Hubbry Logo
Water modelWater modelMain
Open search
Water model
Community hub
Water model
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Water model
Water model
Water model
View on Wikipedia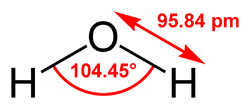
from Wikipedia
A water model is defined by its geometry, together with other parameters such as the atomic charges and Lennard-Jones parameters.

In computational chemistry, a water model is used to simulate and thermodynamically calculate water clusters, liquid water, and aqueous solutions with explicit solvent, often using molecular dynamics or Monte Carlo methods. The models describe intermolecular forces between water molecules and are determined from quantum mechanics, molecular mechanics, experimental results, and these combinations. To imitate the specific nature of the intermolecular forces, many types of models have been developed. In general, these can be classified by the following three characteristics; (i) the number of interaction points or sites, (ii) whether the model is rigid or flexible, and (iii) whether the model includes polarization effects.

An alternative to the explicit water models is to use an implicit solvation model, also termed a continuum model. Examples of this type of model include the COSMO solvation model, the polarizable continuum model (PCM) and hybrid solvation models.[1]

Simple water models

[edit]

The rigid models are considered the simplest water models and rely on non-bonded interactions. In these models, bonding interactions are implicitly treated by holonomic constraints. The electrostatic interaction is modeled using Coulomb's law, and the dispersion and repulsion forces using the Lennard-Jones potential.[2][3] The potential for models such as TIP3P (transferable intermolecular potential with 3 points) and TIP4P is represented by

where kC, the electrostatic constant, has a value of 332.1 Å·kcal/(mol·e²) in the units commonly used in molecular modeling[citation needed];[4][5][6] qi and qj are the partial charges relative to the charge of the electron; rij is the distance between two atoms or charged sites; and A and B are the Lennard-Jones parameters. The charged sites may be on the atoms or on dummy sites (such as lone pairs). In most water models, the Lennard-Jones term applies only to the interaction between the oxygen atoms.

The figure below shows the general shape of the 3- to 6-site water models. The exact geometric parameters (the OH distance and the HOH angle) vary depending on the model.

2-site

[edit]

A 2-site model of water based on the familiar three-site SPC model (see below) has been shown to predict the dielectric properties of water using site-renormalized molecular fluid theory.[7]

3-site

[edit]

Three-site models have three interaction points corresponding to the three atoms of the water molecule. Each site has a point charge, and the site corresponding to the oxygen atom also has the Lennard-Jones parameters. Since 3-site models achieve a high computational efficiency, these are widely used for many applications of molecular dynamics simulations. Most of the models use a rigid geometry matching that of actual water molecules. An exception is the SPC model, which assumes an ideal tetrahedral shape (HOH angle of 109.47°) instead of the observed angle of 104.5°.

The table below lists the parameters for some 3-site models.

TIPS[8] SPC[9] TIP3P[10] SPC/E[11]
r(OH), Å 0.9572 1.0 0.9572 1.0
HOH, deg 104.52 109.47 104.52 109.47
A, 103 kcal Å12/mol 580.0 629.4 582.0 629.4
B, kcal Å6/mol 525.0 625.5 595.0 625.5
q(O) −0.80 −0.82 −0.834 −0.8476
q(H) +0.40 +0.41 +0.417 +0.4238

The SPC/E model adds an average polarization correction to the potential energy function:

where μ is the electric dipole moment of the effectively polarized water molecule (2.35 D for the SPC/E model), μ0 is the dipole moment of an isolated water molecule (1.85 D from experiment), and αi is an isotropic polarizability constant, with a value of 1.608×10−40 F·m2. Since the charges in the model are constant, this correction just results in adding 1.25 kcal/mol (5.22 kJ/mol) to the total energy. The SPC/E model results in a better density and diffusion constant than the SPC model.

The TIP3P model implemented in the CHARMM force field is a slightly modified version of the original. The difference lies in the Lennard-Jones parameters: unlike TIP3P, the CHARMM version of the model places Lennard-Jones parameters on the hydrogen atoms too, in addition to the one on oxygen. The charges are not modified.[12] Three-site model (TIP3P) has better performance in calculating specific heats.[13]

Flexible SPC water model

[edit]
Flexible SPC water model

The flexible simple point-charge water model (or flexible SPC water model) is a re-parametrization of the three-site SPC water model.[14][15] The SPC model is rigid, whilst the flexible SPC model is flexible. In the model of Toukan and Rahman, the O–H stretching is made anharmonic, and thus the dynamical behavior is well described. This is one of the most accurate three-center water models without taking into account the polarization. In molecular dynamics simulations it gives the correct density and dielectric permittivity of water.[16]

Flexible SPC is implemented in the programs MDynaMix and Abalone.

Other models

[edit]
  • Ferguson (flexible SPC)[17]
  • CVFF (flexible)
  • MG (flexible and dissociative)[18]
  • KKY potential (flexible model).[19]
  • BLXL (smear charged potential).[20]

4-site

[edit]

The four-site models have four interaction points by adding one dummy atom near of the oxygen along the bisector of the HOH angle of the three-site models (labeled M in the figure). The dummy atom only has a negative charge. This model improves the electrostatic distribution around the water molecule. The first model to use this approach was the Bernal–Fowler model published in 1933,[21] which may also be the earliest water model. However, the BF model doesn't reproduce well the bulk properties of water, such as density and heat of vaporization, and is thus of historical interest only. This is a consequence of the parameterization method; newer models, developed after modern computers became available, were parameterized by running Metropolis Monte Carlo or molecular dynamics simulations and adjusting the parameters until the bulk properties are reproduced well enough.

The TIP4P model, first published in 1983, is widely implemented in computational chemistry software packages and often used for the simulation of biomolecular systems. There have been subsequent reparameterizations of the TIP4P model for specific uses: the TIP4P-Ew model, for use with Ewald summation methods; the TIP4P/Ice, for simulation of solid water ice; TIP4P/2005, a general parameterization for simulating the entire phase diagram of condensed water; and TIP4PQ/2005, a similar model but designed to accurately describe the properties of solid and liquid water when quantum effects are included in the simulation.[22]

Most of the four-site water models use an OH distance and HOH angle which match those of the free water molecule. One exception is the OPC model, in which no geometry constraints are imposed other than the fundamental C2v molecular symmetry of the water molecule. Instead, the point charges and their positions are optimized to best describe the electrostatics of the water molecule. OPC reproduces a comprehensive set of bulk properties more accurately than several of the commonly used rigid n-site water models. The OPC model is implemented within the AMBER force field.

BF[21] TIPS2[23] TIP4P[10] TIP4P-Ew[24] TIP4P/Ice[25] TIP4P/2005[26] OPC[27] TIP4P-D[28]
r(OH), Å 0.96 0.9572 0.9572 0.9572 0.9572 0.9572 0.8724 0.9572
HOH, deg 105.7 104.52 104.52 104.52 104.52 104.52 103.6 104.52
r(OM), Å 0.15 0.15 0.15 0.125 0.1577 0.1546 0.1594 0.1546
A, 103 kcal Å12/mol 560.4 695.0 600.0 656.1 857.9 731.3 865.1 904.7
B, kcal Å6/mol 837.0 600.0 610.0 653.5 850.5 736.0 858.1 900.0
q(M) −0.98 −1.07 −1.04 −1.04844 −1.1794 −1.1128 −1.3582 −1.16
q(H) +0.49 +0.535 +0.52 +0.52422 +0.5897 +0.5564 +0.6791 +0.58

Others:

  • q-TIP4P/F (flexible) [29]
  • TIP4P/2005f (flexible) [30]

5-site

[edit]

The 5-site models place the negative charge on dummy atoms (labelled L) representing the lone pairs of the oxygen atom, with a tetrahedral-like geometry. An early model of these types was the BNS model of Ben-Naim and Stillinger, proposed in 1971,[citation needed] soon succeeded by the ST2 model of Stillinger and Rahman in 1974.[31] Mainly due to their higher computational cost, five-site models were not developed much until 2000, when the TIP5P model of Mahoney and Jorgensen was published.[32] When compared with earlier models, the TIP5P model results in improvements in the geometry for the water dimer, a more "tetrahedral" water structure that better reproduces the experimental radial distribution functions from neutron diffraction, and the temperature of maximal density of water. The TIP5P-E model is a reparameterization of TIP5P for use with Ewald sums.

BNS[31] ST2[31] TIP5P[32] TIP5P-E[33]
r(OH), Å 1.0 1.0 0.9572 0.9572
HOH, deg 109.47 109.47 104.52 104.52
r(OL), Å 1.0 0.8 0.70 0.70
LOL, deg 109.47 109.47 109.47 109.47
A, 103 kcal Å12/mol 77.4 238.7 544.5 554.3
B, kcal Å6/mol 153.8 268.9 590.3 628.2
q(L) −0.19562 −0.2357 −0.241 −0.241
q(H) +0.19562 +0.2357 +0.241 +0.241
RL, Å 2.0379 2.0160
RU, Å 3.1877 3.1287

Note, however, that the BNS and ST2 models do not use Coulomb's law directly for the electrostatic terms, but a modified version that is scaled down at short distances by multiplying it by the switching function S(r):

Thus, the RL and RU parameters only apply to BNS and ST2.

6-site

[edit]

Originally designed to study water/ice systems, a 6-site model that combines all the sites of the 4- and 5-site models was developed by Nada and van der Eerden.[34] Since it had a very high melting temperature[35] when employed under periodic electrostatic conditions (Ewald summation), a modified version was published later[36] optimized by using the Ewald method for estimating the Coulomb interaction.

Other

[edit]
  • The effect of explicit solute model on solute behavior in biomolecular simulations has been also extensively studied. It was shown that explicit water models affected the specific solvation and dynamics of unfolded peptides, while the conformational behavior and flexibility of folded peptides remained intact.[37]
  • MB model. A more abstract model resembling the Mercedes-Benz logo that reproduces some features of water in two-dimensional systems. It is not used as such for simulations of "real" (i.e., three-dimensional) systems, but it is useful for qualitative studies and for educational purposes.[38]
  • Coarse-grained models. One- and two-site models of water have also been developed.[39] In coarse-grain models, each site can represent several water molecules.
  • Many-body models. Water models built using training-set configurations solved quantum mechanically, which then use machine learning protocols to extract potential-energy surfaces. These potential-energy surfaces are fed into MD simulations for an unprecedented degree of accuracy in computing physical properties of condensed phase systems.[40]
    • Another classification of many body models[41] is on the basis of the expansion of the underlying electrostatics, e.g., the SCME (Single Center Multipole Expansion) model [42]

Computational cost

[edit]

The computational cost of a water simulation increases with the number of interaction sites in the water model. The CPU time is approximately proportional to the number of interatomic distances that need to be computed. For the 3-site model, 9 distances are required for each pair of water molecules (every atom of one molecule against every atom of the other molecule, or 3 × 3). For the 4-site model, 10 distances are required (every charged site with every charged site, plus the O–O interaction, or 3 × 3 + 1). For the 5-site model, 17 distances are required (4 × 4 + 1). Finally, for the 6-site model, 26 distances are required (5 × 5 + 1).

When using rigid water models in molecular dynamics, there is an additional cost associated with keeping the structure constrained, using constraint algorithms (although with bond lengths constrained it is often possible to increase the time step).

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Water model

View on Grokipedia
from Grokipedia
A water model is an empirical mathematical approximation used in computational simulations, particularly (MD), to represent the structure, interactions, and behavior of molecules at the atomic level. These models simplify the quantum mechanical nature of into classical force fields, typically treating molecules as rigid or flexible geometries with point charges and Lennard-Jones potentials to capture electrostatic and van der Waals interactions, respectively. Developed to reproduce essential bulk properties of liquid —such as , self-diffusion coefficient, heat of vaporization, dielectric constant, isobaric , thermal expansion coefficient, and isothermal —they enable realistic modeling of effects in complex systems like biomolecules, materials, and chemical reactions. Water models have evolved since the 1970s, starting with simple three-point representations like the Simple Point Charge (SPC) model, which places partial charges on the oxygen and atoms with fixed bond lengths and angles. Subsequent refinements addressed limitations in reproducing experimental data; for instance, the extended SPC/E model incorporates a polarization correction to better match and coefficients, while four-point models like TIP4P shift charges to a dummy site on the bisector of the H-O-H angle for improved tetrahedral geometry and properties. Polarizable models, such as those using oscillators or inducible dipoles, further enhance accuracy by accounting for electronic polarization, though they increase computational cost; examples include and SWM4-NDP, which perform well in biomolecular contexts but require specialized software. Among non-polarizable models, TIP3P and SPC/E remain widely used due to their balance of efficiency and fidelity, with TIP3P favoring faster simulations despite slight underestimation of . The choice of water model profoundly impacts simulation outcomes, as discrepancies in properties like hydrogen bonding or solvation can alter predicted structures and dynamics in applications ranging from to . Recent advancements, including machine learning-derived potentials, aim to bridge classical and quantum accuracy, but classical models dominate due to scalability in large-scale studies. Overall, water models underscore the interplay between computational tractability and physical realism, continually refined through benchmarking against experimental data to support interdisciplinary research in chemistry, , and .

Fundamentals

Definition and scope

Water models are simplified mathematical representations of the H₂O molecule employed in to approximate its . These models use empirical parameters, such as partial atomic charges and van der Waals coefficients, which are derived from quantum mechanical calculations, experimental measurements, and optimization against bulk properties including , radial distribution functions, and . The scope of water models encompasses simulations of liquid , ice phases, small clusters, and aqueous solutions containing solutes like ions or biomolecules, primarily through and methods. Key components include electrostatic interactions modeled via Coulombic potentials between charged sites on the molecules and van der Waals attractions/repulsions captured by Lennard-Jones potentials. Non-bonded interactions, which dominate intermolecular forces in these models, exclude covalent bonds within the molecule itself and focus on long-range electrostatic and dispersion effects between separate molecules. The general form of the pairwise UU is: U=∑i<jqiqj4πϵ0rij+∑i<j4ϵ[(σrij)12−(σrij)6]U = \sum_{i < j} \frac{q_i q_j}{4 \pi \epsilon_0 r_{ij}} + \sum_{i < j} 4 \epsilon \left[ \left( \frac{\sigma}{r_{ij}} \right)^{12} - \left( \frac{\sigma}{r_{ij}} \right)^6 \right] where qiq_i and qjq_j are partial charges on interaction sites ii and jj, rijr_{ij} is the inter-site distance, ϵ0\epsilon_0 is the vacuum permittivity, and ϵ\epsilon and σ\sigma are Lennard-Jones energy and size parameters, respectively. Water models facilitate large-scale classical simulations of complex aqueous systems where ab initio quantum mechanical approaches are computationally prohibitive due to the need to treat thousands of molecules over extended timescales. This enables detailed studies of solvation dynamics, hydrogen bonding networks, and thermodynamic properties that underpin biological and chemical processes in water. In contrast to continuum solvation models, which approximate the solvent as a homogeneous dielectric continuum without explicit molecules, water models treat water as discrete particles to capture molecular-level details. The first computational use of such a model dates to the 1971 molecular dynamics simulation of liquid water by Rahman and Stillinger.

Historical development

The development of water models began in the early 20th century with theoretical efforts to describe the structure of ice and liquid water based on geometric considerations. In 1933, Bernal and Fowler proposed the first explicit model for water, representing the molecule as a rigid tetrahedron with two hydrogen atoms and a lone pair, emphasizing hydrogen bonding in ice structures without computational simulations. This geometric approach laid foundational insights into water's anomalous properties but lacked dynamic treatment due to the absence of computing resources. The advent of molecular dynamics (MD) simulations in the 1970s marked a pivotal shift toward computational modeling of liquid water. The first MD simulation of liquid water was performed by Rahman and Stillinger in 1971, using a three-site potential to study structural and dynamic properties at ambient conditions, demonstrating the feasibility of simulating water's hydrogen-bond network. By 1974, Stillinger and Rahman refined this with the ST2 model, a six-site rigid water potential incorporating Lennard-Jones interactions and electrostatic charges to better capture short-range repulsion and hydrogen bonding, enabling more accurate reproduction of liquid water's radial distribution functions. Concurrently, the MCY potential, derived from ab initio configuration interaction calculations on water dimers—a pairwise additive model—addressed limitations in transferability across phases. These early efforts were motivated by the need to balance quantum-derived accuracy with the computational demands of MD, though models often overestimated melting points or struggled with dielectric properties. The 1980s saw simplifications for broader applicability, particularly in biomolecular simulations where efficiency was paramount. Jorgensen et al. introduced the three-site TIP3P and four-site TIP4P models in 1983, using fixed partial charges and Lennard-Jones sites to approximate water's electrostatics and dispersion with fewer parameters than ST2, facilitating Monte Carlo and MD studies of aqueous solutions. In 1987, Berendsen et al. developed the SPC/E model, an extension of the earlier SPC three-site potential, by adding a polarization correction via a scaling factor to improve the dielectric constant and radial distribution at liquid densities. These rigid, non-polarizable models prioritized computational speed over detailed many-body effects, responding to challenges in simulating large systems like proteins in water. From the 1990s onward, models evolved to incorporate polarizability and optimize phase behavior. Polarizable models, such as the Gaussian charge transferable model in the 1990s, allowed charges to fluctuate in response to electric fields, enhancing accuracy for interfaces and ionic solutions. Further ab initio-based refinements continued, while the 2000s introduced AMOEBA, a polarizable atomic multipole model that explicitly includes higher-order electrostatics for better thermodynamic properties across temperatures. Optimized rigid models emerged, including TIP4P/2005 in 2005, which improved reproduction of water's phase diagram and anomalies like density maximum, and OPC in 2014, focusing on global optimization of bulk properties using experimental targets. Throughout, motivations centered on reconciling accuracy in reproducing experimental observables—such as the phase diagram, diffusion coefficients, and dielectric response—with computational efficiency, while addressing transferability issues across vapor, liquid, and solid phases. Post-2020, machine learning-based potentials, trained on quantum mechanical data, have begun to enable highly accurate, flexible representations of water's potential energy surface for large-scale simulations.

Classification

By interaction sites

Water models are classified by the number of interaction sites, which are points representing partial charges and van der Waals interactions within the water molecule, including atomic positions (oxygen and hydrogens) or virtual (dummy) sites for lone pairs. These sites enable the modeling of electrostatic forces via Coulombic interactions between partial charges qq and Lennard-Jones potentials for dispersion and repulsion. Increasing the number of sites enhances the accuracy of the electrostatic charge distribution, better capturing the molecular dipole moment and hydrogen bonding geometry, but at the computational expense of more pairwise interactions per molecule pair. Two-site models represent the simplest configuration, with partial charges placed only on the oxygen and a single effective site for the merged hydrogens, omitting explicit hydrogen positions to minimize complexity. This approach is particularly suited for applications requiring efficient predictions of dielectric properties, such as in coarse-grained simulations of bulk water behavior. Three-site models assign partial charges directly to the oxygen and two hydrogen atoms, maintaining a rigid geometry that approximates the experimental structure, for example, with O-H bond lengths of 0.9572 Å and H-O-H angles of 104.52°. This setup balances computational efficiency with reasonable electrostatic representation, making it widely applicable for simulating liquid water properties. Four-site models extend the three-site framework by introducing an off-center virtual negative charge site (M-site) along the angle bisector, typically displaced 0.15 Å from the oxygen, to improve the dipole moment and hydrogen bonding directionality without altering atomic positions. This addition refines the electrostatics for better agreement with experimental solvation and structural data. Five-site models incorporate two positive charges on the hydrogens and two negative charges on virtual sites mimicking the tetrahedral lone pairs, with no charge on the oxygen atom, enhancing the tetrahedral coordination and density anomaly reproduction in liquid water. Six-site models combine elements of four- and five-site designs, adding extra virtual sites to further detail charge distribution, though they are less common and primarily used for specialized simulations of ice-water interfaces near the melting point. Overall, three- and four-site models predominate due to their optimal trade-off between accuracy and computational cost; the number of sites directly influences the pairwise interaction count, such as nine site-site distances for a three-site model pair versus more for higher-site variants.

By molecular flexibility and polarizability

Water models can be classified according to their treatment of molecular flexibility and polarizability, which extend beyond the static geometry and fixed charges of rigid, non-polarizable representations to better capture the dynamic behavior of water molecules in condensed phases. Flexibility refers to the ability of the model to account for intramolecular vibrations, such as oscillations in bond lengths and angles, which are absent in rigid models that enforce fixed geometries using constraint algorithms like SHAKE. In flexible models, these degrees of freedom are governed by intramolecular potential energy functions, typically harmonic forms for stretching and bending: Ubond=kb2(r−r0)2U_{\text{bond}} = \frac{k_b}{2} (r - r_0)^2 Uangle=kθ2(θ−θ0)2U_{\text{angle}} = \frac{k_\theta}{2} (\theta - \theta_0)^2 where kbk_b and kθk_\theta are the respective force constants, and r0r_0 and θ0\theta_0 are the equilibrium bond length and angle. This approach enables the simulation of vibrational modes, improving the representation of dynamic properties like diffusion and spectroscopic signatures compared to constrained rigid baselines. Flexible models, such as variants of the simple point charge (SPC) potential developed in the 1990s, allow bond lengths to vary around experimental gas-phase values, enhancing realism in liquid-state simulations. Polarizability addresses the redistribution of a molecule's electron density in response to the local electric field from neighboring molecules, an effect ignored in fixed-charge models that assume invariant partial charges. In polarizable models, this induction is incorporated either implicitly or explicitly. Implicit schemes approximate the average polarization in bulk water by adjusting fixed charges to an effective value that mimics the enhanced molecular dipole moment, as in the SPC/E model where the charge is set to -0.8476 e on oxygen and +0.4238 e on each hydrogen to account for liquid-phase polarization without dynamic response. Explicit methods, however, directly compute the response, often via inducible point dipoles satisfying μ⃗ind=αE⃗local\vec{\mu}_{\text{ind}} = \alpha \vec{E}_{\text{local}}
Add your contribution
Related Hubs
User Avatar
No comments yet.