Chirp

ChirpMain

Community hub

Chirp

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Chirp

View on Wikipedia

from Wikipedia

Not found

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

A chirp is a signal in which the instantaneous frequency varies continuously with time, typically increasing (up-chirp) or decreasing (down-chirp) in a monotonic fashion, often resembling the sound of a bird's call from which the term derives.^[1]^[2] Chirp signals are fundamental in signal processing and engineering applications due to their ability to achieve high time-bandwidth products, enabling better resolution in time and frequency domains compared to fixed-frequency pulses. The most prevalent form is the linear chirp, where the frequency sweeps linearly from an initial value to a final value over a defined duration, but other variants include quadratic, logarithmic, and exponential chirps that alter the frequency in nonlinear ways.^[3]^[4] In radar and sonar systems, chirps serve as transmitted waveforms to facilitate pulse compression, which enhances range resolution and signal-to-noise ratio without requiring high peak power, thus allowing detection of targets at greater distances or in cluttered environments. For instance, CHIRP (Compressed High-Intensity Radiated Pulse) technology in sonar transmits a sequence of frequencies to produce clearer images of underwater objects by distinguishing echoes based on their time delays. Similarly, in automotive radar, linear frequency-modulated chirps enable simultaneous estimation of range and relative velocity (Doppler shift) for advanced driver-assistance systems, supporting features like adaptive cruise control and collision avoidance.^[5]^[6]^[7] Beyond sensing technologies, chirp-based modulation finds use in communications, particularly chirp spread spectrum (CSS), a technique that spreads the signal across a wide bandwidth using up-chirps or down-chirps to improve robustness against interference, multipath fading, and low-power requirements, making it suitable for Internet of Things (IoT) devices and long-range wireless networks. In photonics and laser systems, chirped pulses—where the frequency varies across the pulse duration—are critical for chirped pulse amplification (CPA), a method that stretches, amplifies, and compresses ultrashort laser pulses to achieve high peak powers without damaging optical components, revolutionizing applications in micromachining, medical imaging, and fusion research.^[8]^[9]^[10]

Fundamentals

Definition

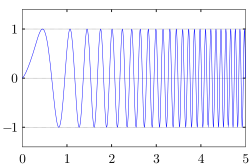
A chirp is a signal in which the frequency changes continuously with time, often increasing or decreasing monotonically.^[1] Unlike constant-frequency signals such as pure tones, which maintain a fixed frequency throughout their duration, a chirp's instantaneous frequency varies over a specified range.^[4] The term "chirp" derives from the short, sharp vocalization produced by birds or insects and was adopted in signal processing during the mid-20th century to describe these frequency-modulated waveforms, owing to the analogous sound generated upon demodulation to audio frequencies.^[11]^[12] This nomenclature first appeared prominently in technical literature around 1960, associated with advancements in radar signal design at Bell Telephone Laboratories.^[13] Chirps are qualitatively described by their direction of frequency sweep: an up-chirp rises from a lower to a higher frequency, while a down-chirp falls from higher to lower.^[1]

Mathematical Representation

A chirp signal is generally represented in the time domain as

s(t) = A \cos(\phi(t))

, where

A

is the amplitude and

\phi(t)

is the instantaneous phase function that encodes the frequency variation over time.^[1] This form captures the essence of a frequency-modulated signal where the phase evolves nonlinearly, distinguishing chirps from constant-frequency sinusoids. Equivalently, the signal can be expressed using sine,

s(t) = A \sin(\phi(t))

, as the choice between cosine and sine is a phase shift convention.^[14] The instantaneous frequency

f(t)

of the chirp is defined as the time derivative of the phase divided by

2\pi

, that is,

f(t) = \frac{1}{2\pi} \frac{d\phi(t)}{dt}

.^[14] This definition arises from the interpretation of the phase's rate of change as the local angular frequency

\omega(t) = \frac{d\phi(t)}{dt}

, with

f(t) = \omega(t)/(2\pi)

. For frequency-modulated chirps, a common phase representation is the quadratic form

\phi(t) = 2\pi \left( f_0 t + \frac{1}{2} k t^2 \right)

, where

f_0

is the starting frequency and

k

is the chirp rate determining the linear frequency sweep; this serves as a foundational model that can be generalized to higher-order polynomials for more complex sweeps.^[1] In ideal chirp signals, the amplitude

A

is typically held constant to focus on frequency modulation, though amplitude modulation can be incorporated as

A(t)

for practical variants without altering the core chirp structure.^[1] A key metric for assessing chirp signal efficiency is the time-bandwidth product

TB = T \cdot B

, where

T

is the signal duration and

B

is the swept bandwidth, quantifying the signal's capacity to achieve high resolution in applications like pulse compression.^[1] This product highlights the chirp's advantage over simple pulses, as larger

TB

values enable greater compression gain while maintaining low sidelobes in matched filtering.

Types

Linear Chirp

A linear chirp is a signal whose instantaneous frequency increases or decreases at a constant rate over time, making it the most fundamental and commonly used form of chirp signal. The instantaneous frequency is defined as

f(t) = f_0 + k t

, where

f_0

is the initial frequency,

k

is the constant chirp rate, and

t

is time, typically for

0 \leq t \leq T

with

T

being the signal duration. The chirp rate

k

is calculated as

k = \frac{f_1 - f_0}{T}

, where

f_1

is the final frequency, determining the linear sweep across the frequency band from

f_0

f_1

.^[15] The phase function of a linear chirp derives from integrating the instantaneous frequency, yielding

\phi(t) = 2\pi \left( f_0 t + \frac{1}{2} k t^2 \right)

, which introduces a quadratic term characteristic of the linear frequency progression.^[16] This quadratic phase distinguishes the linear chirp from constant-frequency signals and enables its representation as a frequency-modulated waveform. The time-domain expression for the linear chirp signal is given by

s(t) = A \cos\left(2\pi \left( f_0 t + \frac{1}{2} k t^2 \right)\right)

for

0 \leq t \leq T

, where

A

is the amplitude, often set to 1 for normalized signals.^[16] This form assumes a real-valued cosine carrier, though complex exponential variants are used in analytical contexts. The constant sweep rate of the linear chirp results in a quadratic phase profile, which simplifies processing in applications requiring predictable frequency evolution. This property makes linear chirps ideal for matched filtering, where the filter's impulse response mirrors the signal's conjugate time-reversed form to achieve pulse compression and improve signal-to-noise ratio.^[17] The bandwidth occupied by the signal approximates

|f_1 - f_0|

, providing a straightforward measure of its spectral extent.^[15] As an example, consider a linear chirp starting at

f_0 = 1

kHz and ending at

f_1 = 10

kHz over

T = 1

second, yielding a chirp rate of

k = 9

kHz/s; this configuration sweeps through 9 kHz of bandwidth in a simple, uniform manner.^[18]

Quadratic Chirp

A quadratic chirp is a signal whose instantaneous frequency varies quadratically with time, resulting in a nonlinear frequency sweep that accelerates or decelerates. The instantaneous frequency is defined as

f(t) = f_0 + \beta t^2

, where

f_0

is the initial frequency and

\beta

is the quadratic chirp rate, typically for

0 \leq t \leq T

with

T

the signal duration. The chirp rate

\beta

is calculated as

\beta = \frac{f_1 - f_0}{T^2}

, where

f_1

is the final frequency, leading to a parabolic frequency progression.^[3] The phase function derives from integrating the instantaneous frequency:

\phi(t) = 2\pi \left( f_0 t + \frac{\beta}{3} t^3 \right)

, introducing a cubic phase term that reflects the quadratic frequency variation. This cubic phase distinguishes quadratic chirps from linear ones and is useful in applications requiring nonlinear frequency modulation. The time-domain expression for the quadratic chirp signal is

s(t) = A \cos\left(2\pi \left( f_0 t + \frac{\beta}{3} t^3 \right)\right)

for

0 \leq t \leq T

, where

A

is the amplitude, often normalized to 1. This assumes a real-valued cosine carrier, with complex forms used analytically. Key properties include the accelerating (for positive

\beta

) or decelerating frequency change, which can provide more uniform energy distribution in certain nonlinear systems or enhance resolution in advanced signal processing. The bandwidth is approximately

|f_1 - f_0|

, but the nonlinear nature affects spectral properties differently from linear chirps.^[3] As an example, a quadratic chirp from

f_0 = 1

kHz to

f_1 = 10

kHz over

T = 1

second has

\beta = 9

kHz/s², resulting in a frequency that starts slowly and accelerates toward the end.^[3]

Exponential Chirp

An exponential chirp is a time-varying signal characterized by an instantaneous frequency that increases or decreases multiplicatively over time. The instantaneous frequency is given by

f(t) = f_0 \cdot \alpha^t,

where

f_0 > 0

is the initial frequency at

t = 0

, and

\alpha > 1

for an up-chirp (increasing frequency) or

0 < \alpha < 1

for a down-chirp. This formulation ensures exponential growth or decay in frequency, contrasting with additive changes in other chirp types. The phase

\phi(t)

of the exponential chirp is derived by integrating the instantaneous angular frequency

2\pi f(\tau)

from 0 to

t

\phi(t) = 2\pi f_0 \int_0^t \alpha^\tau \, d\tau = 2\pi \frac{f_0}{\ln \alpha} (\alpha^t - 1).

The resulting signal form is

s(t) = A \cos\left( \phi(t) + \phi_0 \right),

where

A

is the constant amplitude and

\phi_0

is an optional initial phase offset (often set to 0). This phase structure arises directly from the exponential frequency profile, leading to a nonlinear accumulation of oscillations that accelerates with time for up-chirps. Key properties of the exponential chirp include a linear frequency progression when plotted on a logarithmic scale versus time, which yields a constant relative bandwidth

\Delta f / f \approx \ln \alpha \cdot \Delta t

. This constant relative rate makes it ideal for applications requiring uniform coverage across multiplicative frequency ranges, such as octave-spanning signals where the sweep rate can be specified in octaves per second. For instance, the logarithmic nature ensures equal time allocation per octave, unlike linear chirps that devote more time to higher frequencies.^[19] As a representative example, consider generating an exponential chirp sweeping from 100 Hz to 10 kHz over 1 second. Here,

f_0 = 100

Hz, the final frequency

f_1 = 10{,}000

Hz at

t_1 = 1

s, so

\alpha = (f_1 / f_0)^{1/t_1} = 100

. Equivalently,

\alpha = e^k

with

k = \ln(100) / 1 \approx 4.605

, spanning approximately 6.64 octaves at a rate of 6.64 octaves per second. This setup produces a signal with rapidly increasing perceived pitch, emphasizing the logarithmic scaling.^[20]

Hyperbolic Chirp

A hyperbolic chirp is a frequency-modulated signal characterized by an instantaneous frequency that decreases hyperbolically with time, following an inverse relationship that results in a decaying sweep rate approaching zero. The frequency function is defined as

f(t) = \frac{f_0}{1 + k t}

, where

f_0 > 0

is the starting frequency at

t = 0

, and

k > 0

is the chirp rate parameter with units of inverse time. This form ensures the frequency remains positive and bounded below by zero while starting at

f_0

.^[21] The phase

\phi(t)

of the hyperbolic chirp is derived from the integral of the instantaneous frequency:

\phi(t) = 2\pi \int_0^t f(\tau) \, d\tau = 2\pi \frac{f_0}{k} \ln(1 + k t).

This logarithmic phase accumulation reflects the cumulative effect of the inversely varying frequency. The corresponding signal equation for a real-valued cosine-modulated hyperbolic chirp is then

s(t) = A \cos\left( 2\pi \frac{f_0}{k} \ln(1 + k t) \right),

where

A

is the constant amplitude, typically assuming

t \geq 0

and the signal windowed to a finite duration in practice.^[21] Key properties of the hyperbolic chirp include its frequency asymptoting to zero as

t \to \infty

, which inherently bounds the spectral content from below and prevents unbounded frequency excursions. This structure makes it advantageous for modeling scenarios involving Doppler effects, as the waveform exhibits invariance to Doppler scaling, preserving matched filter performance under velocity-induced shifts. Additionally, the bounded frequency trajectory contributes to controlled spectral occupancy, aiding in applications requiring spectra confined within specific limits.^[21]^[22] A representative example is a hyperbolic chirp starting at

f_0 = 5

kHz and decreasing to 500 Hz over 0.1 seconds, requiring

k = 90

^{-1}

to achieve the desired endpoint frequency via

f(0.1) = \frac{5000}{1 + 90 \times 0.1} = 500

Hz. In limited regimes, such as small

k t

, this form can approximate aspects of an exponential chirp.^[21]

Generation

Analytical Generation

Analytical generation of chirp signals relies on deriving the phase function through direct integration of the specified instantaneous frequency profile, providing closed-form expressions under ideal mathematical conditions. The instantaneous frequency

f(t)

defines the time-varying frequency content, and the phase

\phi(t)

is obtained via

\phi(t) = 2\pi \int_0^t f(\tau) \, d\tau

, assuming a starting time of

t = 0

for simplicity. The resulting chirp signal is then expressed as

s(t) = A \cos(\phi(t) + \phi_0)

, where

A

is the amplitude and

\phi_0

is an initial phase offset, typically set to zero. This integration approach ensures the signal's frequency evolves precisely as prescribed, forming the theoretical foundation for chirp design in signal processing.^[23] For standard chirp types, closed-form solutions for the phase emerge from evaluating the integral explicitly. In the case of a linear chirp, where

f(t) = f_0 + \mu t

with initial frequency

f_0

and chirp rate

\mu

, the phase simplifies to a quadratic form:

\phi(t) = 2\pi \left( f_0 t + \frac{\mu}{2} t^2 \right).

This quadratic phase directly yields the familiar linear frequency sweep over time

t

. For exponential and hyperbolic chirps, the instantaneous frequency follows

f(t) = f_0 \alpha^t

f(t) = \frac{f_0}{1 + \beta t}

, respectively, leading to logarithmic phase expressions:

\phi(t) \propto \ln(1 + \beta t)

for the hyperbolic case, which provides a frequency decrease approaching zero asymptotically. These analytical solutions facilitate precise theoretical modeling without numerical computation.^[24] Asymptotic analysis of chirp envelopes and spectra often employs the stationary phase approximation (SPA), which approximates integrals of the form

\int g(t) e^{i \phi(t)} \, dt

by identifying points where the phase derivative vanishes, i.e., stationary points. For chirp signals, SPA reveals the envelope's behavior in the frequency domain, approximating the magnitude spectrum as

|S(f)| \approx \sqrt{\frac{2\pi}{|\phi''(t_s)|}} |g(t_s)|

∣S(f)∣≈∣ϕ′′(ts)∣2π

∣g(ts)∣ at the stationary time $t_s$ where $\phi'(t_s) = 2\pi f$ , with $\phi''(t)$ the second derivative of the phase. This method is particularly useful for high-frequency or large time-bandwidth products, providing insight into sidelobe structures and resolution limits without full Fourier computation. However, SPA's accuracy diminishes for low-frequency components or near boundaries.^[24] Normalization techniques ensure consistent signal properties across analyses, typically scaling for unit energy or constant amplitude. For unit energy, the signal is divided by its root-mean-square value, such that $\int_{-\infty}^{\infty} |s(t)|^2 \, dt = 1$ , which for a finite-duration chirp of length $T$ approximates to $A = 1 / \sqrt{T}$

under constant amplitude assumptions. Constant amplitude normalization sets $A = 1$ , preserving the envelope shape while focusing on phase modulation. These methods standardize comparisons in theoretical studies, though exact normalization factors depend on the chirp parameters.^[25] Analytical forms assume ideal conditions, such as infinite precision in frequency definition and absence of noise or nonlinearities, which ignore real-world distortions like amplifier saturation or dispersion in transmission media. This idealization supports foundational derivations but requires validation against practical implementations for applied scenarios.^[26]

Practical Generation

Practical generation of chirp signals involves computational and physical methods to approximate the ideal analytical forms, enabling real-time implementation in various systems. Digital synthesis techniques, such as direct digital synthesizers (DDS), utilize phase accumulators to generate chirp signals by incrementally updating the phase based on a time-varying frequency profile. In a DDS architecture, the phase accumulator adds a frequency tuning word at each clock cycle, producing a phase that increases nonlinearly for chirps, which is then converted to amplitude via a sine lookup table or CORDIC algorithm before digital-to-analog conversion. This approach allows for flexible, high-resolution frequency sweeps in applications requiring precise control, such as radar systems.^[27]^[28] Numerical methods for chirp generation rely on discrete-time approximations through sampling of the continuous waveform. A common implementation computes the signal as

s = \cos\left(2\pi \sum_{m=0}^n f \Delta t \right)

, where

f

represents the instantaneous frequency at sample

m

, and

\Delta t

is the sampling interval, effectively discretizing the phase accumulation process. This summation mirrors the integral in analytical forms but is performed iteratively in software or hardware for finite sample lengths, ensuring the signal remains bandlimited within the Nyquist criterion. Such methods are foundational in digital signal processing for generating chirps without dedicated hardware.^[27] Hardware approaches for analog chirp production often employ voltage-controlled oscillators (VCOs) driven by linear voltage ramps to sweep the frequency. A VCO's output frequency varies proportionally with the input control voltage; applying a ramp signal to this input produces a linear chirp, where the ramp's slope determines the chirp rate. This technique is prevalent in analog RF systems for its simplicity, though it requires compensation for VCO nonlinearities to maintain linearity across the sweep.^[29] Software tools facilitate chirp generation in simulation and prototyping environments. In Python, the SciPy library's scipy.signal.chirp function generates a swept-frequency signal specified by initial frequency

f_0

, end time

t_1

, final frequency

f_1

, and method (e.g., 'linear' or 'quadratic'), returning a discrete array evaluated at given times. Similarly, MATLAB's chirp function produces samples of a linear or exponential swept cosine at specified times, with parameters for start/end frequencies and optional phase. These functions implement the discrete approximations internally, supporting rapid development and analysis.^[20]^[3] Implementation challenges in practical chirp generation include managing quantization noise from finite-bit phase accumulators and digital-to-analog converters in DDS systems, which introduces spurs and degrades signal purity, with signal-to-quantization-noise ratio scaling as

1.76 + 6.02B

dB for

B

-bit resolution. Aliasing must be prevented by oversampling the chirp signal, particularly for wideband sweeps where the highest frequency approaches the sampling rate, requiring rates at least twice the maximum instantaneous frequency to avoid spectral folding. Additionally, RF systems face bandwidth limitations due to VCO tuning ranges and component parasitics, often restricting relative bandwidths to under 100% without advanced architectures like multi-stage PLLs.^[27]^[30]

Mathematical Relations

Relation to Impulse Signals

Chirp signals serve as effective approximations to ideal excitation signals for measuring impulse responses in linear systems, particularly in dispersive media where broadband stimulation is required to capture frequency-dependent effects. Unlike a true Dirac delta impulse, which theoretically excites all frequencies equally but is impractical due to its infinite bandwidth and zero energy, a chirp provides a finite-duration signal with a wide frequency sweep, enabling the estimation of the system's impulse response through correlation or deconvolution techniques. This approach is especially valuable in environments with dispersion, as the chirp's linear or nonlinear frequency modulation ensures uniform energy distribution across the spectrum, facilitating accurate reconstruction of the underlying impulse response.^[31] In matched filtering, the output of convolving a transmitted chirp signal

s(t)

with its time-reversed conjugate

s^*(-t)

produces a response that approximates a sinc function, serving as a practical surrogate for an ideal impulse. This compression effect transforms the extended chirp duration into a narrow pulse whose peak corresponds to the time delay, effectively mimicking the delta-like response needed for precise timing or ranging. The dechirping process further enhances this relation by mixing the received chirp echo with a delayed version of the transmitted signal, resulting in a beat frequency that collapses the dispersed energy into a short-duration pulse akin to an impulse, thereby improving resolution in system identification tasks.^[32]^[33] The autocorrelation function of the chirp, which underpins the matched filter output, is given by

R(\tau) = \int_{-\infty}^{\infty} s(t) s(t - \tau) \, dt \approx TB \cdot \delta(\tau),

where

TB

is the time-bandwidth product of the chirp, representing the scaling factor that amplifies the peak while the sinc envelope provides the approximation to the delta function in ideal, noise-free conditions. For a linear frequency-modulated chirp, this correlation yields a main lobe width inversely proportional to the bandwidth, closely emulating an impulse for delay estimation.^[34]^[23] Compared to true impulses, chirps offer significant advantages, including higher total energy due to their longer duration, which translates to improved signal-to-noise ratio (SNR) in noisy or lossy environments without requiring excessive peak power. This energy efficiency makes chirps preferable for practical applications in linear system analysis, where the enhanced SNR enables reliable impulse response measurement even in dispersive channels with attenuation.^[26]

Spectral Properties

The Fourier transform of a linear chirp signal is precisely described by expressions involving Fresnel integrals, which account for the phase modulation induced by the linear frequency sweep. For scenarios where the time-bandwidth product

BT \gg 1

, this transform approximates a rectangular spectrum spanning the full bandwidth

B

, indicating near-ideal energy distribution across the swept frequencies without significant out-of-band components. This approximation arises from the stationary phase method applied to the integral form of the transform, emphasizing the chirp's utility in occupying a wide spectral range efficiently.^[35]^[13] In the time-frequency domain, the Wigner-Ville distribution provides a quadratic representation that captures the chirp's non-stationary nature, manifesting as a prominent linear ridge aligned with the instantaneous frequency trajectory in the time-frequency plane. This ridge achieves near-optimal concentration for linear chirps, free from cross-term interference inherent in multi-component signals, thereby serving as a benchmark for time-frequency analysis tools. The bandwidth-duration product

BT

further governs spectral properties, with large values enabling compressed pulses of duration inversely proportional to

B

, while the overall spectral occupancy directly scales with the frequency sweep extent, enhancing resolvability in broadband applications.^[24]^[13] The ambiguity function of a linear chirp, which jointly evaluates delay and Doppler resolution, displays characteristically low sidelobes following matched filtering, particularly along the delay axis, thereby minimizing false detections and supporting high-fidelity range estimation. This desirable thumbtack-like shape in the ambiguity surface underscores the chirp's resolution advantages over narrowband pulses. In discrete settings, the discrete Fourier transform of sampled chirps is prone to windowing-induced spectral leakage due to the signal's extended duration and frequency variation, often necessitating tapered windows like the Hann or Blackman to suppress edge discontinuities and preserve the approximate rectangular spectral profile.^[36]

Applications

Radar and Sonar

In radar and sonar systems, chirp signals are employed for pulse compression to enhance range resolution and detection capabilities while maintaining high signal-to-noise ratios (SNR). A linear frequency-modulated (LFM) chirp waveform is transmitted as a long-duration pulse with gradually increasing or decreasing frequency, allowing for greater energy transmission compared to short pulses of equivalent peak power. Upon receiving the echo from a target, the signal is processed through matched filtering or dechirping—correlating the received signal with a time-reversed replica of the transmitted chirp—to compress the extended pulse into a short, high-amplitude pulse. This technique effectively achieves the fine range resolution of a short pulse while benefiting from the energy of a longer one, making it ideal for detecting distant or weak targets in environments with power constraints.^[37] The range resolution

\Delta R

provided by chirp pulse compression is determined by the waveform's bandwidth

B

and the propagation speed

c

(speed of light for radar or sound in water for sonar), given by the formula

\Delta R = \frac{c}{2B}

. For instance, a radar chirp with a 100 MHz bandwidth yields a resolution of approximately 1.5 meters in air, while in sonar, a similar bandwidth relative to acoustic frequencies can resolve features on the seafloor to centimeters. This resolution is independent of pulse duration, enabling designers to prioritize energy over brevity for improved SNR without sacrificing precision.^[38] Linear chirps exhibit strong Doppler tolerance, accommodating velocity-induced frequency shifts that would degrade phase-coded waveforms like Barker or polyphase codes. The continuous frequency sweep of a chirp distributes Doppler effects across the signal, minimizing sidelobe degradation and maintaining compression performance for moving targets up to several hundred m/s. This robustness is particularly advantageous in dynamic scenarios, such as tracking aircraft or marine vessels.^[39] Pulse compression with chirps originated in the mid-1950s through independent efforts at Sperry Gyroscope Company and MIT Lincoln Laboratory, building on wartime radar advances to address post-WWII needs for higher resolution without excessive power. These developments demonstrated practical viability, paving the way for modern applications including synthetic aperture radar (SAR) systems that use chirp processing for high-resolution imaging of terrain or ocean surfaces. Key advantages include increased average transmitted power—limited only by duty cycle rather than peak power thresholds—leading to extended detection ranges and reduced vulnerability to noise. In air traffic control, chirp-based radars provide reliable tracking of aircraft in cluttered airspace, while in sonar, CHIRP technology enables detailed underwater imaging for bathymetric mapping and subsea object detection, as seen in multibeam echo sounders.^[40]^[41]

Communications

Chirp spread spectrum (CSS) is a modulation technique employed in wireless communications for robust, low-power signal transmission over long distances, particularly in Internet of Things (IoT) applications. It utilizes wideband linear frequency modulated chirp pulses to spread the signal across a broader bandwidth, enabling efficient operation in unlicensed spectrum bands. A prominent example is the LoRa protocol, which leverages CSS to achieve ranges up to 10 miles in rural areas while supporting battery life exceeding 10 years for end devices.^[42]^[43] In CSS modulation, data bits are encoded by mapping binary symbols to up-chirps (frequency increasing over time) or down-chirps (frequency decreasing), creating orthogonal signals for distinct symbol representation. At the receiver, demodulation occurs through dechirping—multiplying the incoming signal with a locally generated reference chirp—followed by a fast Fourier transform (FFT) to identify peak positions corresponding to the transmitted symbols. This process exploits the correlation properties of chirps to recover data reliably even in noisy channels.^[42] CSS provides strong resistance to multipath fading and interference due to its spread-spectrum nature, which distributes energy across the bandwidth and enhances signal detectability post-correlation. The processing gain, denoted as

G = TB

, where

T

is the chirp duration and

B

is the bandwidth, quantifies this advantage by improving the signal-to-noise ratio by the time-bandwidth product, often exceeding 20 dB in practical systems.^[44]^[43] The IEEE 802.15.4a standard, ratified in 2007, specifies CSS as an optional physical layer for low-data-rate wireless personal area networks (LR-WPANs), supporting rates up to 1 Mb/s in the 2.4 GHz band with features like differential quadrature chirp spread spectrum (DQCSK). It has been applied since the mid-2000s in utility metering and asset tracking, where its jamming resistance (up to 48 dB) and global band compatibility enable reliable deployments in dense environments.^[45] Variants of CSS, such as discrete chirp rate keying (DCRK-CSS), employ discrete frequency shifts or rate variations for digital encoding, offering improved spectral efficiency over traditional analog linear sweeps while maintaining low complexity for LPWANs. These adaptations enhance data throughput in constrained IoT scenarios without sacrificing the core robustness of chirp-based spreading.^[46]

Signal Processing and Acoustics

In signal processing, the chirplet transform serves as a time-frequency analysis tool that generalizes wavelet transforms by employing chirp basis functions, particularly effective for signals with linear frequency modulation (FM). This transform computes the inner product of an input signal

x(t)

with a family of chirplets

\chi_{s,u,c}(t)

, parameterized by scale

s

, time location

u

, and chirp rate

c

, yielding the transform as

C(s, u, c) = \int_{-\infty}^{\infty} x(t) \chi_{s,u,c}^*(t) \, dt,

where

\chi_{s,u,c}^*(t)

is the complex conjugate of the chirplet function, enabling better resolution of chirp-like components compared to traditional spectrograms. Acoustic chirps, often implemented as swept sine waves with logarithmic frequency progression, are widely used to test the frequency response of audio equipment by exciting systems across a broad bandwidth in a short duration, minimizing noise interference and allowing deconvolution to derive impulse responses. For instance, exponential chirps facilitate precise measurement of harmonic distortion and system linearity in loudspeakers and amplifiers.^[31] In musical contexts, exponential chirps model scales where frequencies progress exponentially, aligning with equal temperament tuning by ensuring constant pitch intervals via logarithmic frequency spacing, as seen in representations of Shepard tones that create illusions of continuous rising or falling pitch through octave-layered sweeps.^[47] Chirps also appear in seismic data processing for wavelet estimation, where match-filtering of chirp echoes enhances resolution in sub-bottom profiling to isolate source wavelets and suppress noise, improving subsurface imaging without requiring extensive post-processing. In audio sound design, chirps generate rising or falling pitches to evoke tension or release, commonly applied in film scoring for dynamic auditory effects that mimic perceptual frequency glides.^[48]^[49] The chirplet transform was introduced in the mid-1990s as a foundational method for non-stationary signal analysis. Post-2010 developments have integrated it into machine learning pipelines for spectrogram enhancement, particularly in speech classification and fault detection, where adaptive chirplet bases improve feature extraction robustness to FM variations.^[50]

Info Pages

Talk Pages

Special Pages

Chirp

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Chirp

Chirp

Fundamentals

Definition

Mathematical Representation

Types

Linear Chirp

Quadratic Chirp

Exponential Chirp

Hyperbolic Chirp

Generation

Analytical Generation

Practical Generation

Mathematical Relations

Relation to Impulse Signals

Spectral Properties

Applications

Radar and Sonar

Communications

Signal Processing and Acoustics

References

Add your contribution

Related Hubs

Contribute something

History

Media collections

Chirp

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Chirp

Chirp

Fundamentals

Definition

Mathematical Representation

Types

Linear Chirp

Quadratic Chirp

Exponential Chirp

Hyperbolic Chirp

Generation

Analytical Generation

Add your contribution

Related Hubs

Contribute something