Matched filter

The following section derives the matched filter for a discrete-time system. The derivation for a continuous-time system is similar, with summations replaced with integrals.

The matched filter is the linear filter, ${\displaystyle h}$, that maximizes the output signal-to-noise ratio.

${\displaystyle \ y[n]=\sum _{k=-\infty }^{\infty }h[n-k]x[k],}$

where ${\displaystyle x[k]}$ is the input as a function of the independent variable ${\displaystyle k}$, and ${\displaystyle y[n]}$ is the filtered output. Though we most often express filters as the impulse response of convolution systems, as above (see LTI system theory), it is easiest to think of the matched filter in the context of the inner product, which we will see shortly.

We can derive the linear filter that maximizes output signal-to-noise ratio by invoking a geometric argument. The intuition behind the matched filter relies on correlating the received signal (a vector) with a filter (another vector) that is parallel with the signal, maximizing the inner product. This enhances the signal. When we consider the additive stochastic noise, we have the additional challenge of minimizing the output due to noise by choosing a filter that is orthogonal to the noise.

Let us formally define the problem. We seek a filter, ${\displaystyle h}$, such that we maximize the output signal-to-noise ratio, where the output is the inner product of the filter and the observed signal ${\displaystyle x}$.

Our observed signal consists of the desirable signal ${\displaystyle s}$ and additive noise ${\displaystyle v}$:

${\displaystyle \ x=s+v.\,}$

Let us define the auto-correlation matrix of the noise, reminding ourselves that this matrix has Hermitian symmetry, a property that will become useful in the derivation:

${\displaystyle \ R_{v}=E\{vv^{\mathrm {H} }\}\,}$

where ${\displaystyle v^{\mathrm {H} }}$ denotes the conjugate transpose of ${\displaystyle v}$, and ${\displaystyle E}$ denotes expectation (note that in case the noise ${\displaystyle v}$ has zero-mean, its auto-correlation matrix ${\displaystyle R_{v}}$ is equal to its covariance matrix).

Let us call our output, ${\displaystyle y}$, the inner product of our filter and the observed signal such that

${\displaystyle \ y=\sum _{k=-\infty }^{\infty }h^{*}[k]x[k]=h^{\mathrm {H} }x=h^{\mathrm {H} }s+h^{\mathrm {H} }v=y_{s}+y_{v}.}$

We now define the signal-to-noise ratio, which is our objective function, to be the ratio of the power of the output due to the desired signal to the power of the output due to the noise:

${\displaystyle \mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}}.}$

We rewrite the above:

${\displaystyle \mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{E\{|h^{\mathrm {H} }v|^{2}\}}}.}$

We wish to maximize this quantity by choosing ${\displaystyle h}$. Expanding the denominator of our objective function, we have

${\displaystyle \ E\{|h^{\mathrm {H} }v|^{2}\}=E\{(h^{\mathrm {H} }v){(h^{\mathrm {H} }v)}^{\mathrm {H} }\}=h^{\mathrm {H} }E\{vv^{\mathrm {H} }\}h=h^{\mathrm {H} }R_{v}h.\,}$

Now, our ${\displaystyle \mathrm {SNR} }$ becomes

${\displaystyle \mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{h^{\mathrm {H} }R_{v}h}}.}$

We will rewrite this expression with some matrix manipulation. The reason for this seemingly counterproductive measure will become evident shortly. Exploiting the Hermitian symmetry of the auto-correlation matrix ${\displaystyle R_{v}}$, we can write

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}},}$

We would like to find an upper bound on this expression. To do so, we first recognize a form of the Cauchy–Schwarz inequality:

${\displaystyle \ |a^{\mathrm {H} }b|^{2}\leq (a^{\mathrm {H} }a)(b^{\mathrm {H} }b),\,}$

which is to say that the square of the inner product of two vectors can only be as large as the product of the individual inner products of the vectors. This concept returns to the intuition behind the matched filter: this upper bound is achieved when the two vectors ${\displaystyle a}$ and ${\displaystyle b}$ are parallel. We resume our derivation by expressing the upper bound on our ${\displaystyle \mathrm {SNR} }$ in light of the geometric inequality above:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq {\frac {\left[{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)\right]\left[{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)\right]}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}.}$

Our valiant matrix manipulation has now paid off. We see that the expression for our upper bound can be greatly simplified:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq s^{\mathrm {H} }R_{v}^{-1}s.}$

We can achieve this upper bound if we choose,

${\displaystyle \ R_{v}^{1/2}h=\alpha R_{v}^{-1/2}s}$

where ${\displaystyle \alpha }$ is an arbitrary real number. To verify this, we plug into our expression for the output ${\displaystyle \mathrm {SNR} }$:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}={\frac {\alpha ^{2}|{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{\alpha ^{2}{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)}}={\frac {|s^{\mathrm {H} }R_{v}^{-1}s|^{2}}{s^{\mathrm {H} }R_{v}^{-1}s}}=s^{\mathrm {H} }R_{v}^{-1}s.}$

Thus, our optimal matched filter is

${\displaystyle \ h=\alpha R_{v}^{-1}s.}$

We often choose to normalize the expected value of the power of the filter output due to the noise to unity. That is, we constrain

${\displaystyle \ E\{|y_{v}|^{2}\}=1.\,}$

This constraint implies a value of ${\displaystyle \alpha }$, for which we can solve:

${\displaystyle \ E\{|y_{v}|^{2}\}=\alpha ^{2}s^{\mathrm {H} }R_{v}^{-1}s=1,}$

yielding

${\displaystyle \ \alpha ={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}},}$

giving us our normalized filter,

${\displaystyle \ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.}$

If we care to write the impulse response ${\displaystyle h}$ of the filter for the convolution system, it is simply the complex conjugate time reversal of the input ${\displaystyle s}$.

Though we have derived the matched filter in discrete time, we can extend the concept to continuous-time systems if we replace ${\displaystyle R_{v}}$ with the continuous-time autocorrelation function of the noise, assuming a continuous signal ${\displaystyle s(t)}$, continuous noise ${\displaystyle v(t)}$, and a continuous filter ${\displaystyle h(t)}$.

Alternatively, we may solve for the matched filter by solving our maximization problem with a Lagrangian. Again, the matched filter endeavors to maximize the output signal-to-noise ratio (${\displaystyle \mathrm {SNR} }$) of a filtered deterministic signal in stochastic additive noise. The observed sequence, again, is

${\displaystyle \ x=s+v,\,}$

with the noise auto-correlation matrix,

${\displaystyle \ R_{v}=E\{vv^{\mathrm {H} }\}.\,}$

The signal-to-noise ratio is

${\displaystyle \mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}},}$

where ${\displaystyle y_{s}=h^{\mathrm {H} }s}$ and ${\displaystyle y_{v}=h^{\mathrm {H} }v}$.

Evaluating the expression in the numerator, we have

${\displaystyle \ |y_{s}|^{2}={y_{s}}^{\mathrm {H} }y_{s}=h^{\mathrm {H} }ss^{\mathrm {H} }h.\,}$

and in the denominator,

${\displaystyle \ E\{|y_{v}|^{2}\}=E\{{y_{v}}^{\mathrm {H} }y_{v}\}=E\{h^{\mathrm {H} }vv^{\mathrm {H} }h\}=h^{\mathrm {H} }R_{v}h.\,}$

The signal-to-noise ratio becomes

${\displaystyle \mathrm {SNR} ={\frac {h^{\mathrm {H} }ss^{\mathrm {H} }h}{h^{\mathrm {H} }R_{v}h}}.}$

If we now constrain the denominator to be 1, the problem of maximizing ${\displaystyle \mathrm {SNR} }$ is reduced to maximizing the numerator. We can then formulate the problem using a Lagrange multiplier:

${\displaystyle \ h^{\mathrm {H} }R_{v}h=1}$

${\displaystyle \ {\mathcal {L}}=h^{\mathrm {H} }ss^{\mathrm {H} }h+\lambda (1-h^{\mathrm {H} }R_{v}h)}$

${\displaystyle \ \nabla _{h^{*}}{\mathcal {L}}=ss^{\mathrm {H} }h-\lambda R_{v}h=0}$

${\displaystyle \ (ss^{\mathrm {H} })h=\lambda R_{v}h}$

which we recognize as a generalized eigenvalue problem

${\displaystyle \ h^{\mathrm {H} }(ss^{\mathrm {H} })h=\lambda h^{\mathrm {H} }R_{v}h.}$

Since ${\displaystyle ss^{\mathrm {H} }}$ is of unit rank, it has only one nonzero eigenvalue. It can be shown that this eigenvalue equals

${\displaystyle \ \lambda _{\max }=s^{\mathrm {H} }R_{v}^{-1}s,}$

yielding the following optimal matched filter

${\displaystyle \ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.}$

This is the same result found in the previous subsection.

Matched filtering can also be interpreted as a least-squares estimator for the optimal location and scaling of a given model or template. Once again, let the observed sequence be defined as

${\displaystyle \ x_{k}=s_{k}+v_{k},\,}$

where ${\displaystyle v_{k}}$ is uncorrelated zero mean noise. The signal ${\displaystyle s_{k}}$ is assumed to be a scaled and shifted version of a known model sequence ${\displaystyle f_{k}}$:

${\displaystyle \ s_{k}=\mu _{0}\cdot f_{k-j_{0}}}$

We want to find optimal estimates ${\displaystyle j^{*}}$ and ${\displaystyle \mu ^{*}}$ for the unknown shift ${\displaystyle j_{0}}$ and scaling ${\displaystyle \mu _{0}}$ by minimizing the least-squares residual between the observed sequence ${\displaystyle x_{k}}$ and a "probing sequence" ${\displaystyle h_{j-k}}$:

${\displaystyle \ j^{*},\mu ^{*}=\arg \min _{j,\mu }\sum _{k}\left(x_{k}-\mu \cdot h_{j-k}\right)^{2}}$

The appropriate ${\displaystyle h_{j-k}}$ will later turn out to be the matched filter, but is as yet unspecified. Expanding ${\displaystyle x_{k}}$ and the square within the sum yields

${\displaystyle \ j^{*},\mu ^{*}=\arg \min _{j,\mu }\left[\sum _{k}(s_{k}+v_{k})^{2}+\mu ^{2}\sum _{k}h_{j-k}^{2}-2\mu \sum _{k}s_{k}h_{j-k}-2\mu \sum _{k}v_{k}h_{j-k}\right].}$

The first term in brackets is a constant (since the observed signal is given) and has no influence on the optimal solution. The last term has constant expected value because the noise is uncorrelated and has zero mean. We can therefore drop both terms from the optimization. After reversing the sign, we obtain the equivalent optimization problem

${\displaystyle \ j^{*},\mu ^{*}=\arg \max _{j,\mu }\left[2\mu \sum _{k}s_{k}h_{j-k}-\mu ^{2}\sum _{k}h_{j-k}^{2}\right].}$

Setting the derivative w.r.t. ${\displaystyle \mu }$ to zero gives an analytic solution for ${\displaystyle \mu ^{*}}$:

${\displaystyle \ \mu ^{*}={\frac {\sum _{k}s_{k}h_{j-k}}{\sum _{k}h_{j-k}^{2}}}.}$

Inserting this into our objective function yields a reduced maximization problem for just ${\displaystyle j^{*}}$:

${\displaystyle \ j^{*}=\arg \max _{j}{\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}.}$

The numerator can be upper-bounded by means of the Cauchy–Schwarz inequality:

${\displaystyle \ {\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}\leq {\frac {\sum _{k}s_{k}^{2}\cdot \sum _{k}h_{j-k}^{2}}{\sum _{k}h_{j-k}^{2}}}=\sum _{k}s_{k}^{2}={\text{constant}}.}$

The optimization problem assumes its maximum when equality holds in this expression. According to the properties of the Cauchy–Schwarz inequality, this is only possible when

${\displaystyle \ h_{j-k}=\nu \cdot s_{k}=\kappa \cdot f_{k-j_{0}}.}$

for arbitrary non-zero constants ${\displaystyle \nu }$ or ${\displaystyle \kappa }$, and the optimal solution is obtained at ${\displaystyle j^{*}=j_{0}}$ as desired. Thus, our "probing sequence" ${\displaystyle h_{j-k}}$ must be proportional to the signal model ${\displaystyle f_{k-j_{0}}}$, and the convenient choice ${\displaystyle \kappa =1}$ yields the matched filter

${\displaystyle \ h_{k}=f_{-k}.}$

Note that the filter is the mirrored signal model. This ensures that the operation ${\displaystyle \sum _{k}x_{k}h_{j-k}}$ to be applied in order to find the optimum is indeed the convolution between the observed sequence ${\displaystyle x_{k}}$ and the matched filter ${\displaystyle h_{k}}$. The filtered sequence assumes its maximum at the position where the observed sequence ${\displaystyle x_{k}}$ best matches (in a least-squares sense) the signal model ${\displaystyle f_{k}}$.

The matched filter may be derived in a variety of ways,^[2] but as a special case of a least-squares procedure it may also be interpreted as a maximum likelihood method in the context of a (coloured) Gaussian noise model and the associated Whittle likelihood.^[5] If the transmitted signal possessed no unknown parameters (like time-of-arrival, amplitude,...), then the matched filter would, according to the Neyman–Pearson lemma, minimize the error probability. However, since the exact signal generally is determined by unknown parameters that effectively are estimated (or fitted) in the filtering process, the matched filter constitutes a generalized maximum likelihood (test-) statistic.^[6] The filtered time series may then be interpreted as (proportional to) the profile likelihood, the maximized conditional likelihood as a function of the ("arrival") time parameter.^[7] This implies in particular that the error probability (in the sense of Neyman and Pearson, i.e., concerning maximization of the detection probability for a given false-alarm probability^[8]) is not necessarily optimal. What is commonly referred to as the Signal-to-noise ratio (SNR), which is supposed to be maximized by a matched filter, in this context corresponds to ${\displaystyle {\sqrt {2\log({\mathcal {L}})}}}$, where ${\displaystyle {\mathcal {L}}}$ is the (conditionally) maximized likelihood ratio.^{[7] [nb 1]}

The construction of the matched filter is based on a known noise spectrum. In practice, however, the noise spectrum is usually estimated from data and hence only known up to a limited precision. For the case of an uncertain spectrum, the matched filter may be generalized to a more robust iterative procedure with favourable properties also in non-Gaussian noise.^[7]

When viewed in the frequency domain, it is evident that the matched filter applies the greatest weighting to spectral components exhibiting the greatest signal-to-noise ratio (i.e., large weight where noise is relatively low, and vice versa). In general this requires a non-flat frequency response, but the associated "distortion" is no cause for concern in situations such as radar and digital communications, where the original waveform is known and the objective is the detection of this signal against the background noise. On the technical side, the matched filter is a weighted least-squares method based on the (heteroscedastic) frequency-domain data (where the "weights" are determined via the noise spectrum, see also previous section), or equivalently, a least-squares method applied to the whitened data.

Matched filters are often used in signal detection.^[1] As an example, suppose that we wish to judge the distance of an object by reflecting a signal off it. We may choose to transmit a pure-tone sinusoid at 1 Hz. We assume that our received signal is an attenuated and phase-shifted form of the transmitted signal with added noise.

To judge the distance of the object, we correlate the received signal with a matched filter, which, in the case of white (uncorrelated) noise, is another pure-tone 1-Hz sinusoid. When the output of the matched filter system exceeds a certain threshold, we conclude with high probability that the received signal has been reflected off the object. Using the speed of propagation and the time that we first observe the reflected signal, we can estimate the distance of the object. If we change the shape of the pulse in a specially designed way, the signal-to-noise ratio and the distance resolution can be even improved after matched filtering: this is a technique known as pulse compression.

Additionally, matched filters can be used in parameter estimation problems (see estimation theory). To return to our previous example, we may desire to estimate the speed of the object, in addition to its position. To exploit the Doppler effect, we would like to estimate the frequency of the received signal. To do so, we may correlate the received signal with several matched filters of sinusoids at varying frequencies. The matched filter with the highest output will reveal, with high probability, the frequency of the reflected signal and help us determine the radial velocity of the object, i.e. the relative speed either directly towards or away from the observer. This method is, in fact, a simple version of the discrete Fourier transform (DFT). The DFT takes an ${\displaystyle N}$-valued complex input and correlates it with ${\displaystyle N}$ matched filters, corresponding to complex exponentials at ${\displaystyle N}$ different frequencies, to yield ${\displaystyle N}$ complex-valued numbers corresponding to the relative amplitudes and phases of the sinusoidal components (see Moving target indication).

The matched filter is also used in communications. In the context of a communication system that sends binary messages from the transmitter to the receiver across a noisy channel, a matched filter can be used to detect the transmitted pulses in the noisy received signal.

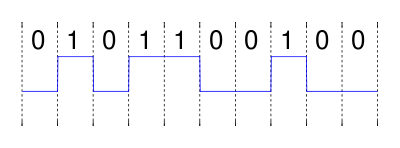
Imagine we want to send the sequence "0101100100" coded in non polar non-return-to-zero (NRZ) through a certain channel.

Mathematically, a sequence in NRZ code can be described as a sequence of unit pulses or shifted rect functions, each pulse being weighted by +1 if the bit is "1" and by -1 if the bit is "0". Formally, the scaling factor for the ${\displaystyle k^{\mathrm {th} }}$ bit is,

${\displaystyle \ a_{k}={\begin{cases}+1,&{\text{if bit }}k{\text{ is }}1,\\-1,&{\text{if bit }}k{\text{ is }}0.\end{cases}}}$

We can represent our message, ${\displaystyle M(t)}$, as the sum of shifted unit pulses:

${\displaystyle \ M(t)=\sum _{k=-\infty }^{\infty }a_{k}\times \Pi \left({\frac {t-kT}{T}}\right).}$

where ${\displaystyle T}$ is the time length of one bit and ${\displaystyle \Pi (x)}$ is the rectangular function.

Thus, the signal to be sent by the transmitter is

If we model our noisy channel as an AWGN channel, white Gaussian noise is added to the signal. At the receiver end, for a Signal-to-noise ratio of 3 dB, this may look like:

A first glance will not reveal the original transmitted sequence. There is a high power of noise relative to the power of the desired signal (i.e., there is a low signal-to-noise ratio). If the receiver were to sample this signal at the correct moments, the resulting binary message could be incorrect.

To increase our signal-to-noise ratio, we pass the received signal through a matched filter. In this case, the filter should be matched to an NRZ pulse (equivalent to a "1" coded in NRZ code). Precisely, the impulse response of the ideal matched filter, assuming white (uncorrelated) noise should be a time-reversed complex-conjugated scaled version of the signal that we are seeking. We choose

${\displaystyle \ h(t)=\Pi \left({\frac {t}{T}}\right).}$

In this case, due to symmetry, the time-reversed complex conjugate of ${\displaystyle h(t)}$ is in fact ${\displaystyle h(t)}$, allowing us to call ${\displaystyle h(t)}$ the impulse response of our matched filter convolution system.

After convolving with the correct matched filter, the resulting signal, ${\displaystyle M_{\mathrm {filtered} }(t)}$ is,

${\displaystyle \ M_{\mathrm {filtered} }(t)=(M*h)(t)}$

where ${\displaystyle *}$ denotes convolution.

Which can now be safely sampled by the receiver at the correct sampling instants, and compared to an appropriate threshold, resulting in a correct interpretation of the binary message.

Matched filters play a central role in gravitational-wave astronomy.^[9] The first observation of gravitational waves was based on large-scale filtering of each detector's output for signals resembling the expected shape, followed by subsequent screening for coincident and coherent triggers between both instruments.^[10] False-alarm rates, and with that, the statistical significance of the detection were then assessed using resampling methods.^[11][12] Inference on the astrophysical source parameters was completed using Bayesian methods based on parameterized theoretical models for the signal waveform and (again) on the Whittle likelihood.^[13][14]

Matched filters find use in seismology to detect similar earthquake or other seismic signals, often using multicomponent and/or multichannel empirically determined templates.^[15] Matched filtering applications in seismology include the generation of large event catalogues to study earthquake seismicity ^[16] and volcanic activity,^[17][18] and in the global detection of nuclear explosions.^[19]

Animals living in relatively static environments would have relatively fixed features of the environment to perceive. This allows the evolution of filters that match the expected signal with the highest signal-to-noise ratio, the matched filter.^[20] Sensors that perceive the world "through such a 'matched filter' severely limits the amount of information the brain can pick up from the outside world, but it frees the brain from the need to perform more intricate computations to extract the information finally needed for fulfilling a particular task."^[21]

• Periodogram
• Filtered backprojection (Radon transform)
• Digital filter
• Statistical signal processing
• Whittle likelihood
• Profile likelihood
• Detection theory
• Multiple comparisons problem
• Channel capacity
• Noisy-channel coding theorem
• Spectral density estimation
• Least mean squares (LMS) filter
• Wiener filter
• MUltiple SIgnal Classification (MUSIC), a popular parametric superresolution method
• SAMV