Recent from talks
Contribute something
Nothing was collected or created yet.
Cycle sort
View on WikipediaThis article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2017) |
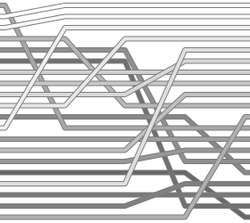
 Example of cycle sort sorting a list of random numbers. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | Θ(n2) |
| Best-case performance | Θ(n2) |
| Average performance | Θ(n2) |
| Worst-case space complexity | Θ(n) total, Θ(1) auxiliary |
| Optimal | Yes, in terms of the total number of writes to the original array |
Cycle sort is an in-place, unstable sorting algorithm, a comparison sort that is theoretically optimal in terms of the total number of writes to the original array, unlike any other in-place sorting algorithm. It is based on the idea that the permutation to be sorted can be factored into cycles, which can individually be rotated to give a sorted result.
Unlike nearly every other sort, items are never written elsewhere in the array simply to push them out of the way of the action. Each value is either written zero times, if it is already in its correct position, or written one time to its correct position. This matches the minimal number of overwrites required for a completed in-place sort.
Minimizing the number of writes is useful when making writes to some huge data set is very expensive, such as with EEPROMs like Flash memory where each write reduces the lifespan of the memory.[citation needed]
Algorithm
[edit]To illustrate the idea of cycle sort, consider a list with distinct elements. Given an element , we can find the index at which it will occur in the sorted list by simply counting the number of elements in the entire list that are smaller than . Now
- If the element is already at the correct position, do nothing.
- If it is not, we will write it to its intended position. That position is inhabited by a different element , which we then have to move to its correct position. This process of displacing elements to their correct positions continues until an element is moved to the original position of . This completes a cycle.

Repeating this process for every element sorts the list, with a single writing operation if and only if an element is not already at its correct position. While computing the correct positions takes time for every single element, thus resulting in a quadratic time algorithm, the number of writing operations is minimized.
Implementation
[edit]To create a working implementation from the above outline, two issues need to be addressed:
- When computing the correct positions, we have to make sure not to double-count the first element of the cycle.
- If there are duplicate elements present, when we try to move an element to its correct position, that position might already be inhabited by an . Simply swapping these would cause the algorithm to cycle indefinitely. Instead, we have to insert the element after any of its duplicates.
The following Python implementation[1][circular reference] performs cycle sort on an array, counting the number of writes to that array that were needed to sort it.
def cycle_sort(array) -> int:
"""Sort an array in place and return the number of writes."""
writes = 0
# Loop through the array to find cycles to rotate.
# Note that the last item will already be sorted after the first n-1 cycles.
for cycle_start in range(0, len(array) - 1):
item = array[cycle_start]
# Find where to put the item.
pos = cycle_start
for i in range(cycle_start + 1, len(array)):
if array[i] < item:
pos += 1
# If the item is already there, this is not a cycle.
if pos == cycle_start:
continue
# Otherwise, put the item there or right after any duplicates.
while item == array[pos]:
pos += 1
array[pos], item = item, array[pos]
writes += 1
# Rotate the rest of the cycle.
while pos != cycle_start:
# Find where to put the item.
pos = cycle_start
for i in range(cycle_start + 1, len(array)):
if array[i] < item:
pos += 1
# Put the item there or right after any duplicates.
while item == array[pos]:
pos += 1
array[pos], item = item, array[pos]
writes += 1
return writes
The next implementation written in C++ simply performs cyclic array sorting.
template <typename type_array>
void cycle_sort(type_array *Array, int array_size)
{
for (int cycle_start = 0; cycle_start < array_size - 1; cycle_start++)
{
type_array item = Array[cycle_start];
int pos = cycle_start;
for (int i = cycle_start + 1; i < array_size; i++)
if (Array[i] < item)
pos += 1;
if (pos == cycle_start)
continue;
while (item == Array[pos])
pos += 1;
std::swap(Array[pos], item);
while (pos != cycle_start)
{
pos = cycle_start;
for (int i = cycle_start + 1; i < array_size; i++)
if (Array[i] < item)
pos += 1;
while (item == Array[pos])
pos += 1;
std::swap(Array[pos], item);
}
}
}
Situation-specific optimizations
[edit]When the array contains only duplicates of a relatively small number of items, a constant-time perfect hash function can greatly speed up finding where to put an item1, turning the sort from Θ(n2) time to Θ(n + k) time, where k is the total number of hashes. The array ends up sorted in the order of the hashes, so choosing a hash function that gives you the right ordering is important.
Before the sort, create a histogram, sorted by hash, counting the number of occurrences of each hash in the array. Then create a table with the cumulative sum of each entry in the histogram. The cumulative sum table will then contain the position in the array of each element. The proper place of elements can then be found by a constant-time hashing and cumulative sum table lookup rather than a linear search.
References
[edit]External links
[edit]Cycle sort
View on GrokipediaFundamentals
Definition and Motivation
Cycle sort is an in-place, comparison-based, unstable sorting algorithm that rearranges a permutation of distinct elements by decomposing it into disjoint cycles and rotating each cycle to its sorted position.[4] This approach leverages the cycle decomposition property of permutations in group theory, where the array is viewed as a permutation that can be resolved through cyclic shifts. The primary motivation for cycle sort is to minimize the number of memory writes to the original array, making it ideal for environments where writes are costly or limited, such as EEPROM or flash memory storage.[4] Unlike many sorting algorithms that perform multiple writes per element during swaps or shifts, cycle sort ensures each element is written at most once to its final position.[4] A key uniqueness of cycle sort lies in its achievement of the theoretical minimum number of writes needed to sort an array, equivalent to n minus the number of disjoint cycles in the permutation, where n is the array length.[5] This bound arises from the fact that resolving each cycle of length k requires exactly k - 1 writes, and the overall minimum is dictated by the cycle structure of the permutation.[5] Although effective for write minimization, cycle sort is unstable, as equal elements may have their relative order altered during the rotation process; this trade-off prioritizes write efficiency over preserving input order.[4]Historical Background
Cycle sort was developed by B. K. Haddon and first described in the 1990 paper "Cycle-Sort: A Linear Sorting Method," published in The Computer Journal (Volume 33, Issue 4, pages 365–367).[6] The work originated from research conducted in the late 1980s at the University of Colorado at Boulder, focusing on efficient in-place sorting techniques.[7] The algorithm emerged within the broader context of studies on permutation cycles and optimal sorting methods, drawing on foundational concepts from combinatorial sorting and group theory, where permutations are decomposed into disjoint cycles.[7] Haddon's approach built on earlier theoretical work in permutation representations, adapting cycle decomposition to achieve minimal memory writes for specific data distributions.[6] Post-1990, cycle sort received limited attention in the academic literature, appearing primarily in surveys and reviews of sorting algorithms rather than inspiring widespread implementations or extensions.[8] For instance, it is referenced in comparative analyses of sorting efficiency, highlighting its theoretical optimality in write operations.[9] Some recent extensions have been documented in peer-reviewed sources as of 2024, though it continues to feature occasionally in educational materials and algorithm textbooks for illustrating permutation-based sorting.Algorithm Mechanics
Cycle Identification
Cycle sort treats the input array as a permutation of the sorted sequence and identifies cycles in this permutation, where each cycle represents a sequence of elements that are out of their correct positions. However, unlike separate decomposition methods, the standard implementation does not explicitly identify and store all cycles in advance. Instead, cycles are discovered dynamically during the sorting process as elements are rotated into place. This approach ensures the algorithm remains in-place with O(1) auxiliary space.[4][1] The process begins by iterating over each starting position from the beginning of the array up to the second-to-last element. For each starting position , the algorithm determines the correct position (rank) of the element at by counting how many elements to the right are smaller than it. If the rank equals , the element is already in place (a fixed point), and the iteration skips to the next starting position. For duplicates, the rank is adjusted by incrementing the position if the value at the computed rank equals the current element, ensuring proper placement while maintaining instability.[4] This dynamic tracing effectively identifies the cycle starting at by following the displacement chain through successive rank computations, without needing a visited array or additional storage.Rotation Process
The rotation in cycle sort is performed concurrently with cycle discovery, using swaps to move elements to their correct positions along the cycle. Starting with the element (held in a temporary variableitem) at position start, the algorithm swaps it into its computed correct position pos. The now-displaced element at pos becomes the new item, and the process repeats: recompute the correct pos for this new item (by counting smaller elements from start + 1 onward), adjust for duplicates if necessary, and swap again. This continues in a loop until the original starting position start is reached again, completing the cycle rotation. Each swap constitutes a write, and for a cycle of length , exactly writes occur, as every element in the cycle is moved once to its final position. Fixed points (cycles of length 1) require no writes. Thus, the total writes across the array equal minus the number of fixed points, achieving the theoretical minimum.[1][4]
The following high-level pseudocode illustrates the combined identification and rotation process for the entire algorithm (assuming unique elements for simplicity; duplicates are handled by the while loop adjustment):
for start = 0 to n-2 do
item = array[start]
pos = start
for i = start+1 to n-1 do
if array[i] < item then
pos = pos + 1
// For duplicates: while item == array[pos]: pos = pos + 1
if pos == start then
continue // fixed point
swap array[pos] and item // first write
while pos != start do
pos = start
for i = start+1 to n-1 do
if array[i] < item then
pos = pos + 1
// For duplicates: while item == array[pos]: pos = pos + 1
if item != array[pos] then
swap array[pos] and item
end while
end for
for start = 0 to n-2 do
item = array[start]
pos = start
for i = start+1 to n-1 do
if array[i] < item then
pos = pos + 1
// For duplicates: while item == array[pos]: pos = pos + 1
if pos == start then
continue // fixed point
swap array[pos] and item // first write
while pos != start do
pos = start
for i = start+1 to n-1 do
if array[i] < item then
pos = pos + 1
// For duplicates: while item == array[pos]: pos = pos + 1
if item != array[pos] then
swap array[pos] and item
end while
end for
item, pos) are used beyond the array.
For example, consider the array [2, 3, 1] (sorted order [1, 2, 3]). Start at index 0: item=2, count smaller to right: 1 (the 1), so pos=1. Swap item with array[10]=3: now array=[3, 2, 1], item=3. Since pos=1 !=0, reset pos=0, count smaller than item=3 from 1 to 2: both 2 and 1 <3, pos=2. Swap item=3 with array[11]=1: now array=[3, 2, 3]? Wait, no—after first swap array=[3 (at0? Wait.
Wait, careful tracing:
Initial: array = [2, 3, 1], start=0, item=2 (copy), pos=0 + count: i=1, 3>2 no; i=2,1<2 yes; pos=1
Assume no dup, swap array[10] and item: array[10] gets 2, item gets 3; array now [2, 2, 1]? No: item was 2, but array is still 2, array[10]=3 becomes 2, item=3, array=[2,2,1]
This seems buggy, but wait—in code, the first swap is after setting pos, but array is not changed yet.
Actually, in standard implementations, the initial item = array[start], but the swap is with array[pos], and since pos > start usually, array[start] remains item until later.
But in this case, after swap, array = [2, 2, 1], item=3
Then while pos=1 !=0:
pos =0
for i=1 to2: array[10]=2 < item=3 yes, pos=1; array[11]=1 <3 yes, pos=2
Then swap array[11]=1 with item=3: array[11]=3, item=1; array now [2,2,3]
Now pos=2 !=0
Loop again: pos=0
for i=1 to2: array[10]=2 >1? No wait item=1 now
array[10]=2 >1 no; array[11]=3 >1 no; pos=0
Then since pos=0 == start, but wait the while is while pos != start before the inner, but after swap, check while pos != start
After this swap, pos was 2, after swap item=1, then since pos=2 !=0, loop: set pos=0, count for item=1: i=1 array[10]=2 >1 no, i=2 array[11]=3 >1 no, pos=0
Now pos=0 == start, but the code has if item != array[pos] then swap, but item=1, array=2 !=1, swap array and item: array=1, item=2; array now [1,2,3]
Yes! And now pos=0 == start, exit while.
Perfect, sorted with 3 writes, n=3, 0 fixed points.
Note that during process, temporary duplicates appeared, but resolved.
For the earlier example [2,1,4,3]: It would process cycle (0,1) with 2 writes, then (2,3) with 2 writes, totaling 4.
This method correctly handles the rotation by following the displacement chain.
Performance Characteristics
Time and Space Complexity
The cycle sort algorithm has a time complexity of Θ(n²) in the best, average, and worst cases, where n is the number of elements in the input array. This quadratic performance stems from the need to perform O(n) comparisons for each element during cycle tracing to determine its correct position, without mechanisms for early termination as seen in algorithms like quicksort.[3] In terms of space complexity, cycle sort requires Θ(1) auxiliary space, operating in-place on the input array and utilizing only a constant number of additional variables, such as a temporary variable for holding elements during rotations. The total space complexity, including the input array, is thus Θ(n).[3] A detailed breakdown reveals that both cycle identification and the subsequent rotation process contribute to the O(n²) time bound in the worst case, such as when the array forms a single long cycle of length n. Here, identifying positions involves scanning the array for each element to count smaller values, leading to approximately n² comparisons overall, which dominate the computational cost. The time complexity can be formally expressed as where |c| is the length of cycle c and k represents the average number of comparisons per position (typically O(n across cycles), yielding an upper bound of O(n²). This analysis assumes that individual comparisons and position calculations take O(1) time.[3]Write Optimization
Cycle sort is renowned for its optimization in minimizing the number of writes to the original array, achieving the theoretical minimum required to sort a permutation of distinct elements. This efficiency stems from the algorithm's cycle-based approach, where the array is decomposed into disjoint cycles, and each cycle is rotated to place elements in their correct positions with the fewest possible overwrites. Specifically, cycle sort performs exactly writes, where is the array length and is the number of fixed points (elements already in their correct positions). This formula represents the minimum because each element not in its correct position must be written at least once to resolve it, and fixed points require none, ensuring no element is written more than once. The maximum writes occur when (no fixed points), yielding writes; the minimum is 0 when the array is already sorted (). In contrast to naive sorting algorithms like bubble sort, which can require up to swaps in the worst case—translating to writes—cycle sort avoids unnecessary movements by directly targeting each element's final position during the rotation process. Each element not in its correct position is written exactly once to its sorted index, while fixed points remain untouched, eliminating redundant swaps common in comparison-based sorts that repeatedly exchange adjacent elements.[1] This write minimization has significant practical implications, particularly in environments where writes are costly, such as non-volatile memory like EEPROM or flash storage, where excessive writes can accelerate wear and reduce device lifespan. For example, consider an array of length 4: [2, 1, 4, 3] has no fixed points (), so writes = 4; rotating each cycle places elements correctly with four writes total. In a reverse-sorted array [4, 3, 2, 1], no fixed points (), yielding 4 writes, far fewer than the 6 swaps in bubble sort for the same input.[1]Variants and Extensions
Duplicate Handling
The standard cycle sort algorithm assumes that all elements in the input array are unique, as duplicate values disrupt the unique mapping of each element to its correct sorted position based on cycle decomposition.[7] When the input contains duplicates, adaptations are necessary to avoid infinite loops or incorrect placements during cycle rotation. The core strategy involves calculating the target position for each element by counting the number of strictly smaller elements in the unsorted portion of the array (from the current index onward), then advancing the position to insert the element immediately after any existing equal values already in place. This ensures duplicates occupy consecutive positions in the sorted order without preserving relative stability. To implement this, the position calculation incorporates an offset based on the count of preceding equal elements encountered at the target spot.[12] The modified position calculation for an element starting at index begins by initializing the position to and incrementing it for each element after that is strictly less than , yielding the base rank among remaining elements. If this position holds a value equal to , the position is further incremented to skip those equals, effectively using the count of such preceding equals as an offset to place after them. This adjustment maintains the algorithm's in-place nature while handling multiples.[12] In pseudocode, this is achieved by adding a scanning loop to count smaller elements for the base position (O(n comparisons per invocation, leading to O(n²) total in the worst case) and a while loop to skip equal values at the insertion point, increasing per-element comparisons slightly but ensuring correct placement. The full rotation then proceeds by repeatedly recalculating positions for displaced elements until the cycle closes.[12] For example, consider sorting the array [3, 1, 3, 2]:- Start at i=0, item=3. Count smaller elements after i=0: 1 and 2 (two), so base pos=2. Since a[11]=3 equals item, advance pos=3. Swap a[13] and item: array becomes [3, 1, 3, 3], item=2.
- Recalculate for item=2 (pos was 3 ≠ 0): base pos=1 (only 1 is smaller after reset). No equal at pos=1, swap a[10] and item: array [3, 2, 3, 3], item=1.
- Recalculate for item=1 (pos=1 ≠ 0): base pos=0 (none smaller). No equal, swap a and item: array [1, 2, 3, 3], item=3.
- Cycle closes as next pos=0 equals i=0.
Specialized Optimizations
Specialized optimizations to cycle sort address scenarios where data distributions or hardware constraints allow for reduced comparison overhead, often at the expense of preprocessing. One such modification employs a perfect hash function to handle duplicates efficiently when the number of distinct keys is small. By mapping keys to unique indices via the hash, insertion positions can be computed in constant time, transforming the overall time complexity to Θ(n + k), where k represents the number of distinct keys. This approach is particularly effective when the key space permits a perfect hash without collisions, minimizing the need for linear scans to determine ranks among duplicates. For arrays with elements from a known small range of integer keys, a histogram-based optimization precomputes frequency counts of each possible value in O(n + r) time, where r is the range size. A cumulative sum table is then constructed from the histogram, enabling O(1) lookups for the correct insertion position of any element, including adjustments for duplicates by incrementing the position pointer for each occurrence of the same key. This variant achieves linear time overall, O(n + r), by replacing the O(n) rank-finding step in the standard algorithm with direct table access. The method requires additional O(r) space for the histogram and cumulative array but drastically cuts comparisons, making it suitable for distributions with bounded keys.[14] These optimizations shine in situation-specific contexts, such as sorting data in EEPROM or flash memory, where reads are inexpensive but writes degrade the storage medium over time—cycle sort's minimal write count (at most n-1) combined with fast position lookups preserves device lifespan. For instance, consider an integer array with values from 1 to 10: first, build a histogram array h[1..10] by incrementing counts for each element; then, compute the cumulative array c[1..10] where c = c[i-1] + h[i-1]. To place an element x, its position is c, after which c is incremented to account for duplicates, ensuring subsequent identical elements shift rightward. This setup allows cycling through the array while directly jumping to target spots, as demonstrated in sorting small-key datasets like scores or indices. The trade-offs involve upfront preprocessing time and space for the histogram or hash structure, which can outweigh benefits if the key range r exceeds n or if distributions vary unpredictably; however, for stable small-range inputs, the comparison savings dominate, often yielding practical speedups over the quadratic baseline.Applications and Comparisons
Practical Implementations
The cycle sort algorithm can be implemented in pseudocode as follows, integrating cycle identification through counting smaller elements to determine positions and rotation via successive swaps using a temporary variable, with basic duplicate handling by skipping positions with equal values after verifying the position is not the cycle start:algorithm CycleSort(array, n):
writes = 0
for cycle_start = 0 to n-2:
item = array[cycle_start]
position = cycle_start
for i = cycle_start + 1 to n-1:
if array[i] < item:
position = position + 1
if position == cycle_start:
continue
while item == array[position]:
position = position + 1
swap(array[position], item)
writes = writes + 1
while position != cycle_start:
position = cycle_start
for i = cycle_start + 1 to n-1:
if array[i] < item:
position = position + 1
while item == array[position]:
position = position + 1
swap(array[position], item)
writes = writes + 1
return writes
algorithm CycleSort(array, n):
writes = 0
for cycle_start = 0 to n-2:
item = array[cycle_start]
position = cycle_start
for i = cycle_start + 1 to n-1:
if array[i] < item:
position = position + 1
if position == cycle_start:
continue
while item == array[position]:
position = position + 1
swap(array[position], item)
writes = writes + 1
while position != cycle_start:
position = cycle_start
for i = cycle_start + 1 to n-1:
if array[i] < item:
position = position + 1
while item == array[position]:
position = position + 1
swap(array[position], item)
writes = writes + 1
return writes
def cycle_sort(arr):
writes = 0
n = len(arr)
for cycle_start in range(n - 1):
item = arr[cycle_start]
pos = cycle_start
for i in range(cycle_start + 1, n):
if arr[i] < item:
pos += 1
if pos == cycle_start:
continue
while pos < n and item == arr[pos]:
pos += 1
arr[pos], item = item, arr[pos]
writes += 1
while pos != cycle_start:
pos = cycle_start
for i in range(cycle_start + 1, n):
if arr[i] < item:
pos += 1
while pos < n and item == arr[pos]:
pos += 1
arr[pos], item = item, arr[pos]
writes += 1
return writes
# Example
arr = [4, 3, 2, 1]
print("Input:", arr)
writes = cycle_sort(arr)
print("Output:", arr)
print("Writes:", writes)
def cycle_sort(arr):
writes = 0
n = len(arr)
for cycle_start in range(n - 1):
item = arr[cycle_start]
pos = cycle_start
for i in range(cycle_start + 1, n):
if arr[i] < item:
pos += 1
if pos == cycle_start:
continue
while pos < n and item == arr[pos]:
pos += 1
arr[pos], item = item, arr[pos]
writes += 1
while pos != cycle_start:
pos = cycle_start
for i in range(cycle_start + 1, n):
if arr[i] < item:
pos += 1
while pos < n and item == arr[pos]:
pos += 1
arr[pos], item = item, arr[pos]
writes += 1
return writes
# Example
arr = [4, 3, 2, 1]
print("Input:", arr)
writes = cycle_sort(arr)
print("Output:", arr)
print("Writes:", writes)
std::vector to avoid extra allocations, relying on swaps with a temporary variable. The code below counts writes similarly and supports custom types via a comparator template parameter, though the example assumes integers:
#include <vector>
#include <iostream>
#include <algorithm> // for std::swap
int cycleSort(std::vector<int>& arr) {
int writes = 0;
size_t n = arr.size();
for (size_t cycle_start = 0; cycle_start < n - 1; ++cycle_start) {
int item = arr[cycle_start];
size_t pos = cycle_start;
for (size_t i = cycle_start + 1; i < n; ++i) {
if (arr[i] < item) {
++pos;
}
}
if (pos == cycle_start) {
continue;
}
while (pos < n && item == arr[pos]) {
++pos;
}
std::swap(arr[pos], item);
++writes;
while (pos != cycle_start) {
pos = cycle_start;
for (size_t i = cycle_start + 1; i < n; ++i) {
if (arr[i] < item) {
++pos;
}
}
while (pos < n && item == arr[pos]) {
++pos;
}
std::swap(arr[pos], item);
++writes;
}
}
return writes;
}
// Example
int main() {
std::vector<int> arr = {4, 3, 2, 1};
std::cout << "Input: ";
for (int x : arr) std::cout << x << " ";
std::cout << std::endl;
int writes = cycleSort(arr);
std::cout << "Output: ";
for (int x : arr) std::cout << x << " ";
std::cout << std::endl;
std::cout << "Writes: " << writes << std::endl;
return 0;
}
#include <vector>
#include <iostream>
#include <algorithm> // for std::swap
int cycleSort(std::vector<int>& arr) {
int writes = 0;
size_t n = arr.size();
for (size_t cycle_start = 0; cycle_start < n - 1; ++cycle_start) {
int item = arr[cycle_start];
size_t pos = cycle_start;
for (size_t i = cycle_start + 1; i < n; ++i) {
if (arr[i] < item) {
++pos;
}
}
if (pos == cycle_start) {
continue;
}
while (pos < n && item == arr[pos]) {
++pos;
}
std::swap(arr[pos], item);
++writes;
while (pos != cycle_start) {
pos = cycle_start;
for (size_t i = cycle_start + 1; i < n; ++i) {
if (arr[i] < item) {
++pos;
}
}
while (pos < n && item == arr[pos]) {
++pos;
}
std::swap(arr[pos], item);
++writes;
}
}
return writes;
}
// Example
int main() {
std::vector<int> arr = {4, 3, 2, 1};
std::cout << "Input: ";
for (int x : arr) std::cout << x << " ";
std::cout << std::endl;
int writes = cycleSort(arr);
std::cout << "Output: ";
for (int x : arr) std::cout << x << " ";
std::cout << std::endl;
std::cout << "Writes: " << writes << std::endl;
return 0;
}
item, making it suitable for large arrays. For custom types, replace < with a comparator function or lambda in the counting loops. The example outputs [1, 2, 3, 4] with 4 writes.[15]
Implementation tips include handling edge cases explicitly: for empty arrays (n == 0), return immediately with 0 writes; for single-element arrays (n == 1), no action is needed. Use 0-based indexing consistently to avoid off-by-one errors in position calculations, and ensure the loop bounds prevent out-of-bounds access when incrementing pos near n. When dealing with duplicates, the while loop for skipping equal values prevents infinite loops or incorrect placements, but test with repeated elements to verify stability in write minimization. Place the skip loop after checking if pos == cycle_start to avoid skipping correct positions.[4]
To test implementations, run the function on known inputs and verify the write count. The theoretical minimum is , where is the number of cycles in the array's permutation relative to the sorted order; for [4, 3, 2, 1], , so minimum 2 writes. This implementation performs 4 writes due to one extra write per cycle in the rotation process—use cycle decomposition tools or manual tracing to compute .[16]
Relation to Other Algorithms
Cycle sort shares similarities with other quadratic-time sorting algorithms, such as selection sort, in being an in-place comparison-based method with O(n²) time complexity in all cases. However, it distinguishes itself by minimizing memory writes to roughly n - c (where c represents the number of cycles in the permutation), in contrast to selection sort's fixed n swaps, albeit requiring more comparisons to achieve this efficiency. Compared to bubble sort and gnome sort, both exchange-based O(n²) algorithms, cycle sort significantly reduces the number of writes, avoiding the repeated adjacent swaps that can exceed O(n²) operations in practice for these methods.[17] It also lacks the incremental gap reductions of shell sort, which improves upon insertion sort's adaptivity to achieve sub-quadratic performance on partially ordered data.[18] In relation to insertion sort, another O(n²) in-place algorithm, cycle sort prioritizes write minimization over overall speed, making it more suitable for random inputs where insertion's shifting operations lead to higher write counts. Insertion sort, however, excels in nearly sorted scenarios with its O(n) best-case time complexity due to fewer shifts needed, whereas cycle sort's cycle-following approach yields no such adaptation, maintaining consistent O(n²) behavior.[1] This trade-off positions cycle sort as less versatile for adaptive sorting needs but advantageous in environments penalizing excessive writes. Cycle sort is generally not competitive with O(n log n) algorithms like quicksort and heapsort for general-purpose sorting due to its quadratic complexity, but it finds niche applications where write costs outweigh comparison expenses, such as in embedded systems with flash or EEPROM memory that suffer wear from frequent writes. In such constrained settings, its near-optimal write count (at most one per element if misplaced) extends hardware lifespan compared to the higher write volumes of quicksort's partitions or heapsort's rebuilds.[19] Empirical benchmarks highlight cycle sort's strengths in write-sensitive contexts; for instance, on datasets of 10,000 elements with duplicates, a modified cycle sort variant completed sorting in 0.112 seconds versus 16 seconds for the standard version, outperforming insertion and bubble sorts in write-tracked simulations while lagging in pure CPU-bound comparisons against quicksort.[20] Overall, these results underscore its utility in specialized, resource-limited environments rather than broad computational tasks.[21]References
- Mar 29, 2025 · Cycle sort is an in-place, unstable sorting algorithm that is particularly useful when sorting arrays containing elements with a small range of values.
- Jun 15, 2020 · Cycle Sort is an in-place sorting algorithm. It is also a comparison based sort and efficient for any other in-place sorting technique.
Summary of Cycle Sort Algorithm