Recent from talks
Contribute something
Nothing was collected or created yet.
Selection sort
View on WikipediaThis article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (May 2019) |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | comparisons, swaps |
| Best-case performance | comparisons, swap |
| Average performance | comparisons, swaps |
| Worst-case space complexity | auxiliary |
| Optimal | No |
In computer science, selection sort is an in-place comparison sorting algorithm. It has a O(n2) time complexity, which makes it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity and has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
The algorithm divides the input list into two parts: a sorted sublist of items which is built up from left to right at the front (left) of the list and a sublist of the remaining unsorted items that occupy the rest of the list. Initially, the sorted sublist is empty and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.
The time efficiency of selection sort is quadratic, so there are a number of sorting techniques which have better time complexity than selection sort.
Example
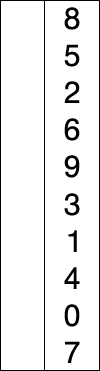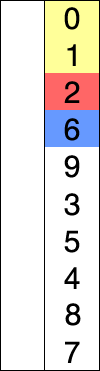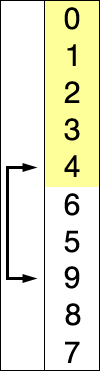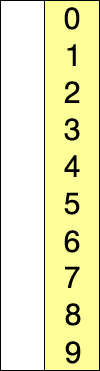
[edit]Here is an example of this sort algorithm sorting five elements:
| Sorted sublist | Unsorted sublist | Least element in unsorted list |
|---|---|---|
| () | (12, 25, 64, 11, 22) | 11 |
| (11) | (25, 64, 12, 22) | 12 |
| (11, 12) | (64, 25, 22) | 22 |
| (11, 12, 22) | (25, 64) | 25 |
| (11, 12, 22, 25) | (64) | 64 |
| (11, 12, 22, 25, 64) | () |
(Nothing appears changed on these last two lines because the last two numbers were already in order.)
Selection sort can also be used on list structures that make add and remove efficient, such as a linked list. In this case it is more common to remove the minimum element from the remainder of the list, and then insert it at the end of the values sorted so far. For example:
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning <11> 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 <12> 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 <22> 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 <25> 64
Implementations
[edit]Below is an implementation in C.
/* a[0] to a[aLength-1] is the array to sort */
int i,j;
int aLength; // initialise to a's length
/* advance the position through the entire array */
/* (could do i < aLength-1 because single element is also min element) */
for (i = 0; i < aLength-1; i++)
{
/* find the min element in the unsorted a[i .. aLength-1] */
/* assume the min is the first element */
int jMin = i;
/* test against elements after i to find the smallest */
for (j = i+1; j < aLength; j++)
{
/* if this element is less, then it is the new minimum */
if (a[j] < a[jMin])
{
/* found new minimum; remember its index */
jMin = j;
}
}
if (jMin != i)
{
swap(&a[i], &a[jMin]);
}
}
Complexity
[edit]Selection sort is not difficult to analyze compared to other sorting algorithms, since none of the loops depend on the data in the array. Selecting the minimum requires scanning elements (taking comparisons) and then swapping it into the first position. Finding the next lowest element requires scanning the remaining elements (taking comparisons) and so on. Therefore, the total number of comparisons is
which is of complexity in terms of number of comparisons.
Comparison to other sorting algorithms
[edit]Among quadratic sorting algorithms (sorting algorithms with a simple average-case of Θ(n2)), selection sort almost always outperforms bubble sort and gnome sort. Insertion sort is very similar in that after the kth iteration, the first elements in the array are in sorted order. Insertion sort's advantage is that it only scans as many elements as it needs in order to place the st element, while selection sort must scan all remaining elements to find the st element.
Simple calculation shows that insertion sort will therefore usually perform about half as many comparisons as selection sort, although it can perform just as many or far fewer depending on the order the array was in prior to sorting. It can be seen as an advantage for some real-time applications that selection sort will perform identically regardless of the order of the array, while insertion sort's running time can vary considerably. However, this is more often an advantage for insertion sort in that it runs much more efficiently if the array is already sorted or "close to sorted."
While selection sort is preferable to insertion sort in terms of number of writes ( swaps versus up to swaps, with each swap being two writes), this is roughly twice the theoretical minimum achieved by cycle sort, which performs at most n writes. This can be important if writes are significantly more expensive than reads, such as with EEPROM or Flash memory, where every write lessens the lifespan of the memory.
Selection sort can be implemented without unpredictable branches for the benefit of CPU branch predictors, by finding the location of the minimum with branch-free code and then performing the swap unconditionally.
Finally, selection sort is greatly outperformed on larger arrays by divide-and-conquer algorithms such as mergesort. However, insertion sort or selection sort are both typically faster for small arrays (i.e. fewer than 10–20 elements). A useful optimization in practice for the recursive algorithms is to switch to insertion sort or selection sort for "small enough" sublists.
Variants
[edit]Heapsort has been described as "nothing but an implementation of selection sort using the right data structure."[1] It greatly improves the basic algorithm by using an implicit heap data structure to find and remove each lowest element in time, instead of normal selection sort's inner loop, reducing the total running time to .
A bidirectional variant of selection sort (called double selection sort or sometimes cocktail sort due to its similarity to cocktail shaker sort) finds both the minimum and maximum values in the list in every pass. This requires three comparisons per two items (a pair of elements is compared, then the greater is compared to the maximum and the lesser is compared to the minimum) rather than regular selection sort's one comparison per item, but requires only half as many passes, a net 25% savings.
Selection sort can be implemented as a stable sort if, rather than swapping in step 2, the minimum value is inserted into the first position and the intervening values shifted up. However, this modification either requires a data structure that supports efficient insertions or deletions, such as a linked list, or it leads to performing writes.
In the bingo sort variant, items are sorted by repeatedly looking through the remaining items to find the greatest value and moving all items with that value to their final location.[2] Like counting sort, this is an efficient variant if there are many duplicate values: selection sort does one pass through the remaining items for each item moved, while Bingo sort does one pass for each value. After an initial pass to find the greatest value, subsequent passes move every item with that value to its final location while finding the next value as in the following pseudocode (arrays are zero-based and the for-loop includes both the top and bottom limits, as in Pascal):
bingo(array A)
{ This procedure sorts in ascending order by
repeatedly moving maximal items to the end. }
begin
last := length(A) - 1;
{ The first iteration is written to look very similar to
the subsequent ones, but without swaps. }
nextMax := A[last];
for i := last - 1 downto 0 do
if A[i] > nextMax then
nextMax := A[i];
while (last > 0) and (A[last] = nextMax) do
last := last - 1;
while last > 0 do begin
{ Each main loop searches for the new nextMax while
swapping items equal to prevMax into place. }
prevMax := nextMax;
nextMax := A[last];
for i := last - 1 downto 0 do
if A[i] > nextMax then
if A[i] <> prevMax then
nextMax := A[i];
else begin
swap(A[i], A[last]);
last := last - 1;
end
while (last > 0) and (A[last] = nextMax) do
last := last - 1;
end;
end;
Thus, if on average there are more than two items with the same value, bingo sort can be expected to be faster because it executes the inner loop fewer times than selection sort.
See also
[edit]References
[edit]- ^ Skiena, Steven (2008). "Searching and Sorting". The Algorithm Design Manual (3rd ed.). Springer. p. 116. doi:10.1007/978-3-030-54256-6_4. ISBN 978-3-030-54255-9.
The name typically given to this algorithm, heapsort, obscures the fact that the algorithm is nothing but an implementation of selection sort using the right data structure.
- ^
 This article incorporates public domain material from Paul E. Black. "Bingo sort". Dictionary of Algorithms and Data Structures. NIST.
This article incorporates public domain material from Paul E. Black. "Bingo sort". Dictionary of Algorithms and Data Structures. NIST.
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison–Wesley, 1997. ISBN 0-201-89685-0. Pages 138–141 of Section 5.2.3: Sorting by Selection.
- Anany Levitin. Introduction to the Design & Analysis of Algorithms, 2nd Edition. ISBN 0-321-35828-7. Section 3.1: Selection Sort, pp 98–100.
- Robert Sedgewick. Algorithms in C++, Parts 1–4: Fundamentals, Data Structure, Sorting, Searching: Fundamentals, Data Structures, Sorting, Searching Pts. 1–4, Second Edition. Addison–Wesley Longman, 1998. ISBN 0-201-35088-2. Pages 273–274
External links
[edit]- Animated Sorting Algorithms: Selection Sort at the Wayback Machine (archived 7 March 2015) – graphical demonstration
Selection sort
View on Grokipediaprocedure selectionSort(array A of size n)
for i from 0 to n-2 do
minIndex = i
for j from i+1 to n-1 do
if A[j] < A[minIndex] then
minIndex = j
swap A[i] with A[minIndex]
procedure selectionSort(array A of size n)
for i from 0 to n-2 do
minIndex = i
for j from i+1 to n-1 do
if A[j] < A[minIndex] then
minIndex = j
swap A[i] with A[minIndex]
Overview
Definition and Principle
A sorting algorithm is a procedure that takes a collection of elements and rearranges them into a specific order, such as non-decreasing, producing a permutation of the input that satisfies the desired ordering relation. These algorithms typically operate on data structures like arrays or lists and rely on comparisons or other operations to achieve the sorted result.[4] Selection sort is an in-place comparison-based sorting algorithm that divides the input list into a sorted sublist, initially empty, and an unsorted sublist, initially the entire list. It builds the sorted sublist incrementally by repeatedly identifying the minimum element from the unsorted portion and placing it at the boundary between the sorted and unsorted parts. The algorithm assumes a total order on the elements, meaning a binary relation that is reflexive, antisymmetric, transitive, and total, allowing consistent comparisons between any pair of elements.[5] The core principle of selection sort involves, for each position i from the start of the list up to the second-to-last element, scanning the unsorted sublist to locate the smallest element and swapping it with the element at position i to extend the sorted sublist. This process ensures that after each iteration, the prefix of the list up to i is sorted, and the remaining suffix contains the unsorted elements.[5][6] Key properties of selection sort include its in-place nature, requiring only a constant amount of extra memory beyond the input array, and its reliance on comparisons without additional data structures. It is not stable, as swaps can alter the relative order of equal elements. While straightforward to implement and educational, selection sort exhibits quadratic time complexity in all cases, making it inefficient for large datasets compared to more advanced algorithms.[5][1]Historical Development
Selection sort traces its origins to the early days of electronic computing, where simple selection-based methods were developed to organize data efficiently on limited hardware. Although no single inventor is attributed, the algorithm's principles resemble manual sorting techniques employed in punch-card data processing systems of the 1920s and 1930s, such as those by IBM, which involved iteratively selecting and separating cards based on specific criteria.[7] This reference, while not establishing the absolute origin, marks a pivotal early documentation amid the rapid growth of computing in the mid-20th century.[8] Donald E. Knuth provided a comprehensive analysis in The Art of Computer Programming, Volume 3: Sorting and Searching (1973), dedicating a section to "Sorting by Selection" and emphasizing its role as an accessible example for understanding comparison-based sorting. Knuth's treatment, grounded in historical context and efficiency analysis, solidified its place in algorithms textbooks, where it was presented alongside insertion and exchange sorts for instructional clarity.[9][5] The core algorithm has remained largely static since its formalization, with evolution limited to pedagogical refinements rather than major redesigns. In the 1970s and 1980s, minor optimizations—such as tournament-based selection to reduce comparisons or bidirectional scanning—were explored in research papers, but these variants retained the inherent quadratic time complexity and did not gain widespread adoption beyond academic interest.[10] Instead, selection sort's enduring legacy lies in its simplicity, making it a foundational topic in introductory computer science education worldwide since the 1970s, where it illustrates key concepts like iterative selection without the complexities of more advanced algorithms.[5]Algorithm Mechanics
Step-by-Step Process
Selection sort operates by repeatedly selecting the minimum element from the unsorted portion of the array and placing it in its correct position within the growing sorted portion, building the sorted array incrementally from the beginning.[6] The process begins with an array of n elements, where the initial sorted portion is empty (for n > 0), and the unsorted portion is the entire array; this sorted segment expands by one element per iteration until it encompasses the entire array.[11] The core iteration proceeds as follows: for each index i ranging from 0 to n-2, the algorithm scans the subarray from position i to n-1, comparing elements to identify the index min_idx of the smallest element in that subarray.[6][11] Upon locating the minimum, if min_idx differs from i, the algorithm swaps the element at position i with the element at min_idx, thereby fixing the next smallest element in its sorted position and extending the sorted portion by one.[6][11] This iteration repeats n-1 times, after which the array is fully sorted in ascending order, as the last element is automatically in place once all preceding minima have been positioned.[6] For edge cases, an empty array (n=0) requires no operations and is considered sorted by default, while a single-element array (n=1) is already sorted and triggers no iterations or swaps.[12] Additionally, input in descending order demands no modifications to the algorithm, as it consistently selects the overall minimum each time, performing the same scans and swaps regardless of initial arrangement.[6]Pseudocode Representation
The standard pseudocode for the selection sort algorithm, as presented in foundational algorithms literature, is a language-agnostic representation that highlights its iterative process of identifying and placing the minimum element in the unsorted portion of the array.procedure selection_sort(A: [array](/page/Array) of integers)
n = length(A)
for i = 0 to n-2 do
min_idx = i
for j = i+1 to n-1 do
if A[j] < A[min_idx] then
min_idx = j
end if
end for
if min_idx != i then
swap A[i] and A[min_idx]
end if
end for
end procedure
procedure selection_sort(A: [array](/page/Array) of integers)
n = length(A)
for i = 0 to n-2 do
min_idx = i
for j = i+1 to n-1 do
if A[j] < A[min_idx] then
min_idx = j
end if
end for
if min_idx != i then
swap A[i] and A[min_idx]
end if
end for
end procedure
Practical Example
Numerical Illustration
To illustrate the selection sort algorithm, consider the input array[64, 25, 12, 22, 11].[13]
In the first pass, the minimum value 11 is found at index 4 and swapped with the element at index 0 (64), resulting in [11, 25, 12, 22, 64]. This fixes the smallest element in position, growing the sorted prefix to length 1 while shrinking the unsorted portion to the remaining 4 elements.[13]
In the second pass, over indices 1 to 4, the minimum value 12 is at index 2 and swapped with the element at index 1 (25), yielding [11, 12, 25, 22, 64]. The sorted prefix now extends to length 2.[13]
In the third pass, over indices 2 to 4, the minimum value 22 is at index 3 and swapped with the element at index 2 (25), producing [11, 12, 22, 25, 64]. The sorted prefix grows to length 3.[13]
In the fourth pass, over indices 3 to 4, the minimum value 25 is at index 3, requiring no swap, so the array remains [11, 12, 22, 25, 64]. With only one element left, the process completes, leaving the fully sorted array [11, 12, 22, 25, 64].[13]
For this array of length , the algorithm performs 4 passes (one fewer than ), involving a total of 10 comparisons (summing ) and 3 swaps (in the first three passes). This numerical tracing demonstrates how selection sort progressively builds the sorted prefix from the beginning, selecting and placing the next smallest element each time.[13]
Visual Step-by-Step
To visualize the selection sort process, consider an initial array represented as a horizontal sequence of rectangular bars or boxes, where each bar's height corresponds to the element's value (e.g., taller bar for 64, shorter for 11), positioned from left to right by index. The example array [64, 25, 12, 22, 11] starts with all bars in blue to indicate the fully unsorted portion, with no sorted elements yet.[14] In the first pass (i=0), a pointer marks the current index i at the leftmost position, scanning rightward to find the minimum value (11 at index 4), highlighted in yellow or green. The unsorted portion remains blue, while an arrow or animated line illustrates the swap between the minimum (11) and the element at i (64), transitioning the bars' positions; post-swap, the leftmost bar (now 11) turns red to denote the growing sorted prefix, with the remaining bars [64, 25, 12, 22] staying blue. Subsequent passes repeat this: for i=1, scan [25, 12, 22] to find 12 (yellow/green highlight), swap with 25, redden the second bar (12), and so on, progressively expanding the red sorted region rightward while shrinking the blue unsorted tail—e.g., after the second pass: [11, 12, 25, 22, 64] (first two red) and [25, 22, 64] blue; third pass swaps 22 with 25, yielding [11, 12, 22, 25, 64] (first three red) and [25, 64] blue; fourth pass requires no swap as the minimum (25) is already in position, reddening the fourth bar and leaving the last (64) to complete the sort trivially.[15][14] Key visual elements include color-coding (blue for unsorted, red for sorted, yellow/green for the current minimum, and temporary black during swaps for emphasis), pointers or labels for i (scanning the unsorted region) and min_idx (tracking the minimum's location), and directional arrows showing element exchanges to clarify the partitioning mechanism.[14][15] In digital formats, this can be animated stepwise with delays (e.g., 500ms per scan or swap) to reveal the iterative selection and placement, allowing viewers to pause and inspect intermediate states; for static diagrams, side-by-side panels depict before-and-after each pass, tracing the array's evolution from [64, 25, 12, 22, 11] (all blue) to [11, 12, 22, 25, 64] (all red).[15] Such visualizations aid intuition by demonstrating how selection sort partitions the array into sorted and unsorted subarrays through repeated minimum extractions, making the algorithm's simplicity and quadratic behavior more tangible without relying on abstract code.[14]Implementation Details
In-Place Implementation
Selection sort operates as an in-place algorithm, utilizing only O(1) extra space by performing all operations directly on the original array through element swaps, thereby avoiding the need for additional auxiliary arrays or data structures.[16] The core code structure employs a double-loop mechanism to maintain efficiency in data movements. The outer loop runs from the first element (index 0) to the second-to-last element (index n-2), where n is the array length, designating each position i as the boundary between the sorted and unsorted portions. Within each outer iteration, the inner loop scans the unsorted subarray from index i+1 to n-1, identifying the index of the minimum value (min_idx) by comparing elements sequentially. This design ensures that swaps occur only once per outer iteration, at most, to place the smallest remaining element at position i, thereby minimizing the total number of exchanges to at most n-1.[5] The swap mechanics are implemented using a single temporary variable to exchange elements without data loss: a temporary variable temp is assigned the value at A, then A receives the value from A[min_idx], and finally A[min_idx] is set to temp; this swap is executed conditionally only if min_idx ≠ i, further reducing operations when the minimum is already correctly positioned.[5]Language-Specific Adaptations
Selection sort implementations vary across programming languages due to differences in syntax, built-in functions, and data structures, but all maintain the core in-place swapping mechanism to minimize memory usage.[17] These adaptations ensure the algorithm's simplicity while leveraging language-specific features for efficiency and readability. In Python, the implementation uses list slicing and tuple unpacking for swaps, emphasizing the language's concise syntax. The following function sorts an array in ascending order:def selection_sort(arr):
n = len(arr)
for i in range(n-1):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
def selection_sort(arr):
n = len(arr)
for i in range(n-1):
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
std::swap from <algorithm>, which provides a safe and efficient exchange operation. The example below uses a std::vector<int> and traditional for-loops:
#include <vector>
#include <algorithm>
void selection_sort(std::vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n-1; ++i) {
int min_idx = i;
for (int j = i+1; j < n; ++j) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
std::swap(arr[i], arr[min_idx]);
}
}
#include <vector>
#include <algorithm>
void selection_sort(std::vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n-1; ++i) {
int min_idx = i;
for (int j = i+1; j < n; ++j) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
std::swap(arr[i], arr[min_idx]);
}
}
int[] or collections such as ArrayList<Integer>, requiring manual swap logic since no built-in swap function exists for arrays. The example uses an int[] for simplicity:
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n-1; i++) {
int min_idx = i;
for (int j = i+1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// Manual swap
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n-1; i++) {
int min_idx = i;
for (int j = i+1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// Manual swap
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
Comparator interface can be passed to the inner loop for comparing objects, enabling sorting by specific attributes (e.g., students.sort(Comparator.comparing(Student::getGPA)) adapted to selection sort).[18] Similarly, C++ uses std::function or functor objects with the < operator overloaded via templates, as in template<typename T> void selection_sort(std::vector<T>& arr, auto cmp) { ... if (cmp(arr[j], arr[min_idx])) ... }.[19] These adaptations support sorting heterogeneous data without altering the algorithm's O(n²) nature.
Selection sort is inherently iterative, avoiding recursion to prevent stack overflow in large arrays and maintain constant space complexity, a design choice preserved across these language implementations.[20]
Complexity Analysis
Time Complexity
The time complexity of selection sort is determined primarily by the number of comparisons performed in its nested loop structure, where an outer loop iterates over the array from the first to the second-to-last element, and an inner loop scans the remaining unsorted portion to find the minimum value.[21] This results in a worst-case and average-case time complexity of , as the algorithm performs approximately comparisons regardless of the input arrangement.[22] To derive this, consider an array of length : the outer loop runs for iterations, and in the -th iteration (starting from ), the inner loop performs comparisons to identify the minimum in the unsorted subarray. The total number of comparisons is thus the sum , which simplifies asymptotically to .[23] In the best case, when the input is already sorted, the algorithm still executes the full inner loops without early termination, yielding the same complexity, as no optimizations skip scans in the standard implementation.[24] The number of swaps is at most , contributing only to the overall time, which is dominated by the quadratic comparisons.[21] Asymptotically, this quadratic time complexity renders selection sort inefficient for large inputs, typically becoming impractical for arrays exceeding 1000 elements due to the rapid growth in operations.[25]Space Complexity and Stability
Selection sort operates as an in-place algorithm, utilizing only a constant amount of auxiliary space—specifically O(1)—for temporary variables during swaps, while the total space complexity remains O(n) due to the input array itself.[2] This minimal extra memory requirement makes it suitable for environments with limited resources, such as embedded systems, where avoiding additional data structures is advantageous.[26] Despite its space efficiency, selection sort is not stable, meaning it does not preserve the relative order of elements with equal keys in the sorted output. Instability arises because the algorithm swaps the selected minimum (or maximum) element with the first position in the unsorted subarray, potentially moving one equal element past another through non-adjacent exchanges. For instance, consider an unsorted subarray starting at index k: [5_a, 5_b, 3], where 5_a and 5_b are equal values distinguished by their original positions (a before b). During the pass for position k, the minimum 3 at index k+2 is identified and swapped with 5_a at k, resulting in [3, 5_b, 5_a]. Here, the relative order of the two 5s is inverted, with 5_b now preceding 5_a.[27] This behavior stems from the selection process choosing the first encountered minimum for swapping, without regard for the positions of subsequent equal elements.[28] The proof of instability follows directly from this mechanism: in each iteration, the algorithm scans the unsorted portion to find the index of the minimum value, starting from the current position, and performs a direct swap regardless of distance, which can reorder equal elements encountered later in the scan.[4] Consequently, applications requiring stability—such as sorting records by multiple keys where secondary order must be maintained—should opt for stable alternatives like merge sort, despite selection sort's in-place advantage.[29] Beyond these properties, selection sort is neither adaptive nor online. It is not adaptive, as it always executes n-1 full scans of the remaining unsorted subarray, irrespective of the input's partial order, leading to no performance gain on nearly sorted data.[30] Similarly, it is not online, requiring access to the complete array upfront to perform its selection passes, unlike algorithms that can process elements incrementally as they arrive.[31]Comparisons
With Insertion Sort
Both selection sort and insertion sort are quadratic-time comparison-based sorting algorithms that perform in-place operations and are straightforward to implement, making them suitable for small arrays or educational purposes. They share the property of incrementally constructing a sorted prefix of the array, one element at a time, through iterative passes over the data.[5] A key difference lies in their approaches to placing elements: selection sort identifies the minimum element in the unsorted subarray via a full linear scan and swaps it directly into its final position at the boundary of the sorted prefix, ensuring exactly one swap per pass. In contrast, insertion sort takes the next unsorted element and inserts it into the correct position within the sorted prefix by shifting larger elements rightward until the spot is found, which can require multiple shifts but no full scans of the unsorted portion. This makes insertion sort more efficient for partially sorted inputs, as it avoids unnecessary scans.[32][5] Performance-wise, selection sort exhibits fixed behavior across all inputs, with approximately comparisons and swaps in the average and worst cases, providing consistent predictability. Insertion sort, however, adapts to the data: it achieves a best-case time complexity of with only comparisons and no shifts for sorted input, though its worst case matches selection sort's comparisons and incurs up to shifts on average. Empirical studies confirm insertion sort often outperforms selection sort on nearly sorted datasets due to fewer operations overall.[32][33] Selection sort is typically favored for uniformly random data where its invariant comparison count minimizes variability, while insertion sort is better suited for nearly sorted arrays or online/streaming applications where elements are processed incrementally.[33][5] Consider a reverse-sorted array such as [5, 4, 3, 2, 1]: selection sort conducts complete minimum searches across the shrinking unsorted subarray in each of the four passes, yielding comparisons, whereas insertion sort performs extensive shifts for each of the four insertions—shifting 1, 2, 3, and 4 elements respectively—resulting in the maximum shifts alongside comparable comparisons.[32]With Bubble Sort
Selection sort and bubble sort are both straightforward, comparison-based sorting algorithms with a time complexity of O(n²) in the worst and average cases, making them suitable for introductory computer science education where they are frequently taught together to illustrate basic sorting principles.[34][35] The primary difference lies in their mechanisms: bubble sort operates by making multiple passes through the array, repeatedly swapping adjacent elements if they are in the wrong order to gradually "bubble" the largest (or smallest) elements to the end, whereas selection sort identifies the global minimum (or maximum) element in the unsorted portion during each pass and swaps it directly into its final position without relying on adjacent exchanges.[35][36] In terms of performance, bubble sort is adaptive and can terminate early if no swaps occur in a pass, indicating the array is sorted, which improves efficiency on nearly sorted data; selection sort lacks this adaptability and always completes all passes regardless of input order.[37] On reverse-sorted inputs, bubble sort performs up to Θ(n²) swaps due to extensive adjacent exchanges, while selection sort requires only n-1 swaps, one per pass to place each minimum element.[38] Bubble sort benefits from optimizations like the cocktail shaker variant, which alternates pass directions to move elements toward both ends more efficiently, whereas selection sort is more challenging to optimize due to its fixed pass structure and direct minimum selection.[39][40] Bubble sort is often preferred in educational contexts for its intuitive, step-by-step adjacent swapping that visually demonstrates disorder resolution, while selection sort excels in scenarios with costly swaps, such as random data distributions, where its minimal n-1 swaps provide an advantage over bubble sort's potentially higher swap count.[41][42]Variants
Bidirectional Selection Sort
Bidirectional selection sort is a variant of the standard selection sort algorithm that enhances efficiency by simultaneously identifying the minimum and maximum elements in the unsorted portion of the array during each iteration.[43] This approach alternates between placing the minimum element at the left end of the unsorted region and the maximum element at the right end, thereby shrinking the unsorted middle section from both sides until the left and right pointers meet.[43] The algorithm initializes two pointers:low at index 0 and high at index n-1, where n is the length of the array. While low < high, it scans the subarray from low to high to locate the indices of the minimum and maximum values. The minimum is swapped into position low, and the maximum is swapped into position high. The pointers are then updated by incrementing low and decrementing high. This process repeats, effectively sorting the array by progressively fixing elements at both extremities of the remaining unsorted portion.[43]
One key benefit of bidirectional selection sort is the reduction in the number of comparisons required, which is approximately halved in the average case to about compared to for the standard selection sort, although the worst-case time complexity remains . This improvement arises from performing roughly half as many passes, as the unsorted region diminishes twice as quickly.
Despite these gains, the algorithm introduces drawbacks such as increased implementation complexity due to the dual tracking of extremes and the need to handle potential overlaps in minimum and maximum positions.[43] It remains unstable, like its predecessor, potentially altering the relative order of equal elements during swaps.[43]
Bidirectional selection sort is particularly useful for medium-sized arrays seeking a modest performance boost over basic selection sort without introducing the space overhead or coding intricacy of more sophisticated algorithms.















