Hubbry Logo
London dispersion forceLondon dispersion forceMain
Open search
London dispersion force
Community hub
London dispersion force
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
London dispersion force
London dispersion force
London dispersion force
View on Wikipedia
from Wikipedia
Interaction energy of an argon dimer. The long-range section is due to London dispersion forces.

London dispersion forces (LDF, also known as dispersion forces, London forces, instantaneous dipole–induced dipole forces, fluctuating induced dipole bonds[1] or loosely as van der Waals forces) are a type of intermolecular force acting between atoms and molecules that are normally electrically symmetric; that is, the electrons are symmetrically distributed with respect to the nucleus.[2] They are part of the van der Waals forces. The LDF is named after the German physicist Fritz London. They are the weakest of the intermolecular forces.

Introduction

[edit]

The electron distribution around an atom or molecule undergoes fluctuations in time. These fluctuations create instantaneous electric fields which are felt by other nearby atoms and molecules, which in turn adjust the spatial distribution of their own electrons. The net effect is that the fluctuations in electron positions in one atom induce a corresponding redistribution of electrons in other atoms, such that the electron motions become correlated. While the detailed theory requires a quantum-mechanical explanation (see quantum mechanical theory of dispersion forces), the effect is frequently described as the formation of instantaneous dipoles that (when separated by vacuum) attract each other. The magnitude of the London dispersion force is frequently described in terms of a single parameter called the Hamaker constant, typically symbolized . For atoms that are located closer together than the wavelength of light, the interaction is essentially instantaneous and is described in terms of a "non-retarded" Hamaker constant. For entities that are farther apart, the finite time required for the fluctuation at one atom to be felt at a second atom ("retardation") requires use of a "retarded" Hamaker constant.[3][4][5]

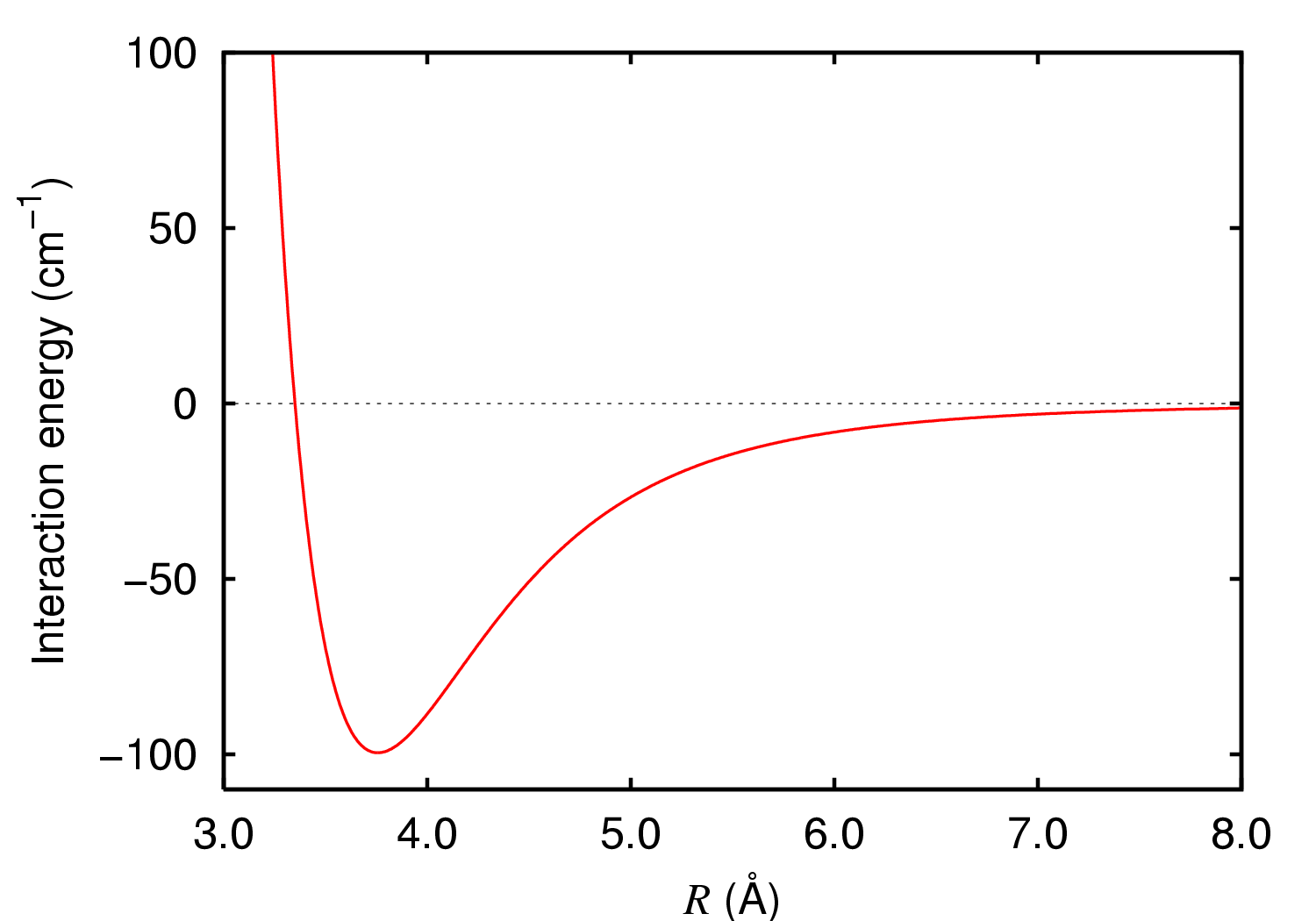
While the London dispersion force between individual atoms and molecules is quite weak and decreases quickly with separation like , in condensed matter (liquids and solids), the effect is cumulative over the volume of materials,[6] or within and between organic molecules, such that London dispersion forces can be quite strong in bulk solid and liquids and decay much more slowly with distance. For example, the total force per unit area between two bulk solids decreases by [7] where is the separation between them. The effects of London dispersion forces are most obvious in systems that are very non-polar (e.g., that lack ionic bonds), such as hydrocarbons and highly symmetric molecules like bromine (Br2, a liquid at room temperature) or iodine (I2, a solid at room temperature). In hydrocarbons and waxes, the dispersion forces are sufficient to cause condensation from the gas phase into the liquid or solid phase. Sublimation heats of e.g. hydrocarbon crystals reflect the dispersion interaction. Liquification of oxygen and nitrogen gases into liquid phases is also dominated by attractive London dispersion forces.

When atoms/molecules are separated by a third medium (rather than vacuum), the situation becomes more complex. In aqueous solutions, the effects of dispersion forces between atoms or molecules are frequently less pronounced due to competition with polarizable solvent molecules. That is, the instantaneous fluctuations in one atom or molecule are felt both by the solvent (water) and by other molecules.

Larger and heavier atoms and molecules exhibit stronger dispersion forces than smaller and lighter ones.[8] This is due to the increased polarizability of molecules with larger, more dispersed electron clouds. The polarizability is a measure of how easily electrons can be redistributed; a large polarizability implies that the electrons are more easily redistributed. This trend is exemplified by the halogens (from smallest to largest: F2, Cl2, Br2, I2). The same increase of dispersive attraction occurs within and between organic molecules in the order RF, RCl, RBr, RI (from smallest to largest) or with other more polarizable heteroatoms.[9] Fluorine and chlorine are gases at room temperature, bromine is a liquid, and iodine is a solid. The London forces are thought to arise from the motion of electrons.

Quantum mechanical theory

[edit]

The first explanation of the attraction between noble gas atoms was given by Fritz London in 1930.[10][11][12] He used a quantum-mechanical theory based on second-order perturbation theory. The perturbation is because of the Coulomb interaction between the electrons and nuclei of the two moieties (atoms or molecules). The second-order perturbation expression of the interaction energy contains a sum over states. The states appearing in this sum are simple products of the stimulated electronic states of the monomers. Thus, no intermolecular antisymmetrization of the electronic states is included, and the Pauli exclusion principle is only partially satisfied.

London wrote a Taylor series expansion of the perturbation in , where is the distance between the nuclear centers of mass of the moieties.

This expansion is known as the multipole expansion because the terms in this series can be regarded as energies of two interacting multipoles, one on each monomer. Substitution of the multipole-expanded form of V into the second-order energy yields an expression that resembles an expression describing the interaction between instantaneous multipoles (see the qualitative description above). Additionally, an approximation, named after Albrecht Unsöld, must be introduced in order to obtain a description of London dispersion in terms of polarizability volumes, , and ionization energies, , (ancient term: ionization potentials).

In this manner, the following approximation is obtained for the dispersion interaction between two atoms and . Here and are the polarizability volumes of the respective atoms. The quantities and are the first ionization energies of the atoms, and is the intermolecular distance.

Note that this final London equation does not contain instantaneous dipoles (see molecular dipoles). The "explanation" of the dispersion force as the interaction between two such dipoles was invented after London arrived at the proper quantum mechanical theory. The authoritative work[13] contains a criticism of the instantaneous dipole model[14] and a modern and thorough exposition of the theory of intermolecular forces.

The London theory has much similarity to the quantum mechanical theory of light dispersion, which is why London coined the phrase "dispersion effect". In physics, the term "dispersion" describes the variation of a quantity with frequency, which is the fluctuation of the electrons in the case of the London dispersion.

Relative magnitude

[edit]

Dispersion forces are usually dominant over the three van der Waals forces (orientation, induction, dispersion) between atoms and molecules, with the exception of molecules that are small and highly polar, such as water. The following contribution of the dispersion to the total intermolecular interaction energy has been given:[15]

Contribution of the dispersion to the total intermolecular interaction energy
Molecule pair % of the total energy of interaction
Ne-Ne 100
CH4-CH4 100
HCl-HCl 86
HBr-HBr 96
HI-HI 99
CH3Cl-CH3Cl 68
NH3-NH3 57
H2O-H2O 24
HCl-HI 96
H2O-CH4 87

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

London dispersion force

View on Grokipedia
from Grokipedia
London dispersion forces, often simply called dispersion forces or London forces, are a fundamental type of weak intermolecular attraction that originates from transient fluctuations in the of atoms or molecules, leading to the formation of instantaneous dipoles that induce complementary dipoles in adjacent particles and produce a net attractive interaction. These forces, theoretically derived by in 1930 through quantum mechanical considerations of , are the weakest component of van der Waals interactions but are universally present between all atoms and molecules, irrespective of their polarity. Unlike dipole-dipole or forces, London dispersion arises even in and nonpolar substances, where no permanent dipoles exist. The magnitude of London dispersion forces depends primarily on the of the interacting species—the ease with which their electron clouds can be distorted—as well as the proximity and number of s involved; thus, they strengthen with increasing molecular size, mass, and surface area, enabling efficient packing in condensed phases. In nonpolar molecules, such as alkanes or , these forces dominate intermolecular attractions, directly influencing macroscopic properties like s, melting points, viscosities, and solubilities; for instance, the higher of iodine compared to reflects stronger dispersion due to greater polarizability. Quantum chemically, dispersion is quantified as a long-range effect that decays with distance, often modeled via methods like with empirical corrections to capture its subtle yet pervasive role. Beyond classical , London dispersion forces have emerged as critical in contemporary applications, including computational simulations of biomolecular binding, where they stabilize protein-ligand complexes and influence ; in , where they modulate selectivity and reactivity in organometallic systems; and in , contributing to in supramolecular structures and . Recent advances in dissecting dispersion energies at the atomic level underscore their context-dependent significance, revealing how they compete or synergize with other interactions in solution and gas phases, thereby demanding precise inclusion in theoretical models for accurate predictions.

Fundamentals

Definition and Characteristics

London dispersion forces are a type of arising from temporary fluctuations in the distribution of atoms or molecules, which create instantaneous dipoles that induce corresponding dipoles in neighboring particles, resulting in an attractive interaction between them. These forces originate from transient correlated momentary dipoles and are fundamentally quantum mechanical in nature. A key characteristic of London dispersion forces is their universal presence in all atoms and molecules, irrespective of whether the particles are polar or nonpolar. They are always attractive and isotropic, meaning they act equally in without dependence on molecular orientation. For pairwise interactions, the strength of these forces decreases rapidly with , following an inverse sixth-power dependence (1/R⁶). Within the broader category of van der Waals forces, London dispersion represents the universal component that applies to every particle containing electrons, in contrast to more specific interactions like permanent dipole-dipole forces or hydrogen bonding, which require fixed charge separations. These dispersion forces enable cohesion in nonpolar substances by providing the weak but essential attractions that allow them to condense into liquids or solids, such as the liquefaction of like or under sufficiently low temperatures and high pressures.

Historical Development

In the late , recognized the existence of attractive forces between molecules in non-polar gases, which deviated from behavior, as incorporated into his 1873 equation of state that accounted for molecular volume and intermolecular attractions through the parameter 'a'. These forces, later understood as a component of van der Waals forces, explained phenomena such as gas liquefaction and compressibility in real gases. Prior to a quantum mechanical interpretation, contributed in by developing the theory of dipole-induced dipole interactions, emphasizing the role of molecular in generating attractive forces between a permanent and an inducible one, though without addressing quantum fluctuations in non-polar systems. Debye's work laid groundwork for understanding induction effects but did not fully explain attractions in non-polar molecules like . The quantum-based explanation for these dispersion interactions emerged in 1930 through Fritz London's seminal paper, where he derived the attractive potential arising from correlated fluctuations and instantaneous dipoles in non-polar atoms and molecules, providing a rigorous theoretical foundation using second-order . London's formulation unified the treatment of intermolecular forces, highlighting their universal presence even in systems lacking permanent dipoles. In the and , 's ideas were refined and integrated into broader theories of intermolecular potentials, including the 1930 derivation of the dispersion interaction by Eisenschitz and . Further developments by various researchers extended these models to applications in condensed phases. The forces became commonly known as dispersion forces in recognition of Fritz 's foundational quantum explanation, solidifying their role in .

Theoretical Basis

Classical Instantaneous Dipole Model

The classical instantaneous dipole model describes London dispersion forces as arising from temporary fluctuations in distribution within neutral atoms or s, leading to attractive interactions without invoking . In this simplified picture, electrons in a are in constant motion due to , occasionally resulting in an uneven charge distribution that creates a transient dipole moment, with one side momentarily more negative and the other more positive. This instantaneous generates an that influences nearby molecules. The mechanism proceeds in three key steps: first, the random movement of electrons in one molecule produces the initial transient dipole; second, the electric field from this dipole polarizes a neighboring molecule by distorting its electron cloud, inducing an oppositely oriented dipole; and third, the positive end of the induced dipole is attracted to the negative end of the original dipole (and vice versa), yielding a net attractive force between the molecules. This process occurs dynamically, with dipoles forming and dissipating rapidly, but their average effect over time results in a weak, cumulative attraction. To illustrate qualitatively, consider two adjacent atoms, each with a symmetric electron cloud under normal conditions. If in one atom momentarily cluster on the side away from the other, it forms a ; this asymmetry repels in the second atom toward its far side, creating an aligned induced . The resulting configuration resembles two bar magnets attracting end-to-end, though the effect is fleeting and probabilistic. Such thought experiments highlight the model's reliance on classical , treating as point charges in orbital motion without wave-like properties. This classical framework qualitatively explains the cohesion observed in nonpolar substances like at low temperatures, where dispersion forces provide the only significant intermolecular attraction, enabling liquefaction of or despite their lack of permanent dipoles. For instance, the model accounts for why molecules aggregate into liquids below 87 K, as transient dipoles foster weak but sufficient binding to overcome thermal disruption. However, the model has notable limitations, as it assumes classical behavior and cannot explain the fundamental origin of the fluctuations, which stem from quantum mechanical correlations rather than purely random motion. It also fails to predict precise interaction strengths or distances, treating the process as a static induction rather than a correlated, time-averaged quantum effect, thus serving primarily as an intuitive precursor to more rigorous derivations.

Quantum Mechanical Derivation

The quantum mechanical foundation of London dispersion forces was established by in through the application of second-order Rayleigh-Schrödinger perturbation theory to the interaction between two neutral atoms. Consider two atoms A and B, each described by their unperturbed Hamiltonians HAH_A and HBH_B, with the total Hamiltonian given by H=HA+HB+VH = H_A + H_B + V, where VV is the perturbative interaction potential arising from the interactions between electrons and nuclei of the two atoms. The interaction VV is expanded in a multipole series, with the leading dipole-dipole term scaling as 1/R31/R^3, where RR is the intermolecular distance. In second-order perturbation theory, the correction to the ground-state energy is δE(2)=∑k≠0∣⟨0∣V∣k⟩∣2E0−Ek,\delta E^{(2)} = \sum_{k \neq 0} \frac{|\langle 0 | V | k \rangle|^2}{E_0 - E_k}, where ∣0⟩|0\rangle is the unperturbed (product of ground states of A and B), and ∣k⟩|k\rangle are the excited states of the combined system. For dispersion forces, the relevant contributions arise from terms where both atoms are virtually excited simultaneously (double excitations), excluding charge-transfer or induction effects. Applying this to the dipole-dipole interaction yields the dispersion energy as Edisp=−∑m≠0A,n≠0B∣⟨0A0B∣Vdd∣mAnB⟩∣2EmAA+EnBB−E0AA−E0BB,E_\text{disp} = -\sum_{m \neq 0_A, n \neq 0_B} \frac{|\langle 0_A 0_B | V_\text{dd} | m_A n_B \rangle|^2}{E_{m_A}^A + E_{n_B}^B - E_{0_A}^A - E_{0_B}^B}, where VddV_\text{dd} is the dipole-dipole operator, and the sums run over excited states mm of A and nn of B. To obtain a closed-form expression, London employed the Unsöld approximation (or closure approximation), replacing the excitation energies with an average value related to the ionization energies IAI_A and IBI_B, and expressing the matrix elements in terms of static dipole polarizabilities αA\alpha_A and αB\alpha_B. This leads to the seminal London formula for the leading-order dispersion energy at large separations: Edisp≈−34αAαBIAIBIA+IB1R6,E_\text{disp} \approx -\frac{3}{4} \frac{\alpha_A \alpha_B I_A I_B}{I_A + I_B} \frac{1}{R^6}, where α\alpha quantifies the ease of inducing a dipole moment (in units of volume, e.g., ų), II approximates the characteristic excitation energy (in energy units, e.g., eV), and the R−6R^{-6} dependence emerges from the second-order treatment of the R−3R^{-3} dipole-dipole potential. This approximation captures the attractive nature of the force while highlighting its quantum origin in correlated electron fluctuations. At very long distances, where retardation effects due to the finite become significant, the R−6R^{-6} form transitions to R−7R^{-7}, as described by the Casimir-Polder formula, which incorporates frequency-dependent polarizabilities integrated over imaginary frequencies. In modern , (DFT) methods, augmented with dispersion corrections like DFT-D3, routinely compute these energies by evaluating the perturbation sum or its approximations directly from electron densities, enabling accurate predictions for complex systems.

Magnitude and Factors

Factors Influencing Strength

The strength of London dispersion forces depends significantly on molecular size and . Larger atoms and molecules possess more s and larger electron clouds, which are more easily distorted to form temporary dipoles, resulting in stronger attractive interactions. For instance, the boiling points of the diatomic rise progressively down the group—from −188 °C for F₂ to 184 °C for I₂—owing to the increasing atomic size and that amplify dispersion forces. (α) scales approximately with molecular volume, as greater volume facilitates larger fluctuations in distribution and thus more pronounced induced dipoles. Molecular shape further modulates the interaction strength by influencing the effective contact area between molecules. Elongated or linear molecules enable closer and more extensive overlap of clouds compared to branched or spherical ones, leading to enhanced dispersion forces. A clear example is provided by the isomers n-pentane and , both C₅H₁₂: n-pentane has a of 36 °C due to its linear structure allowing greater surface interaction, while the more compact boils at 9.5 °C. Temperature affects the manifestation of dispersion forces, as higher thermal energy increases molecular kinetic motion, which disrupts the transient alignment of dipoles and reduces the net attractive effect. Consequently, nonpolar substances remain gaseous at elevated temperatures but condense into liquids or solids upon cooling, when thermal disruption is minimized and dispersion forces can dominate cohesion. The distance between interacting entities governs the force magnitude, with pairwise interactions decaying as 1/R61/R^6, where RR is the intermolecular separation—a dependence originating from quantum mechanical treatments of correlated electron fluctuations. In macroscopic contexts, such as bulk materials or colloidal suspensions, this is aggregated into the Hamaker constant AA, a material-specific parameter quantifying the overall dispersion attraction; for organic substances, AA typically falls in the range of $4 to $7 \times 10^{-20} J. Surrounding environmental conditions also influence dispersion strength. In , forces operate at full intensity without interference, but in , they are attenuated by screening from the medium and competing interactions with solvent molecules. For colloidal systems, dispersion contributes to interparticle attractions at surfaces, promoting aggregation as described in , where the Hamaker constant captures the effective van der Waals component across the medium.

Relative Importance in Intermolecular Forces

London dispersion forces represent the weakest category of intermolecular forces, with typical interaction energies ranging from 0.05 to 40 kJ/mol, though they are ubiquitous and present between all molecular pairs regardless of polarity. In contrast, dipole-dipole interactions typically span 5 to 25 kJ/mol, hydrogen bonding ranges from 10 to 40 kJ/mol, and ionic interactions are substantially stronger, often exceeding 100 kJ/mol for ion-dipole or ion-ion contacts. This hierarchy positions dispersion forces as generally subordinate in systems where stronger interactions dominate, yet their universality ensures they contribute to cohesion in every molecular aggregate. Dispersion forces dominate entirely (100%) in interactions between non-polar molecules, such as or hydrocarbons like (CH₄), where no permanent dipoles exist to enable dipole-dipole or hydrogen bonding. In polar systems, their role is partial, where hydrogen bonding and dipole-dipole forces predominate but dispersion still modulates the total attraction.
Molecular PairDispersion Contribution (%)Qualitative Explanation
CH₄-CH₄100Non-polar symmetric molecules; no dipole-dipole or bonding possible, so dispersion is the sole attractive force.
Dispersion forces play a pivotal role in phase transitions for non-polar substances, where they are the exclusive intermolecular interaction responsible for elevating boiling points relative to ideal gases; for instance, the gradual increase in boiling points across the series (e.g., to ) reflects enhanced dispersion with molecular size.

Examples and Applications

Molecular and Chemical Examples

London dispersion forces are particularly evident in non-polar molecules, where they serve as the primary intermolecular interaction responsible for physical properties such as boiling points. In the series, the boiling points increase significantly from gas (F₂, –188.1°C) to iodine (I₂, 184.3°C), a trend attributed to the increasing molecular size and , which enhance the strength of dispersion forces. Similarly, among the , boiling points rise from (–268.6°C) to (–107.1°C) due to larger atomic radii allowing for greater electron cloud distortion and thus stronger temporary attractions. These examples highlight how dispersion forces scale with molecular or atomic size in systems lacking permanent dipoles.
Noble GasBoiling Point (°C)HalogenBoiling Point (°C)
He–268.6F₂–188.1
Ne–245.9Cl₂–34.6
Ar–185.7Br₂58.8
Kr–152.3I₂184.3
Xe–107.1
Boiling points illustrating the increase due to London dispersion forces with size; data from UTDallas chemistry lecture notes. In hydrocarbons, such as straight-chain alkanes, the boiling point escalates with chain length because longer carbon chains provide more surface area for electron fluctuations, intensifying dispersion interactions; for instance, n-butane boils at –0.5°C, while n-pentane boils at 36.1°C, with dispersion as the sole intermolecular force. This pattern underscores the role of molecular geometry and size in amplifying dispersion effects without contributions from dipole-dipole or hydrogen bonding forces. The liquefaction of non-polar diatomic gases like nitrogen (N₂, boiling point –196°C) and oxygen (O₂, boiling point –183°C) at cryogenic temperatures relies entirely on London dispersion forces to overcome kinetic energy and enable condensation into liquids. These forces induce temporary dipoles in the symmetric molecules, facilitating the phase transition observed in industrial processes like air separation. Experimental manifestations of dispersion forces appear in the physical properties of non-polar solvents, such as the surface tension of oils (typically 20–30 mN/m for hydrocarbons) arising from cohesive attractions between non-polar chains that minimize surface exposure. Likewise, the of these solvents, which increases with molecular weight (e.g., higher in longer-chain hydrocarbons), stems from the resistance to flow imposed by entangled dispersion-mediated interactions. These properties demonstrate the practical impact of dispersion in purely chemical contexts.

Biological and Material Applications

In biological systems, London dispersion forces play a crucial role in stabilizing the hydrophobic cores of proteins, where nonpolar side chains are buried to minimize exposure to . The tight packing within these cores enhances dispersion interactions, contributing significantly to overall protein stability; for instance, burying a –CH₂– group adds approximately 1.1 ± 0.5 kcal/mol to the folding free energy across various proteins. These forces arise from the close proximity of nonpolar residues, providing an attractive energy of about -3.1 kcal/mol per –CH₂– group due to optimized van der Waals contacts in the densely packed interior. Another prominent biological application involves adhesion, where van der Waals forces, predominantly London dispersion, enable strong attachment to diverse surfaces without reliance on chemical residues or . Experimental measurements on individual gecko setae demonstrate adhesion forces of 40–41 μN on both hydrophobic (e.g., with θ = 81.9°) and hydrophilic (e.g., SiO₂ with θ = 0°) substrates, with parallel stress values of 0.213–0.218 N/mm² showing no significant difference (P > 0.5). This indicates that dispersion interactions between the nonpolar spatulae and polarizable surfaces are the dominant mechanism, as confirmed by synthetic analogs like PDMS spatulae yielding 181 nN adhesion consistent with theoretical predictions. In , London dispersion forces underpin polymer cohesion, particularly in , where they act as the primary intermolecular attractions between chain segments in crystalline regions. These weak but cumulative forces, arising from transient dipoles in the chains, enable the formation of crystallites containing 1000–2000 units, where their total strength rivals covalent bonds and contributes to the material's tensile strength and fracture behavior under stress. Similarly, in , dispersion forces drive the and bundling of carbon nanotubes (CNTs), stabilizing aligned structures through pairwise van der Waals attractions; for example, the per interaction scales linearly with CNT circumference (ΔE₁ = 4.028 C_r + 28.28 kcal/mol, R² = 0.995) and length, allowing total bundle energies to reach hundreds of kcal/mol in hexagonal or configurations as modeled by force-field methods. Modern applications leverage dispersion forces in pharmaceutical design, where they influence the of nonpolar drugs by facilitating interactions between solute and molecules in non-aqueous formulations. For nonpolar pharmaceuticals, such as certain steroids or , London dispersion replaces hydrophobic effects in organic solvents, enhancing dissolution and in solid dispersions or amorphous forms. In , anti-fouling coatings exploit reduced dispersion interactions through low materials like (PDMS), where the flexible Si–O–Si backbone and methyl groups minimize van der Waals adhesion of marine organisms, promoting detachment under hydrodynamic shear and achieving over 90% reduction in attachment compared to untreated surfaces. Emerging research in the 2020s employs (DFT) with dispersion corrections to predict and optimize London forces in metal-organic frameworks (MOFs), enabling accurate modeling of their porous structures and gas adsorption properties. Methods like the DFT-D4 model, extended for periodic systems, incorporate charge-dependent dispersion coefficients and reference polarizabilities for elements in MOFs, yielding superior accuracy in lattice energies (mean absolute deviations <5 kJ/mol) and adsorption energies compared to earlier D3 corrections, as validated on molecular crystals and surface interactions. These advancements facilitate the design of MOFs for applications like CO₂ capture, where dispersion dominates framework stability.

References

  1. https://www.sciencedirect.com/topics/pharmacology-toxicology-and-pharmaceutical-science/london-dispersion-force
  2. https://pmc.ncbi.nlm.nih.gov/articles/PMC10702350/
  3. https://www.chem.purdue.edu/gchelp/liquids/disperse.html
  4. https://www.sciencedirect.com/topics/engineering/dispersion-force
  5. https://www.osti.gov/servlets/purl/2311175
  6. https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Introductory_Chemistry_%28CK-12%29/09%253A_Covalent_Bonding/9.18%253A_Van_der_Waals_Forces
  7. https://chem.libretexts.org/Courses/Sacramento_City_College/SCC%253A_CHEM_300_-_Beginning_Chemistry/SCC%253A_CHEM_300_-_Beginning_Chemistry_%28Faculty%29/12%253A_Liquids_Solids_and_Intermolecular_Forces/12.06%253A_Types_of_Intermolecular_Forces-_Dispersion%252C_Dipole%25E2%2580%2593Dipole%252C_Hydrogen_Bonding%252C_and_Ion-Dipole
  8. https://pubs.acs.org/doi/10.1021/acs.jced.9b00264
  9. https://core.ac.uk/download/pdf/291577968.pdf
  10. https://www.ias.ac.in/article/fulltext/reso/015/12/1056-1059
  11. https://pubs.acs.org/doi/10.1021/acscentsci.5c00356
  12. https://www.americanscientist.org/article/engines-powered-by-the-forces-between-atoms
  13. https://chem.libretexts.org/Courses/South_Puget_Sound_Community_College/Chem_121_OER_Textbook/06%253A_Chapter_5B_-_Intermolecular_Forces_and_Molecular_Models/6.03%253A_Intermolecular_Forces/6.3.01%253A_Dipole-Dipole_and_Dispersion_Forces
  14. https://ethz.ch/content/dam/ethz/special-interest/chab/icb/shih-lab-dam/documents/IEM-lecture/Lecture_2022/Notes_2022/Lecture_10_2022.pdf
  15. https://www.sciencedirect.com/science/article/abs/pii/S0065316020300034
  16. https://pubs.aip.org/aip/jcp/article/149/8/084115/565777/A-physically-grounded-damped-dispersion-model-with
  17. https://doi.org/10.1007/BF01421741
  18. https://www.sciencedirect.com/science/article/pii/B9780123750495000049
  19. http://guweb2.gonzaga.edu/faculty/cronk/CHEM101pub/intermolecular_forces.html
  20. https://pubs.rsc.org/en/content/articlepdf/2019/ra/c9ra03003d
  21. https://users.highland.edu/~jsullivan/genchem/s13_imf.html
  22. https://chem.libretexts.org/Courses/Mount_Royal_University/Chem_1201/Unit_5%253A_Intermolecular_Forces/5.2%253A_Intermolecular_Forces
  23. https://pubs.acs.org/doi/10.1021/acs.jpca.9b06433
  24. https://pubs.aip.org/aip/jcp/article/156/19/194306/2841286/The-influence-of-a-solvent-environment-on-direct
  25. https://link.springer.com/article/10.1007/s40828-023-00182-9
  26. https://www.sydney.edu.au/science/chemistry/~george/1611/IntermolecularForces.pdf
  27. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/11%3A_Liquids_and_Intermolecular_Forces/11.02%3A_Intermolecular_Forces
  28. https://personal.utdallas.edu/~son051000/chem1311/Lectures2012/Chapter12a.pdf
  29. https://wou.edu/chemistry/courses/online-chemistry-textbooks/ch105-consumer-chemistry/ch105-chapter-7/
  30. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/physprop.htm
  31. https://intro.chem.okstate.edu/1515SP02/Lecture/Chapter12/Lec2602.html
  32. https://alpha.chem.umb.edu/chemistry/ch116/summer2010/documents/chapter_11au.pdf
  33. https://www2.chemistry.msu.edu/courses/cem151/Intramolecularforces.pdf
  34. https://pmc.ncbi.nlm.nih.gov/articles/PMC4116631/
  35. https://pmc.ncbi.nlm.nih.gov/articles/PMC129431/
  36. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Basic_Principles_of_Organic_Chemistry_(Roberts_and_Caserio)/29%3A_Polymers/29.04%3A_Forces_Between_Polymer_Chains
  37. https://www.mdpi.com/2673-3501/2/2/11
  38. https://pubs.acs.org/doi/10.1021/acs.cgd.0c01102
  39. https://link.springer.com/article/10.1007/s44251-023-00028-z
  40. https://pubs.rsc.org/en/content/articlelanding/2020/cp/d0cp00502a
  41. https://www.cambridge.org/core/journals/journal-of-materials-research/article/recent-trends-on-density-functional-theoryassisted-calculations-of-structures-and-properties-of-metalorganic-frameworks-and-metalorganic-frameworksderived-nanocarbons/71F534F39D70E035C4A6B8D97E2F14B9
Add your contribution
Related Hubs
User Avatar
No comments yet.