Pentagonal polytope

In geometry, a pentagonal polytope is a regular polytope in n dimensions constructed from the H_n Coxeter group. The family was named by H. S. M. Coxeter, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as {5, 3^{n − 2}} (dodecahedral) or {3^{n − 2}, 5} (icosahedral).

The family starts as 1-polytopes and ends with n = 5 as infinite tessellations of 4-dimensional hyperbolic space.

There are two types of pentagonal polytopes; they may be termed the dodecahedral and icosahedral types, by their three-dimensional members. The two types are duals of each other.

The complete family of dodecahedral pentagonal polytopes are:

1. Line segment, { }
2. Pentagon, {5}
3. Dodecahedron, {5, 3} (12 pentagonal faces)
4. 120-cell, {5, 3, 3} (120 dodecahedral cells)
5. Order-3 120-cell honeycomb, {5, 3, 3, 3} (tessellates hyperbolic 4-space (∞ 120-cell facets)

The facets of each dodecahedral pentagonal polytope are the dodecahedral pentagonal polytopes of one less dimension. Their vertex figures are the simplices of one less dimension.

Dodecahedral pentagonal polytopes

n	Coxeter group	Petrie polygon projection	Name Coxeter diagram Schläfli symbol	Facets	Elements
					Vertices	Edges	Faces	Cells	4-faces
1	${\displaystyle H_{1}}$ [ ] (order 2)		Line segment { }	2 vertices	2
2	${\displaystyle H_{2}}$ [5] (order 10)		Pentagon {5}	5 edges	5	5
3	${\displaystyle H_{3}}$ [5,3] (order 120)		Dodecahedron {5, 3}	12 pentagons	20	30	12
4	${\displaystyle H_{4}}$ [5,3,3] (order 14400)		120-cell {5, 3, 3}	120 dodecahedra	600	1200	720	120
5	${\displaystyle {\bar {H}}_{4}}$ [5,3,3,3] (order ∞)		120-cell honeycomb {5, 3, 3, 3}	∞ 120-cells	∞	∞	∞	∞	∞

The complete family of icosahedral pentagonal polytopes are:

1. Line segment, { }
2. Pentagon, {5}
3. Icosahedron, {3, 5} (20 triangular faces)
4. 600-cell, {3, 3, 5} (600 tetrahedron cells)
5. Order-5 5-cell honeycomb, {3, 3, 3, 5} (tessellates hyperbolic 4-space (∞ 5-cell facets)

The facets of each icosahedral pentagonal polytope are the simplices of one less dimension. Their vertex figures are icosahedral pentagonal polytopes of one less dimension.

Icosahedral pentagonal polytopes

n	Coxeter group	Petrie polygon projection	Name Coxeter diagram Schläfli symbol	Facets	Elements
					Vertices	Edges	Faces	Cells	4-faces
1	${\displaystyle H_{1}}$ [ ] (order 2)		Line segment { }	2 vertices	2
2	${\displaystyle H_{2}}$ [5] (order 10)		Pentagon {5}	5 Edges	5	5
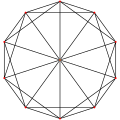
3	${\displaystyle H_{3}}$ [5,3] (order 120)		Icosahedron {3, 5}	20 equilateral triangles	12	30	20
4	${\displaystyle H_{4}}$ [5,3,3] (order 14400)		600-cell {3, 3, 5}	600 tetrahedra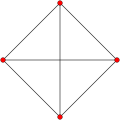	120	720	1200	600
5	${\displaystyle {\bar {H}}_{4}}$ [5,3,3,3] (order ∞)		Order-5 5-cell honeycomb {3, 3, 3, 5}	∞ 5-cells	∞	∞	∞	∞	∞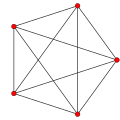

The pentagonal polytopes can be stellated to form new star regular polytopes:

• In two dimensions, we obtain the pentagram {5/2},
• In three dimensions, this forms the four Kepler–Poinsot polyhedra, {3,5/2}, {5/2,3}, {5,5/2}, and {5/2,5}.
• In four dimensions, this forms the ten Schläfli–Hess polychora: {3,5,5/2}, {5/2,5,3}, {5,5/2,5}, {5,3,5/2}, {5/2,3,5}, {5/2,5,5/2}, {5,5/2,3}, {3,5/2,5}, {3,3,5/2}, and {5/2,3,3}.
• In four-dimensional hyperbolic space there are four regular star-honeycombs: {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5}, and {5,5/2,5,3}.

In some cases, the star pentagonal polytopes are themselves counted among the pentagonal polytopes.^[1]

Like other polytopes, regular stars can be combined with their duals to form compounds;

• In two dimensions, a decagrammic star figure {10/2} is formed,
• In three dimensions, we obtain the compound of dodecahedron and icosahedron,
• In four dimensions, we obtain the compound of 120-cell and 600-cell.

Star polytopes can also be combined.

• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25–36]
• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Table I(ii): 16 regular polytopes {p, q, r} in four dimensions, pp. 292–293)