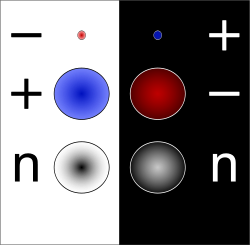Antiparticle

AntiparticleMain

Community hub

Antiparticle

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Antiparticle

View on Wikipedia

from Wikipedia

Not found

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

In particle physics, an antiparticle is a subatomic particle that has the same mass, spin, and lifetime as its corresponding particle in the Standard Model but opposite values for additive quantum numbers, including electric charge, baryon number, lepton number, and certain flavor quantum numbers like strangeness.^[1] For instance, the antiparticle of the negatively charged electron is the positively charged positron, while the antiproton carries a negative charge opposite to the proton's positive charge.^[2] These particles arise naturally within quantum field theory, where fields are quantized and inherently produce both particle and antiparticle states to satisfy mathematical consistency, such as the requirement for charge conjugation symmetry.^[1] The concept of antiparticles was theoretically predicted in 1930 by Paul Dirac in his paper "A Theory of Electrons and Protons," where he interpreted negative-energy solutions in his relativistic quantum equation for the electron as "holes" representing positively charged particles of the same mass—the first indication of antimatter.^[3] This prediction resolved inconsistencies in combining special relativity and quantum mechanics for electrons, suggesting that every fermion has an antiparticle partner.^[4] Experimental confirmation came swiftly: in 1932, Carl David Anderson discovered the positron while studying cosmic rays using a cloud chamber, observing tracks of particles with the mass of an electron but curving in the direction expected for positive charge in a magnetic field.^[5] Antiparticles play a crucial role in fundamental interactions and are routinely produced and studied in high-energy environments. When a particle and its antiparticle collide, they annihilate, converting their combined mass into energy, typically in the form of photons or other particles, as governed by conservation laws in the Standard Model.^[1] Production occurs in particle accelerators like those at Fermilab or CERN, where collisions generate antiparticle-antiparticle pairs, or naturally via cosmic rays and radioactive decays such as beta-plus emission.^[2] Notable milestones include the 1955 discovery of the antiproton at the Berkeley Bevatron by Emilio Segrè and Owen Chamberlain, confirming Dirac's prediction for hadrons and earning them the 1959 Nobel Prize in Physics. Beyond fundamental research, antiparticles have practical applications, particularly in medicine through positron emission tomography (PET) scans, where positrons from radioactive tracers annihilate with electrons to produce detectable gamma rays for imaging.^[2] Antimatter research also probes cosmological questions, such as the observed matter-antimatter asymmetry in the universe, where theories like CP violation in weak interactions explain why matter dominates despite symmetric Big Bang production.^[6] Ongoing experiments at facilities like CERN's Antiproton Decelerator continue to explore antimatter's properties, including antihydrogen spectroscopy, to test whether it behaves identically to matter under gravity and electromagnetism.

Historical Development

Theoretical Predictions

The development of relativistic quantum mechanics in the mid-1920s highlighted the need for a wave equation that reconciled quantum theory with special relativity. The Klein-Gordon equation, independently proposed by Oskar Klein and Walter Gordon in 1926, represented an initial attempt to achieve this by applying the relativistic energy-momentum relation

E^2 = p^2 c^2 + m^2 c^4

to the Schrödinger wave equation, resulting in a second-order differential equation for scalar particles.^[7] However, this equation suffered from significant issues, including the emergence of negative probability densities due to its second-order time dependence, which violated the positive-definite probability interpretation central to quantum mechanics, and solutions with negative energies that lacked physical meaning. These shortcomings motivated physicists, particularly Paul Dirac, to seek a first-order relativistic wave equation that would preserve causality and probabilistic consistency.^[8] In 1928, Dirac formulated a groundbreaking relativistic quantum equation for the electron, known as the Dirac equation, which successfully incorporated both relativity and quantum mechanics while naturally accounting for the electron's spin-1/2 nature. The equation is given by

i \hbar \frac{\partial \psi}{\partial t} = c \vec{\alpha} \cdot \vec{p} \psi + \beta m c^2 \psi,

iℏ∂t∂ψ=cα

⋅p

ψ+βmc2ψ, where $\psi$ is a four-component spinor wave function, $\vec{\alpha}$

and $\beta$ are 4×4 matrices, $\vec{p}$

is the momentum operator, $m$ is the electron mass, $c$ is the speed of light, and $\hbar$ is the reduced Planck's constant.^[9] This first-order form avoided the acausal issues of the Klein-Gordon equation but introduced its own challenge: the energy spectrum included both positive and negative eigenvalues, with negative energy solutions implying unphysical states where electrons could accelerate indefinitely by transitioning to lower energies.^[8] Dirac initially viewed these negative energies as a mathematical artifact requiring reinterpretation to maintain physical realism.^[10] To resolve the negative energy problem, Dirac proposed the "hole theory" in his 1930 paper, interpreting the negative energy states as a completely filled "Dirac sea" of electrons occupying all such levels in accordance with the Pauli exclusion principle, rendering them inaccessible to positive-energy electrons.^[11] Absences or "holes" in this sea would behave as particles of positive energy but opposite charge to the electron—specifically, positively charged particles later identified as positrons—effectively predicting the existence of antimatter as a consequence of relativistic quantum mechanics.^[8] Dirac refined this interpretation in subsequent 1931 work, emphasizing the holes' role in processes like pair production while distancing the theory from earlier misconceptions linking holes to protons. This theoretical framework marked a pivotal prediction of antiparticles, bridging quantum field concepts without invoking full quantum electrodynamics.

Experimental Discovery

The experimental discovery of antiparticles began with the positron, predicted theoretically by Paul Dirac in 1930, interpreting the negative energy solutions from his 1928 relativistic Dirac equation for the electron as "holes" representing positrons. In 1932, Carl D. Anderson at the California Institute of Technology observed the first evidence of the positron while studying cosmic ray tracks in a cloud chamber equipped with a 6 mm lead plate and placed in a uniform magnetic field of about 13,000 gauss.^[5] The key identification criterion was the track's curvature in the magnetic field, which bent in the opposite direction to that of electrons of comparable momentum, indicating a positive charge, while the ionization density and track length confirmed a mass approximately equal to that of the electron.^[12] Anderson photographed multiple such tracks from cosmic rays entering from below, ruling out instrumental artifacts through careful calibration.^[13] For this discovery, Anderson shared the 1936 Nobel Prize in Physics with Victor F. Hess.^[12] The positron's existence was confirmed in 1933 by Patrick M. S. Blackett and Giuseppe P. S. Occhialini at the Cavendish Laboratory using an innovative counter-controlled cloud chamber that automatically triggered expansion only when ionizing particles passed through, allowing efficient capture of rare events from cosmic rays.^[14] Over several months, they analyzed around 700 photographs, identifying approximately 40 events involving electron-positron pair production and 14 clear positron tracks, including spiral paths in the magnetic field that matched Anderson's observations and demonstrated the positron's role in processes like gamma-ray conversion.^[15] These photographic records provided unambiguous evidence, overcoming challenges in distinguishing positrons from protons or other positive ions by measuring track curvature and multiple scattering.^[14] The search for heavier antiparticles extended to the antiproton, discovered in 1955 by Owen Chamberlain and Emilio G. Segrè at the University of California's Berkeley Radiation Laboratory using the newly operational Bevatron accelerator.^[16] Protons accelerated to 6.2 GeV—slightly above the 5.6 GeV threshold required for proton-antiproton pair production—were directed onto a copper target, producing secondary particles that were then momentum-analyzed and detected over a 40-foot path using Cerenkov counters to identify relativistic speeds near that of light and scintillation counters to measure time-of-flight and energy loss.^[17] The team observed about 60 antiproton events, distinguished from negative pi-mesons by their greater mass (inferred from velocity and momentum) and lack of decay in flight, confirming the particles annihilated only upon stopping in matter.^[16] Chamberlain and Segrè received the 1959 Nobel Prize in Physics for this achievement.^[17] The antineutron, the antiparticle of the neutral neutron, was discovered later in 1956 at the same Bevatron by Bruce Cork and colleagues. Antiprotons from the target were directed into a liquid hydrogen target to induce charge exchange reactions (p̄ + p → n̄ + n), producing antineutrons that were identified by their annihilation products—multiple pions—detected in scintillation counters, confirming the antineutron's mass equal to the neutron's and lack of charge. This observation extended the confirmation of antiparticles to neutral hadrons.^[18] The first observation of an antiparticle neutrino came in 1956 through the Cowan-Reines experiment, which detected electron antineutrinos from a nuclear reactor at the Savannah River Plant.^[19] Clyde L. Cowan Jr. and Frederick Reines used a detector consisting of scintillation and water targets doped with cadmium, observing inverse beta decay events (antineutrino + proton → positron + neutron) at a rate of about 3 per hour above background, with the positron's delayed coincidence signal confirming the interaction.^[20] This marked the initial empirical verification of neutrinos as distinct antiparticles, addressing prior challenges in detecting their weak interactions.^[19]

Fundamental Concepts

Definition and Characteristics

An antiparticle is the counterpart to a given elementary particle, possessing identical mass, spin, and lifetime but opposite values for certain quantum numbers, such as electric charge, baryon number, and lepton number. This concept arises from the structure of relativistic quantum field theory, where particles and antiparticles are distinct excitations of the same underlying field.^[21] Key characteristics of antiparticles include adherence to the same relativistic energy-momentum relation as their particle counterparts:

E = \sqrt{(pc)^2 + (mc^2)^2}

E=(pc)2+(mc2)2

where $E$ is energy, $p$ is momentum, $m$ is rest mass, $c$ is the speed of light, and the relation holds equally for both due to their shared mass. Antiparticles exhibit the same interaction strengths in fundamental forces, except for those dependent on the reversed quantum numbers, such as electromagnetic interactions influenced by charge. The CPT theorem, which combines charge conjugation (C), parity (P), and time reversal (T) transformations, rigorously guarantees the existence of an antiparticle for every particle in local quantum field theories with Lorentz invariance and hermiticity, ensuring equality in mass, lifetime, and other intrinsic properties.^[22] A classic example is the positron ( $e^+$ ), the antiparticle of the electron ( $e^-$ ), which has the same mass and spin as the electron but opposite electric charge (+1 versus -1 in elementary charge units). This charge conjugation exemplifies how antiparticles differ from mere mirror images under parity or other symmetries, as the reversal is specifically tied to quantum number inversion rather than spatial reflection alone. For certain neutral particles, such as the photon, the particle is its own antiparticle because it carries no distinguishing quantum numbers like charge, making charge conjugation leave it unchanged.

Symmetry and Conservation

Charge conjugation (C) is a discrete symmetry transformation that interchanges particles with their corresponding antiparticles, effectively swapping the sign of all additive quantum numbers such as electric charge, baryon number, and lepton number.^[23] This symmetry is conserved in strong and electromagnetic interactions, where no violations have been observed, as evidenced by stringent limits on processes like the decay

\pi^0 \to 3\gamma

with branching ratio less than

3.1 \times 10^{-8}

(90% CL, as of 2024).^[23] In contrast, C is violated in weak interactions due to the chiral nature of the weak force, which couples preferentially to left-handed fermions, leading to observable effects such as oscillations between neutral kaons and their antiparticles.^[23] The combined symmetry of charge conjugation (C), parity (P, which inverts spatial coordinates), and time reversal (T, which reverses the direction of time) forms the CPT theorem, which posits that local, Lorentz-invariant quantum field theories must be invariant under CPT transformations.^[24] This invariance implies that particles and antiparticles must have identical masses, lifetimes, and other intrinsic properties, providing a foundational principle for understanding antiparticles in the Standard Model.^[24] Experimental tests, particularly in neutral kaon systems, confirm CPT conservation to high precision, with mass differences between

K^0

and

\overline{K^0}

constrained to less than

4.0 \times 10^{-19}

GeV at 95% confidence level (as of 2024).^[24] Antiparticles carry opposite values of conserved quantum numbers compared to their particles: antibaryons have baryon number

B = -1

while baryons have

B = +1

, and antileptons have lepton number

L = -1

versus

L = +1

for leptons.^[23] Baryon number

B

and total lepton number

L

are conserved in all Standard Model interactions, with no observed violations; for instance, proton lifetime limits exceed

2.4 \times 10^{34}

years for p → e^+ π^0 (90% CL, as of 2024), and neutrinoless double-beta decay searches set half-lives greater than

2.3 \times 10^{26}

years for ^{136}Xe (90% CL, as of 2024).^[23] Individual lepton flavor numbers (e.g., electron, muon, tau) are approximately conserved in charged-current weak interactions but violated by neutrino oscillations.^[23] CP symmetry, the combination of charge conjugation and parity, was discovered to be violated in 1964 through the observation of the decay

K_L^0 \to \pi^+ \pi^-

by the team of Christenson, Cronin, Fitch, and Turlay, with a measured ratio

|\eta_{+-}| = (2.228 \pm 0.011) \times 10^{-3}

(as of 2024).^[25] This violation occurs in weak interactions and contributes to the observed matter-antimatter asymmetry in the universe, as CPT invariance combined with CP violation implies T violation.^[23] In neutral kaon systems, CP violation manifests in mixing and decay asymmetries, such as the semileptonic charge asymmetry measured at

(3.34 \pm 0.07) \times 10^{-3}

(as of 2024), highlighting the non-conservation of C and P separately in weak processes.^[23]

Elementary Antiparticles

Antileptons

Antileptons comprise the antiparticles of the elementary leptons, organized into three generations or families, each featuring a charged antilepton and an associated antineutrino. These particles carry opposite quantum numbers to their lepton counterparts, including opposite electric charge for the charged ones and opposite lepton number. Unlike antiquarks, antileptons do not participate in strong interactions due to the absence of color charge, interacting primarily via the weak and electromagnetic forces.^[26] The first-generation antileptons include the positron (e⁺), the antiparticle of the electron, and the electron antineutrino (

\bar{\nu}_e

). The positron has a positive electric charge of +1 and a rest mass of 0.51099895000(15) MeV/c², identical to that of the electron.^[26] It is stable against decay but can annihilate with electrons, producing gamma rays. The positron was discovered in 1932 by Carl D. Anderson through cloud chamber observations of cosmic ray tracks, where it appeared as a positively charged particle with electron-like curvature in a magnetic field.^[27] The electron antineutrino, electrically neutral and nearly massless (upper limit < 0.8 eV/c² at 90% confidence level), was inferred from the three-body decay kinematics of beta processes, such as neutron decay (n → p + e⁻ +

\bar{\nu}_e

), as early as the 1930s to conserve energy and angular momentum.^[26] Its direct detection via inverse beta decay on protons was achieved in 1956 using antineutrinos from a nuclear reactor.^[28] In the second generation, the antileptons are the antimuon (μ⁺) and the muon antineutrino (

\bar{\nu}_\mu

). The antimuon carries a +1 charge and has a rest mass of 105.6583755(23) MeV/c², approximately 207 times that of the electron.^[26] It is unstable, with a mean lifetime of 2.1969811(22) × 10⁻⁶ s, decaying primarily (≈99.99%) via the weak interaction to a positron, electron antineutrino, and muon neutrino (μ⁺ → e⁺ +

\bar{\nu}_e

+ ν_μ).^[26] The antimuon was identified in 1936 by Carl D. Anderson and Seth Neddermeyer in cosmic ray experiments, distinguishing it from the negatively charged muon through track curvature and penetration depth in a cloud chamber.^[29] Antimuons, produced alongside antimuons in cosmic ray showers, contribute significantly to atmospheric particle fluxes and are routinely observed in detectors like those at sea level. The muon antineutrino, also neutral and with mass < 0.8 eV/c², was inferred from the decay of charged pions (π⁺ → μ⁺ +

\bar{\nu}_\mu

) in the 1940s and later confirmed through neutrino beam experiments distinguishing it from the electron antineutrino.^[26] The third-generation antileptons consist of the antitau (τ⁺) and the tau antineutrino (

\bar{\nu}_\tau

). The antitau has a +1 charge and a much larger rest mass of 1776.93(9) MeV/c², about 3477 times the electron mass.^[26] It decays rapidly with a mean lifetime of 290.3(5) × 10⁻¹⁵ s, predominantly through weak channels producing lighter leptons or hadrons plus neutrinos, such as τ⁺ → μ⁺ +

\bar{\nu}_\mu

+ ν_τ (≈17.39%).^[26] The antitau was discovered in 1977 at the SPEAR electron-positron collider at SLAC, where Martin L. Perl and collaborators observed e⁺μ⁺ + missing energy events consistent with pair production of a new heavy lepton and its antiparticle.^[20] The tau antineutrino, neutral with mass < 0.8 eV/c², is inferred directly from antitau decays and its existence was established by the late 1980s through kinematic reconstruction in tau pair events at e⁺e⁻ colliders.^[26] Hypothetical sterile antineutrinos, which would interact only via gravity and possibly mix with active antineutrinos, remain undetected as of 2025, with ongoing searches motivated by anomalies in neutrino oscillation data but no conclusive evidence.^[30]

Antiquarks and Antihadrons

Antiquarks are the antiparticles of quarks, exhibiting the same six flavors—anti-up (

\bar{u}

), anti-down (

\bar{d}

), anti-strange (

\bar{s}

), anti-charm (

\bar{c}

), anti-bottom (

\bar{b}

), and anti-top (

\bar{t}

)—with identical masses to their quark counterparts but opposite electric charges and color charges. The current quark masses, evaluated in the

\overline{\text{MS}}

scheme at 2 GeV for light flavors, are approximately

m_{\bar{u}} = 2.2^{+0.5}_{-0.4}

MeV/

c^2

m_{\bar{d}} = 4.7^{+0.5}_{-0.4}

MeV/

c^2

, and

m_{\bar{s}} = 95 \pm 5

MeV/

c^2

, while heavier antiquarks have

m_{\bar{c}} \approx 1.275 \pm 0.025

GeV/

c^2

m_{\bar{b}} \approx 4.18^{+0.03}_{-0.02}

GeV/

c^2

, and the anti-top is unstable with a pole mass around 173 GeV/

c^2

. Antiquarks carry anticolor charges (antired, antigreen, antblue), contrasting with the color charges of quarks, and participate in the strong interaction via quantum chromodynamics.^[31]^[32] Antihadrons are composite particles formed by the binding of antiquarks through the strong force, analogous to hadrons but with opposite quantum numbers such as baryon number

B = -1

for antibaryons. The antiproton (

\bar{p} = \bar{u}\bar{u}\bar{d}

) has a mass of 938.272 MeV/

c^2

and is stable against strong and electromagnetic decays, though it can annihilate with protons. The antineutron (

\bar{n} = \bar{u}\bar{d}\bar{d}

) possesses a mass of approximately 939.57 MeV/

c^2

and decays via the weak interaction, primarily to antiproton and positron plus neutrino, with a mean lifetime of 880 seconds. These antibaryons exemplify the mirror symmetry of the quark model, where antiquark combinations yield states with reversed charges and flavors compared to their matter counterparts.^[32] Mesons, being quark-antiquark pairs, frequently incorporate antiquarks and are classified by their flavor content and quantum numbers. The positively charged pion (

\pi^+ = u\bar{d}

) has a mass of 139.57 MeV/

c^2

and spin-parity quantum numbers

J^{PC} = 0^{-+}

, decaying primarily via the weak interaction to a muon and a muon neutrino (

\pi^+ \to \mu^+ \nu_\mu

), with other weak decay modes such as electronic or hadronic channels being minor (branching ratios <0.01%). The negatively charged kaon (

K^- = \bar{u}s

) exhibits a mass of 493.68 MeV/

c^2

with

J^P = 0^-

, undergoing weak decays such as to muon and neutrino, highlighting the role of strangeness in flavor-changing processes. These pseudoscalar mesons illustrate how antiquarks contribute to the light hadron spectrum, with binding energies dominated by the strong interaction.^[32] Antiquarks are primarily produced in high-energy particle collisions through quark-antiquark pair creation, requiring a minimum center-of-mass energy threshold of

2m_q c^2

to conserve energy and quantum numbers; for light antiquarks like

\bar{u}

and

\bar{d}

, this threshold is on the order of a few MeV, while for heavy flavors like

\bar{c}

, it exceeds 2.5 GeV. Due to color confinement in quantum chromodynamics, free antiquarks cannot exist; instead, they immediately combine with quarks or gluons to form color-singlet hadrons, ensuring that observed particles are always neutral under the strong color force. This confinement mechanism underpins the structure of all antihadrons, preventing isolated antiquark detection.^[32]^[33]

Composite Antiparticles

Antinuclei

Antinuclei are composite particles consisting of multiple antiprotons and antineutrons bound together by the strong nuclear force, analogous to ordinary atomic nuclei formed from protons and neutrons. The simplest antinucleus is the antideuteron (

\bar{d} = \bar{p} \bar{n}

), which has a binding energy of approximately 2.2 MeV, identical to that of the deuteron due to charge-parity-time (CPT) symmetry. This binding arises primarily from the strong interaction between the constituent antiquarks, with electromagnetic contributions being negligible compared to the dominant nuclear forces. The antideuteron was first observed in 1965 during proton-beryllium collisions at the CERN Proton Synchrotron, marking the initial experimental confirmation of a bound antimatter nucleus.^[34] Heavier antinuclei, such as antitritium (

\bar{t} = 2\bar{p} + \bar{n}

) and antihelium-3 (

\bar{{}^3\mathrm{He}} = 2\bar{p} + \bar{n}

) or antihelium-4 (

\bar{{}^4\mathrm{He}} = 2\bar{p} + 2\bar{n}

), have been produced in high-energy accelerator experiments, particularly in relativistic heavy-ion collisions at facilities like the Relativistic Heavy Ion Collider (RHIC). For instance, the STAR collaboration at RHIC observed antitritium and antihelium-3 in Au+Au collisions at

\sqrt{s_{NN}} = 200

sNN

=200 GeV, with production yields consistent with coalescence models where antinuclei form from the binding of nearby antiprotons and antineutrons in the collision aftermath. Production cross-sections for these antinuclei are extremely low, typically on the order of $10^{-6}$ relative to antiproton production per collision event, reflecting the rarity of forming bound states from the dilute antimatter fragments generated in such interactions. Antihelium-4, once the heaviest antinucleus observed, was detected in 18 events by the STAR experiment in 2011 during Au+Au collisions at RHIC energies of 200 GeV and 62 GeV per nucleon pair, with no significant deviation from expected statistical yields for matter and antimatter nuclei.^[35] More recently, as of 2024, hyperantinuclei such as antihyperhydrogen-4 (observed by STAR at RHIC) and antihyperhelium-4 (observed by ALICE at the LHC) have been detected, extending the range of known composite antimatter structures.^[36]^[37] The stability of antinuclei mirrors that of their matter counterparts, governed by the strong force that holds them together against decay, but their lifetimes in typical environments are severely limited by interactions with ordinary matter. Upon encountering protons or neutrons, antinuclei undergo rapid annihilation, releasing energy through the conversion of quark-antiquark pairs into mesons and photons, with mean free paths on the order of micrometers in dense media. In vacuum or isolated conditions, such as in cosmic rays, their intrinsic stability is determined by the weak decays of constituents—antiprotons and antineutrons have lifetimes exceeding $10^{10}$ years—but practical observation is constrained by annihilation risks during production and detection. These properties make antinuclei valuable for cosmic ray studies, where searches for rare cosmic antideuterons and heavier antinuclei by experiments like AMS-02 on the International Space Station provide stringent upper limits on fluxes, potentially revealing dark matter annihilation signals amid low astrophysical backgrounds at low energies.^[38]

Anti-Atoms

Anti-atoms are neutral systems formed by the electromagnetic binding of positrons to antinuclei, analogous to ordinary atoms but composed entirely of antimatter. These exotic structures provide a platform for precision tests of fundamental symmetries, such as charge conjugation, parity, and time reversal (CPT) invariance, by comparing their properties to those of their matter counterparts. Unlike antinuclei, which are bound by the strong nuclear force, anti-atoms involve additional leptonic components that enable atomic-scale interactions and spectroscopy. A prominent example of a lepton-only anti-atom is positronium, consisting of an electron and a positron (e⁻ e⁺) bound in a hydrogen-like configuration without nuclear constituents. The ground state of positronium exists in two spin configurations: the singlet para-positronium (p-Ps), which decays primarily into two photons with a lifetime of 0.125 ns, and the triplet ortho-positronium (o-Ps), which has a longer lifetime of approximately 142 ns and decays into three photons. Positronium's short-lived nature makes it challenging to trap but valuable for studies of quantum electrodynamics (QED) corrections. The simplest baryonic anti-atom is antihydrogen (H̄), comprising an antiproton and a positron (p̄ e⁺), with a binding energy of 13.6 eV identical to that of hydrogen due to the universality of electromagnetic interactions. The first antihydrogen atoms were produced in 1995 at CERN's Low Energy Antiproton Ring (LEAR) by the PS210 experiment, where antiprotons were passed through a positronium cloud, leading to charge exchange and neutral atom formation.^[39] Subsequent advances at the Antiproton Decelerator (AD) enabled the production of cold antihydrogen. In 2002, the ATHENA collaboration reported the creation of approximately 50,000 cold antihydrogen atoms by mixing trapped antiprotons and positrons in a nested Penning trap, with the ATRAP collaboration achieving similar results shortly thereafter.^[40]^[41] By the early 2000s, these efforts had scaled to around 10⁵ antihydrogen atoms per experimental run, facilitating laser spectroscopy experiments to measure spectral lines and test CPT symmetry through comparisons with hydrogen transitions.^[42] As of November 2025, the ALPHA collaboration has further advanced production using positron cooling techniques, achieving rates of up to 2000 antihydrogen atoms per hour and trapping over 15,000 atoms, enhancing precision measurements.^[43] More complex anti-atoms, such as those formed from antihelium nuclei (two antiprotons and two antineutrons) bound to two positrons, are theoretically stable under CPT invariance, with predicted spectral lines identical to those of helium atoms. However, neutral antihelium atoms remain unobserved, primarily due to the extreme rarity of antihelium-4 nuclei production—first detected in 2011 at the Relativistic Heavy Ion Collider with only a handful of events—coupled with the challenges of efficient positron binding and isolation from matter. Upon contact with ordinary matter, anti-atoms annihilate rapidly, releasing energy and posing significant experimental containment challenges.

Annihilation Processes

Mechanism and Cross-Sections

Particle-antiparticle annihilation refers to the irreversible process whereby a particle and its antiparticle interact and convert entirely into other forms of energy, typically photons or lighter particles, governed by the relevant gauge interactions such as electromagnetic, strong, or weak forces. This process requires the particle and antiparticle to approach within a distance comparable to their interaction range, allowing their quantum fields to overlap and facilitate the transformation while conserving quantum numbers like charge, baryon number, and lepton number. The minimum center-of-mass energy for annihilation is

2mc^2

, where

m

is the rest mass of the particle and

c

is the speed of light, representing the threshold where kinetic energy is negligible.^[44]^[45] In the case of electron-positron (

e^+ e^-

) annihilation, the dominant channel at low to moderate energies is the production of two photons (

e^+ e^- \to \gamma \gamma

), mediated by the electromagnetic interaction through virtual photon exchange. This process adheres to conservation laws, including angular momentum, which forbids a single-photon outcome due to parity and charge conjugation invariance, necessitating an even number of photons. At high center-of-mass energies

\sqrt{s} \gg 2m_ec^2

≫2mec2, the total cross-section approximates $\sigma \approx \frac{2\pi \alpha^2}{s} \ln \left( \frac{s}{m_e^2} \right)$ , where $\alpha$ is the fine-structure constant, decreasing as $1/s \ln(s)$ characteristic of point-like QED interactions.^[46]^[47] For hadronic annihilation, such as proton-antiproton ( $p \bar{p}$ ), the process occurs primarily through the strong interaction at the quark level, where constituent quarks and antiquarks annihilate via gluon exchange, leading to the production of multiple pions or other hadrons after hadronization. The total cross-section at low energies (near threshold) is approximately 70 millibarns (mb), reflecting the composite nature and strong binding within hadrons. Angular momentum conservation influences the multiplicity of final-state pions, often resulting in an odd number to match the initial spin and parity.^[48]^[49]

Energy Release and Products

In particle-antiparticle annihilation, the total rest mass energy of the pair is fully converted into other forms of energy, governed by the relation

E = 2 m c^2

, where

m

is the rest mass of the particle and

c

is the speed of light. This energy manifests primarily as kinetic energy of the resulting particles or as electromagnetic radiation in the form of photons. For instance, in the low-energy annihilation of an electron (

m_e \approx 0.511

MeV/

c^2

) and positron, the released energy totals 1.022 MeV, typically distributed as two photons each carrying 0.511 MeV when the particles are at rest.^[50] The products of annihilation vary by particle type and interaction. For lepton-antilepton pairs, such as electron-positron, the process is dominated by electromagnetic interactions, yielding primarily photons; in charge conjugation (C)-conserving scenarios like neutral systems at low energies, two photons are produced with a branching ratio of approximately 99.8% for direct annihilation in matter, while three-photon events occur rarely at about 0.2%.^[51] In contrast, for quark-based hadrons like proton-antiproton pairs, strong interactions lead to multi-pion final states, with an average yield of about 5 pions per event at low energies; the ratio of charged to neutral pions (roughly 2:1) reflects isospin symmetry, ensuring balanced production of

\pi^+

\pi^-

, and

\pi^0

.^[52] For neutrino-antineutrino pairs, annihilation at high center-of-mass energies (

\gg m_Z

) proceeds via the weak interaction to produce an on-shell Z boson, which decays into quarks, leptons, or additional neutrinos; at lower energies, the process involves a virtual Z boson exchange within the Standard Model framework.^[53] These annihilation outcomes produce distinct detection signatures in experiments. In high-energy colliders, hadronic annihilations generate pion showers that evolve into detectable hadronic jets, characterized by pion multiplicities and energy spectra that match expected branching ratios, such as the predominant two-photon channel in low-energy lepton cases.^[54]

Theoretical Framework

Dirac Equation and Hole Theory

In the development of relativistic quantum mechanics, Paul Dirac sought to formulate a wave equation for the electron that was first-order in both space and time derivatives, addressing the limitations of the Klein-Gordon equation, which suffered from non-positive definite probability densities and failed to incorporate electron spin naturally.^[55] Dirac proposed a Hamiltonian of the form

H = c \vec{\alpha} \cdot \vec{p} + \beta m c^2

H=cα

⋅p

+βmc2, where $\vec{\alpha} = (\alpha_x, \alpha_y, \alpha_z)$

=(αx,αy,αz) and $\beta$ are four 4×4 matrices satisfying the anticommutation relations $\{\alpha_i, \alpha_j\} = 2\delta_{ij}$ , $\{\alpha_i, \beta\} = 0$ , and $\beta^2 = 1$ .^[55] This leads to the Dirac equation in Hamiltonian form $i\hbar \frac{\partial \psi}{\partial t} = (c \vec{\alpha} \cdot \vec{p} + \beta m c^2) \psi$

⋅p

+βmc2)ψ, where $\psi$ is a four-component spinor.^[56] To express the equation in covariant form, Dirac introduced the gamma matrices $\gamma^\mu$ (with $\mu = 0,1,2,3$ ), defined such that $\gamma^0 = \beta$ and $\gamma^i = \beta \alpha_i$ , satisfying $\{\gamma^\mu, \gamma^\nu\} = 2 g^{\mu\nu}$ where $g^{\mu\nu}$ is the Minkowski metric.^[57] The resulting Dirac equation is $(i \gamma^\mu \partial_\mu - m) \psi = 0$ in natural units ( $\hbar = c = 1$ ), or more generally $i \hbar \gamma^\mu (\partial_\mu + i e A_\mu) \psi = m c \psi$ in the presence of an electromagnetic field.^[57] For free particles, solutions are plane waves $\psi = u(p) e^{-i p \cdot x / \hbar}$ , where the spinor $u(p)$ satisfies $(\gamma^\mu p_\mu - m c) u(p) = 0$ .^[56] The energy-momentum relation yields eigenvalues $E = \pm \sqrt{p^2 c^2 + m^2 c^4}$

, with positive-energy solutions corresponding to electrons and negative-energy solutions initially posing interpretational challenges, as they implied particles with negative kinetic energy and probability issues.^[55] The four-component spinors consist of two independent two-component spinors for each energy sign: for positive energy, large upper components and small lower components (non-relativistic limit), and vice versa for negative energy, reflecting the coupling of spin-1/2 degrees of freedom.^[58] Dirac's 1928 equation successfully predicted the electron's spin magnetic moment as one Bohr magneton and fine structure in hydrogen, but the negative-energy continuum suggested instabilities, such as electrons cascading to lower states without bound.^[55] To resolve these issues, Dirac developed hole theory in 1930, positing an infinite "sea" of negative-energy electron states completely filled according to the Pauli exclusion principle, rendering them inaccessible to positive-energy electrons.^[3] An absence, or "hole," in this sea behaves as a particle with positive charge $+e$ , positive energy $+|E|$ , and momentum $-\vec{p}$

opposite to that of the missing negative-energy electron, effectively describing the positron as a vacancy propagating through the filled sea.^[3] Pair creation occurs when a high-energy photon perturbs the sea, exciting an electron from a negative-energy state to a positive-energy one, leaving a hole that manifests as an electron-positron pair; the process conserves charge and energy, with the photon's energy exceeding $2 m c^2$ .^[59] This interpretation predicted the existence of antiparticles, later validated by Carl Anderson's 1932 discovery of the positron in cosmic ray tracks.^[60] However, hole theory encountered significant limitations, including the infinite negative energy of the filled sea, which implies an unphysical infinite vacuum energy density divergent as $\int_{-\infty}^0 E \, d^3p$ .^[61] Additionally, interactions between multiple holes proved problematic, as the underlying electrons repel via Coulomb forces, leading to ill-defined attractions between holes that violate charge conjugation symmetry in multi-particle scenarios.^[62] By the 1940s, these conceptual and mathematical difficulties, particularly in handling variable vacuum states and renormalization, prompted the transition to quantum field theory, which reformulated particles as excitations of underlying fields without invoking an infinite sea.^[63]

Quantum Field Theory Formalism

In quantum field theory (QFT), particles and antiparticles emerge as quantized excitations of underlying fields, with the vacuum representing the lowest-energy state devoid of such excitations. Creation and annihilation operators act on this vacuum to generate multi-particle states, enabling a consistent relativistic description that accommodates both particles and their antiparticles on equal footing. This formalism resolves issues inherent in single-particle relativistic quantum mechanics by treating fields as operators in a Fock space, where the number of particles is not fixed. For fermionic fields like the Dirac field describing electrons and positrons, the field operator

\psi(x)

is expanded in terms of plane-wave solutions as

\psi(x) = \int \frac{d^3 p}{(2\pi)^3} \frac{1}{\sqrt{2 E_p}} \sum_s \left[ u^s(p) a^s_p e^{-i p \cdot x} + v^s(p) b^{s \dagger}_p e^{i p \cdot x} \right],

ψ(x)=∫(2π)3d3p2Ep

1s∑[us(p)apse−ip⋅x+vs(p)bps†eip⋅x], where $a^s_p$ annihilates a particle (electron) with momentum $p$ and spin $s$ , while $b^{s \dagger}_p$ creates an antiparticle (positron) with the same quantum numbers, $E_p = \sqrt{\mathbf{p}^2 + m^2}$

is the energy, and the sum runs over spin states. The spinors $u^s(p)$ describe particle states, and $v^s(p)$ represent antiparticle states, which are related to the charge conjugates of the particle spinors via $v^s(p) = i \gamma^2 (u^s(p))^*$ in the Dirac representation. Both components involve positive-frequency solutions, ensuring that particles and antiparticles propagate forward in time with positive energy, distinguishing QFT from earlier interpretations. The antiparticle interpretation arises naturally from the anticommutation relations $\{a^s_p, a^{s' \dagger}_{p'}\} = \delta_{ss'} \delta^3(\mathbf{p} - \mathbf{p}')$ and similarly for $b$ , which enforce Fermi-Dirac statistics and prevent negative-energy states from being occupied in the vacuum. This structure predicts phenomena like pair production, where a high-energy photon can create an electron-positron pair in the presence of a nucleus, with cross-sections calculated perturbatively in quantum electrodynamics (QED) scaling asymptotically as $\sigma \approx \frac{28}{9} Z^2 \alpha r_e^2 \ln \left( \frac{2E}{m c^2} \right) - \frac{109}{42} Z^2 \alpha r_e^2$ in the high-energy limit $E \gg m c^2$ ,^[64] confirming experimental rates to high precision. The Feynman–Stückelberg interpretation further elucidates antiparticles in perturbative calculations and Feynman diagrams, viewing them as ordinary particles propagating backward in time. This equivalence holds because the propagator for a Dirac fermion, $S(p) = \frac{i (\not p + m)}{p^2 - m^2 + i \epsilon},$ is invariant under $p^0 \to -p^0$ and charge conjugation, allowing antiparticle lines to be redrawn as particle lines with reversed time direction without altering amplitudes. Originating from Stückelberg's parametrization of proper time evolution and Feynman's path-integral reformulation, this approach simplifies scattering processes involving antiparticles. QFT resolves the infinities plaguing the Dirac sea model—where all negative-energy states are filled—through renormalization, redefining the vacuum and absorbing divergences into physical parameters like mass and charge without invoking an infinite sea. For neutral particles, such as photons or pions, self-conjugate fields use the real Klein-Gordon equation $(\square + m^2) \phi = 0$ , quantized with a single set of creation and annihilation operators $a_p$ and $a^\dagger_p$ , where particles and antiparticles coincide since charge conjugation leaves the field unchanged. The expansion is $\phi(x) = \int \frac{d^3 p}{(2\pi)^3} \frac{1}{\sqrt{2 E_p}} \left[ a_p e^{-i p \cdot x} + a^\dagger_p e^{i p \cdot x} \right],$

1[ape−ip⋅x+ap†eip⋅x], ensuring identical treatment for self-antiparticles in processes like neutral pion decay.

Applications and Implications

In Medicine and Imaging

One of the primary applications of antiparticles in medicine is positron emission tomography (PET), a nuclear medicine imaging technique that utilizes positrons emitted from radioactive isotopes. In PET, short-lived positron-emitting isotopes such as carbon-11 (¹¹C) and fluorine-18 (¹⁸F) are incorporated into radiotracers and administered to patients, where they decay by emitting positrons that subsequently annihilate with surrounding electrons in tissue, producing pairs of back-to-back 511 keV gamma rays detectable by ring-shaped scintillation detectors to reconstruct three-dimensional images of metabolic activity.^[65]^[66]^[67] These gamma rays enable high-sensitivity functional imaging, with typical spatial resolution of 4-6 mm in clinical PET scanners, limited by factors including detector size and positron physics.^[68]^[69] A common radiotracer is ¹⁸F-fluorodeoxyglucose (FDG), which mimics glucose and accumulates in metabolically active cells, such as those in tumors, allowing PET to detect and stage various cancers including lung, breast, and colorectal malignancies with improved accuracy over conventional imaging.^[70]^[71] Approximately 4 million PET/CT scans are performed annually worldwide as of 2024, with volumes continuing to grow and reflecting the technique's growing role in oncology, cardiology, and neurology diagnostics.^[72] Positron-emitting isotopes for PET are primarily produced in on-site cyclotrons, compact particle accelerators that bombard target materials with protons to generate isotopes like ¹⁸F via nuclear reactions, ensuring short half-lives (e.g., 110 minutes for ¹⁸F) for timely imaging.^[67]^[73] The positrons travel a short distance—typically around 1 mm in soft tissue—before annihilation, which introduces some blurring in the reconstructed image due to the displacement from the isotope's decay site, though this effect is minimized for low-energy emitters like ¹⁸F.^[74]^[75] Beyond PET, antiparticles have been explored in experimental cancer therapies, notably through antiproton beams that deposit energy more effectively in tumors via annihilation. The Antiproton Cell Experiment (ACE) at CERN, conducted from 2003 to 2013, demonstrated that antiprotons are up to four times more biologically effective than protons in killing cells at the beam's Bragg peak, suggesting potential for targeted radiotherapy, though applications remain confined to research due to production challenges.^[76]^[77]^[78]

In Cosmology and Fundamental Physics

The Big Bang theory predicts that matter and antimatter were produced in equal quantities in the early universe, leading to complete annihilation if no asymmetry arose.^[79] However, observations reveal a profound imbalance, with matter dominating by a factor quantified by the baryon-to-photon ratio η ≈ 6 × 10^{-10}, indicating roughly one excess baryon per billion photons. This baryon asymmetry necessitates mechanisms that violate baryon number conservation, C and CP symmetries, and involve out-of-equilibrium processes, as outlined in the Sakharov conditions proposed in 1967.^[80] CP violation, essential for generating the asymmetry, arises in the Standard Model through the complex phase in the Cabibbo-Kobayashi-Maskawa (CKM) matrix governing weak interactions.^[81] Searches for antimatter in the cosmos focus on signatures like diffuse gamma-ray emission from matter-antimatter annihilation at domain boundaries, but no evidence for large-scale antimatter regions has been found. The Fermi Large Area Telescope (LAT), observing gamma rays up to energies of several GeV, has surveyed the sky and detected no such signals indicative of macroscopic antimatter domains comparable to the observable universe's scale.^[82] Instead, observed cosmic gamma rays align with known astrophysical processes, constraining any primordial antimatter fractions to below detectable levels. Ongoing experiments at CERN probe antiparticle properties to test fundamental symmetries relevant to the asymmetry. The ALPHA-g collaboration measured the gravitational acceleration of antihydrogen atoms in 2023, finding they fall toward Earth with an acceleration of 0.75 ± 0.13 (statistical and systematic) ± 0.16 (simulation) times the value for ordinary matter (g = 9.81 m/s²), confirming the weak equivalence principle to within experimental uncertainty.^[83] Similarly, the BASE collaboration's 2025 measurement of the antiproton magnetic moment achieved a precision of 1.5 parts per billion, showing no deviation from the proton's value (apart from sign), thus resolving potential CPT-violating anomalies in baryon properties and supporting Standard Model expectations.^[84] These results bolster the framework for asymmetry generation without invoking exotic violations. Beyond Standard Model CP violation, leptogenesis models propose that the decays of heavy right-handed neutrinos in the early universe produce a lepton asymmetry, which sphaleron processes convert into the observed baryon asymmetry, potentially explaining η through seesaw mechanisms for neutrino masses.^[85] Such scenarios align with the Sakharov conditions by incorporating out-of-equilibrium decays and CP-violating interactions in extended sectors.

History

Media collections

Antiparticle

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Antiparticle

Antiparticle

Historical Development

Theoretical Predictions

Applications and Implications

In Medicine and Imaging

In Cosmology and Fundamental Physics

References

Add your contribution

Related Hubs

Contribute something