Recent from talks
Contribute something
Nothing was collected or created yet.
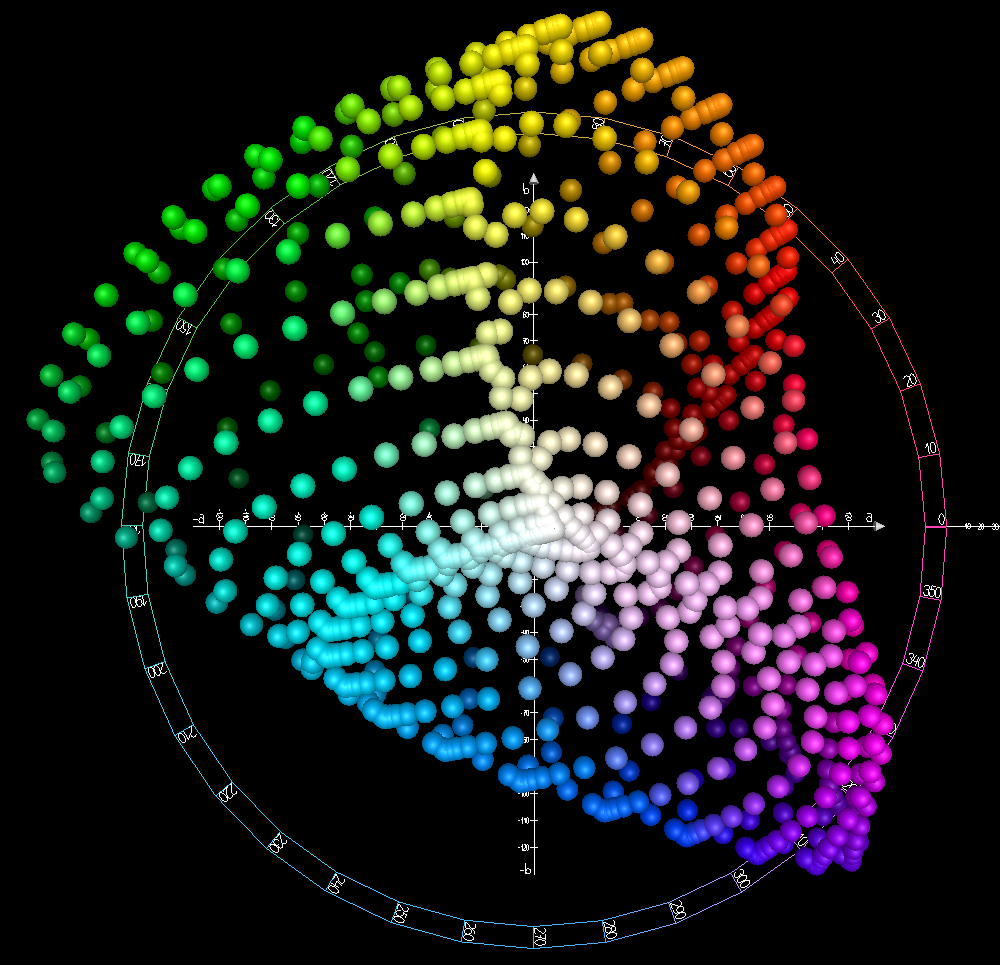
CIELAB color space
View on WikipediaThis article may be too technical for most readers to understand. (November 2010) |



The CIELAB color space, also referred to as L*a*b*, is a color space defined by the International Commission on Illumination (abbreviated CIE) in 1976.[a] It expresses color as three values: L* for perceptual lightness and a* and b* for the four unique colors of human vision: red, green, blue and yellow. CIELAB was intended as a perceptually uniform space, where a given numerical change corresponds to a similar perceived change in color. While the LAB space is not truly perceptually uniform, it nevertheless is useful in industry for detecting small differences in color.
Like the CIEXYZ space it derives from, CIELAB color space is a device-independent, "standard observer" model. The colors it defines are not relative to any particular device such as a computer monitor or a printer, but instead relate to the CIE standard observer which is an averaging of the results of color matching experiments under laboratory conditions.
Coordinates
[edit]The CIELAB space is three-dimensional and covers the entire gamut (range) of human color perception. It is based on the opponent model of human vision, where red and green form an opponent pair and blue and yellow form an opponent pair. This makes CIELAB a Hering opponent color space. The nature of the transformations also characterizes it as a chromatic value color space. The lightness value, L* (pronounced "L star"), defines black at 0 and white at 100. The a* axis is relative to the green–red opponent colors, with negative values toward green and positive values toward red. The b* axis represents the blue–yellow opponents, with negative numbers toward blue and positive toward yellow.
The lightness value, L* in CIELAB is calculated using the cube root of the relative luminance with an offset near black. This results in an effective power curve with an exponent of approximately 0.43 which represents the human eye's response to light under daylight (photopic) conditions.
The a* and b* axes are unbounded and depending on the reference white they can easily exceed ±150 to cover the human gamut. Nevertheless, software implementations often clamp these values for practical reasons. For instance, if integer math is being used it is common to clamp a* and b* in the range of −128 to 127.
CIELAB is calculated relative to a reference white, for which the CIE recommends the use of CIE Standard illuminant D65.[1] D65 is used in the vast majority of industries and applications, with the notable exception being the printing industry which uses D50. The International Color Consortium largely supports the printing industry and uses D50 with either CIEXYZ or CIELAB in the Profile Connection Space, for v2 and v4 ICC profiles.[2]
While the intention behind CIELAB was to create a space that was more perceptually uniform than CIEXYZ using only a simple formula,[3] CIELAB is known to lack perceptual uniformity, particularly in the area of blue hues.[4]
The asterisks (*) after L*, a*, and b* are pronounced star and are part of the full name to distinguish L*a*b* from Hunter's Lab, described below.
Since the L*a*b* model has three axes, it requires a three-dimensional space to be represented completely.[5] Also, because each axis is non-linear, it is not possible to create a two-dimensional chromaticity diagram. Additionally, the visual representations shown in the plots of the full CIELAB gamut on this page are an approximation, as it is impossible for a monitor to display the full gamut of LAB colors.
Perceptual differences
[edit]The nonlinear relations for L*, a* and b* are intended to mimic the nonlinear response of the visual system. Furthermore, uniform changes of components in the L*a*b* color space aim to correspond to uniform changes in perceived color, so the relative perceptual differences between any two colors in L*a*b* can be approximated by treating each color as a point in a three-dimensional space (with three components: L*, a*, b*) and taking the Euclidean distance between them.[6]
RGB and CMYK conversions
[edit]In order to convert RGB or CMYK values to or from L*a*b*, the RGB or CMYK data must be linearized relative to light. The reference illuminant of the RGB or CMYK data must be known, as well as the RGB primary coordinates or the CMYK printer's reference data in the form of a color lookup table (CLUT).
In color managed systems, ICC profiles contains these needed data, which are then used to perform the conversions.
Range of coordinates
[edit]As mentioned previously, the L* coordinate nominally ranges from 0 to 100. The range of a* and b* coordinates is technically unbounded, though it is commonly clamped to the range of −128 to 127 for use with integer code values, though this results in potentially clipping some colors depending on the size of the source color space. The gamut's large size and inefficient utilization of the coordinate space means the best practice is to use floating-point values for all three coordinates.
Advantages
[edit]Unlike the RGB and CMYK color models, CIELAB is designed to approximate human vision. The L* component closely matches human perception of lightness, though it does not take the Helmholtz–Kohlrausch effect into account. CIELAB is less uniform in the color axes, but is useful for predicting small differences in color.
The CIELAB coordinate space represents the entire gamut of human photopic (daylight) vision and far exceeds the gamut for sRGB or CMYK. In an integer implementation such as TIFF, ICC or Photoshop, the large coordinate space results in substantial data inefficiency due to unused code values. Only about 35% of the available coordinate code values are inside the CIELAB gamut with an integer format.[7]
Using CIELAB in an 8-bit per channel integer format typically results in significant quantization errors. Even 16-bit per channel can result in clipping, as the full gamut extends past the bounding coordinate space. Ideally, CIELAB should be used with floating-point data to minimize obvious quantization errors.
CIE standards and documents are copyrighted by the CIE and must be purchased; however, the formulas for CIELAB are available on the CIE website.[8]
Converting between CIELAB and CIE XYZ coordinates
[edit]From CIE XYZ to CIELAB
[edit]where t is or :
X, Y, and Z describe the color stimulus considered and Xn, Yn, Zn describe a specified white achromatic reference illuminant. for the CIE 1931 (2°) standard colorimetric observer and assuming normalization where the reference white has Y = 100, the values are:
For illuminant D50, which is used in the printing industry:
The division of the domain of the f function into two parts was done to prevent an infinite slope at t = 0. The function f was assumed to be linear below some t = t0 and was assumed to match the part of the function at t0 in both value and slope. In other words:
The intercept f(0) = c was chosen so that L* would be 0 for Y = 0: c = 16/116 = 4/29. The above two equations can be solved for m and t0:
where δ = 6/29.[9]
From CIELAB to CIEXYZ
[edit]The reverse transformation is most easily expressed using the inverse of the function f above:
where
and where δ = 6/29.
Cylindrical model
[edit]The "CIELCh" or "CIEHLC" space is a color space based on CIELAB, which uses the polar coordinates C* (chroma, colorfulness of the color) and h° (hue angle, angle of the hue in the CIELAB color wheel) instead of the Cartesian coordinates a* and b*. The CIELAB lightness L* remains unchanged.
The conversion of a* and b* to C* and h° is performed as follows:
Conversely, given the polar coordinates, conversion to Cartesian coordinates is achieved with:
The LCh (or HLC) color space is not the same as the HSV, HSL or HSB color models, although their values can also be interpreted as a base color, saturation and lightness of a color. The HSL values are a polar coordinate transformation of what is technically defined RGB cube color space. LCh is still perceptually uniform.
Further, H and h are not identical, because HSL space uses as primary colors the three additive primary colors red, green and blue (H = 0, 120, 240°). Instead, the LCh system uses the four colors red, yellow, green and blue (h = 0, 90, 180, 270°). Regardless the angle h, C = 0 means the achromatic colors (non saturated), that is, the gray axis.
The simplified spellings LCh, LCh(ab), LCH, LCH(ab) and HLC are common, but the letter presents a different order. HCL color space (Hue-Chroma-Luminance) on the other hand is a commonly used alternative name for the L*C*h(uv) color space, also known as the cylindrical representation or polar CIELUV. This name is commonly used by information visualization practitioners who want to present data without the bias implicit in using varying saturation.[11][12] The name Lch(ab) is sometimes used to differentiate from L*C*h(uv).
Other related color spaces
[edit]A related color space, the CIE 1976 L*u*v* color space (a.k.a. CIELUV), preserves the same L* as L*a*b* but has a different representation of the chromaticity components. CIELAB and CIELUV can also be expressed in cylindrical form (CIELChab[13] and CIELChuv, respectively), with the chromaticity components replaced by correlates of chroma and hue.
Since the work on CIELAB and CIELUV, the CIE has been incorporating an increasing number of color appearance phenomena into their models and difference equations to better predict human color perception. These color appearance models, of which CIELAB is a simple example,[14] culminated with CIECAM02.
Oklab is built on the same spatial structure and achieves greater perceptual uniformity.
Usage
[edit]Some systems and software applications that support CIELAB include:
- CIELAB is used by Datacolor spectrophotometers, including the related color difference calculations.
- CIELAB is used by the PantoneLive library.
- CIELAB is used extensively by X-Rite as a color space with their hardware and software color measuring systems.
- CIELAB D50 is available in Adobe Photoshop, where it is called "Lab mode".[15][16]
- CIELAB is available in Affinity Photo by changing the document's Colour Format to "Lab (16 bit)". The white point, which defaults to D50, can be changed by ICC profile.
- CIELAB D50 is available in ICC profiles as a profile connection space named "Lab color space".[2]
- CIELAB (any white point) is a supported color space in TIFF image files.[17]
- CIELAB (any white point) is available in PDF documents, where it is called the "Lab color space".[18][19]
- CIELAB is an option in Digital Color Meter on macOS described as "L*a*b*".
- CIELAB is available in the RawTherapee photo editor, where it is called the "Lab color space".[20]
- CIELAB is used by GIMP for the hue-chroma adjustment filter, fuzzy-select and paint-bucket. There is also a LCh(ab) color picker.[21]
- Web browser support for CIELAB was introduced as part of CSS Color Module Level 4, and is supported in all major browsers.[22][23]
Hunter Lab
[edit]Hunter Lab (also known as Hunter L,a,b) is a color space defined in 1948[24][25] by Richard S. Hunter. It was designed to be computed via simple formulas from the CIEXYZ space, but to be more perceptually uniform. Hunter named his coordinates L, a and b.
Hunter Lab was a precursor to CIELAB, created in 1976 by the International Commission on Illumination (CIE), which named the coordinates for CIELAB as L*, a*, b* to distinguish them from Hunter's coordinates.[24][25]See also
[edit]Notes
[edit]- ^ Referring to CIELAB as "Lab" without asterisks should be avoided to prevent confusion with Hunter Lab.
References
[edit]- ^ CIE Colorimetry 15 (Third ed.). CIE. 2004. ISBN 3-901-906-33-9.
- ^ a b International Color Consortium, Specification ICC.1:2004-10 (Profile version 4.2.0.0) Image technology color management — Architecture, profile format and data structure, (2006).
- ^ MacEvoy, Bruce. "Explanation of this history".
- ^ A discussion and proposed improvement, Bruce Lindbloom
- ^ 3D representations of the L*a*b* gamut, Bruce Lindbloom.
- ^ Jain, Anil K. (1989). Fundamentals of Digital Image Processing. New Jersey, United States of America: Prentice Hall. pp. 68, 71, 73. ISBN 0-13-336165-9.
- ^ "LAB Integer Gamut —Bruce Lindbloom". brucelindbloom.com. Retrieved 2020-12-12.
- ^ "CIELAB Formula". CIE Terms List. Retrieved 2024-05-10.
- ^ János Schanda (2007). Colorimetry. Wiley-Interscience. p. 61. ISBN 978-0-470-04904-4.
- ^ "CIE 1976 L*a*b* colour space | eilv". eilv.cie.co.at. Archived from the original on 2019-12-28. Retrieved 2020-12-12.
- ^ Zeileis, Achim; Hornik, Kurt; Murrell, Paul (2009). "Escaping RGBland: Selecting Colors for Statistical Graphics" (PDF). Computational Statistics & Data Analysis. 53 (9): 3259–3270. doi:10.1016/j.csda.2008.11.033.
- ^ Stauffer, Reto; Mayr, Georg J.; Dabernig, Markus; Zeileis, Achim (2015). "Somewhere over the Rainbow: How to Make Effective Use of Colors in Meteorological Visualizations" (PDF). Bulletin of the American Meteorological Society. 96 (2): 203–216. Bibcode:2015BAMS...96..203S. doi:10.1175/BAMS-D-13-00155.1. hdl:10419/101098.
- ^ CIE-L*C*h Color Scale
- ^ Fairchild, Mark D. (2005). "Color and Image Appearance Models". Color Appearance Models. John Wiley and Sons. p. 340. ISBN 0-470-01216-1.
- ^ Margulis, Dan (2006). Photoshop Lab Color: The Canyon Conundrum and Other Adventures in the Most Powerful Colorspace. Berkeley, Calif. : London: Peachpit; Pearson Education. ISBN 0-321-35678-0.
- ^ The Lab Color Mode in Photoshop, Adobe TechNote 310838
- ^ TIFF: Revision 6.0 Archived 2000-08-15 at the Wayback Machine Adobe Developers Association, 1992
- ^ Color Consistency and Adobe Creative Suite Archived 2008-07-25 at the Wayback Machine
- ^ Adobe Acrobat Reader 4.0 User Guide "The color model Acrobat Reader uses is called CIELAB…"
- ^ "Lab Adjustments - RawPedia". rawpedia.rawtherapee.com. Retrieved 2018-05-08.[self-published source?]
- ^ "2.6. More use for CIE LAB and CIE LCH". docs.gimp.org.
- ^ "Color Module Level 4". w3.org. Retrieved 2023-10-06.
- ^ "lab() - CSS: Cascading Style Sheets MDN". developer.mozilla.org. Retrieved 2023-10-06.
- ^ a b Hunter, Richard Sewall. "Photoelectric Color-Difference Meter". p. 661. In: "Minutes of the Thirty-First Meeting of the Board of Directors of the Optical Society of America, Incorporated". Journal of the Optical Society of America. 38 (7): 651. July 1948. doi:10.1364/JOSA.38.000651.
- ^ a b Hunter, Richard Sewall. "Accuracy, Precision, and Stability of New Photo-electric Color-Difference Meter". p. 1094. In: "Proceedings of the Thirty-Third Annual Meeting of the Optical Society of America". Journal of the Optical Society of America. 38 (12): 1092–1106. December 1948. doi:10.1364/JOSA.38.001092.
External links
[edit]- Demonstrative color conversion applet
- CIE Colorimetry 15-3 CIE Technical Report Colorimetry 15 third edition (2004). An authoritative reference.
- Whitepaper on understanding colors by X-rite.

![{\displaystyle {\begin{aligned}L^{\star }&=116\,f{{\bigl (}Y/Y_{\mathrm {n} }{\bigr )}}-16,\\[5mu]a^{\star }&=500{\bigl (}f(X/X_{\mathrm {n} })-f(Y/Y_{\mathrm {n} }){\bigr )}\\[5mu]b^{\star }&=200{\bigl (}f(Y/Y_{\mathrm {n} })-f(Z/Z_{\mathrm {n} }){\bigr )}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1ab8e1ba543c6875c7b209476f70fadd48d163a)



![{\displaystyle {\begin{aligned}f(t)&={\begin{cases}{\sqrt[{3}]{t}}&{\text{if }}t>\delta ^{3}\\[4mu]{\tfrac {1}{3}}t\delta ^{-2}+{\tfrac {4}{29}}&{\text{otherwise}}\end{cases}}\\\delta &={\tfrac {6}{29}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aad1d2c8f4c9d68d224d4dbdd46b0bd4057358ff)


![{\displaystyle {\sqrt[{3}]{t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9fd62ad2781d2a017e6fc7f3ea4bc494a22d058)
![{\displaystyle {\begin{aligned}{\sqrt[{3}]{t_{0}}}&=mt_{0}+c&{\text{ (match in value)}}\\[3mu]{\tfrac {1}{3}}\left(t_{0}\right)^{-2/3}&=m&{\text{ (match in slope)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a4533febf64c603011068fe676e57985207ea15)






