Hubbry Logo
Binary decision diagramBinary decision diagramMain
Open search
Binary decision diagram
Community hub
Binary decision diagram
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Binary decision diagram
Binary decision diagram
Binary decision diagram
View on Wikipedia
from Wikipedia

In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.

Similar data structures include negation normal form (NNF), Zhegalkin polynomials, and propositional directed acyclic graphs (PDAG).

Definition

[edit]

A Boolean function can be represented as a rooted, directed, acyclic graph, which consists of several (decision) nodes and two terminal nodes. The two terminal nodes are labeled 0 (FALSE) and 1 (TRUE). Each (decision) node is labeled by a Boolean variable and has two child nodes called low child and high child. The edge from node to a low (or high) child represents an assignment of the value FALSE (or TRUE, respectively) to variable . Such a BDD is called 'ordered' if different variables appear in the same order on all paths from the root. A BDD is said to be 'reduced' if the following two rules have been applied to its graph:

  • Merge any isomorphic subgraphs.
  • Eliminate any node whose two children are isomorphic.

In popular usage, the term BDD almost always refers to Reduced Ordered Binary Decision Diagram (ROBDD in the literature, used when the ordering and reduction aspects need to be emphasized). The advantage of an ROBDD is that it is canonical (unique up to isomorphism) for a particular function and variable order.[1] This property makes it useful in functional equivalence checking and other operations like functional technology mapping.

A path from the root node to the 1-terminal represents a (possibly partial) variable assignment for which the represented Boolean function is true. As the path descends to a low (or high) child from a node, then that node's variable is assigned to 0 (respectively 1).

Example

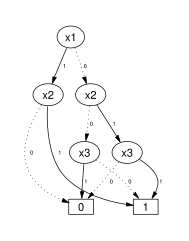
[edit]

The left figure below shows a binary decision tree (the reduction rules are not applied), and a truth table, each representing the function . In the tree on the left, the value of the function can be determined for a given variable assignment by following a path down the graph to a terminal. In the figures below, dotted lines represent edges to a low child, while solid lines represent edges to a high child. Therefore, to find , begin at x1, traverse down the dotted line to x2 (since x1 has an assignment to 0), then down two solid lines (since x2 and x3 each have an assignment to one). This leads to the terminal 1, which is the value of .

The binary decision tree of the left figure can be transformed into a binary decision diagram by maximally reducing it according to the two reduction rules. The resulting BDD is shown in the right figure.

Binary decision tree and truth table for the function , described in notation for Boolean operators.
BDD for the function f

Another notation for writing this Boolean function is .

Complemented edges

[edit]
Representation of a binary decision diagram using complemented edges

An ROBDD can be represented even more compactly, using complemented edges, also known as complement links.[2][3] The resulting BDD is sometimes known as a typed BDD[4] or signed BDD. Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.

Two advantages of using complemented edges when representing BDDs are:

  • computing the negation of a BDD takes constant time
  • space usage (i.e., required memory) is reduced (by a factor at most 2)

However, Knuth[5] argues otherwise:

Although such links are used by all the major BDD packages, they are hard to recommend because the computer programs become much more complicated. The memory saving is usually negligible, and never better than a factor of 2; furthermore, the author's experiments show little gain in running time.

A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.

For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.

An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., . Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.

History

[edit]

The basic idea from which the data structure was created is the Shannon expansion. A switching function is split into two sub-functions (cofactors) by assigning one variable (cf. if-then-else normal form). If such a sub-function is considered as a sub-tree, it can be represented by a binary decision tree. Binary decision diagrams (BDDs) were introduced by C. Y. Lee,[6] and further studied and made known by Sheldon B. Akers[7] and Raymond T. Boute.[8] Independently of these authors, a BDD under the name "canonical bracket form" was realized Yu. V. Mamrukov in a CAD for analysis of speed-independent circuits.[9] The full potential for efficient algorithms based on the data structure was investigated by Randal Bryant at Carnegie Mellon University: his key extensions were to use a fixed variable ordering (for canonical representation) and shared sub-graphs (for compression). Applying these two concepts results in an efficient data structure and algorithms for the representation of sets and relations.[10][11] By extending the sharing to several BDDs, i.e. one sub-graph is used by several BDDs, the data structure Shared Reduced Ordered Binary Decision Diagram is defined.[2] The notion of a BDD is now generally used to refer to that particular data structure.

In his video lecture Fun With Binary Decision Diagrams (BDDs),[12] Donald Knuth calls BDDs "one of the only really fundamental data structures that came out in the last twenty-five years" and mentions that Bryant's 1986 paper was for some time one of the most-cited papers in computer science.

Adnan Darwiche and his collaborators have shown that BDDs are one of several normal forms for Boolean functions, each induced by a different combination of requirements. Another important normal form identified by Darwiche is decomposable negation normal form or DNNF.

Applications

[edit]

BDDs are extensively used in CAD software to synthesize circuits (logic synthesis) and in formal verification. There are several lesser known applications of BDD, including fault tree analysis, Bayesian reasoning, product configuration, and private information retrieval.[13][14][citation needed]

Every arbitrary BDD (even if it is not reduced or ordered) can be directly implemented in hardware by replacing each node with a 2 to 1 multiplexer; each multiplexer can be directly implemented by a 4-LUT in a FPGA. It is not so simple to convert from an arbitrary network of logic gates to a BDD[citation needed] (unlike the and-inverter graph).

BDDs have been applied in efficient Datalog interpreters.[15]

Variable ordering

[edit]

The size of the BDD is determined both by the function being represented and by the chosen ordering of the variables. There exist Boolean functions for which depending upon the ordering of the variables we would end up getting a graph whose number of nodes would be linear (in n) at best and exponential at worst (e.g., a ripple carry adder). Consider the Boolean function Using the variable ordering , the BDD needs nodes to represent the function. Using the ordering , the BDD consists of nodes.

BDD for the function ƒ(x1, ..., x8) = x1x2 + x3x4 + x5x6 + x7x8 using bad variable ordering
Good variable ordering

It is of crucial importance to care about variable ordering when applying this data structure in practice. The problem of finding the best variable ordering is NP-hard.[16] For any constant c > 1 it is even NP-hard to compute a variable ordering resulting in an OBDD with a size that is at most c times larger than an optimal one.[17] However, there exist efficient heuristics to tackle the problem.[18]

There are functions for which the graph size is always exponential—independent of variable ordering. This holds e.g. for the multiplication function.[1] In fact, the function computing the middle bit of the product of two -bit numbers does not have an OBDD smaller than vertices.[19] (If the multiplication function had polynomial-size OBDDs, it would show that integer factorization is in P/poly, which is not known to be true.[20]) Another notorious example is the hidden weight bit function, regarded as the simplest function with an exponential-sized BDD.[21]

Researchers have suggested refinements on the BDD data structure giving way to a number of related graphs, such as BMD (binary moment diagrams), ZDD (zero-suppressed decision diagrams), FBDD (free binary decision diagrams), FDD (functional decision diagrams), PDD (parity decision diagrams), and MTBDDs (multiple terminal BDDs).

Logical operations on BDDs

[edit]

Many logical operations on BDDs can be implemented by polynomial-time graph manipulation algorithms:[22]: 20 

However, repeating these operations several times, for example forming the conjunction or disjunction of a set of BDDs, may in the worst case result in an exponentially big BDD. This is because any of the preceding operations for two BDDs may result in a BDD with a size proportional to the product of the BDDs' sizes, and consequently for several BDDs the size may be exponential in the number of operations. Variable ordering needs to be considered afresh; what may be a good ordering for (some of) the set of BDDs may not be a good ordering for the result of the operation. Also, since constructing the BDD of a Boolean function solves the NP-complete Boolean satisfiability problem and the co-NP-complete tautology problem, constructing the BDD can take exponential time in the size of the Boolean formula even when the resulting BDD is small.

Computing existential abstraction over multiple variables of reduced BDDs is NP-complete.[23]

Model-counting, counting the number of satisfying assignments of a Boolean formula, can be done in polynomial time for BDDs. For general propositional formulas the problem is ♯P-complete and the best known algorithms require an exponential time in the worst case.

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Binary decision diagram

View on Grokipedia
from Grokipedia
A binary decision diagram (BDD) is a that represents a as a rooted, consisting of decision nodes labeled by variables and two terminal nodes labeled 0 and 1, where each decision node has two outgoing edges corresponding to the variable's low (0) and high (1) values. The structure ensures that variables appear in a fixed order along any path from the root to a terminal, and it can be reduced by eliminating redundant nodes where both children are identical or by merging isomorphic subgraphs, resulting in a unique known as a reduced ordered binary decision diagram (ROBDD). The concept of BDDs originated with C. Y. Lee's 1959 work on representing switching circuits using binary-decision programs, which modeled logical functions as decision trees that could be shared for efficiency. This idea was further developed by S. B. Akers in 1978, who formalized binary decision diagrams as a compact method for defining, analyzing, and implementing large digital functions through directed acyclic graphs. The framework gained prominence through Randal E. Bryant's 1986 introduction of graph-based algorithms for manipulating ROBDDs, which provided polynomial-time operations for Boolean functions under fixed variable ordering, enabling practical computation for functions with hundreds of variables. BDDs are fundamental in (CAD) due to their ability to support efficient symbolic manipulation of Boolean functions, including operations like conjunction, disjunction, , and quantification, all performed in time proportional to the product of the sizes of the input diagrams. Their canonical representation facilitates straightforward equivalence checking and model counting, making them essential for applications such as of hardware circuits, where they encode state transitions and constraints to prove properties like or without exhaustive enumeration. Beyond verification, BDDs are employed in logic synthesis for technology mapping and optimization, as well as in areas like , probabilistic , and satisfiability solving, though their size can grow exponentially with poor variable ordering, prompting extensions like edge-valued or multi-terminal variants.

Fundamentals

Definition

A binary decision diagram (BDD) is a rooted, (DAG) used to represent a of n variables, where the vertex set consists of nonterminal vertices (decision nodes) and terminal vertices. Each decision node is labeled with a variable index v from the set {1, ..., n} and has two outgoing edges: a low edge (labeled 0) to the child low(v) and a high edge (labeled 1) to the child high(v), both of which are other vertices in the graph. The terminal vertices are labeled with values 0 (false) or 1 (true), and no decision node points to itself or creates a cycle, ensuring the acyclic property. The structure of a BDD is recursively defined based on the Shannon expansion theorem, which decomposes a f(x_1, ..., x_n) at variable x_i as: f(x1,…,xn)=xˉi⋅f∣xi=0+xi⋅f∣xi=1f(x_1, \dots, x_n) = \bar{x}_i \cdot f|_{x_i=0} + x_i \cdot f|_{x_i=1} where xˉi\bar{x}_i denotes the of x_i, and f∣xi=bf|_{x_i=b} is the cofactor of f with x_i fixed to b ∈ {0,1}. This expansion corresponds to traversing the low or high edge from the decision node for x_i, leading to subgraphs representing the cofactors, until reaching a terminal node that evaluates the function for a given input assignment. A specific form known as the reduced ordered binary decision diagram (ROBDD) imposes two key restrictions: variables appear in a fixed linear order along any path from to terminal (ordered), and no decision node has identical low and high children, with isomorphic subgraphs shared to eliminate (reduced). Under a fixed variable ordering, ROBDDs provide a representation, meaning that every has a unique ROBDD, and two ROBDDs represent the same function if and only if they are isomorphic as graphs. ROBDDs inherit basic properties from general BDDs, including that any over a of variables has a finite BDD representation, as the graph size is bounded by the number of possible subfunctions. Equivalent functions yield isomorphic BDDs, enabling efficient equivalence checking by structural comparison rather than exhaustive evaluation.

Example

To illustrate the construction of a binary decision diagram (BDD), consider the three-variable Boolean function representing odd parity, f(x,y,z)=x′y′z+x′yz′+xy′z′+xyzf(x, y, z) = x'y'z + x'yz' + xy'z' + xyz, where the prime denotes . This function evaluates to true for input combinations with an odd number of 1s: specifically, the minterms 001, 010, 100, and 111. Assume a fixed variable ordering x>y>zx > y > z, meaning decisions are made first on xx, then yy, and finally zz. The BDD is built recursively via Shannon decomposition: f=x⋅fx=1+x′⋅fx=0f = x \cdot f_{x=1} + x' \cdot f_{x=0}, where fx=1f_{x=1} and fx=0f_{x=0} are the cofactors obtained by substituting x=1x = 1 and x=0x = 0, respectively. The cofactor fx=0=y⊕z=y′z+yz′f_{x=0} = y \oplus z = y'z + yz'. Decomposing further on yy: fx=0,y=0=zf_{x=0, y=0} = z and fx=0,y=1=z′f_{x=0, y=1} = z'. Thus, the low branch from the root xx-node leads to a yy-node whose low child is a zz-node (low edge to 0-terminal, high to 1-terminal) and high child is a z′z'-node (low to 1-terminal, high to 0-terminal). The cofactor fx=1=y⊙z=y′z′+yzf_{x=1} = y \odot z = y'z' + yz (where ⊙\odot denotes XNOR). Decomposing on yy: fx=1,y=0=z′f_{x=1, y=0} = z' and fx=1,y=1=zf_{x=1, y=1} = z. Thus, the high branch from the root leads to another yy-node whose low child is the z′z'-node and high child is the zz-node. In the resulting diagram, the is an xx-node with a low edge to one yy-node and a high edge to a distinct yy-node. These yy-nodes branch to shared zz- and z′z'-nodes, which connect to the 0- and 1-terminals. Path compression occurs through subgraph sharing: the zz-node (low: 0, high: 1) and z′z'-node (low: 1, high: 0) are common substructures referenced by both yy-nodes, avoiding duplication. Each path from the to a 1-terminal corresponds to a minterm of the function. For instance, the path xx-low → yy-low → zz-high traces the assignment x=0,y=0,z=1x=0, y=0, z=1 (minterm x′y′zx'y'z), while xx-high → yy-high → zz-high traces x=1,y=1,z=1x=1, y=1, z=1 (minterm xyzxyz). Paths to the 0-terminal represent the complementary minterms (000, 011, 101, 110). This path-based evaluation directly encodes the function's in graphical form. Before reduction, the full decision tree would require 7 non-terminal nodes (1 for xx, 2 for yy, 4 for zz) due to separate copies of the terminal subtrees under each branch. After applying reduction rules—eliminating duplicate subgraphs—the shared zz- and z′z'-nodes reduce the non-terminal count to 5 (1 xx-node, 2 yy-nodes, 2 zz-nodes), plus 2 terminals, demonstrating how BDDs compactly represent the function through detection.

Variants

Reduced Ordered BDDs

An ordered binary decision diagram (OBDD) is a binary decision diagram in which the variables appear in a fixed linear order along each path from the root to a , with no variable repeating on any path. This ordering ensures that the decision nodes for each variable are encountered in a consistent , typically indexed from 1 to n for n variables, where the index of a node is strictly less than the indices of its children. To achieve a canonical representation, OBDDs are reduced by applying two key rules: first, merging any isomorphic subgraphs, meaning distinct nodes with identical structures and labels (including child pointers) are replaced by a single shared node; second, eliminating redundant nodes where the low and high children are the same, as such a node does not depend on its variable and can be bypassed. These reductions transform the OBDD into a that is minimal in size while preserving the represented . The resulting structure, known as a reduced ordered binary decision diagram (ROBDD), ensures no further applications of these rules are possible. A fundamental property of ROBDDs is their : for a given variable ordering, every has exactly one ROBDD representation, up to . This implies that two ROBDDs represent the same function their root nodes are identical, as the reduction process eliminates all non-canonical variations. Formally, if ff and gg are functions with ROBDDs having roots rfr_f and rgr_g, then f≡gf \equiv g if rf=rgr_f = r_g. This theorem enables efficient equivalence checking by simple pointer comparison rather than full function evaluation.

Complemented Edge BDDs

Complemented edge binary decision diagrams (BDDs) extend reduced ordered BDDs by incorporating complemented edges, where the low (0) edge from a node can be marked as complemented, often denoted as 0ˉ\bar{0}, to represent the of the subfunction it points to. This feature allows a single subgraph to represent both a and its complement, avoiding the need for duplicate structures in standard BDDs. The negation operation on a complemented edge BDD is performed in constant time by inverting the complement attribute at the root node, which effectively flips the polarity of the entire represented function without reconstructing the . Modified reduction rules ensure canonicity: during the check, subgraphs are considered equivalent if they match exactly or if one is the complement of the other, eliminating redundant nodes and obviating the need for a separate negative terminal—only the positive terminal (1) is required, with 1ˉ\bar{1} represented via a complemented edge to it. By enabling subgraph sharing for complementary functions, this variant improves space efficiency, potentially reducing the total number of nodes by up to a factor of two in representations involving frequent negations. In particular, for circuits with many XOR operations, which rely heavily on complements, complemented edge BDDs minimize duplication, leading to substantial memory savings during construction and manipulation. For example, the ROBDD for a function f=s⋅d1+sˉ⋅d0f = s \cdot d_1 + \bar{s} \cdot d_0 consists of a root node for ss with a high edge to d1d_1 and a low edge to d0d_0. To represent the complement f′f', the complemented edge variant simply applies a complement mark to the root's incoming edge, inverting the polarity and reusing the same subgraph structure without additional nodes.

Multiterminal and Zero-Suppressed BDDs

Multiterminal binary decision diagrams (MTBDDs) extend standard binary decision diagrams by allowing terminal nodes to hold arbitrary values, such as integers or real numbers, rather than just 0 or 1. This generalization enables the compact representation of multi-output functions, arithmetic circuits, and matrix operations, where the value at each terminal corresponds to the function's output for a given input path. For instance, MTBDDs can efficiently encode the weights or coefficients in expressions or the entries in dense matrices, leveraging the shared substructure of decision diagrams to reduce storage. The structure maintains the ordered variable traversal of reduced ordered BDDs (ROBDDs) but replaces the binary terminals with a of distinct values, ensuring through reduction rules that eliminate redundant nodes where both children are identical. Zero-suppressed binary decision diagrams (ZDDs) represent a variant optimized for encoding families of sparse sets or combinations, such as subsets in combinatorial problems, by applying a specialized reduction rule. In ZDDs, a node for variable xix_i is deleted if its low child (corresponding to xi=0x_i = 0) points to the zero-terminal, preventing the representation of paths that exclude elements unless necessary. This rule contrasts with standard BDD reduction, which skips nodes only when low and high children are identical, allowing ZDDs to compactly store sparse structures like all kk-subsets of an nn-element set without enumerating dense functions. The resulting diagram is isomorphic to the set family it represents, with paths from root to the one-terminal corresponding exactly to valid combinations. The key differences between MTBDDs and ZDDs lie in their terminal semantics and reduction strategies: MTBDDs generalize to non-binary values for multi-valued functions while preserving Boolean-like operations, whereas ZDDs modify the suppression rule to eliminate zero-low nodes, enabling efficient and manipulation without the overhead of representing absent elements. This distinction makes ZDDs particularly suited for set-theoretic operations, such as union or of combinatorial families, where the diagram size scales logarithmically with the number of sets rather than exponentially. In contrast to complemented-edge BDDs, which optimize binary negation, both MTBDDs and ZDDs address non-standard domains—multi-output or sparse—by altering terminal handling and node elimination criteria. Recent advancements since 2020 have applied MTBDDs to quantum circuit simulation. For example, MTBDD-based simulators with symbolic execution and loop summarization accelerate the evaluation of quantum gate operations, achieving several orders of magnitude speedup on iterative circuits like Grover's algorithm compared to state-of-the-art simulators.

Historical Development

Origins and Early Work

The foundational concepts underlying binary decision diagrams emerged from early work in switching theory, particularly Claude Shannon's 1938 master's thesis, "A Symbolic Analysis of Relay and Switching Circuits." In this work, Shannon applied Boolean algebra to model the behavior of relay networks symbolically, demonstrating how switching functions could be analyzed and synthesized using logical expressions rather than physical trial-and-error. This approach provided the theoretical groundwork for decomposing Boolean functions into decision-based structures, influencing subsequent graphical representations of logic circuits. A significant advancement came in 1959 with C. Y. Lee's invention of binary-decision programs, the first explicit structure resembling a binary decision diagram, designed for minimizing relay contact networks in switching circuits. Lee's method represented a switching function as a binary tree, where each internal node tests a binary variable (e.g., a contact's state), with branches leading to sub-programs that resolve the function recursively until reaching a terminal decision (true or false). This tree-based approach enabled systematic enumeration of contact configurations and optimization for minimal series-parallel networks, offering a practical tool for circuit design at Bell Laboratories. Early binary-decision structures, including Lee's programs, suffered from key limitations: they lacked mechanisms for sharing common subgraphs across branches, resulting in redundant computations and exponential space complexity for functions with many variables, particularly without a consistent variable ordering to guide the . Preceding modern refinements, S. B. Akers advanced these ideas in with his introduction of binary decision diagrams as graphical models for digital functions, emphasizing path-based representations that allowed multiple paths to converge on shared decision points. Akers' diagrams served as direct precursors to shared directed acyclic graphs, facilitating analysis and functional testing of while highlighting the potential for compact representations despite persistent space challenges in unrestricted forms.

Modern Advancements

A pivotal advancement in the field of binary decision diagrams (BDDs) came in 1986 with Randal E. Bryant's introduction of reduced ordered BDDs (ROBDDs), which impose a fixed variable ordering and ensure unique representation of subgraphs through sharing and reduction rules. This structure allows for canonical representations of Boolean functions, enabling manipulation operations such as conjunction and quantification to be performed in polynomial time relative to the size of the diagram. In the 1990s, extensions broadened the applicability of BDDs. Complemented edges were introduced in 1990 by Brace, Rudell, and Bryant, permitting efficient representation of function negations by marking edges without duplicating nodes, thereby reducing memory usage by up to a factor of two while maintaining constant-time negation. Multi-terminal BDDs (MTBDDs), proposed by Coudert et al. in 1993, generalize BDDs to represent multi-valued functions and matrices by allowing multiple terminals, facilitating applications in numerical computations and algebraic manipulations. Similarly, zero-suppressed BDDs (ZDDs), developed by Minato in 1993, optimize for sparse sets by suppressing nodes where the zero-child leads to the zero function, enhancing compactness for combinatorial problems. From the 2000s to the 2020s, BDDs integrated with other paradigms, including Boolean satisfiability (SAT) solvers, as exemplified by McMillan's 2003 work combining BDDs with CNF representations for hybrid solving in verification tasks. In , decision diagrams evolved into variants like quantum MDDs (QMDDs) by and Thornton in 2006. A notable 2024 contribution by Méaux and Seuré revisited the hidden weight bit function (HWBF), a benchmark for BDD complexity, proposing a quadratic variant with enhanced cryptographic resistance while preserving high BDD sizes against structural attacks. These developments marked a shift from theoretical constructs to practical tools in (EDA), where BDDs underpin and synthesis in industry-standard flows. Ongoing research focuses on scalable variants, such as multi-core implementations like HermesBDD by Capogrosso et al. in 2023, to handle challenges in verification of large-scale systems.

Construction and Operations

Building BDDs

Binary decision diagrams (BDDs) are constructed from expressions or truth tables using algorithms that leverage the Shannon expansion theorem, which decomposes a function ff with respect to a variable xix_i as f=xifxi=1+xi‾fxi=0f = x_i f_{x_i=1} + \overline{x_i} f_{x_i=0}, where fxi=bf_{x_i=b} denotes the cofactor obtained by setting xi=bx_i = b. This recursive decomposition forms the basis for building the diagram top-down, starting from the root variable and proceeding to terminal nodes (0 or 1). The process ensures sharing of subgraphs through , avoiding redundant computations. The core of the recursive construction is the If-Then-Else (ITE) operator, defined as ITE(x,f1,f0)=xf1+x‾f0\mathrm{ITE}(x, f_1, f_0) = x f_1 + \overline{x} f_0, which directly corresponds to the Shannon expansion for variable xx. To build a BDD for a function ff, the algorithm recursively applies ITE: if ff is constant, return the terminal node; otherwise, select the next variable xix_i in the ordering, compute the BDDs for the cofactors f1=f∣xi=1f_1 = f|_{x_i=1} and f0=f∣xi=0f_0 = f|_{x_i=0}, and create a new decision node with low child f0f_0, high child f1f_1, and variable xix_i. A unique table, typically implemented as a hash table mapping triples (xi,f0,f1)(x_i, f_0, f_1) to existing nodes, enforces sharing and reduction by returning a preexisting node if one matches, or inserting a new one otherwise. This top-down approach has a time complexity bounded by the size of the resulting BDD, often O(2k)O(2^k) in the worst case for kk variables, but efficient in practice due to memoization. The following pseudocode outlines the recursive build function for a Boolean expression, assuming a fixed variable ordering and access to the unique table:

function Build(f, vars): if f is constant c: return terminal(c) if f is already memoized: return memo[f] xi = next variable in vars for f f1 = Build(f|_{xi=1}, vars) f0 = Build(f|_{xi=0}, vars) node = UniqueTable.lookup(xi, f0, f1) if node is null: node = new Node(xi, f0, f1) UniqueTable.insert(xi, f0, f1, node) memo[f] = node return node

function Build(f, vars): if f is constant c: return terminal(c) if f is already memoized: return memo[f] xi = next variable in vars for f f1 = Build(f|_{xi=1}, vars) f0 = Build(f|_{xi=0}, vars) node = UniqueTable.lookup(xi, f0, f1) if node is null: node = new Node(xi, f0, f1) UniqueTable.insert(xi, f0, f1, node) memo[f] = node return node

This algorithm constructs a reduced ordered BDD (ROBDD) directly, as the unique table ensures no duplicate nodes exist for the same variable and children. An alternative bottom-up approach constructs the BDD from a truth table by iteratively inserting minterms (assignments where f=1f = 1) and applying reduction rules on-the-fly. Starting with the terminal nodes, each minterm is added as a path through the diagram following the variable order, creating intermediate nodes as needed and merging with existing ones via the unique table to eliminate redundancies (e.g., nodes with identical children or where low and high branches are the same). For a truth table with 2n2^n entries, this method processes each minterm in time proportional to the path length O(n)O(n), but the total complexity can reach O(2nn)O(2^n n) without sharing; in practice, sharing keeps it efficient for many functions. This approach is particularly useful when the function is given explicitly as a list of satisfying assignments.

Logical Operations

Binary decision diagrams (BDDs) support efficient manipulation through a suite of algorithms for logical operations, leveraging their structure to represent and combine functions compactly. The core approach for binary operations, such as conjunction (AND) and disjunction (OR), employs the algorithm, which recursively applies the operator to corresponding subgraphs while exploiting sharing via unique tables to avoid redundant computations. In the Apply algorithm, for two BDDs G1G_1 and G2G_2 representing functions f1f_1 and f2f_2, the result of f1⊕f2f_1 \oplus f_2 (where ⊕\oplus denotes the binary operator, e.g., ∧\land for AND) is computed by vertices level-wise according to the variable ordering. At terminal vertices, the operator is evaluated directly on their values (0 or 1). For non-terminal vertices u1u_1 in G1G_1 and u2u_2 in G2G_2 at the same variable xix_i, the follows the Shannon cofactors: the low child of the result is low(u1)⊕low(u2)\text{low}(u_1) \oplus \text{low}(u_2), and the high child is high(u1)⊕high(u2)\text{high}(u_1) \oplus \text{high}(u_2). A unique table, often implemented as a , stores pairs of child vertices to identify and reuse identical subgraphs, ensuring the resulting BDD remains reduced and . This "apply-to-all" strategy systematically traverses all relevant vertex pairs, with early termination possible if the operator yields a constant (e.g., 0 for AND when one operand is 0), further . Negation of a BDD representing function ff can be performed in linear time by applying the XOR operator with the constant 1 BDD, which traverses the graph once using the Apply framework. However, in variants using complemented edges—where edges are annotated to indicate the complemented form of the target subgraph—negation requires only constant time by flipping the complement attribute at the root node, without altering the graph structure. This optimization halves potential vertex duplication by sharing a function and its complement, and it is implemented in established BDD packages like BRB. Without complemented edges, negation is performed by applying the XOR operation with the constant 1 BDD using the Apply framework, which traverses the graph once to build the negated BDD in time linear in the graph size. Quantification operations eliminate variables from a BDD, useful for abstraction in verification. Existential quantification ∃xi:f\exists x_i : f, which projects out variable xix_i, is computed as the disjunction of the cofactors: ∃xi:f=f∣xi=0∨f∣xi=1\exists x_i : f = f|_{x_i=0} \lor f|_{x_i=1}, implemented recursively by applying the OR operation (via ) to the low and high children of nodes labeled xix_i, then propagating upward with memoization via a cache keyed on the current vertex and quantified set. Universal quantification ∀xi:f=f∣xi=0∧f∣xi=1\forall x_i : f = f|_{x_i=0} \land f|_{x_i=1} similarly uses conjunction on cofactors, or equivalently ∀xi:f=¬(∃xi:¬f)\forall x_i : f = \neg (\exists x_i : \neg f) via for efficiency. Restriction, the inverse operation of setting xi=bx_i = b (where b∈{0,1}b \in \{0,1\}), redirects all edges from xix_i-nodes to their low (b=0b=0) or high (b=1b=1) children, followed by reduction to eliminate redundant nodes; this takes linear time in the graph size. These algorithms integrate seamlessly with the Apply framework, using unique tables for sharing. The worst-case time complexity for binary operations like AND or OR is O(∣G1∣⋅∣G2∣)O(|G_1| \cdot |G_2|), where ∣G∣|G| denotes the number of vertices, due to potential pairwise traversal, though practical performance is often linear in the output size thanks to unique table hits (typically 40-50% reuse rate) and early termination on constants. Quantification and restriction exhibit O(∣G∣)O(|G|) complexity per variable, scaling with the quantified set size but benefiting from the same sharing mechanisms. These bounds hold under a fixed variable ordering, with complemented edges further accelerating negation and related operations.

Optimization Techniques

Variable Ordering

The choice of variable ordering in ordered binary decision diagrams (OBDDs) critically determines the compactness of the representation, as OBDDs enforce a fixed linear order on the variables encountered along any path from to terminal. A well-chosen ordering can yield an OBDD of linear size in the number of variables n, while a suboptimal one may result in exponential growth, reaching up to 2n nodes in the worst case. This sensitivity arises because the ordering influences the degree of node sharing and elimination during construction and reduction. Determining the optimal variable ordering that minimizes OBDD size for a given is NP-hard, making exact solutions infeasible for large n. Consequently, practical approaches rely on s, such as the sifting implemented in the CUDD package, which dynamically repositions individual variables to minimize size by iteratively swapping adjacent variables and evaluating the impact. Genetic algorithms have also been explored as methods, evolving orderings through selection, crossover, and to approximate optimal configurations. Variable orderings can be static, fixed during OBDD construction based on or initial heuristics, or dynamic, allowing runtime adjustments via variable swaps to adapt to growing diagrams during operations. However, dynamic reordering incurs computational overhead, with each adjacent swap costing O(n) time due to the need to traverse and update the diagram structure. For instance, in the function f = ∑i=1n (xi ∧ yi), an interleaved ordering (x1, y1, ..., xn, yn) produces a linear-sized OBDD with O(n) nodes, whereas grouping all xi before all yj results in an exponential-sized OBDD approximating a full of 2O(n) nodes.

Reduction and Sharing

Binary decision diagrams (BDDs) achieve compactness through reduction rules that eliminate structural redundancies during construction and manipulation. These rules include merging duplicate terminal nodes, where multiple instances of the same (0 or 1) are replaced by a single shared terminal; eliminating non-terminal nodes with identical low and high children, as such nodes provide no decision value; and bypassing nodes where the low and high children are the same, effectively skipping the variable test. Applied recursively, these rules ensure the resulting ordered BDD (OBDD) has no isomorphic subgraphs, minimizing node count while preserving the represented . To enforce uniqueness and promote sharing across subgraphs, BDD implementations maintain a unique table, typically a indexed by a node's variable and its low/high pointers. When creating a new node, the first checks this table; if an identical node exists, the new one is discarded and replaced with a to the existing node, preventing duplication. This mechanism not only reduces memory usage by reusing identical subgraphs but also applies during logical operations, where recursive apply procedures query the table to compose results efficiently. Over time, operations may leave unreachable nodes in , necessitating garbage collection to reclaim space. Implementations trigger collection when the proportion of dead nodes exceeds a threshold. During this process, the unique table (and often a computed table for operation results) is scanned to identify and remove entries referencing unreachable nodes, followed by or marking to free the nodes themselves. Careful timing of garbage collection balances performance, as premature runs waste computation while delayed ones risk exhaustion. The combined effect of reduction rules and the unique table establishes canonicity in reduced OBDDs: for a fixed variable ordering, each Boolean function maps to a unique graph structure. This property enables constant-time equality checks between two functions by simply comparing their root pointers, as identical roots imply identical representations.

Applications

Formal Verification and Synthesis

Binary decision diagrams (BDDs), particularly reduced ordered BDDs (ROBDDs), play a central role in model checking by enabling symbolic representation of transition systems and state spaces. In this approach, the set of states and the transition relation are encoded as BDDs, allowing efficient computation of reachable states through existential quantification and fixed-point iteration. For instance, reachability analysis determines if there exists a path from initial states to error states by iteratively applying the image operator until a fixed point is reached, mitigating the state explosion problem inherent in explicit enumeration. This symbolic method has verified systems with up to 102010^{20} states, far beyond traditional techniques. Equivalence checking leverages the canonicity of ROBDDs to verify functional identity between circuits, a critical step in hardware flows post-synthesis or optimization. For combinational circuits, BDDs are constructed for the outputs of two circuits, and equivalence is confirmed if their ROBDDs are identical, enabling detection of discrepancies without . In sequential equivalence checking, BDDs represent state sets and transitions to compute fixed points of reachable states, comparing the behaviors of two state machines. This method scales to circuits with approximately 100 latches, though variable ordering remains crucial for BDD size control. In logic synthesis, BDDs facilitate multi-level minimization by decomposing Boolean functions and exploiting don't cares to reduce circuit complexity. Techniques involve restricting BDDs with don't-care conditions to simplify subfunctions, followed by factoring and decomposition to generate optimized gate-level networks. For example, internal don't cares derived from unreachable states or observability conditions are used to minimize nodes in a Boolean network, improving area and delay. This BDD-based optimization has been integrated into flows for synthesizing complex controllers. Tools like VIS and ABC incorporate BDDs for verification and synthesis tasks, addressing challenges such as state explosion through symbolic methods. VIS, a system for finite-state hardware verification and synthesis, uses BDDs for , equivalence checking, and , supporting interactive refinement of designs. ABC, while primarily AIG-based, employs BDDs for tasks like don't-care computation and multi-level minimization, enhancing scalability in industrial flows. Despite these advances, BDD size limits persist for very large designs, often requiring hybrid approaches with SAT solvers.

Other Domains

Binary decision diagrams (BDDs) and their variants have found applications in and planning, particularly for knowledge representation. In , a language, BDDs enable efficient evaluation of recursive queries by representing sets of tuples compactly, allowing for scalable inference in knowledge bases. For instance, the bddbddb system uses BDDs to store and manipulate relations, achieving performance improvements over traditional database methods for large-scale . In Bayesian networks, multiterminal BDDs (MTBDDs) extend standard BDDs to handle probabilistic dependencies, representing joint probability distributions over variables with numerical edge weights to compute inference tasks like marginalization efficiently. This approach has been applied in probabilistic reasoning systems, reducing the state space explosion common in exact inference algorithms. Reliability analysis leverages BDDs for evaluating fault trees, which model system failures as logical combinations of component faults. By converting fault trees to BDDs, probabilistic failure rates can be computed through operations like conjunction and disjunction, providing exact results for complex systems where simulations may be inefficient. A seminal application is in nuclear safety assessments, where BDDs quantify the probability of core melt events by handling up to thousands of basic events with minimal memory overhead compared to enumeration methods. This technique emphasizes BDDs' role in achieving precise risk assessments for systems. In cryptography, BDDs have been employed to analyze Boolean functions for resistance to BDD-based attacks. The hidden weight bit (HWB) function is noted for its large BDD size, contributing to cryptographic strength. For example, Méaux and Ozaim (2024) studied the cryptographic properties of weightwise affine and quadratic functions, including HWB, highlighting their algebraic immunity and efficiency in lightweight cryptography. Beyond these, zero-suppressed BDDs (ZDDs) support problems, such as the problem, by efficiently enumerating subsets without supersets, as seen in solving Sudoku puzzles or . MTBDDs also facilitate quantum simulation by representing state vectors in quantum circuits, enabling compact storage and manipulation of superpositions for algorithms like Grover's search on classical hardware.
Add your contribution
Related Hubs
User Avatar
No comments yet.