In mathematical physics and probability and statistics, the Gaussian q-distribution is a family of probability distributions that includes, as limiting cases, the uniform distribution and the normal (Gaussian) distribution. It was introduced by Diaz and Teruel.^{[clarification needed]} It is a q-analog of the Gaussian or normal distribution.

The distribution is symmetric about zero and is bounded, except for the limiting case of the normal distribution. The limiting uniform distribution is on the range -1 to +1.

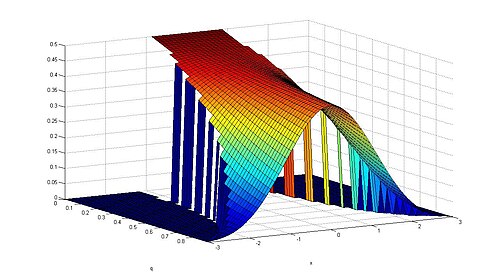
Let q be a real number in the interval [0, 1). The probability density function of the Gaussian q-distribution is given by

where

The q-analogue [t]_q of the real number ${\displaystyle t}$ is given by

The q-analogue of the exponential function is the q-exponential, E^x
_q, which is given by

where the q-analogue of the factorial is the q-factorial, [n]_q!, which is in turn given by

for an integer n > 2 and [1]_q! = [0]_q! = 1.