Hubbry Logo
Kirkwood gapKirkwood gapMain
Open search
Kirkwood gap
Community hub
Kirkwood gap
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Kirkwood gap
Kirkwood gap
Kirkwood gap
View on Wikipedia
from Wikipedia
Histogram showing the four most prominent Kirkwood gaps and a possible division into inner, middle and outer main-belt asteroids:
  inner main-belt (a < 2.5 AU)
  intermediate main-belt (2.5 AU < a < 2.82 AU)
  outer main-belt (a > 2.82 AU)
A plot of inner solar system asteroids and planets as of 2006 May 9, in a manner that exposes the Kirkwood gaps. Similar to the position plot, planets (with trajectories) are orange, Jupiter being the outer most in this view. Various asteroid classes are colour coded: 'generic' main-belt asteroids are white. Inside the main belt, there are the Atens (red), Apollos (green), and Amors (blue). Outside the main belt are the Hildas (blue) and the Trojans (green). All object position vectors have been normalized to the length of the object's semi-major axis. The Kirkwood gaps are visible in the main belt.

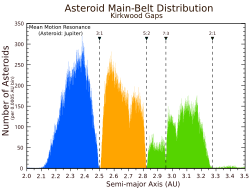
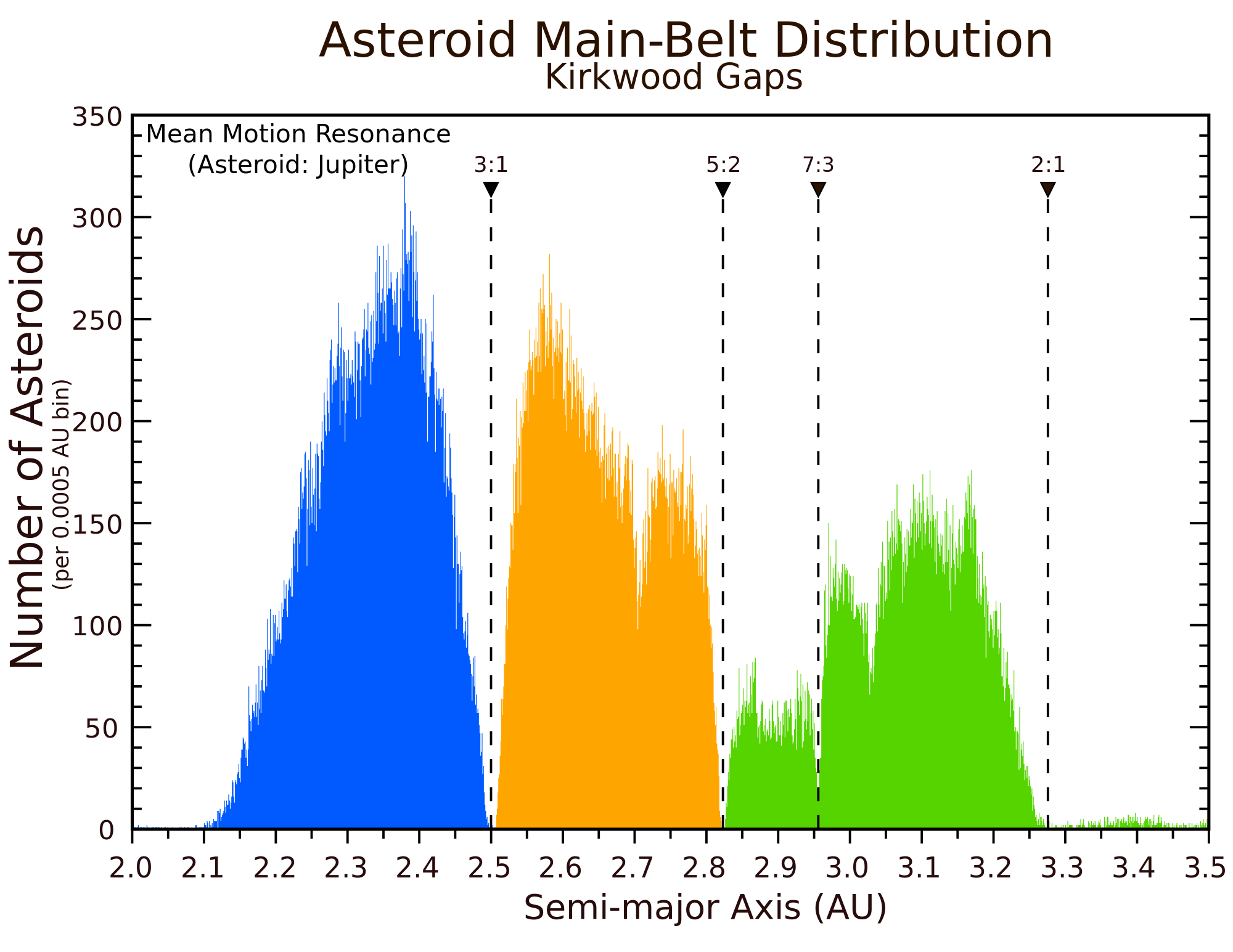
A Kirkwood gap is a gap or dip in the distribution of the semi-major axes (or equivalently of the orbital periods) of the orbits of main-belt asteroids. They correspond to the locations of orbital resonances with Jupiter. The gaps were first noticed in 1866 by Daniel Kirkwood, who also correctly explained their origin in the orbital resonances with Jupiter while a professor at Jefferson College in Canonsburg, Pennsylvania.[1]

For example, there are very few asteroids with semimajor axis near 2.50 AU, period 3.95 years, which would make three orbits for each orbit of Jupiter (hence, called the 3:1 orbital resonance). Other orbital resonances correspond to orbital periods whose lengths are simple fractions of Jupiter's. The weaker resonances lead only to a depletion of asteroids, while spikes in the histogram are often due to the presence of a prominent asteroid family (see List of asteroid families).

Most of the Kirkwood gaps are depleted, unlike the mean-motion resonances (MMR) of Neptune or Jupiter's 3:2 resonance, that retain objects captured during the giant planet migration of the Nice model. The loss of objects from the Kirkwood gaps is due to the overlapping of the ν5 and ν6 secular resonances within the mean-motion resonances. The orbital elements of the asteroids vary chaotically as a result and evolve onto planet-crossing orbits within a few million years.[2] The 2:1 MMR has a few relatively stable islands within the resonance, however. These islands are depleted due to slow diffusion onto less stable orbits. This process, which has been linked to Jupiter and Saturn being near a 5:2 resonance, may have been more rapid when Jupiter's and Saturn's orbits were closer together.[3]

More recently, a relatively small number of asteroids have been found to possess high eccentricity orbits which do lie within the Kirkwood gaps. Examples include the Alinda and Griqua groups. These orbits slowly increase their eccentricity on a timescale of tens of millions of years, and will eventually break out of the resonance due to close encounters with a major planet. This is why asteroids are rarely found in the Kirkwood gaps.

Main gaps

[edit]

The most prominent Kirkwood gaps are located at mean orbital radii of:[4]

  • 1.780 AU (5:1 resonance)
  • 2.065 AU (4:1 resonance)
  • 2.502 AU (3:1 resonance), home to the Alinda group of asteroids
  • 2.825 AU (5:2 resonance)
  • 2.958 AU (7:3 resonance)
  • 3.279 AU (2:1 resonance), Hecuba gap, home to the Griqua group of asteroids.
  • 3.972 AU (3:2 resonance), home to the Hilda asteroids.
  • 4.296 AU (4:3 resonance), home to the Thule group of asteroids.

Weaker and/or narrower gaps are also found at:

  • 1.909 AU (9:2 resonance)
  • 2.258 AU (7:2 resonance)
  • 2.332 AU (10:3 resonance)
  • 2.706 AU (8:3 resonance)
  • 3.031 AU (9:4 resonance)
  • 3.077 AU (11:5 resonance)
  • 3.474 AU (11:6 resonance)
  • 3.517 AU (9:5 resonance)
  • 3.584 AU (7:4 resonance)
  • 3.702 AU (5:3 resonance).

Asteroid zones

[edit]

The gaps are not seen in a simple snapshot of the locations of the asteroids at any one time because asteroid orbits are elliptical, and many asteroids still cross through the radii corresponding to the gaps. The actual spatial density of asteroids in these gaps does not differ significantly from the neighboring regions.[5]

The main gaps occur at the 3:1, 5:2, 7:3, and 2:1 mean-motion resonances with Jupiter. An asteroid in the 3:1 Kirkwood gap would orbit the Sun three times for each Jovian orbit, for instance. Weaker resonances occur at other semi-major axis values, with fewer asteroids found than nearby. (For example, an 8:3 resonance for asteroids with a semi-major axis of 2.71 AU).[6]

The main or core population of the asteroid belt may be divided into the inner and outer zones, separated by the 3:1 Kirkwood gap at 2.5 AU, and the outer zone may be further divided into middle and outer zones by the 5:2 gap at 2.82 AU:[7]

  • 4:1 resonance (2.06 AU)
    • Zone I population (inner zone)
  • 3:1 resonance (2.5 AU)
    • Zone II population (middle zone)
  • 5:2 resonance gap (2.82 AU)
    • Zone III population (outer zone)
  • 2:1 resonance gap (3.28 AU)

4 Vesta is the largest asteroid in the inner zone, 1 Ceres and 2 Pallas in the middle zone, and 10 Hygiea in the outer zone. 87 Sylvia is probably the largest Main Belt asteroid beyond the outer zone.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Kirkwood gap

View on Grokipedia
from Grokipedia
The Kirkwood gaps are regions of depletion within the main , where the distribution of asteroids shows pronounced dips or absences at specific semi-major axes due to mean-motion orbital resonances with . These gaps, first identified in 1866 by American astronomer Daniel Kirkwood while analyzing the orbits of known asteroids, occur at locations where an asteroid's forms a simple integer ratio with Jupiter's 11.86-year orbit, leading to gravitational perturbations that destabilize and eventually eject asteroids from the belt over millions of years. The primary Kirkwood gaps correspond to the 3:1 at approximately 2.50 AU (astronomical units) from the Sun, the 5:2 at about 2.82 AU, the 7:3 at about 2.95 AU, and the 2:1 at roughly 3.28 AU; these locations exhibit far fewer asteroids than the surrounding zones in the belt, which lies between Mars and . 's dominant gravitational influence in these resonant configurations amplifies perturbations, causing asteroids to experience repeated close alignments that increase their orbital eccentricities and inclinations, often resulting in ejection to the outer solar system or collisions. Observations of over 1.3 million asteroids confirm these gaps are not due to collisions but stem from long-term dynamical evolution under 's perturbations. These gaps highlight the sculpted nature of the asteroid belt, influencing our understanding of solar system formation and stability; for instance, they demonstrate how giant planets shape small body populations through resonances, a process relevant to exoplanetary systems as well. While not completely empty, the depletions are stark in histograms of asteroid semi-major axes, underscoring Jupiter's role in clearing resonant zones since the early solar system.

Historical Background

Daniel Kirkwood's Discovery

In the mid-19th century, the systematic cataloging of asteroids was underway, but the field remained limited, with only about 87 asteroids having well-determined orbits by 1867. These minor planets, discovered primarily between 1801 and the 1860s, populated the main between the orbits of Mars and , prompting astronomers to investigate patterns in their semi-major axes. American astronomer and mathematician Daniel Kirkwood (1814–1895), then a professor at , conducted a detailed statistical analysis of this sparse dataset to uncover underlying dynamical structures. Kirkwood presented his findings at the 1866 annual meeting of the American Association for the Advancement of Science, with the paper appearing in the proceedings published in 1867. In this work, he proposed that certain regions in the were depleted due to gravitational interactions with , the dominant perturber in the outer solar system. Kirkwood argued that these interactions arose from orbital resonances, where the periodic alignment of an asteroid's orbit with Jupiter's led to cumulative perturbations that ejected asteroids from those zones over time. Specifically, Kirkwood calculated the locations of these expected empty zones by identifying semi-major axes where orbital periods were simple integer fractions—such as 1/2 or 1/3—of Jupiter's of 11.86 years. Using to relate periods to distances from the Sun, he predicted depletions at distances like approximately 2.5 AU for the 3:1 (period 1/3 of Jupiter's) and 3.3 AU for the 2:1 resonance (period 1/2 of Jupiter's), regions that aligned with the observed scarcity in the limited catalog. This theoretical framework marked an early recognition of resonance-driven instability in the solar system, influencing subsequent studies of .

Early Confirmations and Observations

In the late 19th and early 20th centuries, the rapid increase in asteroid discoveries, facilitated by enhanced observational techniques, provided the empirical data needed to verify Daniel Kirkwood's earlier predictions of orbital depletions. Austrian astronomer Johann Palisa, utilizing visual searches with refracting telescopes at observatories in and Pola, discovered 122 asteroids between 1874 and 1924, significantly expanding the known population and enabling statistical assessments of their semi-major axis distribution. Similarly, German astronomer Max Wolf pioneered photographic starting in 1891 at Heidelberg Observatory, identifying over 200 minor planets and further populating catalogs; these efforts confirmed underdensities at resonant locations, such as the 3:1 mean-motion with at approximately 2.5 AU, where fewer asteroids were observed than in adjacent zones. In 1918, Japanese astronomer Kiyotsugu Hirayama conducted a detailed analysis of 790 orbits from the Berliner Astronomisches Jahrbuch for 1917, examining distributions of s, inclinations, and eccentricities to identify clustering patterns. While noting condensations like the Koronis family (16 asteroids with s around 725" per day), Hirayama highlighted gaps in the distribution attributable primarily to gravitational resonances with , though he also linked some structural features to early asteroid families formed by fragmentation. In a follow-up study published in 1919, Hirayama elaborated on the instability mechanisms, proposing that certain resonant configurations—such as the 2:1—led to abrupt eccentricity growth and dispersal of asteroids, rendering those regions dynamically unstable and explaining the observed depletions beyond mere family dynamics. Early 20th-century orbital catalogs further substantiated these observations through quantitative surveys of counts binned by semi-major axis. For instance, the Observatory's compilations in the 1920s, drawing on thousands of determined orbits, revealed pronounced statistical underdensities aligned with Kirkwood gaps; in one analysis of periods near half of Jupiter's (approximately 2166 days, corresponding to the 2:1 at 3.28 AU), zero asteroids appeared in the 2121–2220 day interval, compared to 8 in the preceding 2100–2120 day bin and 5 in the following 2222–2247 day range, underscoring the resonant clearing effects. These catalogs emphasized that such voids persisted across the main belt, with resonant zones showing 50–80% fewer objects than stable intervals, based on representative samples exceeding 1,000 asteroids.

Orbital Mechanics

Mean-Motion Resonances with

Mean-motion resonances with represent a key dynamical process in the , where an 's (angular speed) is locked in a simple to that of , denoted as a p:q . In this configuration, the completes p orbital revolutions around the Sun while completes q revolutions, leading to periodic gravitational perturbations that align the bodies at regular intervals. These resonances were first proposed by Daniel Kirkwood in as the cause of depletions in the distribution. Jupiter serves as the reference body for these resonances, with its orbit characterized by a semi-major axis of 5.2 AU and a sidereal of 11.86 years. The semi-major axes of resonant asteroids are calculated using Kepler's third , which states that the square of the is proportional to the of the semi-major axis (P2∝a3P^2 \propto a^3). For a p:q , the asteroid's period satisfies P=(q/p)PJP = (q/p) P_J, yielding the resonant semi-major axis a=aJ(q/p)2/3a = a_J (q/p)^{2/3}, where aJa_J and PJP_J are Jupiter's semi-major axis and period, respectively. This formula positions the resonances within the asteroid belt's span of approximately 2.0 to 3.3 AU. Resonances are further classified by their order, determined by the difference |p - q|. resonances, where |p - q| = 1 (e.g., the 3:2 resonance), produce stronger perturbations due to the involvement of lower-order terms in the disturbing function. Second-order resonances, with |p - q| = 2 (e.g., the 5:3 resonance), involve higher-order terms and are generally weaker, though still significant in shaping the belt's structure. These resonance locations cluster between 2.0 and 3.3 AU, influencing the overall distribution of asteroids across the inner, middle, and outer regions of the belt.

Gravitational Instability Mechanisms

The gravitational instability in Kirkwood gaps arises primarily from the interaction between mean-motion resonances (MMRs) with and secular resonances, which collectively destabilize asteroid orbits. In these configurations, asteroids captured in MMRs, such as the 3:1 or 5:2 with , experience repeated gravitational perturbations from the planet that align with their orbital rates, leading to a process known as eccentricity pumping. This secular forcing amplifies the orbital eccentricity over time, gradually increasing it from low values to levels where the asteroid's perihelion approaches or crosses the orbits of inner planets like Mars. As a result, the orbits become unstable, with asteroids either colliding with planets, being ejected from the solar system, or scattered into the inner solar system, thereby clearing the resonant zones. When multiple resonances overlap within a Kirkwood gap—particularly in the 4:1, 3:1, 5:2, and 7:3 MMRs—this interaction generates extensive zones characterized by diffusive motion in . The overlapping secular resonances, such as ν5 and ν6, induce rapid variations in both eccentricity and inclination, promoting diffusion that scatters asteroids unpredictably across . This mechanism efficiently removes material from the gaps by driving asteroids into planet-crossing trajectories or direct ejection, with the behavior extending beyond the nominal widths to explain the observed depletions. Early dynamical models indicate that these instability processes deplete the Kirkwood gaps on timescales of 10 to 100 million years following the formation and dispersal of the primordial asteroid disk, consistent with the age of the solar system. For instance, in the 3:1 gap, chaotic evolution clears most within a few million years through eccentricity growth and close encounters, while broader gaps like the 2:1 require longer diffusive timescales but follow similar perturbation-driven removal.

Gap Locations and Features

Primary Resonances and Gaps

The primary Kirkwood gaps in the main belt arise from mean-motion s with , resulting in regions of significantly reduced asteroid density at specific semi-major axes. These gaps are prominently observed in histograms of asteroid distributions, where the depletions are attributed to gravitational perturbations that destabilize orbits over time. The most notable gaps occur at the 3:1, 5:2, 7:3, and 2:1 resonances. The 3:1 resonance is located at approximately 2.50 AU, where asteroids complete three orbits for every one of Jupiter's; this gap hosts the Alinda group of asteroids, which remain in a stable resonant configuration despite the surrounding depletion. The 5:2 resonance lies at about 2.82 AU, corresponding to five asteroid orbits per two of Jupiter's. Further outward, the 7:3 at roughly 2.95 AU involves seven asteroid orbits for every three of Jupiter's, creating another clear depletion. The outermost primary gap, at the 2:1 around 3.27 AU (or 3.28 AU in some measurements), represents the largest depletion in the main belt, with asteroid density dropping to less than 1% of adjacent regions and spanning approximately 0.1 to 0.2 AU in width.
ResonanceSemi-Major Axis (AU)Notes on Depletion
3:12.50Hosts Alinda asteroids; significant but not total depletion
5:22.82Pronounced gap due to resonant instability
7:32.95Clear depletion, with excess clearing outward
2:13.28Largest and deepest gap, <1% density relative to neighbors
These resonances briefly perturb asteroid orbits through periodic gravitational alignments with , leading to eccentricity growth and eventual ejection from the belt.

Secondary Gaps and Variations

In addition to the primary Kirkwood gaps, higher-order resonances such as the 5:2 and 7:3 mean-motion resonances with produce less pronounced depletions in the at approximately 2.82 AU and 2.95 AU, respectively. These gaps are partially filled by asteroid populations that survive due to the weaker perturbative strength of these higher-order resonances compared to ones like the 3:1. For instance, numerical simulations show that particles can cross the separatrix, leading to some redistribution and partial occupation within these regions without complete clearing. Secular perturbations from the giant planets contribute to the partial filling observed in the 5:2 and 7:3 gaps by coupling with mean-motion resonances, allowing certain orbits to maintain stability over longer timescales through that does not always eject bodies. In the 7:3 gap, a small population of mostly small bodies with diameters under 10 km persists despite the region's instability (about 23 as of ), likely sustained by these secular interactions that modulate eccentricity growth. These effects contrast with the more complete depletions in gaps, highlighting how secular dynamics enable subtle variations in gap occupancy. The 4:1 at approximately 2.06 AU represents a gap in the inner , where depletion is influenced not only by the Jupiter but also by perturbations from Mars, which can destabilize high-inclination orbits near this boundary. The Yarkovsky effect further modifies this gap by inducing semimajor axis drift in smaller asteroids (diameters ~5-20 km), at rates of about 10^{-4} to 10^{-5} AU per million years, allowing some bodies to migrate across the resonance and partially repopulate adjacent zones. Variations in gap shapes include slight asymmetries, with Jupiter-facing boundaries of gaps like the 5:2 and 7:3 showing greater depletion than sunward sides, attributed to historical sweeping during . Inclination effects contribute to these asymmetries by altering the vertical structure of asteroid distributions, with higher inclinations reducing the efficiency of resonant clearing in some orbital planes. Additionally, asteroid size distributions amplify variations, as smaller bodies are more susceptible to the Yarkovsky effect and thus experience enhanced mobility, leading to uneven filling across gap edges compared to larger, less affected objects.

Asteroid Belt Structure

Stable Population Zones

The stable population zones in the are the dynamically secure regions situated between the major Kirkwood gaps, where asteroids can maintain orbits over billions of years without significant perturbation from 's resonances. These zones are bounded by the major Kirkwood gaps at the 3:1 (2.50 AU), 5:2 (2.82 AU), 7:3 (2.95 AU), and 2:1 (3.28 AU) mean-motion resonances with , with the innermost stable region starting around 2.1 AU due to the influence of secular resonances and Mars perturbations. The inner zone, spanning roughly 2.1 to 2.5 AU, exhibits high population density and is dominated by S-type (silicate-rich) asteroids, which constitute the majority of the mass in this region, alongside minor contributions from V-type bodies like those associated with Vesta. Orbits here typically feature low eccentricities (e < 0.15) and moderate inclinations (i ≤ 15°), enabling long-term stability against nearby secular resonances like ν6 near 2.0 AU. This zone includes families such as the Hungaria group (1.8–2.0 AU), characterized by high inclinations (16–35°) and E-type compositions, which contribute to the overall dynamical resilience through limited interactions with Mars. In the middle zone (2.5–2.8 AU), S-type asteroids remain prominent, particularly at smaller sizes, though large C-type objects like Ceres (at 2.77 AU) and Pallas add carbonaceous material, creating a transitional compositional profile. Stability in this region is moderate, with orbits resisting the disruptive influence of the adjacent 3:1 resonance through quasi-periodic evolution and minimal eccentricity diffusion, allowing survival times exceeding 250 million years in numerical models. The outer zones, from 2.8–2.95 AU and 3.0–3.3 AU (separated by the 7:3 ), are primarily composed of C-type (carbonaceous) asteroids, reflecting a in formation conditions cooler than the inner belt, and include the inner portions of the Cybele family near 3.3 AU, which orbits just beyond the 2:1 gap. These zones benefit from protection by the adjacent Kirkwood gaps, limiting Jupiter's direct gravitational influence and fostering semiconfined orbits with eccentricities around 0.1 that remain over gigayear timescales. Key to stability across these zones are orbital criteria such as amplitudes less than 30 degrees in resonant configurations, which prevent entry into domains and ensure avoidance of overlap with secular resonances.

Density Distributions and Depletions

The asteroid belt exhibits a characteristic of approximately 1–10 asteroids per 0.01 AU bin in its stable regions when analyzed using historical catalogs of larger bodies (primarily those with diameters exceeding several kilometers). These catalogs, compiled in the mid-20th century, reveal a non-uniform distribution shaped by dynamical processes, with the overall population concentrated in distinct zones separated by resonant depletions. In contrast, the Kirkwood gaps show drastic reductions, with densities dropping to less than 0.1 asteroids per 0.01 AU bin, reflecting near-complete clearing due to orbital instabilities. Statistical analyses of semimajor axis distributions, often presented in logarithmic histograms, highlight prominent peaks in density at approximately 2.4 (inner belt), 2.7 (central belt), and 3.1 (outer belt), corresponding to dynamically stable populations between major resonances. These peaks represent enrichments relative to the gaps, where depletions reach up to 90% compared to adjacent zones, as evidenced by the scarcity of objects near the 3:1, 5:2, and 2:1 resonances. Such patterns underscore the role of mean-motion resonances in sculpting the belt's structure, with stable zones serving as density maxima amid widespread dynamical erosion. Depletions in the Kirkwood gaps are particularly pronounced for larger asteroids with diameters greater than 1 km, where resonant perturbations efficiently remove bodies over gigayears, leading to sustained low densities. For smaller asteroids (D < 1 km), the gaps are partially refilled through collisional fragmentation of larger parent bodies in nearby zones, which injects debris into resonant orbits, and the Yarkovsky thermal effect, which induces semimajor axis drift and allows transient occupation of unstable regions. This size-dependent behavior results in less severe depletions for sub-kilometer populations, altering the apparent structure of the gaps in surveys sensitive to faint objects.

Modern Insights

Numerical Simulations and Modeling

Numerical simulations have played a crucial role in validating and extending early analytical theories of Kirkwood gap formation by demonstrating the dynamical processes that clear and maintain these regions in the . In the , N-body simulations by Lecar and Franklin modeled the evolution of a primordial under Jupiter's gravitational influence, showing that overlap—particularly involving the 3:1, 4:1, and 2:1 mean-motion s—leads to orbital evolution and rapid ejection of particles. These simulations indicated that the primary Kirkwood gaps form within approximately 10 million years, well under 50 million years, through the overlapping of secular and mean-motion s that destabilize orbits and scatter asteroids into unstable paths. Modern computational models build on these foundations by incorporating additional physical processes such as the Yarkovsky thermal drift and collisional interactions, which explain the observed partial filling of the gaps, particularly for smaller asteroids. The Yarkovsky effect induces semi-major axis drift in kilometer-sized and smaller bodies due to asymmetric photon emission from thermal reradiation, allowing some asteroids to migrate across resonant boundaries and repopulate gap interiors on timescales of tens to hundreds of millions of years; numerical integrations show that this drift enables transit through weaker resonances like the 7:3, with crossing fractions depending on initial obliquity and size. Collisions further contribute by fragmenting larger bodies and injecting debris into gap regions, counteracting depletion for sub-kilometer populations, as revealed in hybrid N-body and statistical models that track orbital evolution over gigayears. These enhancements address limitations in purely gravitational simulations by accounting for non-gravitational forces and stochastic events, revealing that gaps are not completely empty but exhibit size-dependent density gradients. Such models also provide predictions for ongoing and future dynamics in the . Long-term N-body simulations predict continued but slow depletion rates, with resonant scattering as a primary driver rather than collisions, implying that the belt's structure will remain relatively stable over the next billion years barring major perturbations. A 2025 study estimates the current mass loss rate from the asteroid belt at approximately 9×10^{-5} per million years of its collisionally active mass, with about 20% lost as macroscopic bodies and 80% as (~7×10^{16} kg per million years), primarily through dynamical . Moreover, ejections from Kirkwood gap resonances serve as significant sources for populations, with dynamical models indicating that a substantial fraction of NEOs (~20%) originate from the 3:1 resonance, linking gap instability to the delivery of potentially hazardous asteroids to inner Solar System orbits.

Recent Observational Data

The Data Release 3 (DR3), published in 2022, delivered astrometric, photometric, and spectroscopic for over 150,000 solar system objects, including a substantial sample of main-belt asteroids as small as sub-kilometer sizes. This enhanced precision in orbital parameters enabled refined mapping of the asteroid belt's semi-major axis distribution, highlighting subtler depletions and edge structures within the Kirkwood gaps that were underrepresented in prior optical surveys biased toward larger objects. For instance, analysis of rotation periods from DR3 photometry revealed under-abundances of prograde-rotating asteroids near key resonances like the 3:1 and 2:1 Kirkwood gaps, suggesting selective dynamical clearing mechanisms. Infrared observations from the NEOWISE mission during the 2010s provided thermal emission for thousands of main-belt asteroids, uncovering compositional diversity across the belt that varies with distance from the Sun. These reveal a mix of asteroid types throughout the belt, with smaller bodies showing greater mixing due to dynamical processes like the Yarkovsky effect and resonances, offering insights into surface and differences that optical catalogs overlook. Projections from the Vera C. Rubin Observatory's Legacy Survey of Space and Time (LSST), as of 2025, anticipate discovering a large fraction of the main-belt population, including over a million new sub-kilometer objects, that will help confirm voids in Kirkwood gaps with unprecedented resolution (as of 2025). Commissioning observations and Data Preview 1 from 2025 are providing initial data to address incompletenesses in size-limited datasets and reveal transient populations influenced by non-gravitational forces. A 2025 study of near-Earth 2024 YR4, located near the 3:1 Kirkwood gap, utilized long-term orbital tracking to demonstrate chaotic diffusion at gap edges, with the object's high eccentricity (e ≈ 0.66) evolving over decades due to transient captures in Jupiter's resonances. Observations spanning multiple apparitions confirmed irregular variations in its resonant angle, underscoring the unstable nature of gap boundaries and the role of close encounters in injecting material toward inner solar system orbits. Numerical simulations corroborate these empirical findings by reproducing the observed eccentricity excursions.

References

  1. https://www.universetoday.com/articles/astronomy-jargon-101-kirkwood-gaps
  2. https://astro.indiana.edu/about/history/daniel-kirkwood.html
  3. https://ssd.jpl.nasa.gov/diagrams/mb_hist.html
  4. https://astronomy.swin.edu.au/cosmos/Kirkwood+Gaps
  5. https://www.lindahall.org/about/news/scientist-of-the-day/daniel-kirkwood/
  6. https://ssd.jpl.nasa.gov/tools/sbdb_query.html
  7. https://ui.adsabs.harvard.edu/abs/1983Natur.301..201D
  8. https://adsabs.harvard.edu/full/1950JRASC..44..163S
  9. https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/kirkwood-daniel
  10. https://coolcosmos.ipac.caltech.edu/ask/90-How-long-does-it-take-Jupiter-to-go-around-the-Sun-
  11. https://www.britannica.com/biography/Johann-Palisa
  12. https://adsabs.harvard.edu/full/1918AJ.....31..185H
  13. https://www.jstage.jst.go.jp/article/ptmps1907/9/15/9_15_264/_pdf
  14. https://www.pnas.org/doi/pdf/10.1073/pnas.10.6.248
  15. https://iopscience.iop.org/article/10.3847/0004-637X/818/2/159
  16. https://radiojove.gsfc.nasa.gov/education/jupiter/basics/jfacts.htm
  17. https://science.nasa.gov/learn/basics-of-space-flight/chapter1-3/
  18. https://academic.oup.com/mnras/article/390/2/715/1030952
  19. https://ui.adsabs.harvard.edu/abs/1995A&AS..114..325F/abstract
  20. https://doi.org/10.1016/0019-1035(83)90127-6
  21. https://doi.org/10.1038/301201a0
  22. https://ui.adsabs.harvard.edu/abs/2015JRASC.109...55C/abstract
  23. https://asteroidday.org/resources/event-resources/learn-what-are-kirkwood-gaps/
  24. https://www.researchgate.net/figure/Kirkwood-gaps-visible-on-distribution-of-minor-planet-in-inner-part-of-the-Solar-system_fig5_286457029
  25. https://astronomy.swin.edu.au/cosmos/%2A/Kirkwood%2BGaps
  26. https://www.researchgate.net/publication/23833393_Nature_of_the_Kirkwood_gaps_in_the_asteroid_belt
  27. https://arxiv.org/pdf/1211.5603.pdf
  28. https://adsabs.harvard.edu/pdf/1996AJ....111.2453M
  29. https://www.eaps.purdue.edu/minton/docs/Icarus%202010%20Minton.pdf
  30. https://www2.boulder.swri.edu/~bottke/Reprints/Bottke-etal_2001_Science_Yark_Families.pdf
  31. https://www.astro.auth.gr/~varvogli/kirkwood-gaps.pdf
  32. http://www.mit.edu/~fdemeo/publications/DeMeoetal2015_AIV.pdf
  33. https://www2.boulder.swri.edu/~bottke/Reprints/Morbidelli_2015_Asteroids_IV_493_Dynamical_Evol_Asteroid_Belt.pdf
  34. https://www.aanda.org/articles/aa/full_html/2022/01/aa41719-21/aa41719-21.html
  35. https://ui.adsabs.harvard.edu/abs/2015MNRAS.451..244C/abstract
  36. https://www.researchgate.net/publication/222680193_Stable_Chaos_versus_Kirkwood_Gaps_in_the_Asteroid_Belt_A_Comparative_Study_of_Mean_Motion_Resonances
  37. https://adsabs.harvard.edu/full/1976LPSC....7.3603M
  38. https://arxiv.org/pdf/0909.3875
  39. https://adsabs.harvard.edu/full/1996AJ....112.1247F
  40. https://www.aanda.org/articles/aa/full_html/2020/05/aa37261-19/aa37261-19.html
  41. https://www.sciencedirect.com/science/article/abs/pii/S0019103509004953
  42. https://arxiv.org/pdf/2509.21194
  43. https://www.cosmos.esa.int/web/gaia/dr3
  44. https://www.aanda.org/articles/aa/full_html/2024/07/aa49297-24/aa49297-24.html
  45. https://arxiv.org/pdf/1408.2787
  46. https://dp1.lsst.io/index.html
  47. https://www.aanda.org/articles/aa/full_html/2025/07/aa54489-25/aa54489-25.html
Add your contribution
Related Hubs
User Avatar
No comments yet.