Hubbry Logo
Line graphLine graphMain
Open search
Line graph
Community hub
Line graph
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Line graph
Line graph
Line graph
View on Wikipedia
from Wikipedia

In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

The name line graph comes from a paper by Harary & Norman (1960) although both Whitney (1932) and Krausz (1943) used the construction before this.[1] Other terms used for the line graph include the covering graph, the derivative, the edge-to-vertex dual, the conjugate, the representative graph, and the θ-obrazom,[1] as well as the edge graph, the interchange graph, the adjoint graph, and the derived graph.[2]

Hassler Whitney (1932) proved that with one exceptional case the structure of a connected graph G can be recovered completely from its line graph.[3] Many other properties of line graphs follow by translating the properties of the underlying graph from vertices into edges, and by Whitney's theorem the same translation can also be done in the other direction. Line graphs are claw-free, and the line graphs of bipartite graphs are perfect. Line graphs are characterized by nine forbidden subgraphs and can be recognized in linear time.

Various extensions of the concept of a line graph have been studied, including line graphs of line graphs, line graphs of multigraphs, line graphs of hypergraphs, and line graphs of weighted graphs.

Formal definition

[edit]

Given a graph G, its line graph L(G) is a graph such that

  • each vertex of L(G) represents an edge of G; and
  • two vertices of L(G) are adjacent if and only if their corresponding edges share a common endpoint ("are incident") in G.

That is, it is the intersection graph of the edges of G, representing each edge by the set of its two endpoints.[2]

Example

[edit]

The following figures show a graph (left, with blue vertices) and its line graph (right, with green vertices). Each vertex of the line graph is shown labeled with the pair of endpoints of the corresponding edge in the original graph. For instance, the green vertex on the right labeled 1,3 corresponds to the edge on the left between the blue vertices 1 and 3. Green vertex 1,3 is adjacent to three other green vertices: 1,4 and 1,2 (corresponding to edges sharing the endpoint 1 in the blue graph) and 4,3 (corresponding to an edge sharing the endpoint 3 in the blue graph).

  • Graph G
    Graph G
  • Vertices in L(G) constructed from edges in G
    Vertices in L(G) constructed from edges in G
  • Added edges in L(G)
    Added edges in L(G)
  • The line graph L(G)
    The line graph L(G)

Properties

[edit]

Translated properties of the underlying graph

[edit]

Properties of a graph G that depend only on adjacency between edges may be translated into equivalent properties in L(G) that depend on adjacency between vertices. For instance, a matching in G is a set of edges no two of which are adjacent, and corresponds to a set of vertices in L(G) no two of which are adjacent, that is, an independent set.[4]

Thus,

  • The line graph of a connected graph is connected. If G is connected, it contains a path connecting any two of its edges, which translates into a path in L(G) containing any two of the vertices of L(G). However, a graph G that has some isolated vertices, and is therefore disconnected, may nevertheless have a connected line graph.[5]
  • A line graph has an articulation point if and only if the underlying graph has a bridge for which neither endpoint has degree one.[2]
  • For a graph G with n vertices and m edges, the number of vertices of the line graph L(G) is m, and the number of edges of L(G) is half the sum of the squares of the degrees of the vertices in G, minus m.[6]
  • An independent set in L(G) corresponds to a matching in G. In particular, a maximum independent set in L(G) corresponds to maximum matching in G. Since maximum matchings may be found in polynomial time, so may the maximum independent sets of line graphs, despite the hardness of the maximum independent set problem for more general families of graphs.[4] Similarly, a rainbow-independent set in L(G) corresponds to a rainbow matching in G.
  • The edge chromatic number of a graph G is equal to the vertex chromatic number of its line graph L(G).[7]
  • The line graph of an edge-transitive graph is vertex-transitive. This property can be used to generate families of graphs that (like the Petersen graph) are vertex-transitive but are not Cayley graphs: if G is an edge-transitive graph that has at least five vertices, is not bipartite, and has odd vertex degrees, then L(G) is a vertex-transitive non-Cayley graph.[8]
  • If a graph G has an Euler cycle, that is, if G is connected and has an even number of edges at each vertex, then the line graph of G is Hamiltonian. However, not all Hamiltonian cycles in line graphs come from Euler cycles in this way; for instance, the line graph of a Hamiltonian graph G is itself Hamiltonian, regardless of whether G is also Eulerian.[9]
  • If two simple graphs are isomorphic then their line graphs are also isomorphic. The Whitney graph isomorphism theorem provides a converse to this for all but one pair of connected graphs.
  • In the context of complex network theory, the line graph of a random network preserves many of the properties of the network such as the small-world property (the existence of short paths between all pairs of vertices) and the shape of its degree distribution.[10] Evans & Lambiotte (2009) observe that any method for finding vertex clusters in a complex network can be applied to the line graph and used to cluster its edges instead.

Whitney isomorphism theorem

[edit]
The diamond graph (left) and its more-symmetric line graph (right), an exception to the strong Whitney theorem

If the line graphs of two connected graphs are isomorphic, then the underlying graphs are isomorphic, except in the case of the triangle graph K3 and the claw K1,3, which have isomorphic line graphs but are not themselves isomorphic.[3]

As well as K3 and K1,3, there are some other exceptional small graphs with the property that their line graph has a higher degree of symmetry than the graph itself. For instance, the diamond graph K1,1,2 (two triangles sharing an edge) has four graph automorphisms but its line graph K1,2,2 has eight. In the illustration of the diamond graph shown, rotating the graph by 90 degrees is not a symmetry of the graph, but is a symmetry of its line graph. However, all such exceptional cases have at most four vertices. A strengthened version of the Whitney isomorphism theorem states that, for connected graphs with more than four vertices, there is a one-to-one correspondence between isomorphisms of the graphs and isomorphisms of their line graphs.[11]

Analogues of the Whitney isomorphism theorem have been proven for the line graphs of multigraphs, but are more complicated in this case.[12]

Strongly regular and perfect line graphs

[edit]
A line perfect graph. The edges in each biconnected component are colored black if the component is bipartite, blue if the component is a tetrahedron, and red if the component is a book of triangles.

The line graph of the complete graph Kn is also known as the triangular graph, the Johnson graph J(n, 2), or the complement of the Kneser graph KGn,2. Triangular graphs are characterized by their spectra, except for n = 8.[13] They may also be characterized (again with the exception of K8) as the strongly regular graphs with parameters srg(n(n − 1)/2, 2(n − 2), n − 2, 4).[14] The three strongly regular graphs with the same parameters and spectrum as L(K8) are the Chang graphs, which may be obtained by graph switching from L(K8).

The line graph of a bipartite graph is perfect (see Kőnig's theorem), but need not be bipartite as the example of the claw graph shows. The line graphs of bipartite graphs form one of the key building blocks of perfect graphs, used in the proof of the strong perfect graph theorem.[15] A special case of these graphs are the rook's graphs, line graphs of complete bipartite graphs. Like the line graphs of complete graphs, they can be characterized with one exception by their numbers of vertices, numbers of edges, and number of shared neighbors for adjacent and non-adjacent points. The one exceptional case is L(K4,4), which shares its parameters with the Shrikhande graph. When both sides of the bipartition have the same number of vertices, these graphs are again strongly regular.[16] It has been shown that, except for C3 , C4 , and C5 , all connected strongly regular graphs can be made non-strongly regular within two line graph transformations.[17] The extension to disconnected graphs would require that the graph is not a disjoint union of C3.

More generally, a graph G is said to be a line perfect graph if L(G) is a perfect graph. The line perfect graphs are exactly the graphs that do not contain a simple cycle of odd length greater than three.[18] Equivalently, a graph is line perfect if and only if each of its biconnected components is either bipartite or of the form K4 (the tetrahedron) or K1,1,n (a book of one or more triangles all sharing a common edge).[19] Every line perfect graph is itself perfect.[20]

[edit]

All line graphs are claw-free graphs, graphs without an induced subgraph in the form of a three-leaf tree.[21] As with claw-free graphs more generally, every connected line graph L(G) with an even number of edges has a perfect matching;[22] equivalently, this means that if the underlying graph G has an even number of edges, its edges can be partitioned into two-edge paths.

The line graphs of trees are exactly the claw-free block graphs.[23] These graphs have been used to solve a problem in extremal graph theory, of constructing a graph with a given number of edges and vertices whose largest tree induced as a subgraph is as small as possible.[24]

All eigenvalues of the adjacency matrix A of a line graph are at least −2. The reason for this is that A can be written as , where J is the signless incidence matrix of the pre-line graph and I is the identity. In particular, A + 2I is the Gramian matrix of a system of vectors: all graphs with this property have been called generalized line graphs.[25]

Characterization and recognition

[edit]

Clique partition

[edit]
Partition of a line graph into cliques

For an arbitrary graph G, and an arbitrary vertex v in G, the set of edges incident to v corresponds to a clique in the line graph L(G). The cliques formed in this way partition the edges of L(G). Each vertex of L(G) belongs to exactly two of them (the two cliques corresponding to the two endpoints of the corresponding edge in G).

The existence of such a partition into cliques can be used to characterize the line graphs: A graph L is the line graph of some other graph or multigraph if and only if it is possible to find a collection of cliques in L (allowing some of the cliques to be single vertices) that partition the edges of L, such that each vertex of L belongs to exactly two of the cliques.[21] It is the line graph of a graph (rather than a multigraph) if this set of cliques satisfies the additional condition that no two vertices of L are both in the same two cliques. Given such a family of cliques, the underlying graph G for which L is the line graph can be recovered by making one vertex in G for each clique, and an edge in G for each vertex in L with its endpoints being the two cliques containing the vertex in L. By the strong version of Whitney's isomorphism theorem, if the underlying graph G has more than four vertices, there can be only one partition of this type.

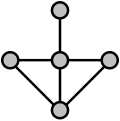
For example, this characterization can be used to show that the following graph is not a line graph:

In this example, the edges going upward, to the left, and to the right from the central degree-four vertex do not have any cliques in common. Therefore, any partition of the graph's edges into cliques would have to have at least one clique for each of these three edges, and these three cliques would all intersect in that central vertex, violating the requirement that each vertex appear in exactly two cliques. Thus, the graph shown is not a line graph.

Forbidden subgraphs

[edit]
The nine minimal non-line graphs, from Beineke's forbidden-subgraph characterization of line graphs. A graph is a line graph if and only if it does not contain one of these nine graphs as an induced subgraph.

Another characterization of line graphs was proven in Beineke (1970) (and reported earlier without proof by Beineke (1968)). He showed that there are nine minimal graphs that are not line graphs, such that any graph that is not a line graph has one of these nine graphs as an induced subgraph. That is, a graph is a line graph if and only if no subset of its vertices induces one of these nine graphs. In the example above, the four topmost vertices induce a claw (that is, a complete bipartite graph K1,3), shown on the top left of the illustration of forbidden subgraphs. Therefore, by Beineke's characterization, this example cannot be a line graph. For graphs with minimum degree at least 5, only the six subgraphs in the left and right columns of the figure are needed in the characterization.[26]

Algorithms

[edit]

Roussopoulos (1973) and Lehot (1974) described linear time algorithms for recognizing line graphs and reconstructing their original graphs. Sysło (1982) generalized these methods to directed graphs. Degiorgi & Simon (1995) described an efficient data structure for maintaining a dynamic graph, subject to vertex insertions and deletions, and maintaining a representation of the input as a line graph (when it exists) in time proportional to the number of changed edges at each step.

The algorithms of Roussopoulos (1973) and Lehot (1974) are based on characterizations of line graphs involving odd triangles (triangles in the line graph with the property that there exists another vertex adjacent to an odd number of triangle vertices). However, the algorithm of Degiorgi & Simon (1995) uses only Whitney's isomorphism theorem. It is complicated by the need to recognize deletions that cause the remaining graph to become a line graph, but when specialized to the static recognition problem only insertions need to be performed, and the algorithm performs the following steps:

  • Construct the input graph L by adding vertices one at a time, at each step choosing a vertex to add that is adjacent to at least one previously-added vertex. While adding vertices to L, maintain a graph G for which L = L(G); if the algorithm ever fails to find an appropriate graph G, then the input is not a line graph and the algorithm terminates.
  • When adding a vertex v to a graph L(G) for which G has four or fewer vertices, it might be the case that the line graph representation is not unique. But in this case, the augmented graph is small enough that a representation of it as a line graph can be found by a brute force search in constant time.
  • When adding a vertex v to a larger graph L that equals the line graph of another graph G, let S be the subgraph of G formed by the edges that correspond to the neighbors of v in L. Check that S has a vertex cover consisting of one vertex or two non-adjacent vertices. If there are two vertices in the cover, augment G by adding an edge (corresponding to v) that connects these two vertices. If there is only one vertex in the cover, then add a new vertex to G, adjacent to this vertex.

Each step either takes constant time, or involves finding a vertex cover of constant size within a graph S whose size is proportional to the number of neighbors of v. Thus, the total time for the whole algorithm is proportional to the sum of the numbers of neighbors of all vertices, which (by the handshaking lemma) is proportional to the number of input edges.

Iterating the line graph operator

[edit]

van Rooij & Wilf (1965) consider the sequence of graphs

They show that, when G is a finite connected graph, only four behaviors are possible for this sequence:

  • If G is a cycle graph then L(G) and each subsequent graph in this sequence are isomorphic to G itself. These are the only connected graphs for which L(G) is isomorphic to G.[27]
  • If G is a claw K1,3, then L(G) and all subsequent graphs in the sequence are triangles.
  • If G is a path graph then each subsequent graph in the sequence is a shorter path until eventually the sequence terminates with an empty graph.
  • In all remaining cases, the sizes of the graphs in this sequence eventually increase without bound.

If G is not connected, this classification applies separately to each component of G.

For connected graphs that are not paths, all sufficiently high numbers of iteration of the line graph operation produce graphs that are Hamiltonian.[28]

Generalizations

[edit]

Medial graphs and convex polyhedra

[edit]
Main article: Medial graph

When a planar graph G has maximum vertex degree three, its line graph is planar, and every planar embedding of G can be extended to an embedding of L(G). However, there exist planar graphs with higher degree whose line graphs are nonplanar. These include, for example, the 5-star K1,5, the gem graph formed by adding two non-crossing diagonals within a regular pentagon, and all convex polyhedra with a vertex of degree four or more.[29]

An alternative construction, the medial graph, coincides with the line graph for planar graphs with maximum degree three, but is always planar. It has the same vertices as the line graph, but potentially fewer edges: two vertices of the medial graph are adjacent if and only if the corresponding two edges are consecutive on some face of the planar embedding. The medial graph of the dual graph of a plane graph is the same as the medial graph of the original plane graph.[30]

For regular polyhedra or simple polyhedra, the medial graph operation can be represented geometrically by the operation of cutting off each vertex of the polyhedron by a plane through the midpoints of all its incident edges.[31] This operation is known variously as the second truncation,[32] degenerate truncation,[33] or rectification.[34]

Total graphs

[edit]

The total graph T(G) of a graph G has as its vertices the elements (vertices or edges) of G, and has an edge between two elements whenever they are either incident or adjacent. The total graph may also be obtained by subdividing each edge of G and then taking the square of the subdivided graph.[35]

Multigraphs

[edit]

The concept of the line graph of G may naturally be extended to the case where G is a multigraph. In this case, the characterizations of these graphs can be simplified: the characterization in terms of clique partitions no longer needs to prevent two vertices from belonging to the same to cliques, and the characterization by forbidden graphs has seven forbidden graphs instead of nine.[36]

However, for multigraphs, there are larger numbers of pairs of non-isomorphic graphs that have the same line graphs. For instance a complete bipartite graph K1,n has the same line graph as the dipole graph and Shannon multigraph with the same number of edges. Nevertheless, analogues to Whitney's isomorphism theorem can still be derived in this case.[12]

Line digraphs

[edit]
Construction of the de Bruijn graphs as iterated line digraphs

It is also possible to generalize line graphs to directed graphs.[37] If G is a directed graph, its directed line graph or line digraph has one vertex for each edge of G. Two vertices representing directed edges from u to v and from w to x in G are connected by an edge from uv to wx in the line digraph when v = w. That is, each edge in the line digraph of G represents a length-two directed path in G. The de Bruijn graphs may be formed by repeating this process of forming directed line graphs, starting from a complete directed graph.[38]

Weighted line graphs

[edit]

In a line graph L(G), each vertex of degree k in the original graph G creates k(k − 1)/2 edges in the line graph. For many types of analysis this means high-degree nodes in G are over-represented in the line graph L(G). For instance, consider a random walk on the vertices of the original graph G. This will pass along some edge e with some frequency f. On the other hand, this edge e is mapped to a unique vertex, say v, in the line graph L(G). If we now perform the same type of random walk on the vertices of the line graph, the frequency with which v is visited can be completely different from f. If our edge e in G was connected to nodes of degree O(k), it will be traversed O(k2) more frequently in the line graph L(G). Put another way, the Whitney graph isomorphism theorem guarantees that the line graph almost always encodes the topology of the original graph G faithfully but it does not guarantee that dynamics on these two graphs have a simple relationship. One solution is to construct a weighted line graph, that is, a line graph with weighted edges. There are several natural ways to do this.[39] For instance if edges d and e in the graph G are incident at a vertex v with degree k, then in the line graph L(G) the edge connecting the two vertices d and e can be given weight 1/(k − 1). In this way every edge in G (provided neither end is connected to a vertex of degree 1) will have strength 2 in the line graph L(G) corresponding to the two ends that the edge has in G. It is straightforward to extend this definition of a weighted line graph to cases where the original graph G was directed or even weighted.[40] The principle in all cases is to ensure the line graph L(G) reflects the dynamics as well as the topology of the original graph G.

Line graphs of hypergraphs

[edit]
Main article: Line graph of a hypergraph

The edges of a hypergraph may form an arbitrary family of sets, so the line graph of a hypergraph is the same as the intersection graph of the sets from the family.

Disjointness graph

[edit]

The disjointness graph of G, denoted D(G), is constructed in the following way: for each edge in G, make a vertex in D(G); for every two edges in G that do not have a vertex in common, make an edge between their corresponding vertices in D(G).[41] In other words, D(G) is the complement graph of L(G). A clique in D(G) corresponds to an independent set in L(G), and vice versa.

Notes

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Line graph

View on Grokipedia
from Grokipedia
In , the line graph L(G)L(G) of an undirected simple graph GG is defined as the graph whose vertex set consists of the edges of GG, with two vertices in L(G)L(G) adjacent if and only if the corresponding edges in GG are incident, meaning they share a common vertex. This construction transforms the edge structure of GG into the vertex structure of L(G)L(G), providing a way to study edge-related properties through vertex analysis. The concept of line graphs originated in the early 20th century, with initial investigations by Hassler Whitney in 1932, who explored isomorphisms between graphs via their line graphs. The term "line graph" was formally introduced by Frank Harary and Robert Z. Norman in 1960, building on earlier work, though the idea had been studied under different names prior to that. Whitney's seminal result, known as Whitney's isomorphism theorem, states that if two connected graphs have isomorphic line graphs, then the original graphs are isomorphic, with the notable exception of the triangle K3K_3 and the star K1,3K_{1,3}, which share the same line graph (a triangle). Line graphs exhibit several characterizing properties that distinguish them within . A nonempty graph is a line graph if and only if its edge set can be partitioned into cliques such that every vertex lies in at most two of these cliques, a result known as Krausz's . If GG is kk-regular, then L(G)L(G) is (2k−2)(2k-2)-regular, reflecting the . Additionally, line graphs are claw-free, meaning they contain no isomorphic to K1,3K_{1,3}, and the line graphs of bipartite graphs are perfect graphs. For recognition, a graph with minimum degree at least 5 is a line graph if it avoids certain forbidden induced subgraphs, such as the Metelsky graphs. Line graphs find applications across various areas of , particularly in translating edge problems to vertex problems. For instance, finding a maximum matching in GG is equivalent to finding a maximum independent set in L(G)L(G), and in GG corresponds to vertex coloring in L(G)L(G). They also aid in studying edge connectivity, as the vertex connectivity of L(G)L(G) relates to the edge connectivity of GG. These properties make line graphs a fundamental tool in , network analysis, and .

Fundamentals

Definition

In , the line graph L(G)L(G) of a simple undirected graph GG is constructed such that its vertex set is in one-to-one correspondence with the edge set of GG, and two vertices in L(G)L(G) are connected by an edge the corresponding edges in GG are incident, meaning they share a common endpoint. This mapping transforms the incidences between edges in the original graph into adjacencies in the line graph, providing a representation where the structure of edge connections is preserved topologically. More precisely, the adjacency condition in L(G)L(G) holds between two vertices if their preimages— the edges in GG—share exactly one endpoint, assuming GG has no multiple edges between the same pair of vertices. For an edge e={u,v}e = \{u, v\} in GG, the degree of the corresponding vertex in L(G)L(G) is given by deg⁡L(G)(e)=deg⁡G(u)+deg⁡G(v)−2\deg_{L(G)}(e) = \deg_G(u) + \deg_G(v) - 2, reflecting the number of other edges incident to uu or vv excluding ee itself. The original graph GG is referred to as the root graph or preimage graph of L(G)L(G), emphasizing the derivational relationship between the two structures.

Example

To illustrate the construction of a line graph, consider the complete graph K3K_3, a triangle with vertices labeled 1, 2, and 3, and edges e1={1,2}e_1 = \{1,2\}, e2={2,3}e_2 = \{2,3\}, and e3={3,1}e_3 = \{3,1\}. The line graph L(K3)L(K_3) has three vertices v1v_1, v2v_2, and v3v_3, each corresponding to one of these edges. Vertices in L(K3)L(K_3) are adjacent if the edges they represent share a common vertex in K3K_3: thus, v1v_1 connects to v2v_2 (sharing vertex 2), v1v_1 to v3v_3 (sharing vertex 1), and v2v_2 to v3v_3 (sharing vertex 3). This adjacency rule yields L(K3)L(K_3) as another triangle with all pairs connected. Visually, K3K_3 appears as an enclosing its three edges. To overlay L(K3)L(K_3), place each vertex viv_i at the of edge eie_i; the induced edges then form a smaller linking these midpoints, with each connection tracing the path around the shared endpoints of the original edges. In K3K_3, every vertex has degree 2, so for any edge e={u,v}e = \{u,v\}, it is adjacent to deg⁡(u)−1+deg⁡(v)−1=2\deg(u) - 1 + \deg(v) - 1 = 2 other edges. Each vertex in L(K3)L(K_3) thus has degree 2, consistent with the structure. This example shows L(K3)≅K3L(K_3) \cong K_3.

Properties

Inherited Properties from the Original Graph

The connectivity of the line graph L(G) mirrors that of the original graph G in a direct manner. Specifically, assuming G has no isolated vertices, L(G) is connected G is connected. If G is disconnected, then L(G) is disconnected, with each connected component of L(G) corresponding to the edges in a connected component of G that contains at least one edge. Bipartiteness in line graphs is also inherited under precise conditions from the structure of G. L(G) is bipartite G is a of even cycles and paths. This ensures that no odd cycles arise in L(G), as even cycles in G map to even cycles in L(G), while paths produce bipartite subgraphs without introducing odd-length structures. The number of edges in L(G) can be expressed in terms of the degrees in G, providing a quantitative link between the two graphs: ∣E(L(G))∣=12∑v∈V(G)(deg⁡(v)2).|E(L(G))| = \frac{1}{2} \sum_{v \in V(G)} \binom{\deg(v)}{2}. This formula arises because each vertex v in G contributes (deg⁡(v)2)\binom{\deg(v)}{2} edges in L(G) among the edges incident to v, with the factor of 1/2 accounting for double-counting across vertices. A defining inherited property is claw-freeness: every line graph L(G) is claw-free, meaning it contains no induced subgraph isomorphic to K_{1,3}. This holds because any three vertices in L(G) corresponding to edges incident to a common vertex in G must form a triangle (if pairwise adjacent) or be connected in a way that avoids the claw structure; non-adjacent edges in G cannot all share a single common neighbor without inducing additional edges. Paths and cycles in G translate directly to similar structures in L(G), preserving much of the original topology. A path in G corresponds to a path in L(G), as consecutive edges in the path become adjacent vertices in L(G). Similarly, every cycle of length at least 4 in G induces a cycle of the same length in L(G), since the edges around the cycle are sequentially adjacent in L(G).

Whitney Isomorphism Theorem

The Whitney isomorphism theorem asserts that if GG and HH are connected graphs that are neither isomorphic to K3K_3 nor to K1,3K_{1,3}, and their line graphs satisfy L(G)≅L(H)L(G) \cong L(H), then G≅HG \cong H. This result establishes that, under these conditions, the line graph operation is injective on the isomorphism classes of connected graphs, providing a near-reversibility to the mapping from graphs to their line graphs. The theorem was established by Hassler Whitney in 1932 as part of his work on graph congruences and connectivity. The exceptions arise specifically for the K3K_3 and the K1,3K_{1,3}, both of which have line graphs isomorphic to K3K_3: in K3K_3, the three edges form a in the line graph due to pairwise vertex sharing; similarly, in K1,3K_{1,3}, the three pendant edges all share the central vertex, inducing the same K3K_3 structure. For connected graphs with more than four vertices, there are no such exceptions, ensuring . A high-level outline of the proof proceeds by leveraging the structural encoding in the line graph. Given an ϕ:L(G)→L(H)\phi: L(G) \to L(H), the degrees in L(G)L(G) reveal the degrees in GG, since the degree of a vertex in L(G)L(G) corresponding to edge uv∈E(G)uv \in E(G) is deg⁡G(u)+deg⁡G(v)−2\deg_G(u) + \deg_G(v) - 2. The adjacency relations in L(G)L(G) allow reconstruction of the endpoint incidences: maximal cliques in L(G)L(G) correspond to the edge stars at vertices of GG (or triangles if present), enabling identification of the bundles of edges incident to each vertex. An ϕ\phi then lifts to a between edges of GG and HH that preserves these incidences, yielding vertex isomorphisms for GG and HH except in the small exceptional cases, which are verified directly. As a corollary, almost all line graphs—specifically, those of connected graphs excluding the exceptions—have a unique root graph up to isomorphism, underscoring the theorem's role in uniquely determining original graphs from their line representations.

Line Graphs of Special Graph Classes

Line graphs derived from special classes of graphs often inherit or exhibit notable structural properties. For instance, when the original graph is strongly regular, its line graph may also be strongly regular under certain conditions. The line graph of the complete graph KmK_m (for m≥4m \geq 4), known as the triangular graph T(m)T(m), is strongly regular with parameters ((m2),2(m−2),m−2,4)\left( \binom{m}{2}, 2(m-2), m-2, 4 \right). Similarly, the line graph of the complete bipartite graph Km,mK_{m,m} (for m≥2m \geq 2), also known as the lattice graph L2(m)L_2(m) or Shrikhande graph in some contexts, is strongly regular with parameters (m2,2(m−1),m−2,2)(m^2, 2(m-1), m-2, 2). Regarding perfect graphs, the line graph L(G)L(G) is perfect whenever GG is bipartite. This follows from the structure of line graphs of bipartite graphs, which contain no induced odd cycles or their complements (odd antiholes), aligning with the strong perfect graph theorem. For example, if GG is a complete bipartite graph Ka,bK_{a,b}, then L(G)L(G) is a whose chromatic number equals its clique number for every . However, if GG is not bipartite, L(G)L(G) need not be perfect; a is the C5C_5, whose line graph is isomorphic to C5C_5 itself, which has clique number 2 but chromatic number 3. The eigenvalues of the of a L(G)L(G) are intimately related to those of the original graph GG through the BB of GG, where the satisfies AL(G)=BTB−2IA_{L(G)} = B^T B - 2I (with II the of order ∣E(G)∣|E(G)|). For a kk- GG with adjacency eigenvalues θ1=k\theta_1 = k (multiplicity 1) and θ2,…,θn\theta_2, \dots, \theta_n (where n=∣V(G)∣n = |V(G)|), the eigenvalues of L(G)L(G) are 2k−22k - 2 (multiplicity 1) and k+θi−2k + \theta_i - 2 for i=2i = 2 to nn, along with −2-2 (with multiplicity ∣E(G)∣−∣V(G)∣|E(G)| - |V(G)|). Line graphs also exhibit Hamiltonian properties tied to Eulerian structures in the original graph. Specifically, L(G)L(G) is Hamiltonian (i.e., contains a Hamiltonian cycle) if GG is Eulerian, meaning GG is connected and every vertex has even degree; in this case, an Eulerian circuit in GG traverses every edge exactly once and induces a Hamiltonian cycle in L(G)L(G). More broadly, L(G)L(G) contains a if GG has an (i.e., GG is connected with exactly zero or two vertices of odd degree).

Connections to Other Graph Families

Line graphs form a subclass of claw-free graphs, as no vertex in a line graph corresponds to an edge incident to three pairwise non-adjacent edges in the original graph. Specifically, if three edges incident to a common edge are pairwise non-adjacent, they would form an induced claw K1,3K_{1,3}, which is impossible in the structure of line graphs. However, the converse does not hold; there exist claw-free graphs that are not line graphs, such as certain quasi-line graphs or more complex structures identified in structural theorems for claw-free graphs. Thus, line graphs constitute a proper subclass of the claw-free family. Line graphs overlap with claw-free perfect graphs by including all complete graphs KnK_n (for n≥1n \geq 1) as special cases, since the line graph of the star graph K1,nK_{1,n} is isomorphic to KnK_n, and complete graphs are both claw-free and perfect. Additionally, line graphs include all cycle graphs CnC_n (for n≥3n \geq 3), as the line graph of CnC_n is isomorphic to CnC_n itself; odd cycles of length at least 5 are claw-free but not perfect, illustrating that line graphs contain both perfect and non-perfect members of the claw-free family. This overlap highlights line graphs as a bridge between perfect and non-perfect claw-free structures. Finally, line graphs are a specific type of : L(G)L(G) is the intersection graph of the edges of GG, where each vertex of L(G)L(G) represents an edge of GG, and two vertices in L(G)L(G) are adjacent the corresponding edges in GG share a common vertex (i.e., their endpoint sets intersect). This representation underscores the geometric and set-theoretic connections of line graphs to the of the original graph.

Characterization and Recognition

Clique Partition Characterization

A graph HH is a line graph if and only if its edge set can be partitioned into cliques such that every vertex of HH lies in at most two of these cliques. This characterization, known as Krausz's theorem, provides a constructive way to verify membership in the class of line graphs by examining edge-disjoint cliques that cover all edges while respecting the degree-two intersection condition at vertices. In this partition, each in H=L(G)H = L(G) corresponds to either the set of edges incident to a single vertex in the original graph GG (forming a star subgraph K1,dK_{1,d} where d=deg⁡(v)d = \deg(v)), or the three edges of a in GG. The size of a star-induced equals the degree of the corresponding vertex in GG, reflecting the where vertices of L(G)L(G) (edges of GG) are adjacent if they share an endpoint. For instance, in the line graph of the K3K_3, which is itself K3K_3, the entire edge set forms a single of size 3, corresponding to the in K3K_3. The root graph's incidence relation underpins these cliques, as adjacency in L(G)L(G) arises precisely from shared endpoints in GG. This partition property implies that verifying the existence of such a can serve as a basis for line graph recognition, though efficient algorithms typically combine it with other structural checks.

Forbidden Induced Subgraphs

Beineke's theorem provides a forbidden characterization of line graphs. A graph is the line graph of some graph it contains none of nine specific induced subgraphs as minimal forbidden configurations. This characterization, established in 1970, is minimal in the sense that removing any one of the nine subgraphs from the list would allow some non-line graphs to be incorrectly classified as line graphs. The nine forbidden induced subgraphs, often referred to collectively as the Beineke graphs, each have between 4 and 6 vertices and represent structural impossibilities in the adjacency of edges within any underlying graph. For instance, the (also known as the ) is a 5-vertex graph consisting of a path of 3 (four vertices) with an additional edge connecting the second vertex to a vertex, forming a configuration resembling a chair; its induced presence implies an incompatible branching of edge adjacencies not possible under the root graph's vertex constraints. The long claw extends the by lengthening one arm to a path of 3, creating a 6-vertex where one path from the center is longer, which forbids it due to the inability to assign consistent incident edges without multiple incidences at a single vertex. The remaining six forbidden subgraphs include variants such as the umbrella (a triangle with two pendant edges attached to different vertices), certain chorded odd cycles like a 5-cycle with a chord, and other attached structures like a complete graph minus an edge (e.g., K5−eK_5 - e) or forked triangles. Each of these corresponds to a local configuration—such as an odd number of edges between partitions or incompatible multiple adjacencies—that cannot be realized as the incidence graph of edges in a simple graph, as proven through exhaustive case analysis of potential root graphs. This approach complements alternative characterizations, such as those based on clique partitions.

Recognition Algorithms

The recognition of line graphs has been advanced through several efficient algorithms that leverage structural characterizations to determine whether a given graph is the line graph of some root graph and, if so, to reconstruct it. One of the seminal approaches is the algorithm developed by Roussopoulos in 1973, which operates in O(\max{n, m}) time, where n is the number of vertices and m the number of edges. This method uses a partition of the edges of the input graph into cliques, corresponding to the stars and triangles in the root graph, to reconstruct the root via a rooting process that identifies odd triangles and builds the adjacency structure accordingly. Independently, Lehot proposed a similar linear-time in 1974, achieving O(n + m) complexity by employing an edge-coloring strategy on the input graph to simulate the matching of edges in the root graph, followed by verification and reconstruction steps that ensure the coloring aligns with the line graph properties. Both Roussopoulos's and Lehot's algorithms not only recognize line graphs but also output the root graph, making them practical for applications requiring inversion. These methods rely on the clique partition characterization rather than exhaustive searches, ensuring efficiency for sparse and dense graphs alike. An alternative recognition strategy involves checking for the absence of Beineke's nine forbidden s, which characterize non-line graphs. While isomorphism is NP-complete in general, the fixed small size (at most six vertices) of these specific subgraphs allows for polynomial-time verification, with naive yielding O(n^6) complexity, though optimized implementations reduce this to O(n^3) or better using multiplications or bounded-degree heuristics. This approach is theoretically foundational but less efficient in practice than the linear-time reconstruction methods for large graphs. Recent advancements have refined these techniques for even greater efficiency and applicability. For instance, the ILIGRA (Inverse Line Graph Recognition Algorithm) by Liu, Trajanovski, and Van Mieghem in 2015 provides a linear-time solution, O(n + m), by iteratively building the root graph through degree-based vertex selection and clique identification, with early termination if inconsistencies arise during construction. Additionally, dynamic algorithms like that of Degiorgi and Simon (1996) extend recognition to handle local graph modifications in O(1 + d) time per update, where d is the size of the modified adjacency list, enabling real-time applications in evolving networks. Up to 2025, no fundamentally new linear-time paradigms have emerged beyond these refinements, though degeneracy-based preprocessing has been integrated into hybrid tools for faster empirical performance on sparse graphs.

Iterated Line Graphs

Construction Process

The iterated line graph Lk(G)L^k(G) of a graph GG is constructed by recursively applying the line graph operator LL, where L1(G)=L(G)L^1(G) = L(G) and Lk(G)=L(Lk−1(G))L^k(G) = L(L^{k-1}(G)) for k≥2k \geq 2. This process begins with the standard line graph, in which vertices represent the edges of GG and adjacency exists between vertices if the corresponding edges in GG share a common vertex, and extends it through successive transformations. In the second iteration, L2(G)L^2(G), the vertices correspond to the edges of L(G)L(G), which themselves represent pairs of incident edges from the original graph GG; thus, each vertex in L2(G)L^2(G) encodes a path of length 2 in GG. The edges of L(G)L(G), and hence the vertices of L2(G)L^2(G), number ∑v∈V(G)(deg⁡G(v)2)\sum_{v \in V(G)} \binom{\deg_G(v)}{2}, reflecting quadratic growth relative to the degrees in GG for graphs with higher connectivity. Subsequent iterations amplify this effect, with the number of vertices in Lk(G)L^k(G) determined by the edge count of Lk−1(G)L^{k-1}(G), leading to rapid expansion in graphs where minimum degree is at least 3. For a finite connected graph GG, the sequence G,L(G),L2(G),…G, L(G), L^2(G), \dots exhibits one of four behaviors under iteration: the number of vertices steadily increases indefinitely; the sequence remains constant (as with cycle graphs); it stabilizes after one step (as with the star K1,3K_{1,3}); or it decreases to the empty graph (as with paths or disjoint edges). In small cases, such as those with all degrees at most 2, the process terminates or stabilizes quickly, while others grow without bound. As an example, iteration on a PnP_n (with n≥3n \geq 3) produces L(Pn)≅Pn−1L(P_n) \cong P_{n-1}, continuing to shorten the path until reaching the empty graph after n−1n-1 steps, thereby stabilizing thereafter.

Properties and Uniqueness

The k-iterated line graph L^k(G) of a connected graph G remains connected for all k ≥ 1, as the line graph operator preserves connectivity for graphs without isolated edges. Furthermore, if G is a connected of degree at least 3, the vertex-connectivity of L^k(G) equals its degree for sufficiently large k (specifically k ≥ 5), achieving the maximum possible connectivity. For a connected graph G that is not a path, cycle, or (termed prolific), the of L^k(G) satisfies diam(L^{k+1}(G)) = diam(L^k(G)) + 1 for all sufficiently large k, implying a linear growth in with the iteration depth. This behavior establishes an upper bound on the of L^k(G) that is at most 2k - 1 under standard assumptions on the initial of L(G) ≤ 2 for connected graphs excluding paths. Unlike the single iteration case, where Whitney's isomorphism theorem guarantees that most graphs are uniquely reconstructible from their line graph (except for K_3 and K_{1,3}), higher iterations do not preserve uniqueness of the graph. Multiple non-isomorphic graphs can yield isomorphic -iterated line graphs for > 1, as the mapping from G to L^(G) loses structural information through successive applications of the line graph operator, with known counterexamples for second-iterated line graphs. This failure of generalization limits reconstruction to specialized cases or additional constraints. The spectral properties of iterated line graphs for regular graphs exhibit distinctive patterns in their eigenvalues. For an r-regular graph G with r ≥ 3, all negative eigenvalues of L^k(G) are equal to -2 for every k ≥ 1. The adjacency matrix of L(G) relates to the incidence matrix B of G via A(L(G)) = B B^T - 2I, and eigenvalues of iterated versions arise from powers of this operator, with the largest eigenvalue (spectral radius) of L(G) being 2(r - 1) and subsequent iterations amplifying positive eigenvalues while stabilizing the negative spectrum at -2. As k increases, L^k(G) for a connected graph G with |E(G)| = m exhibits asymptotic toward a highly dense structure on an exponentially growing number of vertices, where the minimum degree and connectivity approach the theoretical maximum relative to the order, resembling properties of complete graphs in terms of expansion and linkage but on |E(L^{k-1}(G))| vertices. For large k, the graph becomes maximally connected, with growing linearly while the vertex count expands, leading to effective completeness in local neighborhoods.

Generalizations

Multigraph and Digraph Variants

In the context of , which permit multiple edges between the same pair of vertices, the line graph L(G) is constructed with vertices corresponding to the edges of G, and two such vertices are adjacent in L(G) if the corresponding edges in G share a common incident vertex. If G contains parallel edges, L(G) may itself be a , with the multiplicity of edges in L(G) reflecting the number of shared incidences between the original edges. This extension preserves the while accommodating parallels, distinguishing it from the simple graph case where at most one edge exists between any pair. Loops in a G, which are edges connecting a vertex to itself, are handled in the such that a loop at vertex becomes a vertex in L(G) adjacent to all vertices corresponding to other edges incident to , since they share . Some formulations may exclude loops or adjust degrees, but the standard definition integrates them via incidence. For directed graphs, or digraphs, the analogous structure is the line digraph L(D), where vertices correspond to the arcs of D. There is a directed edge in L(D) from the vertex representing arc (u, v) to the vertex representing arc (x, y) precisely when v = x, capturing head-to-tail incidence. This definition extends the undirected incidence relation to respect directionality, focusing on sequential connectivity along arcs. Line digraphs inherit key connectivity properties from their root digraphs. Specifically, L(D) is strongly connected if and only if D is strongly connected, assuming D has at least two vertices, thereby preserving the ability to traverse all vertices via directed paths. Regarding degrees, the out-degree in L(D) of the vertex for arc (u, v) equals the out-degree of v in D, while its in-degree equals the in-degree of u in D; this relation ensures that local arc behaviors translate to global degree patterns in the line digraph.

Total and Weighted Line Graphs

The total graph T(G)T(G) of a graph GG is defined as the graph with vertex set V(G)∪E(G)V(G) \cup E(G), where two vertices in T(G)T(G) are adjacent if and only if they correspond to elements of GG that are either adjacent vertices, incident vertex-edge pairs, or adjacent edges (sharing a common endpoint). This construction was introduced by Behzad in 1970 as part of a study of such graphs. The edges of T(G)T(G) thus consist of three disjoint types: the original edges of GG (connecting vertices in V(G)V(G)), the edges of the line graph L(G)L(G) (connecting vertices in E(G)E(G)), and the bipartite incidence edges between V(G)V(G) and E(G)E(G) (connecting a vertex to each of its incident edges). This structure positions T(G)T(G) as a natural extension that incorporates both vertex and edge information from GG, facilitating analyses that bridge vertex and edge properties, such as total colorings or traversability studies. For instance, the degree of a vertex vv in T(G)T(G) is deg⁡G(v)+deg⁡G(v)=2deg⁡G(v)\deg_G(v) + \deg_G(v) = 2\deg_G(v), while the degree of an edge-vertex e=uve = uv in T(G)T(G) is deg⁡G(u)+deg⁡G(v)\deg_G(u) + \deg_G(v). Total graphs of regular graphs exhibit strong regularity properties, often leading to strongly regular graphs when GG is complete. Weighted line graphs extend the line graph construction to weighted graphs GG, where each edge e∈E(G)e \in E(G) has an associated attribute such as or capacity, denoted w(e)w(e). In the weighted line graph WL(G)WL(G), the vertices correspond to E(G)E(G) as in the standard line graph, with adjacency preserved based on shared endpoints in GG; however, the edges of WL(G)WL(G) are assigned weights derived from the attributes of the corresponding original edges, for example, via a that normalizes the product of weights adjusted by endpoint strengths to account for degree heterogeneity. This weighting preserves incidence relations while encoding edge-specific metrics, enabling applications like community detection in weighted networks. In network flow contexts, such weighted line graphs model edge capacities or costs, transforming edge-flow problems into vertex-based analyses on WL(G)WL(G), where flow constraints on original edges become properties of vertices or weighted adjacencies. For multigraphs with parallel edges, weighted line graphs handle parallels by assigning distinct vertices in WL(G)WL(G) to each parallel edge, with weights reflecting their individual attributes.

Hypergraph and Disjointness Extensions

In hypergraph theory, the line graph of a H=(V,E)H = (V, E) is defined as the graph L(H)L(H) whose vertex set corresponds to the hyperedges in EE, with two vertices adjacent if and only if the corresponding hyperedges have a non-empty . This construction generalizes the classical line graph of a graph, where hyperedges replace edges and intersection replaces shared vertices. Seminal work by Berge refers to L(H)L(H) interchangeably as the line graph or representative graph of HH, emphasizing its role in capturing hyperedge overlaps. Two primary variants of line graphs for hypergraphs exist: intersection line graphs and incidence line graphs. The intersection line graph, as defined above, focuses on pairwise overlaps among hyperedges and is the direct analog of the graph line graph. In contrast, the incidence line graph is bipartite, with one part consisting of the vertices of HH and the other part consisting of the hyperedges of HH, where an edge connects a vertex to a hyperedge if the vertex belongs to that hyperedge; this structure encodes membership relations without emphasizing intersections. For kk-uniform hypergraphs (where all hyperedges have exactly kk vertices), the intersection line graph can be further specialized; for instance, if HH is linear (any two hyperedges intersect in at most one vertex), the resulting graph belongs to the class I1(k)I_1(k). The disjointness graph provides an abstract dual variant to the intersection line graph. For a such as the hyperedges of HH, the disjointness graph has the sets as vertices, with an edge between two vertices if the corresponding sets are disjoint. This construction inverts the adjacency condition of the intersection line graph, making it useful for studying complementary overlap properties in set systems. Hypergraph line graphs extend key properties of classical line graphs to higher uniformity. Notably, the line graphs of 2-uniform s (ordinary graphs) are claw-free, meaning they contain no induced K1,3K_{1,3} subgraph. For k≥3k \geq 3, the intersection graphs of linear kk-uniform s generalize this by avoiding infinite families of forbidden induced subgraphs, such as chains of diamond graphs, though they are not necessarily claw-free without additional constraints like minimum degree conditions (e.g., finite forbidden subgraph characterizations exist for minimum degree at least 2k2−3k+12k^2 - 3k + 1). These properties highlight how line graphs capture structural generalizations of claw-freeness, with recognition problems being NP-complete for k≥3k \geq 3.

Medial Graphs and Polyhedral Applications

In the context of plane graphs, the medial graph of a plane graph GG is constructed by placing a vertex at the of each edge of GG, with edges in the medial graph connecting these midpoints whenever the corresponding edges of GG are consecutive along the boundary of a face in the embedding of GG. This construction yields a 4-regular plane graph, as each original edge borders two faces and has two consecutive neighbors on each face boundary. Medial graphs bear a close relationship to line graphs, particularly for 3-regular (cubic) plane graphs. For a cubic plane graph GG, the medial graph coincides exactly with the line graph L(G)L(G), because the embedding ensures that edges incident at each vertex are consecutive along the faces, making the adjacency conditions equivalent. More generally, medial graphs of 3-connected planar graphs are 4-regular line graphs, inheriting planarity and connectivity from the original . In polyhedral applications, line graphs of the 1-skeletons of convex polyhedra play a key role in embedding theory. The 1-skeleton of a 3-dimensional convex polyhedron is a 3-connected planar graph by Steinitz's theorem, which states that a graph is realizable as the 1-skeleton of a convex 3-polytope if and only if it is planar and 3-connected. For a cubic 3-polytope Γ\Gamma, its line graph L(Γ)L(\Gamma) (equivalently, the medial graph M(Γ)M(\Gamma)) is a 4-regular 3-connected planar graph, hence also realizable as the 1-skeleton of another convex 3-polytope by Steinitz's theorem. This correspondence allows line graphs to map polyhedral structures to new embeddable graphs on surfaces, facilitating studies in geometric graph theory and polyhedral realizations. A representative example is the , whose 1-skeleton is a cubic 3-polytope with 8 vertices and 12 edges. The medial graph of this skeleton coincides with its line graph, forming a 4-regular graph with 12 vertices that is the 1-skeleton of the , another convex 3-polytope. This illustrates how medial and line graph constructions preserve polyhedral embeddability.

References

  1. https://faculty.etsu.edu/gardnerr/5340/notes-Godsil-Royle/Algebraic-GT-GR-1-7.pdf
  2. https://people.math.binghamton.edu/zaslav/Oldcourses/381.S11/line-graphs.pdf
  3. https://fs.unm.edu/IJMC/ANoteOnLineGraphs.pdf
  4. https://www.khoury.northeastern.edu/home/rhoshino/papers/gt3.pdf
  5. https://mathworld.wolfram.com/MetelskyGraphs.html
  6. https://www.sciencedirect.com/science/article/pii/S0012365X18302887
  7. https://www.math.kent.edu/~reichel/publications/linegraph.pdf
  8. https://www.zib.de/userpage/groetschel/teaching/WS1314/BondyMurtyGTWA.pdf
  9. https://mathworld.wolfram.com/LineGraph.html
  10. https://www.jetir.org/papers/JETIR1906S71.pdf
  11. http://people.math.binghamton.edu/zaslav/Oldcourses/381.S13/line-graphs.pdf
  12. https://math.wvu.edu/~hlai2/ClawFreeGraphs-10-20-2012.pdf
  13. https://web.math.princeton.edu/~mchudnov/claws_survey.pdf
  14. https://mathworld.wolfram.com/Claw-FreeGraph.html
  15. https://doc.sagemath.org/html/en/reference/graphs/sage/graphs/line_graph.html
  16. https://www.tandfonline.com/doi/full/10.1080/09728600.2022.2093146
  17. https://doi.org/10.1016/S0021-9800(70)80019-9
  18. https://math.wvu.edu/~hlai2/Pdf/Hong-Jian_Lai_Pdf/062-JCTB_2001.pdf
  19. https://www.sciencedirect.com/science/article/abs/pii/002001907390029X
  20. https://dl.acm.org/doi/10.1145/321850.321853
  21. https://link.springer.com/article/10.1007/s10852-014-9251-2
  22. https://link.springer.com/chapter/10.1007/3-540-60618-1_64
  23. https://arxiv.org/pdf/2105.02496
  24. https://www.math.sk/knor/PREP/p026.pdf
  25. https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1396&context=rhumj
  26. https://www.sciencedirect.com/science/article/pii/S0166218X0200197X
  27. https://www.researchgate.net/publication/220620185_Distances_in_iterated_line_graphs
  28. https://arxiv.org/abs/2105.08610
  29. https://onlinelibrary.wiley.com/doi/abs/10.1002/jgt.3190120218
  30. https://www.sciencedirect.com/science/article/pii/S0893965904003799
  31. https://arxiv.org/pdf/2105.08610
  32. https://www.dmlett.com/archive/v6/DML21_v6_pp68-83.pdf
  33. https://camo.ici.ro/journal/vol15/v15a7.pdf
  34. https://www.researchgate.net/publication/343081259_TOTAL_GRAPH_OF_REGULAR_GRAPHS
  35. https://iarjset.com/wp-content/uploads/2019/04/IARJSET.2019.6313.pdf
  36. https://arxiv.org/pdf/0912.4389
  37. https://www.nature.com/articles/s41598-022-07249-6
  38. https://arxiv.org/pdf/1809.08472
  39. https://www.sciencedirect.com/science/article/pii/0012365X77901273
  40. https://epjdatascience.springeropen.com/articles/10.1140/epjds/s13688-020-00231-0
  41. https://hypernetx.readthedocs.io/en/latest/hypergraph101.html
  42. https://arxiv.org/pdf/2112.05991
  43. https://nathanlindzey.com/disjointness_graphs_fpsac24.pdf
  44. https://www.sciencedirect.com/science/article/pii/S0012365X07010539
  45. https://arxiv.org/abs/2404.07819
  46. https://www.sciencedirect.com/science/article/pii/S0012365X06005279
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.