Hubbry Logo
Logic puzzleLogic puzzleMain
Open search
Logic puzzle
Community hub
Logic puzzle
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Logic puzzle
Logic puzzle
Logic puzzle
View on Wikipedia
from Wikipedia
Part of a series on
Puzzles
Jigsaw piece
Types
Guessing
Logic
Mechanical
Word and Number
Puzzle video games
Metapuzzles
Topics
Lists

A logic puzzle is a puzzle deriving from the mathematical field of deduction.

A logic puzzle grid. The only information filled in is that only Simon is 15 and Jane does not like the color green.

History

[edit]

The logic puzzle was first produced by Charles Lutwidge Dodgson, who is better known under his pen name Lewis Carroll, the author of Alice's Adventures in Wonderland. In his book The Game of Logic he introduced a game to solve problems such as confirming the conclusion "Some greyhounds are not fat" from the statements "No fat creatures run well" and "Some greyhounds run well".[1] Puzzles like this, where we are given a list of premises and asked what can be deduced from them, are known as syllogisms.[citation needed] Dodgson goes on to construct much more complex puzzles consisting of up to 8 premises.[citation needed]

In the second half of the 20th century mathematician Raymond M. Smullyan continued and expanded the branch of logic puzzles with books such as The Lady or the Tiger?, To Mock a Mockingbird and Alice in Puzzle-Land. He popularized the "knights and knaves" puzzles, which involve knights, who always tell the truth, and knaves, who always lie.[citation needed]

There are also logic puzzles that are completely non-verbal in nature. Some popular forms include Sudoku, which involves using deduction to correctly place numbers in a grid; the nonogram, also called "Paint by Numbers", which involves using deduction to correctly fill in a grid with black-and-white squares to produce a picture; and logic mazes, which involve using deduction to figure out the rules of a maze.[2]

Logic grid puzzles

[edit]

Another form of logic puzzle, popular among puzzle enthusiasts and available in magazines dedicated to the subject, is a format in which the set-up to a scenario is given, as well as the object (for example, determine who brought what dog to a dog show, and what breed each dog was), certain clues are given ("neither Misty nor Rex is the German Shepherd"), and then the reader fills out a matrix with the clues and attempts to deduce the solution. These are often referred to as "logic grid" puzzles. The data set of a logic grid puzzles can be any number of categories, but are limited by the corresponding increase in complexity, with most having only two, three, or even four categories.

While designed more as a table-based puzzle than a matrix, the most famous example of a logic-grid puzzle may be the so-called Zebra Puzzle, which asks the question Who Owned the Zebra?.

Common in logic puzzle magazines are derivatives of the logic grid puzzle called "table puzzles" that are deduced in the same manner as grid puzzles, but lack the grid either because a grid would be too large, or because some other visual aid is provided. For example, a map of a town might be present in lieu of a grid in a puzzle about the location of different shops.

See also

[edit]

References

[edit]

Sources

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Logic puzzle

View on Grokipedia
from Grokipedia
A logic puzzle is a type of challenge that relies on to arrive at a unique solution, providing all necessary clues within the problem itself without requiring external such as or specialized vocabulary. These puzzles derive from the mathematical field of deduction, often presenting scenarios involving relationships, constraints, or patterns that must be systematically resolved through logical inference. They emphasize precision in thinking, rewarding solvers who eliminate impossibilities and build conclusions step by step to reveal the complete answer. The roots of logic puzzles trace back to ancient philosophy, particularly Aristotle's development of syllogistic logic in the 4th century BCE, which laid the groundwork for formal deduction through structured arguments. In the 19th century, British mathematician and author (Charles Dodgson) significantly popularized the form by transforming abstract logical principles into accessible games and diagrams, as seen in his 1887 work The Game of Logic, which used visual aids to solve syllogisms, and his later Symbolic Logic (1896), introducing innovative methods like Carroll diagrams for handling complex propositions. The 20th century saw further evolution with contributions from logician , who crafted narrative-driven puzzles involving truth-tellers and liars on imaginary islands, connecting recreational logic to advanced concepts like . Common types of logic puzzles encompass a variety of formats designed to hone different aspects of reasoning. Grid-based elimination puzzles, such as those popularized in the and akin to (though its attribution to is apocryphal), require matching categories like people, items, and attributes using clues to fill a constraint table. Other prominent varieties include syllogisms, which test categorical deductions (e.g., "All A are B; some B are C"); truth-teller and liar problems, where statements from characters must be evaluated for consistency; river-crossing scenarios, like the classic wolf, goat, and cabbage puzzle; and modern numerical grids like Sudoku, which enforce rules on uniqueness within rows, columns, and blocks. These puzzles not only entertain but also build skills in analytical thinking, pattern recognition, and problem-solving, with applications in education, standardized testing (e.g., the LSAT's logic games section (1982–2024)), and even computational logic.

Definition and Characteristics

Core Definition

A logic puzzle is a type of intellectual challenge that requires from a set of given to deduce a unique solution, typically through the application of constraints to eliminate invalid possibilities. These puzzles emphasize systematic inference, where solvers build conclusions step by step based solely on the provided information, without needing external knowledge or chance. Unlike mathematical proofs, which aim to establish general truths applicable across infinite or broad domains using formal rigor, logic puzzles are confined to finite, self-contained scenarios designed for targeted problem-solving. In contrast to riddles, which often rely on wordplay, misdirection, or veiled meanings for resolution, logic puzzles prioritize explicit logical inference and consistency checking over linguistic tricks. The fundamental components of a logic puzzle include clues that supply the initial , variables representing entities such as , objects, or positions, and relations that define possible connections or assignments among them, such as or adjacency. These elements form a structured framework where interdependencies guide the elimination process toward the sole valid outcome.

Key Features and Elements

Logic puzzles are characterized by a finite set of possibilities, typically represented through discrete elements such as categories, items, or positions that solvers must assign or match according to given rules. These elements form a bounded search space, ensuring that the puzzle can be exhaustively explored without infinite options, as seen in grid-based variants where categories contain a fixed number of unique items (e.g., four clients, four prices, and four masseuses in a standard setup). Interdependent clues provide the constraints that link these elements across categories, creating a web of relationships that must be resolved collectively rather than in isolation; for instance, a clue stating "Hannah paid more than Teri’s client" ties specific entities together, forcing deductions that propagate through the entire structure. Well-formed logic puzzles emphasize ambiguity avoidance by guaranteeing a unique solution verifiable solely through logical deduction, eliminating the need for trial-and-error or external . This is a core design principle, as multiple solutions would undermine the deductive process, leading to inconsistencies or reliance on arbitrary choices; puzzle creators like those at Nikoli enforce absolute to maintain fairness and solvability. Constraints such as one-to-one mappings—where each item in one category pairs exclusively with one item in another—further enforce this, preventing overlaps and ensuring every element is utilized exactly once in the final arrangement. Cognitively, logic puzzles demand pattern recognition to identify recurring structures or implications within the clues and partial solutions, such as spotting unavoidable placements in a grid. Solvers engage in hypothesis testing by tentatively assigning elements and verifying them against the rules, refining or discarding ideas based on consistency, which mirrors formal proof construction. A key requirement is the avoidance of assumptions beyond the provided clues, training disciplined reasoning that relies only on explicit information to prevent errors from extraneous inferences.

Historical Development

Ancient and Early Examples

The earliest known examples of logic puzzles trace back to ancient , where riddles inscribed on cuneiform tablets required to interpret metaphors and scenarios from daily life, , and . Dating to around 1500 BCE in the Old Babylonian period, these riddles, such as a involving a ruler's deceit, challenged scribes to apply logical inference in educational contexts like surveyor training. These proto-logic forms prefigure modern puzzles by emphasizing constraint-based deduction without explicit rules. In , developed syllogistic logic in the 4th century BCE, laying the groundwork for formal deduction through structured arguments consisting of two premises leading to a conclusion, such as "All men are mortal; is a man; therefore, is mortal." His works in the formalized categorical propositions and syllogisms, influencing philosophical and for centuries and serving as a basis for later puzzle constructions. During the 5th century BCE, developed paradoxes that probed the foundations of motion, space, and infinity through seemingly contradictory logical arguments. Notable among them is the Achilles and the tortoise paradox, where Achilles cannot overtake a slower tortoise due to infinite subdivisions of distance, forcing readers to confront assumptions about continuity and . Similarly, the dichotomy paradox argues that to traverse any distance, one must first cover half, then half of the remainder, , rendering motion impossible—a challenge resolved only centuries later through but highlighting early rigorous logical debate. Medieval Islamic scholarship advanced mechanical logic through ingenious devices that incorporated automated sequences and feedback mechanisms, akin to puzzle-like automata. In the 9th century CE, the Banū Mūsā brothers—Muḥammad, Aḥmad, and al-Ḥasan—authored The Book of Ingenious Devices (c. 850 CE), detailing around 100 inventions including self-regulating fountains and trick vessels that operated via hidden logical principles, such as siphons triggering based on water levels to surprise users. These contraptions, blending with recreational intellect, demonstrated proto-computational logic in physical form, influencing later automata designs.

Modern Evolution and Popularization

In the , (Charles Lutwidge Dodgson) bridged verbal and formal logic with playful that demanded systematic transformation and inference. His "doublets," introduced in 1879, required changing one word into another by altering a single letter per step while forming valid English words, as in transforming "head" to "tail" via intermediates like "heal" and "teal." Published in works like The Game of Logic (1886), these puzzles used diagrams to visualize syllogisms, serving as accessible precursors to structured deduction in . The of logic puzzles began in the early with the pioneering work of British puzzle designer Henry Ernest Dudeney, whose collections such as The Canterbury Puzzles (1907) and Amusements in Mathematics (1917) systematized recreational logic problems, drawing on earlier traditions while introducing innovative mechanical and geometrical challenges that influenced subsequent creators. Dudeney's contributions, including the first crossnumber puzzle in 1926, helped elevate logic puzzles from casual diversions to structured intellectual exercises, fostering a growing audience through newspaper and magazine publications. In the 1930s, the launch of Publishing's puzzle magazines marked a significant milestone in mass dissemination, beginning with Dell Crossword Puzzles in 1931 and expanding to include logic and math-based formats that reached millions of readers annually. This periodical tradition continued unabated, providing consistent outlets for logic puzzles amid the rise of print media. The mid-20th century saw further popularization through Martin Gardner's "Mathematical Games" column in , which ran from 1957 to 1980 and introduced concepts like polyominoes and to a broad readership, sparking widespread interest in . Complementing this, Raymond Smullyan's books in the 1970s, such as What Is the Name of This Book? (1978) and The Chess Mysteries of (1979), blended logic with narrative storytelling, making accessible and engaging for non-specialists. A pivotal development came in 1979 with the invention of Sudoku (originally "Number Place") by American architect Howard Garns, published in Dell Math Puzzles & Logic Problems, which combined grid constraints with numerical deduction in a format ripe for global appeal. Though initially modest, Sudoku exploded in popularity after its 1984 adoption and renaming by Japan's Nikoli magazine, culminating in worldwide mania by 2005 following its introduction in () and major U.S. outlets, with sales of puzzle books surpassing millions and inspiring international competitions. The digital revolution from the 1990s onward transformed logic puzzles by enabling computer generation and interactive delivery, with early examples like (1990) introducing grid-based deduction to personal computers. Software advancements, such as Hong Kong judge Wayne Gould's 1997 program for creating unique Sudoku variants, facilitated endless puzzle variations and powered the shift to apps and online platforms in the , dramatically increasing accessibility via mobile devices and broadening participation beyond print media.

Major Types

Grid and Constraint-Based Puzzles

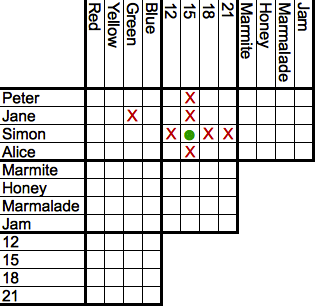
Grid and constraint-based puzzles, often referred to as logic grid puzzles, are deduction-based challenges that involve matching elements across multiple categories using provided clues to satisfy all constraints. These puzzles typically consist of an equal number of elements in each category—such as suspects, locations, or attributes—and require identifying the unique one-to-one correspondences that fulfill the conditions. The format draws from problems, where clues impose relational restrictions, and the goal is to derive the complete assignment through iterative elimination. The core structure utilizes a cross-referencing grid, a tabular matrix with rows for one category (e.g., individuals) and columns for others (e.g., professions, items), enabling visual tracking of possibilities. Solvers mark cells to indicate impossibilities (often with an "X") based on contradictory clues or confirmed matches (e.g., with a checkmark), progressively narrowing options until only valid pairings remain. This method leverages bijectivity—ensuring each element pairs uniquely across categories—and transitivity in deductions, such as inferring that if A relates to B and B excludes C, then A excludes C. For illustration, a simplified 3x3 grid for matching three friends to drinks and hobbies might start empty and evolve as clues eliminate options:
FriendTeaCoffeeHobby1Hobby2
Alice????
BobX??X
Carol??X?
Such grids promote systematic reasoning without requiring computational tools for small instances. Prominent examples include the , originally published in Life International magazine on December 17, 1962, featuring five houses distinguished by color, nationality, drink, cigarette, and pet, with the objective of determining the zebra's owner and the water drinker. This puzzle exemplifies the format's use of positional and relational clues, such as "the Norwegian lives next to the blue house," to constrain the grid. Logic grid variants extend to "who-dun-it" scenarios, common in mystery-themed puzzles, where categories like suspects, weapons, motives, and crime scenes are aligned to pinpoint the perpetrator through exclusionary evidence. These examples highlight the puzzle type's adaptability to narrative contexts while maintaining structural rigor. Weighing puzzles represent another form of constraint-based logic puzzles, employing a balance scale to identify an anomalous item (such as a heavier ball) among identical ones through a limited number of weighings. A classic example involves nine balls, one heavier, and two weighings: divide into three groups of three, weigh two groups against each other; the heavier group contains the heavy ball (or the unweighed if balanced), then repeat on the three suspects to identify it. Effective design principles focus on ensuring solvability via a unique solution derivable from logical , achieved by balancing clue density to avoid under- or over-constraint. Clues are crafted as atomic relations (e.g., equality, ordering, ) that interact multiplicatively, with redundancy minimized to prevent triviality; for instance, including implicit bijectivity constraints allows chain reactions in eliminations. Difficulty is modulated by clue ordering—presenting direct matches first to bootstrap deductions—while preserving human-solvable , typically for grids up to 5x5 categories without algorithmic aid. These principles underpin the puzzles' educational value in teaching constraint , akin to deductive techniques in broader logic solving.

Verbal and Lateral Thinking Puzzles

Verbal and lateral thinking puzzles constitute a category of logic puzzles that emphasize narrative scenarios, linguistic interpretation, and non-linear inference rather than strict deductive chains. These puzzles typically present an unusual situation with incomplete details, prompting the solver to probe through yes-or-no questions or to reframe assumptions for a resolution that defies initial expectations. Coined by in his 1967 book The Use of Lateral Thinking, the term "" describes a process of restructuring conventional thought patterns to generate novel solutions, often by incorporating seemingly irrelevant elements or escaping habitual logic. In puzzle form, this manifests as "situation puzzles" where the goal is to uncover hidden explanations through iterative questioning, fostering skills. A representative example is the "man in the " puzzle: A man lives on the tenth floor and takes the elevator to the ground floor each morning, but in the evening, he rides only to the seventh floor unless it is raining, in which case he goes to the tenth. The solution reveals that the man is a dwarf who cannot reach the higher buttons without using his as an extension on rainy days. Another example is the three switches and one light puzzle, where three switches outside a room control one light inside (only one is connected). The solver turns one switch on for several minutes then off, turns a second on, and enters the room once: if the light is on, it is the second switch; if off but the bulb is warm, it is the first; if off and cold, it is the third. This requires considering the bulb's temperature as an additional state. One prominent subtype is river-crossing puzzles, which involve transporting a set of entities—such as animals, people, or objects—across a river using a boat with limited capacity, while adhering to constraints that prevent incompatible combinations from being left unsupervised. These puzzles require planning a sequence of trips to satisfy all conditions, often balancing multiple risks simultaneously. The classic ", , and cabbage" variant, attributed to the 9th-century scholar of in his work Propositiones ad Acuendos Juvenes, tasks a farmer with ferrying the three items across without the wolf devouring the goat or the goat eating the cabbage; the boat holds only the farmer and one item at a time. This subtype highlights spatial and temporal reasoning within a framework, with solutions typically demanding back-and-forth traversals to isolate threats. Another key subtype comprises liar and truthteller dilemmas, where characters are divided into those who always tell the truth and those who always lie, and the solver must analyze their statements to identify types, resolve contradictions, or select correct actions like choosing a safe path. These puzzles rely on propositional logic embedded in dialogue, where self-referential or interdependent claims create paradoxes that demand case analysis. For instance, of truth-tellers and liars, if inhabitant A says "B is a liar" and B says "A is a truth-teller," deduction reveals both as liars since consistent truth would contradict the statements. A prominent example is the two doors and two guards puzzle, where one door leads to freedom and the other to doom; the solver asks one guard "If I asked the other guard which door leads to freedom, what would he say?" and chooses the opposite door. This exploits the interplay of truth-telling and lying to identify the correct path. Originating in ancient riddles but formalized in modern , such dilemmas train systematic elimination of impossible scenarios. Solving verbal and puzzles presents unique challenges, particularly in navigating linguistic and cultural influences . Wording in these puzzles often carries multiple meanings or relies on unstated assumptions, requiring solvers to clarify through precise questioning to avoid misdirection. Additionally, cultural shapes how scenarios are perceived; for example, assumptions about social norms or environmental elements in riddles can vary, leading to diverse solutions or dead ends across societies. These elements underscore the puzzles' role in promoting flexible , as popularized in the through de Bono's techniques and recreational literature.

Solving Methods

Deductive Reasoning Techniques

in logic puzzles involves a systematic process of drawing specific conclusions from given or clues, ensuring each logically follows without gaps. Solvers start by scanning all clues to identify direct implications, such as a statement that immediately assigns a value or eliminates a possibility within the puzzle's constraints. For instance, in a grid-based puzzle, a clue stating that "A is not B" allows marking exclusions directly. This initial scan establishes foundational truths upon which further deductions build. Once direct implications are noted, deductions extends the reasoning by linking multiple clues sequentially. If one clue implies a relationship (e.g., A implies B), and another excludes an option based on B (e.g., B excludes C), the solver infers that A excludes C, propagating information across the puzzle. This chain continues iteratively, updating the solution space until no new implications arise or the puzzle resolves. Such is essential in constraint-based puzzles like Einstein's riddle, where interdependencies require tracking multiple variables. Key techniques enhance this process, particularly in grid puzzles. Cross-hatching, a scanning method used in Sudoku-like puzzles, involves examining rows and columns within blocks to eliminate candidates for a specific number, revealing positions where it must fit. By systematically checking each row against a block's columns, solvers deduce hidden singles—cells with only one possible value—without advanced marking. Another technique, assumption-contradiction testing, applies proof by contradiction: assume a tentative assignment (e.g., a statement is true), derive consequences, and if they lead to an impossibility (e.g., violating a clue), reject the assumption. This method is particularly useful in verbal puzzles involving truth-tellers and liars, where assuming one role propagates contradictions to reveal the consistent solution. Common pitfalls in deductive reasoning include jumping to conclusions by integrating only partial clues, leading to invalid chains that overlook later contradictions. Solvers may also start with erroneous premises, such as misinterpreting a clue's scope, or apply flawed logic despite correct initial scans, resulting in configurations that violate uniqueness rules (e.g., multiple assignments in one category). To mitigate these, thorough re-scanning after each deduction ensures all clues remain consistent.

Systematic and Algorithmic Approaches

Systematic and algorithmic approaches to solving logic puzzles formalize the resolution through structured search strategies, enabling automated and scalable solutions beyond manual deduction. These methods model puzzles as problems (CSPs), where variables represent unknown elements (such as cell values or assignments), domains specify possible values, and constraints define compatibility rules derived from puzzle rules. algorithms serve as a foundational technique, systematically exploring the search space by assigning values to variables in sequence, checking constraints at each step, and retracting (backtracking) from invalid partial solutions to infeasible branches. This trial-and-error with significantly reduces computational effort compared to exhaustive . In CSP modeling, logic puzzles like Einstein's riddle or grid-based variants are encoded to leverage constraint propagation techniques, such as arc consistency, which eliminate inconsistent values from domains early to narrow the search space. can be enhanced with heuristics, like most-constrained-variable ordering, to prioritize variables with the fewest remaining options, further improving efficiency. For specific puzzle types, optimized implementations exist; for instance, Knuth's efficiently solves Sudoku by representing the problem as an instance using doubly-linked lists for rapid row and column updates during search. This structure allows O(1) time operations for adding and removing constraints, making it highly effective for combinatorial puzzles. Similarly, Prolog's (CLP) paradigm declaratively specifies puzzle rules and queries solutions via built-in and unification, as demonstrated in solving zebra puzzles or logic grids through finite domain constraints. Regarding efficiency, many logic puzzles exhibit , meaning that while solutions can be verified in polynomial time, finding one is computationally hard in the worst case, with no known polynomial-time for general instances. For example, the Sudoku completion problem—determining if a partially filled grid can be completed—is NP-complete, implying that or CSP solvers may require exponential time for difficult cases, though practical puzzles often solve quickly due to strong initial constraints. These approaches thus provide universal frameworks for puzzle resolution, balancing completeness with pragmatic performance.

Notable Examples

Classic Puzzles

One of the most renowned logic puzzles is Einstein's Riddle, also known as the , which involves deducing the arrangement of attributes across five adjacent houses. Each house is distinguished by its color (yellow, blue, red, white, or green), the nationality of its owner (British, Swedish, Danish, Norwegian, or German), the owner's pet (dog, birds, cats, horse, or fish), the preferred drink (tea, coffee, milk, beer, or water), and the brand of cigarette smoked (Pall Mall, Dunhill, Blends, Blue Master, or Prince). The puzzle provides 15 interlocking clues that eliminate possibilities through process of elimination, culminating in the question of who owns the fish. Although popularly attributed to as a boy in the early 1930s, the puzzle's origins are uncertain and the Einstein connection is widely regarded as a ; it first appeared in published form in Life International magazine on December 17, 1962, titled "Who Owns the Zebra?" The presents a counterintuitive probability dilemma inspired by the structure of the American game show , hosted by from 1963 to 1986. In the setup, a contestant selects one of three doors, one hiding a valuable prize (such as a car) and the other two concealing lesser prizes (s). The host, aware of the contents, deliberately reveals a behind one of the unchosen doors and then invites the contestant to switch their selection to the remaining unopened door. The core mechanic revolves around whether adhering to the original choice or switching maximizes the odds of winning, with analysis showing that switching yields a 2/3 probability of success compared to 1/3 for staying. Statistician Steve Selvin first formalized and solved the problem in correspondence published in The American Statistician in 1975, drawing directly from the show's mechanics. The Blue-Eyed Islanders puzzle exemplifies inductive logic through a of among perfect reasoners. It describes an isolated tribe where residents have either blue or brown eyes but are forbidden by custom from learning their own or discussing it; they observe others' eyes daily and depart the island at midnight if they deduce their own eye color is blue. A publicly states that she sees at least one person with blue eyes, providing information that was previously private but now shared. This announcement initiates a cascading deduction: if there were only one blue-eyed person, they would leave on the ; observing no departure allows others to infer higher counts, leading all blue-eyed islanders (say, n in number) to leave simultaneously on the nth night. As a modern variant of epistemic logic puzzles emphasizing iterated knowledge, it highlights how public declarations can synchronize private beliefs without direct communication. The light switch puzzle involves three switches outside a room containing one light bulb, where only one switch controls the bulb and the others do nothing. The solver may flip the switches freely but can enter the room only once to observe the bulb. The solution uses the heat retained by an incandescent bulb: turn the first switch on for several minutes then off, turn the second switch on, and enter the room. If the bulb is on, it is controlled by the second switch; if off but warm, by the first; if off and cold, by the third. The two doors and guards puzzle, a classic knights and knaves scenario, features two doors (one leading to freedom, one to doom) and two guards (one always tells the truth, one always lies). The solver may ask one question to one guard to determine the safe door. The effective question is: "If I asked the other guard which door leads to freedom, what would he say?" The response will indicate the door to doom, so the solver chooses the opposite door. The ball weighing puzzle requires identifying the single heavier ball among nine identical balls using a balance scale in only two weighings. The strategy divides the balls into three groups of three, weighs two groups against each other: if balanced, the heavier is in the unused group (weigh two from it to identify); if unbalanced, the heavier is in the heavier group (weigh two from it to identify).

Contemporary Variants

Contemporary logic puzzles have evolved through technological integration and cultural diversification, introducing interactive elements and global influences that build on traditional deductive frameworks. One prominent example is , invented in 2004 by Japanese math educator Tetsuya Miyamoto as a grid-based puzzle that combines Sudoku-like uniqueness rules with arithmetic constraints in defined "cages," where players must perform operations like addition, subtraction, multiplication, or division to reach target values. This variant emphasizes mathematical reasoning alongside logical placement, gaining widespread adoption in publications such as since 2009. Narrative-driven series like , launched in 2007 for the , further illustrate contemporary adaptations by embedding logic puzzles within storylines, where players solve brain teasers—ranging from spatial reasoning to riddles—to advance mysteries alongside protagonists Professor Layton and his apprentice Luke. Developed by Level-5, the series integrates over 150 puzzles per installment, rewarding solutions with in-game items that unlock additional challenges, thus blending entertainment with cognitive engagement. Global influences are evident in non-Western variants such as , a Japanese puzzle first published in by Nikoli under the authorship of れーにん, which merges binary logic with visual by requiring players to shade cells to form connected "islands" of specified sizes amid an "ocean" of black cells, avoiding isolated groups or 2x2 black blocks. This aesthetic-logical hybrid draws from imagery of invisible walls, promoting and connectivity deduction. Technology has spurred digital twists, including apps that incorporate timed logic challenges, such as decoding sequences or spatial manipulations under pressure to "escape" virtual environments, as seen in popular titles like Escape Time, which test and in themed scenarios. Additionally, AI-generated puzzles represent an innovative frontier, with algorithms automating the creation of cellular logic variants like ; for instance, techniques generate solvable grids by encoding constraints and ensuring unique solutions, enabling scalable, procedurally varied content. Advanced puzzles involving multi-level epistemic reasoning also appear in contemporary contexts, such as the K-level thinking puzzle where three students—Calvin, Zandra, and Eli—each receive a positive integer, with the numbers summing to 14. Calvin states, "I know that Zandra and Eli have different numbers." Zandra replies, "I already knew that all three of our numbers were different." Eli then deduces everyone's number. The solution is Calvin has 1, Zandra has 7, and Eli has 6. This puzzle illustrates higher-order reasoning about others' knowledge.

Applications and Impact

Educational and Cognitive Uses

Logic puzzles serve as effective tools for enhancing and problem-solving abilities in educational settings, fostering skills essential for analyzing complex scenarios and drawing reasoned conclusions. These activities encourage learners to identify patterns, test hypotheses, and eliminate inconsistencies systematically, which directly supports . Research indicates that regular engagement with logic puzzles improves such as , , and , contributing to overall mental agility. For instance, a neuroimaging study of middle-aged adults found that frequent participation in games and puzzles correlated with larger gray matter volumes in regions like the caudal , associated with executive processing, and better performance on neuropsychological tests of speed, flexibility, and verbal learning. In formal education, logic puzzles have been incorporated into curricula since the , particularly in gifted and talented programs to build STEM readiness by bridging abstract reasoning with practical applications in science, technology, engineering, and mathematics. These puzzles, such as grid-based constraint problems, help students develop deductive skills applicable to mathematical proofs and scientific inquiry, preparing them for higher-level STEM challenges. In philosophy classrooms, programs like , initiated in the late and expanded through the , use logic puzzles to teach argumentative reasoning and ethical analysis, promoting collaborative inquiry among students as young as elementary age. Similarly, in , visual and verbal logic puzzles are employed to reinforce logical structures, such as sequences and spatial relations, enhancing problem-solving proficiency without relying solely on rote . Beyond traditional classrooms, logic puzzles find applications in therapeutic contexts for individuals with cognitive disorders, including and , where they form part of cognitive remediation strategies to maintain or restore mental functions. A 2024 randomized controlled trial involving 375 older adults demonstrated that an 8-week intervention with brain stimulation significantly slowed cognitive decline over six years, particularly in those with remitted depression and impairment, as measured by standardized cognitive assessments. This approach, which includes puzzles and logic problems, leverages such activities to target by encouraging sustained attention and , offering a non-pharmacological method to support in clinical settings. Such evidence underscores the role of logic puzzles in bridging educational and rehabilitative goals, with benefits extending to improved daily functioning and reduced progression of cognitive deficits.

Cultural and Entertainment Roles

Logic puzzles have long served as a cornerstone of , embedding into , media, and interactive formats to engage audiences intellectually while providing leisure. In the late 19th century, Lewis Carroll (Charles Dodgson) pioneered their recreational use through works such as Pillow Problems (1893) and A Tangled Tale (1885), where he presented syllogistic challenges and paradoxes as whimsical diversions, making Aristotelian logic approachable for general readers beyond academic circles. This literary integration transformed puzzles from dry exercises into narrative elements, influencing subsequent authors to blend logic with storytelling for amusement. The 20th century saw further popularization through Raymond Smullyan's prolific output, beginning with What Is the Name of This Book? (1978), which framed knight-and-knave dilemmas—tales of truth-tellers and liars—as entertaining mysteries akin to , thereby illuminating concepts like in an accessible, playful manner. Smullyan's approach extended to television, as evidenced by his 1982 appearance on , where he shared logic riddles with host , exposing millions to such brainteasers as lighthearted fare. Meanwhile, print media amplified their reach; grid-based logic puzzles debuted in Magazines' Math Puzzles and Logic Problems in the late 1970s, evolving into fixtures of newspapers and magazines that fostered daily habits of problem-solving among diverse readerships. A hallmark of their cultural permeation came with Sudoku's explosion in popularity around 2005, when the number-placement puzzle was syndicated across hundreds of global newspapers, topping bestseller lists for puzzle books and symbolizing modern amid rising stress levels in urban life. In digital entertainment, the video game series, developed by Level-5 and released starting in , exemplifies this evolution by weaving over 150 logic puzzles per title into adventure narratives, achieving sales exceeding 18 million units worldwide as of 2023 and appealing to players through touch-screen interactivity on platforms. More recently, escape rooms—originating in in 2007 via company SCRAP's real-life adventure games—have become a thriving interactive genre, centering on collaborative logic challenges like ciphers and deduction grids to "escape" themed scenarios, with the format proliferating to approximately 2,350 venues in the U.S. alone as of 2019 and about 2,000 as of late 2024 following pandemic-related declines. These roles underscore logic puzzles' enduring appeal as both solitary diversions and communal spectacles, bridging intellectual rigor with widespread amusement.

References

  1. https://www.nytimes.com/2023/12/18/crosswords/logic-puzzles-how-to.html
  2. https://www.psychologytoday.com/us/blog/brain-workout/202009/what-is-logic-puzzle
  3. https://ima.org.uk/18429/games-for-your-mind-the-history-and-future-of-logic-puzzles/
  4. https://iep.utm.edu/lewis-carroll-logic/
  5. https://brilliant.org/wiki/logical-puzzles/
  6. https://www.lsac.org/blog/what-to-expect-starting-with-august-2024-lsat
  7. https://minds.wisconsin.edu/bitstream/handle/1793/61769/PaulaStevens.pdf?sequence=1&isAllowed=y
  8. https://arxiv.org/abs/2501.01433
  9. https://aclanthology.org/D15-1118.pdf
  10. http://gapdjournal.com/style/gapd-sample.pdf
  11. https://www.psychologytoday.com/ie/blog/brain-workout/201907/the-challenge-knights-and-knaves-puzzles
  12. https://www.livescience.com/18147-ancient-riddles-decoded-mesopotamia.html
  13. https://www.biblicalarchaeology.org/daily/news/riddle-me-this-king-nebuchadnezzar/
  14. https://plato.stanford.edu/entries/aristotle-logic/
  15. https://iep.utm.edu/zenos-paradoxes/
  16. https://www.1001inventions.com/banu-musa/
  17. https://invention.si.edu/invention-stories/ingenious-devices
  18. https://www.cs.brandeis.edu/~storer/JimPuzzles/BOOKS/DudeneyBooks/KnuthDudeneyStrandIndex.pdf
  19. https://people.uncw.edu/hermanr/Documents/Talks/Puzzles_and_Games___Smullyan.pdf
  20. https://www.pennydellpuzzles.com/about-us/
  21. https://www.martin-gardner.org/SciAm1.html
  22. https://philosophy.indiana.edu/about/history/in-memoriam/smullyan.html
  23. https://crownhillhf.org/howard-s-garns-inventor-of-sudoku/
  24. https://www.conceptispuzzles.com/index.aspx?uri=puzzle/sudoku/history
  25. https://dl.acm.org/doi/pdf/10.1287/ited.2014.0129
  26. http://www.math.ntua.gr/~papanico/PUZZLES/Zebra_Puzzle.pdf
  27. https://puzzling.stackexchange.com/questions/284/n-balls-and-a-scale
  28. https://www.sciencedirect.com/science/article/pii/S0004370221001016
  29. https://www.penguin.co.uk/books/178835/lateral-thinking-by-edward-de-bono/9780241257548
  30. https://journals.lww.com/nurseeducatoronline/fulltext/2019/07000/lateral_thinking_puzzles_encourage_creative.8.aspx
  31. https://www.sciencedirect.com/topics/psychology/lateral-thinking
  32. https://www.popularmechanics.com/science/math/a25716/solution-to-riddle-of-the-week-20/
  33. https://meetings.ams.org/math/jmm2025/meetingapp.cgi/Paper/39927
  34. https://www.psychologytoday.com/us/blog/brain-workout/201006/alcuins-river-crossing-puzzles-and-common-sense
  35. https://sites.millersville.edu/bikenaga/math-proof/truth-teller-or-liar/truth-teller-or-liar.html
  36. https://puzzling.stackexchange.com/questions/2188/two-doors-with-two-guards-one-lies-one-tells-the-truth
  37. https://webpages.charlotte.edu/~hbreiter/Exotic/Logic.pdf
  38. https://explore.gcts.edu/gacor1-03/pdf?docid=ZHM34-4365&title=analytical-puzzles.pdf
  39. https://neuroanthropology.net/2008/01/20/puzzles-and-cultural-differences/
  40. https://www.e-iji.net/dosyalar/iji_2020_1_30.pdf
  41. https://logic.puzzlebaron.com/how-to-solve-a-logic-puzzle.php
  42. https://www.stolaf.edu/people/hansonr/sudoku/explain.htm
  43. https://www.math.ucdavis.edu/~gravner/MAT108/materials/lp.pdf
  44. https://darkwing.uoregon.edu/~harrow/psy330/OFStudyGuide.htm
  45. https://www2.cs.sfu.ca/CourseCentral/417/havens/papers/Dechter_CSP_Rev.pdf
  46. http://aima.cs.berkeley.edu/newchap05.pdf
  47. https://cdn.aaai.org/AAAI/2007/AAAI07-361.pdf
  48. https://link.springer.com/chapter/10.1007/978-3-540-24662-6_11
  49. https://www.aswinvanwoudenberg.com/posts/who-owns-the-zebra/
  50. https://www.tandfonline.com/doi/abs/10.1080/00031305.1975.10479121
  51. https://www.popularmechanics.com/science/math/a26557/riddle-of-the-week-27-blue-eyed-islanders/
  52. https://plus.maths.org/content/puzzle-page-50
  53. https://plus.maths.org/content/weighing-balls
  54. https://www.kenkenpuzzle.com/about_facts
  55. https://gamerant.com/professor-layton-games-nintendo-consoles/
  56. https://www.gmpuzzles.com/blog/nurikabe-rules-and-info/
  57. https://teambuilding.com/blog/virtual-escape-rooms
  58. http://www.cs.uky.edu/ai/papers.dir/genpuzzles.pdf
  59. https://pmc.ncbi.nlm.nih.gov/articles/PMC4417099/
  60. https://doi.org/10.1007/s11682-014-9329-5
  61. https://p4c.com/about-p4c/history-of-p4c/
  62. https://www.beammath.org/beam-discovery-logic
  63. https://jamanetwork.com/journals/jamapsychiatry/fullarticle/2825463
  64. https://www.utsouthwestern.edu/newsroom/articles/year-2024/oct-combination-therapy-cognitive-decline.html
  65. https://press.princeton.edu/ideas/can-logic-be-fun
  66. https://press.princeton.edu/books/hardcover/9780691174075/games-for-your-mind
  67. https://www.ebsco.com/research-starters/mathematics/puzzles
  68. https://www.economist.com/business/2005/05/19/do-you-sudoku
  69. https://gamingbolt.com/professor-layton-series-has-sold-over-18-million-units-worldwide
  70. https://www.trapdoorescape.com/history-of-escape-rooms/
  71. https://roomescapeartist.com/2019/08/08/5-year-us-escape-room-industry-report-august-2019/
  72. https://roomescapeartist.com/2024/12/29/us-escape-room-industry-report-december-2024/
Add your contribution
Related Hubs
User Avatar
No comments yet.