Hubbry Logo
ZenithZenithMain
Open search
Zenith
Community hub
Zenith
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Zenith
Zenith
Zenith
View on Wikipedia
from Wikipedia
Diagram showing the relationship between the zenith, the nadir, and different types of horizon

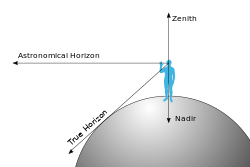
The zenith (UK: /ˈzɛnɪθ/, US: /ˈziː-/)[1][2] is the imaginary point on the celestial sphere directly "above" a particular location. "Above" means in the vertical direction (plumb line) opposite to the gravity direction at that location (nadir). The zenith is the "highest" point on the celestial sphere. The direction opposite of the zenith is the nadir.

Origin

[edit]

The word zenith derives from an inaccurate reading of the Arabic expression سمت الرأس (samt al-raʾs), meaning "direction of the head" or "path above the head", by Medieval Latin scribes in the Middle Ages (during the 14th century), possibly through Old Spanish.[3] It was reduced to samt ("direction") and miswritten as senit/cenit, the m being misread as ni. Through the Old French cenith, zenith first appeared in the 17th century.[4]

Relevance and use

[edit]
Angles and planes of a celestial sphere
The shadows of trees are the shortest on Earth when the Sun is directly overhead (at the zenith). This happens only at solar noon on certain days in the tropics, where the trees' latitude and the Sun's declination are equal.
See also: Culmination

The term zenith sometimes means the highest point, way, or level reached by a celestial body on its daily apparent path around a given point of observation.[5] This sense of the word is often used to describe the position of the Sun ("The sun reached its zenith..."), but to an astronomer, the Sun does not have its own zenith and is at the zenith only if it is directly overhead.

In a scientific context, the zenith is the direction of reference for measuring the zenith angle (or zenith angular distance), the angle between a direction of interest (e.g. a star) and the local zenith - that is, the complement of the altitude angle (or elevation angle).

The Sun reaches the observer's zenith when it is 90° above the horizon, and this only happens between the Tropic of Cancer and the Tropic of Capricorn. The point where this occurs is known as the subsolar point. In Islamic astronomy, the passing of the Sun over the zenith of Mecca becomes the basis of the qibla observation by shadows twice a year on 27/28 May and 15/16 July.[6][7]

At a given location during the course of a day, the Sun reaches not only its zenith but also its nadir, at the antipode of that location 12 hours from solar noon.

In astronomy, the altitude in the horizontal coordinate system and the zenith angle are complementary angles, with the horizon perpendicular to the zenith. The astronomical meridian is also determined by the zenith, and is defined as a circle on the celestial sphere that passes through the zenith, nadir, and the celestial poles.

A zenith telescope is a type of telescope designed to point straight up at or near the zenith, and used for precision measurement of star positions, to simplify telescope construction, or both. The NASA Orbital Debris Observatory and the Large Zenith Telescope are both zenith telescopes, since the use of liquid mirrors meant these telescopes could only point straight up.

On the International Space Station, zenith and nadir are used instead of up and down, referring to directions within and around the station, relative to the earth.

Zenith star

[edit]

Zenith stars (also "star on top", "overhead star", "latitude star")[8] are stars whose declination equals the latitude of the observers location, and hence at some time in the day or night pass culminate (pass) through the zenith. When at the zenith the right ascension of the star equals the local sidereal time at your location. In celestial navigation this allows latitude to be determined, since the declination of the star equals the latitude of the observer. If the current time at Greenwich is known at the time of the observation, the observers longitude can also be determined from the right ascension of the star. Hence "Zenith stars" lie on or near the circle of declination equal to the latitude of the observer ("zenith circle"). Zenith stars are not to be confused with "steering stars"[8] of a sidereal compass rose of a sidereal compass.

See also

[edit]

Media related to Zenith (topography) at Wikimedia Commons

References

[edit]

Further reading

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Zenith

View on Grokipedia
from Grokipedia
The zenith is the point on the directly above an observer at a particular on , defined by the vertical direction opposite to . It represents the highest point in the sky from the observer's perspective, forming one endpoint of the zenith distance used to measure the angular of celestial objects. The opposite point, directly below the observer, is known as the . In astronomy, the zenith plays a key role in the alt-azimuth coordinate system, where it corresponds to an altitude of 90°, aiding in the precise location of stars, planets, and other celestial bodies relative to the horizon. Observers at different latitudes experience varying zenith positions; for instance, at the , the passes through the zenith at certain times, while at the poles, the zenith aligns with the . This concept is fundamental to , including determining via meridian transits and calibrating instruments like telescopes. The term "zenith" entered English in the late via and , derived from the Arabic phrase samt ar-raʾs, meaning "path over the head" or "direction of the head," originally referring to the vertical path of celestial bodies. A scribal in medieval translations altered the Arabic samt (path) to something resembling cenit, which evolved into the modern spelling. Beyond its astronomical meaning, "zenith" is commonly used figuratively to denote the peak or culmination of any process, such as the highest point in a or the apex of achievement, , or influence. This metaphorical extension underscores its cultural significance in , , and everyday to describe moments of utmost or .

Etymology and Fundamentals

Etymology

The term "zenith" derives from the Arabic phrase samt ar-rās, meaning "path over the head" or "direction of the head," referring to the overhead point in the sky. This phrase originated in medieval Islamic astronomical texts, where it described the vertical path above an observer. The word entered European languages through translations of Arabic works during the Islamic Golden Age, reflecting the profound influence of Muslim scholars on Western astronomy; for instance, terms like zenith entered Latin via such transmissions, alongside concepts from astronomers like Al-Farghani (known in Latin as Alfraganus), whose 9th-century Elements of Astronomy was widely translated in Europe. In , the term appeared as cenit or zenit, often resulting from scribal misreadings of the , where the letter m in samt was confused with ni. It passed into as cenith by the late before entering English in the late in its astronomical sense, initially through scholarly texts on and . The word's adoption highlights the broader transmission of Islamic astronomical terminology to , including related terms like and . Variations persist across modern languages, such as French zénith (with an on the e) and Italian zenit, maintaining the core while adapting to local .

Definition

In astronomy, the zenith is defined as the point on the directly overhead an observer, representing the intersection of an upward vertical line—perpendicular to the local horizon plane—with the imaginary dome of the sky. This point lies at an altitude of 90° above the horizon and is diametrically opposite the , the corresponding point directly beneath the observer. The zenith thus marks the highest point in the observer's local sky, serving as a fundamental reference in celestial coordinate systems. Geometrically, the zenith aligns with an imaginary line passing from straight upward through the Earth's and extending to the on the far side of the planet, emphasizing its role as the apex of the local vertical axis. This configuration assumes a model and ignores minor local gravitational variations that might slightly deflect the plumb line defining "up." A distinction exists between the astronomical zenith, defined by the local direction of (plumb line), and the geocentric zenith, defined by the radial line from Earth's through the observer. Local irregularities, such as mountains, can cause slight deflections (up to arcminutes) between these directions, except at the and poles where they coincide due to symmetry. Atmospheric affects the apparent positions of celestial objects near the zenith minimally, as the effect decreases to zero at the zenith itself, but corrections are applied in precise measurements.

Celestial Geometry

Position on the Celestial Sphere

The celestial sphere is conceptualized as an imaginary sphere of infinite radius centered on the Earth, serving as a projection surface onto which the positions of stars and other celestial objects are mapped to simplify astronomical observations. Within this framework, the zenith represents the point on the sphere directly overhead an observer, defined by the local vertical direction perpendicular to the Earth's surface at that location. This positions the zenith as the north pole of the observer's personal horizon system, analogous to how the north celestial pole functions in the equatorial coordinate system. The horizon coordinate system, or alt-azimuth system, uses the observer's local horizon as its fundamental plane and the as its upper pole to describe celestial positions. In this system, any point on the is located using two coordinates: altitude, which measures the angular height above the horizon (ranging from 0° at the horizon to 90° at the ), and , which measures the horizontal direction clockwise from along the horizon (ranging from 0° to 360°). At the itself, the altitude is exactly 90°, but the becomes undefined, as the point lies at the convergence of all horizontal directions, similar to how is undefined at the Earth's geographic poles. Earth's rotation on its axis, completing one full turn approximately every 24 hours, causes the apparent motion of the relative to the observer. From the perspective of (which define an inertial reference frame), the zenith's direction in space shifts continuously westward, tracing a daily path on the celestial sphere that parallels the at an angular distance equal to the observer's . Consequently, different stars pass through the zenith over the course of a sidereal day, altering which celestial objects appear directly overhead at any given time.

Relation to Nadir and Horizon Coordinates

In the horizon , the serves as the to the , located directly below the observer at the opposite end of the local vertical axis. This positions the 180° away from the along the plumb line, forming a straight line that passes through the observer and the center of the , assuming a spherical model. The horizon, in turn, is defined as the on the that lies precisely 90° from both the zenith and the , perpendicular to the local vertical axis through the observer. This configuration places the horizon at an altitude of 0°, serving as the fundamental reference for measuring elevations above or below it in the alt-azimuth system. Within this framework, azimuth circles—also known as vertical circles or hour circles in the local system—function as meridians connecting the zenith to the , each representing a path along which altitude is measured for celestial objects. These circles are oriented by angles, typically measured clockwise from (or sometimes south in conventions) along the horizon to the point where the circle intersects it, enabling precise localization in the horizon-based used in .

Measurement and Properties

Zenith Distance

The zenith distance (ZD) of a celestial object is the angular separation between the object's position on the and the observer's zenith, measured along the that passes through both points. This measurement is fundamental in horizon-based coordinate systems, where it directly relates to the object's altitude above the horizon. The zenith distance is calculated using the formula
ZD=90∘−h,\text{ZD} = 90^\circ - h,
where hh is the altitude of the object. This relation holds because the zenith is at 90° altitude, making ZD the complement of the . In astronomical observations, zenith distance plays a key role in applying corrections for , which bends light rays and alters apparent positions. is minimal at the zenith (ZD = 0°) but increases toward the horizon, and standard refraction tables are typically indexed by ZD for precise adjustments up to about 45° or more. For instance, formulas for across all zenith distances incorporate terms that depend on ZD to account for varying atmospheric density effects. As an example, if a is observed at an altitude of 30°, its zenith distance is 60°, requiring a corresponding correction from tables to determine the true position. Historically, zenith distance computations from sextant-measured altitudes were essential for determination in , as detailed in standard texts like The American Practical Navigator.

Zenith Passage

Zenith passage, also known as at the zenith, refers to the moment when a celestial body reaches its highest point in the sky directly overhead, attaining a maximum altitude of 90 degrees where the zenith distance is zero. This event marks the upper of the body as it crosses the observer's meridian. The timing of zenith passage occurs when the celestial body's is zero, signifying its alignment with the local meridian at the peak of its daily path. For , which maintain fixed , this passage only happens for observers whose matches the star's , allowing the star to transit directly overhead. For instance, equatorial with a declination of 0 degrees pass through the zenith exclusively at the . A star that transits the zenith for a particular latitude is termed a zenith star, providing a unique observational reference point for that location. An example is Sirius, the brightest star in the night sky, with a declination of approximately -16.7 degrees, which culminates at the zenith for observers at latitudes around 16.7 degrees south. Observationally, is significant because it offers the clearest view of the celestial body, minimizing and distortion effects along the vertical , which aids in precise astronomical measurements and historical timekeeping.

Applications

In Astronomy

In astronomy, the zenith serves as a critical reference point for observations, minimizing atmospheric distortions and enabling precise measurements of celestial objects. Specialized instruments known as zenith telescopes are designed to point directly overhead or near the zenith, facilitating accurate determinations of star positions as they cross the meridian. These telescopes, often fixed in a vertical orientation, were pivotal in early precise , allowing astronomers to observe transits with reduced instrumental errors compared to more versatile but less stable equatorial mounts. One notable example is the zenith sector employed by Nevil Maskelyne in the 18th century. During his 1761 expedition to St. Helena to observe the transit of Venus, Maskelyne utilized a 10-foot zenith sector to measure stellar positions, addressing design challenges that improved portability and accuracy for remote observations. This instrument, a precursor to modern zenith telescopes, consisted of a telescope mounted on a sector frame to track stars near the zenith, contributing to advancements in meridian astronomy. Earlier, James Bradley commissioned a 12½-foot zenith sector in 1727, crafted by George Graham, which aided in his discoveries of stellar aberration and nutation through high-precision transit timings. The zenith's position also plays a key role in atmospheric corrections, particularly , which bends light rays and displaces apparent celestial positions. is minimal at the zenith—effectively zero under ideal conditions—and increases dramatically toward the horizon, reaching approximately 0.57° for standard and . This necessitates corrections in observations, with zenith-pointed measurements requiring the least adjustment, thus enhancing reliability for photometric and astrometric studies. Zenith , the angular separation from the zenith, is often referenced in these corrections to quantify refraction effects accurately. In modern astronomy, zenith observations remain valuable for reducing interference and improving precision. In , telescopes are frequently pointed near the zenith to minimize interference from terrestrial sources and atmospheric opacity, which is lowest overhead, allowing clearer detection of faint cosmic signals. Similarly, for satellite tracking, observations at or near the zenith provide the highest precision due to reduced and scintillation, enabling sub-arcsecond resolutions essential for orbital parameter refinements and monitoring.

In Navigation

In celestial navigation, the zenith serves as a key reference point for determining an observer's through the zenith distance (ZD) method. This technique involves measuring the from the zenith to a celestial body, such as the Sun or a , at the moment of its , or meridian passage, when it reaches its highest altitude above the horizon. The ZD is simply 90° minus the observed altitude of the body, and it relates directly to the observer's latitude (φ) and the body's (δ) via the equation ZD = |φ - δ|. Latitude is then computed as φ = δ + ZD or φ = δ - ZD, depending on whether the observer and the celestial body are on the same side of the (same-name case) or opposite sides (contrary-name case). This method provides a reliable way to fix position at sea without relying on electronic aids. For the pole star , with a of approximately 89°, the is nearly equal to 90° - ZD when culminates near the zenith, offering a straightforward in northern . A classic example is the noon sight of the Sun, taken at local apparent noon when the Sun crosses the meridian. If the observed altitude (h) is 50° and the Sun's is 20° N (with the observer in the and the Sun appearing south of the zenith), the ZD is 40°; the is then φ = 20° + 40° = 60° N. This calculation assumes the same-name case where exceeds . Historically, navigators employed instruments like the and the quadrant to measure altitudes for deriving ZD. The , an evolution of ancient designs popularized in the by explorers, was a handheld disk with a rotating for sighting celestial bodies against the horizon, enabling altitude measurements at sea despite ship motion. The quadrant, a quarter-circle device often used from the onward, was suspended vertically with a to align sights, allowing direct estimation of angles from the vertical (zenith) to the body in some configurations, though most measured horizon altitudes from which ZD was computed. In contemporary practice, while GPS has become the primary , celestial navigation based on zenith principles remains an essential backup for scenarios involving GPS denial, such as jamming or satellite failure. The U.S. reinstated celestial navigation training in , incorporating ZD calculations into curricula for officers to maintain proficiency independent of electronic systems. This ensures resilience in high-stakes maritime operations where traditional methods can still achieve positional accuracy within a few nautical miles under clear conditions.

References

  1. https://science.nasa.gov/learn/basics-of-space-flight/chapter2-2/
  2. https://www.physics.unlv.edu/~jeffery/astro/glossary/zenith.html
  3. https://graphics.stanford.edu/projects/gantry/design/astronomical_terms.html
  4. https://astro4edu.org/resources/glossary/term/390/
  5. https://www.etymonline.com/word/zenith
  6. https://www.merriam-webster.com/dictionary/zenith
  7. https://www.dictionary.com/browse/zenith
  8. https://islam-science.net/islamic-astronomy-by-owen-gingerich-3780/
  9. https://courses.ems.psu.edu/astro801/content/l1_p2.html
  10. http://astronomy.nmsu.edu/nicole/teaching/astr505/lectures/lecture08/slide02.html
  11. https://ui.adsabs.harvard.edu/abs/2005BaltA..14..277M
  12. https://vikdhillon.staff.shef.ac.uk/teaching/phy105/celsphere/phy105_celsphere_intro.html
  13. https://www.gb.nrao.edu/GBTopsdocs/primer/horizon_coordinate_system.htm
  14. https://astronomy.swin.edu.au/cosmos/h/Horizontal%2BCoordinate%2BSystem
  15. http://www.weatherscapes.com/Techniques/celestialsphere.php
  16. https://srmastro.uvacreate.virginia.edu/astr1230/LECTURES/LECTURE2/lecture2D-s13.html
  17. https://w.astro.berkeley.edu/~basri/astro10-03/lectures/StarMotions.htm
  18. https://www.synapses.co.uk/astro/earthmot.html
  19. https://astro.unl.edu/naap/motion2/observer.html
  20. https://aty.sdsu.edu/explain/sphere.html
  21. https://www.oxfordreference.com/display/10.1093/oi/authority.20110803133425459
  22. https://www.math.ubc.ca/~cass/courses/m308-02b/projects/jackson/Page2.html
  23. https://www.dictionary.com/browse/zenith-distance
  24. https://www.oxfordreference.com/display/10.1093/oi/authority.20110803095432203
  25. https://onlinelibrary.wiley.com/doi/pdf/10.1002/asna.2113180507
  26. https://skyandtelescope.org/astronomy-news/lie-back-look-up-and-find-your-zenith-stars/
  27. https://astro4edu.org/resources/glossary/term/147/
  28. http://lcd-www.colorado.edu/feathern/1030/coordinates.pdf
  29. https://gml.noaa.gov/ozwv/dobson/papers/report6/apph.html
  30. https://www.uibk.ac.at/en/the-historical-observatory/historical-instruments/the-oppolzer-zenith-telescope/
  31. http://dissertationreviews.org/nevil-maskelyne-the-zenith-sector/
  32. https://www.royalobservatorygreenwich.org/articles.php?article=1065
  33. https://britastro.org/2019/atmospheric-refraction
  34. https://ntrs.nasa.gov/api/citations/20140003876/downloads/20140003876.pdf
  35. https://www.dfmengineering.com/news_satellite_tracking_telescopes.html
  36. https://thenauticalalmanac.com/Formulas.html
  37. https://code7700.com/celestial_navigation.htm
  38. https://cseligman.com/laboratory/navcalc.htm
  39. https://www.marinenavigationbooks.com/images/pdfs/Chapter-06-Latitude-by-Noon-Sight.pdf
  40. https://oceanservice.noaa.gov/education/dyw-astrolabe.html
  41. https://celestialnavigation.net/resources/navigational-instruments/
  42. https://www.militarytimes.com/news/your-military/2015/11/01/naval-academy-reinstates-celestial-navigation/
  43. https://www.usni.org/magazines/proceedings/2025/january/ships-must-practice-celestial-navigation
Add your contribution
Related Hubs
User Avatar
No comments yet.