Community hub
0 subscribers7 pages, 0 posts
Recent from talks
All channels
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to Double-precision floating-point format.
Nothing was collected or created yet.
Double-precision floating-point format
View on Wikipediafrom Wikipedia
Double-precision floating-point format (sometimes called FP64 or float64) is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide range of numeric values by using a floating radix point.
Double precision may be chosen when the range or precision of single precision would be insufficient.
In the IEEE 754 standard, the 64-bit base-2 format is officially referred to as binary64; it was called double in IEEE 754-1985. IEEE 754 specifies additional floating-point formats, including 32-bit base-2 single precision and, more recently, base-10 representations (decimal floating point).
One of the first programming languages to provide floating-point data types was Fortran.[citation needed] Before the widespread adoption of IEEE 754-1985, the representation and properties of floating-point data types depended on the computer manufacturer and computer model, and upon decisions made by programming-language implementers. E.g., GW-BASIC's double-precision data type was the 64-bit MBF floating-point format.
| Floating-point formats |
|---|
| IEEE 754 |
|
| Other |
| Alternatives |
| Tapered floating point |
IEEE 754 double-precision binary floating-point format: binary64
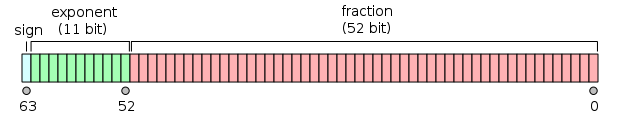
[edit]Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, in spite of its performance and bandwidth cost. It is commonly known simply as double. The IEEE 754 standard specifies a binary64 as having:
- Sign bit: 1 bit
- Exponent: 11 bits
- Significand precision: 53 bits (52 explicitly stored)
The sign bit determines the sign of the number (including when this number is zero, which is signed).
The exponent field is an 11-bit unsigned integer from 0 to 2047, in biased form: an exponent value of 1023 represents the actual zero. Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers.
The 53-bit significand precision gives from 15 to 17 significant decimal digits precision (2−53 ≈ 1.11 × 10−16). If a decimal string with at most 15 significant digits is converted to the IEEE 754 double-precision format, giving a normal number, and then converted back to a decimal string with the same number of digits, the final result should match the original string. If an IEEE 754 double-precision number is converted to a decimal string with at least 17 significant digits, and then converted back to double-precision representation, the final result must match the original number.[1]
The format is written with the significand having an implicit integer bit of value 1 (except for special data, see the exponent encoding below). With the 52 bits of the fraction (F) significand appearing in the memory format, the total precision is therefore 53 bits (approximately 16 decimal digits, 53 log10(2) ≈ 15.955). The bits are laid out as follows:
The real value assumed by a given 64-bit double-precision datum with a given biased exponent and a 52-bit fraction is
or
Between 252=4,503,599,627,370,496 and 253=9,007,199,254,740,992 the representable numbers are exactly the integers. For the next range, from 253 to 254, everything is multiplied by 2, so the representable numbers are the even ones, etc. Conversely, for the previous range from 251 to 252, the spacing is 0.5, etc.
The spacing as a fraction of the numbers in the range from 2n to 2n+1 is 2n−52. The maximum relative rounding error when rounding a number to the nearest representable one (the machine epsilon) is therefore 2−53.
The 11 bit width of the exponent allows the representation of numbers between 10−308 and 10308, with full 15–17 decimal digits precision. By compromising precision, the subnormal representation allows even smaller values up to about 5 × 10−324.
Exponent encoding
[edit]The double-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 1023; also known as exponent bias in the IEEE 754 standard. Examples of such representations would be:
e =000000000012=00116=1:
|
(smallest exponent for normal numbers) | ||
e =011111111112=3ff16=1023:
|
(zero offset) | ||
e =100000001012=40516=1029:
|
|||
e =111111111102=7fe16=2046:
|
(highest exponent) |
The exponents 00016 and 7ff16 have a special meaning:
000000000002=00016is used to represent a signed zero (if F = 0) and subnormal numbers (if F ≠ 0); and111111111112=7ff16is used to represent ∞ (if F = 0) and NaNs (if F ≠ 0),
where F is the fractional part of the significand. All bit patterns are valid encoding.
Except for the above exceptions, the entire double-precision number is described by:
In the case of subnormal numbers (e = 0) the double-precision number is described by:
Endianness
[edit]
Although many processors use little-endian storage for all types of data (integer, floating point), there are a number of hardware architectures where floating-point numbers are represented in big-endian form while integers are represented in little-endian form.[2] There are ARM processors that have mixed-endian floating-point representation for double-precision numbers: each of the two 32-bit words is stored as little-endian, but the most significant word is stored first. VAX floating point stores little-endian 16-bit words in big-endian order. Because there have been many floating-point formats with no network standard representation for them, the XDR standard uses big-endian IEEE 754 as its representation. It may therefore appear strange that the widespread IEEE 754 floating-point standard does not specify endianness.[3] Theoretically, this means that even standard IEEE floating-point data written by one machine might not be readable by another. However, on modern standard computers (i.e., implementing IEEE 754), one may safely assume that the endianness is the same for floating-point numbers as for integers, making the conversion straightforward regardless of data type. Small embedded systems using special floating-point formats may be another matter, however.
Double-precision examples
[edit]0 01111111111 00000000000000000000000000000000000000000000000000002 ≙ 3FF0 0000 0000 000016 ≙ +20 × 1 = 1
0 01111111111 00000000000000000000000000000000000000000000000000012 ≙ 3FF0 0000 0000 000116 ≙ +20 × (1 + 2−52) ≈ 1.0000000000000002220 (the smallest number greater than 1)
0 01111111111 00000000000000000000000000000000000000000000000000102 ≙ 3FF0 0000 0000 000216 ≙ +20 × (1 + 2−51) ≈ 1.0000000000000004441 (the second smallest number greater than 1)
0 10000000000 00000000000000000000000000000000000000000000000000002 ≙ 4000 0000 0000 000016 ≙ +21 × 1 = 2
1 10000000000 00000000000000000000000000000000000000000000000000002 ≙ C000 0000 0000 000016 ≙ −21 × 1 = −2
0 10000000000 10000000000000000000000000000000000000000000000000002 ≙ 4008 0000 0000 000016 ≙ +21 × 1.12 = 112 = 3
0 10000000001 00000000000000000000000000000000000000000000000000002 ≙ 4010 0000 0000 000016 ≙ +22 × 1 = 1002 = 4
0 10000000001 01000000000000000000000000000000000000000000000000002 ≙ 4014 0000 0000 000016 ≙ +22 × 1.012 = 1012 = 5
0 10000000001 10000000000000000000000000000000000000000000000000002 ≙ 4018 0000 0000 000016 ≙ +22 × 1.12 = 1102 = 6
0 10000000011 01110000000000000000000000000000000000000000000000002 ≙ 4037 0000 0000 000016 ≙ +24 × 1.01112 = 101112 = 23
0 01111111000 10000000000000000000000000000000000000000000000000002 ≙ 3F88 0000 0000 000016 ≙ +2−7 × 1.12 = 0.000000112 = 0.01171875 (3/256)
0 00000000000 00000000000000000000000000000000000000000000000000012 ≙ 0000 0000 0000 000116 ≙ +2−1022 × 2−52 = 2−1074 ≈ 4.9406564584124654 × 10−324 (smallest positive subnormal number)
0 00000000000 11111111111111111111111111111111111111111111111111112 ≙ 000F FFFF FFFF FFFF16 ≙ +2−1022 × (1 − 2−52) ≈ 2.2250738585072009 × 10−308 (largest subnormal number)
0 00000000001 00000000000000000000000000000000000000000000000000002 ≙ 0010 0000 0000 000016 ≙ +2−1022 × 1 ≈ 2.2250738585072014 × 10−308 (smallest positive normal number)
0 11111111110 11111111111111111111111111111111111111111111111111112 ≙ 7FEF FFFF FFFF FFFF16 ≙ +21023 × (2 − 2−52) ≈ 1.7976931348623157 × 10308 (largest normal number)
0 00000000000 00000000000000000000000000000000000000000000000000002 ≙ 0000 0000 0000 000016 ≙ +0 (positive zero)
1 00000000000 00000000000000000000000000000000000000000000000000002 ≙ 8000 0000 0000 000016 ≙ −0 (negative zero)
0 11111111111 00000000000000000000000000000000000000000000000000002 ≙ 7FF0 0000 0000 000016 ≙ +∞ (positive infinity)
1 11111111111 00000000000000000000000000000000000000000000000000002 ≙ FFF0 0000 0000 000016 ≙ −∞ (negative infinity)
0 11111111111 00000000000000000000000000000000000000000000000000012 ≙ 7FF0 0000 0000 000116 ≙ NaN (sNaN on most processors, such as x86 and ARM)
0 11111111111 10000000000000000000000000000000000000000000000000012 ≙ 7FF8 0000 0000 000116 ≙ NaN (qNaN on most processors, such as x86 and ARM)
0 11111111111 11111111111111111111111111111111111111111111111111112 ≙ 7FFF FFFF FFFF FFFF16 ≙ NaN (an alternative encoding of NaN)
0 01111111101 01010101010101010101010101010101010101010101010101012 ≙ 3FD5 5555 5555 555516 ≙ +2−2 × (1 + 2−2 + 2−4 + ... + 2−52) ≈ 0.33333333333333331483 (closest approximation to 1/3)
0 10000000000 10010010000111111011010101000100010000101101000110002 ≙ 4009 21FB 5444 2D1816 ≈ 3.141592653589793116 (closest approximation to π)
Encodings of qNaN and sNaN are not completely specified in IEEE 754 and depend on the processor. Most processors, such as the x86 family and the ARM family processors, use the most significant bit of the significand field to indicate a quiet NaN; this is what is recommended by IEEE 754. The PA-RISC processors use the bit to indicate a signaling NaN.
By default, 1/3 rounds down, instead of up like single precision, because of the odd number of bits in the significand.
In more detail:
Given the hexadecimal representation 3FD5 5555 5555 555516,
Sign = 0
Exponent = 3FD16 = 1021
Exponent Bias = 1023 (constant value; see above)
Fraction = 5 5555 5555 555516
Value = 2(Exponent − Exponent Bias) × 1.Fraction – Note that Fraction must not be converted to decimal here
= 2−2 × (15 5555 5555 555516 × 2−52)
= 2−54 × 15 5555 5555 555516
= 0.333333333333333314829616256247390992939472198486328125
≈ 1/3
Execution speed with double-precision arithmetic
[edit]Using double-precision floating-point variables is usually slower than working with their single precision counterparts. One area of computing where this is a particular issue is parallel code running on GPUs. For example, when using Nvidia's CUDA platform, calculations with double precision can take, depending on hardware, from 2 to 32 times as long to complete compared to those done using single precision.[4]
Additionally, many mathematical functions (e.g., sin, cos, atan2, log, exp and sqrt) need more computations to give accurate double-precision results, and are therefore slower.
Precision limitations on integer values
[edit]- Integers from −253 to 253 (−9,007,199,254,740,992 to 9,007,199,254,740,992) can be exactly represented.
- Integers between 253 and 254 = 18,014,398,509,481,984 round to a multiple of 2 (even number).
- Integers between 254 and 255 = 36,028,797,018,963,968 round to a multiple of 4.
- Integers between 2n and 2n+1 round to a multiple of 2n−52.
Implementations
[edit]Doubles are implemented in many programming languages in different ways. On processors with only dynamic precision, such as x86 without SSE2 (or when SSE2 is not used, for compatibility purpose) and with extended precision used by default, software may have difficulties to fulfill some requirements.
C and C++
[edit]C and C++ offer a wide variety of arithmetic types. Double precision is not required by the standards (except by the optional annex F of C99, covering IEEE 754 arithmetic), but on most systems, the double type corresponds to double precision. However, on 32-bit x86 with extended precision by default, some compilers may not conform to the C standard or the arithmetic may suffer from double rounding.[5]
Fortran
[edit]Fortran provides several integer and real types, and the 64-bit type real64, accessible via Fortran's intrinsic module iso_fortran_env, corresponds to double precision.
Common Lisp
[edit]Common Lisp provides the types SHORT-FLOAT, SINGLE-FLOAT, DOUBLE-FLOAT and LONG-FLOAT. Most implementations provide SINGLE-FLOATs and DOUBLE-FLOATs with the other types appropriate synonyms. Common Lisp provides exceptions for catching floating-point underflows and overflows, and the inexact floating-point exception, as per IEEE 754. No infinities and NaNs are described in the ANSI standard, however, several implementations do provide these as extensions.
Java
[edit]On Java before version 1.2, every implementation had to be IEEE 754 compliant. Version 1.2 allowed implementations to bring extra precision in intermediate computations for platforms like x87. Thus a modifier strictfp was introduced to enforce strict IEEE 754 computations. Strict floating point has been restored in Java 17.[6]
JavaScript
[edit]As specified by the ECMAScript standard, all arithmetic in JavaScript shall be done using double-precision floating-point arithmetic.[7]
JSON
[edit]The JSON data encoding format supports numeric values, and the grammar to which numeric expressions must conform has no limits on the precision or range of the numbers so encoded. However, RFC 8259 advises that, since IEEE 754 binary64 numbers are widely implemented, good interoperability can be achieved by implementations processing JSON if they expect no more precision or range than binary64 offers.[8]
Rust and Zig
[edit]See also
[edit]
Notes and references
[edit]- ^ William Kahan (1 October 1997). "Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic" (PDF). p. 4. Archived (PDF) from the original on 8 February 2012.
- ^ Savard, John J. G. (2018) [2005], "Floating-Point Formats", quadibloc, archived from the original on 2018-07-03, retrieved 2018-07-16
- ^ "pack – convert a list into a binary representation". Archived from the original on 2009-02-18. Retrieved 2009-02-04.
- ^ "Nvidia's New Titan V Pushes 110 Teraflops From A Single Chip". Tom's Hardware. 2017-12-08. Retrieved 2018-11-05.
- ^ "Bug 323 – optimized code gives strange floating point results". gcc.gnu.org. Archived from the original on 30 April 2018. Retrieved 30 April 2018.
- ^ Darcy, Joseph D. "JEP 306: Restore Always-Strict Floating-Point Semantics". Retrieved 2021-09-12.
- ^ ECMA-262 ECMAScript Language Specification (PDF) (5th ed.). Ecma International. p. 29, §8.5 The Number Type. Archived (PDF) from the original on 2012-03-13.
- ^ Bray, Tim (December 2017). "The JavaScript Object Notation (JSON) Data Interchange Format". Internet Engineering Task Force. Retrieved 2022-02-01.
- ^ "Data Types - The Rust Programming Language". doc.rust-lang.org. Retrieved 10 August 2024.
- ^ "Documentation - The Zig Programming Language". ziglang.org. Retrieved 10 August 2024.
Double-precision floating-point format
View on Grokipediafrom Grokipedia
Overview and Fundamentals
Definition and Purpose
Double-precision floating-point format, also known as binary64 in the IEEE 754 standard, is a 64-bit computational representation designed to approximate real numbers using a sign bit, an 11-bit exponent, and a 52-bit significand (mantissa).[6] This structure allows for the encoding of a wide variety of numerical values in binary scientific notation, where the number is expressed as ±(1 + fraction) × 2^(exponent - bias), providing a normalized form for most representable values.[7] The format was standardized in IEEE 754-1985 to ensure consistent representation and arithmetic operations across different computer systems, promoting portability in software and hardware implementations.[8] The primary purpose of double-precision format in computing is to achieve a balance between numerical range and precision suitable for scientific simulations, engineering analyses, and general-purpose calculations that require higher accuracy than single-precision alternatives.[9] It supports a dynamic range of approximately 10^{-308} to 10^{308}, enabling the representation of extremely large or small magnitudes without excessive loss of detail, and offers about 15 decimal digits of precision due to the 53-bit effective significand (including the implicit leading 1).[10] This precision is sufficient for most applications where relative accuracy matters more than absolute exactness, such as in physics modeling or financial computations. Compared to fixed-point or integer formats, double-precision floating-point significantly reduces the risks of overflow and underflow by dynamically adjusting the binary point through the exponent, allowing seamless handling of scales from subatomic to astronomical without manual rescaling.[11] This feature makes it indispensable for iterative algorithms and data processing where input values vary widely, ensuring computational stability and efficiency in diverse fields.[7]Historical Development and Standardization
The development of double-precision floating-point formats emerged in the 1950s and 1960s amid the growing need for mainframe computers to handle scientific and engineering computations requiring greater numerical range and accuracy than single-precision or integer formats could provide. The IBM 704, introduced in 1954 as the first mass-produced computer with dedicated floating-point hardware, supported single-precision (36-bit) and double-precision (72-bit) binary formats, enabling more reliable processing of complex mathematical operations in fields like physics and aerodynamics.[12][13] Subsequent IBM systems, such as the 7094 in 1962, expanded these capabilities with hardware support for double-precision operations and index registers, further solidifying floating-point arithmetic as essential for high-performance computing.[14] Pre-IEEE implementations varied significantly, contributing to interoperability challenges, but several influenced the eventual standard. The DEC PDP-11 minicomputer series, launched in 1970, featured a 64-bit double-precision floating-point format (G-floating) with an 8-bit exponent, 55-bit significand, and hidden-bit normalization, which bore close resemblance to the later IEEE design despite differences in exponent bias (129 versus 1023) and handling of subnormals; this format's structure informed discussions on binary representation during standardization efforts.[15][16] In the 1970s, divergent floating-point implementations across architectures led to severe portability issues, such as inconsistent rounding behaviors and unreliable results (e.g., distinct nonzero values yielding zero under subtraction), inflating software development costs and limiting numerical reliability. To address this "anarchy," the IEEE formed the Floating-Point Working Group in 1977 under the Microprocessor Standards Subcommittee, with initial meetings in November of that year; William Kahan, a key consultant to Intel and co-author of influential drafts, chaired efforts that balanced precision, range, and exception handling needs from industry stakeholders. The resulting IEEE 754-1985 standard formalized the 64-bit binary double-precision format (binary64), specifying a 1-bit sign, 11-bit biased exponent, and 52-bit significand (with implicit leading 1), thereby establishing a portable foundation for floating-point arithmetic in binary systems.[17][5][18] The core binary64 format has remained stable through subsequent revisions, which focused on enhancements rather than fundamental changes. IEEE 754-2008 introduced fused multiply-add (FMA) operations—computing with a single rounding step to minimize error accumulation—along with decimal formats and refined exception handling, while preserving the unchanged structure of binary64 for backward compatibility. The 2019 revision (IEEE 754-2019) delivered minor bug fixes, clarified operations like augmented addition, and ensured upward compatibility, without altering the binary64 specification to maintain ecosystem stability.[19][20][21][22] Adoption accelerated in the late 1980s, driven by hardware implementations that embedded the standard into mainstream processors. The Intel 80387 floating-point unit, released in 1987 as a coprocessor for the 80386, provided full support for IEEE 754 double-precision arithmetic, including 64-bit operations with 53-bit precision and exception handling, enabling widespread use in x86-based personal computers and scientific applications by the 1990s.[23][24]IEEE 754 Binary64 Specification
Bit Layout and Components
The double-precision floating-point format, designated as binary64 in the IEEE 754 standard, employs a fixed 64-bit structure to encode real numbers, balancing range and precision for computational applications. This layout divides the 64 bits into three primary fields: a sign bit, an exponent field, and a significand field.[25] The sign bit occupies the most significant position (bit 63), with a value of 0 denoting a positive number and 1 indicating a negative number. The exponent field spans the next 11 bits (bits 62 through 52), serving as an unsigned integer that scales the overall magnitude. The significand field, also known as the mantissa or fraction, comprises the least significant 52 bits (bits 51 through 0), capturing the binary digits that define the number's precision.[25][7] For normalized numbers, the represented value is given by the formula: where is the sign bit (0 or 1), is the significand bits interpreted as a 52-bit integer, and is the exponent field value as an 11-bit unsigned integer.[25][7] The sign bit straightforwardly controls the number's polarity. The exponent field adjusts the binary scale factor, while the significand encodes the fractional part after the radix point. In normalized form, the significand assumes an implicit leading 1 (the "hidden bit") before the explicit 52 bits, yielding a total of 53 bits of precision for the mantissa. This hidden bit convention ensures efficient use of storage by omitting the redundant leading 1 in normalized representations.[25][7] The 64-bit structure, with its 53-bit effective significand precision, supports approximately 15.95 decimal digits of accuracy, calculated as .[26][25]| Field | Bit Positions | Width (bits) | Purpose |
|---|---|---|---|
| Sign | 63 | 1 | Polarity (0: positive, 1: negative) |
| Exponent | 62–52 | 11 | Scaling factor (biased) |
| Significand | 51–0 | 52 | Precision digits (with hidden bit) |
Exponent Encoding and Bias
In the IEEE 754 binary64 format, the exponent is represented by an 11-bit field that stores a biased value to accommodate both positive and negative exponents using an unsigned binary encoding.[27] This bias mechanism adds a fixed offset to the true exponent, allowing the field to range from 0 to 2047 while mapping to effective exponents that span negative and positive values.[17] The bias value for binary64 is 1023, calculated as .[27] The true exponent is obtained by subtracting the bias from the encoded exponent : This formula enables the representation of normalized numbers with exponents ranging from to .[27] For normalized values, ranges from 1 to 2046, ensuring an implicit leading significand bit of 1 and full precision.[27] When the exponent field is all zeros (), it denotes subnormal (denormalized) numbers, providing gradual underflow toward zero rather than abrupt flushing.[27] In this case, the effective exponent is fixed at , and the value is computed as , where is the sign bit and is the 52-bit significand field interpreted as a fraction less than 1.[27] The all-ones exponent field () is reserved for special values.[27] The use of biasing allows the exponent to be stored as an unsigned integer, supporting signed effective exponents without the complexities of two's complement representation, such as asymmetric ranges or additional hardware for sign handling.[17] This design choice simplifies comparisons of floating-point magnitudes by treating the biased exponents as unsigned values and promotes efficient implementation across diverse hardware architectures.[17]Significand Representation and Normalization
In the IEEE 754 binary64 format, the significand, also known as the mantissa, consists of 52 explicitly stored bits in the trailing significand field, augmented by an implicit leading bit of 1 for normalized numbers, resulting in an effective precision of 53 bits. This design allows the significand to represent values in the range [1, 2) in binary, where the explicit bits capture the fractional part following the implicit integer bit. The choice of 53 bits provides a relative precision of approximately for numbers near 1, enabling the representation of about 15 to 17 decimal digits of accuracy.[28][2] Normalization ensures that the significand is adjusted to have its leading bit as 1, maximizing the use of available bits for precision. During the normalization process, the binary representation of a number is shifted left or right until the most significant bit is 1, with corresponding adjustments to the exponent to maintain the overall value; this implicit leading 1 is not stored, freeing up space for additional fractional bits. For a normalized binary64 number, the significand value is thus given by , where is the 52-bit fraction and is the unbiased exponent (with the biased exponent referenced from the encoding scheme). This normalization applies to all finite nonzero numbers except subnormals, ensuring consistent precision across the representable range.[28][2] Denormalized (or subnormal) numbers are used to represent values smaller than the smallest normalized number, extending the range toward zero without underflow to zero. In this case, the exponent field is set to zero, and there is no implicit leading 1; instead, the significand is interpreted as , where is the 52-bit fraction, resulting in reduced precision that gradually decreases as more leading zeros appear in the significand. This mechanism fills the gap between zero and the minimum normalized value of , with the smallest positive subnormal being .[28][2]Special Values and Exceptions
In the IEEE 754 binary64 format, zero is encoded with an exponent field of all zeros (unbiased value 0) and a significand of all zeros, where the sign bit determines positive zero (+0) or negative zero (-0). Signed zeros are preserved in arithmetic operations and are significant in contexts like division, where they affect the sign of the resulting infinity (e.g., and ). This distinction ensures consistent handling of directional rounding and branch cuts in complex arithmetic. Positive and negative infinity are represented by setting the exponent field to all ones (biased value 2047) and the significand to all zeros, with the sign bit specifying the direction. These values arise from operations like overflow, where a result exceeds the largest representable finite number (approximately ), or division by zero, producing or based on operand signs. Infinity propagates through most arithmetic operations, such as , maintaining the expected mathematical behavior while signaling potential issues. Not-a-Number (NaN) values indicate indeterminate or invalid results and are encoded with the exponent field set to 2047 and a non-zero significand. NaNs are categorized as quiet NaNs (qNaNs), which have the most significant bit of the significand set to 1 and silently propagate through operations without raising exceptions, or signaling NaNs (sNaNs), which have that bit set to 0 and trigger the invalid operation exception upon use. The remaining 51 bits of the significand serve as a payload, allowing implementations to embed diagnostic information, such as the operation that generated the NaN, in line with IEEE 754 requirements for NaN propagation in arithmetic (e.g., ). IEEE 754 defines five floating-point exceptions to handle edge cases, with default results that maintain computational continuity: the invalid operation exception, triggered by operations like or , yields a NaN; division by zero produces infinity; overflow rounds to infinity; underflow delivers a denormalized number or zero when the result is subnormal; and inexact indicates rounding occurred, though it does not alter the result. Implementations may enable traps for these exceptions, but the standard mandates non-trapping default behavior to ensure portability.Representation and Conversion
Converting Decimal to Binary64
Converting a decimal number to the binary64 format involves decomposing the number into its sign, exponent, and significand components according to the IEEE 754 standard.[28] For positive decimal numbers, the process begins by separating the integer and fractional parts. The integer part is converted to binary by repeated division by 2, recording the remainders as bits from least to most significant. The fractional part is converted by repeated multiplication by 2, recording the integer parts (0 or 1) until the fraction terminates or a sufficient number of bits (up to 53 for binary64) is obtained.[29] The combined binary representation is then normalized to the form , where is the fractional significand and is the unbiased exponent, by shifting the binary point left or right as needed. The significand is taken as the first 52 bits after the leading 1 (implicit in normalized form), with rounding applied if more bits are generated. The exponent is biased by adding 1023 to produce the 11-bit encoded exponent field.[28] For negative numbers, the process follows the same steps for the absolute value, after which the sign bit is set to 1.[28] Consider the decimal 3.5 as an illustrative outline. The integer part 3 is 11 in binary, and the fractional part 0.5 is 0.1 in binary, yielding 11.1. Normalizing gives , so the significand is 11 followed by 50 zeros (padded and rounded if necessary), the unbiased exponent is 1, and the biased exponent is , encoded in binary as 10000000000.[28] The reverse conversion from binary64 to decimal extracts the sign bit to determine positivity or negativity. The biased exponent is unbiased by subtracting 1023, and the significand is reconstructed as where is the 52-bit fraction. The value is then , which can be converted to decimal by scaling and summing powers of 2, though software typically handles the final decimal output.[28] Not all decimal numbers are exactly representable in binary64; for instance, 0.1 requires an infinite repeating binary fraction (0.0001100110011...), which is rounded to the nearest representable value, leading to approximation.[30]Endianness in Memory Storage
The IEEE 754 standard for binary floating-point arithmetic, including the double-precision (binary64) format, defines the logical bit layout—consisting of 1 sign bit, 11 exponent bits, and 52 significand bits—but does not specify the byte order in which these 64 bits are stored in memory.[31] This omission allows implementations to vary based on the underlying hardware architecture, leading to differences in how binary64 values are serialized into the 8 bytes of memory they occupy.[31] In big-endian storage, common in network protocols and certain processors, the most significant byte is placed at the lowest memory address, followed by successively less significant bytes. Conversely, little-endian storage, prevalent in x86 architectures, places the least significant byte first. For example, the double-precision representation of the value 1.0 has the 64-bit pattern 0x3FF0000000000000, where the sign bit is 0, the biased exponent is 0x3FF (1023 in decimal), and the significand is 0 (implied leading 1). In big-endian memory, this appears as the byte sequence 3F F0 00 00 00 00 00 00; in little-endian, it is reversed to 00 00 00 00 00 00 F0 3F.[31][32] These variations create portability challenges, particularly when transmitting binary64 data across systems or networks, where big-endian is the conventional order (as established in protocols like TCP/IP). Programmers must use byte-swapping functions—analogous to htonl/ntohl for integers but extended for 64-bit floats, such as via unions or explicit swaps—to ensure correct interpretation on heterogeneous platforms. Failure to account for endianness can result in corrupted values, as a little-endian system's output read on a big-endian system would reinterpret the bytes in reverse order. Platform-specific behaviors further highlight these differences: x86 processors (e.g., Intel and AMD) universally employ little-endian storage for binary64 values, while PowerPC architectures default to big-endian but support a little-endian mode configurable at runtime.[33] ARM processors, used in many embedded and mobile systems, also support both modes, with the double-precision format split into two 32-bit words: in big-endian, the most significant word (containing the sign, exponent, and high significand bits) precedes the least significant word; the reverse holds in little-endian.[32] Some processors, such as certain MIPS implementations, offer bi-endian flexibility, allowing software to select the order for compatibility in diverse environments.Double-Precision Numerical Examples
The double-precision floating-point format, as defined by the IEEE 754 standard, encodes real numbers using a 1-bit sign, 11-bit biased exponent, and 52-bit significand, allowing for precise representations of many values but approximations for others due to binary constraints.[27] To illustrate this encoding, consider the representation of the integer 1.0, which is a normalized value with an unbiased exponent of 0 and an implicit leading significand bit of 1 followed by all zeros.[34] For 1.0, the sign bit is 0 (positive), the biased exponent is 1023 (binary 01111111111, as the bias is 1023 for double precision), and the significand bits are all 0 (representing 1.0 exactly).[27] This yields the 64-bit binary pattern:0 01111111111 0000000000000000000000000000000000000000000000000000
0 01111111111 0000000000000000000000000000000000000000000000000000
0 00000000000 0000000000000000000000000000000000000000000000000001
0 00000000000 0000000000000000000000000000000000000000000000000001
Precision and Limitations
Exact Representation of Integers
In the IEEE 754 binary64 format, also known as double-precision floating-point, all integers with absolute values up to and including (exactly 9,007,199,254,740,992) can be represented exactly without any rounding error.[35] This range arises because the 53-bit significand, including the implicit leading 1, provides sufficient precision to encode every integer in this interval as a normalized binary floating-point number with no fractional part.[35] For any integer satisfying , the representation is unique and precise, ensuring that conversion to and from this format preserves the exact value.[36] Beyond , not all integers are exactly representable due to the fixed 53-bit significand length, which limits the density of representable values in higher magnitude ranges.[35] However, certain larger integers remain exact if their binary representation fits within the 53-bit significand after normalization; for instance, powers of 2 such as are exactly representable because they require only a single bit in the significand (the implicit 1) and an appropriate exponent.[37] In contrast, cannot be exactly represented, as it would require an additional bit beyond the significand's capacity, leading to rounding to the nearest representable value, which is .[37] For magnitudes greater than , the unit in the last place (ulp) increases with the exponent, meaning representable integers are spaced by multiples of , where is the unbiased exponent corresponding to the number's scale.[35] Thus, in the range from to , only even integers are representable, and the spacing doubles with each subsequent power-of-2 interval, skipping more values as the magnitude grows.[35] This behavior ensures that while some sparse integers remain exact within the overall exponent range (up to approximately ), dense integer sequences cannot be preserved without loss.[37] In programming contexts, this limit implies that integer computations in double-precision are safe and exact for values up to , beyond which developers must resort to integer types, big-integer libraries, or explicit casting to avoid unintended rounding during arithmetic operations or storage.[35] For example, adding 1 to in double-precision yields no change, highlighting the need for awareness in applications involving large counters or identifiers.[36]Rounding Errors and Precision Loss
In double-precision floating-point arithmetic, as defined by the IEEE 754 standard, computations may introduce inaccuracies due to the finite precision of the 53-bit significand (including the implicit leading 1). These inaccuracies arise primarily from rounding during operations like addition, subtraction, multiplication, and division, where the exact result cannot be represented exactly in the binary64 format. The standard specifies four rounding modes to control how these inexact results are handled: round to nearest (the default, which rounds to the closest representable value, with ties to even), round toward zero (truncation), round toward positive infinity, and round toward negative infinity.[38][4] To enable accurate rounding in hardware implementations, floating-point units typically employ extra bits beyond the 52 stored significand bits: a guard bit (capturing the first bit discarded during normalization or alignment), a round bit (the next bit), and a sticky bit (an OR of all remaining lower-order bits). These guard, round, and sticky bits (collectively GRS) allow the rounding decision to consider the full precision of intermediate results, minimizing the rounding error to at most half a unit in the last place (ulp). For instance, without these bits, alignment shifts in addition could lead to larger errors, but their use ensures compliance with IEEE 754's requirement for correctly rounded operations in the default mode.[35][6] Representation errors occur when a real number cannot be exactly encoded in binary64, such as the fraction 1/3, which is approximately 0.333... in decimal but requires an infinite binary expansion (0.010101...₂), resulting in the closest representable value of about 0.33333333333333331. Subtraction can exacerbate errors through catastrophic cancellation, where two nearly equal numbers are subtracted, yielding a result with significantly reduced precision; for example, subtracting two close approximations can amplify relative errors by orders of magnitude due to the loss of leading digits.[35] The unit roundoff, denoted ε and equal to 2^{-53} ≈ 1.11 × 10^{-16}, represents the maximum relative rounding error for a single operation in round-to-nearest mode, bounding the error by ε/2. In multi-step computations, such as summing terms in a series approximation for π (e.g., the Leibniz formula π/4 = 1 - 1/3 + 1/5 - ...), errors accumulate: each addition introduces a new rounding error of up to ε/2 times the current partial sum, leading to a total error that grows roughly linearly with the number of terms, potentially reaching O(n ε) for n additions in naive summation. Techniques like compensated summation can mitigate this growth, but unoptimized implementations may lose several digits of precision over many operations.[39][35] In long-term astronomical computations, such as calculating ephemerides of Earth's position, the limitations of double-precision become particularly evident due to the chaotic dynamics of the solar system. Double-precision provides approximately 15-17 decimal digits of precision, which is sufficient for accurate predictions over timescales up to about 50-300 million years using constrained astronomical solutions. However, over billions of years, the exponential sensitivity to initial conditions—characterized by Lyapunov times of 3-5 million years for inner planets—causes trajectories to diverge rapidly, rendering unique long-term predictions impossible with this format's finite precision.[40]Comparison to Single-Precision Format
The double-precision floating-point format, also known as binary64 in the IEEE 754 standard, utilizes 64 bits to represent a number, consisting of 1 sign bit, 11 exponent bits, and 52 significand bits, providing an effective precision of 53 bits (including the implicit leading 1 for normalized numbers). In contrast, the single-precision format, or binary32, employs 32 bits with 1 sign bit, 8 exponent bits, and 23 significand bits, yielding 24 bits of precision.[31] This structural expansion in double precision allows for greater representational capacity compared to single precision.[41] Regarding dynamic range, double precision accommodates normalized numbers from approximately (about ) to (about ), far exceeding the single-precision range of approximately (about ) to (about ).[31] This broader exponent field in double precision (11 bits versus 8) enables handling of much larger and smaller magnitudes without overflow or underflow in applications requiring extensive scales.[4] In terms of precision, double precision supports roughly 15 to 16 significant decimal digits, compared to 7 to 8 digits for single precision, due to the additional significand bits that minimize relative rounding errors.[31] This enhanced precision is particularly beneficial in iterative algorithms, where accumulated rounding errors in single precision can lead to significant divergence, whereas double precision maintains accuracy over more iterations by reducing the impact of each rounding step.[35] Double precision serves as the default for most scientific and engineering computations demanding high fidelity, such as simulations and data analysis, while single precision is favored in graphics rendering and machine learning inference to conserve memory and boost computational throughput.[41] A key property of conversions between formats is that transforming a single-precision value to double precision preserves the exact bit-for-bit representation by padding the significand with zeros, but the reverse conversion may introduce rounding errors if the value exceeds single precision's capabilities.[31]| Aspect | Single Precision (binary32) | Double Precision (binary64) |
|---|---|---|
| Total Bits | 32 | 64 |
| Significand Bits | 23 (24 effective) | 52 (53 effective) |
| Exponent Bits | 8 | 11 |
| Approx. Decimal Digits | 7–8 | 15–16 |
| Normalized Range | to | to |
Performance and Hardware
Execution Speed in Arithmetic Operations
The execution speed of double-precision floating-point arithmetic operations varies significantly depending on the operation type and hardware platform. On modern CPUs such as Intel Skylake and later microarchitectures, basic operations like addition (ADDPD) and multiplication (MULPD) exhibit latencies of approximately 4 cycles and reciprocal throughputs of 0.5 cycles per operation, enabling high throughput in pipelined execution. In contrast, more complex operations like division (DIVPD) and square root (SQRTSD) are notably slower, with latencies ranging from 14 to 23 cycles for division and 17 to 21 cycles for square root, alongside reciprocal throughputs of 6 to 11 cycles for division and 8 to 12 cycles for square root. These differences arise because addition and multiplication leverage dedicated, high-speed functional units, while division and square root require iterative algorithms such as SRT or Goldschmidt methods, which demand more computational steps.[42] A key optimization for improving both speed and accuracy in double-precision computations is the fused multiply-add (FMA) instruction, which computes in a single operation without intermediate rounding, unlike separate multiply and add instructions that introduce an extra rounding step. On Intel CPUs supporting FMA3 (e.g., Haswell and later), the VFMADDPD instruction has a latency of 4 cycles and a reciprocal throughput of 0.5 cycles, matching that of individual multiply or add operations but effectively doubling the performance for the combined computation in terms of instruction efficiency and reduced error accumulation. This can yield up to 2x speedup over separate operations in scenarios where multiply and add are chained dependently, as it avoids pipeline serialization and extra rounding overhead.[42][43] Performance bottlenecks in double-precision arithmetic often stem from the need for exponent alignment during addition and subtraction, where the mantissas of operands with differing exponents must be shifted to normalize them before summation, potentially introducing variable latency based on the exponent difference. In out-of-order execution pipelines, such alignments can lead to stalls if subsequent dependent operations cannot proceed while waiting for normalization or carry propagation resolution. On graphics processing units (GPUs), double-precision operations face additional hardware trade-offs; for instance, on NVIDIA's Volta architecture (e.g., Tesla V100), peak double-precision (FP64) performance reaches 7.8 TFLOPS, compared to 15.7 TFLOPS for single-precision (FP32), resulting in double-precision being roughly half the speed due to optimized tensor cores and CUDA cores prioritizing parallel single-precision workloads for graphics and machine learning.[44][45] Recent trends in CPU design emphasize single instruction, multiple data (SIMD) extensions to boost double-precision throughput. Intel's AVX-512 instructions enable vectorization across 512-bit registers, processing 8 double-precision elements simultaneously per instruction, which can deliver up to 8x the throughput of scalar double-precision operations on compatible processors like Skylake-X or Ice Lake, particularly in vectorizable workloads such as matrix multiplications or simulations. This improvement is contingent on compiler auto-vectorization or explicit intrinsics, and it scales performance while maintaining the per-element latency of underlying operations.[46][47]Hardware Support and Implementations
The Intel 8087, introduced in 1980 as a coprocessor for the 8086 microprocessor, provided early hardware support for double-precision floating-point operations, handling 64-bit IEEE 754-compliant formats alongside single-precision and extended-precision modes.[48] Today, double-precision support is ubiquitous in modern processors, though some architectures like RISC-V require optional extensions for full IEEE 754 compliance, such as the D extension for 64-bit floating-point registers and operations.[49] In x86 architectures, the Intel 80486 microprocessor, released in 1989, was the first to integrate a floating-point unit (FPU) on-chip, enabling native double-precision arithmetic without a separate coprocessor.[50] The Streaming SIMD Extensions 2 (SSE2), introduced with the Pentium 4 in 2000, further mandated comprehensive support for packed double-precision floating-point operations across 128-bit XMM registers, enhancing vectorized performance.[51] ARM architectures incorporate double-precision support through the NEON advanced SIMD extension, particularly in AArch64 mode, where it enables vectorized double-precision operations fully compliant with IEEE 754. In graphics processing units (GPUs), NVIDIA's CUDA cores provide double-precision capabilities starting from compute capability 1.3, but older architectures like those in the Maxwell family (compute capability 5.x) deliver only about 1/32 the throughput of single-precision operations due to limited dedicated hardware units.[52] Double-precision operations generally consume roughly twice the energy of single-precision ones, owing to the use of wider 64-bit registers and data paths that increase switching activity and capacitance.[53]Software Implementations
In C and Related Languages
In the C programming language, thedouble type is used to represent double-precision floating-point numbers, which occupy 64 bits and conform to the binary64 format defined by IEEE 754. The float type, in contrast, represents single-precision values using 32 bits in the binary32 format. These types provide the foundation for floating-point arithmetic in C and related languages like C++.[54]
The C99 standard (ISO/IEC 9899:1999) includes optional support for IEC 60559, the international equivalent of IEEE 754-1985, through its informative Annex F, though most modern implementations fully conform to these requirements for portability and predictability. This support ensures that floating-point types and operations adhere to IEEE 754 semantics, including normalized representations, subnormal numbers, infinities, and NaNs. The header <float.h> provides macros for querying implementation limits, such as DBL_MAX (the maximum representable finite value, approximately 1.7976931348623157 × 10^308) and DBL_MIN (the minimum normalized positive value, approximately 2.2250738585072014 × 10^{-308}), enabling portable bounds checking.[55][56]
C provides standard library functions in <math.h> for manipulating double-precision values according to IEEE 754 rules. For example, the frexp function decomposes a double-precision number into its significand (a value between 0.5 and 1.0) and an integral exponent to the base 2, facilitating exponent extraction for custom arithmetic or analysis. The C11 standard (ISO/IEC 9899:2011) enhances this with normative Annex F, which mandates fuller IEC 60559 (IEEE 754-2008 equivalent) compliance when the __STDC_IEC_559__ macro is defined, including precise exception handling via <fenv.h> and support for rounding modes like FE_TONEAREST.[57][54]
Developers must be aware of common pitfalls in handling double-precision values. Signed zeros (+0.0 and -0.0) are distinct representations that can affect operations like division (e.g., 1.0 / -0.0 yields -infinity), and comparisons involving NaNs always fail equality checks (NaN != NaN), as per IEEE 754 semantics. To safely test for special values, use functions like isnan (from <math.h>) for NaNs and isfinite for finite numbers, avoiding direct == comparisons which can lead to unexpected behavior.[58]
Compilers such as GCC and Clang offer optimization flags that can impact IEEE 754 strictness. The -ffast-math flag enables aggressive floating-point optimizations by assuming no NaNs or infinities, reordering operations, and relaxing rounding, which can improve performance but risks non-compliant results, such as incorrect handling of signed zeros or exceptions; it is not recommended for code requiring exact IEEE conformance.[59]
In related languages, Fortran's DOUBLE PRECISION type, introduced in Fortran 77 and retained in modern standards like Fortran 2003 and 2018, typically maps to the C double type, providing 64-bit IEEE 754 binary64 precision when using the ISO_C_BINDING module for interoperability (e.g., REAL(KIND=C_DOUBLE)).[60]
In Java and JavaScript
In Java, thedouble primitive type implements the IEEE 754 double-precision 64-bit floating-point format, providing approximately 15 decimal digits of precision for representing real numbers.[61] The Double class serves as an object wrapper for double values, enabling their use in object-oriented contexts such as collections and enabling methods for conversion, parsing, and string representation.[61] To ensure predictable rounding behavior across different hardware platforms, Java provides the StrictMath class, which implements mathematical functions with strict adherence to IEEE 754 semantics, avoiding platform-specific optimizations that could alter results.[62] Java Virtual Machines (JVMs) have been required to support IEEE 754 floating-point operations, including subnormal numbers and gradual underflow, since the initial release of JDK 1.0 in January 1996.[63]
In JavaScript, the Number type exclusively uses double-precision 64-bit IEEE 754 format for all numeric values, with no distinct single-precision type available, which simplifies numeric handling but limits exact integer representation to the safe range of -2^53 to 2^53.[64] This format was standardized in the first edition of ECMA-262 in June 1997, defining Number as the set of double-precision IEEE 754 values.[65] For integers exceeding this safe range, ECMAScript 2020 introduced the BigInt primitive, which supports arbitrary-precision integers without floating-point approximations.[66] Major engines like Google's V8 and Mozilla's SpiderMonkey fully implement IEEE 754 for Number, ensuring consistent behavior for operations such as addition, multiplication, and special values like NaN and Infinity.[67] However, JavaScript's loose equality operator == treats NaN as not equal to itself (returning false), a quirk of the language specification; the Object.is() method provides strict equality that correctly handles NaN comparisons.
Both Java and JavaScript assume host platform conformance to IEEE 754 for portability, but embedded JavaScript engines, such as those in resource-constrained devices, may introduce variations in precision or special value handling to optimize for limited hardware, potentially deviating from full standard compliance.
In Other Languages and Standards
In Fortran, double-precision floating-point numbers are declared using theDOUBLE PRECISION type or the non-standard REAL*8 specifier, both of which allocate 8 bytes and provide approximately 15 decimal digits of precision.[68][69] These types conform to the IEEE 754 binary64 format when compiled with modern Fortran processors supporting the standard. Fortran provides intrinsic functions to query limits, such as HUGE(), which returns the largest representable positive value for a given double-precision variable, approximately 1.7976931348623157 × 10^308.[70]
Common Lisp defines the DOUBLE-FLOAT type as a subtype of FLOAT, representing IEEE 754 double-precision values with 53 bits of mantissa precision.[71] This type supports IEEE special values including infinities, NaNs, and subnormals, enabling robust handling of exceptional conditions in numerical computations across Common Lisp implementations like SBCL and LispWorks.[72][73]
In Rust, the f64 primitive type implements the IEEE 754 binary64 double-precision format, offering 64 bits of storage with operations that adhere to the standard's requirements for accuracy and exceptions.[74] For interoperability with C code, f64 can be used with the #[repr(C)] attribute on structs to ensure layout compatibility, while the std::os::raw::c_double alias explicitly maps to f64 for foreign function interfaces.[75] Rust's std::f64 module enforces round-to-nearest-ties-to-even rounding as the default mode for arithmetic operations, consistent with IEEE 754 semantics.[74]
Zig's double-precision support mirrors C's double type through its f64 type, which is defined as an IEEE 754 binary64 float to facilitate seamless C ABI compatibility and low-level systems programming.[76]
In JSON, numeric values are serialized assuming IEEE 754 double-precision representation, as per RFC 8259, but the format provides no explicit guarantee of precision preservation during transmission or parsing, potentially leading to artifacts like 0.1 + 0.2 yielding 0.30000000000000004 in JavaScript environments.[77] The specification warns that numbers exceeding double-precision limits, such as very large exponents, should trigger errors to avoid silent precision loss.[77]References
- https://en.wikichip.org/wiki/intel/80486