Recent from talks
Nothing was collected or created yet.
Meantone temperament
View on WikipediaMeantone temperaments are musical temperaments;[1] that is, a variety of tuning systems constructed, similarly to Pythagorean tuning, as a sequence of equal fifths, both rising and descending, scaled to remain within the same octave. But rather than using perfect fifths, consisting of frequency ratios of value , these are tempered by a suitable factor that narrows them to ratios that are slightly less than , in order to bring the major or minor thirds closer to the just intonation ratio of or , respectively. Among temperaments constructed as a sequence of fifths, a regular temperament is one in which all the fifths are chosen to be of the same size.
Twelve-tone equal temperament (12 TET) is obtained by making all semitones the same size, with each equal to one-twelfth of an octave; i.e. with ratios 12√2 : 1. Relative to Pythagorean tuning, it narrows the perfect fifths by about 2 cents or 1/ 12 of a Pythagorean comma to give a frequency ratio of . This produces major thirds that are wide by about 13 cents, or 1/ 8 of a semitone. Twelve-tone equal temperament is almost exactly the same as 1/ 11 syntonic comma meantone tuning (1.955 cents vs. 1.95512).
Notable meantone temperaments
[edit]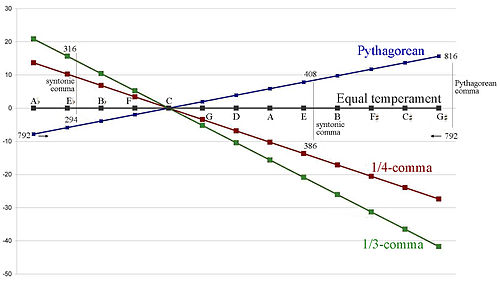
Quarter-comma meantone, which tempers each of the twelve perfect fifths by 1 / 4 of a syntonic comma, is the best known type of meantone temperament, and the term meantone temperament is often used to refer to it specifically. Four ascending fifths (as C G D A E) tempered by 1 / 4 comma (and then lowered by two octaves) produce a just major third (C E) (with ratio 5 : 4), which is one syntonic comma (or about 22 cents) narrower than the Pythagorean third that would result from four perfect fifths.
It was commonly used from the early 16th century till the early 18th, after which twelve-tone equitemperament eventually came into general use. For church organs and some other keyboard purposes, it continued to be used well into the 19th century, and is sometimes revived in early music performances today. Quarter-comma meantone can be well approximated by a division of the octave into 31 equal steps.
It proceeds in the same way as Pythagorean tuning; i.e., it takes the fundamental (say, C) and goes up by six successive fifths (always adjusting by dividing by powers of 2 to remain within the octave above the fundamental), and similarly down, by six successive fifths (adjusting back to the octave by multiplying by powers of 2 ). However, instead of using the 3 / 2 ratio, which gives perfect fifths, this must be divided by the fourth root of 81 / 80 , which is the syntonic comma: The ratio of the Pythagorean third 81 / 64 to the just major third 5 / 4 . Equivalently, one can use 4√5 instead of 3 / 2 , which produces the same slightly reduced fifths. This results in the interval C E being a just major third 5 / 4 , and the intermediate seconds (C D, D E) dividing C E uniformly, so D C and E D are equal ratios, whose square is 5 / 4 . The same is true of the major second sequences F G A and G A B.
However, there is a residual gap in quarter-comma meantone tuning between the last of the upper sequence of six fifths and the last of the lower sequence; e.g. between F♯ and G♭ if the starting point is chosen as C, which, adjusted for the octave, are in the ratio of 125 / 128 or −41.06 cents. This is in the sense opposite to the Pythagorean comma (i.e. the upper end is flatter than the lower one) and nearly twice as large.
In third-comma meantone, the fifths are tempered by 1 / 3 of a syntonic comma. It follows that three descending fifths (such as A D G C) produce a just minor third (A C) of ratio 6 / 5 , which is one syntonic comma wider than the minor third resulting from Pythagorean tuning of three perfect fifths. Third-comma meantone can be very well approximated by a division of the octave into 19 equal steps.
The tone as a mean
[edit]The name "meantone temperament" derives from the fact that in all such temperaments the size of the whole tone, within the diatonic scale, is somewhere between the major and minor tones (9:8 and 10:9 respectively) of just intonation, which differ from each other by a syntonic comma. In any regular system [1] the whole tone (as C D) is reached after two fifths (as C G D) (lowered by an octave), while the major third is reached after four fifths (C G D A E) (lowered by two octaves). It follows that in 1 / 4 comma meantone the whole tone is exactly half of the just major third (in cents) or, equivalently, the square root of the frequency ratio of 5 / 4 .
Thus, one sense in which the tone is a mean is that, as a frequency ratio, it is the geometric mean of the major tone and the minor tone: equivalent to 193.157 cents: the quarter-comma whole-tone size. However, any intermediate tone qualifies as a "mean" in the sense of being intermediate, and hence as a valid choice for some meantone system.
In the case of quarter-comma meantone, where the major third is made narrower by a syntonic comma, the whole tone is made half a comma narrower than the major tone of just intonation (9:8), or half a comma wider than the minor tone (10:9). This is the sense in which quarter-tone temperament is often considered "the" exemplary meantone temperament since, in it, the whole tone lies midway (in cents) between its possible extremes.[1]
History of meantone temperament and its practical implementation
[edit]Mention of tuning systems that could possibly refer to meantone were published as early as 1496 (Gaffurius).[2] Pietro Aron[3] (Venice, 1523) was unmistakably discussing quarter-comma meantone. Lodovico Fogliani[4] mentioned the quarter-comma system, but offered no discussion of it. The first mathematically precise meantone tuning descriptions are to be found in late 16th century treatises by Zarlino[5] and de Salinas.[6] Both these authors described the 1 / 4 comma, 1 / 3 comma, and 2 / 7 comma meantone systems. Marin Mersenne described various tuning systems in his seminal work on music theory, Harmonie universelle,[7] including the 31 tone equitempered one, but rejected it on practical grounds.
Meantone temperaments were sometimes referred to under other names or descriptions. For example, in 1691 Huygens[8] advocated the use of the 31 tone equitempered system (31 TET) as an excellent approximation for the 1 / 4 comma meantone system, mentioning prior writings of Zarlino and Salinas, and dissenting from the negative opinion of Mersenne (1639). He made a detailed comparison of the frequency ratios in the 31 TET system and the quarter-comma meantone temperament, which he referred to variously as temperament ordinaire, or "the one that everyone uses". (See references cited in the article Temperament Ordinaire.)
Of course, the quarter-comma meantone system (or any other meantone system) could not have been implemented with high accuracy until much later, since devices that could accurately measure all pitch frequencies didn't exist until the mid-19th century. But tuners could apply the same methods that "by ear" tuners have always used: Go up by fifths, and down by octaves, or down by fifths, and up by octaves, tempering the fifths so they are slightly smaller than the just 3/ 2 ratio. How tuners could identify a "quarter comma" reliably by ear is a bit more subtle. Since this amounts to about 0.3% of the frequency which, near middle C (~264 Hz), is about one hertz, they could do it by using perfect fifths as a reference and adjusting the tempered note to produce beats at this rate. However, the frequency of the beats would have to be slightly adjusted, proportionately to the frequency of the note. Alternatively the diatonic scale major thirds can be adjusted to just major thirds, of ratio 5/ 4 , by eliminating the beats.
For 12 tone equally-tempered tuning, the fifths have to be tempered by considerably less than a 1/4 comma (very close to a 1/11 syntonic comma, or a 1/12 Pythagorean comma), since they must form a perfect cycle, with no gap at the end ("circle of fifths"). For 1/4 comma meantone tuning, if one artificially stops after filling the octave with only 12 pitches, one has a residual gap between sharps and their enharmonic flats that is slightly smaller than the Pythagorean one, in the opposite direction. Both quarter-comma meantone and the Pythagorean system do not have a circle but rather a spiral of fifths, which continues indefinitely. Slightly tempered versions of the two systems that do close into a much larger circle of fifths are 31 TET for meantone, and 53 TET for Pythagorean.
Although meantone is best known as a tuning system associated with earlier music of the Renaissance and Baroque, there is evidence of its continuous use as a keyboard temperament well into the 19th century.
- "The mode of tuning which prevailed before the introduction of equal temperament, is called the Meantone System. It has hardly yet died out in England, for it may still be heard on a few organs in country churches. According to Don B. Yñiguez, organist of Seville Cathedral, the meantone system is generally maintained on Spanish organs, even at the present day." — Grove (1890)[9]
It has had a considerable revival for early music performance in the late 20th century and in newly composed works specifically demanding meantone by some composers, such as Adams, Ligeti, and Leedy.
Meantone temperaments
[edit]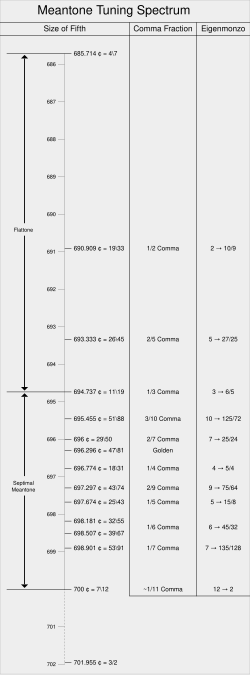
A meantone temperament is a regular temperament, distinguished by the fact that the correction factor to the Pythagorean perfect fifths, given usually as a specific fraction of the syntonic comma, is chosen to make the whole tone intervals equal, as closely as possible, to the geometric mean of the major tone and the minor tone. Historically, commonly used meantone temperaments, discussed below, occupy a narrow portion of this tuning continuum, with fifths ranging from approximately 695 to 699 cents.
Meantone temperaments can be specified in various ways: By what fraction of a syntonic comma the fifth is being flattened (as above), the width of the tempered perfect fifth in cents, or the ratio of the whole tone (in cents) to the diatonic semitone. This last ratio was termed "R" by American composer, pianist and theoretician Easley Blackwood. If R happens to be a rational number then is the closest approximation to the corresponding meantone tempered fifth within the equitempered division of the octave into equal parts. Such divisions of the octave into a number of small parts greater than 12 are sometimes refererred to as microtonality, and the smallest intervals called microtones.
In these terms, some historically notable meantone tunings are listed below, and compared with the closest equitempered microtonal tuning. The first column gives the fraction of the syntonic comma by which the perfect fifths are tempered in the meantone system. The second lists 5 limit rational intervals that occur within this tuning. The third gives the fraction of an octave, within the corresponding equitempered microinterval system, that best approximates the meantone fifth. The fourth gives the difference between the two, in cents. The fifth is the corresponding value of the fraction and the fifth is the number of equitempered (ET ) microtones in an octave.
| Meantone fraction of (syntonic) comma |
5-limit rational intervals | Size of ET fifths as fractions of an octave |
Error between meantone fifths and ET fifths (in cents) |
Blackwood’s ratio R = |
Number of ET microtones |
|---|---|---|---|---|---|
|
1/ 315 (very nearly |
For all practical purposes,
the fifth is a "perfect" 3 / 2 . |
31 / 53 | +0.000066
(+6.55227×10−5) |
9 / 4 = 2.25 | 53 |
|
1/ 11 ( or 1/ 12 Pythagorean comma) |
16384 / 10935 = 214 / 37 × 5 ( Kirnberger fifth: a just fifth flattened by a schisma.
|
7 / 12 | +0.000116
(+1.16371×10−4) |
2 / 1 = 2.00 | 12 |
| 1 / 6 | 45 / 32 and 64 / 45
(tritones) |
32 / 55 | −0.188801 | 9 / 5 = 1.80 | 55 |
| 1 / 5 |
16/ 15 and 15/ 8 (diatonic semitone and major seventh) |
25 / 43 | +0.0206757 | 7 / 4 = 1.75 | 43 |
| 1 / 4 |
5 / 4 and 8 / 5 (just major third and minor sixth) |
18 / 31 | +0.195765 | 5 / 3 = 1.66 | 31 |
| 2 / 7 |
25 / 24 and 48 / 25 (chromatic semitone and major seventh ) |
29 / 50 | +0.189653 | 8 / 5 = 1.60 | 50 |
| 1 / 3 |
6/ 5 and 5/ 3 (just minor third and major sixth) |
11 / 19 | −0.0493956 | 3 / 2 = 1.50 | 19 |
| 2 / 5 | 27/ 25
(large limma) |
26 / 45 | +0.0958 | 7 / 5 = 1.40 | 45 |
| 1 / 2 | 10/ 9 and 9/ 5
(just minor tone and diminished seventh) |
19 / 33 | −0.292765 | 5/ 4 = 1.25 | 33 |
Equal temperaments
[edit]In neither the twelve tone equitemperament nor the quarter-comma meantone is the fifth a rational fraction of the octave, but several tunings exist which approximate the fifth by such an interval; these are a subset of the equal temperaments ( "N TET" ), in which the octave is divided into some number (N) of equally wide intervals.
Equal temperaments that are useful as approximations to meantone tunings include (in order of increasing generator width) 19 TET (~ + 1 / 3 comma), 50 TET (~ + 2 / 7 comma), 31 TET (~ + 1 / 4 comma), 43 TET (~ + 1 / 5 comma), 55 TET (~ + 1 / 6 comma), 12 TET (= + 1 / 11 comma), and 53 TET (~ + 1 / 315 comma). 53 TET almost perfectly fits both Pythagorean tuning and 5 limit just intonation, with a few 7 limit and 11 limit intervals. The farther the tuning gets away from quarter-comma meantone, however, the less related the tuning is to harmonic ratios. This can be overcome by tempering the partials to match the tuning, which is possible, however, only on electronic synthesizers.[10] The following table gives various meantone temperaments

| 12 ET | 19 ET | 31 ET | 43 ET | 50 ET | 53 ET | 55 ET |
|---|---|---|---|---|---|---|
| = + 1 / 11 comma | ~ + 1 / 3 comma | ~ + 1 / 4 comma | ~ + 1 / 5 comma | ~ + 2 / 7 comma | ~ + 1 / 315 comma | ~ + 1 / 6 comma |
 |
 |
 |
 |
 |
 |
 |
Wolf intervals
[edit]A whole number of just perfect fifths will never add up to a whole number of octaves, because log2 3 is an irrational number. If a whole number of perfect fifths is stacked-up, then in order to close that stack to fit an octave, at least one of the intervals that is enharmonically equivalent to a fifth must have a different width than all the other fifths. For example, to make a 12 note chromatic scale in Pythagorean tuning close at the octave, one of the fifth intervals must be lowered ("out-of-tune") by the Pythagorean comma; this altered fifth is called a "wolf fifth" because it sounds similar to a fifth in its interval size and seems like an out-of-tune fifth, but is actually a diminished sixth (e.g. between G♯ and E♭). Likewise, 11 of the 12 perfect fourths are also in tune, but the remaining fourth is actually an augmented third (rather than a true fourth).
Wolf intervals are not inherent to a complete tuning system, rather they are an artifact of inadequate keyboards that do not have enough keys for all of the in-tune notes used in any given piece. Keyboard players then create a "wolf" by substituting a key that is actually in-tune with a different pitch, nearby the actual notated pitch, but not quite near enough to pass.[11]

The issue can be most easily shown by using an isomorphic keyboard, with many more than just 12 keys per octave, such as that shown in Figure 2 (on an isomorphic keyboard, any given musical interval has the same shape wherever it appears, except at the edges). Here's an example: On the keyboard shown in Figure 2, from any given note, the note that's a perfect fifth higher is always upward-and-rightward adjacent to the given note. There are no wolf intervals within the note-span of this keyboard. The problem is at the edge, on the note E♯. The note that's a perfect fifth higher than E♯ is B♯, which is not included on the keyboard shown (although it could be included in a larger keyboard, placed just to the right of A♯, hence maintaining the keyboard's consistent note-pattern). Because there is no B♯ button, when playing an E♯ power chord (open fifth chord), one must choose some other note, such as C, to play instead of the missing B♯.
Even edge conditions produce wolf intervals only if the isomorphic keyboard has fewer buttons per octave than the tuning has enharmonically-distinct notes.[12] For example, the isomorphic keyboard in Figure 2 has 19 buttons per octave, so the above-cited edge-condition, from E♯ to C, is not a wolf interval in 12 tone equal temperament (TET), 17 TET, or 19 TET; however, it is a wolf interval in 26 TET, 31 TET, and 50 ET. In these latter tunings, using electronic transposition could keep the current key's notes on the isomorphic keyboard's white buttons, such that these wolf intervals would very rarely be encountered in tonal music, despite modulation to exotic keys.[13]
Isomorphic keyboards expose the invariant properties of the meantone tunings of the syntonic temperament isomorphically (that is, for example, by exposing a given interval with a single consistent inter-button shape in every octave, key, and tuning) because both the isomorphic keyboard and temperament are two-dimensional (i.e., rank 2) entities.[14] One-dimensional N key keyboards (where N is some number) can expose accurately the invariant properties of only a single one-dimensional tuning in N TET; hence, the one-dimensional piano-style keyboard, with 12 keys per octave, can expose the invariant properties of only one tuning: 12 TET.
When the perfect fifth is exactly 700 cents wide (that is, tempered by almost exactly 1/11 of a syntonic comma, or exactly 1/12 of a Pythagorean comma) then the tuning is identical to the familiar 12 tone equal temperament. This appears in the table above when R = 2:1 .
Because of the compromises (and wolf intervals) forced on meantone tunings by the limitation of having only 12 key per octave on a conventional piano-style keyboard, well temperaments and eventually equal temperament became more popular.
Using standard interval names, twelve fifths equal six octaves plus one augmented seventh; seven octaves are equal to eleven fifths plus one diminished sixth. Given this, three "minor thirds" are actually augmented seconds (for example, B♭ to C♯), and four "major thirds" are actually diminished fourths (for example, B to E♭). Several triads (like B E♭ F♯ and B♭ C♯ F) contain both these intervals and have normal fifths.
Extended meantones
[edit]All meantone tunings fall into the valid tuning range of the syntonic temperament, so all meantone tunings are syntonic tunings. All syntonic tunings, including the meantones and the various just intonations, conceivably have an infinite number of notes in each octave, that is, seven natural notes, seven sharp notes (F♯ to B♯), seven flat notes (B♭ to F♭) (which is the limit of the orchestral harp, which allows 21 distinct pitches per octave); then double sharp notes (F![]() to B
to B![]() ), double flat notes (F
), double flat notes (F![]() to B
to B![]() ), triple sharps and flats, and so on. In fact, double sharps and flats are uncommon, but still needed, but triple sharps and flats are almost never seen, so might be skipped or compromised. In any syntonic tuning that happens to divide the octave into a small number of equally wide smallest intervals (such as 12, 19, or 31 ET), this extended set of notes still exists, but is not infinite, since some notes will be equivalent. For example, in 19 ET, E♯ and F♭ are the same pitch; in 31 ET, C
), triple sharps and flats, and so on. In fact, double sharps and flats are uncommon, but still needed, but triple sharps and flats are almost never seen, so might be skipped or compromised. In any syntonic tuning that happens to divide the octave into a small number of equally wide smallest intervals (such as 12, 19, or 31 ET), this extended set of notes still exists, but is not infinite, since some notes will be equivalent. For example, in 19 ET, E♯ and F♭ are the same pitch; in 31 ET, C![]() ♯ and E
♯ and E![]() are identical, as are E
are identical, as are E![]() and G
and G![]() ; and in just intonation for C major, C♯ D
; and in just intonation for C major, C♯ D![]() are within 8.1 ¢, and so can be tempered to be identical, with the compromise note being only a tolerable 4 ¢ off for each.
are within 8.1 ¢, and so can be tempered to be identical, with the compromise note being only a tolerable 4 ¢ off for each.
Many musical instruments are capable of very fine distinctions of pitch, such as the human voice, the trombone, unfretted strings such as the violin family and fretless guitars, and lutes with movable frets. These instruments are well-suited to the use of meantone tunings.
On the other hand, the conventional piano keyboard only has twelve note-producing keys per octave, making it poorly suited to any tunings other than 12 ET or well temperaments. Almost all of the historic problems with the meantone temperament are caused by the failure to map meantone's infinite number of notes per octave to a finite number of piano keys. This is, for example, the source of the "wolf fifth" discussed above. When choosing which notes to map to the piano's black keys, it is convenient to choose those notes that are common to a small number of closely related keys, but this will only work up to the edge of the octave; when crossing up or down to an adjacent octave, for some of the intervals must be a "wolf fifth" – that is, slightly flatter than the others, as described above.
The existence of the "wolf fifth" is one of the reasons why, before the introduction of well temperament, instrumental music generally stayed in a number of "safe" tonalities that did not involve the "wolf fifth" (which was generally put between G♯ and E♭).
Throughout the Renaissance and Enlightenment, theorists as varied as Nicola Vicentino, Francisco de Salinas, Fabio Colonna, Marin Mersenne, Christiaan Huygens, and Isaac Newton advocated the use of meantone tunings that were extended beyond the keyboard's twelve notes,[1][15][16] and hence these are now called "extended" meantone tunings. Such efforts required a corresponding extension of keyboard instruments to provide means of producing more than 12 notes per octave; examples include Vincento's archicembalo, Mersenne's 19 ET harpsichord, Colonna's 31 ET sambuca rota, and Huygens's 31 ET harpsichord.[17]
Other instruments extended the keyboard by only a few notes. Some period harpsichords and organs have split D♯ / E♭ keys, such that both E major / C♯ minor (4 sharps) and E♭ major / C minor (3 flats) can be played with no wolf fifths. Many of those instruments also have split G♯ / A♭ keys, and a few have all the five accidental keys split.
All of these alternative instruments were "complicated" and "cumbersome" (Isacoff 2009), due to
- (a) not being isomorphic, and
- (b) not having a transposing mechanism,
which can significantly reduce the number of note-controlling buttons needed on an isomorphic keyboard (Plamondon 2009). Both of these criticisms could be addressed by electronic isomorphic keyboard instruments (such as the open-source hardware jammer keyboard), which could be simpler, less cumbersome, and more expressive than existing keyboard instruments.[18]
See also
[edit]References
[edit]- ^ a b c d Barbour, James Murray (1951). Tuning and Temperament: A historical survey. Dover Books On Music: History. Dover Publications (2013). Chapters III, IV and VII. ISBN 978-0-4864-3406-3.
{{cite book}}: ISBN / Date incompatibility (help) - ^ Gaffurius, Franchinus (1496). Practicae musica (in Italian). Milan: Gulielmum signer Rothomagensem.
- ^ Aron, Pietro (1523). Thoscanello de la musica (in Italian). Venice: Marchio Sessa.
- ^ Fogliani, Lodovico. Musica theorica. Bibliotheca Musica Bononiensis. Vol. II/13, 88 pp. (Line-cut of the Venice, 1529 ed.). Bologna, IT: Civico Museo Bibliografico Musicale.
- ^ Zarlino, Gioseffo (1558). Le istitutioni harmoniche (in Italian). Venice.
- ^ de Salinas, Francisco (1577). De musica libri septem. Salamanca: Mathias Gastius.
- ^ Mersenne, M. (1639). Harmonie universelle (1st online ed.). Paris, FR: Gallica.
Translation to English by Roger E. Chapman (The Hague, 1957)
- ^ Huygens, Christiaan (1691). Lettre à Henri Basnage de Beauval touchant le cycle harmonique, citée dans: "Histoire des Ouvrages des Sçavans" [Letter concerning the harmonic cycle] (in French). Rotterdam, NL – via huygens-fokker.org.
- ^ Grove, G., ed. (1890). "[no title cited]". A Dictionary of Music and Musicians. Vol. IV (1st ed.). London, UK: Macmillan. p. 72.
- ^ Sethares, W.A.; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. (2009). "Spectral tools for dynamic tonality and audio morphing". Computer Music Journal. 33 (2): 71–84. CiteSeerX 10.1.1.159.838. doi:10.1162/comj.2009.33.2.71. S2CID 216636537. Project MUSE 266411.
- ^ Milne, Andrew; Sethares, W.A.; Plamondon, J. (March 2008). "Tuning continua and keyboard layouts" (PDF). Journal of Mathematics and Music. 2 (1): 1–19. doi:10.1080/17459730701828677.
- ^ Milne, Andrew; Sethares, W.A.; Plamondon, J. (Winter 2007). "Isomorphic controllers and dynamic tuning: Invariant fingering over a tuning continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15.
- ^ Milne, Andrew; Sethares, W.A.; Plamondon, J. (2009). Dynamic tonality: Extending the framework of tonality into the 21st century (PDF). Annual Conference of the South Central Chapter of the College Music Society – via sethares.engr.wisc.edu.
- ^ Milne, Sethares & Plamondon 2007.
- ^ Duffin, Ross W. (2007). How Equal Temperament Ruined Harmony (and why you should care). W.W. Norton & Company. ISBN 978-0-393-06227-4.[page needed]
- ^ Isacoff, Stuart (2009). Temperament: How music became a battleground for the great minds of western civilization. Knopf Doubleday Publishing Group. ISBN 978-0-307-56051-3.[page needed]
- ^ Stembridge, Christopher (1993). "The cimbalo cromatico and other Italian keyboard instruments with nineteen or more divisions to the octave". Performance Practice Review. VI (1): 33–59. doi:10.5642/perfpr.199306.01.02.
- ^ Paine, G.; Stevenson, I.; Pearce, A. (2007). The Thummer mapping project (ThuMP) (PDF). 7th International Conference on New Interfaces for Musical Expression (NIME 07). pp. 70–77.
External links
[edit]- An explanation of constructing Quarter Comma Meantone Tuning
- How to tune quarter-comma meantone
- Archive index at the Wayback Machine Music fragments played in different temperaments - mp3s not archived
- Kyle Gann's Introduction to Historical Tunings has an explanation of how the meantone temperament works.
- Willem Kroesbergen, Andrew cruickshank: Meantone, unequal and equal temperament during J.S. Bach's life https://www.academia.edu/9189419/Blankenburg_Equal_or_unequal_temperament_during_J.S._Bach_s_life
- Meantone Temperament | Definition & Meaning | M5 Music - M5 Music
Meantone temperament
View on GrokipediaFundamentals
Definition and Core Principles
Meantone temperament is a family of musical tuning systems that approximate 5-limit just intonation by prioritizing consonant major thirds, achieved through the deliberate tempering of perfect fifths. In these systems, the major third is tuned closer to the pure ratio of 5:4 (approximately 386 cents), while the perfect fifth is flattened from its just intonation value of 702 cents to a range of roughly 696–700 cents. This adjustment enhances the purity of thirds in diatonic scales, making them more harmonious for vocal and instrumental music of the Renaissance and Baroque periods, at the cost of slightly narrowing some fifths.[5][6] At its core, meantone temperament operates by distributing the syntonic comma—an interval with the ratio 81:80, measuring about 22 cents—across multiple perfect fifths to create a "mean" or averaged tone that balances interval sizes. The syntonic comma represents the discrepancy between a Pythagorean major third (81:64, about 408 cents) and its just counterpart (5:4), and tempering it allows for the generation of scales where major thirds are more accurately represented than in untempered systems like Pythagorean tuning. This principle focuses on producing diatonic scales with improved thirds, even if it introduces minor inconsistencies in fifths, contrasting with modern equal temperament where all intervals are uniformly compromised. To measure these intervals precisely, cents are used as a logarithmic unit, with one octave equaling 1200 cents, enabling fine distinctions in tuning. Generator intervals, such as the tempered fifth, serve as the foundational building block for constructing the scale.[5][6] The basic scale in meantone temperament is generated by starting from a reference pitch, such as C, and stacking successive tempered fifths (e.g., C to G, G to D) until the chromatic octave is filled, typically resulting in 12 distinct tones per octave for common variants. This process ensures that four tempered fifths equate to two pure octaves plus a just major third, thereby tempering the syntonic comma equally across those fifths to yield a mean whole tone of about 193.2 cents, positioned midway between the just major seconds of 9:8 (204 cents) and 10:9 (182 cents). Unlike pure just intonation, which avoids tempering but limits modulation, meantone provides a practical compromise for fixed-pitch instruments, supporting limited key changes while maintaining consonance in primary tonalities.[5][6]Relation to Just Intonation
Just intonation is a tuning system that employs simple integer frequency ratios to achieve acoustically pure intervals, such as the perfect fifth of 3:2 (approximately 702 cents) and the major third of 5:4 (approximately 386 cents). These ratios derive from the harmonics of a single fundamental tone, promoting maximal consonance in vertical harmonies. However, extending just intonation to a complete chromatic scale by stacking successive pure fifths (3:2) produces the Pythagorean scale, in which closing the circle of 12 fifths exceeds seven octaves by the Pythagorean comma (531441:524288, approximately 23.5 cents), resulting in an imperfect alignment. The syntonic comma (81:80, about 21.5 cents) is the discrepancy between the Pythagorean major third (81:64) and the just major third (5:4).[7][8] Meantone temperament emerges as a practical adaptation of just intonation for fixed-pitch instruments, resolving the syntonic comma by slightly flattening each perfect fifth—typically by a fraction of the comma—to ensure the circle of fifths closes evenly. This process "means" or averages tones between sharper Pythagorean-derived versions and flatter just alternatives, distributing the comma across multiple fifths and enabling key modulation without instrument retuning. The approach prioritizes 5-limit tuning, incorporating prime numbers up to 5 to favor consonant thirds essential for polyphonic music.[7][8][9] A key precursor issue addressed by meantone is the wide major thirds in Pythagorean tuning, which relies solely on 3-limit ratios (powers of 2 and 3) and yields thirds of 81:64 (approximately 408 cents)—over 20 cents sharper than the just 5:4. These "Pythagorean thirds" produce audible beats and dissonance in harmonic contexts like Renaissance polyphony, where vertical sonorities demand purer intervals. Meantone partially remedies this by tempering fifths to approximate just thirds, enhancing consonance in closely related keys.[9][7] The trade-offs in meantone reflect its compromise nature: while major thirds become nearly just, supporting expressive harmonic progressions in 5-limit music, the flattened fifths (around 697 cents) introduce subtle dissonance, and remote keys feature a harsh "wolf" interval, limiting full chromatic freedom compared to untempered just intonation's theoretical purity. This usability gain for keyboard and ensemble instruments outweighed the restrictions during periods emphasizing tonal harmony.[8][4][9]Mathematical Foundations
The Mean Tone Mechanism
Meantone temperament achieves its characteristic sound by setting all whole tones equal to the arithmetic mean, in cents, between the major tone (9/8, approximately 203.91 cents) and the minor tone (10/9, approximately 182.40 cents) from just intonation, yielding a mean tone of about 193.16 cents. This compromise ensures more consonant major thirds compared to Pythagorean tuning, where tones vary in size. The mechanism centers on tempering the perfect fifth (3/2, 701.955 cents) downward by a fraction of the syntonic comma (81/80, 21.506 cents), distributing the adjustment across the circle of fifths to approximate pure intervals while maintaining a closed system.[7] The size of the tempered fifth in cents is given by where is the denominator of the comma fraction (e.g., for quarter-comma meantone, tempering each fifth by 1/4 comma or ~5.377 cents). This formula subtracts a portion of the comma from the pure fifth, flattening it to better align the derived intervals with just intonation ratios. In the circle of fifths, 12 such tempered fifths span 7 octaves minus a discrepancy cents, where cents (syntonic comma) and cents (Pythagorean comma); for , cents, accommodated in the wolf interval (an enlarged fifth of ~737.64 cents). For positive tempering (typical in meantone), the fifths are narrowed to favor purer thirds, while negative tempering would sharpen them, as in systems emphasizing fifths over thirds.[7][10] A key interval relationship in meantone is the major third, derived as two tempered fifths minus one octave, resulting in approximately 386 cents—close to the just major third (5/4, 386.31 cents)—which produces the pure-sounding thirds central to the system's appeal. This construction ensures that chains of mean tones build to consonant triads, prioritizing harmonic stability in 5-limit tuning over the dissonant thirds of untempered Pythagorean scales.[7]Calculation of Intervals
In a generic meantone temperament, intervals are calculated using the tempered perfect fifth as the generator, with its size determined by a parameter , the denominator of the comma fraction (e.g., for quarter-comma meantone, tempering by cents from 701.955 cents). The formula for the tempered fifth is thus cents.[10] This parameterization allows for variants like quarter-comma meantone (), where cents. Key intervals are derived by stacking multiples of this fifth and reducing modulo the octave (1200 cents), ensuring consistency within the 12-note scale while absorbing discrepancies into a "wolf" fifth. The major third, central to meantone, is obtained by stacking four fifths and subtracting two octaves: cents, yielding approximately 386.314 cents for , matching the just major third of 5:4. The major second (mean tone) follows as two fifths minus one octave: cents, or about 193.156 cents for . The perfect fourth is the octave complement of the fifth: cents, approximately 503.422 cents for . The tritone (augmented fourth) is six fifths minus three octaves: cents, roughly 579.468 cents for . Smaller intervals like the minor second and minor third require positions from the fifth chain. The minor second (chromatic semitone, e.g., C to C♯) is seven fifths minus six octaves (or 7f mod 1200): cents (adjusted for mod), approximately 76.049 cents for . The minor third (e.g., C to E♭) is nine fifths minus five octaves (9f mod 1200): cents, or about 269.221 cents for . Alternatively, the minor third can be computed as the major second plus chromatic semitone (193.156 + 76.049 = 269.205 cents), confirming the stacking approach. Other intervals follow similarly: for instance, the minor sixth is the octave minus the major third (813.686 cents for ), and the major sixth is three fifths minus one octave (889.734 cents for ). The following table presents a representative set of interval sizes in cents for quarter-comma meantone (), computed via the above derivations and standard chain positions avoiding the wolf fifth:| Interval | Cents (approximate) |
|---|---|
| Unison | 0.000 |
| Minor second | 76.049 |
| Major second | 193.156 |
| Minor third | 269.221 |
| Major third | 386.314 |
| Perfect fourth | 503.422 |
| Tritone | 579.468 |
| Perfect fifth | 696.578 |
| Octave | 1200.000 |
Historical Context
Origins in Renaissance Theory
The roots of meantone temperament lie in 15th-century monochord divisions, where music theorists experimented with interval constructions to address the dissonant major thirds inherent in Pythagorean tuning, laying groundwork for more consonant 5-limit systems.[14] Figures like Bartolomeo Ramis de Pareja in his 1482 Musica practica advocated just intonation via monochord measurements to achieve pure fifths and thirds, influencing subsequent reforms that tempered intervals for polyphonic harmony. These early efforts marked a departure from strict Pythagorean ditones (81/64), prioritizing sensory consonance over purely mathematical ratios.[15] A pivotal advancement came in 1523 with Pietro Aaron's Toscanella, where he proposed tempering the perfect fifth by a quarter of the syntonic comma (approximately 5.4 cents flatter than just) to yield pure major thirds (5:4) on keyboard instruments, an innovation aimed at resolving the "harshness" of traditional tunings in ensemble settings. This suggestion represented the first explicit description of a meantone system, bridging theoretical monochord work with practical tuning adjustments.[1] Gioseffo Zarlino further refined these ideas in his influential 1558 treatise Le Istitutioni harmoniche, advocating a 2/7 syntonic comma temperament that divided the major third into two equal whole tones, ensuring pure thirds essential for the rich polyphony of Renaissance sacred music. Zarlino's approach emphasized the theoretical realization of just intonation principles within a tempered framework, promoting it as superior for harmonic progressions in multiple voices.[15] Theoretical debates of the era highlighted the shift from Pythagorean ditonics to 5-limit meantone for enhanced consonance, as theorists sought tunings that balanced interval purity with chromatic usability. In 1577, Francisco Salinas contributed to this discourse in De musica libri septem by proposing an arithmetic mean method to bisect the just major third (5:4) into equal "mean tones," yielding a 1/3 comma temperament that extended to a 19-note scale for greater flexibility. Underpinning these innovations was Renaissance humanism's focus on sensory pleasure in music, which revived ancient Greek ideas of harmonia and ethos to justify tuning reforms that prioritized auditory delight over medieval scholasticism.[15] Humanists like Zarlino integrated classical sources with empirical observation, viewing consonant intervals as key to emotional expression in polyphonic compositions.Practical Implementation in Instruments
By the late 16th century, quarter-comma meantone had become the predominant tuning system for keyboard instruments such as organs and harpsichords across Europe, enabling performers to achieve pure major thirds in common keys while accommodating the growing polyphonic repertoire of the Renaissance. This adoption, first explicitly advocated by theorist Pietro Aaron in 1523 for practical keyboard use, allowed instruments to support the modal structures and harmonic progressions central to the era's music, with widespread implementation by around 1600. To address the limitations of the 12-note keyboard in meantone—particularly the dissonant wolf interval between G♯ and E♭—some designs incorporated split black keys, dividing notes like B♭/F♯ into separate halves tuned to their distinct meantone pitches, as seen in Italian and German harpsichords from the early 17th century.[16] Tuning these instruments required precise methods to establish the narrowed perfect fifths characteristic of meantone, typically beginning with a pure major third divided into four tempered fifths. Organ builders often employed reed pipes as reference tones to set the foundational intervals, adjusting the pipe lengths or reed tongues for accuracy, while harpsichord and clavichord tuners favored the monochord—a stretched wire device—for measuring divisions with calipers or auditory beats. Michael Praetorius, in his 1619 treatise Syntagma musicum, provided detailed instructions for organ temperament in quarter-comma meantone, advocating the tuning of pure major thirds (such as C-E) followed by successive flat fifths, and recommending a 19-note cembalo with split keys for enhanced flexibility in 1/3-comma variants. These techniques ensured consonant diatonic harmonies but demanded skilled artisans, as slight deviations could amplify the wolf interval's harshness. In ensemble settings, meantone temperament influenced the intonation of fretted string instruments like viols and lutes, which were tuned to align with keyboard temperaments during Renaissance and Baroque consort music, promoting blended sonorities in polyphonic works by composers such as William Byrd or Claudio Monteverdi.[17] Viols, often played in matched consorts of three to six instruments, adapted by fretting to approximate meantone's pure thirds, while lutes used tied frets or movable gut ties to fine-tune intervals for harmonic consonance within the group.[17] However, transposing wind instruments like recorders faced challenges, as their fixed bores and fingerings struggled to match meantone's irregular semitones across keys, limiting seamless modulation and requiring players to adjust breath pressure or select specific sizes (e.g., treble in F or bass in C) to stay within usable tonalities. The practical constraints of meantone, including its restricted key palette due to the wolf interval, contributed to its decline in the 18th century as composers increasingly demanded freer modulation in works by figures like Johann Sebastian Bach. This shift toward well-tempered and equal systems accelerated in northern Europe by the 1720s, though meantone persisted in French organs and harpsichords until approximately 1750, supported by the conservative stylistic preferences of the Versailles court.[18]Key Variants
Quarter-Comma Meantone
Quarter-comma meantone is a specific variant of meantone temperament in which each perfect fifth is tempered flat by one quarter of the syntonic comma (approximately 5.377 cents), resulting in a fifth of 696.578 cents and a pure major third of 386.314 cents.[19] This tempering distributes the syntonic comma (81/80, approximately 21.506 cents) evenly across four fifths to achieve consonance in major thirds, aligning them with the just intonation ratio of 5:4.[20] The sonic profile of quarter-comma meantone features particularly sweet and resonant major thirds and minor sixths due to their near-purity relative to just intonation, while the slightly flattened fifths contribute a subtle warmth compared to sharper Pythagorean fifths; however, this comes at the cost of dissonant wolf intervals in remote keys.[19] It served as the predominant tuning system for keyboard and other fixed-pitch instruments across Europe during the 16th and 17th centuries, influencing Renaissance and early Baroque composition.[21] The scale is generated by stacking tempered fifths of 696.578 cents, with intervals derived modulo the octave. The following table lists key intervals in quarter-comma meantone, including their sizes in cents, corresponding just intonation values (syntonic scale), and deviations:| Interval | Meantone (cents) | Just (cents) | Deviation (cents) |
|---|---|---|---|
| Unison | 0.000 | 0.000 | 0.000 |
| Diatonic minor second | 117.108 | 111.731 | +5.377 |
| Major second | 193.157 | 203.910 | -10.754 |
| Minor third | 310.264 | 315.641 | -5.377 |
| Major third | 386.314 | 386.314 | 0.000 |
| Perfect fourth | 503.422 | 498.045 | +5.377 |
| Diminished fifth (small tritone) | 579.471 | 590.225 | -10.754 |
| Perfect fifth | 696.578 | 701.955 | -5.377 |
| Minor sixth | 813.686 | 813.686 | 0.000 |
| Major sixth | 889.736 | 884.359 | +5.377 |
| Minor seventh | 1006.844 | 996.090 | +10.754 |
| Octave | 1200.000 | 1200.000 | 0.000 |










