Hubbry Logo
Octahedral molecular geometryOctahedral molecular geometryMain
Open search
Octahedral molecular geometry
Community hub
Octahedral molecular geometry
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Octahedral molecular geometry
Octahedral molecular geometry
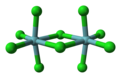
Octahedral molecular geometry
View on Wikipedia
from Wikipedia
Octahedral molecular geometry
ExamplesSF6, Mo(CO)6
Point groupOh
Coordination number6
Bond angle(s)90°
μ (Polarity)0

In chemistry, octahedral molecular geometry, also called square bipyramidal,[1] describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The octahedron has eight faces, hence the prefix octa. The octahedron is one of the Platonic solids, although octahedral molecules typically have an atom in their centre and no bonds between the ligand atoms. A perfect octahedron belongs to the point group Oh. Examples of octahedral compounds are sulfur hexafluoride SF6 and molybdenum hexacarbonyl Mo(CO)6. The term "octahedral" is used somewhat loosely by chemists, focusing on the geometry of the bonds to the central atom and not considering differences among the ligands themselves. For example, [Co(NH3)6]3+, which is not octahedral in the mathematical sense due to the orientation of the N−H bonds, is referred to as octahedral.[2]

The concept of octahedral coordination geometry was developed by Alfred Werner to explain the stoichiometries and isomerism in coordination compounds. His insight allowed chemists to rationalize the number of isomers of coordination compounds. Octahedral transition-metal complexes containing amines and simple anions are often referred to as Werner-type complexes.

Structure of sulfur hexafluoride, an example of a molecule with the octahedral coordination geometry.

Isomerism in octahedral complexes

[edit]
Main article: Stereochemistry

When two or more types of ligands (La, Lb, ...) are coordinated to an octahedral metal centre (M), the complex can exist as isomers. The naming system for these isomers depends upon the number and arrangement of different ligands.

cis and trans

[edit]

For MLa
4Lb
2, two isomers exist. The cis isomer has the two Lb ligands adjacent to each other, whereas the trans isomer has them 180° to each other. It was the analysis of such complexes that led Alfred Werner to the 1913 Nobel Prize–winning postulation of octahedral complexes.

  • cis-[CoCl2(NH3)4]+
    cis-[CoCl2(NH3)4]+
  • trans-[CoCl2(NH3)4]+
    trans-[CoCl2(NH3)4]+

Facial and meridional isomers

[edit]

For MLa
3Lb
3, two isomers are possible. The facial isomer (fac) has each set of three identical ligands occupying one face of the octahedron surrounding the central atom; all of the identical ligands are cis to each other. The meridional isomer (mer) has each set of three identical ligands occupying a plane passing through the central atom; two of the three are trans to each other and the third is cis to the first two.

  • fac-[CoCl3(NH3)3]
    fac-[CoCl3(NH3)3]
  • mer-[CoCl3(NH3)3]
    mer-[CoCl3(NH3)3]

Δ vs Λ isomers

[edit]

Complexes with three bidentate ligands or two cis bidentate ligands can exist as enantiomeric pairs. Examples are shown below.

Other

[edit]

For MLa
2Lb
2Lc
2, a total of five geometric isomers and six stereoisomers are possible.[3]

  1. One isomer in which all three pairs of identical ligands are trans
  2. Three isomers in which one pair of identical ligands (La or Lb or Lc) is trans while the other two pairs of ligands are mutually cis.
  3. Two enantiomeric pair in which all three pairs of identical ligands are cis. These are equivalent to the Δ vs Λ isomers mentioned above.

The number of possible isomers can reach 30 for an octahedral complex with six different ligands (in contrast, only two stereoisomers are possible for a tetrahedral complex with four different ligands). The following table lists all possible combinations for monodentate ligands:

Formula Number of isomers Number of enantiomeric pairs
ML6 1 0
MLa
5Lb		 1 0
MLa
4Lb
2		 2 0
MLa
4LbLc		 2 0
MLa
3Lb
3		 2 0
MLa
3Lb
2Lc		 3 0
MLa
3LbLcLd		 5 1
MLa
2Lb
2Lc
2		 6 1
MLa
2Lb
2LcLd		 8 2
MLa
2LbLcLdLe		 15 6
MLaLbLcLdLeLf 30 15

Thus, all 15 diastereomers of MLaLbLcLdLeLf are chiral, whereas for MLa
2LbLcLdLe, six diastereomers are chiral and three are not (the ones where La are trans). One can see that octahedral coordination allows much greater complexity than the tetrahedron that dominates organic chemistry. The tetrahedron MLaLbLcLd exists as a single enantiomeric pair. To generate two diastereomers in an organic compound, at least two carbon centers are required.

Deviations from ideal symmetry

[edit]

Jahn–Teller effect

[edit]
Main article: Jahn–Teller effect

The term can also refer to octahedral influenced by the Jahn–Teller effect, which is a common phenomenon encountered in coordination chemistry. This reduces the symmetry of the molecule from Oh to D4h and is known as a tetragonal distortion.

Distorted octahedral geometry

[edit]

Some molecules, such as XeF6 or IF−
6, have a lone pair that distorts the symmetry of the molecule from Oh to C3v.[4][5] The specific geometry is known as a monocapped octahedron, since it is derived from the octahedron by placing the lone pair over the centre of one triangular face of the octahedron as a "cap" (and shifting the positions of the other six atoms to accommodate it).[6] These both represent a divergence from the geometry predicted by VSEPR, which for AX6E1 predicts a pentagonal pyramidal shape.

Bioctahedral structures

[edit]

Pairs of octahedra can be fused in a way that preserves the octahedral coordination geometry by replacing terminal ligands with bridging ligands. Two motifs for fusing octahedra are common: edge-sharing and face-sharing. Edge- and face-shared bioctahedra have the formulas [M2L8(μ-L)]2 and M2L6(μ-L)3, respectively. Polymeric versions of the same linking pattern give the stoichiometries [ML2(μ-L)2]∞ and [M(μ-L)3]∞, respectively.

The sharing of an edge or a face of an octahedron gives a structure called bioctahedral. Many metal pentahalide and pentaalkoxide compounds exist in solution and the solid with bioctahedral structures. One example is niobium pentachloride. Metal tetrahalides often exist as polymers with edge-sharing octahedra. Zirconium tetrachloride is an example.[7] Compounds with face-sharing octahedral chains include MoBr3, RuBr3, and TlBr3.

Trigonal prismatic geometry

[edit]
Main article: trigonal prismatic molecular geometry
"Trigonal prism" redirects here. For the three-sided prism, see Triangular prism.

For compounds with the formula MX6, the chief alternative to octahedral geometry is a trigonal prismatic geometry, which has symmetry D3h. In this geometry, the six ligands are also equivalent. There are also distorted trigonal prisms, with C3v symmetry; a prominent example is W(CH3)6. The interconversion of Δ- and Λ-complexes, which is usually slow, is proposed to proceed via a trigonal prismatic intermediate, a process called the "Bailar twist". An alternative pathway for the racemization of these same complexes is the Ray–Dutt twist.

Splitting of d-orbital energies

[edit]
Main article: Ligand field theory

For a free ion, e.g. gaseous Ni2+ or Mo0, the energy of the d-orbitals are equal in energy; that is, they are "degenerate". In an octahedral complex, this degeneracy is lifted. The energy of the dz2 and dx2−y2, the so-called eg set, which are aimed directly at the ligands are destabilized. On the other hand, the energy of the dxz, dxy, and dyz orbitals, the so-called t2g set, are stabilized. The labels t2g and eg refer to irreducible representations, which describe the symmetry properties of these orbitals. The energy gap separating these two sets is the basis of crystal field theory and the more comprehensive ligand field theory. The loss of degeneracy upon the formation of an octahedral complex from a free ion is called crystal field splitting or ligand field splitting. The energy gap is labeled Δo, which varies according to the number and nature of the ligands. If the symmetry of the complex is lower than octahedral, the eg and t2g levels can split further. For example, the t2g and eg sets split further in trans-MLa
4Lb
2.

Ligand strength has the following order for these electron donors:

weak: iodine < bromine < fluorine < acetate < oxalate < water < pyridine < cyanide :strong

So called "weak field ligands" give rise to small Δo and absorb light at longer wavelengths.

Reactions

[edit]

Given that a virtually uncountable variety of octahedral complexes exist, it is not surprising that a wide variety of reactions have been described. These reactions can be classified as follows:

  • Ligand substitution reactions (via a variety of mechanisms)
  • Ligand addition reactions, including among many, protonation
  • Redox reactions (where electrons are gained or lost)
  • Rearrangements where the relative stereochemistry of the ligand changes within the coordination sphere.

Many reactions of octahedral transition metal complexes occur in water. When an anionic ligand replaces a coordinated water molecule the reaction is called an anation. The reverse reaction, water replacing an anionic ligand, is called aquation. For example, the [CoCl(NH3)5]2+ slowly yields [Co(NH3)5(H2O)]3+ in water, especially in the presence of acid or base. Addition of concentrated HCl converts the aquo complex back to the chloride, via an anation process.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Octahedral molecular geometry

View on Grokipedia
from Grokipedia
Octahedral molecular geometry is a coordination arrangement in which a central atom is bonded to six surrounding atoms or ligands positioned at the vertices of a regular , resulting in bond angles of 90° between adjacent ligands and 180° between opposite ligands. This geometry arises primarily from the valence shell repulsion () theory, which predicts that six s around a central atom adopt this configuration to minimize electrostatic repulsions. In main-group chemistry, octahedral geometry is exemplified by molecules such as (SF₆), where the central atom is surrounded by six fluorine atoms in an AX₆ electron and , leading to a nonpolar, symmetric structure. Variations occur when lone pairs are present, such as in (BrF₅), which has AX₅E geometry and adopts a square pyramidal molecular shape with bond angles slightly less than 90° due to lone pair-bond pair repulsions. Similarly, AX₄E₂ systems like the tetrachloridoiodate(III) ([ICl₄]⁻) result in square planar geometry. Octahedral geometry is particularly prevalent in coordination complexes, where the coordination number is six, and ligands such as , , or occupy the octahedral positions around the metal center. Common examples include the hexaaquacobalt(II) ion ([Co(H₂O)₆]²⁺) and tris(ethylenediamine)chromium(III) ([Cr(en)₃]³⁺), which exhibit 90° bond angles and can display geometric isomerism (cis and trans) as well as optical isomerism in certain cases. These complexes are crucial in fields like , (e.g., in groups), and due to their electronic properties influenced by crystal field splitting in the octahedral ligand field.

Fundamentals of Octahedral Geometry

Definition and Characteristics

Octahedral molecular geometry describes a coordination arrangement in which six ligands surround a central atom, positioned at the vertices of a regular octahedron, corresponding to a coordination number of 6. This structure arises commonly in coordination compounds and molecules where the central atom, often a transition metal, bonds to six identical or similar ligands in a highly symmetric fashion. In the ideal octahedral geometry, the bond angles between adjacent ligands are 90°, while the angles between ligands in opposite positions are 180°. These angles reflect the geometric constraints of the , ensuring maximal separation of the ligands to minimize repulsion in valence shell electron pair repulsion (. The resulting structure exhibits O_h , characterized by 48 symmetry operations including rotations, reflections, and inversions, which impart isotropic properties to the molecule. Due to this high and the presence of an inversion center, ideal octahedral molecules possess a zero dipole moment, as individual bond dipoles cancel out completely. The geometric positions of the ligands can be mathematically represented in a , with the central atom at the origin (0, 0, 0) and the ligands located along the principal axes at coordinates (±d,0,0)(\pm d, 0, 0), (0,±d,0)(0, \pm d, 0), and (0,0,±d)(0, 0, \pm d), where dd denotes the metal-ligand bond distance. This foundational concept in coordination chemistry was established by in the early 1900s through his pioneering work on the spatial arrangements in coordination compounds, for which he received the in 1913.

Examples in Chemistry

Octahedral molecular geometry is observed in various main group compounds, particularly those with six equivalent ligands surrounding a central atom from the p-block. (SF₆) exemplifies this with its central atom bonded to six atoms, forming S–F bonds of about 1.56 Å and bond angles of exactly 90° and 180°, resulting in a highly symmetric structure. This compound is chemically inert due to the filled octet on and strong electronegativity difference with , making it useful as an electrical insulator despite its role as a long-lived . (XeF₆) displays a fluxional structure with minor distortions from ideal octahedral geometry caused by a stereochemically active on , yet electron diffraction studies confirm a mean Xe–F bond length of 1.89 Å and overall octahedral arrangement. The iodide hexafluoride anion (IF₆⁻) adopts a distorted octahedral geometry in solid salts, with iodine at the center coordinated to six fluorines, stabilized by the negative charge distributing . In coordination chemistry, octahedral geometry dominates for six-coordinate complexes of d-block elements, favored by ligand field stabilization energies that lower the energy of specific d-orbital configurations relative to other geometries. For example, the hexafluorocobaltate(III) ion ([CoF₆]³⁻) features a high-spin d⁶ (III) center in an octahedral field, with Co–F bonds around 1.93 , exhibiting due to four unpaired electrons. The hexaaquairon(II) cation ([Fe(H₂O)₆]²⁺) forms pale green solutions in water, with Fe–O bonds of approximately 2.12 in its high-spin d⁶ octahedral structure, commonly encountered in aqueous iron(II) salts. Similarly, the hexachloroplatinate(IV) anion ([PtCl₆]²⁻) shows a low-spin d⁶ (IV) center with Pt–Cl bonds near 2.33 , known for its stability and use in . The hexaamminechromium(III) cation ([Cr(NH₃)₆]³⁺) is a yellow, kinetically inert complex with Cr–N bonds of about 2.07 , illustrating octahedral coordination with neutral ligands.
Central AtomLigandsChargeKey Properties
S6 F0Highly stable, nonpolar, used as ; potent with atmospheric lifetime >1000 years
Xe6 F0Fluxional with distortion; reactive fluorinating agent
I6 F-1Stable in ionic salts; exhibits distorted
Co6 F-3High-spin paramagnetic; weak-field example
Fe6 H₂O+2High-spin; forms green aqueous solutions, prone to oxidation
Pt6 Cl-2Low-spin diamagnetic; stable, used in
Cr6 NH₃+3High-spin, kinetically inert; yellow color, classic Werner complex; paramagnetic (3 unpaired electrons)

Isomerism in Octahedral Complexes

Geometric Isomers: Cis and Trans

Geometric isomerism, also known as cis-trans isomerism, arises in octahedral coordination complexes of the type MA₄B₂, where M is the central metal ion and A and B are monodentate ligands, as well as in M(AA)₂B₂, where AA represents a bidentate ligand. These isomers are diastereomers, differing in the spatial arrangement of the ligands without being mirror images, and were first systematically identified by Alfred Werner in his studies of cobalt(III) ammine complexes. In the trans isomer of MA₄B₂, the two B ligands occupy opposite positions at a 180° relative to the metal center, resulting in a symmetric structure with a zero net dipole moment due to the cancellation of opposing bond dipoles. A classic example is the trans form of [Co(NH₃)₄Cl₂]⁺, which appears green and exhibits higher stability when B ligands are bulky, as the trans configuration minimizes steric repulsions between ligands. Conversely, the cis isomer features the two B ligands in adjacent positions at a 90° angle, leading to an asymmetric arrangement and a non-zero dipole moment. For [Co(NH₃)₄Cl₂]⁺, the cis form is violet and less stable than its trans counterpart for similar reasons of increased ligand-ligand repulsion. In M(AA)₂B₂ complexes, such as cis-[Co(en)₂Cl₂]⁺ (where en is ), the cis configuration can further exhibit optical activity due to the chelating ligands creating a chiral environment. The energy difference between cis and trans isomers primarily stems from variations in ligand-ligand repulsions; the trans form is generally more stable, particularly with bulky B ligands, as computational studies confirm lower steric strain in the 180° arrangement. Spectroscopically, these isomers can be distinguished using infrared (IR) spectroscopy: the trans isomer displays a single IR-active band for the M-B stretching modes due to its higher symmetry (D₄h ), while the cis isomer shows two such bands (C_{2v} point group), reflecting the degeneracy lifting of the vibrational modes. This distinction is evident in the Raman and IR spectra of [Co(NH₃)₄Cl₂]⁺ isomers.

Facial and Meridional Isomers

In octahedral complexes of the type MA₃B₃, where M is the central metal ion and A and B are different monodentate ligands, geometric isomerism arises from the distinct arrangements of the three identical A ligands relative to the three B ligands. The (fac) isomer positions the three A ligands on one triangular face of the , resulting in all A–M–A bond angles of 90°. Conversely, the meridional (mer) isomer arranges the three A ligands along a meridian, or equatorial plane, of the , yielding two A–M–A angles of 90° and one of 180°./Coordination_Chemistry/Structure_and_Nomenclature_of_Coordination_Compounds/Isomers/Stereoisomers:_Geometric_Isomers_in_Transition_Metal_Complexes) A representative example is the cobalt(III) complex [Co(NH₃)₃(NO₂)₃], where both fac and mer isomers have been isolated and characterized. These isomers differ in their physical properties due to variations in ligand symmetry and electronic environment. The fac and mer forms of this complex were first observed and systematically studied by in his foundational work on coordination compounds, which earned him the in 1913. The stability of these isomers depends on the nature of the ligands and the metal center. In the fac isomer, the clustering of the three A ligands leads to greater steric repulsion between them compared to the more spread-out arrangement in the mer isomer, often making the mer form thermodynamically preferred for complexes with bulky or charged monodentate ligands. The point group symmetries of these isomers further distinguish their behavior. The fac isomer belongs to the C_{3v} point group, exhibiting higher that results in simpler NMR spectra and potentially different reactivity profiles, while the mer isomer has C_{2v} , with a C₂ axis and two mirror planes that influence its spectroscopic signatures and substitution patterns./09:Coordination_Chemistry_I-_Structure_and_Isomers/9.04:_Isomerism)

Optical Isomers: Delta and Lambda

Optical isomerism in octahedral complexes arises primarily from the arrangement of chelating ligands that create a chiral environment lacking a plane of , leading to non-superimposable mirror images known as enantiomers. This phenomenon is common in complexes of the type [M(AA)₃], where M is a central metal and AA represents symmetrical bidentate ligands such as (en), forming a propeller-like helical structure around the metal center. Similarly, cis-[M(AA)₂B₂] complexes, with two bidentate ligands and two monodentate ligands B in adjacent positions, can exhibit due to the twisted conformation of the chelates. The enantiomers are designated using the Δ and Λ notation, which describes the helical of the ligand arrangement. The Δ configuration corresponds to a right-handed , where the ligands twist clockwise when viewed along the C₃ axis from a point above the plane containing the metal and the midpoints of the chelate rings. Conversely, the Λ configuration features a left-handed, anticlockwise twist. This system, recommended by IUPAC, relies on the Cahn-Ingold-Prelog priority rules to assign the based on the orientation of the donor atoms. A classic example is the tris(ethylenediamine)cobalt(III) , [Co(en)₃]³⁺, which exists as a pair of enantiomers: Δ-[Co(en)₃]³⁺ and Λ-[Co(en)₃]³⁺. These were first resolved in 1914 by A. Werner using d-tartrate as a chiral resolving agent, forming diastereomeric salts that could be separated by fractional due to their differing solubilities. The pure enantiomers exhibit opposite optical rotations; the Λ isomer is dextrorotatory ([α]ᵉ₅₈₉ > 0), while the Δ isomer is levorotatory, with reported values around +135° and -135° for the iodide salts in , respectively. Optical isomerism is absent in trans-[M(AA)₂B₂] forms because these possess a plane of that renders them achiral. In contrast, the [M(AA)₃] arrangement lacks a plane of and supports as a propeller-like structure with Δ and Λ enantiomers. These chiral octahedral complexes find applications in asymmetric , where the metal-centered influences stereoselectivity in reactions such as or epoxidation. Additionally, Δ/Λ isomers serve as models for in biological systems, including cobalt-containing proteins involved in and enzymatic processes.

Additional Isomer Types

In octahedral molecular geometry, additional types of isomerism beyond geometric and optical forms include constitutional isomers, which arise from differences in connectivity or composition within the . These structural variants are particularly relevant for complexes with ambidentate ligands or those involving counterions and solvents. Unlike stereoisomers, constitutional isomers exhibit distinct chemical reactivities and spectroscopic properties due to variations in . Linkage isomerism occurs when an ambidentate coordinates to the metal center through different donor atoms, leading to s with the same overall formula but different structures. A classic example is the nitrite (NO₂⁻), which can bind via the nitrogen atom to form the nitro or via the oxygen atom to form the nitrito . In (III) ammine complexes, [Co(NH₃)₅(NO₂)]²⁺ represents the nitro form, while [Co(NH₃)₅(ONO)]²⁺ is the nitrito form; the nitrito is less and tends to convert to the nitro under heating or acidic conditions. Ionization isomerism involves the exchange of a and a between the inner and the outer sphere, resulting in compounds that yield different ions in solution. For instance, in pentaamminecobalt(III) complexes, [Co(NH₃)₅Br]SO₄ releases Br⁻ as the coordinated and SO₄²⁻ as the , whereas the ionization isomer [Co(NH₃)₅(SO₄)]Br has SO₄²⁻ coordinated and releases Br⁻; this distinction can be confirmed by precipitation tests with appropriate like Ba²⁺ or Ag⁺. Hydrate isomerism, a specific case of solvate isomerism, features the migration of molecules between the and lattice positions as of hydration. Chromium(III) chloride hexahydrate provides well-known examples: the violet [Cr(H₂O)₆]Cl₃ has all molecules coordinated, while the blue-green [Cr(H₂O)₅Cl]Cl₂·H₂O has one replacing a molecule in the inner , with the displaced as hydration; further isomers include dark green [Cr(H₂O)₄Cl₂]Cl·2H₂O and pale green [Cr(H₂O)₃Cl₃]·3H₂O, each differing in color and solubility due to the varying number of coordinated waters. Coordination isomerism is observed in ionic compounds where both the cation and anion are complex ions, allowing ligand distribution to vary between them while maintaining the overall formula. An example is the pair [Co(NH₃)₆][Cr(CN)₆] and [Cr(NH₃)₆][Co(CN)₆], where in the former, ligands coordinate to and to , while the latter reverses this arrangement; these isomers differ in their electronic properties and reactivity toward ligand substitution. These constitutional isomer types are less prevalent in simple mononuclear octahedral complexes compared to other geometries like tetrahedral or square planar, where steric constraints limit such variations, but they become more significant in polynuclear or charged systems with flexible ligand environments.

Distortions and Deviations

Jahn-Teller Effect

The Jahn-Teller theorem asserts that any nonlinear molecular system possessing a spatially degenerate electronic is unstable and will distort along a vibrational mode that lowers the , thereby removing the degeneracy and reducing the overall energy. This fundamental principle arises from the coupling between electronic and vibrational , ensuring that stable equilibrium configurations cannot maintain both high and electronic degeneracy simultaneously. In octahedral coordination complexes, the Jahn-Teller effect manifests prominently in transition metal ions with degenerate ground states, particularly high-spin d4\mathrm{d^4} and d9\mathrm{d^9} configurations, where the uneven occupancy of the eg\mathrm{e_g} orbital set—derived from the octahedral splitting of d-orbitals into lower-energy t2g\mathrm{t_{2g}} and higher-energy \mathrm{e_g}} levels—drives the distortion. For high-spin d4\mathrm{d^4} (e.g., Mn3+\mathrm{Mn^{3+}}) and d9\mathrm{d^9} (e.g., Cu2+\mathrm{Cu^{2+}}) ions, the single electron (or hole) in the degenerate eg\mathrm{e_g} orbitals (dz2\mathrm{d_{z^2}} and dx2−y2\mathrm{d_{x^2 - y^2}}) leads to preferential stabilization by elongating the two axial bonds along the z-axis or, less commonly, compressing them, resulting in a tetragonal distortion that reduces the symmetry from OhO_h to D4hD_{4h}. This elongation is far more typical than compression, as the latter requires specific ligand field or environmental factors to favor it. A classic example is the hexaqua copper(II) ion, [Cu(H2O)6]2+[\mathrm{Cu(H_2O)_6}]^{2+}, where the Jahn-Teller produces four shorter equatorial Cu-O bonds at approximately 1.96 and two longer axial bonds at 2.32 , reflecting the stabilization of the dx2−y2\mathrm{d_{x^2 - y^2}} orbital in the equatorial plane. Spectroscopic evidence for such distortions appears in UV-Vis absorption spectra as broadened d-d transition bands, arising from the dynamic averaging of multiple distorted geometries due to vibronic interactions, which split and widen the otherwise sharp octahedral transitions. Theoretically, this behavior in octahedral systems stems from linear vibronic coupling of the doubly degenerate 2Eg^2\mathrm{E_g} electronic state with the doubly degenerate eg\mathrm{e_g} vibrational modes, denoted as the E⊗e\mathrm{E \otimes e} problem in OhO_h symmetry, which generates three equivalent minima on the potential energy surface corresponding to the possible tetragonal distortions. This coupling constant determines the magnitude of the distortion, with stronger interactions yielding more pronounced elongation.

Other Structural Distortions

Steric distortions in octahedral complexes arise primarily from the spatial demands of bulky or multidentate ligands, which impose constraints on ideal bond angles and lengths. For instance, bidentate ligands like (en) in [Ni(en)3]2+ exhibit a characteristic bite angle of approximately 83°, deviating from the ideal 90° octahedral angle due to the ligand's fixed geometry, leading to a compressed and overall angular distortion. This effect is exacerbated by larger ligands such as phosphines (e.g., PPh3), which introduce steric crowding that bends equatorial planes or elongates axial bonds to minimize repulsion. Such distortions are common in complexes where ligand size limits the approach to perfect , influencing electronic properties and reactivity without invoking electronic degeneracy. Environmental factors, including solvation in polar solvents, can induce subtle distortions by asymmetrically solvating the complex, often resulting in slight elongation or compression along polar axes. In polar media like or , the dielectric environment stabilizes charged ligands unevenly, causing variations on the order of 1-3% in complexes such as [Co(NH3)6]3+, as observed through spectroscopic shifts and computational modeling. These solvent-induced perturbations maintain the overall octahedral framework but alter vibrational modes and ligand-metal interactions, contributing to solvatochromism in solution. Pseudo-octahedral geometries occur in cases where coordination appears sixfold but includes a weak or distant sixth , effectively mimicking five-coordinate structures within an octahedral envelope. A representative example is the [XeF5]+ cation, which adopts a pseudo-octahedral AX5E arrangement under , with the occupying an axial position and faint interactions from counterions simulating the sixth , resulting in a square-pyramidal base distorted toward . This configuration is stabilized in solid-state salts like XeF5Ni(AsF6)3, where structures reveal Xe-F bond lengths varying by up to 10% due to the pseudo-coordination. Additional examples illustrate lone pair or dynamic effects leading to distortions while preserving the octahedral motif. The [IF6]- anion features a distorted octahedral due to a stereochemically active in the valence shell, causing C4v with elongated axial I-F bonds (approximately 2.05 ) compared to equatorial ones (1.89 ), as confirmed by NMR and diffraction studies. Similarly, the [NbF6]- ion adopts a nearly regular octahedral , with minimal distortions due to dynamic Jahn-Teller effects in its d¹ configuration, resulting in averaged bond lengths of about 1.91 as observed in solid-state and solution studies. These non-Jahn-Teller distortions are typically quantified using , where significant deviations are identified by bond length variations exceeding 5% from the mean (e.g., Δr/r > 0.05) or angular deviations >5° from 90°/180°, providing metrics for comparing ideal versus perturbed geometries in both and solution phases.

Bioctahedral Structures

Bioctahedral structures arise when two octahedral coordination units share either an edge or a face, forming discrete dimeric clusters that are prevalent in the chemistry of early and middle transition metals. These configurations lower the overall symmetry compared to isolated octahedra (O_h) and often feature metal-metal multiple bonds that stabilize the assembly, enabling unique electronic properties. Edge-sharing bioctahedra involve two bridging ligands between the metals, while face-sharing involves three, leading to shorter intermetallic distances and stronger interactions in the latter. In edge-sharing bioctahedra, the shared edge typically consists of two halide or chalcogenide ligands, resulting in structures with D_{4h} symmetry. A prototypical example is the [Mo_2Cl_8]^{4-} anion, where two Mo(III) centers (each formally d^3) are linked by a quadruple Mo-Mo bond with a length of approximately 0.214 nm, comprising one σ, two π, and one δ components derived from d-orbital overlap. This bonding motif, first characterized crystallographically in 1964, exemplifies how electron-rich metals form robust multiple bonds to achieve stability, with the chloride ligands providing four terminal positions per metal. Similar edge-sharing dimers occur in rhenium clusters like Re_3Cl_9, where pairwise edge-sharing among three metals forms a triangular core supported by metal-metal bonds. Face-sharing bioctahedra feature three bridging ligands, often adopting approximate D_{3h} symmetry, and are less common in discrete molecules due to steric demands but appear in certain oxide-fluoride systems. The [Mo_2O_6F_3]^{3-} anion represents such a structure, with two Mo(VI) centers bridged by three fluoride ions and each metal bearing three terminal oxo groups; the Mo-Mo distance is about 0.317 nm, with weak or no direct metal-metal bonding due to the long distance. In cluster chemistry, face-sharing motifs extend to larger assemblies, such as the [Nb_6Cl_{12}]^{2+} core (with additional terminal ligands like in [Nb_6Cl_{12}(CN)_6]^{4-}), where the six niobium atoms form an octahedral metal framework bridged by chlorides on faces and edges, effectively incorporating multiple shared faces for delocalized bonding. These clusters exhibit 14 valence electrons per metal octahedron, following the cluster electron-counting rules. The reduced symmetry in bioctahedral structures (e.g., D_{4h} for edge-sharing) influences spectroscopic properties and reactivity, often leading to anisotropic ligand fields. Applications leverage these features: edge-sharing dimers like [Mo_2Cl_8]^{4-} derivatives serve as precursors for in due to their robust metal-metal bonds, while octahedral clusters such as Nb_6 and Ta_6 halides form building blocks for coordination polymers with luminescent or supramolecular properties. In , related Mo_6 octahedral clusters in Chevrel phases (e.g., PbMo_6S_8) exhibit high critical magnetic fields and up to 13 K, attributed to the delocalized electrons within the cluster framework.

Trigonal Prismatic Geometry

Trigonal prismatic geometry represents an alternative coordination arrangement for six ligands around a central metal atom, where the ligands occupy the vertices of a . In this structure, the three ligands in each triangular face are eclipsed, resulting in equatorial metal-ligand-metal angles of approximately 60°, in contrast to the 90° angles characteristic of octahedral geometry. This geometry is less common than octahedral but occurs in specific electronic configurations, particularly for early transition metals with d⁰ or d¹⁰ counts, where ligand-ligand repulsions are minimized and covalent interactions are favored over ionic ones. For instance, in d⁰ systems, the absence of d electrons allows for closer ligand approaches without electronic destabilization, as seen in layered materials like TaS₂, where adopts trigonal prismatic coordination with atoms. Similarly, d¹⁰ configurations, often involving soft donor ligands, stabilize the prismatic form due to filled d orbitals that reduce angular strain preferences. The preference for trigonal prismatic over octahedral geometry in these systems arises from reduced - interactions and better overlap of metal- orbitals in the prismatic arrangement. In d⁰ complexes like W(CH₃)₆, the structure adopts a distorted trigonal prismatic form with C₃ , where the methyl groups enable fluxional behavior through low-energy inversions and rotations, averaging the environments in solution. For d¹⁰ examples, precursors such as [MoS₄]²⁻ (Mo(VI), d⁰, but illustrative of sulfur-rich environments leading to prismatic clusters) highlight how soft ligands promote prismatic coordination in subsequent assemblies. In contrast, MoF₆ maintains an octahedral but features trigonal prismatic transition states approximately 27.5–45.5 kJ/mol higher in energy, underscoring the energetic accessibility of prismatic forms in fluoride systems. Interconversion between octahedral and trigonal prismatic geometries in hexacoordinate complexes typically proceeds via a Bailar twist mechanism, involving rotation of the triangular faces to pass through a trigonal prismatic , akin to an extension of pseudorotation principles for higher coordination numbers. This pathway has a higher energy barrier for second- and third-row transition metals compared to first-row analogs, due to stronger metal-ligand bonds and increased relativistic effects; for example, tungsten complexes like W(CH₃)₆ exhibit barriers around 20 kJ/mol for prismatic inversion, higher than in lighter congeners. Spectroscopic methods, particularly , can distinguish trigonal prismatic from octahedral geometries through differences in vibrational modes. In prismatic structures, the eclipsed arrangement leads to distinct symmetric stretching modes (e.g., A₁' in D₃h ), while octahedral complexes show degenerate E_g modes; for instance, in MoS₂ polymorphs, the trigonal prismatic 2H phase displays prominent E₂g and A₁g bands at ~380 cm⁻¹ and ~408 cm⁻¹, differing from the octahedral 1T phase's lower-frequency shifts and additional J₂ modes. This distinction aids in identifying the geometry in solid-state or solution samples without crystallographic analysis.

Electronic Structure and Orbital Splitting

d-Orbital Energy Splitting

(CFT) models the interaction between a and its surrounding ligands by treating the ligands as point negative charges that generate an electrostatic field. This field lifts the degeneracy of the five d-orbitals, splitting them into groups of different energies due to differential repulsion from the ligands. In an octahedral ligand field, the d-orbitals divide into a threefold degenerate lower-energy t_{2g} set (comprising the d_{xy}, d_{xz}, and d_{yz} orbitals) and a twofold degenerate higher-energy e_g set (comprising the d_{z^2} and d_{x^2-y^2} orbitals). The t_{2g} orbitals, which point between the -metal axes, experience less electrostatic repulsion than the e_g orbitals, which point directly toward the ligands. The energy separation between these sets is defined as the octahedral splitting parameter Δ_o, where Δ_o = E_{e_g} - E_{t_{2g}}. Relative to the barycenter (the average energy of the unsplit d-orbitals), the t_{2g} set lies at -0.4 Δ_o and the e_g set at +0.6 Δ_o, ensuring no net change in total d-orbital energy. This splitting pattern is illustrated in the following energy diagram: eg(+0.6Δo)t2g(−0.4Δo)\begin{array}{c} \text{e}_\text{g} \quad (+0.6 \Delta_\text{o}) \\ \hline \\ \text{t}_\text{2g} \quad (-0.4 \Delta_\text{o}) \end{array} The magnitude of Δ_o varies based on several key factors. Higher metal oxidation states increase Δ_o because they enhance the effective nuclear charge (Z_eff), strengthening the electrostatic interaction with the ligands. For instance, Δ_o is larger for Co(III) complexes than for Co(II) analogs with the same ligands. Additionally, Δ_o rises with increasing principal quantum number of the metal's valence electrons (n), as orbitals with higher n extend farther from the nucleus and overlap more effectively with ligand orbitals; thus, splitting follows the order 5d > 4d > 3d metals./05%3A_Coordination_Chemistry/5.06%3A_Crystal_Field_Theory/5.6.04%3A_Factors_That_Affect_the_Magnitude_of_o) The most significant influence on Δ_o comes from ligand field strength, quantified by the spectrochemical series, which ranks ligands by their ability to split d-orbitals: I⁻ < Br⁻ < S²⁻ < SCN⁻ < Cl⁻ < NO₃⁻ < N₃⁻ < F⁻ < OH⁻ < C₂O₄²⁻ ≈ H₂O < NCS⁻ < CH₃CN < py < NH₃ < en < bipy < phen < NO₂⁻ < PPh₃ < CN⁻ < CO. Weak-field ligands (left side) produce small Δ_o, while strong-field ligands (right side) produce large Δ_o. Within CFT, Δ_o scales proportionally with Z_eff and the ligand's electrostatic field strength, approximated as Δ_o ∝ Z_eff × (ligand field parameter). For example, in [Co(NH₃)₆]³⁺, where NH₃ is a moderate-field ligand and Co is in the +3 oxidation state (3d metal), Δ_o ≈ 23,000 cm⁻¹.

Implications for Crystal Field Theory

In octahedral complexes, the crystal field splitting parameter Δo\Delta_o plays a crucial role in determining the electron configuration for d⁴ to d⁷ ions by comparing it to the pairing energy PP, which is the energy required to pair two electrons in the same orbital. When Δo<P\Delta_o < P, electrons occupy both t₂g and e_g orbitals singly before pairing, resulting in a high-spin configuration with more unpaired electrons; conversely, if Δo>P\Delta_o > P, electrons pair in the lower-energy t₂g orbitals, yielding a low-spin configuration with fewer unpaired electrons. This distinction arises because weak-field ligands produce small Δo\Delta_o values, favoring high-spin states, while strong-field ligands generate larger Δo\Delta_o values, promoting low-spin states. A representative example is the d⁶ Fe²⁺ ion: in [Fe(H₂O)₆]²⁺, acts as a weak-field , leading to a high-spin t₂g⁴ e_g² configuration with four unpaired electrons, rendering the complex pale green and paramagnetic. In contrast, [Fe(CN)₆]⁴⁻ features as a strong-field , resulting in a low-spin t₂g⁶ configuration with no unpaired electrons, making it diamagnetic. The octahedral splitting Δo\Delta_o also governs the colors of these complexes through d-d transitions, where electrons are excited from t₂g to e_g orbitals, absorbing visible light. For first-row transition metals, Δo\Delta_o typically falls in the visible range (around 10,000–20,000 cm⁻¹), causing absorption of specific wavelengths and transmission of , such as the pale green of high-spin [Fe(H₂O)₆]²⁺ due to absorption in the red-orange region. Magnetism in octahedral complexes stems from the number of unpaired electrons dictated by the spin state, quantified by the spin-only magnetic moment formula μ=n(n+2)\mu = \sqrt{n(n+2)}
Add your contribution
Related Hubs
User Avatar
No comments yet.