Hubbry Logo
JitterJitterMain
Open search
Jitter
Community hub
Jitter
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Jitter
Jitter
Jitter
View on Wikipedia
from Wikipedia

In electronics and telecommunications, jitter is the deviation from true periodicity of a presumably periodic signal, often in relation to a reference clock signal. In clock recovery applications it is called timing jitter.[1] Jitter is a significant, and usually undesired, factor in the design of almost all communications links.

Jitter can be quantified in the same terms as all time-varying signals, e.g., root mean square (RMS), or peak-to-peak displacement. Also, like other time-varying signals, jitter can be expressed in terms of spectral density.

Jitter period is the interval between two times of maximum effect (or minimum effect) of a signal characteristic that varies regularly with time. Jitter frequency, the more commonly quoted figure, is its inverse. ITU-T G.810 classifies deviation lower frequencies below 10 Hz as wander and higher frequencies at or above 10 Hz as jitter.[2]

Jitter may be caused by electromagnetic interference and crosstalk with carriers of other signals. Jitter can cause a display monitor to flicker, affect the performance of processors in personal computers, introduce clicks or other undesired effects in audio signals, and cause loss of transmitted data between network devices. The amount of tolerable jitter depends on the affected application.

Metrics

[edit]

For clock jitter, there are three commonly used metrics:[contradictory]

Absolute jitter
The absolute difference in the position of a clock's edge from where it would ideally be.
Maximum time interval error (MTIE)
Maximum error committed by a clock under test in measuring a time interval for a given period of time.
Period jitter (a.k.a. cycle jitter)
The difference between any one clock period and the ideal or average clock period. Period jitter tends to be important in synchronous circuitry such as digital state machines where the error-free operation of the circuitry is limited by the shortest possible clock period (average period less maximum cycle jitter), and the performance of the circuitry is set by the average clock period. Hence, synchronous circuitry benefits from minimizing period jitter, so that the shortest clock period approaches the average clock period.
Cycle-to-cycle jitter
The difference in duration of any two adjacent clock periods. It can be important for some types of clock generation circuitry used in microprocessors and RAM interfaces.

In telecommunications, the unit used for the above types of jitter is usually the unit interval (UI) which quantifies the jitter in terms of a fraction of the transmission unit period. This unit is useful because it scales with clock frequency and thus allows relatively slow interconnects such as T1 to be compared to higher-speed internet backbone links such as OC-192. Absolute units such as picoseconds are more common in microprocessor applications. Units of degrees and radians are also used.

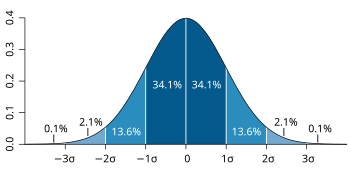
In the normal distribution one standard deviation from the mean (dark blue) accounts for about 68% of the set, while two standard deviations from the mean (medium and dark blue) account for about 95% and three standard deviations (light, medium, and dark blue) account for about 99.7%.

If jitter has a Gaussian distribution, it is usually quantified using the standard deviation of this distribution. This translates to an RMS measurement for a zero-mean distribution. Often, jitter distribution is significantly non-Gaussian. This can occur if the jitter is caused by external sources such as power supply noise. In these cases, peak-to-peak measurements may be more useful. Many efforts have been made to meaningfully quantify distributions that are neither Gaussian nor have a meaningful peak level. All have shortcomings but most tend to be good enough for the purposes of engineering work.

In computer networking, jitter can refer to packet delay variation, the variation (statistical dispersion) in the delay of the packets.

Types

[edit]

One of the main differences between random and deterministic jitter is that deterministic jitter is bounded and random jitter is unbounded.[3][4]

Random jitter

[edit]

Random jitter, also called Gaussian jitter, is unpredictable electronic timing noise. Random jitter typically follows a normal distribution[5][6] due to being caused by thermal noise in an electrical circuit.

Deterministic jitter

[edit]

Deterministic jitter is a type of clock or data signal jitter that is predictable and reproducible. The peak-to-peak value of this jitter is bounded, and the bounds can easily be observed and predicted. Deterministic jitter has a known non-normal distribution. Deterministic jitter can either be correlated to the data stream (data-dependent jitter) or uncorrelated to the data stream (bounded uncorrelated jitter). Examples of data-dependent jitter are duty-cycle dependent jitter (also known as duty-cycle distortion) and intersymbol interference.

Total jitter

[edit]
n BER
6.4 10−10
6.7 10−11
7 10−12
7.3 10−13
7.6 10−14

Total jitter (T) is the combination of random jitter (R) and deterministic jitter (D) and is computed in the context to a required bit error rate (BER) for the system:[7]

T = Dpeak-to-peak + 2nRrms,

in which the value of n is based on the BER required of the link.

A common BER used in communication standards such as Ethernet is 10−12.

Examples

[edit]

Sampling jitter

[edit]

In analog-to-digital and digital-to-analog conversion of signals, the sampling is normally assumed to be periodic with a fixed period—the time between every two samples is the same. If there is jitter present on the clock signal to the analog-to-digital converter or a digital-to-analog converter, the time between samples varies and instantaneous signal error arises. The error is proportional to the slew rate of the desired signal and the absolute value of the clock error. The effect of jitter on the signal depends on the nature of the jitter. Random jitter tends to add broadband noise while periodic jitter tends to add errant spectral components, "birdys". In some conditions, less than a nanosecond of jitter can reduce the effective bit resolution of a converter with a Nyquist frequency of 22 kHz to 14 bits.[8]

Sampling jitter is an important consideration in high-frequency signal conversion, or where the clock signal is especially prone to interference.

In digital antenna arrays ADC and DAC jitters are the important factors determining the direction of arrival estimation accuracy[9] and the depth of jammers suppression.[10]

Packet jitter in computer networks

[edit]

In the context of computer networks, packet jitter or packet delay variation (PDV) is the variation in latency as measured in the variability over time of the end-to-end delay across a network. A network with constant delay has no packet jitter.[11] Packet jitter is expressed as an average of the deviation from the network mean delay.[12] PDV is an important quality of service factor in assessment of network performance.

Transmitting a burst of traffic at a high rate followed by an interval or period of lower or zero rate transmission may also be seen as a form of jitter, as it represents a deviation from the average transmission rate. However, unlike the jitter caused by variation in latency, transmitting in bursts may be seen as a desirable feature,[citation needed] e.g. in variable bitrate transmissions.

Video and image jitter

[edit]

Video or image jitter occurs when the horizontal lines of video image frames are randomly displaced due to the corruption of synchronization signals or electromagnetic interference during video transmission. Model-based dejittering study has been carried out under the framework of digital image and video restoration.[13]

Testing

[edit]

Jitter in serial bus architectures is measured by means of eye patterns. There are standards for jitter measurement in serial bus architectures. The standards cover jitter tolerance, jitter transfer function and jitter generation, with the required values for these attributes varying among different applications. Where applicable, compliant systems are required to conform to these standards.

Testing for jitter and its measurement is of growing importance to electronics engineers because of increased clock frequencies in digital electronic circuitry to achieve higher device performance. Higher clock frequencies have commensurately smaller eye openings, and thus impose tighter tolerances on jitter. For example, modern computer motherboards have serial bus architectures with eye openings of 160 picoseconds or less. This is extremely small compared to parallel bus architectures with equivalent performance, which may have eye openings on the order of 1000 picoseconds.

Jitter is measured and evaluated in various ways depending on the type of circuit under test.[14] In all cases, the goal of jitter measurement is to verify that the jitter will not disrupt normal operation of the circuit.

Testing of device performance for jitter tolerance may involve injection of jitter into electronic components with specialized test equipment.

A less direct approach—in which analog waveforms are digitized and the resulting data stream analyzed—is employed when measuring pixel jitter in frame grabbers.[15]

Mitigation

[edit]

Anti-jitter circuits

[edit]

Anti-jitter circuits (AJCs) are a class of electronic circuits designed to reduce the level of jitter in a clock signal. AJCs operate by re-timing the output pulses so they align more closely to an idealized clock. They are widely used in clock and data recovery circuits in digital communications, as well as for data sampling systems such as the analog-to-digital converter and digital-to-analog converter. Examples of anti-jitter circuits include phase-locked loop and delay-locked loop.

Jitter buffers

[edit]

Jitter buffers or de-jitter buffers are buffers used to counter jitter introduced by queuing in packet-switched networks to ensure continuous playout of an audio or video media stream transmitted over the network.[16] The maximum jitter that can be countered by a de-jitter buffer is equal to the buffering delay introduced before starting the play-out of the media stream. In the context of packet-switched networks, the term packet delay variation is often preferred over jitter.

Some systems use sophisticated delay-optimal de-jitter buffers that are capable of adapting the buffering delay to changing network characteristics. The adaptation logic is based on the jitter estimates computed from the arrival characteristics of the media packets. Adjustments associated with adaptive de-jittering involves introducing discontinuities in the media play-out which may be noticeable to the listener or viewer. Adaptive de-jittering is usually carried out for audio play-outs that include voice activity detection that allows the lengths of the silence periods to be adjusted, thus minimizing the perceptual impact of the adaptation.

Dejitterizer

[edit]

A dejitterizer is a device that reduces jitter in a digital signal.[17] A dejitterizer usually consists of an elastic buffer in which the signal is temporarily stored and then retransmitted at a rate based on the average rate of the incoming signal. A dejitterizer may not be effective in removing low-frequency jitter (wander).

Filtering and decomposition

[edit]

A filter can be designed to minimize the effect of sampling jitter.[18]

A jitter signal can be decomposed into intrinsic mode functions (IMFs), which can be further applied for filtering or dejittering.[citation needed]

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Jitter

View on Grokipedia
from Grokipedia
Jitter is the short-term variation in the timing of significant instants of a from their ideal positions in time. This phenomenon, also described as the noise modulation due to random time shifts on an otherwise ideal signal transition, primarily affects high-frequency digital signals in and systems. Jitter arises in contexts such as clock signals, data transmission, and network communications, where precise timing is essential for reliable performance. In communications systems, jitter can lead to bit errors by shifting sampling instants relative to the transmitted data, thereby degrading the (BER). It is distinguished from longer-term variations known as wander, with jitter typically referring to phase changes above 10 Hz. Jitter accumulates along signal paths, influenced by factors like electrical , device imperfections, (EMI), and bandwidth limitations. Jitter is categorized into two main types: random jitter (RJ), which is unbounded and follows a Gaussian distribution due to sources like thermal ; and deterministic jitter (DJ), which is bounded and caused by predictable factors such as data patterns or . Total jitter (TJ) combines these, often expressed as the sum of DJ and a multiple of RJ based on the desired BER, such as 7σ or 14σ for low error rates. Deterministic jitter includes subtypes like periodic jitter from fixed-frequency (e.g., power supply ) and data-dependent jitter varying with signal duty cycles. Measurement and management of jitter are critical in standards like and Fiber Channel, which define it in terms of deviations from ideal timing to ensure system interoperability and performance. Techniques such as phase-locked loops (PLLs) and jitter cleaners are employed to filter RJ while addressing DJ through improved circuit design. In clock systems, jitter estimation often derives from measurements, integrating spectral densities over relevant frequency bands using power-law noise models.

Fundamentals

Definition

Jitter refers to the deviation in the timing of a periodic signal from its ideal uniform period. Specifically, it is defined as the short-term variations of the significant instants of a from their ideal positions in time. This phenomenon manifests as small, rapid fluctuations in the timing of signal edges or transitions, typically quantified in time units such as picoseconds (ps) or femtoseconds (fs), or occasionally as a of the signal's period. Jitter differs from related timing and signal impairments: unlike , which involves random variations in signal , jitter pertains exclusively to phase or timing deviations without affecting . It also contrasts with wander, which represents long-term variations in the significant instants of a timing signal, often due to slower frequency drifts over extended periods. These distinctions ensure that jitter focuses on high-frequency, short-term instabilities in periodic signals. Mathematically, jitter can be represented as the standard deviation of the time deviations for successive signal cycles, expressed as J=σ(Δti)J = \sigma(\Delta t_i), where Δti\Delta t_i denotes the deviation of the ii-th cycle from its ideal timing. This formulation captures the statistical variation in edge arrival times relative to a perfect reference clock. Jitter arises in various technical domains, including electronics where it affects clock signal stability, communications systems for maintaining data synchronization, and computing environments for precise processor timing.

Significance

Jitter significantly degrades in electronic systems by introducing timing variations that distort the , potentially closing the eye diagram and reducing the valid sampling window for . This leads to increased bit error rates (BER), as excessive jitter can cause signal transitions to occur on the incorrect side of the decision threshold at the receiver, resulting in misinterpreted bits. In high-speed digital communications, such degradation also causes loss between transmitter and receiver clocks, leading to misalignment and frame errors. Furthermore, jitter limits achievable rates by consuming a substantial portion of the unit interval (UI), the time slot for each bit, thereby constraining overall system throughput in environments exceeding 1 Gbps. The economic and reliability costs of uncontrolled jitter are substantial, manifesting in system failures that demand costly redesigns and maintenance. In , jitter contributes to degraded in voice-over-IP (VoIP) networks, where variations in packet arrival times exceed jitter buffer tolerances, leading to audio distortions, choppy voice, and user dissatisfaction. In applications, jitter induces timing violations in processors by shortening clock pulses below the minimum required for stages, causing setup/hold time failures and halting operations, which compromises reliability in data centers and embedded systems. These issues elevate operational expenses through higher error correction overhead and reduced equipment lifespan, underscoring jitter's role as a key reliability bottleneck. To mitigate these effects, engineers employ jitter budgets that allocate allowable timing variations across system components, ensuring total jitter remains below critical thresholds for reliable operation. A general design guideline specifies that peak-to-peak jitter should be less than 10% of the bit period to maintain low BER, such as 10^{-12}, providing adequate margin for and inter-symbol interference. These budgets are essential in high-speed interfaces, where even small deviations can propagate and amplify risks. The importance of controlling jitter has intensified since the with the transition from megahertz to gigahertz clock speeds in modern , as higher frequencies shrink the UI proportionally, making even picosecond-level jitter a dominant factor in performance limitations. This evolution, driven by demands for faster data processing in applications like 10-Gigabit Ethernet and multi-core processors, has necessitated advanced jitter analysis and mitigation techniques to sustain at rates up to 2 GHz and beyond.

Types

Random Jitter

Random jitter constitutes the stochastic component of timing variations in electrical signals, arising from unpredictable noise sources that introduce Gaussian-distributed deviations from ideal edge positions. Primary sources include thermal noise, which stems from random molecular motion in conductors; , resulting from the discrete nature of charge carriers in semiconductors; and fluctuations in noise that contribute broadband random effects. These mechanisms ensure that random jitter exhibits no repeatable pattern and accumulates through independent, uncorrelated events across the signal path. Statistically, random jitter is modeled using a , characterized by its root-mean-square (RMS) value, denoted as σ\sigma. For system reliability assessments, such as in high-speed serial links, the peak-to-peak random jitter JrJ_r is often bounded at a specific (BER); at a BER of 10−1210^{-12}, Jr≈14.1σJ_r \approx 14.1 \sigma, reflecting the tail of the distribution where errors become negligible. This modeling assumes independence from other jitter types and focuses on the unbounded nature of the distribution, where extreme deviations, though improbable, can theoretically extend indefinitely. In practice, random jitter's characteristics include its theoretical unbounded extent, limited only by constraints, and a tendency to grow with extended periods as more samples are captured, widening the effective distribution. of random jitter typically employs histogram-based techniques on time-interval to construct the (PDF), enabling estimation of σ\sigma and validation of the Gaussian shape. This method provides a visual and quantitative representation of the jitter's statistical profile, essential for isolating random contributions in evaluations.

Deterministic Jitter

Deterministic jitter (DJ) refers to predictable and systematic deviations in the timing of signal edges caused by repeatable external or internal influences in digital systems. Unlike random jitter, which is characterized by statistical distributions, deterministic jitter exhibits bounded behavior with finite minimum and maximum extents that can be predicted based on observed patterns. DJ encompasses several subtypes, including data-dependent jitter (DDJ), periodic jitter (PJ), duty-cycle distortion (DCD), and bounded uncorrelated jitter (BUJ). DDJ arises from interactions between the data pattern and the channel response, such as , leading to timing shifts that depend on preceding bits. PJ results from periodic interference sources, manifesting as sinusoidal or modulations on the signal. DCD occurs due to asymmetries in the clock or signal , causing even and odd edges to shift differently. BUJ includes other bounded components not correlated with data or strictly periodic, such as those from or reflections. Common sources of DJ include between adjacent signal lines, reflections from impedance mismatches, and clock modulation from power supplies. For instance, PJ can be induced by 50/60 Hz hum coupling into the system, creating low-frequency periodic variations. These sources produce repeatable effects that degrade in high-speed serial links. DJ is often modeled using sinusoidal or periodic functions to represent its predictable nature; for example, periodic jitter can be expressed as PJ(t)=Asin⁡(2πft+ϕ)PJ(t) = A \sin(2\pi f t + \phi), where AA is the , ff is the of the interfering signal, and ϕ\phi is the phase offset. Due to its bounded characteristics, DJ is analyzed through eye diagrams, which visualize the peak-to-peak extent of timing variations and their impact on the signal eye opening without relying on probabilistic methods.

Total Jitter

Total jitter (TJ) is the aggregate timing variation in a signal, encompassing both random jitter (RJ) and deterministic jitter (DJ), and serves as a comprehensive measure for assessing overall signal integrity at a specified bit error rate (BER). The composition of TJ is determined by combining the unbounded Gaussian distribution of RJ with the bounded components of DJ, typically expressed as TJ(BER)=DJp−p+2⋅Q−1(BER2)⋅RJ,TJ(BER) = DJ_{p-p} + 2 \cdot Q^{-1}\left(\frac{BER}{2}\right) \cdot RJ, where Q−1Q^{-1} denotes the inverse Q-function, which quantifies the tail extent of the Gaussian distribution corresponding to the target BER (e.g., Q−1(5×10−13)≈7.03Q^{-1}(5 \times 10^{-13}) \approx 7.03 for BER = 10−1210^{-12}, yielding approximately 14 RJ for the random contribution), and RJ is the RMS random jitter. This formulation arises from the bathtub curve analysis in eye diagrams, where TJ defines the total closure of the timing margin at low BER levels. The dual-Dirac model provides an efficient approximation of the total jitter (PDF) by convolving a Gaussian PDF for RJ with two Dirac delta functions offset by the DJ peak-to-peak value, effectively bounding the deterministic contributions. This model simplifies the estimation of TJ(BER) for complex signals, enabling rapid prediction without full statistical sampling, and is particularly useful for validating system margins in serial data communications. In the design and verification of high-speed serial links, TJ is the key parameter for compliance testing, as it directly determines the eye opening and adequacy. For example, standards such as PCIe Gen2 specify a maximum TJ of 0.6 unit intervals (UI) for receiver jitter tolerance at BER = 10−1210^{-12}, ensuring robust operation amid accumulated impairments. Decomposing TJ into RJ and DJ components presents challenges due to the convolution of their distributions, which can obscure boundaries in measured histograms, requiring advanced fitting techniques like dual-Dirac analysis for accurate separation. Such decomposition is essential for root-cause diagnosis—identifying thermal noise in RJ versus crosstalk in DJ—but TJ itself remains the definitive metric for specification compliance, as isolated components alone do not predict end-to-end BER performance.

Applications and Examples

Sampling Jitter

Sampling jitter refers to the random or deterministic variations in the timing of sampling clock edges within analog-to-digital converters (ADCs), which introduce aperture uncertainty and result in errors during the quantization of the input signal. This uncertainty manifests as a deviation in the exact moment the sample-and-hold circuit captures the analog voltage, leading to inaccuracies proportional to the signal's rate of change, particularly for high-frequency inputs. The primary sources of sampling jitter in ADCs include instability in the , such as from oscillators, and noise introduced by phase-locked loops (PLLs) used for clock synthesis or multiplication. Internal aperture jitter within the ADC's sample-and-hold circuitry also contributes, often combining with external clock jitter to form the total timing error. These timing variations degrade the signal-to-noise ratio (SNR) of the ADC, with the impact becoming more severe at higher signal frequencies due to the increased voltage error from rapid signal slopes. The theoretical SNR limited by jitter can be approximated by the formula SNR=−20log⁡10(2πfJ\rms)\text{SNR} = -20 \log_{10} (2 \pi f J_{\rms}) where ff is the input signal frequency in Hz and J\rmsJ_{\rms} is the root-mean-square (RMS) jitter in seconds; this equation assumes a sinusoidal input and random jitter dominating other noise sources. For instance, at 100 MHz with 1 ps RMS jitter, the SNR drops to approximately 66 dB, limiting effective resolution in high-speed applications. In practical examples, such as high-speed oscilloscopes used for analysis, sampling jitter must be minimized to below 1 ps RMS to preserve timing accuracy for gigahertz-range signals without significant . Similarly, in high-fidelity audio sampling ADCs operating at 192 kHz with 24-bit resolution, jitter levels around 50 ps RMS, as measured in modern equipment, are sufficient to avoid audible artifacts.

Packet Jitter in Networks

Packet jitter in networks refers to the variation in inter-packet arrival times experienced by data packets traversing computer and networks, primarily arising from decisions, congestion at network nodes, and variable queuing delays at routers or switches. This phenomenon became particularly prominent in the with the widespread adoption of packet-switched networks, such as the early , where the integration of real-time applications like voice and video over IP highlighted the need for (QoS) mechanisms to manage delay variability. As networks evolved into high-speed infrastructures like and modern , packet jitter remains a key challenge for ensuring reliable performance in latency-sensitive services. Measurement of packet jitter is commonly performed using Inter-Packet Delay Variation (IPDV), defined as the difference between the one-way delays of successive packets in a stream, allowing for assessment of short-term delay fluctuations. In real-time protocols like RTP for VoIP, jitter is calculated as the smoothed absolute difference between expected and actual interarrival times, providing a metric in units to quantify network variability. Standards such as RFC 3393 emphasize IPDV for applications requiring bounded delay variation, with practical thresholds for VoIP typically recommending levels below 30 ms to maintain acceptable call quality, as higher values degrade audio clarity. The impacts of packet jitter are most evident in real-time applications, where inconsistent packet arrival times can lead to buffer underflow—resulting in dropped packets and audio gaps—or , causing excessive latency that disrupts . For instance, in video streaming, jitter exceeding acceptable bounds contributes to lip-sync discrepancies between audio and video tracks, impairing user experience in conferencing or broadcast services. Deterministic components of jitter, often induced by periodic traffic patterns, can exacerbate these issues in structured network environments. Overall, uncontrolled jitter undermines QoS guarantees, necessitating careful network design to support emerging applications in ecosystems.

Audio and Video Jitter

In digital audio playback systems, clock jitter in digital-to-analog converters (DACs) affects the timing of sample reconstruction, leading to and similar to ADC sampling jitter. For high-quality 24-bit audio, modern DACs tolerate jitter up to 500 ps RMS in the low-frequency band (0-40 kHz) while maintaining above 100 dB and low THD+N. For example, in interfaces, excessive jitter can introduce audible smearing or harshness, though levels below 200 ps are typically targeted for applications. In video , jitter refers to variations in the timing of or pixel clock signals, which can cause visual artifacts such as horizontal line displacement, twinkling, or sync instability. In broadcast and professional video, standards like for 3G-SDI interfaces specify tolerances including timing jitter below 2.0 unit intervals (UI, approximately 0.67 ns at 2.97 Gbps ) and alignment jitter below 0.3 UI to prevent signal degradation in transmission chains. For instance, in HD video , uncontrolled jitter may result in noticeable picture instability during editing or playback.

Measurement and Testing

Testing Techniques

Time-domain analysis represents a primary for jitter measurement, focusing on the direct capture of timings relative to an ideal clock reference. This approach typically employs oscilloscopes to record time interval errors (TIE), where deviations in edge arrival times are quantified over multiple cycles. By accumulating these TIE values, histograms can be generated to visualize the distribution of jitter, enabling the identification of both random and deterministic components through statistical analysis of the edge timings. Two fundamental techniques underpin time-domain measurements: real-time sampling, which captures all edges in a single acquisition for high-speed signals, and equivalent-time sampling, which builds a composite from multiple acquisitions to enhance resolution for repetitive patterns. These methods allow for precise and histogram construction, often revealing bounded and unbounded jitter behaviors. For instance, histograms of TIE data facilitate the separation of jitter peaks, providing insights into peak-to-peak variations without requiring frequency transformations. Frequency-domain methods complement time-domain approaches by analyzing jitter through spectral representations, particularly useful for isolating periodic components. The (FFT) applied to TIE sequences converts time-domain jitter into a jitter , highlighting deterministic jitter as discrete tones while random jitter appears as a . spectral density, measured as single-sideband phase noise in dBc/Hz at specific offsets from the carrier, serves as an equivalent metric for random jitter, linking time-domain deviations to frequency-domain noise profiles. This technique is especially effective for low-frequency jitter components that may be obscured in direct time measurements. Statistical sampling is essential for characterizing random jitter (RJ), which follows a Gaussian distribution and requires extensive data accumulation to achieve reliable low-probability estimates. Measurements typically involve capturing at least 10^6 clock cycles to build a sufficient sample , allowing of RJ standard deviation to bit error ratios (BER) as low as 10^{-12} using tail-fitting techniques. This long-term accumulation ensures statistical confidence in RJ estimation, as shorter datasets may underestimate the unbounded tails critical for high-reliability applications. Such often employs models like the dual-Dirac for total jitter, briefly referencing its decomposition into random and deterministic parts. Automated testing procedures have largely supplanted manual methods, leveraging software tools integrated with oscilloscopes to streamline jitter analysis and BER correlation. These tools automatically detect clock patterns, compute histograms, and perform decompositions, reducing operator error and enabling real-time BER predictions through generation. Plugins or built-in algorithms correlate jitter components directly to error rates by simulating decision thresholds, offering faster iterations compared to manual edge-by-edge verification. This automation is particularly valuable for validating in complex systems, ensuring measurements align with extrapolated BER targets.

Equipment and Standards

Jitter measurement requires specialized high-bandwidth oscilloscopes capable of operating at frequencies exceeding 10 GHz to capture high-speed signals accurately, with examples including the Keysight 86100C series that supports over 80 GHz bandwidth and integrates jitter analysis capabilities. Time domain reflectometry (TDR) and transmission (TDT) modules are essential for assessing signal reflections and integrity in interconnects, often incorporated as plug-in options in these oscilloscopes to enable precise impedance analysis. Dedicated jitter analyzers, such as those embedded in Tektronix DSA8200 sampling oscilloscopes, provide ultra-low intrinsic jitter floors below 100 fs to ensure measurement fidelity for picosecond-scale phenomena. Software suites enhance automation in jitter decomposition, with Keysight's D9020JITA offering algorithms for separating random jitter (RJ) from deterministic jitter (DJ) through histogram-based and spectral methods on Infiniium oscilloscopes. Similarly, Tektronix's Advanced Jitter Analysis (DJA) software automates RJ/DJ isolation using tail fitting and dual-Dirac modeling, integrated directly with their real-time oscilloscopes for streamlined compliance testing. Relevant standards govern jitter specifications for various interfaces, including the Optical Internetworking Forum's Common Electrical I/O (OIF-CEI) implementation agreements, which define jitter budgets and measurement methodologies for optical and electrical interfaces up to 112 Gb/s, such as OIF-CEI-112G for long-reach and very short-reach operations. As of November 2025, the OIF published OIF-EEI-112G-RTLR-01.0 for energy-efficient 112 Gb/s retimed transmitter linear receiver electrical and optical interfaces. For USB interfaces, the (USB-IF) specifies jitter limits in the electrical compliance methodology, requiring random jitter below 4.3 ps RMS (pk-pk 60 ps or 0.3 UI) at a bit error ratio of 10^{-12} for SuperSpeed signaling at 5 Gb/s. To achieve picosecond-range accuracy, of measurement equipment must be to the National Institute of Standards and Technology (NIST), ensuring that jitter results account for instrument noise, bandwidth limitations, and timing references with uncertainties below 1 ps RMS. Such is verified through electro-optic sampling systems and precision waveform calibrators aligned with NIST standards, minimizing systematic errors in high-speed serial data assessments.

Mitigation

Hardware Solutions

Hardware solutions for jitter mitigation primarily involve specialized circuits and components designed to stabilize clock signals and minimize timing variations at the physical layer. Phase-locked loops (PLLs) and delay-locked loops (DLLs) serve as key anti-jitter circuits for clock recovery in high-speed systems. PLLs synchronize an output clock to a reference by adjusting phase through a feedback loop, effectively filtering input jitter while introducing trade-offs in loop bandwidth: narrower bandwidths reduce high-frequency jitter but slow acquisition time, whereas wider bandwidths improve tracking of low-frequency variations at the cost of amplifying noise. DLLs, which align phases without frequency synthesis, exhibit inherent jitter peaking that cannot be fully eliminated, with maximum peaking around 0.66 dB in typical configurations; this peaking trades off against tracking bandwidth, where higher bandwidth enhances acquisition but increases high-frequency jitter amplification by up to 0.63 dB for white noise sources. To mitigate DLL limitations, loop filtering adds poles (e.g., at 6.5 MHz) to suppress peaking to 0.1 dB, while phase filtering via injection locking (e.g., 20 MHz bandwidth) attenuates high-frequency components in multiplying applications. Clock distribution networks employ low-jitter oscillators and buffers to curb jitter, which arises from signal and noise accumulation along transmission paths. Oven-controlled crystal oscillators (OCXOs) provide ultra-stable references with low , often locked to GPS or standards, minimizing jitter contributions from thermal, , or supply disturbances in synchronous systems. buffers, such as the LMK00105, distribute clock signals across multiple outputs while adding minimal jitter (e.g., 30 fs RMS at 156.25 MHz over 12 kHz to 20 MHz), achieving low delay (0.85–2.8 ns) and output skew (6 ps max) through high inputs and adjustable supplies. Power supply filtering addresses deterministic jitter (DJ) induced by , such as periodic ripple from switching regulators, by isolating sensitive clock circuits. Decoupling capacitors (e.g., 10–22 µF low-ESR for low frequencies and 0.1 µF for high frequencies) placed near supply pins create low-impedance paths to shunt , reducing its into clock buffers and thereby lowering DJ spurs in spectra. Linear regulators further enhance rejection by converting noisy switching supplies to cleaner outputs, with parallel capacitors optimizing broadband filtering to prevent ripple amplification in high-slew-rate clocks. In transceivers, spread-spectrum clocking (SSC) averages out periodic jitter (PJ) by modulating the clock frequency slightly (e.g., 0.8–6.3 GHz range with 5000 ppm spread), reducing peak spectral energy while maintaining low RMS jitter (under 3.5 ps) and achieving up to 20 dB electromagnetic interference suppression without excessive power draw (7 mW at 1.2 V). These techniques collectively target DJ sources like and supply noise, as detailed in prior sections on deterministic jitter.

Software Solutions

Software solutions for jitter mitigation primarily involve algorithmic techniques implemented in operating systems, network protocols, and applications to compensate for timing variations in streams. These approaches focus on buffering, , and error handling to ensure smooth playback without introducing excessive latency. Jitter buffers, also known as playout buffers, are a core software mechanism used in (VoIP) and (RTP) systems to absorb variations in packet arrival times. In RTP, receivers employ these buffers to reorder out-of-sequence packets and delay playback until sufficient data arrives, reconstructing the original timing based on RTP timestamps and sequence numbers. Adaptive jitter buffers dynamically adjust their size—typically ranging from 20 ms to 200 ms—according to estimated network jitter variance, using interarrival jitter calculations derived from RTCP reports to balance low latency against the risk of underflow or overflow. For instance, the jitter estimation formula in RTP, J(i) = J(i-1) + (|D(i-1,i)| - J(i-1))/16, where D represents the difference in packet transit times, enables fine-tuned adaptation to network conditions. This approach improves voice quality by minimizing audible disruptions during talkspurts, as validated in VoIP implementations that monitor buffer depth and link status to detect and respond to jitter spikes. Clock synchronization protocols provide another software layer for reducing jitter in distributed networks by aligning timestamps across devices. The (PTP), defined in IEEE 1588, achieves sub-microsecond synchronization accuracy over Ethernet by exchanging timestamped messages between master and slave clocks, compensating for propagation delays and clock drifts. PTP operates in software on network interfaces or hosts, using algorithms to measure one-way delays and adjust local clocks, thereby minimizing timing jitter in applications like industrial automation and . Implementations often leverage hardware timestamping for enhanced precision, but the protocol's core logic runs in software stacks to handle message parsing and offset calculations. Forward Error Correction (FEC) techniques in software protocols tolerate timing errors by adding redundant data to streams, allowing reconstruction of lost or delayed packets without retransmissions that could exacerbate jitter. In RTP-based systems, FEC as specified in RFC 5109 uses parity packets—such as XOR-based schemes or Unequal Level Protection (ULP)—to recover up to 48 source packets per FEC packet, preserving timing integrity through included timestamps. This method is particularly effective in real-time environments like VoIP, where due to jitter-induced drops is common, enabling immediate delivery of received data while deferring recovery only as needed to avoid additional delay. These software solutions are commonly implemented in operating system kernels, network libraries, and real-time applications. For example, WebRTC's NetEQ jitter buffer module employs adaptive algorithms to estimate inter-arrival times and maintain a target buffer level, using a cost function that weighs delay against underflow probability to dynamically scale the buffer (default capacity: 200 packets). NetEQ further incorporates timescale modification techniques, such as packet or expansion, during silent periods to adjust without audible artifacts, and burst-aware discarding to handle overflow efficiently, reducing in high-jitter scenarios like networks. Such integrations ensure robust performance in browser-based communication, drawing on RTP standards for jitter estimation while optimizing for web constraints.

Advanced Decomposition Methods

Advanced decomposition methods in jitter analysis employ sophisticated techniques to isolate and characterize individual jitter components, such as random jitter (RJ), periodic jitter (PJ), and wander, from the total jitter histogram. These methods are essential for predicting system performance in high-speed applications, where separating bounded uncorrelated jitter (BUJ) from RJ enables accurate extrapolation of bit error rates. Filtering plays a central role, with high-pass filters applied to isolate short-term RJ by attenuating low-frequency wander components, typically using a around 5 kHz or as defined by standards like G.810 at 10 Hz for the boundary between jitter and wander. Conversely, low-pass filters remove high-frequency jitter to focus on wander, often implemented as Butterworth filters in tools and Ethernet standards for their flat passband response; for instance, fourth-order Butterworth filters with specific cutoffs are used in receiver modeling to simulate real-world separation. Decomposition algorithms further refine this isolation by modeling jitter distributions. Tail fitting extrapolates RJ by assuming a Gaussian tail in the histogram and fitting it to predict unbounded behavior beyond the acquisition window, a technique that enhances accuracy for low-probability events in serial links. For PJ, sinusoidal fitting decomposes periodic components via , identifying dominant frequencies and amplitudes to subtract them from the total jitter, thereby clarifying interactions with other deterministic elements. These approaches, often integrated into real-time software, rely on the dual-Dirac model to convolve RJ and deterministic jitter (DJ) components for total jitter estimation. Dejitterizers implement active correction using (DSP) blocks that predict and mitigate jitter in real time. Kalman filters, prized for their optimal state estimation under noise, track clock offsets and skew to reconstruct timing, effectively reducing accumulated jitter in packet-based systems like Ethernet by adaptively adjusting intervals. In hardware DSP implementations, these filters serve as predictive equalizers, estimating future sample times to counteract RJ and DJ, particularly in clock data recovery circuits. Recent advances in the leverage for automated jitter separation in complex, high-data-rate environments such as 100G+ Ethernet links. models, including 1D convolutional neural networks, analyze jitter histograms to decompose components with higher precision than traditional methods by learning non-linear patterns from training data. These AI-driven tools, applied in analysis software, facilitate rapid of multi-gigabit signals where conventional filtering falls short due to overlap.

References

  1. https://www.analog.com/en/resources/technical-articles/an-introduction-to-jitter-in-communications-systems.html
  2. https://tf.nist.gov/general/pdf/1895.pdf
  3. https://www.microchip.com/en-us/about/media-center/blog/2020/what-is-jitter
  4. https://www.tek.com/en/documents/application-note/jitter-timing-fundamentals
  5. https://www.sitime.com/support/resource-library/application-notes/an10007-clock-jitter-definitions-and-measurement-methods
  6. https://www.nextiva.com/blog/network-jitter.html
  7. https://www.keysight.com/us/en/assets/7018-01139/brochures/5988-8427.pdf
  8. https://grouper.ieee.org/groups/802/3/av/public/2008_03/3av_0803_ben-amram_1.pdf
  9. https://www.signalintegrityjournal.com/blogs/8-for-good-measure/post/1817-evaluating-oscillator-power-supply-noise-rejection-its-the-total-jitter-that-matters
  10. https://www.analog.com/en/resources/technical-articles/a-proposed-framework-for-measuring-identifying-and-eliminating-clock-and-data-jitter.html
  11. https://www.analog.com/en/resources/technical-articles/three-key-physical-layer-phy-performance-metrics-for-a-jesd204b-transmitter.html
  12. https://www.edn.com/basic-jitter-measurements-using-an-oscilloscope/
  13. https://download.tek.com/document/55W_16146_5_MR_Letter.pdf
  14. https://www.ieee.li/pdf/viewgraphs/jitter_basics_advanced.pdf
  15. https://www.teledynelecroy.com/doc/understanding-dj-ddj-pj-jitter-calculations
  16. https://helpfiles.keysight.com/scopes/FlexDCA-UG/Content/Topics/Jitter-Mode/Meas-Toolbar/dj.htm
  17. https://www.renesas.com/en/document/apn/815-understanding-jitter-units
  18. https://www.highfrequencyelectronics.com/Apr04/HFE0404_Hancock.pdf
  19. https://www.eetimes.com/measuring-deterministic-jitter-with-a-scope/
  20. https://www.renesas.com/document/apn/838-peak-peak-jitter-calculations
  21. https://ewh.ieee.org/r6/san_diego/sscs/events/slides/2019_08_23_BasicsOfJitterInWirelineCommunications_AliSheikholeslami.pdf
  22. https://grouper.ieee.org/groups/802/3/bj/public/sep12/ran_3bj_01a_0912.pdf
  23. https://people.engr.tamu.edu/spalermo/ecen689/jitter_dual_dirac_agilent.pdf
  24. https://www.keysight.com/us/en/assets/7018-01309/white-papers/5989-3206.pdf
  25. https://ransomsnotes.com/index_htm_files/RansomStephensJitter360Pt2DualDirac.pdf
  26. https://escholarship.mcgill.ca/downloads/mp48sd21q.pdf
  27. https://grouper.ieee.org/groups/802/3/bm/public/cuadhoc/meetings/aug6_13/latchman_01_080613_CAUI.pdf
  28. https://ieeexplore.ieee.org/iel7/9364948/9364949/09364950.pdf
  29. https://www.analog.com/media/en/training-seminars/design-handbooks/data-conversion-handbook/chapter2.pdf
  30. https://www.analog.com/media/en/training-seminars/design-handbooks/Basic-Linear-Design/Chapter6.pdf
  31. https://www.ti.com/lit/pdf/snaa334
  32. https://pubs.aip.org/asa/jasa/article/154/1/443/2903757/Absolute-measurement-of-sampling-jitter-in-audio
  33. https://datatracker.ietf.org/doc/html/rfc3393
  34. https://www.comsoc.org/publications/ctn/quick-and-dead-rise-deterministic-networks
  35. https://datatracker.ietf.org/doc/html/rfc3550
  36. https://www.cisco.com/c/en/us/td/docs/ios/solutions_docs/qos_solutions/QoSVoIP/QoSVoIP.html
  37. https://www.cisco.com/c/en/us/support/docs/voice/voice-quality/18902-jitter-packet-voice.html
  38. https://www.analog.com/en/resources/technical-articles/analyzing-audio-dac-jitter-sensitivity.html
  39. https://www.ti.com/lit/pdf/snla178
  40. https://ww1.microchip.com/downloads/aemDocuments/documents/VOP/ApplicationNotes/ApplicationNotes/AN6172-Clock-Jitter-Basics-DS00006172.pdf
  41. https://www.tek.com/en/documents/application-note/characterizing-and-troubleshooting-jitter-your-oscilloscope
  42. https://www.analog.com/en/resources/app-notes/an-1067.html
  43. https://www.rohde-schwarz.com/us/applications/comparison-of-jitter-measurements-in-the-time-and-frequency-domain-application-card_56279-468544.html
  44. https://hpwiki.mcguirescientificservices.com/_media/application_notes:5989-2933en.pdf
  45. https://cdn.teledynelecroy.com/files/whitepapers/understanding_sdaiii_jitter_calculation_methods.pdf
  46. https://www.keysight.com/us/en/assets/7018-05976/application-notes/5992-2676.pdf
  47. https://www.keysight.com/us/en/product/86100C/infiniium-dcaj-wideband-oscilloscope-mainframe.html
  48. https://www.keysight.com/us/en/products/oscilloscopes/infiniium-dca-equivalent-time-sampling-oscilloscopes/dca-x-sampling-oscilloscopes.html
  49. https://www.tek.com/en/datasheet/dsa8200
  50. https://www.keysight.com/us/en/product/D9020JITA/jitter-vertical-phase-noise-analysis-software-90000-v-z-uxr.html
  51. https://www.tek.com/en/solutions/application/high-speed-serial-communication/jitter-measurement-and-timing-analysis
  52. https://www.oiforum.com/wp-content/uploads/00311c-OIF-112G-OFC-slides_ofc20_presentation.pdf
  53. https://www.oiforum.com/technical-work/implementation-agreements-ias/
  54. https://www.usb.org/sites/default/files/USB_3_0_e-Compliance_methodology_0p5_whitepaper.pdf
  55. https://download.tek.com/document/61W_18786_2.pdf
  56. https://www.nist.gov/document/haletraceable-waveformtimoct2009pdf
  57. https://ieeexplore.ieee.org/document/4450561/
  58. http://cva.stanford.edu/publications/2003/lee_dlltheory.pdf
  59. https://www.ti.com/lit/gpn/LMK00105
  60. https://www.ti.com/lit/an/scaa110a/scaa110a.pdf
  61. https://ieeexplore.ieee.org/document/5696211/
  62. https://hpwiki.mcguirescientificservices.com/_media/application_notes:5988-6254en.pdf
  63. https://ieeexplore.ieee.org/document/9363151
Add your contribution
Related Hubs
User Avatar
No comments yet.