Hubbry Logo
DuoprismDuoprismMain
Open search
Duoprism
Community hub
Duoprism
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Duoprism
Duoprism
Duoprism
View on Wikipedia
from Wikipedia
Set of uniform p-q duoprisms
Type Prismatic uniform 4-polytopes
Schläfli symbol {p}×{q}
Coxeter-Dynkin diagram
Cells p q-gonal prisms,
q p-gonal prisms
Faces pq squares,
p q-gons,
q p-gons
Edges 2pq
Vertices pq
Vertex figure
disphenoid
Symmetry [p,2,q], order 4pq
Dual p-q duopyramid
Properties convex, vertex-uniform
 
Set of uniform p-p duoprisms
Type Prismatic uniform 4-polytope
Schläfli symbol {p}×{p}
Coxeter-Dynkin diagram
Cells 2p p-gonal prisms
Faces p2 squares,
2p p-gons
Edges 2p2
Vertices p2
Symmetry [p,2,p] = [2p,2+,2p], order 8p2
Dual p-p duopyramid
Properties convex, vertex-uniform, Facet-transitive
A close up inside the 23-29 duoprism projected onto a 3-sphere, and perspective projected to 3-space. As m and n become large, a duoprism approaches the geometry of duocylinder just like a p-gonal prism approaches a cylinder.

In geometry of 4 dimensions or higher, a double prism[1] or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

The lowest-dimensional duoprisms exist in 4-dimensional space as 4-polytopes being the Cartesian product of two polygons in 2-dimensional Euclidean space. More precisely, it is the set of points:

where P1 and P2 are the sets of the points contained in the respective polygons. Such a duoprism is convex if both bases are convex, and is bounded by prismatic cells.

Nomenclature

[edit]

Four-dimensional duoprisms are considered to be prismatic 4-polytopes. A duoprism constructed from two regular polygons of the same edge length is a uniform duoprism.

A duoprism made of n-polygons and m-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a triangular-pentagonal duoprism is the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

  • q-gonal-p-gonal prism
  • q-gonal-p-gonal double prism
  • q-gonal-p-gonal hyperprism

The term duoprism is coined by George Olshevsky, shortened from double prism. John Horton Conway proposed a similar name proprism for product prism, a Cartesian product of two or more polytopes of dimension at least two. The duoprisms are proprisms formed from exactly two polytopes.

Example 16-16 duoprism

[edit]
Schlegel diagram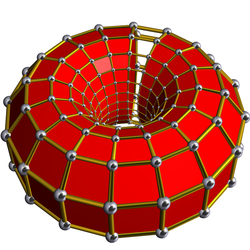

Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown. 		net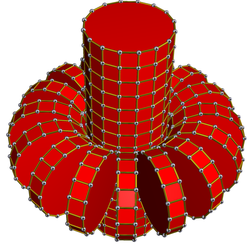

The two sets of 16-gonal prisms are shown. The top and bottom faces of the vertical cylinder are connected when folded together in 4D.

Geometry of 4-dimensional duoprisms

[edit]

A 4-dimensional uniform duoprism is created by the product of a regular n-sided polygon and a regular m-sided polygon with the same edge length. It is bounded by n m-gonal prisms and m n-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

  • When m and n are identical, the resulting duoprism is bounded by 2n identical n-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
  • When m and n are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to the tesseract.

The m-gonal prisms are attached to each other via their m-gonal faces, and form a closed loop. Similarly, the n-gonal prisms are attached to each other via their n-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

As m and n approach infinity, the corresponding duoprisms approach the duocylinder. As such, duoprisms are useful as non-quadric approximations of the duocylinder.

Nets

[edit]

3-3

3-4
4-4

3-5
4-5
5-5

3-6
4-6
5-6
6-6

3-7
4-7
5-7
6-7
7-7

3-8
4-8
5-8
6-8
7-8
8-8

3-9
4-9
5-9
6-9
7-9
8-9
9-9

3-10
4-10
5-10
6-10
7-10
8-10
9-10
10-10

Perspective projections

[edit]

A cell-centered perspective projection makes a duoprism look like a torus, with two sets of orthogonal cells, p-gonal and q-gonal prisms.

Schlegel diagrams
6-prism 6-6 duoprism
A hexagonal prism, projected into the plane by perspective, centered on a hexagonal face, looks like a double hexagon connected by (distorted) squares. Similarly a 6-6 duoprism projected into 3D approximates a torus, hexagonal both in plan and in section.

The p-q duoprisms are identical to the q-p duoprisms, but look different in these projections because they are projected in the center of different cells.

Schlegel diagrams

3-3
3-4
3-5
3-6
3-7
3-8

4-3
4-4
4-5
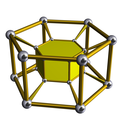4-6
4-7
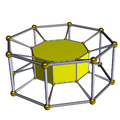4-8

5-3
5-4
5-5
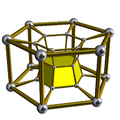5-6
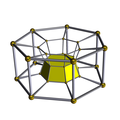5-7
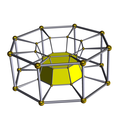5-8

6-3
6-4
6-5
6-6
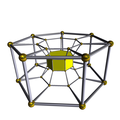6-7
6-8

7-3
7-4
7-5
7-6
7-7
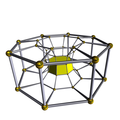7-8

8-3
8-4
8-5
8-6
8-7
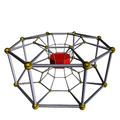8-8

Orthogonal projections

[edit]

Vertex-centered orthogonal projections of p-p duoprisms project into [2n] symmetry for odd degrees, and [n] for even degrees. There are n vertices projected into the center. For 4,4, it represents the A3 Coxeter plane of the tesseract. The 5,5 projection is identical to the 3D rhombic triacontahedron.

Orthogonal projection wireframes of p-p duoprisms
Odd
3-3 5-5 7-7 9-9
[3] [6] [5] [10] [7] [14] [9] [18]
Even
4-4 (tesseract) 6-6 8-8 10-10
[4] [8] [6] [12] [8] [16] [10] [20]
[edit]
A stereographic projection of a rotating duocylinder, divided into a checkerboard surface of squares from the {4,4|n} skew polyhedron

The regular skew polyhedron, {4,4|n}, exists in 4-space as the n2 square faces of a n-n duoprism, using all 2n2 edges and n2 vertices. The 2n n-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not regular.)

Duoantiprism

[edit]
p-q duoantiprism vertex figure, a gyrobifastigium
Great duoantiprism, stereographic projection, centred on one pentagrammic crossed-antiprism

Like the antiprisms as alternated prisms, there is a set of 4-dimensional duoantiprisms: 4-polytopes that can be created by an alternation operation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the 4-4 duoprism (tesseract) which creates the uniform (and regular) 16-cell. The 16-cell is the only convex uniform duoantiprism.

The duoprisms , t0,1,2,3{p,2,q}, can be alternated into , ht0,1,2,3{p,2,q}, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of the tesseract , t0,1,2,3{2,2,2}, with its alternation as the 16-cell, , s{2}s{2}.

The only nonconvex uniform solution is p=5, q=5/3, ht0,1,2,3{5,2,5/3}, , constructed from 10 pentagonal antiprisms, 10 pentagrammic crossed-antiprisms, and 50 tetrahedra, known as the great duoantiprism (gudap).[2][3]

Ditetragoltriates

[edit]

Also related are the ditetragoltriates or octagoltriates, formed by taking the octagon (considered to be a ditetragon or a truncated square) to a p-gon. The octagon of a p-gon can be clearly defined if one assumes that the octagon is the convex hull of two perpendicular rectangles; then the p-gonal ditetragoltriate is the convex hull of two p-p duoprisms (where the p-gons are similar but not congruent, having different sizes) in perpendicular orientations. The resulting polychoron is isogonal and has 2p p-gonal prisms and p2 rectangular trapezoprisms (a cube with D2d symmetry) but cannot be made uniform. The vertex figure is a triangular bipyramid.

Double antiprismoids

[edit]

Like the duoantiprisms as alternated duoprisms, there is a set of p-gonal double antiprismoids created by alternating the 2p-gonal ditetragoltriates, creating p-gonal antiprisms and tetrahedra while reinterpreting the non-corealmic triangular bipyramidal spaces as two tetrahedra. The resulting figure is generally not uniform except for two cases: the grand antiprism and its conjugate, the pentagrammic double antiprismoid (with p = 5 and 5/3 respectively), represented as the alternation of a decagonal or decagrammic ditetragoltriate. The vertex figure is a variant of the sphenocorona.

k22 polytopes

[edit]

The 3-3 duoprism, -122, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k22 series. The 3-3 duoprism is the vertex figure for the second, the birectified 5-simplex. The fourth figure is a Euclidean honeycomb, 222, and the final is a paracompact hyperbolic honeycomb, 322, with Coxeter group [32,2,3], . Each progressive uniform polytope is constructed from the previous as its vertex figure.

k22 figures in n dimensions
Space Finite Euclidean Hyperbolic
n 4 5 6 7 8
Coxeter
group 		A2A2 E6 =E6+ =E6++
Coxeter
diagram
Symmetry [[32,2,-1]] [[32,2,0]] [[32,2,1]] [[32,2,2]] [[32,2,3]]
Order 72 1440 103,680 ∞
Graph ∞ ∞
Name −122 022 122 222 322

See also

[edit]

Notes

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Duoprism

View on Grokipedia
from Grokipedia
A duoprism is a in four or more dimensions formed as the of two polytopes, each of dimension two or higher. In the specific case of two polygons with p and q sides, the result is a four-dimensional polychoron known as a p-q duoprism, with vertices corresponding to all pairwise combinations of the polygons' vertices. This construction yields a polytope when the input polygons are regular, exhibiting rotational symmetries derived from the dihedral groups of the polygons. The cellular structure of a p-q duoprism consists of p prisms with q-gonal bases and q prisms with p-gonal bases, totaling p + q three-dimensional cells. For instance, the 3-3 duoprism, the of two triangles, has 9 vertices, 18 edges, 15 faces (6 triangles and 9 squares), and 6 triangular prismatic cells, with a of order 72. Notable examples include the 4-4 duoprism, which is equivalent to the or {4,3,3}. Duoprisms generalize lower-dimensional prisms and serve as building blocks in higher-dimensional , appearing in studies of polytopal products and tessellations.

Definition and Construction

Cartesian Product Basis

A duoprism is a constructed as the of two polygons PmP_m and PnP_n embedded in 4-dimensional . This product combines every point of the first polygon with every point of the second, forming a higher-dimensional analogue of prismatic figures. The term "duoprism" was introduced by H.S.M. Coxeter to describe such products of polygonal bases. The explicit construction is given by the set Pm×Pn={(x,y,z,w)∣(x,y)∈Pm,(z,w)∈Pn},P_m \times P_n = \{ (x, y, z, w) \mid (x, y) \in P_m, (z, w) \in P_n \}, where PmP_m lies in the xyxy-plane and PnP_n in the orthogonal zwzw-plane. This ensures the resulting figure inherits the geometric structure from both components, with vertices corresponding to pairwise products of the polygons' vertices. The serves as a fundamental operation in geometry, extending lower-dimensional examples such as the product of a and a line interval, which yields a in 3-dimensional space. In general, the duoprism occupies 4 dimensions, though it degenerates to 3 dimensions if one is a (a degenerate 2-gon equivalent to a ). The resulting duoprism is convex if and only if both constituent polygons are convex, as the preserves convexity from its factors.

Elemental Composition

A duoprism, formed as the of an m-gon and an n-gon, consists of m n vertices, each corresponding to a unique pairing of a vertex from the m-gon with a vertex from the n-gon.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] The edges total 2 m n, comprising two sets: m n edges from the edges of the m-gon paired with vertices of the n-gon, and m n edges from the edges of the n-gon paired with vertices of the m-gon.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] The faces are of three types: n copies of the m-gon, arising from the full m-gon paired with each vertex of the n-gon; m copies of the n-gon, from the full n-gon paired with each vertex of the m-gon; and m n quadrilaterals, generated from each edge of the m-gon paired with each edge of the n-gon.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] Thus, the total number of faces is m + n + m n.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] The cells consist of n prisms with m-gonal bases, obtained by extruding the m-gon along each edge of the n-gon, and m prisms with n-gonal bases, from extruding the n-gon along each edge of the m-gon.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] The total number of cells is therefore m + n.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.] These counts satisfy the Euler characteristic for a convex 4-polytope, χ = V − E + F − C = 0. For instance, in the 3-3 duoprism, V = 9, E = 18, F = 15 (6 triangles and 9 quadrilaterals), and C = 6, yielding 9 − 18 + 15 − 6 = 0.[Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover Publications, p. 124.]

Convexity and Uniformity

A duoprism, formed as the of two s PmP_m and PnP_n in orthogonal planes, inherits convexity from its base polygons. Specifically, the duoprism is convex if and only if both PmP_m and PnP_n are convex polygons, as the of convex sets in preserves convexity. duoprisms arise when both base polygons are regular and share the same edge length, rendering the resulting vertex-transitive with prismatic cells. In this case, the cells consist of 3-dimensional prisms, where each cell is formed by extruding one base polygon along the edges of the other, ensuring all cells are polyhedra. If the base polygons are irregular, the duoprism remains well-defined and convex (provided the bases are convex) but loses ity, as the and transitivity properties degrade. The symmetry group of a uniform duoprism is the direct product of the dihedral groups Dm×DnD_m \times D_n of the base polygons, acting independently on each 2-dimensional plane, with order 4mn4mn. When m=nm = n, an additional symmetry arises from interchanging the identical factors, doubling the order to 8m28m^2. Uniform duoprisms are vertex-transitive by construction but are cell-transitive (facet-transitive) only when m=nm = n, as the two types of prismatic cells become indistinguishable; otherwise, the distinct cell types prevent full cell-transitivity. They are not face-transitive in general, as there are distinct types of faces: the polygonal faces from the bases and the quadrilateral faces from edge products. Only in the special case m = n = 4, where the duoprism is the tesseract with all square faces, is it face-transitive.

Nomenclature and History

Naming Conventions

The standard for duoprisms designates them as p-q duoprisms, where p and q (p ≤ q) denote the number of sides of the two regular polygons whose forms the . This convention ensures uniqueness by ordering the factors, avoiding redundancy in naming isomorphic structures. For instance, the 3-4 duoprism arises from the product of a regular triangle and . In symbolic notation, duoprisms employ the extended Schläfli symbol {p} × {q}, reflecting their construction as the product of two regular p-gons and q-gons; this differs from the standard Schläfli symbols for prisms ({p,3}) and antiprisms ({p,3/2}), which incorporate a triangular factor for extrusion along a line. The term "duoprism" itself, a contraction of "double prism," was coined by George Olshevsky in the 1990s during his compilation of a catalog of uniform polychora. An alternative designation, "proprism," was introduced by to describe the more general of two or more polytopes each of dimension at least two, encompassing duoprisms as a special case. Some notations occasionally conflate duoprisms with duopyramids, but the latter are the duals of duoprisms, formed instead by connecting corresponding vertices of the base polygons with edges.

Origins and Terminology Evolution

The roots of duoprism concepts trace back to 19th-century advancements in higher-dimensional geometry, particularly Ludwig Schläfli's work from 1850 to 1852, where he introduced the notion of polytopes (termed "polyschemes") as generalizations of polyhedra to n dimensions and developed for their classification. Although Schläfli's contributions laid foundational groundwork for multidimensional polytopes, including the identification of six regular 4-polytopes, he did not explicitly address Cartesian products in the context of duoprisms. In the 20th century, H. S. M. Coxeter's Regular Polytopes (first edition 1948, third edition 1973) explored prismatic constructions and Cartesian products of polytopes in higher dimensions, providing early theoretical support for such structures, though duoprisms as uniform 4-polytopes were not yet formalized. Related early enumeration efforts included Norman W. Johnson's 1966 Ph.D. dissertation, The Theory of Uniform Polytopes and Honeycombs, which classified 75 non-prismatic uniform 4-polytopes under advisor Coxeter, while duoprisms form part of the infinite prismatic families explored in the broader theory. The term "duoprism" was coined by George Olshevsky in the late 1990s, specifically during his 1997–2000 development of an online catalog of uniform polychora, where it denoted the of two polygons as a for "double prism." In 2008, John H. Conway, in The Symmetries of Things, proposed the alternative term "proprism" for general s of s, emphasizing their isogonal (vertex-transitive) properties and integrating them into broader discussions. Post-2000, duoprisms gained practical visibility through integration into visualization software such as Stella4D, which supports the generation and rendering of uniform duoprisms and antiduoprisms. Duoprisms continue to hold potential applications within abstract polytope theory, particularly in studies of products and symmetries.

Geometric Properties

Vertex, Edge, and Face Counts

In a uniform p-q duoprism, formed as the of regular p-gons and q-gons, the number of vertices is given by V=pqV = p q, as each vertex arises from pairing one vertex of the p-gon with one of the q-gon. The number of edges is E=2pqE = 2 p q, consisting of pqp q edges from the p-gon directions (each vertex of the q-gon connected along the p-gon's edges) and pqp q from the q-gon directions. The faces comprise three types: qq regular p-gonal faces (one for each vertex of the q-gon, spanning the full p-gon), pp regular q-gonal faces (one for each vertex of the p-gon, spanning the full q-gon), and pqp q square faces (arising from each edge of the p-gon paired with each edge of the q-gon, forming rectangular products that are squares in the uniform case). Thus, the total number of faces is F=p+q+pqF = p + q + p q. The cells number C=p+qC = p + q, with pp q-gonal prisms (each q-gonal face extruded along the p-gon's edges) and qq p-gonal prisms (each p-gonal face extruded along the q-gon's edges); each such cell is uniform with square lateral faces. These counts satisfy the Euler characteristic for 4-polytopes, V−E+F−C=0V - E + F - C = 0. For instance, in the 3-3 duoprism, V=9V = 9, E=18E = 18, F=15F = 15 (6 triangles and 9 squares), and C=6C = 6 triangular prisms, yielding 9−18+15−6=09 - 18 + 15 - 6 = 0. The 4-4 duoprism is the , with V=16V = 16, E=32E = 32, F=24F = 24 squares, and C=8C = 8 cubes. The following table summarizes the element counts for a uniform p-q duoprism:
ElementCountComponents/Details
Vertices (V)pqp qProduct of vertices from each polygon
Edges (E)2pq2 p qpqp q in p-direction + pqp q in q-direction
Faces (F)p+q+pqp + q + p qqq p-gons + pp q-gons + pqp q squares
Cells (C)p+qp + qpp q-gonal prisms + qq p-gonal prisms

Cell Structures and Symmetries

A duoprism, formed as the of a regular pp-gon and a regular qq-gon, possesses two distinct types of 3-dimensional cells: qq cells that are pp-gonal prisms and pp cells that are qq-gonal prisms. These prismatic cells are when p≥3p \geq 3 and q≥3q \geq 3, consisting of two parallel regular kk-gonal bases (where k=pk = p or qq) connected by rectangular lateral faces, which become squares under orthogonal with equal edge lengths in the product construction. The regularity of these cells derives from the regularity of the base polygons and the orthogonal nature of the , which preserves angles and edge lengths within each factor's plane while separating the dimensions. In the pp-gonal prism cells, the two pp-gonal bases lie in parallel hyperplanes, with lateral edges perpendicular to these bases spanning the qq-gon's edge direction. The generated by the construction is the of the s Dph×DqhD_{ph} \times D_{qh}, where DkhD_{kh} denotes the full of order $2k including reflections, of order $4pq (doubled to $8pqwhenwhenp=qduetotheabilitytoswapidenticalfactors).Thisgroupactsindependentlyonthedue to the ability to swap identical factors). This group acts independently on thep−gonand-gon and q−gonfactors,rotatingandreflectingthesetsofcellsseparately:actionsfrom-gon factors, rotating and reflecting the sets of cells separately: actions from D_{qh}cyclethecycle theq p−gonalprismcellsaroundthe-gonal prism cells around the q−gon′saxis,while-gon's axis, while D_{ph}cyclesthecycles thep q$-gonal prism cells; reflections in either factor map cells to themselves or adjacent ones within their orbit. However, in special cases such as the 4-4 duoprism, the admits a larger full . Uniform duoprisms are always vertex-transitive under this , as vertices correspond to products of vertices, which are transitively permuted in each factor. However, they are generally not cell-transitive, featuring two distinct orbits of cells—the pp-gonal prisms and qq-gonal prisms—unless p=qp = q, in which case the orbits coincide and the duoprism becomes cell-transitive. The at each vertex is a disphenoid , with three pairs of equal opposite edges corresponding to the directions in the product construction, though it projects as a p×qp \times q grid in orthogonal views.

Special Cases and Degeneracies

The {4,4} duoprism, formed by the of two squares, is identical to the or 4-cube, a with Schläfli symbol {4,3,3}. It consists of 8 cubic cells and 24 square faces, exhibiting the full symmetry of the hypercubic group. The {3,3} duoprism, the product of two equilateral triangles, is a comprising 6 triangular prismatic cells, with 9 square faces and 6 triangular faces. This structure arises directly from the of the triangular tiling with itself in orthogonal planes. Degeneracies occur when one of the base polygons reduces to a digon (p=2), in which case the duoprism collapses to a q-gonal embedded in 3D rather than a true 4D . Similarly, setting q=2 yields a p-gonal . These cases highlight the prism product's dimensional reduction when one factor is degenerate. The {5,5} duoprism, derived from two regular pentagons, features 10 pentagonal prismatic cells, including 10 pentagonal faces and 25 square faces. This polytope maintains convexity and prismatic uniformity in 4D. As an example of a larger duoprism, the {16,16} duoprism consists of 32 16-gonal prismatic cells. In its , it appears as two layers of orthogonal 16-gonal prisms, illustrating the layered structure inherent to the construction. In the limiting case where both p and q approach infinity, the duoprism approximates a , the 4D analogue of the product of two circles, transitioning from polygonal facets to curved surfaces.

Visualizations

Net Diagrams

A net of a duoprism is a three-dimensional unfolding of the 4-polytope's surface into Euclidean 3-space, analogous to the two-dimensional nets of three-dimensional polyhedra, allowing visualization of cell adjacencies without projection distortions. Such nets are obtained via unfoldings, where cuts are made along a of the of the two-dimensional ridges (square faces), enabling isometric development of the three-dimensional cells into 3-space. For a {p,q} duoprism, comprising q copies of p-gonal prisms and p copies of q-gonal prisms as cells, the net arranges unfolded prism cells—each a two-dimensional net of rectangular sides and polygonal bases—interconnected along matching square faces to reflect the 4D topology. This interlocked configuration ensures the boundary's connectivity is preserved, with p sets of q-prism unfoldings meshing with q sets of p-prism unfoldings. Computational generation is essential due to the complexity, as manual arrangement risks overlaps or distortions in 3D. Representative examples illustrate this structure. The 3-3 duoprism net unfolds its six cells into a 3D assembly where three prisms form a ring connected via squares to another set of three, creating a compact topological model that highlights the uniform adjacency of four cells per vertex when refolded. The 4-4 duoprism, or , features eight cubic cells and admits 261 distinct non-overlapping 3D nets, often visualized as arrangements such as a cross-shaped core of four cubes with four additional cubes attached orthogonally in 3D branches. Similarly, the 5-5 duoprism net deploys ten unfoldings in an interleaved radial pattern, with each pentagonal base net (five rectangles plus two pentagons) linked by squares to adjacent cells, forming a more elaborate 3D skeleton. Challenges in duoprism net construction include potential self-intersections when embedding nets in 3D, particularly for higher p and q where the dihedral angles of polygonal bases complicate planar-to-3D transitions; however, for symmetric cases like the , all unfoldings avoid overlaps. Software such as Stella4D facilitates generation by automating cuts and 3D layouts, producing exportable models that reveal the duoprism's (V - E + F - C = 0 for closed 4D surfaces) through direct cell counting. Interpreting these nets enhances topological insight: for instance, tracing square connections in a 3-3 duoprism net demonstrates the cyclic linking of s, mirroring the duoprism's [3,2,3] and aiding comprehension of how the surface closes in 4D without gaps or tears. In textual layout terms, a simplified 3-3 net might position one centrally, attach three others to its rectangular faces via intervening squares extruded in planes, and cap with the remaining two in offset layers to complete the sphere-like .

Perspective Projections

Perspective projections of duoprisms into three-dimensional space are achieved by selecting a viewpoint in four-dimensional space outside the polytope and projecting rays from that point onto a three-dimensional hyperplane, creating a realistic depth effect with receding cells. This method, known as central projection, utilizes homogeneous coordinates to compute the projected positions of vertices. For a four-dimensional point (x,y,z,w)(x, y, z, w) relative to a viewpoint aligned along the ww-axis at (0,0,0,d)(0, 0, 0, d) where d>max⁡wd > \max w, the projected three-dimensional coordinates are given by (xd−w,yd−w,zd−w),\left( \frac{x}{d - w}, \frac{y}{d - w}, \frac{z}{d - w} \right), assuming the projection hyperplane is at w=dw = d; this formula scales the coordinates to simulate convergence at a vanishing point. The vertices of an mm- nn duoprism are first generated as the Cartesian product of two regular polygons: one in the xyxy-plane with vertices (cos⁡(2πi/m),sin⁡(2πi/m),0,0)(\cos(2\pi i/m), \sin(2\pi i/m), 0, 0) for i=0,…,m−1i = 0, \dots, m-1, and the other in the zwzw-plane with vertices (0,0,cos⁡(2πj/n),sin⁡(2πj/n))(0, 0, \cos(2\pi j/n), \sin(2\pi j/n)) for j=0,…,n−1j = 0, \dots, n-1, scaled appropriately for unit size. In these projections, duoprisms typically appear as ring-like or toroidal structures in three dimensions, where the two sets of polygonal prism cells interlock like chain links, with one set forming a cycle around the other due to the cyclic symmetries of the base polygons. The viewpoint distance dd influences the degree of : a larger dd yields less foreshortening and more parallelism among distant edges, while a smaller dd (but still outside the ) enhances the perspective effect, making outer cells appear larger and inner ones compressed toward the center. It is common to align one of the base planes (e.g., the xyxy-plane) parallel to the projection hyperplane to minimize initial and highlight the interlocking . For example, the projection of a 3-4 duoprism, centered on a , reveals four triangular prisms forming a ring interlocked with three cubes, appearing as deformed frustums and extruded shapes that spiral under , emphasizing the chain-like arrangement. Similarly, a 6-6 duoprism projects as a torus-like form with cells arranged in two concentric cycles, where the uniform hexagonal bases create a symmetric, doughnut-shaped envelope with visible interlocking seams. In the 3-5 duoprism, the projection shows a pentagonal ring of five triangular prisms encircling three pentagonal prisms, resulting in an asymmetric toroidal appearance with the triangular cells appearing to weave through the larger pentagonal . These visualizations underscore the duoprism's as a product of cycles, often requiring software like for rendering to handle the coordinate transformations accurately.

Orthogonal Projections

Orthogonal projections provide a means to visualize duoprisms in three dimensions by employing parallel rays perpendicular to a chosen projection hyperplane, preserving angles and lengths within the projected subspace without the convergence of perspective views. These projections are typically aligned with the duoprism's symmetry axes to highlight structural features, such as vertex arrangements or cell configurations. The method involves selecting a direction vector orthogonal to the 3D subspace, often corresponding to a vertex, edge, or cell center, and computing the projection of 4D coordinates onto that subspace using the formula for orthogonal projection: for a point v\mathbf{v} and direction d\mathbf{d}, the projected point is v−v⋅d∥d∥2d\mathbf{v} - \frac{\mathbf{v} \cdot \mathbf{d}}{\|\mathbf{d}\|^2} \mathbf{d}, yielding 3D coordinates for rendering. A simple case is coordinate-aligned projection, such as ignoring the ww-coordinate of vertices embedded with the pp-gon in the xyxy-plane and the qq-gon in the zwzw-plane, resulting in a 3D extrusion of the pp-gon along the projected qq-gon interval in zz. In vertex-centered orthogonal projections, the direction vector points toward a vertex from the center, centering that vertex in the 3D view and producing a whose vertices correspond directly to the duoprism's pqpq vertices. For instance, the 4-4 duoprism () projects to a when aligned along a coordinate axis. The 8-8 duoprism's vertex-centered projection is shown in figures of views. These views are computed by normalizing the direction vector to the target vertex, such as d=(1,1,1,1)\mathbf{d} = (1,1,1,1) for a corner vertex in the , ensuring rotational around the projection axis. Cell-centered orthogonal projections focus on a specific cell at the center, with surrounding cells arranged symmetrically around it, revealing the duoprism's product structure. For the 3-4 duoprism, comprising 3 square and 4 triangular , a cell-centered view positions one square centrally, encircled by the 4 triangular along its equatorial belt, while the remaining square appear as orthogonal layers. The projection direction aligns with the cell's symmetry axis, such as perpendicular to the bases of the central , to maintain uniformity. This approach highlights how the pp of one type interlock with the qq of the other, forming a toroidal-like arrangement in projection without actual . Further orthogonal projection of these 3D images into 2D, often along a principal axis of the 3D view, produces wireframe diagrams or filled polygonal representations suitable for print or analysis. These 2D views prioritize edge connectivity over depth, using shading or color to distinguish overlapping elements from distinct 4D features.

Duoantiprisms

Duoantiprisms are isogonal 4-polytopes constructed by alternating the vertices of a duoprism, which staggers the positions of one or both base polygons to produce antiprismatic cells rather than prismatic ones. This process involves selecting every other vertex in the duoprism's vertex set, effectively twisting the arrangement and connecting the resulting structure with disphenoidal cells. When the base polygons have an even number of sides, the alternation halves the vertex count of the original duoprism; for odd-sided polygons, the construction alternates a duoprism with doubled side counts, such as the hexagonal duoprism for the 3-3 case. The cells of a duoantiprism typically consist of two orthogonal rings of antiprisms from the alternated bases, interconnected by digonal disphenoids; if the bases are identical, these become tetragonal disphenoids. The faces are primarily triangles from the antiprisms and disphenoids, with the original polygonal faces transformed into twisted or gyroprismatic equivalents. Element counts follow adjusted formulas from the parent duoprism: for an {p,q} duoantiprism, vertices number (p q)/2 for even cases, edges are roughly twice the vertices due to the dual sets of connecting and base edges, and cells include p q-gonal antiprisms, q p-gonal antiprisms, and p q digonal disphenoids. For instance, the 3-3 duoantiprism has 18 vertices, 72 edges (36 short and 36 long), 84 triangular faces, and 30 cells (12 triangular antiprisms and 18 tetragonal disphenoids). Uniform duoantiprisms occur in specific cases where edge lengths match, yielding high symmetry. The convex example is the (hexadecachoron, {3,3,4}), obtained by fully alternating the 4-4 duoprism (), resulting in 16 regular tetrahedral cells, 32 triangular faces, 24 edges, and 8 vertices with . A nonconvex case is the great duoantiprism (5-5/2 or 5-5/3 in crossed notation), featuring 50 tetrahedral cells, 20 antiprismatic/retroprismatic cells (10 pentagonal antiprisms and 10 pentagrammic retroprisms), 200 edges, 220 faces (200 triangles, 10 pentagons, and 10 pentagrams), and 50 vertices, with icosahedral symmetry of order 200 and central density 3. These exhibit enhanced rotational symmetries compared to their duoprism parents, particularly when both bases are alternated, leading to isogonal vertex figures like the (a twisted ). The alternation process can be derived by rectifying the graph of the two polygons—removing mid-edges to stagger vertices—or by applying independent rotary symmetries to each base polygon, ensuring uniform vertex connectivity without self-intersections in convex cases. Duoantiprisms are distinct from snub duoprisms, which involve denser chiral operations, though both leverage rotational elements for their twisted geometries.

Ditetragoltriates and Variants

Ditetragoltriates represent a family of isogonal 4-polytopes derived as variants of duoprisms through a involving scaled bases. Specifically, an n-gonal ditetragoltriate is formed as the convex hull of two similarly oriented semi-uniform {n,n} duoprisms, one with an enlarged base in the xy-plane and the other with an enlarged base in the zw-plane, ensuring all edges in the hull are of equal length. This results in a convex, vertex-transitive polychoron with cells comprising 2n n-gonal prisms and n² rectangular trapezoprisms. The emphasizes conceptual uniformity at vertices while allowing cell diversity, distinguishing it from standard uniform duoprisms. The term "ditetragoltriate" stems from John Conway's polyhedral notation extended to higher dimensions, where it denotes a power operation applying the ditetragon—an isogonal variant of the , also called a truncated square—to a p-gonal base, effectively linking to octagon-p-gon duoprism products like {8,p}. For instance, the {8,3} duoprism serves as a foundational example, possessing 24 vertices, 48 edges, and cells consisting of 8 triangular prisms and 3 prisms, with symmetries from the of dihedral groups D_{8h} × D_{3h} of order 96. The ditetragoltriate variant generalizes this by the hull method, yielding 2p p-gonal prisms (e.g., 6 triangular prisms for p=3) and incorporating trapezoprismatic cells, while inheriting enhanced isogonal properties and components in select realizations. Key variants arise from alternating the ditetragoltriate, producing double antiprismoids—nonconvex polychora with cells of p-gonal s and regular tetrahedra. These alternations remove every other vertex, transforming the structure into a star polytope uniform only for specific p, such as p=5, where the resulting grand antiprism is a polychoron bounded by 20 pentagonal antiprisms and 300 tetrahedra. Discovered by John Conway and Michael Guy in 1965, this uniform case highlights the variants' role in bridging convex and nonconvex 4-polytopes. Ditetragoltriates are invariably convex and isogonal, with vertex figures as notches or triangular bipyramids, but non-uniform due to varying cell types; uniformity emerges only in alternated forms for p=3 and p=5. They maintain prismatic symmetries scaled by n, such as order 72 for the triangular case (A_2 ≀ S_2). Geometrically, they fill gaps in isogonal series related to abstract polytopes, prioritizing vertex equivalence over cell regularity in duoprism extensions. A representative example, the triangular ditetragoltriate, features 18 vertices, 45 edges, 42 faces (6 triangles + 18 rectangles + 18 isosceles trapezoids), and 15 cells, underscoring the construction's efficiency in generating diverse yet symmetric structures.

Connections to Uniform 4-Polytopes

Duoprisms form an infinite family within the 4-polytopes, as they are vertex-transitive polychora with regular polygonal faces and polyhedral cells constructed via the of two regular polygons. While the 75 4-polytopes typically refer to those generated by irreducible reflection groups with connected Coxeter-Dynkin diagrams, duoprisms belong to the prismatic with reducible (product) groups; specific convex examples, such as the triangular-square and square-pentagonal duoprisms, are enumerated in classifications of 4-polytopes. The triangular duoprism (3-3 duoprism) serves as the base for the k22 family of uniform polytopes, a dimensional series denoted by Coxeter that extends from 4D to higher dimensions, including rectified forms, runcinated variants like the runcicapped triangular duopyramid, sphenocorona compounds, and ultimately paracompact honeycombs in Euclidean 4D space. This series highlights how the 3-3 duoprism's , a product of two triangular groups, generates further uniforms through Wythoff constructions involving alternations and truncations on the disconnected Coxeter-Dynkin diagram. As a subset of prismatic uniform 4-polytopes, duoprisms correspond to those with effectively equivalent to Schläfli symbols {p,q,4} in a product sense, where the fourth node represents the prismatic direction, distinguishing them from non-prismatic uniforms derived from irreducible groups like A4 or F4. Their duals, known as duopyramids, are also uniform 4-polytopes, formed as the convex hulls of two orthogonal regular polygons and exhibiting reciprocal cell structures, such as disphenoidal cells in p,p cases. In higher dimensions, duoprisms generalize to duotriprisms and beyond, such as 5D products of three polygons, maintaining uniformity through product symmetries and fitting into extended Wythoffian constructions for prismatic families. Duoprisms integrate into the overall uniform framework via their disconnected Coxeter-Dynkin diagrams (e.g., two separate branches for the polygonal factors), which allow generation from base prisms via operations like rectification, filling gaps in the enumeration of reducible-group uniforms beyond the 75 irreducible cases.

References

  1. https://www.qfbox.info/4d/duoprism
  2. https://polytope.miraheze.org/wiki/Duoprism
  3. https://graphsearch.epfl.ch/en/concept/41745711
  4. https://arxiv.org/abs/2205.02720
  5. https://books.google.com/books/about/Regular_Polytopes.html?id=iWvXsVInpgMC
  6. https://ejmt.mathandtech.org/Contents/eJMT_v18n1p5.pdf
  7. https://arxiv.org/pdf/2210.16722
  8. https://www.cs.cmu.edu/~suvrit/teach/l1_cvxsets.pdf
  9. https://repository.library.northeastern.edu/files/neu:rx915b81t/fulltext.pdf
  10. http://www.polytope.net/hedrondude/duoprisms.htm
  11. https://www.math.harvard.edu/media/AllenLiuTheStarsAboveUsThesis.pdf
  12. https://mathshistory.st-andrews.ac.uk/Biographies/Schlafli/
  13. https://bendwavy.org/polytile/NWJ/tup.html
  14. http://www.polytope.net/hedrondude/polychora.htm
  15. https://graphsearch.epfl.ch/en/concept/2114155
  16. http://www.software3d.com/Stella.php
  17. https://bendwavy.org/klitzing/explain/product.htm
  18. https://bendwavy.org/klitzing/explain/round.htm
  19. https://drops.dagstuhl.de/storage/00lipics/lipics-vol224-socg2022/LIPIcs.SoCG.2022.67/LIPIcs.SoCG.2022.67.pdf
  20. https://unfolding.apperceptual.com/
  21. https://www.heldermann-verlag.de/jgg/jgg01_05/jgg0404.pdf
  22. https://laustep.github.io/stlahblog/posts/Duoprism.html
  23. https://aaltodoc.aalto.fi/server/api/core/bitstreams/0656fafe-a009-4107-98a0-2bfb26f36b52/content
  24. https://www.qfbox.info/4d/3%2C4-duoprism
  25. https://polytope.miraheze.org/wiki/Duoantiprism
  26. https://polytope.miraheze.org/wiki/Triangular_duoantiprism
  27. https://polytope.miraheze.org/wiki/Hexadecachoron
  28. https://polytope.miraheze.org/wiki/Great_duoantiprism
  29. https://polytope.miraheze.org/wiki/Ditetragoltriate
  30. https://cavac.at/cavacopedia/duoprism
  31. https://polytope.miraheze.org/wiki/Triangular-octagonal_duoprism
  32. https://polytope.miraheze.org/wiki/Triangular_ditetragoltriate
  33. http://t.archive.bridgesmathart.org/2000/bridges2000-239.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.