Recent from talks
Nothing was collected or created yet.
Allometry
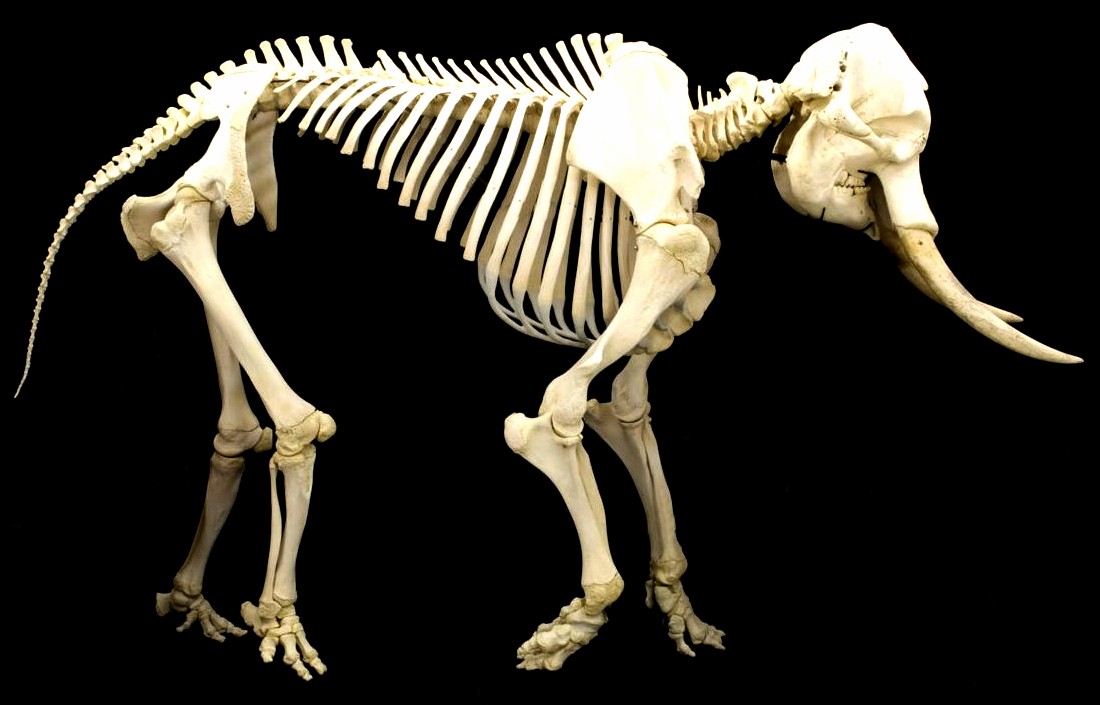
View on WikipediaThe proportionately thicker bones in the elephant are an example of allometric scaling
Allometry (Ancient Greek ἄλλος állos "other", μέτρον métron "measurement") is the study of the relationship of body size to shape,[1] anatomy, physiology and behaviour,[2] first outlined by Otto Snell in 1892,[3] by D'Arcy Thompson in 1917 in On Growth and Form[4] and by Julian Huxley in 1932.[5]
Overview
[edit]Allometry is a well-known study, particularly in statistical shape analysis for its theoretical developments, as well as in biology for practical applications to the differential growth rates of the parts of a living organism's body. One application is in the study of various insect species (e.g., Hercules beetles), where a small change in overall body size can lead to an enormous and disproportionate increase in the dimensions of appendages such as legs, antennae, or horns.[6] The relationship between the two measured quantities is often expressed as a power law equation (allometric equation) which expresses a remarkable scale symmetry:[7]

or in a logarithmic form,
or similarly,
where is the scaling exponent of the law. Methods for estimating this exponent from data can use type-2 regressions, such as major axis regression or reduced major axis regression, as these account for the variation in both variables, contrary to least-squares regression, which does not account for error variance in the independent variable (e.g., log body mass). Other methods include measurement-error models and a particular kind of principal component analysis.
The allometric equation can also be acquired as a solution of the differential equation
Allometry often studies shape differences in terms of ratios of the objects' dimensions. Two objects of different size, but common shape, have their dimensions in the same ratio. Take, for example, a biological object that grows as it matures. Its size changes with age, but the shapes are similar. Studies of ontogenetic allometry often use lizards or snakes as model organisms both because they lack parental care after birth or hatching and because they exhibit a large range of body sizes between the juvenile and adult stage. Lizards often exhibit allometric changes during their ontogeny.[9]
In addition to studies that focus on growth, allometry also examines shape variation among individuals of a given age (and sex), which is referred to as static allometry.[10] Comparisons of species are used to examine interspecific or evolutionary allometry (see also Phylogenetic comparative methods).
Isometric scaling and geometric similarity
[edit]| Group | Factor | Length range |
|---|---|---|
| Insects | 1000 | 10−4 to 10−1 m |
| Fish | 1000 | 10−2 to 10+1 m |
| Mammals | 1000 | 10−1 to 10+2 m |
| Vascular plants | 10,000 | 10−2 to 10+2 m |
| Algae | 100,000 | 10−5 to 100 m |
Isometric scaling happens when proportional relationships are preserved as size changes during growth or over evolutionary time. An example is found in frogs—aside from a brief period during the few weeks after metamorphosis, frogs grow isometrically.[12] Therefore, a frog whose legs are as long as its body will retain that relationship throughout its life, even if the frog itself increases in size tremendously.
Isometric scaling is governed by the square–cube law. An organism which doubles in length isometrically will find that the surface area available to it will increase fourfold, while its volume and mass will increase by a factor of eight. This can present problems for organisms. In the case of above, the animal now has eight times the biologically active tissue to support, but the surface area of its respiratory organs has only increased fourfold, creating a mismatch between scaling and physical demands. Similarly, the organism in the above example now has eight times the mass to support on its legs, but the strength of its bones and muscles is dependent upon their cross-sectional area, which has only increased fourfold. Therefore, this hypothetical organism would experience twice the bone and muscle loads of its smaller version. This mismatch can be avoided either by being "overbuilt" when small or by changing proportions during growth, called allometry.
Isometric scaling is often used as a null hypothesis in scaling studies, with 'deviations from isometry' considered evidence of physiological factors forcing allometric growth.
Allometric scaling
[edit]Allometric scaling is any change that deviates from isometry. A classic example discussed by Galileo in his Dialogues Concerning Two New Sciences is the skeleton of mammals. The skeletal structure becomes much stronger and more robust relative to the size of the body as the body size increases.[13] Allometry is often expressed in terms of a scaling exponent based on body mass, or body length (snout–vent length, total length, etc.). A perfectly allometrically scaling organism would see all volume-based properties change proportionally to the body mass, all surface area-based properties change with mass to the power of 2/3, and all length-based properties change with mass to the power of 1/3. If, after statistical analyses, for example, a volume-based property was found to scale to mass to the 0.9th power, then this would be called "negative allometry", as the values are smaller than predicted by isometry. Conversely, if a surface area-based property scales to mass to the 0.8th power, the values are higher than predicted by isometry and the organism is said to show "positive allometry". One example of positive allometry occurs among species of monitor lizards (family Varanidae), in which the limbs are relatively longer in larger-bodied species.[14] The same is true for some fish, e.g. the muskellunge, the weight of which grows with about the power of 3.325 of its length.[15] A 30-inch (76 cm) muskellunge will weigh about 8 pounds (3.6 kg), while a 40-inch (100 cm) muskellunge will weigh about 18 pounds (8.2 kg), so 33% longer length will more than double the weight.
Determining if a system is scaling with allometry
[edit]To determine whether isometry or allometry is present, an expected relationship between variables needs to be determined to compare data to. This is important in determining if the scaling relationship in a dataset deviates from an expected relationship (such as those that follow isometry). Using tools such as dimensional analysis is very helpful in determining expected slope.[16][17][18] This 'expected' slope, as it is known, is essential for detecting allometry because scaling variables are comparisons to other things. Saying that mass scales with a slope of 5 in relation to length doesn't have much meaning unless knowing the isometric slope is 3, meaning in this case, the mass is increasing extremely fast. For example, different sized frogs should be able to jump the same distance according to the geometric similarity model proposed by Hill 1950[19] and interpreted by Wilson 2000,[20] but in actuality larger frogs do jump longer distances.
Data gathered in science do not fall neatly in a straight line, so data transformations are useful. It is also important to remember what is being compared in the data. Comparing a characteristic such as head length to head width might yield different results from comparing head length to body length. That is, different characteristics may scale differently.[21] A common way to analyze data such as those collected in scaling is to use log-transformation.
There are two reasons why logarithmic transformation should be used to study allometry —a biological reason and a statistical reason. Log-log transformation places numbers into a geometric domain so that proportional deviations are represented consistently, independent of the scale and units of measurement. In biology, this is appropriate because many biological phenomena (e.g., growth, reproduction, metabolism, sensation) are fundamentally multiplicative.[22] Statistically, it is beneficial to transform both axes using logarithms and then perform a linear regression. This will normalize the data set and make it easier to analyze trends using the slope of the line.[23] Before analyzing data, it is important to have a predicted slope of the line to compare the analysis to.
After data are log-transformed and linearly regressed, comparisons can then use least squares regression with 95% confidence intervals or reduced major axis analysis. Sometimes, the two analyses can yield different results, but often they do not. If the expected slope is outside the confidence intervals, allometry is present. If the mass in this imaginary animal scaled with a slope of 5, which was a statistically significant value, then mass would scale very fast in this animal versus the expected value. It would scale with positive allometry. If the expected slope were 3 and in reality, in a certain organism mass scaled with 1 (assuming this slope is statistically significant), it would be negatively allometric.
Examples
[edit]
To find the expected slope for the relationship between mass and the characteristic length of an animal (see figure), the units of mass (M) from the y-axis are divided by the units of the x-axis, Length (L). The expected slope on a double-logarithmic plot of L3 / L is 3 (). This is the slope of a straight line.
Another example: Force is dependent on the cross-sectional area of muscle (CSA), which is L2. If comparing force to a length, then the expected slope is 2. Alternatively, this analysis may be accomplished with a power regression. Plot the relationship between the data onto a graph. Fit this to a power curve (depending on the stats program, this can be done multiple ways), and it will give an equation with the form: y=Zxn, where n is the number. That "number" is the relationship between the data points. The downside, to this form of analysis, is that it makes it a little more difficult to do statistical analyses.
Physiological scaling
[edit]Many physiological and biochemical processes (such as heart rate, respiration rate or the maximum reproduction rate) show scaling, mostly associated with the ratio between surface area and mass (or volume) of the animal.[7] The metabolic rate of an individual animal is also subject to scaling.
Metabolic rate and body mass
[edit]In plotting an animal's basal metabolic rate (BMR) against the animal's own body mass, a logarithmic straight line is obtained, indicating a power-law dependence. Overall metabolic rate in animals is generally accepted to show negative allometry, scaling to mass to a power of ≈ 0.75, known as Kleiber's law, 1932. This means that larger-bodied species (e.g., elephants) have lower mass-specific metabolic rates and lower heart rates, as compared with smaller-bodied species (e.g., mice). The straight line generated from a double logarithmic scale of metabolic rate in relation to body mass is known as the "mouse-to-elephant curve".[24] These relationships of metabolic rates, times, and internal structure have been explained as, "an elephant is approximately a blown-up gorilla, which is itself a blown-up mouse."[25]
Max Kleiber contributed the following allometric equation for relating the BMR to the body mass of an animal.[24] Statistical analysis of the intercept did not vary from 70 and the slope was not varied from 0.75, thus:
- (although the universality of this relation has been disputed both empirically and theoretically[26][27])
where is body mass, and metabolic rate is measured in kcal per day.
Consequently, the body mass itself can explain the majority of the variation in the BMR. After the body mass effect, the taxonomy of the animal plays the next most significant role in the scaling of the BMR. The further speculation that environmental conditions play a role in BMR can only be properly investigated once the role of taxonomy is established. The challenge with this lies in the fact that a shared environment also indicates a common evolutionary history and thus a close taxonomic relationship. There are strides currently in research to overcome these hurdles; for example, an analysis in muroid rodents,[24] the mouse, hamster, and vole type, took into account taxonomy. Results revealed the hamster (warm dry habitat) had lowest BMR and the mouse (warm wet dense habitat) had the highest BMR. Larger organs could explain the high BMR groups, along with their higher daily energy needs. Analyses such as these demonstrate the physiological adaptations to environmental changes that animals undergo.
Energy metabolism is subjected to the scaling of an animal and can be overcome by an individual's body design. The metabolic scope for an animal is the ratio of resting and maximum rate of metabolism for that particular species as determined by oxygen consumption. Oxygen consumption VO2 and maximum oxygen consumption VO2 max. Oxygen consumption in species that differ in body size and organ system dimensions show a similarity in their charted VO2 distributions indicating that, despite the complexity of their systems, there is a power law dependence of similarity; therefore, universal patterns are observed in diverse animal taxonomy.[28]
Across a broad range of species, allometric relations are not necessarily linear on a log-log scale. For example, the maximal running speeds of mammals show a complicated relationship with body mass, and the fastest sprinters are of intermediate body size.[29][30]
Allometric muscle characteristics
[edit]The muscle characteristics of animals are similar in a wide range of animal sizes, though muscle sizes and shapes can and often do vary depending on environmental constraints placed on them. The muscle tissue itself maintains its contractile characteristics and does not vary depending on the size of the animal. Physiological scaling in muscles affects the number of muscle fibers and their intrinsic speed to determine the maximum power and efficiency of movement in a given animal. The speed of muscle recruitment varies roughly in inverse proportion to the cube root of the animal's weight (compare the intrinsic frequency of the sparrow's flight muscle to that of a stork).
For inter-species allometric relations related to such ecological variables as maximal reproduction rate, attempts have been made to explain scaling within the context of dynamic energy budget theory and the metabolic theory of ecology. However, such ideas have been less successful.
Allometry of legged locomotion
[edit]Methods of study
[edit]Allometry has been used to study patterns in locomotive principles across a broad range of species.[31][32][33][34] Such research has been done in pursuit of a better understanding of animal locomotion, including the factors that different gaits seek to optimize.[34] Allometric trends observed in extant animals have even been combined with evolutionary algorithms to form realistic hypotheses concerning the locomotive patterns of extinct species.[33] These studies have been made possible by the remarkable similarities among disparate species' locomotive kinematics and dynamics, "despite differences in morphology and size".[31]
Allometric study of locomotion involves the analysis of the relative sizes, masses, and limb structures of similarly shaped animals and how these features affect their movements at different speeds.[34] Patterns are identified based on dimensionless Froude numbers, which incorporate measures of animals' leg lengths, speed or stride frequency, and weight.[33][34]
Alexander incorporates Froude-number analysis into his "dynamic similarity hypothesis" of gait patterns. Dynamically similar gaits are those between which there are constant coefficients that can relate linear dimensions, time intervals, and forces. In other words, given a mathematical description of gait A and these three coefficients, one could produce gait B, and vice versa. The hypothesis itself is as follows: "animals of different sizes tend to move in dynamically similar fashion whenever the ratio of their speed allows it." While the dynamic similarity hypothesis may not be a truly unifying principle of animal gait patterns, it is a remarkably accurate heuristic.[34]
It has also been shown that living organisms of all shapes and sizes utilize spring mechanisms in their locomotive systems, probably in order to minimize the energy cost of locomotion.[35] The allometric study of these systems has fostered a better understanding of why spring mechanisms are so common,[35] how limb compliance varies with body size and speed,[31] and how these mechanisms affect general limb kinematics and dynamics.[32]
Principles of legged locomotion identified through allometry
[edit]- Alexander found that animals of different sizes and masses traveling with the same Froude number consistently exhibit similar gait patterns.[34]
- Duty factors—percentages of a stride during which a foot maintains contact with the ground—remain relatively constant for different animals moving with the same Froude number.[34]
- The dynamic similarity hypothesis states that "animals of different sizes tend to move in dynamically similar fashion whenever the ratio of their speed allows it".[34]
- Body mass has even more of an effect than speed on limb dynamics.[32]
- Leg stiffness, , is proportional to , where is body mass.[32]
- Peak force experienced throughout a stride is proportional to .[32]
- The amount by which a leg shortens during a stride (i.e. its peak displacement) is proportional to .[32]
- The angle swept by a leg during a stride is proportional to .[32]
- The mass-specific work rate of a limb is proportional to .[32]
Drug dose scaling
[edit]The physiological effect of drugs and other substances in many cases scales allometrically. For example, plasma concentration of carotenoids scales to the three-quarter power of mass in nine predatory and scavenger raptor species.[36]
West, Brown, and Enquist in 1997 derived a hydrodynamic theory to explain the universal fact that metabolic rate scales as the 3⁄4 power with body weight. They also showed why lifespan scales as the +1⁄4 power and heart rate as the -1⁄4 power. Blood flow (+3⁄4) and resistance (-3⁄4) scale in the same way, leading to blood pressure being constant across species.[37]
Hu and Hayton in 2001 discussed whether the basal metabolic rate scale is a 2⁄3 or 3⁄4 power of body mass. The exponent of 3⁄4 might be used for substances that are eliminated mainly by metabolism, or by metabolism and excretion combined, while 2⁄3 might apply for drugs that are eliminated mainly by renal excretion.[38]
An online allometric scaler of drug doses based on the above work is available.[39]
The US Food and Drug Administration (FDA) published guidance in 2005 giving a flow chart that presents the decisions and calculations used to generate the maximum recommended starting dose in drug clinical trials from animal data.[40]
Allometric scaling in fluid locomotion
[edit]This article may need to be rewritten to comply with Wikipedia's quality standards. (August 2022) |
The mass and density of an organism have a large effect on the organism's locomotion through a fluid. For example, a tiny organism uses flagella and can effectively move through a fluid it is suspended in, while on the other end of the scale, a blue whale is much more massive and dense relative to the viscosity of the fluid compared to a bacterium in the same medium. The way in which the fluid interacts with the external boundaries of the organism is important with locomotion through the fluid. For streamlined swimmers, the resistance or drag determines the performance of the organism. This drag or resistance can be seen in two distinct flow patterns: laminar flow, where the fluid is relatively uninterrupted after the organism moves through it, and turbulent flow, where the fluid moves roughly around an organism, creating vortices that absorb energy from the propulsion or momentum of the organism. Scaling also affects locomotion through a fluid because of the energy needed to propel an organism and keep up velocity through momentum. The rate of oxygen consumption per gram body size decreases consistently with increasing body size.[41]
In general, smaller, more streamlined organisms create laminar flow (R < 0.5x106), whereas larger, less streamlined organisms produce turbulent flow (R > 2.0×106).[19] Also, increase in velocity (V) increases turbulence, which can be proved using the Reynolds equation. In nature however, organisms such as a 6-foot-6-inch (1.98 m) dolphin moving at 15 knots does not have the appropriate Reynolds numbers for laminar flow (R = 107), but exhibit it in nature. G. A. Steven observed and documented dolphins moving at 15 knots alongside his ship leaving a single trail of light when phosphorescent activity in the sea was high. The factors that contribute are:
- the surface area of the organism and its effect on the fluid in which the organism lives.
- the velocity of an organism through fluid, which changes the dynamic of the flow around that organism – the shape of the organism becomes more important for laminar flow as velocity increases.
- the density and viscosity of the fluid.
- the length of the organism, as the surface area of just the front 2/3 of the organism has an effect on the drag.
The resistance to the motion of an approximately stream-lined solid through a fluid can be expressed by the formula: Cfρ(total surface)V2/2,[19] where:
- V = velocity
- ρ = density of fluid
- Cf = 1.33R − 1 (laminar flow)
- R = Reynolds number
The Reynolds number R is given by R = VL/ν, where:
- V = velocity
- L = axial length of organism
- ν = kinematic viscosity (viscosity/density)
Notable Reynolds numbers:
- R < 0.5 million = laminar flow threshold
- R > 2.0 million = turbulent flow threshold
Scaling also has an effect on the performance of organisms in fluid. This is extremely important for marine mammals and other marine organisms that rely on atmospheric oxygen for respiration and survival. This can affect how fast an organism can propel itself efficiently or how long and deep it can dive. Heart mass and lung volume are important in determining how scaling can affect metabolic function and efficiency.
Aquatic mammals, like other mammals, have the same size heart proportional to their bodies. In general, mammals have hearts about 0.6% of their total body mass: , where M is the body mass of the individual.[41] Lung volume is also directly related to body mass in mammals (slope = 1.02). The lung has a volume of 63 ml for every kg of body mass, with the tidal volume at rest being 1/10 the lung volume. In addition, respiration costs with respect to oxygen consumption is scaled in the order of .[41] This shows that mammals, regardless of size, have similarly scaled respiratory and cardiovascular systems and the same relative amount of blood: about 5.5% of body mass. This means that for similarly designed marine mammals, a larger individual can travel more efficiently, as it takes the same effort to move one body length. For example, large whales can migrate far distance in the oceans and not stop for rest. It is metabolically less expensive to be larger in body size.[41] This goes for terrestrial and flying animals as well: smaller animals consume more oxygen per unit body mass than larger ones. The metabolic advantage in larger animals makes it possible for larger marine mammals to dive for longer durations of time than their smaller counterparts. That the heart rate is lower means that larger animals can carry more blood, which carries more oxygen. In conjuncture with the fact that mammals reparation costs scales in the order of , this shows having a larger body mass can be advantageous. More simply, a larger whale can hold more oxygen and at the same time demand less metabolically than a smaller whale.
Traveling long distances and deep dives are a combination of good stamina and also moving an efficient speed and in an efficient way to create laminar flow, reducing drag and turbulence. In sea water as the fluid, it traveling long distances in large mammals, such as whales, is facilitated by their neutral buoyancy and have their mass completely supported by the density of the sea water. On land, animals have to expend a portion of their energy during locomotion to fight the effects of gravity.
Flying organisms such as birds are also considered as moving through a fluid. In scaling birds of similar shape, it has also been seen that larger individuals have less metabolic costs per kg, as expected. Birds also have a variance in wing beat frequency. Beyond the compensation of larger wings per unit body mass, larger birds also have slower wing beat frequencies, allowing them to fly at higher altitudes, longer distances, and faster absolute speeds than smaller birds. Because of the dynamics of lift-based locomotion and the fluid dynamics, birds have a U-shaped curve for metabolic cost and velocity. Because flight, in air as the fluid, is metabolically more costly at the lowest and the highest velocities. On the other end, small organisms such as insects can make gain advantage from the viscosity of the fluid (air) that they are moving in. A wing-beat timed perfectly can effectively uptake energy from the previous stroke (Dickinson 2000). This form of wake capture allows an organism to recycle energy from the fluid or vortices within that fluid created by the organism itself. This same sort of wake capture occurs in aquatic organisms as well, and for organisms of all sizes. This dynamic of fluid locomotion allows smaller organisms to gain advantage because the effect on them from the fluid is much greater because of their relatively smaller size.[41][42]
Allometric engineering
[edit]Allometric engineering is a method for manipulating allometric relationships within or among groups.[43]
In characteristics of a city
[edit]Arguing that there are a number of analogous concepts and mechanisms between cities and biological entities, Bettencourt et al. showed a number of scaling relationships between observable properties of a city and the city size. GDP, "supercreative" employment, number of inventors, crime, spread of disease,[25] and even pedestrian walking speeds[44] scale with city population. This phenomenon goes under the name of urban scaling. Theoretical explanations for the presence of allometry in cities propose different mechanisms. Bettencourt’s model suggests that superlinear scaling arises from the quadratic growth of social interactions with population size under budget constraints.[45] A different mechanism was proposed by Gomez-Lievano et al. in which superlinear scaling is linked to the exponential growth in outputs resulting from the combination of diverse, complementary factors (or capabilities) found in cities, which scale logarithmically with city size.[46]
Examples
[edit]Some examples of allometric laws:
- Kleiber's law, metabolic rate is proportional to body mass raised to the power:
- breathing and heart rate are both inversely proportional to body mass raised to the power:
- mass transfer contact area and body mass :
- the proportionality between the optimal cruising speed of flying bodies (insects, birds, airplanes) and body mass raised to the power :
Determinants of size in different species
[edit]Many factors go into the determination of body mass and size for a given animal. These factors often affect body size on an evolutionary scale, but conditions such as availability of food and habitat size can act much more quickly on a species. Other examples include the following:
- Physiological design
- Basic physiological design plays a role in the size of a given species. For example, animals with a closed circulatory system are larger than animals with open or no circulatory systems.[24]
- Mechanical design
- Mechanical design can also determine the maximum allowable size for a species. Animals with tubular endoskeletons tend to be larger than animals with exoskeletons or hydrostatic skeletons.[24]
- Habitat
- An animal's habitat throughout its evolution is one of the largest determining factors in its size. On land, there is a positive correlation between body mass of the top species in the area and available land area.[47] However, there are a much greater number of "small" species in any given area. This is most likely determined by ecological conditions, evolutionary factors, and the availability of food; a small population of large predators depend on a much greater population of small prey to survive. In an aquatic environment, the largest animals can grow to have a much greater body mass than land animals where gravitational weight constraints are a factor.[19]
See also
[edit]- Biomass allocation – Concept in plant biology
- Biomechanics – Study of the mechanics of biological systems
- Body roundness index – Body scale based on waist circumference and height
- Comparative physiology – Study of the diversity of functional characteristics of organisms
- Cranial evolutionary allometry – Theory regarding evolutionary trends in the shape of mammalian skulls
- Evolutionary physiology – Study of evolutionary changes in physiological characteristics
- Metabolic theory of ecology – Theory concerning metabolism and observed patterns in ecology
- Phylogenetic comparative methods – Use of information on the historical relationships of lineages to test evolutionary hypotheses
- Power law – Functional relationship between two quantities (also known as a scaling law)
- Rensch's rule – A biological rule concerning sexual size dimorphism
- Tree allometry – Quantitative relations between some key characteristic dimensions of trees
- Urban scaling – Quantitative relations between urban characteristics and city population size
References
[edit]- ^ Small, Christopher G. (1996). The Statistical Theory of Shape. Springer. p. 4. ISBN 978-0-387-94729-7.
- ^ Damuth J (February 2001). "Scaling of growth: plants and animals are not so different". Proc. Natl. Acad. Sci. U.S.A. 98 (5): 2113–4. Bibcode:2001PNAS...98.2113D. doi:10.1073/pnas.051011198. PMC 33381. PMID 11226197.
- ^ Otto Snell (1892). "Die Abhängigkeit des Hirngewichts von dem Körpergewicht und den geistigen Fähigkeiten". Arch. Psychiatr. 23 (2): 436–446. doi:10.1007/BF01843462. S2CID 30692188.
- ^ Thompson, D'Arcy W (1992). On Growth and Form (Canto ed.). Cambridge University Press. ISBN 978-0-521-43776-9.
- ^ Huxley, Julian S. (1972). Problems of Relative Growth (2nd ed.). New York: Dover. ISBN 978-0-486-61114-3.
- ^ E.L. McCullough, K.J. Ledger, D.M. O'Brien, D.J. Emlen (2015) Variation in the allometry of exaggerated rhinoceros beetle horns. Animal Behaviour 109: 133–140. doi:10.1016/j.anbehav.2015.08.013.
- ^ a b Longo, Giuseppe; Montévil, Maël (2014-01-01). Perspectives on Organisms. Lecture Notes in Morphogenesis. Springer Berlin Heidelberg. pp. 23–73. doi:10.1007/978-3-642-35938-5_2. ISBN 9783642359378.
- ^ Frydrýšek, Karel (2019). Biomechanika 1. Ostrava, Czech Republic: VSB – Technical University of Ostrava, Faculty of Mechanical Engineering, Department of Applied Mechanics. p. 461. ISBN 978-80-248-4263-9.
- ^ Garland, T. Jr.; P. L. Else (March 1987). "Seasonal, sexual, and individual variation in endurance and activity metabolism in lizards" (PDF). Am J Physiol. 252 (3 Pt 2): R439–49. doi:10.1152/ajpregu.1987.252.3.R439. PMID 3826408. Archived from the original (PDF) on 2020-10-25. Retrieved 2009-01-23.
- ^ Bonduriansky, Russell; Day, Troy (2003). "The Evolution of Static Allometry in Sexually Selected Traits". Evolution. 57 (11): 2450–2458. doi:10.1111/j.0014-3820.2003.tb01490.x. PMID 14686522. S2CID 221262390.
- ^ Vogel, Steven (1988). Life's Devices: The Physical World of Animals and Plants. Princeton University Press. p. 39. ISBN 978-0-691-02418-9. Retrieved 29 March 2014.
- ^ Emerson S. B. (September 1978). "Allometry and Jumping in Frogs: Helping the Twain to Meet". Evolution. 32 (3): 551–564. doi:10.2307/2407721. JSTOR 2407721. PMID 28567959.
- ^ Schmidt-Nielsen 1984
- ^ Christian, A.; Garland T., Jr. (1996). "Scaling of limb proportions in monitor lizards (Squamata: Varanidae)" (PDF). Journal of Herpetology. 30 (2): 219–230. doi:10.2307/1565513. JSTOR 1565513. Archived from the original (PDF) on 2016-11-30. Retrieved 2010-03-15.
- ^ R. O. Anderson and R. M. Neumann, Length, Weight, and Associated Structural Indices, in Fisheries Techniques, second edition, B.E. Murphy and D.W. Willis, eds., American Fisheries Society, 1996.
- ^ Pennycuick, Colin J. (1992). Newton Rules Biology. Oxford University Press. p. 111. ISBN 978-0-19-854021-2.
- ^ Schmidt-Nielsen 1984, p. 237
- ^ Gibbings, J.C. (2011). Dimensional Analysis. Springer. ISBN 978-1-84996-317-6.
- ^ a b c d Hill, A.V. (November 12, 1949). "The dimensions of animals and their muscular dynamics". Nature. 164 (4176): 820. Bibcode:1949Natur.164R.820.. doi:10.1038/164820b0. S2CID 4082708.
- ^ Wilson RS, Franklin CE, James RS (June 2000). "Allometric scaling relationships of jumping performance in the striped marsh frog Limnodynastes peronii". J. Exp. Biol. 203 (Pt 12): 1937–46. doi:10.1242/jeb.203.12.1937. PMID 10821750.
- ^ Robinson, Michael; Motta, Philip (2002). "Patterns of growth and the effects of scale on the feeding kinematics of the nurse shark (Ginglymostoma cirratum)". Journal of Zoology, London. 256 (4): 449–462. CiteSeerX 10.1.1.524.9341. doi:10.1017/S0952836902000493.
- ^ Kerkhoff, A.J.; Enquist, B.J. (2009). "Multiplicative by nature: Why logarithmic transformation is necessary in allometry". Journal of Theoretical Biology. 257 (3): 519–521. Bibcode:2009JThBi.257..519K. doi:10.1016/j.jtbi.2008.12.026.
- ^ O'Hara, R.B.; Kotze, D.J. (2010). "Do not log-transform count data". Methods in Ecology and Evolution. 1 (2): 118–122. Bibcode:2010MEcEv...1..118O. CiteSeerX 10.1.1.466.9313. doi:10.1111/j.2041-210X.2010.00021.x. S2CID 92046364.
- ^ a b c d e Willmer, Pat (2009). Environmental Physiology of Animals. Wiley-Blackwell.
- ^ a b Bettencourt LM, Lobo J, Helbing D, Kühnert C, West GB (April 2007). "Growth, innovation, scaling, and the pace of life in cities". Proc. Natl. Acad. Sci. U.S.A. 104 (17): 7301–6. Bibcode:2007PNAS..104.7301B. doi:10.1073/pnas.0610172104. PMC 1852329. PMID 17438298.
- ^ Dodds PS, Rothman DH, Weitz JS (March 2001). "Re-examination of the "3/4-law" of metabolism". Journal of Theoretical Biology. 209 (1): 9–27. arXiv:physics/0007096. Bibcode:2001JThBi.209....9D. doi:10.1006/jtbi.2000.2238. PMID 11237567. S2CID 9168199.>
- ^ Rothman DH, Weitz JS (Nov 2005). "Beyond the '3/4-power law': variation in the intra- and interspecific scaling of metabolic rate in animals". Biological Reviews. 80 (4): 611–662. doi:10.1017/S1464793105006834. PMID 16221332. S2CID 8546506.>
- ^ Labra FA, Marquet PA, Bozinovic F (June 2007). "Scaling metabolic rate fluctuations". Proc. Natl. Acad. Sci. U.S.A. 104 (26): 10900–3. Bibcode:2007PNAS..10410900L. doi:10.1073/pnas.0704108104. PMC 1904129. PMID 17578913.
- ^ Garland Jr., T. (1983). "The relation between maximal running speed and body mass in terrestrial mammals" (PDF). Journal of Zoology, London. 199 (2): 157–170. doi:10.1111/j.1469-7998.1983.tb02087.x. Archived from the original (PDF) on 2018-08-31. Retrieved 2010-03-16.
- ^ Chappell, R. (1989). "Fitting bent lines to data, with applications to allometry". Journal of Theoretical Biology. 138 (2): 235–256. Bibcode:1989JThBi.138..235C. doi:10.1016/S0022-5193(89)80141-9. PMID 2607772.
- ^ a b c Daley, Monica A.; Usherwood, James R. (2010). "Two explanations for the compliant running paradox: reduced work of bouncing viscera and increased stability in uneven terrain". Biology Letters. 6 (3): 418–421. doi:10.1098/rsbl.2010.0175. PMC 2880072. PMID 20335198.
- ^ a b c d e f g h Farley CT, Glasheen J, McMahon TA (December 1993). "Running springs: speed and animal size". J. Exp. Biol. 185 (1): 71–86. doi:10.1242/jeb.185.1.71. PMID 8294853.[permanent dead link]
- ^ a b c Sellers, William Irving; Manning, Phillip Lars (2007). "Estimating dinosaur maximum running speeds using evolutionary robotics". Proceedings of the Royal Society B. 274 (1626): 2711–6. doi:10.1098/rspb.2007.0846. PMC 2279215. PMID 17711833.
- ^ a b c d e f g h Alexander, R. McN. (1984). "The gaits of bipedal and quadrupedal animals". The International Journal of Robotics Research. 3 (2): 49–59. doi:10.1177/027836498400300205. S2CID 120138903.
- ^ a b Roberts, Thomas J.; Azizi, Emanuel (2011). "Fleximble mechanisms: the diverse roles of biological springs in vertebrate movement". The Journal of Experimental Biology. 214 (3): 353–361. doi:10.1242/jeb.038588. PMC 3020146. PMID 21228194.
- ^ Blanco, G.; Bautista, L.M.; Hornero-Méndez, D.; Lambertucci, S.A.; Wiemeywer, G.; Sánchez-Zapata, J.A.; Hiraldo, F.; Donazar, J.A. (2014). "Allometric deviations of plasma carotenoids in raptors" (PDF). Ibis. 156 (3): 668–675. doi:10.1111/ibi.12155. hdl:10261/98308.
- ^ West, G. B.; Brown, J.H.; Enquist, B. J. (1997). "A general model for the origin of allometric scaling laws in biology". Science. 276 (5309): 122–126. doi:10.1126/science.276.5309.122. PMID 9082983. S2CID 3140271.
- ^ T. M. Hu; W. L. Hayton (2001). "Allometric scaling of xenobiotic clearance: uncertainty versus universality". AAPS PharmSci. 3 (4): E29. doi:10.1208/ps030429. PMC 2751218. PMID 12049492.
- ^ "Allometric Scaling Calculator". Clymer.altervista.org. 13 May 2012. Retrieved 15 December 2015. Online allometric scaling calculator, with explanation and source.
- ^ US FDA: Estimating the Safe Starting Dose in Clinical Trials for Therapeutics in Adult Healthy Volunteers, July 2005
- ^ a b c d e Schmidt-Nielsen, Knut (10 April 1997). Animal Physiology: Adaptation and Environment (5th ed.). Cambridge University Press. ISBN 978-0-521-57098-5.
- ^ Dickinson MH, Farley CT, Full RJ, Koehl MA, Kram R, Lehman S (April 2000). "How animals move: an integrative view". Science. 288 (5463): 100–6. Bibcode:2000Sci...288..100D. doi:10.1126/science.288.5463.100. PMID 10753108.
- ^ Sinervo, B.; Huey, R. (1990). "Allometric Engineering: An Experimental Test of the Causes of Interpopulational Differences in Performance" (PDF). Science. 248 (4959): 1106–9. Bibcode:1990Sci...248.1106S. doi:10.1126/science.248.4959.1106. PMID 17733374. S2CID 3068221.
- ^ Bornstein MH, Bornstein HG (19 February 1976). "The Pace of Life". Nature. 259 (5544): 557–9. Bibcode:1976Natur.259..557B. doi:10.1038/259557a0. S2CID 4176349.
- ^ Bettencourt, Luís M. A. (2013-06-21). "The Origins of Scaling in Cities". Science. 340 (6139): 1438–1441. doi:10.1126/science.1235823. ISSN 0036-8075.
- ^ Gomez-Lievano, Andres; Patterson-Lomba, Oscar; Hausmann, Ricardo (2016-12-22). "Explaining the prevalence, scaling and variance of urban phenomena". Nature Human Behaviour. 1 (1). arXiv:1604.07876. doi:10.1038/s41562-016-0012. ISSN 2397-3374.
- ^ Burness, G. P.; Diamond, Jared; Flannery, Timothy (2001). "Dinosaurs, dragons, and dwarfs: The evolution of maximal body size". Proc. Natl. Acad. Sci. U.S.A. 98 (25): 14518–23. Bibcode:2001PNAS...9814518B. doi:10.1073/pnas.251548698. PMC 64714. PMID 11724953.
Further reading
[edit]- Calder, W. A. (1984). Size, function and life history. Harvard University Press. ISBN 978-0-674-81070-9.
- McMahon, T. A.; Bonner, J. T. (1983). On Size and Life. Scientific American Library. ISBN 978-0-7167-5000-0.
- Niklas, K. J. (1994). Plant allometry: The scaling of form and process. University of Chicago Press. ISBN 978-0-226-58081-4.
- Peters, R. H. (1983). The ecological implications of body size. Cambridge University Press. ISBN 978-0-521-28886-6.
- Reiss, M. J. (1989). The allometry of growth and reproduction. Cambridge University Press. ISBN 978-0-521-42358-8.
- Schmidt-Nielsen, K. (1984). Scaling: why is animal size so important?. Cambridge: Cambridge University Press. ISBN 978-0-521-31987-4.
- Samaras, Thomas T. (2007). Human body size and the laws of scaling: physiological, performance, growth, longevity and ecological ramifications. Nova Publishers. ISBN 978-1-60021-408-0.
External links
[edit]- FDA Guidance for Estimating Human Equivalent Dose Archived 2009-05-11 at the Wayback Machine (For "first in human" clinical trials of new drugs)
Allometry
View on GrokipediaIntroduction
Overview
Allometry is the study of size-dependent changes in the shape, physiology, anatomy, or other traits of organisms, capturing how these attributes vary disproportionately with overall body size.[2] This field examines relationships often expressed through power-law models of the form , where represents a trait, is body size, is a constant, and signifies non-proportional (allometric) scaling, distinguishing it from isometric cases where . Such patterns arise during growth, across species, or in static comparisons, revealing fundamental principles of biological form and function.[9] The importance of allometry extends across biology, informing processes like growth and development, where it explains how organisms adapt to size changes without proportional adjustments in all features.[2] In evolution, allometric scaling highlights selective pressures that shape trait exaggeration or constraint, such as in morphological diversity among related species.[10] Ecologically, it underpins community dynamics and resource use by linking body size to interaction strengths.[11] Beyond biology, allometric principles apply to engineered systems and urban planning, where scaling laws predict infrastructure demands or socioeconomic outputs in growing cities, analogous to metabolic rates in organisms.[12] Key pioneers, including D'Arcy Thompson in his seminal work On Growth and Form, emphasized allometry's role in integrating mathematics and biology to uncover universal scaling rules.[13] Overall, allometry illuminates non-proportional scaling in living systems, demonstrating how size influences efficiency, adaptation, and organization from cells to ecosystems.[14]Historical Development
The concept of allometry emerged in the early 20th century as biologists sought to understand disproportionate growth patterns in organisms. D'Arcy Wentworth Thompson's influential book On Growth and Form, published in 1917, provided a foundational perspective by emphasizing the geometric and morphological principles that govern biological structures during development, influencing subsequent studies on form and scaling. This work highlighted how physical laws shape organic forms, setting the stage for quantitative analyses of relative growth. In 1932, Max Kleiber's analysis revealed a foundational relationship between body mass and metabolic rate, demonstrating that metabolic rate across species scales approximately as the three-quarters power of body mass—a pattern later termed Kleiber's law—which became a benchmark for understanding energy allocation in physiology. Julian Huxley's 1932 monograph Problems of Relative Growth formalized the field by developing mathematical frameworks to model heterogonic growth, where parts grow at rates differing from the whole, drawing on empirical data from diverse species, such as fiddler crabs and salamanders, and thus establishing allometry as a core tool in developmental biology.[15][6] The term "allometry" was coined in 1936 by Huxley and Georges Teissier in a joint paper to describe the study of size-dependent variations in the proportions of body parts. His contributions shifted focus from descriptive morphology to predictive modeling of growth trajectories. Following World War II, allometric approaches extended further into physiological scaling and other areas. During the 1970s and 1980s, allometry broadened into ecology and evolutionary biology, integrating scaling principles with population dynamics and life-history traits. Robert H. Peters' 1983 synthesis The Ecological Implications of Body Size compiled extensive interspecific data to show how body size governs ecological patterns, such as population density and resource use, thereby linking allometry to broader environmental processes.[16] This era also saw evolutionary applications, with researchers like William A. Calder exploring size-related invariants in life histories. Building on these, Geoffrey West and collaborators in the late 20th century unified allometric scaling with network theory to explain universal patterns in biology. From 2020 to 2025, allometric research has increasingly adopted interdisciplinary methods, particularly computational models for applications like tree allometry. Advances in remote sensing, such as LiDAR integration, have refined biomass estimation models.[17] These developments enhance predictions of carbon sequestration and ecosystem resilience, extending allometry's utility to global environmental modeling.[18]Core Concepts
Isometric Scaling
Isometric scaling describes the proportional growth of structures where shape and proportions remain unchanged as overall size varies, characterized by the power-law relationship with the scaling exponent . In this case, any linear dimension (such as length) increases directly in proportion to the reference size , ensuring geometric similarity across different scales. This form of scaling, first formalized in studies of relative growth, contrasts with deviations where proportions alter, but it represents the baseline expectation for uniform expansion.[19] The principles of geometric similarity underpin isometric scaling, dictating how dimensions transform with size. Linear dimensions scale directly with the overall size factor, while surface areas scale with its square and volumes with its cube. As a result, linear dimensions are proportional to the cube root of volume, since volume implies , where is a linear measure. This relationship holds in idealized systems, preserving form without distortion, and serves as a reference for analyzing real-world growth patterns.[20] Examples of isometric scaling appear in non-biological systems like crystal growth, where uniform environmental conditions allow crystals to enlarge while maintaining fixed proportions, such as in isometric mineral habits like those of garnet or halite. Similarly, ideal geometric shapes, such as spheres or cubes, exemplify this scaling: enlarging a cube doubles its edge length results in volumes eight times larger, but the shape remains identical, with all faces and angles unchanged. These cases illustrate pure geometric fidelity without adaptive modifications. In biology, heart mass often scales isometrically with body mass in mammals, maintaining relative proportions across body sizes.[1] In uniformly scaling structures under isometric principles, implications for mechanical integrity arise, particularly regarding stress and strength. Structural strength depends on cross-sectional area, which scales with the square of linear dimensions (), whereas gravitational loads like weight scale with volume (). Consequently, stress (load per unit area) increases with size, as the cube-to-square ratio grows, making larger isometric structures prone to failure under their own weight unless reinforced— a challenge evident in hypothetical uniform scaling of load-bearing elements like beams or limbs. This scaling mismatch highlights why pure isometry becomes unsustainable beyond certain sizes in weight-bearing designs.[21]Allometric Scaling
Allometric scaling refers to the disproportionate change in the size of a biological trait relative to the overall size of an organism, typically described by a power-law relationship where the scaling exponent deviates from unity. In this framework, the size of a trait scales with body size according to the equation , where is a constant and is the allometric exponent; when , the trait does not grow proportionally with the body, leading to changes in shape or proportions.[1][4] Positive allometry occurs when , indicating that the trait grows faster than the body as a whole, such as in certain exaggerated structures; conversely, negative allometry arises when , where the trait grows more slowly, resulting in relatively smaller proportions in larger individuals.[1] This concept was formalized by Julian Huxley in his 1932 work Problems of Relative Growth, building on earlier observations of relative growth patterns in organisms.[4] Allometric scaling manifests in three primary types, distinguished by the scale of observation. Ontogenetic allometry describes changes within an individual during its development, where the exponent reflects differences in growth rates between the trait and overall body size over time.[1][22] Static allometry examines variation among individuals of the same species at a single developmental stage, capturing intraspecific differences in relative trait sizes.[1][22] Evolutionary allometry, in contrast, compares traits across species or populations, revealing interspecific patterns shaped by phylogenetic history.[1][22] These types highlight how scaling relationships can differ depending on whether the focus is individual growth, population variation, or macroevolutionary trends.[23] For empirical analysis, the power-law relationship is often transformed into a log-linear form to facilitate linear regression. Taking the logarithm (base 10 or natural) of both sides of yields , where the slope of the resulting straight line on a log-log plot directly estimates the exponent , and the intercept corresponds to .[1][4] This derivation simplifies the detection of nonlinear scaling patterns and allows for statistical testing of deviations from isometry (where ).[1] The value of the exponent is influenced by underlying biological processes, including developmental constraints and natural selection pressures. Developmental constraints, such as shared regulatory mechanisms for growth, can limit the evolvability of on short timescales, stabilizing scaling relationships within populations or species.[24][25] Selection pressures, acting on body size or specific traits, can drive shifts in over evolutionary time, as seen in cases where functional demands alter relative growth rates.[25][24] For instance, stabilizing selection may maintain particular exponents to preserve adaptive proportions, while directional selection can promote deviations in response to ecological or mating pressures.[25]Analytical Methods
Identifying Scaling Relationships
To identify scaling relationships in allometric studies, researchers commonly apply ordinary least squares (OLS) regression to log-transformed data, which linearizes the relationship between two variables and allows estimation of the scaling exponent as the slope of the fitted line.[26] This approach tests for isometry by evaluating whether , indicating proportional scaling, or , signifying allometry with either positive () or negative () deviation. Statistical inference on the slope involves t-tests to assess significant deviation from isometry () or examination of 95% confidence intervals that exclude 1 as evidence of allometry.[27] For bivariate datasets where measurement error affects both variables equally, reduced major axis (RMA) or standardized major axis (SMA) regression is preferred over OLS, as these methods account for symmetric error structures and provide unbiased slope estimates.[26] Phylogenetic confounding, arising from shared evolutionary history among species, can bias standard regressions; this is addressed using phylogenetically independent contrasts (PIC), which compute differences in traits along phylogenetic branches to yield independent data points for analysis. Alternatively, phylogenetic generalized least squares (PGLS) incorporates the phylogenetic covariance matrix directly into the regression model, adjusting for non-independence while estimating slopes and testing deviations from isometry. These methods ensure robust detection of scaling patterns by isolating evolutionary signals from historical correlations.Examples of Analysis
One illustrative example of allometric analysis involves examining the relationship between bird wing length and body mass to detect scaling patterns relevant to flight capabilities. In a study of diverse avian species, total wing bone length (comprising humerus, ulna, and manus) was found to scale against body mass with an exponent of approximately 0.37 to 0.39, indicating positive allometry since this exceeds the isometric expectation of 1/3 for linear dimensions versus mass.[28] This positive scaling suggests that larger birds develop relatively longer wings, which may enhance lift generation and reduce wing loading for sustained flight.[28] To demonstrate this, consider a simplified dataset from representative bird species spanning small to large body sizes. The following table presents sample body mass and corresponding wing length measurements (total bone length, approximate):| Species Example | Body Mass (g) | Wing Length (cm) |
|---|---|---|
| Hummingbird | 5 | 4.0 |
| Sparrow | 30 | 8.5 |
| Crow | 500 | 30.0 |
| Eagle | 5000 | 42.0 |
| Species Example | Body Length (mm) | Hind Femur Length (mm) |
|---|---|---|
| Small cricket | 10 | 6.0 |
| Medium grasshopper | 25 | 12.5 |
| Large katydid | 60 | 25.0 |