Hubbry Logo
Mass numberMass numberMain
Open search
Mass number
Community hub
Mass number
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Mass number
Mass number
Mass number
View on Wikipedia
from Wikipedia
Nuclear physics
Models of the nucleus
Nuclides' classification
Nuclear stability
Radioactive decay
Nuclear fission
Capturing processes
High-energy processes
Nucleosynthesis and
nuclear astrophysics
High-energy nuclear physics
Scientists

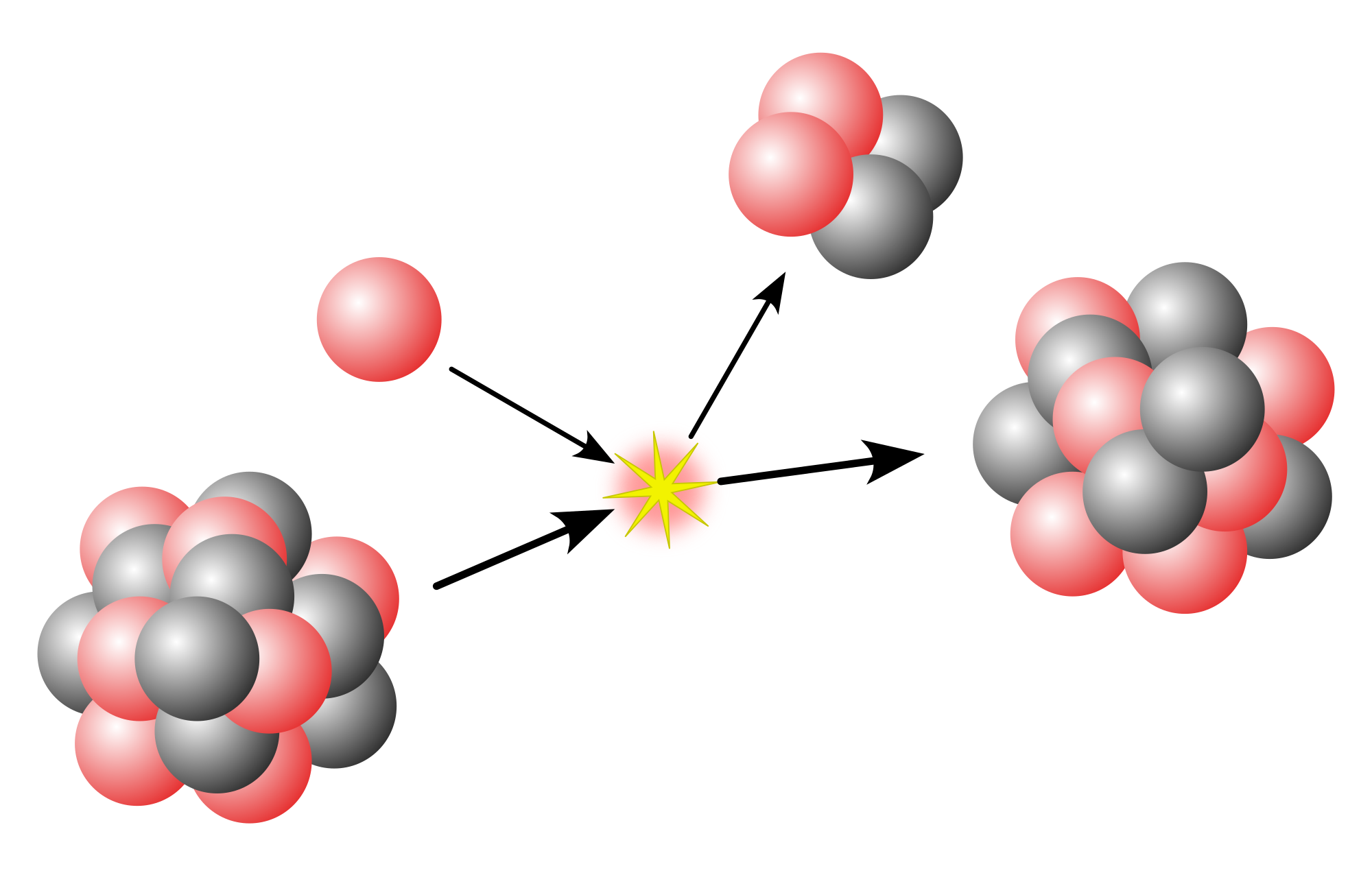
The mass number (symbol A, from the German word: Atomgewicht, "atomic weight"),[1] also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It is approximately equal to the atomic (also known as isotopic) mass of the atom expressed in daltons. Since protons and neutrons are both baryons, the mass number A is identical with the baryon number B of the nucleus (and also of the whole atom or ion). The mass number is different for each isotope of a given chemical element, and the difference between the mass number and the atomic number Z gives the number of neutrons (N) in the nucleus: N = A − Z.[2]

The mass number is written either after the element name or as a superscript to the left of an element's symbol. For example, the most common isotope of carbon is carbon-12, or 12
C, which has 6 protons and 6 neutrons. The full isotope symbol would also have the atomic number (Z) as a subscript to the left of the element symbol directly below the mass number: 12
6C.[3]

Mass number changes in radioactive decay

[edit]

Different types of radioactive decay are characterized by their changes in mass number as well as atomic number, according to the radioactive displacement law of Fajans and Soddy. For example, uranium-238 usually decays by alpha decay, where the nucleus loses two neutrons and two protons in the form of an alpha particle. Thus the atomic number and the number of neutrons each decrease by 2 (Z: 92 → 90, N: 146 → 144), so that the mass number decreases by 4 (A = 238 → 234); the result is an atom of thorium-234 and an alpha particle (4
2He2+
):[4]

238
92U 		 →  234
90Th 		 +  4
2He2+

On the other hand, carbon-14 decays by beta decay, whereby one neutron is transmuted into a proton with the emission of an electron and an antineutrino. Thus the atomic number increases by 1 (Z: 6 → 7) and the mass number remains the same (A = 14), while the number of neutrons decreases by 1 (N: 8 → 7).[5] The resulting atom is nitrogen-14, with seven protons and seven neutrons:

14
6C 		 →  14
7N 		 +  e−
 		 +  ν
e

Beta decay is possible because different isobars[6] have mass differences on the order of a few electron masses. If possible, a nuclide will undergo beta decay to an adjacent isobar with lower mass. In the absence of other decay modes, a cascade of beta decays terminates at the isobar with the lowest atomic mass.

Another type of radioactive decay without change in mass number is emission of a gamma ray from a nuclear isomer or metastable excited state of an atomic nucleus. Since all the protons and neutrons remain in the nucleus unchanged in this process, the mass number is also unchanged.

Mass number and isotopic mass

[edit]

The mass number gives an estimate of the isotopic mass measured in daltons (Da). For 12C, the isotopic mass is exactly 12, since the dalton is defined as 1/12 of the mass of 12C. For other isotopes, the isotopic mass is usually within 0.1 Da of the mass number. For example, 35Cl (17 protons and 18 neutrons) has a mass number of 35 and an isotopic mass of 34.96885.[7] The difference of the actual isotopic mass minus the mass number of an atom is known as the mass excess,[8] which for 35Cl is –0.03115. Mass excess should not be confused with mass defect, which is the difference between the mass of an atom and its constituent particles (namely protons, neutrons and electrons).

There are two reasons for mass excess:

  1. The neutron is slightly heavier than the proton. This increases the mass of nuclei with more neutrons than protons relative to the dalton based on 12C with equal numbers of protons and neutrons.
  2. Nuclear binding energy varies between nuclei. A nucleus with greater binding energy has a lower total energy, and therefore a lower mass according to Einstein's mass–energy equivalence relation E = mc2. For 35Cl, the isotopic mass is less than 35, so this must be the dominant factor.

Relative atomic mass of an element

[edit]

The mass number should also not be confused with the standard atomic weight (also called atomic weight) of an element, which is the ratio of the average atomic mass of the different isotopes of that element (weighted by abundance) to the atomic mass constant.[9] The atomic weight is a mass ratio, while the mass number is a counted number (and so an integer).

This weighted average can be quite different from the near-integer values for individual isotopic masses. For instance, there are two main isotopes of chlorine: chlorine-35 and chlorine-37. In any given sample of chlorine that has not been subjected to mass separation there will be roughly 75% of chlorine atoms which are chlorine-35 and only 25% of chlorine atoms which are chlorine-37. This gives chlorine a relative atomic mass of 35.5 (actually 35.4527 g/mol).

Moreover, the weighted average mass can be near-integer, but at the same time not corresponding to the mass of any natural isotope. For example, bromine has only two stable isotopes, 79Br and 81Br, naturally present in approximately equal fractions, which leads to the standard atomic mass of bromine close to 80 (79.904 g/mol),[10] even though the isotope 80Br with such mass is unstable.

References

[edit]

Further reading

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Mass number

View on Grokipedia
from Grokipedia
The mass number, denoted by the symbol A and also known as the , is defined as the total number of protons and neutrons (collectively called ) present in the nucleus of an atom. It represents an integer value that approximates the of the in unified atomic mass units (u), since both protons and neutrons have masses very close to 1 u each. The mass number is calculated as A = Z + N, where Z is the (the number of protons) and N is the number of neutrons. In standard chemical notation, the mass number appears as a left superscript to the of the element, often alongside the as a left subscript, in the form ZAX^{A}_{Z}\mathrm{X}, where X is the element ; for example, is written as 612C^{12}_{6}\mathrm{C}. This notation uniquely identifies a , as the combination of and mass number specifies both the element and its isotopic form. The mass number plays a crucial role in and chemistry, particularly in distinguishing isotopes—variants of the same element that share the same but differ in mass number to varying counts. Unlike the (or ), which is a weighted average of the atomic masses of an element's naturally occurring based on their abundances, the mass number applies specifically to individual and is always an . For instance, the two stable —612C^{12}_{6}\mathrm{C} (mass number 12) and 613C^{13}_{6}\mathrm{C} (mass number 13)—have the same of 6 but different mass numbers, leading to distinct nuclear properties. The radioactive isotope 614C^{14}_{6}\mathrm{C} (mass number 14) is used in . Mass numbers greater than 208 are typically unstable and radioactive, influencing stability trends across the periodic table.

Fundamentals

Definition

The mass number, denoted by the symbol AA, is defined as the total number of protons and neutrons—collectively referred to as nucleons—in the nucleus of an atom. This integer value provides a fundamental measure of the nuclear composition, distinguishing it from the ZZ, which counts only the protons in the nucleus and determines the chemical identity of the element. The number of neutrons NN is calculated as N=A−ZN = A - Z. As an approximation, the mass number represents the mass of the nucleus in atomic mass units (u), where each contributes roughly 1 u to the total, though actual isotopic masses deviate slightly due to binding effects. For instance, the isotope (12C^{12}\text{C}) has a mass number of 12, comprising 6 protons and 6 s, which approximates its nuclear mass at 12 u. of an element share the same but differ in mass number due to varying neutron counts.

Notation

The mass number AA is conventionally represented as a left superscript preceding the of the element in nuclide notation, as in AX^{A}X, where XX denotes the . This form is used when the ZZ is either unnecessary or implied by context. For complete specification, the is included as a left subscript, yielding the standard ZAX_{Z}^{A}X, which uniquely identifies a particular by indicating both the number of protons (ZZ) and the total number of nucleons (AA). Alternative notations simplify representation in certain contexts. For instance, AXA X omits the atomic number subscript when ZZ is clear, while X−AX-A places the mass number after the symbol separated by a hyphen, such as C-12 for carbon-12. In verbal or informal , a hyphenated form is common for isotopes, exemplified by or U-235, where the element name or symbol precedes the mass number. These variants facilitate in publications and discussions without altering the underlying meaning. Isobars, defined as nuclides sharing the same mass number AA but differing in ZZ, are often denoted using the simplified AX^{A}X form to emphasize the common AA value across different elements, such as 14C^{14}\mathrm{C} and 14N^{14}\mathrm{N} for and nitrogen-14. This notation highlights structural similarities in contexts. The International Union of Pure and Applied Chemistry (IUPAC) provides guidelines for these notations in , recommending the left-superscript placement for mass number to ensure precision and consistency, particularly in isotopically specified compounds and nuclear data compilations. Arabic numerals are used exclusively for AA and ZZ, with the symbols italicized only if representing variables rather than fixed labels.

Isotopes and Identification

Isotopes

Isotopes are nuclides of the same chemical element that have the same atomic number ZZ but different mass numbers AA, arising from variations in the number of neutrons in the nucleus. This difference in neutron count results in atoms that are chemically nearly identical but differ in mass and nuclear stability. Isotopes are classified as stable or unstable (radioactive), depending on whether they undergo spontaneous radioactive decay. Stable isotopes persist indefinitely without decaying, while unstable ones decay over time into other nuclides. In nature, elements typically occur as mixtures of isotopes with varying abundances; for instance, carbon consists primarily of the stable isotope carbon-12 (approximately 99% abundance) and a smaller fraction of carbon-13 (approximately 1% abundance). These natural abundances reflect the relative proportions in which the isotopes are found in Earth's materials. The of an element, as listed in periodic tables, is calculated as the amount-weighted average of the atomic masses of its , using their fractional abundances as weights. This averaging accounts for the isotopic composition of the element in standard terrestrial samples, providing a practical value for chemical calculations rather than the mass of any single isotope. Isotopes play key roles in chemistry and due to subtle differences in their physical properties. For example, (hydrogen-2, with one proton and one ) exhibits a , where reactions involving C–H bonds proceed faster than those with C–D bonds because of the heavier mass of , which strengthens the bond and raises the . In , stable isotopes like deuterium oxide are employed as tracers to study metabolic processes, such as turnover in the body, without introducing radioactivity. The discovery of isotopes is credited to early 20th-century work using , notably by Francis Aston, who in 1919 identified (masses 20 and 22) with his improved mass spectrograph at the , confirming J.J. Thomson's earlier observations and enabling widespread isotopic analysis. Isotopes are conventionally denoted in isotopic notation, such as ZAX^{A}_{Z}\mathrm{X}.

Isotopic Notation

Isotopic notation specifies the mass number AA to distinguish isotopes of the same element, building on general symbolism where the mass number is placed as a left superscript to the element , such as 12C^{12}\mathrm{C} for or 2H^{2}\mathrm{H} for . This convention, recommended by the International Union of Pure and Applied Chemistry (IUPAC), ensures precise identification by highlighting the total number of protons and neutrons, with the implied by the element . An alternative verbal or abbreviated form uses a followed by the mass number, as in or C-12, which is commonly employed in textual descriptions and databases. For the hydrogen isotopes, standard notation designates protium as 1H^{1}\mathrm{H} or H-1, deuterium as 2H^{2}\mathrm{H} or H-2, and tritium as 3H^{3}\mathrm{H} or H-3, reflecting their increasing mass numbers due to additional neutrons. These examples illustrate how the superscript mass number directly conveys the isotopic variant without ambiguity. IUPAC guidelines in the Nomenclature of Organic Chemistry (Blue Book, Chapter P-8) recommend using roman type for the element symbol with the mass number as an italicized superscript in equations and tables, reserving italicization for locants in compound names. For instance, in chemical equations, 12CH4^{12}\mathrm{CH_4} denotes with a specific carbon isotope, and nuclides should be ordered alphabetically by symbol or by increasing mass number when multiple are present. Notation for isotopic mixtures or enriched samples extends these conventions to indicate composition variations. Natural mixtures are often denoted simply by the element symbol (e.g., C for natural carbon, comprising ~98.93% 12C^{12}\mathrm{C} and ~1.07% 13C^{13}\mathrm{C}), while enriched samples use prefixes like "enr" followed by the nuclide symbol, such as enr-13C^{13}\mathrm{C} for carbon enriched in the 13 isotope. Isotopically deficient mixtures employ "def" (e.g., def-13C^{13}\mathrm{C}), adhering to IUPAC standards for labeling in analytical contexts. In and , the mass number facilitates peak identification by correlating spectral peaks with specific isotopes, as each produces distinct m/z values based on its mass. For example, in the of (C₂H₅OH), the molecular at m/z 46 corresponds to the most abundant 12C2^{12}\mathrm{C}_2 form, while adjacent M+1 (m/z 47) and M+2 (m/z 48) peaks arise from 13C^{13}\mathrm{C} and 18O^{18}\mathrm{O} substitutions, respectively, allowing deduction of elemental composition from mass number patterns and natural abundances. This reliance on mass number enables quantitative analysis of isotopic distributions in complex samples.

Mass Relations

Isotopic Mass

The isotopic mass of a refers to the experimentally measured of its neutral atom, including the masses of its electrons, expressed in unified atomic mass units (u). This value is typically a non-integer, reflecting the mass defect caused by the conversion of a portion of the nucleons' rest mass into during the formation of the nucleus. The isotopic mass mm approximates the mass number AA, but a more precise conceptual relation is given by m≈ZmH+Nmn−Δmc2c2,m \approx Z m_\mathrm{H} + N m_\mathrm{n} - \frac{\Delta m c^2}{c^2}, where ZZ is the atomic number (number of protons), N=A−ZN = A - Z is the number of neutrons, mHm_\mathrm{H} is the mass of a neutral hydrogen atom, mnm_\mathrm{n} is the neutron mass, Δm\Delta m is the mass defect, and cc is the speed of light. The mass defect Δm\Delta m is defined as the difference between the total mass of the separated protons, neutrons, and electrons (ZmH+NmnZ m_\mathrm{H} + N m_\mathrm{n}) and the actual measured atomic mass; this defect corresponds to the nuclear binding energy via Einstein's equation Eb=Δmc2E_b = \Delta m c^2, which quantifies the energy required to disassemble the nucleus into its constituent particles. Isotopic masses are determined through high-precision , a technique that ionizes atoms and separates them based on their in electric and magnetic fields to yield accurate mass values. A key reference is the isotope (12C^{12}\mathrm{C}), defined by the International Union of Pure and Applied Chemistry (IUPAC) in 1961 as having an isotopic mass of exactly 12 u for its neutral atom in the , establishing the unified atomic mass unit as one-twelfth of this value. In distinction from the mass number AA, which is the dimensionless integer approximating the total number of nucleons, the isotopic mass is an empirical quantity derived from measurement. For example, the isotopic mass of (16O^{16}\mathrm{O}) is 15.994915 u, slightly less than 16 due to the mass defect.

Relative Atomic Mass

The relative atomic mass, denoted Ar(E)A_r(E), of an element EE is defined as the ratio of the average mass per atom of the element in its standard isotope composition to one-twelfth the mass of an atom of the carbon-12 isotope. This value is dimensionless and represents a weighted average of the relative isotopic masses of the element's naturally occurring isotopes, scaled such that the relative mass of 12C^{12}\mathrm{C} is exactly 12. The calculation accounts for the fractional abundances of each isotope, ensuring the result reflects the typical composition found in normal terrestrial materials. The formula for relative atomic mass is given by Ar(E)=∑ixi⋅Ai,A_r(E) = \sum_i x_i \cdot A_i, where xix_i is the (fractional abundance) of isotope ii, and AiA_i is the relative isotopic mass of that isotope. The mass number AA of each , which approximates the sum of protons and neutrons, determines the range of isotopic masses around this ; for elements with multiple isotopes differing in AA, the weighted often falls between the nearest integers. For example, has two isotopes, 35Cl^{35}\mathrm{Cl} (A=35A = 35, relative mass 34.96885 u, abundance approximately 75.8%) and 37Cl^{37}\mathrm{Cl} (A=37A = 37, relative mass 36.96590 u, abundance approximately 24.2%), yielding a relative atomic mass of approximately 35.45. Standard atomic weights, as recommended by the Commission on Isotopic Abundances and Atomic Weights (CIAAW), incorporate uncertainties to account for natural variations in isotopic abundances across terrestrial sources, expressed as intervals like [35.446, 35.457] for . These variations arise from isotopic processes in nature, such as or biological uptake, differing from more uniform laboratory-synthesized samples where fixed abundances can yield precise values without brackets. This physics-based scale, with 12C=12^{12}\mathrm{C} = 12, was adopted internationally in 1961 by IUPAC and the International Union of Pure and Applied Physics, replacing the earlier chemical scale based on set to 16 to unify measurements across disciplines and align with standards.

Nuclear Processes

Radioactive Decay

Radioactive decay involves the spontaneous transformation of an unstable into a more stable configuration, often altering the mass number AA, which is the total number of protons and neutrons in the nucleus. In this process, the mass number of the daughter nucleus can change depending on the decay mode, while conservation of number ensures that the total AA across all massive decay products remains constant, as neutrinos or antineutrinos emitted have negligible mass. Alpha decay occurs when a nucleus emits an , which is a nucleus (24α^{4}_{2}\alpha) consisting of two protons and two neutrons, thereby reducing the mass number of the nucleus by 4. This mode is common in heavy nuclides with A>[200](/page/200)A > [200](/page/200), as it helps achieve greater stability by lowering the proton-to-neutron . For example, undergoes to thorium-234: 92238U→90234Th+24α^{238}_{92}\mathrm{U} \to ^{234}_{90}\mathrm{Th} + ^{4}_{2}\alpha. Beta minus (β−\beta^-) decay transforms a neutron into a proton, emitting an electron and an antineutrino, which leaves the mass number unchanged since the total number of nucleons remains the same, but increases the atomic number ZZ by 1. This process typically occurs in neutron-rich nuclei and shifts the nuclide toward stability. A representative example is the decay of carbon-14 to nitrogen-14: 614C→714N+e−+νˉe^{14}_{6}\mathrm{C} \to ^{14}_{7}\mathrm{N} + e^- + \bar{\nu}_e. Beta plus (β+\beta^+) decay and electron capture both convert a proton into a neutron, resulting in no change to the mass number but a decrease in the atomic number by 1; in β+\beta^+ decay, a positron and neutrino are emitted, while electron capture involves an inner-shell electron combining with a proton to form a neutron and emitting a neutrino. These modes are prevalent in proton-rich nuclei lighter than bismuth. Gamma decay involves the emission of a high-energy from an excited nucleus, with no alteration to the mass number or , as it merely releases excess energy without changing the nuclear composition. This often follows other decay modes to de-excite the daughter nucleus. For instance, an excited nucleus decays to its : 2760Co∗→2760Co+γ^{60}_{27}\mathrm{Co}^* \to ^{60}_{27}\mathrm{Co} + \gamma. In decay chains, such as the series, alpha decays progressively reduce the mass number by 4 in each step, interspersed with beta decays that preserve AA, ultimately leading to stable lead-206 after 14 decays (8 alpha and 6 beta). This stepwise reduction illustrates how mass number evolves toward stability in heavy-element series.

Nuclear Reactions

In nuclear reactions, the mass number AA, defined as the total number of protons and neutrons in a nucleus, is strictly conserved, reflecting the preservation of under the strong . This conservation principle ensures that the sum of the mass numbers of all reactants equals that of all products in any induced nuclear process, distinguishing it from - equivalence where slight differences in atomic masses contribute to the reaction's energy release via the Q-value, calculated as Q=(∑mreactants−∑mproducts)c2Q = (\sum m_{\text{reactants}} - \sum m_{\text{products}}) c^2, with the mass defect arising from differences while AA remains unchanged. Nuclear fission exemplifies this conservation in the induced splitting of a heavy nucleus. For instance, in the thermal neutron-induced fission of , the reaction 235U+n→^{235}\mathrm{U} + n \rightarrow fission fragments (e.g., one with A≈95A \approx 95 and another with A≈139A \approx 139) + 2-3 neutrons results in products whose total mass number sums to 236, matching the reactants' combined AA. This process, central to nuclear reactors and atomic bombs, releases energy from the mass defect but maintains AA balance, with the distribution of mass numbers among fragments typically peaking around asymmetric splits due to nuclear shell effects. In contrast, nuclear fusion combines light nuclei to form heavier ones, again conserving total AA. A key example is the deuterium-tritium reaction, 2H+3H→4He+n^2\mathrm{H} + ^3\mathrm{H} \rightarrow ^4\mathrm{He} + n, where the reactants' total A=5A = 5 equals the products' A=5A = 5, powering stars through sequential fusions that progressively build elements up to iron (mass number around 56) in stellar cores via processes like the proton-proton chain or CNO cycle. Neutron capture reactions further illustrate AA alteration at the individual nucleus level: in 59Co+n→60Co+γ^{59}\mathrm{Co} + n \rightarrow ^{60}\mathrm{Co} + \gamma, the target's mass number increases by 1 as the neutron is incorporated, a process vital for producing isotopes like cobalt-60 used in medicine and contributing to the rapid buildup of heavier elements in stellar nucleosynthesis.

References

  1. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_Chemistry_-_The_Central_Science_%28Brown_et_al.%29/02:_Atoms_Molecules_and_Ions/2.04:_The_Atomic_Theory_of_Matter
  2. https://www.khanacademy.org/science/chemistry/atomic-structure-and-properties/introduction-to-the-atom/a/atomic-number-atomic-mass-and-isotopes-article
  3. https://www.isotopesmatter.com/lessons/glossary.html
  4. https://goldbook.iupac.org/terms/view/M03726
  5. https://www2.lbl.gov/abc/wallchart/glossary/glossary.html
  6. https://www.isotopes.gov/isotope-basics
  7. https://iupac.org/wp-content/uploads/2025/03/IUPAC-GB4Abridged.pdf
  8. https://iupac.org/wp-content/uploads/2019/05/IUPAC-GB3-2012-2ndPrinting-PDFsearchable.pdf
  9. https://goldbook.iupac.org/terms/view/I03331
  10. https://iupac.org/wp-content/uploads/2015/02/IPTEI_postprint_20190301.pdf
  11. https://iupac.org/wp-content/uploads/2018/02/July11_supplement_hi_res.pdf
  12. https://iupac.org/cms/wp-content/uploads/2016/04/Guidelines-for-the-use-of-atomic-weights.pdf
  13. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_(Morsch_et_al.)/11%3A_Reactions_of_Alkyl_Halides-_Nucleophilic_Substitutions_and_Eliminations/11.08%3A_The_E2_Reaction_and_the_Deuterium_Isotope_Effect
  14. https://pmc.ncbi.nlm.nih.gov/articles/PMC7561496/
  15. https://pubs.rsc.org/en/content/articlehtml/1998/dt/a804629h
  16. https://iupac.qmul.ac.uk/BlueBook/PDF/P8.pdf
  17. https://www.ciaaw.org/carbon.htm
  18. https://pmc.ncbi.nlm.nih.gov/articles/PMC3679491/
  19. https://goldbook.iupac.org/terms/view/U06554
  20. https://physics.bu.edu/~duffy/sc546_notes10/mass_defect.html
  21. https://www.chem.purdue.edu/gchelp/howtosolveit/Nuclear/nuclear_binding_energy.htm
  22. http://physics.bu.edu/~duffy/sc546_notes10/mass_defect.html
  23. https://www.nist.gov/pml/atomic-weights-and-isotopic-compositions-relative-atomic-masses
  24. https://www.chem.ualberta.ca/~massspec/atomic_mass_abund.pdf
  25. https://goldbook.iupac.org/terms/view/R05258
  26. https://www.ciaaw.org/chlorine.htm
  27. https://ciaaw.org/historical-atomic-weights.htm
  28. https://physics.bu.edu/~duffy/py106/Radioactivity.html
  29. https://www2.lbl.gov/abc/wallchart/chapters/03/0.html
  30. https://www2.lbl.gov/abc/wallchart/chapters/03/1.html
  31. https://users.highland.edu/~jsullivan/genchem/s15_nuclear_rxns.html
  32. https://www2.lbl.gov/abc/wallchart/chapters/03/2.html
  33. http://ch302.cm.utexas.edu/nuclear/radioactivity/selector.php?name=decay-type
  34. https://www.ncbi.nlm.nih.gov/books/NBK585729/
  35. https://wou.edu/chemistry/courses/online-chemistry-textbooks/ch103-allied-health-chemistry/ch103-chapter-3-radioactivity/
  36. https://open.byu.edu/chem_101/vytpchylxq
  37. https://www4.uwsp.edu/physastr/kmenning/fendt/phen/decaychains_en.htm
  38. https://www-pub.iaea.org/MTCD/Publications/PDF/te_1506_web.pdf
  39. https://www.iaea.org/sites/default/files/gc/gc50inf-3-att6_en.pdf
  40. https://www-pub.iaea.org/MTCD/Publications/PDF/te_1168_prn.pdf
  41. https://inis.iaea.org/collection/NCLCollectionStore/_Public/37/086/37086874.pdf
  42. https://www.energy.gov/science/doe-explainsdeuterium-tritium-fusion-fuel
  43. https://ntrs.nasa.gov/api/citations/20040085477/downloads/20040085477.pdf
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.