Hubbry Logo
Minimum spanning treeMinimum spanning treeMain
Open search
Minimum spanning tree
Community hub
Minimum spanning tree
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Minimum spanning tree
Minimum spanning tree
Minimum spanning tree
View on Wikipedia
from Wikipedia

A planar graph and its minimum spanning tree. Each edge is labeled with its weight, which here is roughly proportional to its length.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.[1] That is, it is a spanning tree whose sum of edge weights is as small as possible.[2] More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

There are many use cases for minimum spanning trees. One example is a telecommunications company trying to lay cable in a new neighborhood. If it is constrained to bury the cable only along certain paths (e.g. roads), then there would be a graph containing the points (e.g. houses) connected by those paths. Some of the paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. Currency is an acceptable unit for edge weight – there is no requirement for edge lengths to obey normal rules of geometry such as the triangle inequality. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects every house; there might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost, representing the least expensive path for laying the cable.

Properties

[edit]

Possible multiplicity

[edit]

If there are n vertices in the graph, then each spanning tree has n − 1 edges.

This figure shows there may be more than one minimum spanning tree in a graph. In the figure, the two trees below the graph are two possibilities of minimum spanning tree of the given graph.

There may be several minimum spanning trees of the same weight; in particular, if all the edge weights of a given graph are the same, then every spanning tree of that graph is minimum.

Uniqueness

[edit]

If each edge has a distinct weight then there will be only one, unique minimum spanning tree. This is true in many realistic situations, such as the telecommunications company example above, where it's unlikely any two paths have exactly the same cost. This generalizes to spanning forests as well.

Proof:

  1. Assume the contrary, that there are two different MSTs A and B.
  2. Since A and B differ despite containing the same nodes, there is at least one edge that belongs to one but not the other. Among such edges, let e1 be the one with least weight; this choice is unique because the edge weights are all distinct. Without loss of generality, assume e1 is in A.
  3. As B is an MST, {e1} ∪ B must contain a cycle C with e1.
  4. As a tree, A contains no cycles, therefore C must have an edge e2 that is not in A.
  5. Since e1 was chosen as the unique lowest-weight edge among those belonging to exactly one of A and B, the weight of e2 must be greater than the weight of e1.
  6. As e1 and e2 are part of the cycle C, replacing e2 with e1 in B therefore yields a spanning tree with a smaller weight.
  7. This contradicts the assumption that B is an MST.

More generally, if the edge weights are not all distinct then only the (multi-)set of weights in minimum spanning trees is certain to be unique; it is the same for all minimum spanning trees.[3]

Minimum-cost subgraph

[edit]

If the weights are positive, then a minimum spanning tree is, in fact, a minimum-cost subgraph connecting all vertices, since if a subgraph contains a cycle, removing any edge along that cycle will decrease its cost and preserve connectivity.

Cycle property

[edit]

For any cycle C in the graph, if the weight of an edge e of C is larger than any of the individual weights of all other edges of C, then this edge cannot belong to an MST.

Proof: Assume the contrary, i.e. that e belongs to an MST T1. Then deleting e will break T1 into two subtrees with the two ends of e in different subtrees. The remainder of C reconnects the subtrees, hence there is an edge f of C with ends in different subtrees, i.e., it reconnects the subtrees into a tree T2 with weight less than that of T1, because the weight of f is less than the weight of e.

Cut property

[edit]
This figure shows the cut property of MSTs. T is the only MST of the given graph. If S = {A,B,D,E}, thus V – S = {C,F}, then there are 3 possibilities of the edge across the cut (S, V – S), they are edges BC, EC, EF of the original graph. Then, e is one of the minimum-weight-edge for the cut, therefore S ∪ {e} is part of the MST T.

For any cut C of the graph, if the weight of an edge e in the cut-set of C is strictly smaller than the weights of all other edges of the cut-set of C, then this edge belongs to all MSTs of the graph.

Proof: Assume that there is an MST T that does not contain e. Adding e to T will produce a cycle, that crosses the cut once at e and crosses back at another edge e'. Deleting e' we get a spanning tree T∖{e' } ∪ {e} of strictly smaller weight than T. This contradicts the assumption that T was a MST.

By a similar argument, if more than one edge is of minimum weight across a cut, then each such edge is contained in some minimum spanning tree.

Minimum-cost edge

[edit]

If the minimum cost edge e of a graph is unique, then this edge is included in any MST.

Proof: if e was not included in the MST, removing any of the (larger cost) edges in the cycle formed after adding e to the MST, would yield a spanning tree of smaller weight.

Contraction

[edit]

If T is a tree of MST edges, then we can contract T into a single vertex while maintaining the invariant that the MST of the contracted graph plus T gives the MST for the graph before contraction.[4]

Algorithms

[edit]

In all of the algorithms below, m is the number of edges in the graph and n is the number of vertices.

Classic algorithms

[edit]

The first algorithm for finding a minimum spanning tree was developed by Czech scientist Otakar Borůvka in 1926 (see Borůvka's algorithm). Its purpose was an efficient electrical coverage of Moravia. The algorithm proceeds in a sequence of stages. In each stage, called Boruvka step, it identifies a forest F consisting of the minimum-weight edge incident to each vertex in the graph G, then forms the graph G1 = G \ F as the input to the next step. Here G \ F denotes the graph derived from G by contracting edges in F (by the Cut property, these edges belong to the MST). Each Boruvka step takes linear time. Since the number of vertices is reduced by at least half in each step, Boruvka's algorithm takes O(m log n) time.[4]

A second algorithm is Prim's algorithm, which was invented by Vojtěch Jarník in 1930 and rediscovered by Prim in 1957 and Dijkstra in 1959. Basically, it grows the MST (T) one edge at a time. Initially, T contains an arbitrary vertex. In each step, T is augmented with a least-weight edge (x,y) such that x is in T and y is not yet in T. By the Cut property, all edges added to T are in the MST. Its run-time is either O(m log n) or O(m + n log n), depending on the data-structures used.

A third algorithm commonly in use is Kruskal's algorithm, which also takes O(m log n) time.

A fourth algorithm, not as commonly used, is the reverse-delete algorithm, which is the reverse of Kruskal's algorithm. Its runtime is O(m log n (log log n)3).

All four of these are greedy algorithms. Since they run in polynomial time, the problem of finding such trees is in FP, and related decision problems such as determining whether a particular edge is in the MST or determining if the minimum total weight exceeds a certain value are in P.

Faster algorithms

[edit]

Several researchers have tried to find more computationally-efficient algorithms.

In a comparison model, in which the only allowed operations on edge weights are pairwise comparisons, Karger, Klein & Tarjan (1995) found a linear time randomized algorithm based on a combination of Borůvka's algorithm and the reverse-delete algorithm.[5][6]

The fastest non-randomized comparison-based algorithm with known complexity, by Bernard Chazelle, is based on the soft heap, an approximate priority queue.[7][8] Its running time is O(m α(m,n)), where α is the classical functional inverse of the Ackermann function. The function α grows extremely slowly, so that for all practical purposes it may be considered a constant no greater than 4; thus Chazelle's algorithm takes very close to linear time.

Linear-time algorithms in special cases

[edit]

Dense graphs

[edit]

If the graph is dense (i.e. m/n ≥ log log log n), then a deterministic algorithm by Fredman and Tarjan finds the MST in time O(m).[9] The algorithm executes a number of phases. Each phase executes Prim's algorithm many times, each for a limited number of steps. The run-time of each phase is O(m + n). If the number of vertices before a phase is n', the number of vertices remaining after a phase is at most . Hence, at most log*n phases are needed, which gives a linear run-time for dense graphs.[4]

There are other algorithms that work in linear time on dense graphs.[7][10]

Integer weights

[edit]

If the edge weights are integers represented in binary, then deterministic algorithms are known that solve the problem in O(m + n) integer operations.[11] Whether the problem can be solved deterministically for a general graph in linear time by a comparison-based algorithm remains an open question.

Planar graphs

[edit]

Deterministic algorithms are known that solve the problem for planar graphs in linear time.[12][13] By the Euler characteristic of planar graphs, m ≤ 3n - 6 ∈ O(n), so this is in time O(n).

Decision trees

[edit]

Given graph G where the nodes and edges are fixed but the weights are unknown, it is possible to construct a binary decision tree (DT) for calculating the MST for any permutation of weights. Each internal node of the DT contains a comparison between two edges, e.g. "Is the weight of the edge between x and y larger than the weight of the edge between w and z?". The two children of the node correspond to the two possible answers "yes" or "no". In each leaf of the DT, there is a list of edges from G that correspond to an MST. The runtime complexity of a DT is the largest number of queries required to find the MST, which is just the depth of the DT. A DT for a graph G is called optimal if it has the smallest depth of all correct DTs for G.

For every integer r, it is possible to find optimal decision trees for all graphs on r vertices by brute-force search. This search proceeds in two steps.

A. Generating all potential DTs

  • There are different graphs on r vertices.
  • For each graph, an MST can always be found using r(r − 1) comparisons, e.g. by Prim's algorithm.
  • Hence, the depth of an optimal DT is less than r2.
  • Hence, the number of internal nodes in an optimal DT is less than .
  • Every internal node compares two edges. The number of edges is at most r2 so the different number of comparisons is at most r4.
  • Hence, the number of potential DTs is less than

B. Identifying the correct DTs To check if a DT is correct, it should be checked on all possible permutations of the edge weights.

  • The number of such permutations is at most (r2)!.
  • For each permutation, solve the MST problem on the given graph using any existing algorithm, and compare the result to the answer given by the DT.
  • The running time of any MST algorithm is at most r2, so the total time required to check all permutations is at most (r2 + 1)!.

Hence, the total time required for finding an optimal DT for all graphs with r vertices is:[4]

which is less than

See also: Decision tree model

Optimal algorithm

[edit]

Seth Pettie and Vijaya Ramachandran have found a provably optimal deterministic comparison-based minimum spanning tree algorithm.[4] The following is a simplified description of the algorithm.

  1. Let r = log log log n, where n is the number of vertices. Find all optimal decision trees on r vertices. This can be done in time O(n) (see Decision trees above).
  2. Partition the graph to components with at most r vertices in each component. This partition uses a soft heap, which "corrupts" a small number of the edges of the graph.
  3. Use the optimal decision trees to find an MST for the uncorrupted subgraph within each component.
  4. Contract each connected component spanned by the MSTs to a single vertex, and apply any algorithm which works on dense graphs in time O(m) to the contraction of the uncorrupted subgraph
  5. Add back the corrupted edges to the resulting forest to form a subgraph guaranteed to contain the minimum spanning tree, and smaller by a constant factor than the starting graph. Apply the optimal algorithm recursively to this graph.

The runtime of all steps in the algorithm is O(m), except for the step of using the decision trees. The runtime of this step is unknown, but it has been proved that it is optimal - no algorithm can do better than the optimal decision tree. Thus, this algorithm has the peculiar property that it is provably optimal although its runtime complexity is unknown.

Parallel and distributed algorithms

[edit]
Further information: Parallel algorithms for minimum spanning trees

Research has also considered parallel algorithms for the minimum spanning tree problem. With a linear number of processors it is possible to solve the problem in O(log n) time.[14][15]

The problem can also be approached in a distributed manner. If each node is considered a computer and no node knows anything except its own connected links, one can still calculate the distributed minimum spanning tree.

MST on complete graphs with random weights

[edit]

Alan M. Frieze showed that given a complete graph on n vertices, with edge weights that are independent identically distributed random variables with distribution function satisfying , then as n approaches +∞ the expected weight of the MST approaches , where is the Riemann zeta function (more specifically is Apéry's constant). Frieze and Steele also proved convergence in probability. Svante Janson proved a central limit theorem for weight of the MST.

For uniform random weights in , the exact expected size of the minimum spanning tree has been computed for small complete graphs.[16]

Vertices Expected size Approximate expected size
2
⁠1/2⁠
 0.5
3
⁠3/4⁠
 0.75
4
⁠31/35⁠
 0.8857143
5
⁠893/924⁠
 0.9664502
6
⁠278/273⁠
 1.0183151
7
⁠30739/29172⁠
 1.053716
8
⁠199462271/184848378⁠
 1.0790588
9
⁠126510063932/115228853025⁠
 1.0979027

Fractional variant

[edit]

There is a fractional variant of the MST, in which each edge is allowed to appear "fractionally". Formally, a fractional spanning set of a graph (V,E) is a nonnegative function f on E such that, for every non-trivial subset W of V (i.e., W is neither empty nor equal to V), the sum of f(e) over all edges connecting a node of W with a node of V\W is at least 1. Intuitively, f(e) represents the fraction of e that is contained in the spanning set. A minimum fractional spanning set is a fractional spanning set for which the sum is as small as possible.

If the fractions f(e) are forced to be in {0,1}, then the set T of edges with f(e)=1 are a spanning set, as every node or subset of nodes is connected to the rest of the graph by at least one edge of T. Moreover, if f minimizes, then the resulting spanning set is necessarily a tree, since if it contained a cycle, then an edge could be removed without affecting the spanning condition. So the minimum fractional spanning set problem is a relaxation of the MST problem, and can also be called the fractional MST problem.

The fractional MST problem can be solved in polynomial time using the ellipsoid method.[17]: 248  However, if we add a requirement that f(e) must be half-integer (that is, f(e) must be in {0, 1/2, 1}), then the problem becomes NP-hard,[17]: 248  since it includes as a special case the Hamiltonian cycle problem: in an -vertex unweighted graph, a half-integer MST of weight can only be obtained by assigning weight 1/2 to each edge of a Hamiltonian cycle.

Other variants

[edit]
Minimum Steiner trees of vertices of regular polygons with N = 3 to 8 sides. The lowest network length L for N > 5 is the circumference less one side. Squares represent Steiner points.
  • The Steiner tree of a subset of the vertices is the minimum tree that spans the given subset. Finding the Steiner tree is NP-complete.[18]
  • The k-minimum spanning tree (k-MST) is the tree that spans some subset of k vertices in the graph with minimum weight.
  • A set of k-smallest spanning trees is a subset of k spanning trees (out of all possible spanning trees) such that no spanning tree outside the subset has smaller weight.[19][20][21] (Note that this problem is unrelated to the k-minimum spanning tree.)
  • The Euclidean minimum spanning tree is a spanning tree of a graph with edge weights corresponding to the Euclidean distance between vertices which are points in the plane (or space).
  • The rectilinear minimum spanning tree is a spanning tree of a graph with edge weights corresponding to the rectilinear distance between vertices which are points in the plane (or space).
  • The distributed minimum spanning tree is an extension of MST to the distributed model, where each node is considered a computer and no node knows anything except its own connected links. The mathematical definition of the problem is the same but there are different approaches for a solution.
  • The capacitated minimum spanning tree is a tree that has a marked node (origin, or root) and each of the subtrees attached to the node contains no more than c nodes. c is called a tree capacity. Solving CMST optimally is NP-hard,[22] but good heuristics such as Esau-Williams and Sharma produce solutions close to optimal in polynomial time.
  • The degree-constrained minimum spanning tree is a MST in which each vertex is connected to no more than d other vertices, for some given number d. The case d = 2 is a special case of the traveling salesman problem, so the degree constrained minimum spanning tree is NP-hard in general.
  • An arborescence is a variant of MST for directed graphs. It can be solved in time using the Chu–Liu/Edmonds algorithm.
  • A maximum spanning tree is a spanning tree with weight greater than or equal to the weight of every other spanning tree. Such a tree can be found with algorithms such as Prim's or Kruskal's after multiplying the edge weights by −1 and solving the MST problem on the new graph. A path in the maximum spanning tree is the widest path in the graph between its two endpoints: among all possible paths, it maximizes the weight of the minimum-weight edge.[23] Maximum spanning trees find applications in parsing algorithms for natural languages[24] and in training algorithms for conditional random fields.
  • The dynamic MST problem concerns the update of a previously computed MST after an edge weight change in the original graph or the insertion/deletion of a vertex.[25][26][27]
  • The minimum labeling spanning tree problem is to find a spanning tree with least types of labels if each edge in a graph is associated with a label from a finite label set instead of a weight.[28]
  • A bottleneck edge is the highest weighted edge in a spanning tree. A spanning tree is a minimum bottleneck spanning tree (or MBST) if the graph does not contain a spanning tree with a smaller bottleneck edge weight. A MST is necessarily a MBST (provable by the cut property), but a MBST is not necessarily a MST.[29][30]
  • A minimum-cost spanning tree game is a cooperative game in which the players have to share among them the costs of constructing the optimal spanning tree.
  • The optimal network design problem is the problem of computing a set, subject to a budget constraint, which contains a spanning tree, such that the sum of shortest paths between every pair of nodes is as small as possible.

Applications

[edit]

Minimum spanning trees have direct applications in the design of networks, including computer networks, telecommunications networks, transportation networks, water supply networks, and electrical grids (which they were first invented for, as mentioned above).[31] They are invoked as subroutines in algorithms for other problems, including the Christofides algorithm for approximating the traveling salesman problem,[32] approximating the multi-terminal minimum cut problem (which is equivalent in the single-terminal case to the maximum flow problem),[33] and approximating the minimum-cost weighted perfect matching.[34]

Other practical applications based on minimal spanning trees include:

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Minimum spanning tree

View on Grokipedia
from Grokipedia
A minimum spanning tree (MST) of a connected, edge-weighted undirected graph is a of the edges that connects all vertices without forming cycles and has the minimum total edge weight among all possible spanning trees. This structure ensures the graph remains connected while minimizing the sum of edge weights, making it fundamental in optimization problems where cost or distance must be reduced. The minimum spanning tree problem was first addressed in 1926 by Otakar Borůvka with a greedy algorithm for constructing such trees. It was independently rediscovered in the mid-20th century by Joseph Kruskal, who described an algorithm in 1956 that sorts edges by weight and adds the smallest non-cycle-forming edges until all vertices are connected, and by Robert C. Prim, who proposed a related method in 1957, starting from an arbitrary vertex and iteratively adding the minimum-weight edge connecting a new vertex to the growing tree. Both Kruskal's and Prim's algorithms run in O(E log E) or O(E log V) time complexity, where E is the number of edges and V is the number of vertices, using union-find data structures for cycle detection in Kruskal's case or priority queues in Prim's. MSTs exhibit key properties that guarantee their optimality, such as the cut property: for any cut partitioning the graph, the minimum-weight crossing edge belongs to some MST. If all edge weights are distinct, the MST is unique; otherwise, multiple MSTs may exist. These properties enable polynomial-time solutions, distinguishing MSTs from harder problems like the traveling salesman problem, which Kruskal also connected to spanning trees in his original work. Applications of MSTs span network design, where they minimize wiring or routing costs in , transportation, and computer systems; data clustering, by treating distances as edge weights to group similar points; and approximation algorithms for problems like facility location or . For instance, in planning, MSTs optimize connections between power stations to reduce total cable length.

Definition and Background

Formal Definition

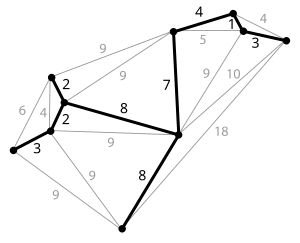
In , a of a connected undirected graph G=(V,E)G = (V, E) is a subgraph that includes all vertices in VV and is both connected and acyclic, necessarily containing exactly ∣V∣−1|V| - 1 edges. A minimum spanning tree (MST) of a connected, undirected, edge-weighted graph G=(V,E)G = (V, E) with edge weights w(e)w(e) for each edge e∈Ee \in E is a T⊆ET \subseteq E whose total weight ∑e∈Tw(e)\sum_{e \in T} w(e) is minimized among all possible spanning trees of GG. To illustrate, consider a simple connected undirected graph with four vertices V={A,B,C,D}V = \{A, B, C, D\} and five weighted edges: A−BA-B with weight 1, A−CA-C with weight 2, B−CB-C with weight 3, B−DB-D with weight 4, and C−DC-D with weight 1. One possible MST consists of the edges A−BA-B (weight 1), A−CA-C (weight 2), and C−DC-D (weight 1); this subgraph connects all four vertices without cycles and has a total weight of 4, which is minimal.

Graph Theory Prerequisites

In , an undirected graph GG is formally defined as a pair (V,E)(V, E), where VV is a of vertices (also called nodes) and EE is a set of edges, each edge being an unordered pair of distinct vertices from VV. This structure models symmetric relationships, such as mutual connections between entities, without implying direction. Connectivity in an undirected graph refers to the existence of a path—a sequence of adjacent edges—between any pair of vertices; a graph is connected if such paths exist for every pair. Many applications of undirected graphs involve weights assigned to edges to represent costs, distances, or capacities, forming a weighted undirected graph where each edge e∈Ee \in E has a weight w(e)w(e). Weights are often non-negative in contexts like network design. If a graph is not connected, it decomposes into two or more connected components, each being a maximal connected subgraph; isolated vertices form singleton components. For a minimum spanning tree to exist and span all vertices, the graph must be connected, as disconnected components cannot be linked without additional edges. A is a connected undirected graph that contains no cycles and thus has exactly ∣V∣−1|V| - 1 edges, where ∣V∣|V| denotes the number of vertices. This minimal connectivity ensures a unique path between any pair of vertices. A of a connected undirected graph G=(V,E)G = (V, E) is a subgraph that is a and includes every vertex in VV, effectively providing a skeletal structure of GG without redundancy. A cycle in an undirected graph is a closed path where the starting and ending vertices are the same, and no other vertices repeat, forming a loop of at least three edges. Cycles introduce redundancy in connectivity, distinguishing them from trees. A cut, or edge cut, arises from a partition of the vertex set VV into two nonempty subsets SS and V∖SV \setminus S; the edges with one endpoint in SS and the other in V∖SV \setminus S form the cutset, representing the connections across the partition. These concepts underpin the structure of spanning trees, where avoiding cycles while crossing necessary cuts ensures full connectivity.

Fundamental Properties

Existence, Uniqueness, and Multiplicity

In any connected, undirected graph with real-valued edge weights (typically assumed non-negative), a minimum spanning (MST) exists. This follows from the non-emptiness of the set of spanning trees in a connected graph and the finiteness of this set, ensuring that the total edge weights achieve a minimum value among them. One proceeds inductively: begin with a single vertex as a trivial MST, then repeatedly add the minimum-weight edge connecting a new vertex to the current without forming a cycle, leveraging the cut to guarantee optimality at each step. This greedy approach aligns with the existence guaranteed by the optimization over the compact set of spanning trees. The uniqueness of an MST depends on the edge weights. If all edge weights in the graph are distinct, then there is exactly one MST. To see this, suppose there are two distinct MSTs TT and T′T'. Consider an edge ee of minimum weight in the TΔT′T \Delta T', and assume e∈Te \in T but e∉T′e \notin T'. The unique path in T′T' between the endpoints of ee must contain some edge ff with weight strictly greater than that of ee (due to distinct weights). Replacing ff with ee in T′T' yields a with lower total weight, contradicting the minimality of T′T'. Thus, no such distinct MSTs can exist. When edge weights are not all distinct, multiple MSTs may exist, all sharing the same minimum total weight but differing in their edge sets. For instance, consider a cycle graph on four vertices a,b,c,da, b, c, d with all edges of equal weight 1; the MSTs are any three edges forming a path (e.g., aa-bb-cc-dd or aa-dd-cc-bb), each with total weight 3, while including all four edges would create a cycle. In general, multiplicity arises when there are ties in weights that allow alternative edge selections without increasing the total cost, as seen in graphs with symmetric structures or equal-weight parallel options.

Cycle Property

The cycle property of minimum spanning trees states that, for any cycle CC in an undirected connected weighted graph GG, the edge ff with the maximum weight in CC cannot belong to any minimum spanning tree (MST) of GG. This property holds under the simplifying assumption that all edge weights in GG are distinct, which ensures uniqueness in comparisons for the general case. To prove this, assume for contradiction that some MST T∗T^* of GG contains the maximum-weight edge ff from cycle CC. Removing ff from T∗T^* disconnects the graph into two components, defining a cut (S,V−S)(S, V - S) where SS is one component and V−SV - S is the other. Since ff crosses this cut and also lies on cycle CC, there must exist another edge ee in CC that also crosses the cut (as CC connects vertices on ). The spanning tree T′=T∗∪{e}∖{f}T' = T^* \cup \{e\} \setminus \{f\} connects all vertices and has no cycles, so T′T' is also a spanning tree. Moreover, since ee has strictly lower weight than ff (by the choice of ff), the total weight of T′T' is less than that of T∗T^*, contradicting the minimality of T∗T^*. Thus, no MST can include ff. A direct of the cycle property is that every MST of GG is acyclic, reinforcing its tree structure: if an MST contained a cycle, its maximum-weight edge would violate the property, leading to a contradiction. For illustration, consider a simple with three vertices AA, BB, and CC, and edges ABAB with 1, BCBC with 2, and CACA with 3. The unique MST is the tree {AB,BC}\{AB, BC\} with total 3. The {AB,CA}\{AB, CA\} has total 4, which is not minimum. CA cannot be part of any MST, as it is the heaviest edge in the cycle, and its inclusion would allow replacement by the lighter BCBC to reduce the total without disconnecting the graph.

Cut Property

The cut property states that, in a connected undirected graph G=(V,E)G = (V, E) with nonnegative edge weights w:E→Rw: E \to \mathbb{R}, for any partition of the vertex set into two nonempty disjoint subsets S⊆VS \subseteq V and V∖SV \setminus S, if ee is a minimum-weight edge with one endpoint in SS and the other in V∖SV \setminus S, then ee belongs to some minimum spanning tree of GG. If all edge weights in GG are distinct, then ee belongs to every minimum spanning tree of GG. To prove the cut property, consider an arbitrary minimum spanning tree TT of GG. If TT already contains ee, the property holds. Otherwise, add ee to TT, forming a cycle CC. Since ee crosses the cut (S,V∖S)(S, V \setminus S), CC must contain at least one other edge ff that also crosses the cut (as cycles cross cuts an even number of times). The edge ff has weight w(f)≥w(e)w(f) \geq w(e), so the graph T′=T∪{e}∖{f}T' = T \cup \{e\} \setminus \{f\} is a spanning tree with total weight at most that of TT. Thus, T′T' is also a minimum spanning tree containing ee. If weights are distinct, then w(f)>w(e)w(f) > w(e), so any MST excluding ee can be improved by this exchange, implying ee is in every MST. This property holds even if multiple edges share the minimum crossing weight; any such edge can be included in some MST without increasing the total weight. For example, consider a graph with vertices A,B,C,DA, B, C, D and edges ABAB (weight 1), CDCD (weight 2), ACAC (weight 3), BDBD (weight 4), ADAD (weight 5), BCBC (weight 6). For the cut S={A,B}S = \{A, B\} and V∖S={C,D}V \setminus S = \{C, D\}, the crossing edges are ACAC (3), ADAD (5), BCBC (6), BDBD (4); the minimum-weight crossing edge is ACAC (3). One MST is {AB,AC,CD}\{AB, AC, CD\} with total weight 6, which includes ACAC.

Proof Techniques and Equivalences

Contraction

In , the contraction of an edge e=(u,v)e = (u, v) in an undirected, edge-weighted graph G=(V,E,w)G = (V, E, w) merges the vertices uu and vv into a single supernode, denoted as uvuv, such that all edges originally incident to uu or vv (except ee itself) become incident to uvuv; any resulting self-loops are removed, and for any pair of supernodes with multiple parallel edges, only the minimum-weight edge is retained. This operation reduces the number of vertices by one while preserving the connectivity and relative weights of the remaining edges. Contracting an edge that belongs to some minimum spanning tree (MST) of GG maintains key structural properties of the MST in the resulting contracted graph G′G', ensuring that the minimum spanning forest of G′G' corresponds to a partial MST of GG. Specifically, if FF is a forest consisting of edges from an MST of GG, contracting the edges in FF yields a graph where the supernodes represent the connected components induced by FF, and the MST of this contracted graph can be expanded to complete an MST of the original graph. In algorithmic contexts, contraction serves as a reduction technique for constructing MSTs by iteratively identifying and contracting "safe" edges—those that appear in some MST—thereby simplifying the graph while building the MST incrementally from the contracted edges. This process ensures that the final MST is formed by the union of all contracted edges, as each contraction step preserves the optimality invariant. A fundamental theorem underpinning this approach states that if TT is a forest in GG and G′G' is obtained by contracting all edges in TT, then combining TT with any MST T′T' of G′G' (expanded by restoring the supernodes in TT) yields an MST of GG. This equivalence holds because contraction does not introduce new cycles or alter the minimum weights across cuts in a way that violates MST optimality.

Minimum-Cost Edge and Subgraph

A minimum spanning tree (MST) of a connected, edge-weighted undirected graph G=(V,E)G = (V, E) with nonnegative edge weights is not only the minimum-weight spanning tree but also the minimum-weight connected spanning subgraph of GG. That is, among all subgraphs of GG that connect every pair of vertices in VV, the total edge weight of an MST is the smallest possible. This property underscores that adding extra edges to an MST can only increase or maintain the total cost, but never decrease it below that of the MST. To see why, consider any connected spanning subgraph HH of GG. If HH is acyclic (i.e., a tree), then by the definition of an MST, the weight of HH is at least that of the MST TT. If HH contains cycles, repeatedly apply the cycle property: in any cycle of HH, remove the maximum-weight edge, which disconnects no component since the remaining path connects the endpoints. Each such removal yields a connected spanning subgraph of equal or strictly lower weight (if the removed edge had positive weight). Continuing until HH becomes acyclic produces a spanning tree whose weight is at most that of the original HH. Since TT is an MST, its weight is no greater than that of this derived tree, and thus no greater than that of HH. A key is that the minimum-weight edge in GG belongs to some MST of GG. This follows as a special case of the cut property: let e=(u,v)e = (u, v) be the minimum-weight edge in GG, and consider the cut ({u},V∖{u})(\{u\}, V \setminus \{u\}). Then ee is the minimum-weight edge crossing this cut (as it is the global minimum), so ee lies on some MST. This implies that solving for an MST yields the optimal solution not just among trees but over the broader class of all connected spanning subgraphs, justifying the focus on structures in algorithms for this problem.

Decision Tree Characterization

In the comparison-based model for solving the minimum spanning tree (MST) problem, the decision tree represents an algorithm's query process as a structure. Each internal node corresponds to a between the weights of two specific edges in the graph, with the two branches representing the outcomes: one where the weight of the first edge is less than the second, and the other where it is greater (assuming distinct weights for simplicity). The leaves of the tree each specify a particular set of edges that form the MST, consistent with the sequence of comparison outcomes leading to that leaf. This model captures the information gained solely through weight comparisons, without assuming access to the actual numerical values. The structure of this provides a of the MST problem's query . The of the denotes the worst-case number of comparisons required to identify the MST. A key insight is that the number of leaves must be at least as large as the number of distinct possible MSTs in the graph, since each possible MST must be output for some assignment of edge weights consistent with the comparisons. Consequently, the height is bounded below by the base-2 logarithm of the number of possible MSTs, offering an information-theoretic lower bound on the comparisons needed. When the MST is unique for generic weight assignments, the decision tree has fewer paths, simplifying the query process. This characterization is leveraged to establish lower bounds on comparison-based MST algorithms. For instance, the number of possible MSTs implies that distinguishing among them requires sufficient comparisons, but tighter bounds arise from adversarial arguments. In particular, consider a with |E| edges; the MST excludes the unique heaviest edge, and identifying it demands Ω(|E|) comparisons in the worst case, as this reduces to finding the maximum among |E| unordered elements. Thus, any comparison-based MST algorithm requires Ω(|E|) comparisons in the worst case for general graphs. Chazelle formalized this by proving that the decision-tree complexity of the MST problem is Θ(|E| α(|E|, n)), where α is the inverse , and demonstrated an algorithm achieving this bound, thereby fully characterizing the problem's complexity in the comparison model.

Classic Algorithms

Kruskal's algorithm is a greedy method for computing a minimum spanning tree (MST) in a connected, undirected graph with non-negative edge weights. Introduced by Joseph B. Kruskal in , it constructs the MST by progressively adding the lightest edges that do not form cycles. The algorithm begins by sorting all edges in non-decreasing order of weight. It maintains a of trees, initially consisting of |V| singleton trees, one for each vertex. Using a disjoint-set (Union-Find) to track connected components, it iterates through the sorted edges: for each edge (u, v) with weight w, if u and v belong to different components, the edge is added to the forest and the components are merged via union operation. This process continues until the forest contains a single tree spanning all vertices. via the find operation ensures no redundant edges are included. Here is the pseudocode for Kruskal's algorithm:

function Kruskal(G = (V, E), w): MST = empty set for each vertex v in V: make-set(v) // Initialize Union-Find sort E by increasing w(e) for each edge e = (u, v) in sorted E: if find(u) ≠ find(v): MST = MST ∪ {e} union(u, v) return MST

function Kruskal(G = (V, E), w): MST = empty set for each vertex v in V: make-set(v) // Initialize Union-Find sort E by increasing w(e) for each edge e = (u, v) in sorted E: if find(u) ≠ find(v): MST = MST ∪ {e} union(u, v) return MST

The Union-Find structure employs path compression and union by rank to achieve amortized nearly constant time per operation. The dominant cost is sorting the edges, yielding a time complexity of O(|E| log |E|), where |E| is the number of edges; the Union-Find operations add only O(|E| α(|V|)), with α being the slow-growing inverse Ackermann function, which is effectively constant for practical graph sizes. The correctness of follows from the cut property of MSTs: for any cut of the graph, the minimum-weight edge crossing the cut can be safely included in some MST without loss of optimality. At each step, the current partitions the vertices into components, defining multiple cuts; the next candidate edge, being the globally smallest unused one, must be the minimum-weight crossing edge for the cut separating its endpoints' components, making it safe to add. If it connected the same component, it would violate the cycle property by forming a cycle with lighter edges already included. By induction, the final is an MST. To illustrate, consider a graph with vertices {A, B, C, D} and edges AB (weight 2), AC (3), BC (1), BD (4), AD (6), CD (5). The edges sorted by weight are: BC (1), AB (2), AC (3), BD (4), CD (5), AD (6).
  • Start with components {A}, {B}, {C}, {D}.
  • Add BC (1): merges to {A}, {B,C}, {D}; MST weight = 1.
  • Add AB (2): B and A differ, merges to {A,B,C}, {D}; MST weight = 3.
  • Skip AC (3): A and C same component.
  • Add BD (4): B and D differ, merges to {A,B,C,D}; MST weight = 7.
  • Skip remaining edges: all vertices connected.
The resulting MST edges are BC, AB, BD with total weight 7.

Prim's Algorithm

Prim's algorithm is a greedy method for constructing a (MST) in a connected, undirected graph with weighted edges. Developed by Robert C. Prim, the algorithm begins with an arbitrary starting vertex and iteratively grows a by adding the minimum-weight edge that connects a vertex in the current tree to a vertex outside it. This process continues until all vertices are included, ensuring the result is an MST. The algorithm maintains a to track the minimum key (edge weight) for each vertex not yet in the , along with the parent vertex that provides this key. It starts by setting the key of the starting vertex to 0 and all others to , then repeatedly extracts the vertex with the minimum key, adds it to the , and relaxes (updates) the keys of its adjacent vertices if a cheaper connection is found. for using a generic is as follows:

PRIM(G, w, r) for each vertex u in G.V key[u] ← ∞ parent[u] ← NIL key[r] ← 0 create a priority queue Q containing all vertices in G.V while Q is not empty u ← EXTRACT-MIN(Q) for each vertex v adjacent to u if w(u, v) < key[v] key[v] ← w(u, v) parent[v] ← u DECREASE-KEY(Q, v, key[v]) return the tree defined by the parent array

PRIM(G, w, r) for each vertex u in G.V key[u] ← ∞ parent[u] ← NIL key[r] ← 0 create a priority queue Q containing all vertices in G.V while Q is not empty u ← EXTRACT-MIN(Q) for each vertex v adjacent to u if w(u, v) < key[v] key[v] ← w(u, v) parent[v] ← u DECREASE-KEY(Q, v, key[v]) return the tree defined by the parent array

This implementation relies on priority queue operations like extract-min, decrease-key, and insert. The time complexity depends on the priority queue implementation. With a binary heap, which supports extract-min in O(log |V|) and decrease-key in O(log |V|), the overall time is O(|E| log |V|), as there are O(|V|) extracts and up to O(|E|) decrease-keys. Using a , which amortizes decrease-key to O(1) and extract-min to O(log |V|), the time improves to O(|E| + |V| log |V|). Correctness follows from the cut property of MSTs: at each step, the edge added is the minimum-weight edge crossing the cut between the current tree and the remaining vertices, making it safe to include without violating optimality. By induction, the partial tree at every iteration is a minimum spanning forest for the vertices it spans. For example, consider a graph with vertices A, B, C, and D, and edges A-B (weight 2), A-C (3), B-C (1), B-D (4), C-D (1). Starting from A, the algorithm first adds A to the tree (key 0). It then selects the minimum edge A-B (weight 2), adding B. Next, from {A, B}, the minimum crossing edge is B-C (1), adding C. Finally, from {A, B, C}, the minimum is C-D (1), adding D. The resulting MST has edges A-B, B-C, C-D with total weight 4.

Borůvka's Algorithm

Borůvka's algorithm, introduced in 1926 by Czech mathematician Otakar Borůvka, provides an early solution to the minimum spanning tree problem, motivated by the design of efficient electrical networks for Moravia. This approach predates the more widely known Kruskal's and Prim's algorithms by several decades and represents a foundational contribution to combinatorial optimization. The algorithm operates in phases on a connected, undirected graph with weighted edges, starting with each vertex as its own connected component. In each phase, for every current component, the minimum-weight edge that connects it to any vertex outside the component is identified and selected. These selections occur simultaneously across all components, with each component choosing its cheapest outgoing edge independently; if an edge is the minimum outgoing for multiple components (such as both endpoints), it is still included only once. The selected edges are added to the spanning forest, connecting multiple components into larger ones. The newly connected components are then merged into single supervertices via contraction, and parallel edges between supervertices are handled appropriately (e.g., keeping the minimum weight if needed), with intra-super vertex edges discarded. The process repeats over multiple phases until only one component remains, yielding the minimum spanning tree. In cases of multiplicity, where multiple edges have the same minimum weight outgoing from a component, the algorithm selects an arbitrary one to ensure progress without affecting optimality. The correctness of Borůvka's algorithm follows from the cut property of minimum spanning trees: each selected edge is the lightest edge crossing the cut defined by its originating component and the rest of the graph, ensuring it belongs to some minimum spanning tree, and the contractions preserve the minimum spanning tree structure for the reduced graph. With respect to time complexity, the algorithm requires at most O(log⁡∣V∣)O(\log |V|) phases, as each phase reduces the number of components by at least half, and each phase can be implemented in O(∣E∣)O(|E|) time by scanning all edges to find the minimum outgoing edges for components. Thus, the overall running time is O(∣E∣log⁡∣V∣)O(|E| \log |V|).

Advanced Algorithms

Deterministic Improvements

The development of deterministic algorithms for computing minimum spanning trees (MSTs) has evolved significantly since the introduction of the classic methods in the mid-20th century, with key refinements emerging in the late 20th and early 21st centuries to achieve near-linear worst-case running times. Early algorithms, such as Kruskal's from 1956 and Prim's from 1957, achieved O(|E| log |E|) time using union-find structures and priority queues, but subsequent work focused on reducing the logarithmic factors through advanced data structures and filtering techniques. By the 1980s, researchers introduced sophisticated heap variants and decomposition methods to push complexities closer to linear, culminating in algorithms that incorporate the slowly growing inverse Ackermann function in the 2000s. Improvements to Kruskal's and Prim's algorithms often employ filtering techniques to eliminate edges unlikely to be in the MST without full sorting or exhaustive priority queue operations, thereby reducing the number of edges considered in subsequent steps. In Kruskal's context, filtering identifies and discards edges that violate the cycle property—those forming cycles with lower-weight edges already processed—allowing partial sorting or bucketing of the remaining candidate edges. For Prim's algorithm, similar filtering integrates with priority queues to prune high-weight incident edges early, leveraging cut properties to bound the search space. These techniques, while initially practical, have been formalized in theoretical frameworks to guarantee worst-case efficiency gains, often halving the effective edge set size in dense graphs. A landmark deterministic improvement is the algorithm by Gabow, Galil, Spencer, and Tarjan from 1986, which computes an MST in O(|E| log |V| / log log |V|) time for a graph with |V| vertices and |E| edges. This method combines Borůvka-style phase contractions with specialized Fibonacci-like heaps (F-heaps) that support efficient decrease-key and extract-min operations, enabling faster merging of components during union steps. The algorithm processes edges in logarithmic phases, using the heaps to select minimum crossing edges across cuts, and achieves its bound through amortized analysis of heap operations that minimize logarithmic overhead. This represents a substantial refinement over earlier O(|E| log |V|) implementations, particularly for sparse graphs where the denominator term provides asymptotic speedup. The most advanced deterministic MST algorithm, developed by Chazelle in 2000, runs in O(|E| \alpha(|V|)) time, where \alpha is the inverse Ackermann function, which grows slower than any iterated logarithm and is effectively constant for all practical graph sizes. This algorithm iterates Borůvka phases but uses soft heaps—an approximate priority queue allowing controlled errors in key values—to filter and contract components efficiently, ensuring errors do not propagate to the final MST. It builds on Borůvka phases with multilevel edge filtering, using soft heaps to manage approximate priorities during component contractions. The soft heap's error rate of O(1/n) per extraction guarantees exact MST recovery after a linear number of phases, marking the tightest known worst-case bound for comparison-based models without randomization. These refinements highlight a progression from brute-force greedy selections in the 1950s to structure-aware optimizations by the 2000s, with each advance building on cut and cycle properties while minimizing data structure overhead. The inverse-Ackermann complexity of Chazelle's method is widely regarded as optimal up to constants in the decision-tree model, influencing subsequent work on dynamic and parallel MST variants.

Randomized and Near-Linear Time Algorithms

The Karger-Klein-Tarjan algorithm provides a randomized method for computing a minimum spanning tree in an undirected, connected graph with nonnegative edge weights, achieving an expected running time of O(m), where m is the number of edges. This Las Vegas algorithm, which always produces the correct MST but with randomized runtime, combines random edge sampling with a linear-time verification procedure to efficiently sparsify the graph while preserving the MST structure. Building on the contraction phases of Borůvka's algorithm, the approach iteratively identifies and contracts minimum-weight edges incident to each component, but incorporates randomization to address the issue of dense subgraphs slowing down progress. In each phase, a subset of edges is randomly sampled such that each edge is included independently with probability p = 1/2, ensuring, via the sampling lemma, that the MSF of the sampled graph allows safe filtering of heavy edges, preserving the original MST while bounding the number of candidate edges. Following sampling, a verification step discards edges that cannot belong to any MST by checking against the cut property, reducing the edge count to O(n) in expectation per phase, where n is the number of vertices. Contractions then merge components, repeating until a single tree remains. The expected time analysis hinges on probabilistic guarantees for component reduction: with high probability (at least 1 - 1/n^c for constant c), each phase contracts a constant fraction of the vertices, leading to O(log n) phases overall. A key sampling lemma proves that the probability of failing to contract a particular vertex is exponentially small, bounding the expected number of surviving edges and ensuring the total time is linear despite occasional denser phases. This backward analysis technique simplifies proving the preservation of MST edges under sampling. In practice, the algorithm's expected linear time makes it particularly efficient for large, sparse graphs, often outperforming deterministic methods like improved versions of or in empirical studies due to reduced constant factors in edge processing.

Parallel and Distributed Algorithms

Parallel algorithms for minimum spanning trees leverage the inherent parallelism in methods like , where each phase involves independently selecting minimum-weight outgoing edges from graph components. In the parallel approach, these phases are executed concurrently across components in the PRAM model, with each iteration reducing the number of components by a constant factor, leading to O(log |V|) rounds until a single component remains. Graph contraction techniques, such as tree or star contraction, are used to merge components efficiently while updating cross edges, ensuring the selected edges form part of the MST. This parallelization achieves work-efficient performance, matching the sequential bound of O(|E| log |V|) total operations, with span (parallel time) of O(log² |V|) or O(log³ |V|) depending on the contraction method. Modern implementations, such as filter-enhanced variants, further optimize for distributed-memory systems by combining Borůvka phases with edge filtering, yielding expected work O(|E| + |V| log |V| log(|E|/|V|)) and polylogarithmic span, enabling scalability on thousands of cores. In distributed settings, the Gallager-Humblet-Spira (GHS) algorithm provides a foundational message-passing protocol for constructing MSTs in asynchronous networks. Nodes initiate fragments and iteratively merge them by exchanging messages to identify and select minimum-weight outgoing edges, progressing through levels up to O(log |V|) to form the spanning tree. The algorithm uses specific message types (e.g., Connect, Accept, Reject) for coordination, incurring O(|E| + |V| log |V|) total messages and O(|V| log |V|) time in the worst case, though synchronous variants achieve O(log |V|) rounds. These parallel and distributed MST algorithms find applications in large-scale networks, such as wireless sensor and peer-to-peer systems, where they facilitate energy-efficient data aggregation and routing by minimizing total edge costs. In sensor networks, distributed MSTs reduce communication overhead for broadcasting and fusion tasks, with approximations like neighbor-neighbor-tree methods achieving O(|V|) expected messages compared to GHS's higher complexity, thus conserving battery life in resource-constrained environments.

Special Cases and Complexity

Dense Graphs

In dense graphs, where the number of edges ∣E∣|E| is on the order of ∣V∣2|V|^2 with ∣V∣|V| denoting the number of vertices, minimum spanning tree (MST) algorithms exploit the graph's structure to achieve running times linear in the input size. The input representation, such as an adjacency matrix, requires Θ(∣V∣2)\Theta(|V|^2) space and time to process, making O(∣V∣2)O(|V|^2) algorithms asymptotically optimal for this regime. A straightforward approach adapts Prim's algorithm using a dense representation like an adjacency matrix, where the priority queue is simulated by linearly scanning the rows to select the minimum-weight edge connecting the growing tree to an unvisited vertex. This implementation runs in O(∣V∣2)O(|V|^2) time, independent of explicit heap structures, as each of the ∣V∣|V| iterations examines up to ∣V∣|V| potential edges. For example, in a complete graph, scanning the adjacency matrix rows directly identifies the cheapest connection at each step, avoiding the overhead of sparse data structures. The Fredman-Tarjan algorithm provides a deterministic O(∣E∣+∣V∣log⁡∣V∣)O(|E| + |V| \log |V|) solution using adapted for priority queue operations, which reduces to O(∣V∣2)O(|V|^2) in dense cases since ∣E∣=Θ(∣V∣2)|E| = \Theta(|V|^2). This bound is linear relative to the input size, as processing all edges and vertices scales with the Θ(∣V∣2)\Theta(|V|^2) input complexity.

Integer Edge Weights

When edge weights are small non-negative integers, a variant of Kruskal's algorithm using bucket sort can compute the minimum spanning tree in linear time. The edges are distributed into buckets indexed by their weights, ranging from 0 to W, where W is the maximum edge weight. These buckets are then processed sequentially in increasing order of weight, adding an edge to the spanning tree if it connects distinct components in the union-find structure. This avoids the O(m log m) cost of general sorting, replacing it with O(m + W) time for bucketing and scanning, while union-find operations with path compression and union by rank take nearly linear time O(m α(m, n)), where α is the inverse Ackermann function. The overall running time is thus linear in m when W = O(m). This bucket sort approach is efficient when edge weights are small, such as W = O(m). For larger integer weights up to polynomial in |V|, linearity in sorting can be achieved via radix sort or advanced integer sorting techniques, maintaining the total time linear in the input size. For integer weights up to poly(|V|), a deterministic linear-time algorithm in the trans-dichotomous RAM model was developed by Fredman and Willard, leveraging fusion trees for priority queue operations in a Borůvka-style framework to simulate efficient edge selection without explicit sorting. The running time is O(|E| + |V|), assuming operations on words of size log |V| bits. This seminal result exploits the integer structure to perform integer comparisons and manipulations in constant time per word.

Optimal Deterministic Algorithms

The fastest known deterministic algorithm for computing a minimum spanning tree of a connected undirected graph with ∣V∣|V| vertices and ∣E∣|E| edges runs in O(∣E∣α(∣V∣))O(|E| \alpha(|V|)) time, where α\alpha denotes the extremely slow-growing inverse Ackermann function. This algorithm, developed by , builds upon earlier techniques such as link-cut trees and soft heaps to achieve near-linear performance while remaining fully deterministic. It processes the graph by iteratively contracting components and using a sophisticated data structure to select edges efficiently, ensuring the time bound holds across all graph densities. A fundamental lower bound for the minimum spanning tree problem arises from its decision-tree complexity, which is Ω(∣E∣)\Omega(|E|) in the comparison model. This bound, established by showing that the problem's computational complexity matches its decision-tree depth, implies that any deterministic algorithm must examine Ω(∣E∣)\Omega(|E|) edge weight comparisons in the worst case, equivalent to at least scanning the entire input. Consequently, no deterministic solution can asymptotically outperform this threshold without additional assumptions on the input model. As of 2025, it remains an open question whether a deterministic O(∣E∣)O(|E|)-time algorithm exists for the general case, with Chazelle's result representing the closest known approach to this linear bound. Although asymptotically superior to classical methods like Kruskal's or Prim's algorithms, which require O(∣E∣log⁡∣V∣)O(|E| \log |V|) time, Chazelle's implementation is highly intricate, involving advanced amortized analysis and specialized data structures that render it impractical for real-world use.

Variants

Minimum Spanning Trees with Random Weights

In the study of minimum spanning trees (MSTs) with random weights, the standard model considers the complete graph KnK_n on nn vertices where each edge weight is an independent identically distributed (i.i.d.) random variable drawn from a continuous distribution, such as the uniform distribution on [0,1][0,1] or the exponential distribution with rate 1 (mean 1). This setup captures the behavior of MSTs in dense networks where all possible connections exist, and weights represent random costs or distances. The i.i.d. assumption ensures that the relative ordering of edge weights is a uniform random permutation, which simplifies analysis via algorithms like , as the MST is formed by adding the lightest non-cycle-forming edges in sorted order. The expected total weight of the MST in this model has been rigorously analyzed for distributions with positive density at 0. For both the uniform [0,1][0,1] and exponential (rate 1) distributions, which have density f(0)=1f(0) = 1 at the origin, the expected cost converges asymptotically to ζ(3)≈1.2020569\zeta(3) \approx 1.2020569 as n→∞n \to \infty, where ζ(3)=∑k=1∞1/k3\zeta(3) = \sum_{k=1}^\infty 1/k^3 is Apéry's constant. This constant arises from the local analysis near weight 0, where the density determines the likelihood of small edges being selected, and the MST effectively samples from the lightest available cross-component edges without heavy tails dominating. More generally, for distributions with density ff differentiable from the left at 0 with f(0)>0f(0) > 0 and finite variance, the limit is ζ(3)/f(0)\zeta(3)/f(0). For certain other distributions, such as those leading to incremental merging costs in union-find structures under random ordering, exact expected costs can take the form ∑k=1n−11/k=Hn−1\sum_{k=1}^{n-1} 1/k = H_{n-1}, the (n−1)(n-1)-th , which grows as ≈ln⁡n+γ\approx \ln n + \gamma (where γ≈0.57721\gamma \approx 0.57721 is the Euler-Mascheroni constant); however, this form is specific to models like exponentially distributed increments in component merging rather than direct i.i.d. edge weights. Key properties of the random-weight MST highlight its concentration around light edges. With high probability (approaching 1 as n→∞n \to \infty), all edges in the MST have weights at most O((log⁡n)/n)O((\log n)/n), ensuring no "heavy" edges (relative to the scale of the lightest possible connections) are included; this follows from the fact that the maximum edge weight in the MST is the weight at which the graph becomes connected in the random ordering, which occurs before the threshold for cycles in heavy edges. Moreover, under continuous distributions like or exponential, the MST is unique with probability 1, as ties in edge weights have probability 0. These properties underscore the robustness of the MST to perturbations in dense random settings. This random-weight model on s provides a foundational framework for understanding MSTs in more structured random environments, such as random geometric graphs where vertices are placed uniformly in a unit cube and edge weights are Euclidean distances. In the geometric case, the complete graph with i.i.d. weights approximates the behavior when points are in and distances are "random-like," though geometric MSTs exhibit different scaling (e.g., Θ(n(d−1)/d)\Theta(n^{(d-1)/d}) in dd dimensions); the i.i.d. model thus isolates probabilistic effects without spatial correlations, aiding theoretical bounds and simulations for network design in or applications.

Fractional Minimum Spanning Tree

The fractional minimum spanning tree is defined as the optimal solution to the of the integer linear program for the minimum spanning tree problem. In this relaxation, the binary variables xe∈{0,1}x_e \in \{0,1\} indicating whether an edge ee is included in the are replaced by continuous variables xe∈[0,1]x_e \in [0,1]. The constraints are designed to ensure that an integer solution corresponds to a —providing connectivity across the graph and preventing cycles—but the acyclicity condition is inherently relaxed in the fractional setting, allowing solutions that may fractionally "cover" cycles. Connectivity is enforced either through cut-based constraints or equivalently via multicommodity flow constraints in polynomial-size formulations. A standard exponential-size formulation of this LP uses cut constraints derived from the cut property of MSTs: min⁡∑e∈Ewexe\min \sum_{e \in E} w_e x_e subject to ∑e∈δ(S)xe≥1∀S⊂V, ∅≠S≠V\text{subject to } \sum_{e \in \delta(S)} x_e \geq 1 \quad \forall S \subset V, \, \emptyset \neq S \neq V 0≤xe≤1∀e∈E0 \leq x_e \leq 1 \quad \forall e \in E Here, δ(S)\delta(S) denotes the set of edges with one endpoint in SS and the other in V∖SV \setminus S. This LP relaxation is exact for the MST problem: its optimal value equals the cost of a minimum spanning tree, and every basic optimal solution is integral, corresponding precisely to the characteristic vector of an MST. Consequently, the integrality gap is zero, as the polytope defined by the constraints—the spanning tree polytope—has integer vertices. This property follows from the total unimodularity of the constraint matrix or the matroid polytope structure. For a polynomial-size alternative, connectivity can be modeled using multicommodity flows: introduce flow variables fpef_p^e for paths pp and edges ee, requiring that unit demand can be routed between all vertex pairs (or from a fixed to all others) subject to capacities xex_e on edges. The objective minimizes ∑wexe\sum w_e x_e while satisfying flow conservation and demand constraints, with acyclicity relaxed through the minimization. This formulation yields an equivalent optimal value to the cut-based LP and supports the same integrality guarantee. The fractional MST LP forms the foundation for approximation algorithms in harder variants, such as the minimum bounded-degree spanning tree, where randomized or iterative methods applied to the fractional solution yield guarantees like O(log⁡n/log⁡log⁡n)O(\log n / \log \log n)-. It also underpins matroid intersection algorithms, as a is a maximum common independent set in the intersection of the graphic matroid (cycle-free subsets) and a partition (size at most n−1n-1); the LP relaxation enables efficient separation oracles and procedures in such frameworks.

Other Variants

The bottleneck minimum spanning tree (BMST), also known as the minimum maximin spanning tree, is a that minimizes the weight of the heaviest edge in the tree. This variant prioritizes avoiding high-cost edges over total weight minimization, with applications in network reliability and where the determines performance. A BMST can be computed in linear time using Camerini's algorithm, which iteratively contracts components and finds MSTs on reduced graphs, or equivalently via by sorting edges and adding until connectivity, with the final edge's weight as the bottleneck. Interestingly, any minimum spanning tree of the graph is also a BMST, as the property holds for undirected graphs under the bottleneck objective. For disconnected graphs, the minimum spanning forest (MSF) generalizes the MST by forming a collection of minimum spanning trees, one for each connected component, such that the total edge weight is minimized across all components. This structure preserves acyclicity and connects all vertices within their respective components, serving as a foundational tool in graph partitioning and clustering tasks on non-connected inputs. Standard MST algorithms like Prim's or Kruskal's naturally produce an MSF when applied to disconnected graphs, running in O(m log n) time where m and n are the number of edges and vertices. Dynamic minimum spanning tree algorithms address the challenge of maintaining an MST under edge insertions and deletions, enabling efficient updates in evolving graphs such as communication networks or databases. Early approaches leverage link-cut trees, a supporting link (add edge) and cut (remove edge) operations in O(log n) amortized time, which can represent the and facilitate MST recomputation by handling path queries and aggregations. For fully dynamic settings, the seminal Holm-de Lichtenberg-Thorup (HDT) algorithm achieves deterministic polylogarithmic update time of O(log² n) per operation by maintaining multiple levels of spanning s and replacement edges, ensuring amortized efficiency across updates. Recent advancements have refined these to improved polylogarithmic update times, incorporating randomized techniques for denser graphs while preserving guarantees. In geometric settings, the (EMST) connects a set of points in d-dimensional space using straight-line edges of minimal total length, forming the MST of the complete geometric graph. Unlike dense complete graphs, the EMST in 2D is a subgraph of the —a with O(n) edges constructed in O(n log n) time—allowing efficient EMST computation by applying Kruskal's or solely on the triangulation's edges, achieving the same time bound. This approximation property extends to higher dimensions with O(n^{⌈d/2⌉}) edges in the Delaunay complex, though practical algorithms often use randomized incremental construction for speed. For sparse approximations, techniques like well-separated pair decomposition further reduce candidates to O(n) edges while providing constant-factor length guarantees.

Applications

Network Design and Optimization

In the design of telecommunication backbone networks, minimum spanning trees (MSTs) are utilized to connect a set of nodes—such as regional hubs or centers—with the minimum total edge cost, ensuring full connectivity without cycles. Edge weights typically represent installation costs, distances, or capacities for optic links, allowing network operators to optimize deployment for reliable, low-cost transmission across large areas. For example, in a national telecom grid, an MST can select optimal routes among potential city connections, reducing overall while maintaining redundancy-free . MSTs find direct application in cable laying and wiring problems, where the objective is to interconnect discrete points, such as buildings in a neighborhood or components on a circuit board, using the shortest total length of cable to avoid cycles and excess . By modeling locations as vertices and possible cable paths as weighted edges (based on Euclidean distances or terrain factors), the MST yields a that minimizes wiring costs and simplifies installation logistics. This approach is widely adopted in electrical and utility engineering to balance connectivity with . For scenarios requiring potential intermediate junctions, MSTs provide a foundational 2-approximation for the metric minimum , where additional Steiner points can be added to further shorten connections in communication or transportation networks. The method involves constructing a on the required terminals using shortest-path distances as edge weights, then computing the MST of this graph; its total weight is at most twice the optimal Steiner tree cost, as the optimal solution can be traversed in a tour of length less than twice its own, and the MST bounds that tour length. This is particularly valuable in dense urban network , where exact Steiner solutions are computationally intensive.

Clustering and Data Analysis

In single-linkage hierarchical clustering, the minimum spanning tree (MST) provides a foundational structure for merging data points into clusters based on their pairwise distances. The MST connects all points with the minimum total edge weight, where each edge represents the shortest path distance between clusters during agglomeration. By treating the MST edges as sequential merges ordered by increasing weight, the clustering process mirrors , and cutting the tree at a specified threshold—such as the (k-1) longest edges for k clusters—yields the desired number of connected components forming the clusters. This equivalence allows the of to be directly derived from the MST, offering an efficient visualization of hierarchical relationships without recomputing distances at each step. In data mining applications, MSTs facilitate by highlighting deviations in the graph structure, such as isolated leaves or edges with weights significantly larger than the average, which indicate outliers relative to the main data manifold. For instance, a two-stage MST approach first builds a global tree to identify anomalous sub-clusters, then refines with local MSTs on subsets to score individual points. Additionally, MSTs underpin spanning tree-based similarity graphs, where the tree's edges preserve essential nearest-neighbor relationships for downstream tasks like or visualization in high-dimensional spaces. A practical example involves applying to point cloud data, such as 3D sensor readings, by constructing the with Euclidean distances as edge weights, computing the MST, and partitioning it by removing the longest edges to form k clusters; this method efficiently groups spatial points while handling noise, as demonstrated in parallel implementations for large-scale datasets. One key advantage of MST-based clustering is its ability to effectively capture non-Euclidean distances, enabling robust grouping in arbitrary metric spaces like graph distances or custom similarities without reliance on vector embeddings.

Approximation in NP-Hard Problems

The minimum spanning tree (MST) plays a central role in designing algorithms for several NP-hard graph problems, particularly those involving connectivity and tours, by providing a low-cost acyclic structure that can be augmented or pruned to satisfy additional constraints. In metric spaces, where edge weights satisfy the , the MST offers a bounded to optimal solutions, enabling constant-factor guarantees without solving the full problem exactly. This utility stems from the polynomial-time computability of MSTs and their total weight being at most the optimum for many related problems. A prominent example is the traveling salesman problem (TSP) in metric graphs, which seeks a minimum-cost Hamiltonian cycle and is NP-hard. The achieves a 3/2- by first computing an MST of the graph, whose total weight is at most that of the optimal TSP tour. It then identifies the odd-degree vertices in the MST (at most n/2 such vertices) and adds a minimum-weight on those vertices, ensuring the resulting has all even degrees. A minimum-cost Eulerian tour is found in this , and shortcutting repeated vertices yields a valid TSP tour whose cost is at most the MST cost plus half the matching cost, bounding the total by 3/2 times the optimum. In 2023, this was slightly improved to a (3/2 - ε)- for a tiny ε > 0. This remains one of the best known approximation ratios for metric TSP as of 2025, and it is conjectured that no polynomial-time achieves a better constant approximation than 3/2 unless P=NP. In the prize-collecting Steiner tree problem (PCST), which generalizes the NP-hard Steiner tree problem by allowing vertices to be excluded at a penalty cost to minimize the total edge and penalty costs while connecting a subset of terminals, MST-based techniques enable strong approximations through primal-dual methods and post-processing. The problem models budgeted connectivity scenarios, such as network design with optional nodes. Goemans and Williamson's primal-dual 2-approximation constructs a tree by growing components via lagrangian relaxation of the LP formulation, then applies iterative pruning to remove low-density leaves until a valid solution emerges; an MST computation on the contracted graph can further refine the solution by replacing suboptimal subtrees, improving practical performance while preserving the guarantee. Recent refinements, such as iterative rounding and adaptive variants, achieve factors as low as 1.79 by combining these with dynamic edge updates, but the core reliance on MST-like structures for pruning persists. The fractional MST, as the LP relaxation of the spanning tree polytope, underpins these approaches by providing integral solutions upon rounding. A key theoretical foundation for these approximations is the integrality of the MST linear program in tree packing contexts. The standard cut-based formulation for the MST—minimizing edge costs subject to degree constraints and subtour elimination via cuts for every proper S of vertices—has integer optimal solutions for undirected graphs, as its polytope is the polytope with integral vertices. This integrality extends to many multi-commodity flow and tree packing LPs, where fractional solutions can be rounded to MSTs without increasing , enabling exact or near-exact decompositions in schemes for problems like multi-cut or survivable network .

References

  1. https://algs4.cs.princeton.edu/43mst/
  2. https://mathworld.wolfram.com/MinimumSpanningTree.html
  3. https://www.sciencedirect.com/science/article/pii/S0012365X00002247
  4. https://5010.mathed.usu.edu/Fall2018/THigham/Krukskal.pdf
  5. https://www.utdallas.edu/~besp/teaching/mst-applications.pdf
  6. https://www.zib.de/userpage/groetschel/teaching/WS1314/BondyMurtyGTWA.pdf
  7. https://www.cs.cmu.edu/afs/cs/academic/class/15210-f14/www/lectures/graph-intro.pdf
  8. https://www.cs.yale.edu/homes/aspnes/pinewiki/GraphTheory.html
  9. https://www.cs.hunter.cuny.edu/~sweiss/course_materials/csci335/lecture_notes/chapter09.pdf
  10. http://web.stanford.edu/class/archive/cs/cs103/cs103.1204/lectures/10-GraphsI/GraphsI.2.pdf
  11. https://web.mit.edu/neboat/Public/6.042/graphtheory3.pdf
  12. https://facultyweb.kennesaw.edu/mlavrov/courses/graph-theory/lecture10.pdf
  13. https://stanford.edu/~rezab/discrete/Notes/2.pdf
  14. https://www.math.toronto.edu/swastik/courses/rutgers/graphtheory-F11/flow.pdf
  15. https://jeffe.cs.illinois.edu/teaching/algorithms/book/07-mst.pdf
  16. https://courses.cs.duke.edu/spring18/compsci330/Notes/mst.pdf
  17. http://homepages.math.uic.edu/~leon/cs-mcs401-s08/handouts/mst.pdf
  18. https://www.cs.princeton.edu/~wayne/kleinberg-tardos/pearson/04MinimumSpanningTrees-2x2.pdf
  19. https://courses.cs.duke.edu/spring15/compsci590.1/scribing/cps590_lec15.pdf
  20. https://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/14/Small14.pdf
  21. https://courses.cs.washington.edu/courses/cse421/18au/lecture/lecture-10.pdf
  22. https://www.geeksforgeeks.org/dsa/properties-of-minimum-spanning-tree-mst/
  23. https://courses.grainger.[illinois](/page/Illinois).edu/cs374/fa2018/slides/19-mst.pdf
  24. https://www.cs.cmu.edu/afs/cs/academic/class/15210-s12/www/lectures/lecture18.pdf
  25. https://people.eecs.berkeley.edu/~jordan/courses/174-spring02/notes/note9.pdf
  26. https://www.cs.jhu.edu/~jason/papers/eisner.mst-tutorial.pdf
  27. https://www.math.ias.edu/~avi/STUDENTS/dpthesis.pdf
  28. https://dl.acm.org/doi/10.1145/505241.505243
  29. http://www.cs.yale.edu/homes/lans/readings/routing/kruskal-1956.pdf
  30. https://www.cs.princeton.edu/courses/archive/spring21/cos226/lectures/43MinimumSpanningTrees.pdf
  31. https://www.programiz.com/dsa/kruskal-algorithm
  32. https://ia601308.us.archive.org/17/items/bstj36-6-1389/bstj36-6-1389.pdf
  33. https://www.cs.jhu.edu/~mdinitz/IntroAlgorithms/Lectures/lecture14.pdf
  34. https://people.cs.umass.edu/~marius/class/cs311-fa18/lec8-nup.pdf
  35. https://www.cmat.edu.uy/~marclan/TAG/Sellanes/boruvka.pdf
  36. https://www.cs.cornell.edu/courses/cs4820/2021sp/lectures/notes/cs4820-2021-02-17.pdf
  37. https://www.csie.ntu.edu.tw/~kmchao/tree07spr/mst.pdf
  38. https://www.cs.princeton.edu/~chazelle/pubs/mst.pdf
  39. https://www2.seas.gwu.edu/~simhaweb/champalg/mst/papers/GabowMST.pdf
  40. https://ae.iti.kit.edu/documents/teaching/algorithm-engineering/ws23/fkruskal.pdf
  41. https://link.springer.com/article/10.1007/BF02579168
  42. http://www.cs.cmu.edu/afs/cs/academic/class/15859-f05/www/documents/p1012-chazelle.pdf
  43. https://www.cs.utexas.edu/~vlr/papers/optmsf-jacm.pdf
  44. https://www.math.ucsd.edu/~ronspubs/85_07_minimum_spanning_tree.pdf
  45. https://dl.acm.org/doi/10.1145/201019.201022
  46. https://www.sciencedirect.com/science/article/pii/S002001909800129X
  47. https://www.sciencedirect.com/science/article/abs/pii/S0305054800000071
  48. https://www.cs.cmu.edu/~15210/algobook/mst/par.pdf
  49. https://arxiv.org/pdf/2302.12199
  50. https://users.dimi.uniud.it/~gabriele.puppis/teaching/Distributed%20Systems/Additional%20material/Code%20examples/Erlang/minimum_spanning_tree/GHS_enhanced.pdf
  51. http://www.maleqkhan.net/papers/TPDS.pdf
  52. https://dl.acm.org/doi/10.1145/28869.28874
  53. https://www.sciencedirect.com/science/article/pii/S0022000005800649
  54. https://dl.acm.org/doi/10.1145/355541.355562
  55. https://webdocs.cs.ualberta.ca/~mreza/courses/AdvancedF25/Scribed5.pdf
  56. https://www2.seas.gwu.edu/~simhaweb/champalg/mst/mst.html
  57. https://projecteuclid.org/journals/annals-of-probability/volume-45/issue-5/The-scaling-limit-of-the-minimum-spanning-tree-of-the/10.1214/16-AOP1132.full
  58. https://people.orie.cornell.edu/dpw/orie6300/Recitations/Rec10.pdf
  59. https://www.columbia.edu/~cs2035/courses/ieor6614.S16/mst-lp.pdf
  60. https://courses.cs.duke.edu/fall15/compsci532/scribe_notes/lec15.pdf
  61. https://theory.epfl.ch/osven/courses/Approx13/Notes/lecture9and10.pdf
  62. http://www.contrib.andrew.cmu.edu/~ravi/bdmst06.pdf
  63. https://dl.acm.org/doi/10.1145/2145816.2145842
  64. https://www.cs.cornell.edu/courses/JavaAndDS/files/spanningTree2.pdf
  65. https://people.idsia.ch/~grandoni/Pubblicazioni/BGRS12jacm.pdf
  66. https://academic.oup.com/jrsssc/article/18/1/54/6882518
  67. https://www.semanticscholar.org/paper/Worst-Case-Analysis-of-a-New-Heuristic-for-the-Christofides/9677131fd6775e1352dca36f63bc81dfe95b58b0
  68. https://pubsonline.informs.org/doi/10.1287/opre.2022.2338
  69. https://theory.epfl.ch/anhc/pathslil.pdf
  70. https://math.mit.edu/~goemans/PAPERS/GoemansWilliamson-1995-AGeneralApproximationTechniqueForConstrainedForestProblems.pdf
  71. http://dspace.mit.edu/bitstream/handle/1721.1/86544/46921794-MIT.pdf?sequence=2
  72. https://arxiv.org/abs/2405.03792
Add your contribution
Related Hubs
User Avatar
No comments yet.