Scoring rule

Consider a sample space ${\displaystyle \Omega }$, a σ-algebra ${\displaystyle {\mathcal {A}}}$ of subsets of ${\displaystyle \Omega }$ and a convex class ${\displaystyle {\mathcal {F}}}$ of probability measures on ${\displaystyle (\Omega ,{\mathcal {A}})}$. A function defined on ${\displaystyle \Omega }$ and taking values in the extended real line, ${\displaystyle {\overline {\mathbb {R} }}=[-\infty ,\infty ]}$, is ${\displaystyle {\mathcal {F}}}$-quasi-integrable if it is measurable with respect to ${\displaystyle {\mathcal {A}}}$ and is quasi-integrable with respect to all ${\displaystyle F\in {\mathcal {F}}}$.

A probabilistic forecast is any probability measure ${\displaystyle F\in {\mathcal {F}}}$. I.e. it is a distribution of potential future observations.

A scoring rule is any extended real-valued function ${\displaystyle \mathbf {S} :{\mathcal {F}}\times \Omega \rightarrow \mathbb {R} }$ such that ${\displaystyle \mathbf {S} (F,\cdot )}$ is ${\displaystyle {\mathcal {F}}}$-quasi-integrable for all ${\displaystyle F\in {\mathcal {F}}}$. ${\displaystyle \mathbf {S} (F,y)}$ represents the loss or penalty when the forecast ${\displaystyle F\in {\mathcal {F}}}$ is issued and the observation ${\displaystyle y\in \Omega }$ materializes.

A point forecast is a functional, i.e. a potentially set-valued mapping ${\displaystyle F\rightarrow T(F)\subseteq \Omega }$.

A scoring function is any real-valued function ${\displaystyle S:\Omega \times \Omega \rightarrow \mathbb {R} }$ where ${\displaystyle S(x,y)}$ represents the loss or penalty when the point forecast ${\displaystyle x\in \Omega }$ is issued and the observation ${\displaystyle y\in \Omega }$ materializes.

Scoring rules ${\displaystyle \mathbf {S} (F,y)}$ and scoring functions ${\displaystyle S(x,y)}$ are negatively (positively) oriented if smaller (larger) values mean better. Here we adhere to negative orientation, hence the association with "loss".

We write for the expected score of a prediction ${\displaystyle F}$ under ${\displaystyle Q\in {\mathcal {F}}}$ as the expected score of the predicted distribution ${\displaystyle F\in {\mathcal {F}}}$, when sampling observations from distribution ${\displaystyle Q}$.

${\displaystyle \mathbb {E} _{Y\sim Q}[S(F,Y)]=\int \mathbf {S} (F,\omega )\mathrm {d} Q(\omega )}$

Many probabilistic forecasting models are training via the sample average score, in which a set of predicted distributions ${\displaystyle F_{1},\ldots ,F_{n}\in {\mathcal {F}}}$ is evaluated against a set of observations ${\displaystyle y_{1},\ldots ,y_{n}\in \Omega }$.

${\displaystyle {\mathcal {L}}={\frac {1}{n}}\sum _{i=1}^{n}S(F_{i},y_{i})}$

Strictly proper scoring rules and strictly consistent scoring functions encourage honest forecasts by maximization of the expected reward: If a forecaster is given a reward of ${\displaystyle -\mathbf {S} (F,y)}$ if ${\displaystyle y}$ realizes (e.g. ${\displaystyle y=rain}$), then the highest expected reward (lowest score) is obtained by reporting the true probability distribution.^[1]

A scoring rule ${\displaystyle \mathbf {S} }$ is proper relative to ${\displaystyle {\mathcal {F}}}$ if (assuming negative orientation) its expected score is minimized when the forecasted distribution matches the distribution of the observation.

${\displaystyle \mathbb {E} _{Y\sim Q}[S(Q,Y)]\leq \mathbb {E} _{Y\sim Q}[S(F,Y)]}$ for all ${\displaystyle F,Q\in {\mathcal {F}}}$.

It is strictly proper if the above equation holds with equality if and only if ${\displaystyle F=Q}$.

A scoring function ${\displaystyle S}$ is consistent for the functional ${\displaystyle T}$ relative to the class ${\displaystyle {\mathcal {F}}}$ if

${\displaystyle \mathbb {E} _{Y\sim F}[S(t,Y)]\leq \mathbb {E} _{Y\sim F}[S(x,Y)]}$ for all ${\displaystyle F\in {\mathcal {F}}}$, all ${\displaystyle t\in T(F)}$ and all ${\displaystyle x\in \Omega }$.

It is strictly consistent if it is consistent and equality in the above equation implies that ${\displaystyle x\in T(F)}$.

An example of probabilistic forecasting is in meteorology where a weather forecaster may give the probability of rain on the next day. One could note the number of times that a 25% probability was quoted, over a long period, and compare this with the actual proportion of times that rain fell. If the actual percentage was substantially different from the stated probability we say that the forecaster is poorly calibrated. A poorly calibrated forecaster might be encouraged to do better by a bonus system. A bonus system designed around a proper scoring rule will incentivize the forecaster to report probabilities equal to his personal beliefs.^[3]

In addition to the simple case of a binary decision, such as assigning probabilities to 'rain' or 'no rain', scoring rules may be used for multiple classes, such as 'rain', 'snow', or 'clear', or continuous responses like the amount of rain per day.

The image shows an example of a scoring rule, the logarithmic scoring rule, as a function of the probability reported for the event that actually occurred. One way to use this rule would be as a cost based on the probability that a forecaster or algorithm assigns, then checking to see which event actually occurs.

Scoring rules can be used beyond evaluation metrics to directly serve as loss function to construct estimators.^[4]

There are an infinite number of scoring rules, including entire parameterized families of strictly proper scoring rules. The ones shown below are simply popular examples.

For a categorical response variable with ${\displaystyle m}$ mutually exclusive events, ${\displaystyle Y\in \Omega =\{1,\ldots ,m\}}$, a probabilistic forecaster or algorithm will return a probability vector ${\displaystyle \mathbf {r} }$ with a probability for each of the ${\displaystyle m}$ outcomes.

The logarithmic scoring rule is a local strictly proper scoring rule. This is also the negative of surprisal, which is commonly used as a scoring criterion in Bayesian inference; the goal is to minimize expected surprise. This scoring rule has strong foundations in information theory.

${\displaystyle L(\mathbf {r} ,i)=\ln(r_{i})}$

Here, the score is calculated as the logarithm of the probability estimate for the actual outcome. That is, a prediction of 80% that correctly proved true would receive a score of ln(0.8) = −0.22. This same prediction also assigns 20% likelihood to the opposite case, and so if the prediction proves false, it would receive a score based on the 20%: ln(0.2) = −1.6. The goal of a forecaster is to maximize the score and for the score to be as large as possible, and −0.22 is indeed larger than −1.6.

If one treats the truth or falsity of the prediction as a variable x with value 1 or 0 respectively, and the expressed probability as p, then one can write the logarithmic scoring rule as x ln(p) + (1 − x) ln(1 − p). Note that any logarithmic base may be used, since strictly proper scoring rules remain strictly proper under linear transformation. That is:

${\displaystyle L(\mathbf {r} ,i)=\log _{b}(r_{i})}$

is strictly proper for all ${\displaystyle b>1}$.

The quadratic scoring rule is a strictly proper scoring rule

${\displaystyle Q(\mathbf {r} ,i)=2r_{i}-\mathbf {r} \cdot \mathbf {r} =2r_{i}-\sum _{j=1}^{C}r_{j}^{2}}$

where ${\displaystyle r_{i}}$ is the probability assigned to the correct answer and ${\displaystyle C}$ is the number of classes.

The Brier score, originally proposed by Glenn W. Brier in 1950,^[5] can be obtained by an affine transform from the quadratic scoring rule.

${\displaystyle B(\mathbf {r} ,i)=\sum _{j=1}^{C}(y_{j}-r_{j})^{2}}$

Where ${\displaystyle y_{j}=1}$ when the ${\displaystyle j}$th event is correct and ${\displaystyle y_{j}=0}$ otherwise and ${\displaystyle C}$ is the number of classes.

An important difference between these two rules is that a forecaster should strive to maximize the quadratic score ${\displaystyle Q}$ yet minimize the Brier score ${\displaystyle B}$. This is due to a negative sign in the linear transformation between them.

The spherical scoring rule is also a strictly proper scoring rule

${\displaystyle S(\mathbf {r} ,i)={\frac {r_{i}}{\lVert \mathbf {r} \rVert }}={\frac {r_{i}}{\sqrt {r_{1}^{2}+\cdots +r_{C}^{2}}}}}$

The ranked probability score ^[6] (RPS) is a strictly proper scoring rule, that can be expressed as:

${\displaystyle RPS(\mathbf {r} ,i)=\sum _{k=1}^{C-1}\left(\sum _{j=1}^{k}r_{j}-y_{j}\right)^{2}}$

Where ${\displaystyle y_{j}=1}$ when the ${\displaystyle j}$th event is correct and ${\displaystyle y_{j}=0}$ otherwise, and ${\displaystyle C}$ is the number of classes. Other than other scoring rules, the ranked probability score considers the distance between classes, i.e. classes 1 and 2 are considered closer than classes 1 and 3. The score assigns better scores to probabilistic forecasts with high probabilities assigned to classes close to the correct class. For example, when considering probabilistic forecasts ${\displaystyle \mathbf {r} _{1}=(0.5,0.5,0)}$ and ${\displaystyle \mathbf {r} _{2}=(0.5,0,0.5)}$, we find that ${\displaystyle RPS(\mathbf {r} _{1},1)=0.25}$, while ${\displaystyle RPS(\mathbf {r} _{2},1)=0.5}$, despite both probabilistic forecasts assigning identical probability to the correct class.

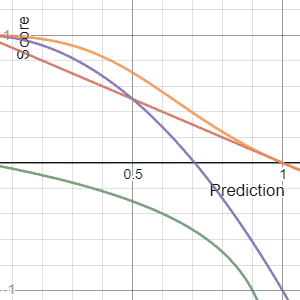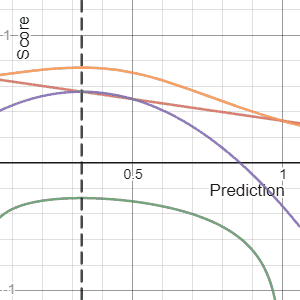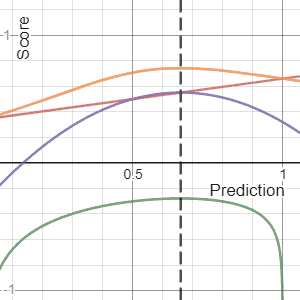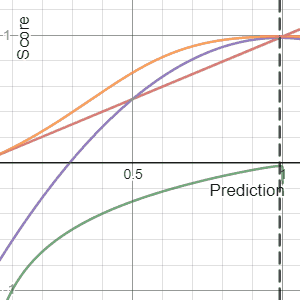
Shown below on the left is a graphical comparison of the Logarithmic, Quadratic, and Spherical scoring rules for a binary classification problem. The x-axis indicates the reported probability for the event that actually occurred.

It is important to note that each of the scores have different magnitudes and locations. The magnitude differences are not relevant however as scores remain proper under affine transformation. Therefore, to compare different scores it is necessary to move them to a common scale. A reasonable choice of normalization is shown in the picture where all scores intersect the points (0.5,0) and (1,1). This ensures that they yield 0 for a uniform distribution (two probabilities of 0.5 each), reflecting no cost or reward for reporting what is often the baseline distribution. All normalized scores below also yield 1 when the true class is assigned a probability of 1.

The scoring rules listed below aim to evaluate probabilistic predictions when the predicted distributions are univariate continuous probability distribution's, i.e. the predicted distributions are defined over a univariate target variable ${\displaystyle X\in \mathbb {R} }$ and have a probability density function ${\displaystyle f:\mathbb {R} \to \mathbb {R} _{+}}$.

The logarithmic score is a local strictly proper scoring rule. It is defined as

${\displaystyle L(D,y)=-\ln(f_{D}(y))}$

where ${\displaystyle f_{D}}$ denotes the probability density function of the predicted distribution ${\displaystyle D}$. It is a local, strictly proper scoring rule. The logarithmic score for continuous variables has strong ties to Maximum likelihood estimation. However, in many applications, the continuous ranked probability score is often preferred over the logarithmic score, as the logarithmic score can be heavily influenced by slight deviations in the tail densities of forecasted distributions.^[7]

The continuous ranked probability score (CRPS)^[8] is a strictly proper scoring rule much used in meteorology. It is defined as

${\displaystyle CRPS(D,y)=\int _{\mathbb {R} }(F_{D}(x)-H(x-y))^{2}dx}$

where ${\displaystyle F_{D}}$ is the cumulative distribution function of the forecasted distribution ${\displaystyle D}$, ${\displaystyle H}$ is the Heaviside step function and ${\displaystyle y\in \mathbb {R} }$ is the observation. For distributions with finite first moment, the continuous ranked probability score can be written as:^[1]

${\displaystyle CRPS(D,y)=\mathbb {E} _{X\sim D}[|X-y|]-{\frac {1}{2}}\mathbb {E} _{X,X'\sim D}[|X-X'|]}$

where ${\displaystyle X}$ and ${\displaystyle X'}$ are independent random variables, sampled from the distribution ${\displaystyle D}$. This is the energy form of CRPS and opens the door to estimating the CRPS via Monte Carlo sampling (through approximating the expectation value).

Furthermore, when the cumulative probability function ${\displaystyle F}$ is continuous, the continuous ranked probability score can also be written as^[9]

${\displaystyle CRPS(D,y)=\mathbb {E} _{X\sim D}[|X-y|]+\mathbb {E} _{X\sim D}[X]-2\mathbb {E} _{X\sim D}[X\cdot F_{D}(X)]}$

The continuous ranked probability score can be seen as both a continuous extension of the ranked probability score, as well as quantile regression. The continuous ranked probability score over the empirical distribution ${\displaystyle {\hat {D}}_{q}}$ of an ordered set points ${\displaystyle q_{1}\leq \ldots \leq q_{n}}$ (i.e. every point has ${\displaystyle 1/n}$ probability of occurring), is equal to twice the mean quantile loss applied on those points with evenly spread quantiles ${\displaystyle (\tau _{1},\ldots ,\tau _{n})=(1/(2n),\ldots ,(2n-1)/(2n))}$:^[10]

${\displaystyle CRPS\left({\hat {D}}_{q},y\right)={\frac {2}{n}}\sum _{i=1}^{n}\tau _{i}(y-q_{i})_{+}+(1-\tau _{i})(q_{i}-y)_{+}}$

For many popular families of distributions, closed-form expressions for the continuous ranked probability score have been derived. The continuous ranked probability score has been used as a loss function for artificial neural networks, in which weather forecasts are postprocessed to a Gaussian probability distribution.^[11][12]

CRPS was also adapted to survival analysis to cover censored events.^[13]

CRPS is also known as Cramer–von Mises distance and can be seen as an improvement of Wasserstein distance (often used in machine learning) and further Cramer distance performed better in ordinal regression than KL distance or the Wasserstein metric.^[14]

While CRPS is widely used for evaluating probabilistic forecasts, it has critical theoretical limitations. It has been shown that CRPS can produce systematically misleading evaluations by favoring probabilistic forecasts whose medians are close to the observed outcome, regardless of the actual probability assigned to that region, potentially resulting in higher scores for forecasts that allocate negligible (or even zero) probability mass to the true outcome. Furthermore, CRPS is not invariant under smooth transformations of the forecast variable, and its ranking of forecast systems may reverse under such transformations, raising concerns about its consistency for evaluation purposes.^[15]

The interval score measures the calibration and sharpness of an interval prediction ${\displaystyle (l,u)}$ at nominal coverage ${\displaystyle 1-\alpha }$:

${\displaystyle S_{\alpha }(l,u;y)=(u-l)+{\frac {2}{\alpha }}(l-y)\,\mathbf {1} \{y<l\}+{\frac {2}{\alpha }}(y-u)\,\mathbf {1} \{y>u\}}$

"The forecaster is rewarded for narrow prediction intervals, and he or she incurs a penalty, the size of which de- pends on α, if the observation misses the interval"^[16]

The scoring rules listed below aim to evaluate probabilistic predictions when the predicted distributions are univariate continuous probability distribution's, i.e. the predicted distributions are defined over a multivariate target variable ${\displaystyle X\in \mathbb {R} ^{n}}$ and have a probability density function ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} _{+}}$.

The multivariate logarithmic score is similar to the univariate logarithmic score:

${\displaystyle L(D,y)=-\ln(f_{D}(y))}$

where ${\displaystyle f_{D}}$ denotes the probability density function of the predicted multivariate distribution ${\displaystyle D}$. It is a local, strictly proper scoring rule.

The Hyvärinen scoring function (of a density p) is defined by^[17]

${\displaystyle s(p)=2\Delta _{y}\log p(y)+\|\nabla _{y}\log p(y)\|_{2}^{2}}$

Where ${\displaystyle \Delta }$ denotes the Hessian trace and ${\displaystyle \nabla }$ denotes the gradient. This scoring rule can be used to computationally simplify parameter inference and address Bayesian model comparison with arbitrarily-vague priors.^[17][18] It was also used to introduce new information-theoretic quantities beyond the existing information theory.^[19]

The energy score is a multivariate extension of the continuous ranked probability score:^[1]

${\displaystyle ES_{\beta }(D,Y)=\mathbb {E} _{X\sim D}[\lVert X-Y\rVert _{2}^{\beta }]-{\frac {1}{2}}\mathbb {E} _{X,X'\sim D}[\lVert X-X'\rVert _{2}^{\beta }]}$

Here, ${\displaystyle \beta \in (0,2)}$, ${\displaystyle \lVert \rVert _{2}}$ denotes the ${\displaystyle n}$-dimensional Euclidean distance and ${\displaystyle X,X'}$ are independently sampled random variables from the probability distribution ${\displaystyle D}$. The energy score is strictly proper for distributions ${\displaystyle D}$ for which ${\displaystyle \mathbb {E} _{X\sim D}[\lVert X\rVert _{2}]}$ is finite. It has been suggested that the energy score is somewhat ineffective when evaluating the intervariable dependency structure of the forecasted multivariate distribution.^[20] The energy score is equal to twice the energy distance between the predicted distribution and the empirical distribution of the observation.

The variogram score of order ${\displaystyle p}$ is given by:^[21]

${\displaystyle VS_{p}(D,Y)=\sum _{i,j=1}^{n}w_{ij}(|Y_{i}-Y_{j}|^{p}-\mathbb {E} _{X\sim D}[|X_{i}-X_{j}|^{p}])^{2}}$

Here, ${\displaystyle w_{ij}}$ are weights, often set to 1, and ${\displaystyle p>0}$ can be arbitrarily chosen, but ${\displaystyle p=0.5,1}$ or ${\displaystyle 2}$ are often used. ${\displaystyle X_{i}}$ is here to denote the ${\displaystyle i}$'th marginal random variable of ${\displaystyle X}$. The variogram score is proper for distributions for which the ${\displaystyle (2p)}$'th moment is finite for all components, but is never strictly proper. Compared to the energy score, the variogram score is claimed to be more discriminative with respect to the predicted correlation structure.

The conditional continuous ranked probability score (Conditional CRPS or CCRPS) is a family of (strictly) proper scoring rules. Conditional CRPS evaluates a forecasted multivariate distribution ${\displaystyle D}$ by evaluation of CRPS over a prescribed set of univariate conditional probability distributions of the predicted multivariate distribution:^[22]

${\displaystyle CCRPS_{\mathcal {T}}(D,Y)=\sum _{i=1}^{k}CRPS(P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i}),Y_{v_{i}})}$

Here, ${\displaystyle X_{i}}$ is the ${\displaystyle i}$'th marginal variable of ${\displaystyle X\sim D}$, ${\displaystyle {\mathcal {T}}=(v_{i},{\mathcal {C}}_{i})_{i=1}^{k}}$ is a set of tuples that defines a conditional specification (with ${\displaystyle v_{i}\in \{1,\ldots ,n\}}$ and ${\displaystyle {\mathcal {C}}_{i}\subseteq \{1,\ldots ,n\}\setminus \{v_{i}\}}$), and ${\displaystyle P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i})}$ denotes the conditional probability distribution for ${\displaystyle X_{v_{i}}}$ given that all variables ${\displaystyle X_{j}}$ for ${\displaystyle j\in {\mathcal {C}}_{i}}$ are equal to their respective observations. In the case that ${\displaystyle P_{X\sim D}(X_{v_{i}}|X_{j}=Y_{j}{\text{ for }}j\in {\mathcal {C}}_{i})}$ is ill-defined (i.e. its conditional event has zero likelihood), CRPS scores over this distribution are defined as infinite. Conditional CRPS is strictly proper for distributions with finite first moment, if the chain rule is included in the conditional specification, meaning that there exists a permutation ${\displaystyle \phi _{1},\ldots ,\phi _{n}}$ of ${\displaystyle 1,\ldots ,n}$ such that for all ${\displaystyle 1\leq i\leq n}$: ${\displaystyle (\phi _{i},\{\phi _{1},\ldots ,\phi _{i-1}\})\in {\mathcal {T}}}$.

All proper scoring rules are equal to weighted sums (integral with a non-negative weighting functional) of the losses in a set of simple two-alternative decision problems that use the probabilistic prediction, each such decision problem having a particular combination of associated cost parameters for false positive and false negative decisions. A strictly proper scoring rule corresponds to having a nonzero weighting for all possible decision thresholds. Any given proper scoring rule is equal to the expected losses with respect to a particular probability distribution over the decision thresholds; thus the choice of a scoring rule corresponds to an assumption about the probability distribution of decision problems for which the predicted probabilities will ultimately be employed, with for example the quadratic loss (or Brier) scoring rule corresponding to a uniform probability of the decision threshold being anywhere between zero and one. The classification accuracy score (percent classified correctly), a single-threshold scoring rule which is zero or one depending on whether the predicted probability is on the appropriate side of 0.5, is a proper scoring rule but not a strictly proper scoring rule because it is optimized (in expectation) not only by predicting the true probability but by predicting any probability on the same side of 0.5 as the true probability.^{[23][24][25][26][27][28]}

A strictly proper scoring rule, whether binary or multiclass, after an affine transformation remains a strictly proper scoring rule.^[3] That is, if ${\displaystyle S(\mathbf {r} ,i)}$ is a strictly proper scoring rule then ${\displaystyle a+bS(\mathbf {r} ,i)}$ with ${\displaystyle b\neq 0}$ is also a strictly proper scoring rule, though if ${\displaystyle b<0}$ then the optimization sense of the scoring rule switches between maximization and minimization.

A proper scoring rule is said to be local if its estimate for the probability of a specific event depends only on the probability of that event. This statement is vague in most descriptions but we can, in most cases, think of this as the optimal solution of the scoring problem "at a specific event" is invariant to all changes in the observation distribution that leave the probability of that event unchanged. All binary scores are local because the probability assigned to the event that did not occur is determined so there is no degree of flexibility to vary over.

Affine functions of the logarithmic scoring rule are the only strictly proper local scoring rules on a finite set that is not binary.

The expectation value of a proper scoring rule ${\displaystyle S}$ can be decomposed into the sum of three components, called uncertainty, reliability, and resolution,^[29][30] which characterize different attributes of probabilistic forecasts:

${\displaystyle E(S)=\mathrm {UNC} +\mathrm {REL} -\mathrm {RES} .}$

If a score is proper and negatively oriented (such as the Brier Score), all three terms are positive definite. The uncertainty component is equal to the expected score of the forecast which constantly predicts the average event frequency. The reliability component penalizes poorly calibrated forecasts, in which the predicted probabilities do not coincide with the event frequencies.

The equations for the individual components depend on the particular scoring rule. For the Brier Score, they are given by

${\displaystyle \mathrm {UNC} ={\bar {x}}(1-{\bar {x}})}$

${\displaystyle \mathrm {REL} =E(p-\pi (p))^{2}}$

${\displaystyle \mathrm {RES} =E(\pi (p)-{\bar {x}})^{2}}$

where ${\displaystyle {\bar {x}}}$ is the average probability of occurrence of the binary event ${\displaystyle x}$, and ${\displaystyle \pi (p)}$ is the conditional event probability, given ${\displaystyle p}$, i.e. ${\displaystyle \pi (p)=P(x=1\mid p)}$

• Coherence
• Decision rule

• Strictly Proper Scoring Rules, Prediction, and Estimation. Tilmann Gneiting &Adrian E Raftery Pages 359-378, https://doi.org/10.1198/016214506000001437, pdf