Position of the Sun

These equations, from the Astronomical Almanac,^[4][5] can be used to calculate the apparent coordinates of the Sun, mean equinox and ecliptic of date, to a precision of about 0°.01 (36″), for dates between 1950 and 2050. Similar equations are coded into a Fortran 90 routine in Ref.^[3] and are used to calculate the solar zenith angle and solar azimuth angle as observed from the surface of the Earth.

Start by calculating n, the number of days (positive or negative, including fractional days) since Greenwich noon, Terrestrial Time, on 1 January 2000 (J2000.0). If the Julian date for the desired time is known, then

${\displaystyle n=\mathrm {JD} -2451545.0}$

The mean longitude of the Sun, corrected for the aberration of light, is:

${\displaystyle L=280.460^{\circ }+0.9856474^{\circ }n}$

The mean anomaly of the Sun (actually, of the Earth in its orbit around the Sun, but it is convenient to pretend the Sun orbits the Earth), is:

${\displaystyle g=357.528^{\circ }+0.9856003^{\circ }n}$

Put ${\displaystyle L}$ and ${\displaystyle g}$ in the range 0° to 360° by adding or subtracting multiples of 360° as needed‍— which is to say, ${\displaystyle L}$ and ${\displaystyle g}$ are really to be evaluated (mod 360).

Finally, the ecliptic longitude of the Sun is:

${\displaystyle \lambda =L+1.915^{\circ }\sin g+0.020^{\circ }\sin 2g}$

The ecliptic latitude of the Sun is nearly:

${\displaystyle \beta =0}$,

as the ecliptic latitude of the Sun never exceeds 0.00033° (a little over 1″),^[6] and the distance of the Sun from the Earth, in astronomical units, is:

${\displaystyle R=1.00014-0.01671\cos g-0.00014\cos 2g}$.

Where the obliquity of the ecliptic is not obtained elsewhere, it can be approximated:

${\displaystyle \epsilon =23.439^{\circ }-0.0000004^{\circ }n}$

${\displaystyle \lambda }$, ${\displaystyle \beta }$ and ${\displaystyle R}$ form a complete position of the Sun in the ecliptic coordinate system. This can be converted to the equatorial coordinate system by calculating the obliquity of the ecliptic, ${\displaystyle \epsilon }$, and continuing:

Right ascension,

${\displaystyle \alpha =\arctan(\cos \epsilon \tan \lambda )}$, where ${\displaystyle \alpha }$ is in the same quadrant as ${\displaystyle \lambda }$,

To get RA at the right quadrant on computer programs use double argument Arctan function such as ATAN2(y,x)

${\displaystyle \alpha =\arctan 2(\cos \epsilon \sin \lambda ,\cos \lambda )}$

and declination,

${\displaystyle \delta =\arcsin(\sin \epsilon \sin \lambda )}$.

Right-handed rectangular equatorial coordinates in astronomical units are:

${\displaystyle X=R\cos \lambda }$

${\displaystyle Y=R\cos \epsilon \sin \lambda }$

${\displaystyle Z=R\sin \epsilon \sin \lambda }$

Where ${\displaystyle X}$ axis is in the direction of the March equinox, the ${\displaystyle Y}$ axis towards June Solstice, and the ${\displaystyle Z}$ axis towards the North celestial pole.^[7]

The Sun appears to move northward during the northern spring, crossing the celestial equator on the March equinox. Its declination reaches a maximum equal to the angle of Earth's axial tilt (23.44° or 23°26')^[8][9] on the June solstice, then decreases until reaching its minimum (−23.44° or -23°26') on the December solstice, when its value is the negative of the axial tilt. This variation produces the seasons.

A line graph of the Sun's declination during a year resembles a sine wave with an amplitude of 23.44°, but one lobe of the wave is several days longer than the other, among other differences.

The following phenomena would occur if Earth were a perfect sphere, in a circular orbit around the Sun, and if its axis were tilted 90°, so that the axis itself is on the orbital plane (similar to Uranus). At one date in the year, the Sun would be directly overhead at the North Pole, so its declination would be +90°. For the next few months, the subsolar point would move toward the South Pole at constant speed, crossing the circles of latitude at a constant rate, so that the solar declination would decrease linearly with time. Eventually, the Sun would be directly above the South Pole, with a declination of −90°; then it would start to move northward at a constant speed. Thus, the graph of solar declination, as seen from this highly tilted Earth, would resemble a triangle wave rather than a sine wave, zigzagging between plus and minus 90°, with linear segments between the maxima and minima.

If the 90° axial tilt is decreased, then the absolute maximum and minimum values of the declination would decrease, to equal the axial tilt. Also, the shapes of the maxima and minima on the graph would become less acute, being curved to resemble the maxima and minima of a sine wave. However, even when the axial tilt equals that of the actual Earth, the maxima and minima remain more acute than those of a sine wave.

In reality, Earth's orbit is elliptical.^{[note 1]} Earth moves more rapidly around the Sun near perihelion, in early January, than near aphelion, in early July. This makes processes like the variation of the solar declination happen faster in January than in July. On the graph, this makes the minima more acute than the maxima. Also, since perihelion and aphelion do not happen on the exact dates as the solstices, the maxima and minima are slightly asymmetrical. The rates of change before and after are not quite equal. Furthermore, Earth's subsolar point only occurs within the tropics.

The graph of apparent solar declination is therefore different in several ways from a sine wave. Calculating it accurately involves some complexity, as shown below.

The declination of the Sun, δ_☉, is the angle between the rays of the Sun and the plane of the Earth's equator. The Earth's axial tilt (called the obliquity of the ecliptic by astronomers) is the angle between the Earth's axis and a line perpendicular to the Earth's orbit. The Earth's axial tilt changes slowly over thousands of years but its current value of about ε = 23.44° is nearly constant, so the change in solar declination during one year is nearly the same as during the next year.

At the solstices, the angle between the rays of the Sun and the plane of the Earth's equator reaches its maximum value of 23.44°. Therefore, δ_☉ = +23.44° at the northern summer solstice and δ_☉ = −23.44° at the southern summer solstice.

At the moment of each equinox, the center of the Sun appears to pass through the celestial equator, and δ_☉ is 0°.

The Sun's declination at any given moment is calculated by:

${\displaystyle \delta _{\odot }=\arcsin \left[\sin \left(-23.44^{\circ }\right)\cdot \sin \left(EL\right)\right]}$

where EL is the ecliptic longitude (essentially, the Earth's position in its orbit). Since the Earth's orbital eccentricity is small, its orbit can be approximated as a circle which causes up to 1° of error. The circle approximation means the EL would be 90° ahead of the solstices in Earth's orbit (at the equinoxes), so that sin(EL) can be written as sin(90+NDS)=cos(NDS) where NDS is the number of days after the December solstice. By also using the approximation that arcsin[sin(d)·cos(NDS)] is close to d·cos(NDS), the following frequently used formula is obtained:

${\displaystyle \delta _{\odot }=-23.44^{\circ }\cdot \cos \left[{\frac {360^{\circ }}{365}}\cdot \left(N+10\right)\right]}$

where N is the day of the year beginning with N=0 at midnight Universal Time (UT) as January 1 begins (i.e. the days part of the ordinal date −1). The number 10, in (N+10), is the approximate number of days after the December solstice to January 1. This equation overestimates the declination near the September equinox by up to +1.5°. The sine function approximation by itself leads to an error of up to 0.26° and has been discouraged for use in solar energy applications.^[2] The 1971 Spencer formula^[10] (based on a Fourier series) is also discouraged for having an error of up to 0.28°.^[11] An additional error of up to 0.5° can occur in all equations around the equinoxes if not using a decimal place when selecting N to adjust for the time after UT midnight for the beginning of that day. So the above equation can have up to 2.0° of error, about four times the Sun's angular width, depending on how it is used.

The declination can be more accurately calculated by not making the two approximations, using the parameters of the Earth's orbit to more accurately estimate EL:^[12]

${\displaystyle \delta _{\odot }=\arcsin \left[\sin \left(-23.44^{\circ }\right)\cdot \cos \left({\frac {360^{\circ }}{365.24}}\left(N+10\right)+{\frac {360^{\circ }}{\pi }}\cdot 0.0167\sin \left({\frac {360^{\circ }}{365.24}}\left(N-2\right)\right)\right)\right]}$

which can be simplified by evaluating constants to:

${\displaystyle \delta _{\odot }=-\arcsin \left[0.39779\cos \left(0.98565^{\circ }\left(N+10\right)+1.914^{\circ }\sin \left(0.98565^{\circ }\left(N-2\right)\right)\right)\right]}$

N is the number of days since midnight UT as January 1 begins (i.e. the days part of the ordinal date −1) and can include decimals to adjust for local times later or earlier in the day. The number 2, in (N-2), is the approximate number of days after January 1 to the Earth's perihelion. The number 0.0167 is the current value of the eccentricity of the Earth's orbit. The eccentricity varies very slowly over time, but for dates fairly close to the present, it can be considered to be constant. The largest errors in this equation are less than ± 0.2°, but are less than ± 0.03° for a given year if the number 10 is adjusted up or down in fractional days as determined by how far the previous year's December solstice occurred before or after noon on December 22. These accuracies are compared to NOAA's advanced calculations^[13][14] which are based on the 1999 Jean Meeus algorithm that is accurate to within 0.01°.^[15]

(The above formula is related to a reasonably simple and accurate calculation of the Equation of Time, which is described here.)

More complicated algorithms^[16][17] correct for changes to the ecliptic longitude by using terms in addition to the 1st-order eccentricity correction above. They also correct the 23.44° obliquity which changes very slightly with time. Corrections may also include the effects of the moon in offsetting the Earth's position from the center of the pair's orbit around the Sun. After obtaining the declination relative to the center of the Earth, a further correction for parallax is applied, which depends on the observer's distance away from the center of the Earth. This correction is less than 0.0025°. The error in calculating the position of the center of the Sun can be less than 0.00015°. For comparison, the Sun's width is about 0.5°.

The declination calculations described above do not include the effects of the refraction of light in the atmosphere, which causes the apparent angle of elevation of the Sun as seen by an observer to be higher than the actual angle of elevation, especially at low Sun elevations.^[2] For example, when the Sun is at an elevation of 10°, it appears to be at 10.1°. The Sun's declination can be used, along with its right ascension, to calculate its azimuth and also its true elevation, which can then be corrected for refraction to give its apparent position.^[2][14][18]

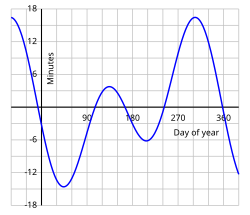
In addition to the annual north–south oscillation of the Sun's apparent position, corresponding to the variation of its declination described above, there is also a smaller but more complex oscillation in the east–west direction. This is caused by the tilt of the Earth's axis, and also by changes in the speed of its orbital motion around the Sun produced by the elliptical shape of the orbit.^[2] The principal effects of this east–west oscillation are variations in the timing of events such as sunrise and sunset, and in the reading of a sundial compared with a clock showing local mean time. As the graph shows, a sundial can be up to about 16 minutes fast or slow, compared with a clock. Since the Earth rotates at a mean speed of one degree every four minutes, relative to the Sun, this 16-minute displacement corresponds to a shift eastward or westward of about four degrees in the apparent position of the Sun, compared with its mean position. A westward shift causes the sundial to be ahead of the clock.

Since the main effect of this oscillation concerns time, it is called the equation of time, using the word "equation" in a somewhat archaic sense meaning "correction". The oscillation is measured in units of time, minutes and seconds, corresponding to the amount that a sundial would be ahead of a clock. The equation of time can be positive or negative.

An analemma is a diagram that shows the annual variation of the Sun's position on the celestial sphere, relative to its mean position, as seen from a fixed location on Earth. (The word analemma is also occasionally, but rarely, used in other contexts.) It can be considered as an image of the Sun's apparent motion during a year, which resembles a figure-8. An analemma can be pictured by superimposing photographs taken at the same time of day, a few days apart for a year.

An analemma can also be considered as a graph of the Sun's declination, usually plotted vertically, against the equation of time, plotted horizontally. Usually, the scales are chosen so that equal distances on the diagram represent equal angles in both directions on the celestial sphere. Thus 4 minutes (more precisely 3 minutes, 56 seconds), in the equation of time, are represented by the same distance as 1° in the declination, since Earth rotates at a mean speed of 1° every 4 minutes, relative to the Sun.

An analemma is drawn as it would be seen in the sky by an observer looking upward. If north is shown at the top, then west is to the right. This is usually done even when the analemma is marked on a geographical globe, on which the continents, etc., are shown with west to the left.

Some analemmas are marked to show the position of the Sun on the graph on various dates, a few days apart, throughout the year. This enables the analemma to be used to make simple analog computations of quantities such as the times and azimuths of sunrise and sunset. Analemmas without date markings are used to correct the time indicated by sundials.^[19]

We see light from the Sun about 20 angle seconds from where the Sun is when the light is seen. See Solar annual aberration.