Hubbry Logo
WavefrontWavefrontMain
Open search
Wavefront
Community hub
Wavefront
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Wavefront
Wavefront
Wavefront
View on Wikipedia
from Wikipedia

In physics, the wavefront of a time-varying wave field is the set (locus) of all points having the same phase.[1] The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined).

Wavefronts usually move with time. For waves propagating in a unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surfaces in a three-dimensional one.

The wavefronts of a plane wave are planes.
Wavefronts change shape after going through a lens.

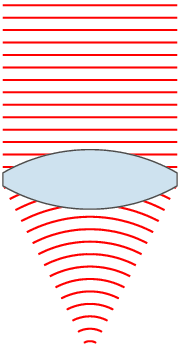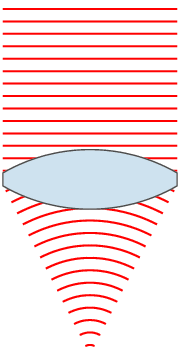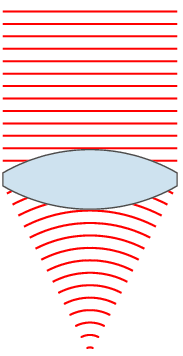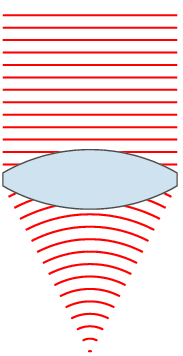
For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefronts may change by refraction. In particular, lenses can change the shape of optical wavefronts from planar to spherical, or vice versa.

In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets.[2] The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength, as shown in the inserted image. This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of different lengths to the registering surface. If there are multiple, closely spaced openings (e.g., a diffraction grating), a complex pattern of varying intensity can result.

Simple wavefronts and propagation

[edit]

Optical systems can be described with Maxwell's equations, and linear propagating waves such as sound or electron beams have similar wave equations. However, given the above simplifications, Huygens' principle provides a quick method to predict the propagation of a wavefront through, for example, free space. The construction is as follows: Let every point on the wavefront be considered a new point source. By calculating the total effect from every point source, the resulting field at new points can be computed. Computational algorithms are often based on this approach. Specific cases for simple wavefronts can be computed directly. For example, a spherical wavefront will remain spherical as the energy of the wave is carried away equally in all directions. Such directions of energy flow, which are always perpendicular to the wavefront, are called rays creating multiple wavefronts.[3]

Rays and wavefronts

The simplest form of a wavefront is the plane wave, where the rays are parallel to one another. The light from this type of wave is referred to as collimated light. The plane wavefront is a good model for a surface-section of a very large spherical wavefront; for instance, sunlight strikes the earth with a spherical wavefront that has a radius of about 150 million kilometers (1 AU). For many purposes, such a wavefront can be considered planar over distances of the diameter of Earth.

In an isotropic medium wavefronts travel with the same speed in all directions.

Wavefront aberrations

[edit]
Main article: Optical aberration

Methods using wavefront measurements or predictions can be considered an advanced approach to lens optics, where a single focal distance may not exist due to lens thickness or imperfections. For manufacturing reasons, a perfect lens has a spherical (or toroidal) surface shape though, theoretically, the ideal surface would be aspheric. Shortcomings such as these in an optical system cause what are called optical aberrations. The best-known aberrations include spherical aberration and coma.[4]

However, there may be more complex sources of aberrations such as in a large telescope due to spatial variations in the index of refraction of the atmosphere. The deviation of a wavefront in an optical system from a desired perfect planar wavefront is called the wavefront aberration. Wavefront aberrations are usually described as either a sampled image or a collection of two-dimensional polynomial terms. Minimization of these aberrations is considered desirable for many applications in optical systems.

Wavefront sensor and reconstruction techniques

[edit]

A wavefront sensor is a device which measures the wavefront aberration in a coherent signal to describe the optical quality or lack thereof in an optical system.[5] There are many applications that include adaptive optics, optical metrology and even the measurement of the aberrations in the eye itself. In this approach, a weak laser source is directed into the eye and the reflection off the retina is sampled and processed. Another application of software reconstruction of the phase is the control of telescopes through the use of adaptive optics.

Mathematical techniques like phase imaging or curvature sensing are also capable of providing wavefront estimations. [6][7]These algorithms compute wavefront images from conventional brightfield images at different focal planes without the need for specialised wavefront optics. [6]While Shack-Hartmann lenslet arrays are limited in lateral resolution to the size of the lenslet array, techniques such as these are only limited by the resolution of digital images used to compute the wavefront measurements. That said, those wavefront sensors suffer from linearity issues and so are much less robust than the original SHWFS, in term of phase measurement.

There are several types of wavefront sensors, including:

Although an amplitude splitting interferometer such as the Michelson interferometer could be called a wavefront sensor, the term is normally applied to instruments that do not require an unaberrated reference beam to interfere with.

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Wavefront

View on Grokipedia
from Grokipedia
A wavefront is a surface or curve that connects all points in a propagating wave disturbance—such as , , or water waves—where the phase of the is identical at a given instant. This locus represents the instantaneous position of the wave's , with the direction of normal to the surface. For plane waves, wavefronts appear as parallel planes, whereas for spherical waves emanating from a , they form expanding concentric spheres. The concept of the wavefront originated in the 17th century with Dutch , who in 1678 proposed his eponymous principle as part of an early wave theory of light. According to Huygens' principle, every point on an existing wavefront serves as a source of secondary spherical wavelets that propagate forward, and the new wavefront is the tangent envelope to these wavelets, enabling predictions of wave behavior beyond straight-line propagation. This framework resolved inconsistencies in earlier particle models of light and laid the groundwork for understanding , , and interference. In modern , wavefronts underpin both wave and ray theories: in , they approximate wave propagation for short wavelengths, where rays—lines to the wavefronts—trace paths efficiently. Aberrations, or distortions in wavefront shape, degrade image quality in optical systems, prompting techniques like wavefront reconstruction to measure and correct phase errors. Applications extend to in telescopes, which compensate for atmospheric turbulence by dynamically reshaping wavefronts to achieve diffraction-limited , and to biomedical fields, where wavefront shaping focuses through scattering media for enhanced and .

Definition and Fundamentals

Definition

A wavefront is defined as the locus of all points in a wave field that have the same phase at a given instant in time, forming an imaginary surface or curve connecting these points. This concept applies primarily to sinusoidal or monochromatic waves, where phase coherence allows for clear identification of such surfaces. The term "wavefront" was introduced by in his 1678 manuscript Traité de la Lumière, where he developed a wave theory of light that explained reflection and refraction through the propagation of secondary wavelets from points on the wavefront. This built upon earlier wave-like ideas proposed by figures such as and , marking a shift toward understanding light as a wave phenomenon rather than purely corpuscular. Wavefronts differ from ray paths in wave optics; rays represent the direction of energy propagation and are lines perpendicular (or orthogonal) to the wavefront at every point, tracing to the phase surface. For visualization, consider the expanding circular crests formed by ripples on a surface after dropping a , where each crest constitutes a two-dimensional wavefront, or the spherical wavefronts emanating from a of in air, propagating outward as variations. Wavefronts emerge as fundamental features in solutions to the wave equation, which governs the propagation of disturbances in media, providing a geometric interpretation of phase constancy without requiring detailed derivations.

Mathematical Representation

In wave optics, a wavefront is mathematically described through the phase of the wavefield. The complex scalar wavefield ψ(r,t)\psi(\mathbf{r}, t) at position r\mathbf{r} and time tt is expressed in phasor form as ψ(r,t)=A(r)exp⁡[i(ϕ(r)−ωt)]\psi(\mathbf{r}, t) = A(\mathbf{r}) \exp[i (\phi(\mathbf{r}) - \omega t)], where A(r)A(\mathbf{r}) is the real-valued amplitude function, ϕ(r)\phi(\mathbf{r}) is the phase function, and ω\omega is the angular frequency. Wavefronts are defined as the isosurfaces where the phase ϕ(r)\phi(\mathbf{r}) is constant, representing loci of points with identical optical path length from the source. The evolution of the wavefield ψ\psi satisfies the scalar in an inhomogeneous medium with n(r)n(\mathbf{r}): ∇2ψ−n2(r)c2∂2ψ∂t2=0\nabla^2 \psi - \frac{n^2(\mathbf{r})}{c^2} \frac{\partial^2 \psi}{\partial t^2} = 0, where cc is the in . Within this framework, wavefronts correspond to the level sets of the phase function ϕ(r)\phi(\mathbf{r}), as the rapid oscillations in the exponential term dominate the wave behavior. For high-frequency approximations, where the wavelength is much smaller than the scale of variations in the medium, the eikonal equation governs the phase: ∣∇ϕ∣=n(r)ω/c|\nabla \phi| = n(\mathbf{r}) \omega / c. This equation is derived by substituting the phasor form into the Helmholtz equation ∇2ψ+k2n2(r)ψ=0\nabla^2 \psi + k^2 n^2(\mathbf{r}) \psi = 0 (with k=ω/ck = \omega / c) and neglecting second-order derivatives of the phase relative to the first-order gradient in the short-wavelength limit. The eikonal approximation thus reduces the wave equation to a first-order partial differential equation for ϕ\phi, enabling ray-tracing methods to describe wavefront propagation geometrically. Specific coordinate systems simplify the mathematical description depending on the wavefront geometry. In Cartesian coordinates, plane wavefronts are represented by a linear phase ϕ(r)=k⋅r\phi(\mathbf{r}) = \mathbf{k} \cdot \mathbf{r}, where k\mathbf{k} is the wave vector with ∣k∣=nk|\mathbf{k}| = n k. For spherical wavefronts emanating from a point source, spherical coordinates (ρ,θ,φ)(\rho, \theta, \varphi) are appropriate, yielding ϕ(ρ)=nkρ\phi(\rho) = n k \rho with amplitude scaling as A(ρ)∝1/ρA(\rho) \propto 1/\rho to conserve energy. Given appropriate initial conditions—such as the initial wavefield ψ(r,0)\psi(\mathbf{r}, 0) and its time ∂ψ/∂t(r,0)\partial \psi / \partial t (\mathbf{r}, 0)—the solution to the wave equation, and thus the evolution of the wavefronts as phase level sets, is unique in bounded domains or under suitable boundary conditions, as established by arguments or maximum principles for hyperbolic PDEs.

Types of Wavefronts

Plane Wavefronts

A plane wavefront is defined as an idealized surface of constant phase that forms an infinite plane perpendicular to the direction of wave propagation, where the phase ϕ=k⋅r\phi = \mathbf{k} \cdot \mathbf{r} remains constant across the surface. This implies that all points on the wavefront oscillate in unison, with the wave vector k\mathbf{k} pointing normal to the plane, ensuring uniform advancement in the propagation direction without . Key properties of plane wavefronts include constant amplitude throughout the infinite extent and the absence of in the ideal case, as the wavefront's uniformity prevents phase variations that cause spreading. Rays associated with such wavefronts are parallel and perpendicular to the plane, facilitating straightforward prediction of wave behavior in homogeneous media. These characteristics make plane wavefronts a foundational model for analyzing uniform propagation, where the wave maintains its planar shape indefinitely. Plane wavefronts can be generated using collimated beams from lasers, which produce nearly rays approximating infinite planes over practical distances, or from distant point sources where spherical wavefronts flatten due to the source's remoteness. For instance, incident on can be treated as a plane wavefront, as the Sun's subtends a small , rendering the incoming waves effectively flat across the planet's scale. In paraxial , plane wavefronts simplify mathematical modeling by allowing linear approximations for ray tracing and phase calculations, reducing complex problems to manageable scalar forms. They are particularly valuable in , where flat reference wavefronts enable precise measurement of phase differences for surface testing and alignment. However, real-world implementations face limitations, as finite apertures in sources or introduce , causing wavefronts to diverge and deviate from ideality even for initially collimated beams.

Curved Wavefronts

Curved wavefronts arise from localized sources, such as point or line emitters, resulting in surfaces of constant phase that exhibit rather than uniformity. Unlike plane wavefronts, these propagate with varying intensity and directionality due to their . Spherical wavefronts emanate from a in an isotropic medium, forming expanding spheres centered at the source. The radius of these spheres increases linearly with time as r=ctr = ct, where cc is the wave speed and tt is the propagation time. The phase at a rr from the source is given by ϕ=kr\phi = kr, with k=2π/λk = 2\pi / \lambda as the and λ\lambda the . This configuration describes divergent propagation, where the wavefront's surface area grows as 4πr24\pi r^2, leading to intensity diminution proportional to 1/r21/r^2. Cylindrical wavefronts originate from an infinite line source, producing circular arcs in planes perpendicular to the line, with no variation along the source axis. These maintain and expand such that intensity decreases as 1/[r](/page/R)1/[r](/page/R) with radial distance [r](/page/R)[r](/page/R). In acoustics, line sources like elongated emitters generate such wavefronts for applications requiring uniform coverage over distance. Cylindrical lenses similarly manipulate wavefronts to focus or diverge in one , converting a into a line image. Converging or diverging curved wavefronts occur when optical elements alter the direction. A converging lens imparts positive to an incoming plane wavefront, causing rays to meet at a focus, while a diverging lens induces negative , spreading rays apart. The RR of the post-lens wavefront relates to the lens ff through the lensmaker's formula, where 1/f=(n−1)(1/R1−1/R2)1/f = (n-1)(1/R_1 - 1/R_2) for nn and surface radii R1,R2R_1, R_2; this determines the vergence change from infinite (plane) to 1/f1/f. Representative examples include from a , which arrives nearly as a plane wavefront due to the great distance from the point-like source, though it is fundamentally a diverging spherical wavefront. Similarly, from a point-like speaker in the near field propagates as an approximate spherical wavefront, with evident close to the source before transitioning toward plane-like behavior at greater distances. Refraction at an interface bends wavefront segments differently based on the speed change in each medium, thereby altering local while preserving the overall topological structure, such as or cylindricity. This effect enables wavefront reshaping without fragmentation.

Propagation Principles

Huygens-Fresnel Principle

The Huygens-Fresnel principle provides a foundational framework for understanding wavefront through and interference in wave . Originally proposed by in 1678 as a geometric construction for wave , the principle posits that every point on an existing wavefront serves as a source of secondary spherical wavelets that expand outward at the speed of the wave. The new wavefront at a later time is then formed as the envelope tangent to these secondary wavelets, effectively describing how waves advance while accounting for their spreading nature. This geometric approach, detailed in Huygens' 1690 treatise Traité de la Lumière, revolutionized the wave theory of light by explaining phenomena like without relying on particle models. Augustin-Jean Fresnel extended Huygens' idea in 1818 by incorporating the wave nature of light, particularly interference among the secondary wavelets, to quantitatively predict diffraction effects. In his prize-winning memoir on diffraction submitted to the French Academy of Sciences, Fresnel introduced an obliquity factor to adjust the amplitude contributions from each secondary source, recognizing that wavelets emitted at oblique angles relative to the observation direction contribute less due to the transverse polarization of light. The obliquity factor is given by (1+cos⁡θ)/2(1 + \cos \theta)/2, where θ\theta is the angle between the normal to the wavefront at the source point and the line connecting it to the observation point; this factor ensures that forward-propagating wavelets (θ≈0\theta \approx 0) contribute fully, while backward ones (θ≈π\theta \approx \pi) are suppressed. This modification transformed the principle into a tool for calculating interference patterns, validating the wave theory against experimental observations like the Poisson spot. The Huygens-Fresnel principle is mathematically formalized through the diffraction , which computes the wave field at an point PP from the field distribution ψ(Q)\psi(Q) over a wavefront surface SS: ψ(P)=1iλ∬Sψ(Q)1+cos⁡θ2rexp⁡(ikr) dS,\psi(P) = \frac{1}{i\lambda} \iint_S \psi(Q) \frac{1 + \cos \theta}{2 r} \exp(ikr) \, dS, where λ\lambda is the , rr is the distance from source point QQ to PP, k=2π/λk = 2\pi / \lambda is the , and the sums the complex amplitudes of the obliquity-weighted spherical waves. This expression, derived from applied to the under the far-field approximation, allows precise prediction of the propagated wavefront by treating it as a superposition of secondary waves. In applications to wavefront , the principle elucidates patterns such as those observed in single-slit experiments, where the wavefront bends around edges to produce alternating bright and dark fringes due to constructive and destructive interference of secondary wavelets. It also explains wave bending around obstacles, as seen in shadow edges, where the envelope of wavelets from the undisturbed portion of the wavefront reconstructs the field beyond the barrier, preventing perfect geometric shadows. These predictions align with experimental validations, including Fresnel's own demonstrations of diffraction halos, and extend to broader wave phenomena like sound around barriers.

Ray Approximation

In geometric optics, rays are defined as lines that are normal to the wavefronts and aligned with the direction of the wave vector k\mathbf{k}, representing the direction of energy propagation perpendicular to the phase fronts. These rays trace the large-scale evolution of wavefronts in media where the wavelength is much smaller than the scale of variations in the refractive index. When a wavefront encounters an interface between two media with different refractive indices, rays refract according to Snell's law, which states that n1sin⁡θ1=n2sin⁡θ2n_1 \sin \theta_1 = n_2 \sin \theta_2, where nn is the refractive index and θ\theta is the angle of incidence or refraction relative to the normal. This refraction bends the rays, causing the wavefront to change direction as one part of the front slows down upon entering the denser medium, thereby altering the overall propagation path. The ray paths followed in this approximation adhere to , which posits that light travels along paths of stationary , minimizing or maximizing the time taken between two points. This principle is mathematically equivalent to the , ∣∇S∣=n|\nabla S| = n, where SS is the function, ensuring rays correspond to the shortest-time trajectories in inhomogeneous media. For rays propagating close to the , the paraxial assumes small angles (θ≪1\theta \ll 1 ), allowing sin⁡θ≈tan⁡θ≈θ\sin \theta \approx \tan \theta \approx \theta. Under this simplification, reduces to n1θ1≈n2θ2n_1 \theta_1 \approx n_2 \theta_2, enabling linear matrix methods to derive lensmaker's formulas and predict without higher-order terms. The ray approximation holds for smooth wavefront propagation but breaks down near caustics—envelopes of ray families where rays converge—or at focal points, where singularities arise and effects dominate, necessitating a transition to full wave optics. In these regions, the geometric model fails to capture interference and amplitude variations accurately.

Wavefront Aberrations

Types of Optical Aberrations

Optical aberrations represent deviations of the actual from the ideal shape, such as a converging spherical wavefront for focused imaging, leading to imperfect point spread functions in optical systems. These aberrations are typically analyzed in monochromatic light, where the errors arise from the geometry of the optical elements rather than wavelength dispersion, though chromatic effects introduce additional wavelength-dependent variations. The primary of monochromatic aberrations uses the Seidel , which decomposes them into five fundamental types based on third-order wave aberrations. Spherical aberration occurs when rays parallel to the optical axis but at different distances from it fail to converge to the same focal point, resulting in a circumferential blur around the ideal focus for on-axis points. Coma, an off-axis aberration, causes asymmetric blurring where point sources appear comet-shaped, with the tail oriented away from the optical axis, due to varying focal lengths for rays in the meridional and sagittal planes. Astigmatism produces two mutually perpendicular line foci instead of a point image for off-axis points, as the tangential and sagittal foci separate along the optical axis. Petzval field curvature warps the image plane into a curved surface, making peripheral points focus inside or outside the nominal focal plane, while central points remain in focus. Distortion, the least affecting resolution but impacting geometry, causes pincushion or barrel warping of the image field, where off-axis points are radially displaced without blurring the local image quality. A more general and orthogonal representation of wavefront aberrations employs , which form a complete set of functions over a unit disk and allow decomposition of the wavefront error into modes ordered by radial degree and azimuthal frequency. For example, the Zernike mode Z20Z_2^0 corresponds to defocus, shifting the best focus position, while Z31Z_3^1 and Z3−1Z_3^{-1} represent horizontal and vertical , capturing the asymmetric tilt in the wavefront. Higher-order terms, such as those for (Z40Z_4^0) or (Z3±3Z_3^{\pm 3}), describe more complex deviations beyond Seidel's third-order approximation. Wavefront error is quantified as the difference (OPD), the deviation in phase or path length from the ideal reference wavefront, often expressed in units of waves (λ) at a specific . The root-mean-square (RMS) wavefront error provides a statistical measure of this deviation, calculated as the standard deviation of the OPD across the , with values below λ/14 typically yielding diffraction-limited performance. These aberrations degrade image quality by broadening and distorting the point spread function (PSF), which convolves with the object to produce blurred images, and by reducing the , defined as the ratio of the observed peak intensity to that of an ideal aberration-free system, where ratios above 0.8 indicate near-diffraction-limited . For instance, primary Seidel aberrations like or introduce asymmetric tails or elongation in the PSF, while creates a halo around the central peak, collectively lowering contrast and resolution.

Causes in Optical Systems

In optical systems, wavefront aberrations often originate from imperfections in the components themselves. Deviations from the ideal aspheric profile of lenses, due to manufacturing challenges in achieving precise s, primarily induce by causing peripheral rays to focus at different points than axial rays, distorting the wavefront . Misalignment of elements, such as tilts or decenterings in multi-lens assemblies, introduces asymmetric phase errors that propagate as higher-order aberrations. Additionally, material inhomogeneities—variations in within the glass arising from uneven or stress during fabrication—create localized phase delays, further degrading wavefront uniformity and contributing to irregular aberration patterns. Atmospheric turbulence represents a primary environmental source of wavefront aberrations, particularly in ground-based astronomical and free-space optical systems. This turbulence follows the Kolmogorov spectrum, a statistical model describing the energy cascade in turbulent eddies over scales from millimeters to kilometers. Random fluctuations in air temperature and pressure generate corresponding variations in the refractive index, with a typical structure constant Cn2C_n^2 ranging from 10−1710^{-17} to 10−1310^{-13} m−2/3^{-2/3} depending on altitude and weather. These index perturbations refract incoming light rays irregularly, imposing phase distortions on the wavefront that manifest as scintillation (rapid intensity fluctuations) and tip-tilt (low-order angular deviations causing image wander). Certain system design limitations inherently produce wavefront aberrations to balance competing requirements like and compactness. In wide-field telescopes, off-axis optical layouts avoid central obscurations for better light collection but introduce field-dependent aberrations, such as , where off-axis points form comet-like images due to asymmetric wavefront tilts. diffraction sets a baseline wavefront error via the Airy pattern, with the diffraction limit defined by θ≈1.22λ/D\theta \approx 1.22 \lambda / D for aperture diameter DD, but suboptimal designs can amplify this into larger phase variations across the . Manufacturing tolerances directly influence wavefront quality by controlling how closely fabricated elements match their specifications. Surface figure errors, quantified as peak-to-valley (P-V) deviations from the nominal shape, translate to wavefront errors roughly twice that for reflective surfaces or scaled by the number of elements in transmissive systems. To achieve diffraction-limited performance—where the exceeds 0.8—tolerances are typically held to λ/4\lambda/4 P-V or better at the operating wavelength λ\lambda, ensuring the root-mean-square (RMS) wavefront error stays below λ/14\lambda/14 per the Rayleigh criterion and minimizing scatter into the of the point spread function. Propagation through media introduces additional wavefront aberrations via material and intensity-dependent effects. Dispersion in optical glasses or fibers causes wavelength-dependent phase velocities, leading to chromatic wavefront errors that broaden pulses or defocus polychromatic beams, with group velocity dispersion quantified by D=d2β/dω2D = d^2\beta / d\omega^2 where β\beta is the . For high-intensity beams, the —a third-order nonlinearity—produces an intensity-dependent change Δn=n2I\Delta n = n_2 I, where n2n_2 is the nonlinear and II the intensity, resulting in self-phase modulation that warps the wavefront and can induce self-focusing or filamentation over propagation distances.

Measurement and Correction

Wavefront Sensing Techniques

Wavefront sensing techniques enable the direct or indirect measurement of wavefront distortions in optical systems, providing essential data for aberration correction in applications such as . These methods typically quantify local slopes, curvatures, or phase differences across the wavefront, with devices like sensors and interferometers converting optical distortions into detectable signals, such as spot displacements or intensity variations. The Shack-Hartmann sensor employs a microlens array to divide the incoming wavefront into sub-apertures, each focusing light onto a (CCD) detector to form an array of spots. Local wavefront are determined by calculating the shifts of these spots relative to their undistorted positions, allowing reconstruction of the overall wavefront shape through integration of the slope data. Developed in the early 1970s at the , this technique achieves a resolution typically supporting 10-100 actuators, with accuracy on the order of λ/20, where λ is the . Recent advances include meta-lens array-based Shack-Hartmann sensors, which enhance phase imaging resolution and compactness using metasurfaces, as demonstrated in studies up to 2024. Interferometric methods measure phase variations by interfering the wavefront with a or sheared copy of itself. In lateral shearing interferometry, the wavefront is displaced relative to itself by a small amount, producing fringes whose patterns encode the local phase gradients or slopes; this approach is particularly effective for high-resolution phase mapping without a separate beam. The Mach-Zehnder interferometer, a classic configuration, splits the into two paths—one distorted and one —recombining them to generate contour maps of the phase differences across the wavefront. These techniques offer high sensitivity to phase changes and are often used for precise, absolute measurements in controlled environments. The pyramid sensor utilizes a pyramid-shaped placed at the focal plane to divide the incoming beam into four overlapping images on a detector. Wavefront slopes are inferred from the differential intensities among these images, with the sensor's response providing a measure of the local tilt; modulation via prism oscillation enhances and prevents saturation for large aberrations. Proposed by Ragazzoni in 1996, this method excels in sensitivity for faint or extended sources, such as in astronomical , and allows adjustable gain by varying the modulation amplitude. Curvature sensing estimates the second derivatives of the wavefront phase by capturing intensity distributions in two defocused images, one before and one after the nominal focus. The difference in normalized intensities between these planes relates directly to the Laplacian of the phase, enabling inference of wavefront without direct measurement; this is grounded in the conservation of across defocus planes. Introduced by Roddier in the late 1980s, the technique is computationally simple and efficient for systems with many actuators, though it requires careful selection of defocus distance to balance sensitivity and dynamic range. Performance metrics for these techniques vary by design and application, with key factors including , sensitivity to low-order aberrations like defocus and , and noise sources such as photon noise. Shack-Hartmann and sensors offer wide dynamic ranges limited primarily by detector size or saturation, achieving high sensitivity (e.g., detecting slopes as small as λ/100) but susceptible to photon noise in low-light conditions; interferometric methods provide superior sensitivity to higher-order aberrations with narrower dynamic ranges dependent on shear or path length, while being robust to some . sensing excels in sensitivity for low-order modes but has a more restricted dynamic range due to focus ambiguity, with photon noise and scintillation as primary limitations. Emerging deep learning-based enhancements to these sensors, such as modified ResNet networks for improved performance in high-speed Shack-Hartmann systems, have shown promise in experimental setups as of 2025. Overall, selection depends on the balance of optical efficiency, computational demands, and environmental factors.

Reconstruction and Adaptive Methods

Reconstruction of the wavefront phase from sensor-derived slope measurements is a critical step in systems, enabling the estimation of aberrations across the . Modal reconstruction represents the wavefront as a linear combination of basis functions, typically or Karhunen-Loève functions, where coefficients are determined by least-squares fitting to minimize the discrepancy between observed slopes and those predicted by the model. , being orthogonal over a circular , efficiently capture low-order aberrations like defocus and , while Karhunen-Loève functions, derived from statistics, provide optimal representation for atmospheric distortions by maximizing variance in the leading modes. This approach reduces dimensionality, facilitating computation in real-time systems, though it assumes the aberration lies within the span of the truncated basis. Zonal reconstruction, in contrast, directly estimates phase values at discrete points corresponding to actuator locations on the corrective device, avoiding global basis assumptions and better suiting high-order or irregular aberrations. In the Southwell geometry, slopes are related to phase differences between adjacent points in a square grid, leading to a sparse matrix formulation solvable via least-squares inversion for efficient wavefront estimation. The Fried geometry modifies this by averaging slopes at subaperture centers, improving stability for hexagonal or irregular arrays common in large telescopes, and is particularly effective when slope measurements align with phase differences over overlapping regions. Both zonal methods enable precise control of discrete actuators but can suffer from noise amplification in ill-conditioned matrices, necessitating regularization techniques. Recent data-driven approaches, including and deep neural networks, have advanced wavefront reconstruction by handling non-linear and high-dimensional data more effectively than traditional methods. These techniques, reviewed in studies up to 2025, enable faster processing and better performance in complex scenarios like strong or media, often integrating with existing modal or zonal frameworks for hybrid systems. The control loop integrates reconstruction with correction: wavefront slopes from the sensor are processed by the reconstructor to compute phase commands, which drive a deformable mirror (DM) or () to apply the conjugate phase, with residual errors fed back for iterative refinement at rates up to several kilohertz. This closed-loop operation compensates for evolving aberrations, maintaining Strehl ratios above 0.5 in moderate after convergence. Deformable mirrors serve as the primary corrective elements, with micro-electro-mechanical systems () offering high density (up to 1000s per device) and piezoelectric stacks providing robust actuation; typical strokes reach λ/2 to λ (where λ is the operating , e.g., 500 nm for visible light), sufficient for quarter-wave correction, while resonant frequencies exceed 1 kHz to track temporal changes in atmospheric seeing. , often liquid-crystal based, complement DMs in lab settings by enabling pixelated without mechanical motion. Iterative algorithms enhance reconstruction accuracy and speed, particularly under varying conditions. For static aberrations, least-squares minimization iteratively solves the overdetermined system of slope equations, converging to the minimum-variance estimate with preconditioning to handle large matrices. In dynamic scenarios like atmospheric turbulence, Kalman filtering extends this by modeling the wavefront as a state evolving under a linear process noise (e.g., wind-driven Taylor hypothesis), predicting future phases and updating with new measurements to reduce latency and suppress noise, achieving prediction horizons of 10-20 ms with residual errors below λ/10 RMS.

Applications

In Optics and Imaging

In optical systems, wavefront analysis plays a pivotal role in enhancing imaging quality by compensating for distortions introduced by the atmosphere, biological tissues, or manufacturing imperfections. (AO) systems, which rely on real-time wavefront sensing and correction, have revolutionized astronomical imaging since the 1990s. At the Keck Observatory, the first AO system on the 10-meter Keck II became operational in 1999, using natural guide stars to achieve near-diffraction-limited performance at near- wavelengths, with resolutions improving from 1 arcsecond (seeing-limited) to about 0.06 arcseconds at 2.2 micrometers. Similarly, the (VLT) at ESO implemented AO on its Unit Telescopes starting in the early , with the NAOS-CONICA instrument enabling high-contrast imaging of faint companions, such as exoplanets around , by correcting atmospheric turbulence over wide fields. These advancements have allowed ground-based telescopes to rival space-based observatories like Hubble in resolution for infrared observations. In , wavefront sensing has transformed by enabling customized correction of higher-order aberrations in the eye. The Shack-Hartmann aberrometer, adapted from astronomical AO, measures the eye's wavefront distortions by analyzing the deflection of rays through a microlens array, providing a map of aberrations like and . Clinical adoption accelerated after 2000, with FDA approval of the LADARVision system in 2002 for wavefront-guided , allowing surgeons to tailor laser ablation profiles to individual aberration patterns and achieve visual outcomes superior to conventional , including reduced halos and improved contrast sensitivity. By the mid-2000s, aberrometry became standard in custom procedures, with studies showing up to 90% of patients achieving 20/20 uncorrected vision or better, compared to 70-80% in non-wavefront-guided treatments. Wavefront correction is equally critical in advanced and , where high (NA) objectives demand precise phase control to maintain resolution. In , objectives with integrated wavefront aberration control, such as those achieving a exceeding 95%, minimize phase errors across the field, ensuring stable imaging for high-NA systems (NA > 1.0) used in biological sample analysis. This correction compensates for mismatches in refractive indices between immersion media and samples, preserving resolution down to 200 nanometers. In (EUV) , wavefront systems monitor and adjust phase aberrations in projection to sub-nanometer levels, enabling patterning of features below 7 nanometers for logic chips. For instance, wavefront sensors in EUV tools detect phase variations, allowing active control that boosts overlay accuracy and yield in high-volume . Recent advances up to 2025 have expanded wavefront applications through computational and hardware innovations. Spatial light modulators (SLMs) enable dynamic wavefront shaping for deep-tissue optical imaging, where scattering in biological media is reversed using iterative optimization algorithms to focus light at depths exceeding 1 millimeter, enhancing fluorescence signals by factors of 100 or more. In 2024, AI-assisted reconstruction methods, such as modified ResNet convolutional neural networks integrated with Shack-Hartmann sensors, accelerated wavefront processing by reducing computation time from seconds to milliseconds while improving accuracy in noisy environments, facilitating real-time correction in portable imaging devices. Overall, these wavefront techniques yield significant performance gains, particularly in resolution. By compensating aberrations, AO systems in and astronomy restore diffraction-limited , effectively pushing effective resolution beyond the uncorrected limit— for example, in super-resolution setups, AO has enabled 50-100 nanometer localization precision in live-cell imaging by minimizing wavefront errors that otherwise blur sub-diffraction features. In astronomy, this has translated to Strehl ratios above 50% at 2 micrometers, allowing detection of objects 100 times fainter than without correction.

In Acoustics and Other Wave Phenomena

In acoustics, wavefronts describe the loci of points where sound waves maintain constant phase as they propagate through elastic media, such as air or water. The propagation speed of these acoustic waves in fluids is determined by c=Bρc = \sqrt{\frac{B}{\rho}}
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.