Recent from talks
Nothing was collected or created yet.
Binary data
View on WikipediaThis article needs additional citations for verification. (April 2019) |
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra.
Binary data occurs in many different technical and scientific fields, where it can be called by different names including bit (binary digit) in computer science, truth value in mathematical logic and related domains and binary variable in statistics.
Mathematical and combinatoric foundations
[edit]A discrete variable that can take only one state contains zero information, and 2 is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information.
A collection of n bits may have 2n states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more (1024) states than three decimal digits (1000). 10k bits are more than sufficient to represent an information (a number or anything else) that requires 3k decimal digits, so information contained in discrete variables with 3, 4, 5, 6, 7, 8, 9, 10... states can be ever superseded by allocating two, three, or four times more bits. So, the use of any other small number than 2 does not provide an advantage.
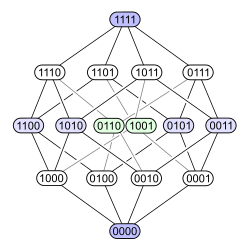
Moreover, Boolean algebra provides a convenient mathematical structure for collection of bits, with a semantic of a collection of propositional variables. Boolean algebra operations are known as "bitwise operations" in computer science. Boolean functions are also well-studied theoretically and easily implementable, either with computer programs or by so-named logic gates in digital electronics. This contributes to the use of bits to represent different data, even those originally not binary.
In statistics
[edit]In statistics, binary data is a statistical data type consisting of categorical data, that can take exactly two possible values, such as "A" and "B", or "heads" and "tails". It is also called dichotomous data, and an older term is quantal data.[1] The two values are often referred to generically as "success" and "failure".[1] As a form of categorical data, binary data is nominal data, meaning the values are qualitatively different and cannot be compared numerically. However, the values are frequently represented as 1 or 0, which corresponds to counting the number of successes in a single trial: 1 (success…) or 0 (failure); see § Counting. More intuitively, binary data can be represented as count data.
Often, binary data is used to represent one of two conceptually opposed values, e.g.:
- the outcome of an experiment ("success" or "failure")
- the response to a yes–no question ("yes" or "no")
- presence or absence of some feature ("is present" or "is not present")
- the truth or falsehood of a proposition ("true" or "false", "correct" or "incorrect")
However, it can also be used for data that is assumed to have only two possible values, even if they are not conceptually opposed or conceptually represent all possible values in the space. For example, binary data is often used to represent the party choices of voters in elections in the United States, i.e. Republican or Democratic. In this case, there is no inherent reason why only two political parties should exist, and indeed, other parties do exist in the U.S., but they are so minor that they are generally simply ignored. Modeling continuous data (or categorical data of more than 2 categories) as a binary variable for analysis purposes is called dichotomization (creating a dichotomy). Like all discretization, it involves discretization error, but the goal is to learn something valuable despite the error: treating it as negligible for the purpose at hand, but remembering that it cannot be assumed to be negligible in general.
Binary variables
[edit]A binary variable is a random variable of binary type, meaning with two possible values. Independent and identically distributed (i.i.d.) binary variables follow a Bernoulli distribution, but in general binary data need not come from i.i.d. variables. Total counts of i.i.d. binary variables (equivalently, sums of i.i.d. binary variables coded as 1 or 0) follow a binomial distribution, but when binary variables are not i.i.d., the distribution need not be binomial.
Counting
[edit]Like categorical data, binary data can be converted to a vector of count data by writing one coordinate for each possible value, and counting 1 for the value that occurs, and 0 for the value that does not occur.[2] For example, if the values are A and B, then the data set A, A, B can be represented in counts as (1, 0), (1, 0), (0, 1). Once converted to counts, binary data can be grouped and the counts added. For instance, if the set A, A, B is grouped, the total counts are (2, 1): 2 A's and 1 B (out of 3 trials).
Since there are only two possible values, this can be simplified to a single count (a scalar value) by considering one value as "success" and the other as "failure", coding a value of the success as 1 and of the failure as 0 (using only the coordinate for the "success" value, not the coordinate for the "failure" value). For example, if the value A is considered "success" (and thus B is considered "failure"), the data set A, A, B would be represented as 1, 1, 0. When this is grouped, the values are added, while the number of trial is generally tracked implicitly. For example, A, A, B would be grouped as 1 + 1 + 0 = 2 successes (out of trials). Going the other way, count data with is binary data, with the two classes being 0 (failure) or 1 (success).
Counts of i.i.d. binary variables follow a binomial distribution, with the total number of trials (points in the grouped data).
Regression
[edit]Regression analysis on predicted outcomes that are binary variables is known as binary regression; when binary data is converted to count data and modeled as i.i.d. variables (so they have a binomial distribution), binomial regression can be used. The most common regression methods for binary data are logistic regression, probit regression, or related types of binary choice models.
Similarly, counts of i.i.d. categorical variables with more than two categories can be modeled with a multinomial regression. Counts of non-i.i.d. binary data can be modeled by more complicated distributions, such as the beta-binomial distribution (a compound distribution). Alternatively, the relationship can be modeled without needing to explicitly model the distribution of the output variable using techniques from generalized linear models, such as quasi-likelihood and a quasibinomial model; see Overdispersion § Binomial.
In computing
[edit]
As modern computers are designed for binary operations and storage, computer data is binary data. Each bit is stored in hardware that stores one of two states.[a][3]
A computer generally accesses memory as a sequence memory locations that consist of a fixed number of bits; often an 8-bit byte but this varies by memory hardware. Higher-level groupings are often defined as well. For example, word typically refers to a group of bytes and a group of words might be called long word or quadword.
Although binary data can be interpreted as purely numeric, some data is more abstract; representing other concepts based on a mapping scheme. For example, memory can contain computer instructions that can control the computer (i.e. via a computer program).
Memory can also contain data that represents text per a character encoding that encodes human-readable information. Although all computer data is binary data, in practice, binary data generally excludes this text data; plain text. Although technically text data is binary data (as all computer data is binary), a distinction is made between data that encoded as text vs. data that is not. Content that represents text can be binary such as an image of text but only data stored as encoded characters is considered text data. All other data is classified as (non-text) binary.
See also
[edit]Notes
[edit]References
[edit]- ^ a b Collett 2002, p. 1.
- ^ Agresti, Alan (2012). "1.2.2 Multinomial Distribution". Categorical Data Analysis (3rd ed.). Wiley. p. 6. ISBN 978-0470463635.
- ^ Gul, Najam (2022-08-18). "How do different types of Data get stored in form of 0 and 1?". Curiosity Tea. Retrieved 2023-01-05.
Collett, David (2002). Modelling Binary Data (Second ed.). CRC Press. ISBN 9781420057386.
Binary data
View on GrokipediaFundamentals
Definition and Properties
Binary data consists of information expressed as a sequence of bits, where each bit represents one of two distinct states, typically denoted as 0 or 1.[5] These states are often analogous to on/off switches in electronic systems or true/false values in logical operations, forming the foundational unit for digital representation.[6] In computing, bits serve as the smallest indivisible elements of data, enabling the encoding of more complex structures through combinations.[7] A key property of binary data is its discreteness, which contrasts with analog data's continuous variation; binary values are confined to exact, finite states without intermediate gradations, making them robust against noise in transmission and storage.[8] The base-2 system is immutable in its structure, relying solely on powers of two for representation, which ensures consistent interpretation across digital systems.[5] Each bit carries unit of information, quantifying the choice between two equally likely alternatives as the fundamental measure in information theory.[9] Binary data's efficiency in electronic representation stems from its two-state simplicity, which aligns directly with the on/off behavior of transistors and switches, unlike decimal systems requiring ten states that complicate hardware implementation.[10] This simplicity enhances reliability and reduces power consumption in digital circuits compared to multi-state alternatives like decimal, where representation is less efficient for storage and processing.[11] For instance, the bit pattern 1010 represents the decimal value 10 or can serve as a flag indicating a specific condition, such as an enabled feature in software.[12]Historical Context
The concept of binary data traces its roots to early philosophical and mathematical explorations of dualistic systems. Gottfried Wilhelm Leibniz outlined his dyadic arithmetic, a binary number system representing numbers using only 0 and 1, in 1679, which he explicitly drew from the ancient Chinese I Ching's hexagrams composed of broken and unbroken lines. He published this as "Explication de l'Arithmétique Binaire" in 1703, positioning binary as a universal language akin to the I Ching's divinatory framework.[13] Complementing these ideas, George Boole introduced algebraic logic in his 1854 book An Investigation of the Laws of Thought, formalizing operations on binary variables (true/false) that laid the groundwork for logical computation without direct reference to numerical representation.[14] The 20th century marked the practical adoption of binary in engineering and computing. Claude Shannon's 1937 master's thesis, "A Symbolic Analysis of Relay and Switching Circuits," demonstrated how Boolean algebra could optimize electrical switching circuits using binary states, bridging abstract logic to physical digital devices.[15] This insight influenced early computers, culminating in John von Neumann's 1945 "First Draft of a Report on the EDVAC," which formalized binary encoding as the basis for stored-program architecture in electronic computing systems.[16] Key milestones included Samuel Morse's development of the electromagnetic telegraph and Morse code in the late 1830s and early 1840s, employing binary on/off signals via dots and dashes for long-distance communication, which predated computational uses but exemplified binary signaling in practice.[17] Standardization accelerated in the mid-20th century amid the transition from decimal to binary systems. The ENIAC, completed in 1945, represented an early adoption of electronic digital computation, though it primarily used decimal rings; its design influenced subsequent binary implementations like the EDVAC. IBM pioneered binary-coded decimal (BCD) in the 1940s for punch-card systems and early machines, encoding decimal digits in binary to facilitate data processing in business applications.[18] By the 1950s, mainframes such as the IBM 701 (1952) and UNIVAC I (1951) shifted to pure binary arithmetic for efficiency in scientific computing, marking a widespread move away from decimal machinery.[19] Post-1991, Unicode evolved binary encoding standards, starting with its inaugural version in 1991 and introducing UTF-8 in 1993 to support global characters via variable-length binary sequences, ensuring compatibility across diverse data systems.[20]Mathematical Foundations
Combinatorics and Counting
The number of distinct binary strings of length is , as each of the positions can independently be either 0 or 1.[21] For example, when , there are 8 possible strings: 000, 001, 010, 011, 100, 101, 110, and 111.[21] Binary strings of length also correspond to the subsets of an -element set, where each 1 indicates inclusion of an element and each 0 indicates exclusion.[22] Consequently, the power set of an -element set contains exactly subsets.[23] This equivalence underpins the binomial theorem, which expands , where counts the number of ways to choose positions for 1s in a binary string of length .[24] The Hamming weight of a binary string is defined as the number of 1s it contains.[25] The Hamming distance between two binary strings and of equal length is the number of positions at which they differ, given by , where denotes the bitwise XOR operation and is the Hamming weight.[26] In coding theory, these concepts enable error detection. For instance, a parity bit can be appended to a binary string to ensure an even number of 1s overall; for the string 101 (which has two 1s), adding a 0 yields 1010, preserving even parity.[27] If transmission flips a bit, the received string will have odd parity, signaling an error.[27]Information Theory Basics
In information theory, binary data serves as the foundational unit for quantifying uncertainty and information content, where each binary digit (bit) represents the smallest indivisible unit of information. Self-information measures the surprise or information conveyed by a specific binary event, defined as , where is the probability of the event occurring; for a binary event like receiving a 1 with probability , this yields bits, establishing bits as the fundamental currency of information in binary systems.[28] For a binary source emitting symbols 0 and 1 independently with probability for 1 (and for 0), the average information per symbol is captured by the Shannon entropy, also known as the binary entropy function: This function reaches its maximum value of 1 bit when , indicating maximum uncertainty for a fair coin flip, and decreases symmetrically to 0 as approaches 0 or 1, reflecting predictability in biased sources.[28] In communication channels, binary data transmission is often modeled by the binary symmetric channel (BSC), where bits are flipped with error probability independently of the input. The channel capacity, representing the maximum mutual information achievable, is , measured in bits per channel use; for , capacity is 1 bit (noiseless), while it approaches 0 as nears 0.5, highlighting the impact of noise on reliable binary communication.[28] Huffman coding provides an optimal method for lossless compression of binary data sources with known probabilities, constructing prefix-free codes that minimize average codeword length. For symbol probabilities {0.5, 0.25, 0.25}, the algorithm assigns code lengths of 1, 2, and 2 bits respectively (e.g., 0 for the most probable, 10 and 11 for the others), achieving an average length of 1.5 bits per symbol, which equals the entropy bound for efficient encoding.[29]Statistical Applications
Binary Variables and Distributions
In statistics, a binary variable is a categorical random variable that assumes exactly one of two possible values, typically coded as 0 or 1 to represent distinct outcomes such as failure/success or false/true.[30] This coding facilitates quantitative analysis while preserving the dichotomous nature of the data.[31] The Bernoulli distribution provides the foundational probabilistic model for a single binary variable , defined by a single parameter representing the probability of success.[30] Specifically, the probability mass function is given by: The expected value (mean) is , and the variance is , which achieves its maximum of 0.25 when .[30] This distribution, first rigorously developed by Jacob Bernoulli in his seminal 1713 treatise Ars Conjectandi, underpins much of modern probability theory for two-state systems.[32] For scenarios involving multiple independent binary trials, the binomial distribution models the count of successes in fixed Bernoulli trials, each with the same success probability .[33] The probability mass function is: where denotes the binomial coefficient.[30] The mean is and the variance is , reflecting the additive properties of independent trials.[33] This distribution is particularly useful for aggregating binary outcomes over repeated experiments. Common applications include modeling coin flips, where a fair coin has , yielding symmetric probabilities for heads or tails in a single trial under the Bernoulli distribution or multiple flips under the binomial.[30] In hypothesis testing, binary outcomes appear in A/B tests, such as comparing conversion rates (success as user engagement) between two website variants, where the binomial distribution quantifies the number of successes in each group to assess differences in .[34]Regression and Modeling
In statistical modeling, binary data often serves as the response variable in regression analyses where the outcome is dichotomous, such as success/failure or presence/absence. Logistic regression is a foundational method for this purpose, modeling the probability of the positive outcome through the logit link function. For a binary response taking values 0 or 1, the model specifies , where is a predictor and are parameters estimated via maximum likelihood.[35] The exponentiated coefficient represents the odds ratio, quantifying how the odds of change with a one-unit increase in .[35] An alternative to logistic regression is the probit model, which links the probability to the inverse cumulative distribution function of the standard normal distribution. Here, , where is the normal CDF, providing a similar interpretation but assuming an underlying normal latent variable.[36] Probit models are particularly common in econometrics and biostatistics for their connection to threshold models of decision-making.[36] Binary data can also appear as predictors in regression models, typically encoded as dummy variables that take values 0 or 1 to represent categories. In a linear regression context, including a dummy variable shifts the intercept by when , with the coefficient interpreted as the average difference in the response between the two groups, holding other variables constant.[37] This approach allows categorical binary information, such as treatment versus control, to be incorporated without assuming continuity.[37] Evaluating models with binary outcomes requires metrics beyond mean squared error, as they assess classification performance. The area under the receiver operating characteristic curve (AUC-ROC) measures the model's ability to discriminate between classes, with values ranging from 0.5 (random) to 1 (perfect separation); it represents the probability that a randomly chosen positive instance ranks higher than a negative one.[38] For instance, in predicting disease presence (coded as ) from clinical predictors, an AUC-ROC of 0.85 indicates strong discriminatory power for identifying at-risk patients.[38]Computer Science Usage
Representation and Encoding
Binary data in computing systems is typically represented using standardized encoding schemes that map higher-level data types, such as characters and numbers, into fixed or variable-length sequences of bits. These encodings ensure compatibility across hardware and software platforms for storage and transmission. One of the earliest and most foundational schemes is the American Standard Code for Information Interchange (ASCII), which uses 7 bits to represent 128 characters, including uppercase and lowercase letters, digits, and control symbols; for example, the character 'A' is encoded as 01000001 in binary.[39] Extended 8-bit versions, such as ISO-8859-1, allow for 256 characters by utilizing the full byte, accommodating additional symbols like accented letters. For broader international support, modern systems employ UTF-8, a variable-length encoding of the Unicode character set that uses 1 to 4 bytes per character, preserving ASCII compatibility for the first 128 code points while efficiently handling over a million possible characters with longer sequences for rarer symbols.[40] This scheme is particularly advantageous for transmission, as it minimizes bandwidth for English text (1 byte per character) while scaling for multilingual content, such as encoding the Unicode character U+1F600 (grinning face) as the 4-byte sequence 11110000 10011111 10011000 10000000.[40] Numerical values are encoded in binary using conventions that support both integers and floating-point numbers. Signed integers commonly use two's complement representation, where the most significant bit indicates the sign (0 for positive, 1 for negative), and negative values are formed by inverting all bits of the absolute value and adding 1; for instance, -5 in 8-bit two's complement is 11111011, allowing arithmetic operations to treat positive and negative numbers uniformly without special hardware.[41] Floating-point numbers follow the IEEE 754 standard, which defines binary formats with a sign bit, an exponent field, and a mantissa (significand); the single-precision (32-bit) format allocates 1 bit for the sign, 8 bits for the biased exponent, and 23 bits for the mantissa, enabling representation of numbers from approximately ±1.18 × 10⁻³⁸ to ±3.40 × 10³⁸ with about 7 decimal digits of precision.[42] In file formats, binary data contrasts with text files by storing information in a machine-readable structure rather than human-readable characters, often without line endings or delimiters that imply textual interpretation; text files encode data as sequences of printable characters (e.g., via ASCII), while binary files directly embed raw bytes for efficiency.[43] A prominent example is the JPEG image format, where the file header begins with the binary bytes FF D8 (Start of Image marker) followed by application-specific data in binary, such as JFIF identifiers and quantization tables, before the compressed image data.[44] Compression techniques tailored to binary data exploit its bit-level simplicity, particularly for repetitive patterns. Run-length encoding (RLE) is a lossless method ideal for binary images, where sequences of identical bits (runs of 0s or 1s) are replaced by a count and the bit value; for a row like 0000011110 in a black-and-white image, it might be encoded as (5 zeros, 4 ones, 1 zero), reducing storage for sparse or uniform regions like scanned documents.[45] This approach achieves high compression ratios on binary data due to the prevalence of long runs, though it performs poorly on complex patterns.Storage and Operations
Binary data is stored in computer memory as sequences of bits, where each bit represents either a 0 or 1 state. In random-access memory (RAM), particularly dynamic RAM (DRAM), individual bits are stored using capacitors that hold a charge to indicate 1 or discharge for 0, refreshed periodically to prevent data loss. Static RAM (SRAM), used in caches, employs flip-flops—circuits that maintain state using feedback transistors—to store bits without refresh. Read-only memory (ROM) stores bits more permanently, often via fuses, mask programming, or floating-gate transistors in flash ROM, ensuring data persistence even without power.[46] Memory is organized into bytes, each comprising 8 bits, allowing efficient addressing and access.[47] Addresses themselves are binary numbers, with the central processing unit (CPU) using these to locate specific bytes via address lines in hardware.[47] Arithmetic operations on binary data mimic decimal processes but operate bit by bit. Binary addition sums two bits plus any carry-in, producing a sum bit and carry-out: for instance, 0 + 0 = 0 (no carry), 1 + 1 = 0 with carry 1, and 1 + 1 + 1 (with carry-in) = 1 with carry 1.[48] Subtraction uses two's complement representation, where the subtrahend is inverted and added to the minuend plus 1, propagating borrows akin to carries.[49] Multiplication is achieved through shifts and additions: the multiplicand is shifted left (multiplying by 2) for each 1 bit in the multiplier, then added to an accumulator, as in the basic shift-and-add algorithm.[50] Bitwise operations enable direct manipulation of binary representations for tasks like masking or encryption. The AND operation (&) outputs 1 only if both input bits are 1, useful for clearing bits; for example,1010 & 1100 = 1000 (10 in decimal AND 12 = 8).[51] OR (|) outputs 1 if at least one input is 1, setting bits; XOR (^) outputs 1 for differing bits, aiding parity checks; and NOT (~) inverts all bits (0 to 1, 1 to 0).[52] Left shift (<<) moves bits toward higher significance, equivalent to multiplication by powers of 2 (e.g., x << 1 = x * 2), while right shift (>>) divides by powers of 2, filling with zeros (unsigned) or sign bits (signed).[53]
In CPU processing, the arithmetic logic unit (ALU) executes these operations on binary data fetched from registers or memory.[54] The ALU handles bitwise logic, shifts, and arithmetic using combinational circuits like full adders for carries. Instructions are encoded as binary machine code; in x86 architecture, for example, the ADD operation between registers uses opcode 0x01 followed by ModR/M bytes specifying operands, such as 01 18 for ADD [EAX], EBX in certain encodings.[55] This binary encoding allows the CPU to decode and route signals to the ALU for execution.[56]
Broader Applications
In Digital Electronics and Engineering
In digital electronics, binary data forms the foundation of logic circuits, where binary states (0 and 1) are represented and manipulated using electronic components to perform computational operations. Logic gates are the basic building blocks, implementing Boolean functions through transistor networks that process binary inputs to produce binary outputs. These gates enable the construction of complex digital systems by combining simple binary decisions. The fundamental logic gates include AND, OR, NOT, and XOR, each defined by their truth tables that specify outputs for all possible binary input combinations. For the AND gate, the output is 1 only if both inputs are 1; otherwise, it is 0.[57]| A | B | AND Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | OR Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A | NOT Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
| A | B | XOR Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |



