| Truncated 5-demicube Cantic 5-cube | |
|---|---|
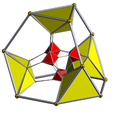
 D5 Coxeter plane projection | |
| Type | uniform 5-polytope |
| Schläfli symbol | h2{4,3,3,3} t{3,32,1} |
| Coxeter-Dynkin diagram | |
| 4-faces | 42 total: 16 r{3,3,3} 16 t{3,3,3} 10 t{3,3,4} |
| Cells | 280 total: 80 {3,3} 120 t{3,3} 80 {3,4} |
| Faces | 640 total: 480 {3} 160 {6} |
| Edges | 560 |
| Vertices | 160 |
| Vertex figure |  ( )v{ }×{3} |
| Coxeter groups | D5, [32,1,1] |
| Properties | convex |
In geometry of five dimensions or higher, a cantic 5-cube, cantihalf 5-cube, truncated 5-demicube is a uniform 5-polytope, being a truncation of the 5-demicube. It has half the vertices of a cantellated 5-cube.
The Cartesian coordinates for the 160 vertices of a cantic 5-cube centered at the origin and edge length 6√2 are coordinate permutations:
with an odd number of plus signs.
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 
|

|
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [4] |
It has half the vertices of the cantellated 5-cube, as compared here in the B5 Coxeter plane projections:
 Cantic 5-cube |
 Cantellated 5-cube |
This polytope is based on the 5-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
| n | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| Symmetry [1+,4,3n-2] |
[1+,4,3] = [3,3] |
[1+,4,32] = [3,31,1] |
[1+,4,33] = [3,32,1] |
[1+,4,34] = [3,33,1] |
[1+,4,35] = [3,34,1] |
[1+,4,36] = [3,35,1] |
| Cantic figure |

|
|
|

|

|

|
| Coxeter | = |
= |
= |
= |
= |
= |
| Schläfli | h2{4,3} | h2{4,32} | h2{4,33} | h2{4,34} | h2{4,35} | h2{4,36} |
There are 23 uniform 5-polytope that can be constructed from the D5 symmetry of the 5-demicube, of which are unique to this family, and 15 are shared within the 5-cube family.
| D5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 h{4,3,3,3} |
 h2{4,3,3,3} |
 h3{4,3,3,3} |
 h4{4,3,3,3} |
 h2,3{4,3,3,3} |
 h2,4{4,3,3,3} |
 h3,4{4,3,3,3} |
 h2,3,4{4,3,3,3} | ||||