Hubbry Logo
Structural isomerStructural isomerMain
Open search
Structural isomer
Community hub
Structural isomer
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Structural isomer
Structural isomer
Structural isomer
View on Wikipedia
from Wikipedia

In chemistry, a structural isomer (or constitutional isomer in the IUPAC nomenclature[1]) of a compound is a compound that contains the same number and type of atoms, but with a different connectivity (i.e. arrangement of bonds) between them.[2][3] The term metamer was formerly used for the same concept.[4]

For example, butanol H3C−(CH2)3−OH, methyl propyl ether H3C−(CH2)2−O−CH3, and diethyl ether (H3CCH2−)2O have the same molecular formula C4H10O but are three distinct structural isomers.

The concept applies also to polyatomic ions with the same total charge. A classical example is the cyanate ion O=C=N− and the fulminate ion C−≡N+−O−. It is also extended to ionic compounds, so that (for example) ammonium cyanate [NH4]+[O=C=N]− and urea (H2N−)2C=O are considered structural isomers,[4] and so are methylammonium formate [H3C−NH3]+[HCO2]− and ammonium acetate [NH4]+[H3C−CO2]−.

Structural isomerism is the most radical type of isomerism. It is opposed to stereoisomerism, in which the atoms and bonding scheme are the same, but only the relative spatial arrangement of the atoms is different.[5][6] Examples of the latter are the enantiomers, whose molecules are mirror images of each other, and the cis and trans versions of 2-butene.

Among the structural isomers, one can distinguish several classes including skeletal isomers, positional isomers (or regioisomers), functional isomers, tautomers,[7] and structural isotopomers.[8]

Skeletal isomerism

[edit]

A skeletal isomer of a compound is a structural isomer that differs from it in the atoms and bonds that are considered to comprise the "skeleton" of the molecule. For organic compounds, such as alkanes, that usually means the carbon atoms and the bonds between them.

For example, there are three skeletal isomers of pentane: n-pentane (often called simply "pentane"), isopentane (2-methylbutane) and neopentane (dimethylpropane).[9]

Skeletal isomers of pentane
n-Pentane Isopentane Neopentane

If the skeleton is acyclic, as in the above example, one may use the term chain isomerism.

Position isomerism (regioisomerism)

[edit]
See also: Arene substitution pattern § Ortho, meta, and para substitution

Position isomers (also positional isomers or regioisomers) are structural isomers that can be viewed as differing only on the position of a functional group, substituent, or some other feature on the same "parent" structure.[10]

For example, replacing one of the 12 hydrogen atoms –H by a hydroxyl group –OH on the n-pentane parent molecule can give any of three different position isomers:

Pentan-1-ol Pentan-2-ol Pentan-3-ol

Another example of regioisomers are α-linolenic and γ-linolenic acids, both octadecatrienoic acids, each of which has three double bonds, but on different positions along the chain.

Functional isomerism

[edit]

Functional isomers are structural isomers which have different functional groups, resulting in significantly different chemical and physical properties.[11]

An example is the pair propanal H3C–CH2–C(=O)-H and acetone H3C–C(=O)–CH3: the first has a –C(=O)H functional group, which makes it an aldehyde, whereas the second has a C–C(=O)–C group, that makes it a ketone.

Another example is the pair ethanol H3C–CH2–OH (an alcohol) and dimethyl ether H3C–O–CH2H (an ether). In contrast, 1-propanol and 2-propanol are structural isomers, but not functional isomers, since they have the same significant functional group (the hydroxyl –OH) and are both alcohols.

Besides the different chemistry, functional isomers typically have very different infrared spectra. The infrared spectrum is largely determined by the vibration modes of the molecule, and functional groups like hydroxyl and esters have very different vibration modes. Thus 1-propanol and 2-propanol have relatively similar infrared spectra because of the hydroxyl group, which are fairly different from that of methyl ethyl ether.[citation needed]

Structural isotopomers

[edit]
Main article: Isotopomer

In chemistry, one usually ignores distinctions between isotopes of the same element. However, in some situations (for instance in Raman, NMR, or microwave spectroscopy) one may treat different isotopes of the same element as different elements. In the second case, two molecules with the same number of atoms of each isotope but distinct bonding schemes are said to be structural isotopomers.

Thus, for example, ethene would have no structural isomers under the first interpretation; but replacing two of the hydrogen atoms (1H) by deuterium atoms (2H) may yield any of two structural isotopomers (1,1-dideuteroethene and 1,2-dideuteroethene), if both carbon atoms are the same isotope. If, in addition, the two carbons are different isotopes (say, 12C and 13C), there would be three distinct structural isotopomers, since 1-13C-1,1-dideuteroethene would be different from 1-13C-2,2-dideuteroethene. And, in both cases, the 1,2-dideutero structural isotopomer would occur as two stereoisotopomers, cis and trans.

Structural equivalence and symmetry

[edit]

Structural equivalence

[edit]

Two molecules (including polyatomic ions) A and B have the same structure if each atom of A can be paired with an atom of B of the same element, in a one-to-one way, so that for every bond in A there is a bond in B, of the same type, between corresponding atoms; and vice versa.[3] This requirement applies also to complex bonds that involve three or more atoms, such as the delocalized bonding in the benzene molecule and other aromatic compounds.

Depending on the context, one may require that each atom be paired with an atom of the same isotope, not just of the same element.

Two molecules then can be said to be structural isomers (or, if isotopes matter, structural isotopomers) if they have the same molecular formula but do not have the same structure.

Structural symmetry and equivalent atoms

[edit]

Structural symmetry of a molecule can be defined mathematically as a permutation of the atoms that exchanges at least two atoms but does not change the molecule's structure. Two atoms then can be said to be structurally equivalent if there is a structural symmetry that takes one to the other.[12]

Thus, for example, all four hydrogen atoms of methane are structurally equivalent, because any permutation of them will preserve all the bonds of the molecule.

Likewise, all six hydrogens of ethane (C
2H
6) are structurally equivalent to each other, as are the two carbons; because any hydrogen can be switched with any other, either by a permutation that swaps just those two atoms, or by a permutation that swaps the two carbons and each hydrogen in one methyl group with a different hydrogen on the other methyl. Either operation preserves the structure of the molecule. That is the case also for the hydrogen atoms in cyclopentane, allene, 2-butyne, hexamethylenetetramine, prismane, cubane, dodecahedrane, etc.

On the other hand, the hydrogen atoms of propane are not all structurally equivalent. The six hydrogens attached to the first and third carbons are equivalent, as in ethane, and the two attached to the middle carbon are equivalent to each other; but there is no equivalence between these two equivalence classes.

Symmetry and positional isomerism

[edit]

Structural equivalences between atoms of a parent molecule reduce the number of positional isomers that can be obtained by replacing those atoms for a different element or group. Thus, for example, the structural equivalence between the six hydrogens of ethane C
2H
6 means that there is just one structural isomer of ethanol C
2H
5OH, not 6. The eight hydrogens of propane C
3H
8 are partitioned into two structural equivalence classes (the six on the methyl groups, and the two on the central carbon); therefore there are only two positional isomers of propanol (1-propanol and 2-propanol). Likewise there are only two positional isomers of butanol, and three of pentanol or hexanol.

Symmetry breaking by substitutions

[edit]

Once a substitution is made on a parent molecule, its structural symmetry is usually reduced, meaning that atoms that were formerly equivalent may no longer be so. Thus substitution of two or more equivalent atoms by the same element may generate more than one positional isomer.

The classical example is the derivatives of benzene. Its six hydrogens are all structurally equivalent, and so are the six carbons; because the structure is not changed if the atoms are permuted in ways that correspond to flipping the molecule over or rotating it by multiples of 60 degrees. Therefore, replacing any hydrogen by chlorine yields only one chlorobenzene. However, with that replacement, the atom permutations that moved that hydrogen are no longer valid. Only one permutation remains, that corresponds to flipping the molecule over while keeping the chlorine fixed. The five remaining hydrogens then fall into three different equivalence classes: the one opposite to the chlorine is a class by itself (called the para position), the two closest to the chlorine form another class (ortho), and the remaining two are the third class (meta). Thus a second substitution of hydrogen by chlorine can yield three positional isomers: 1,2- or ortho-, 1,3- or meta-, and 1,4- or para-dichlorobenzene.

ortho-Dichlorobenzene meta-Dichlorobenzene para-Dichlorobenzene
1,2-Dichlorobenzene 1,3-Dichlorobenzene 1,4-Dichlorobenzene

For the same reason, there is only one phenol (hydroxybenzene), but three benzenediols; and one toluene (methylbenzene), but three toluols, and three xylenes.

On the other hand, the second replacement (by the same substituent) may preserve or even increase the symmetry of the molecule, and thus may preserve or reduce the number of equivalence classes for the next replacement. Thus, the four remaining hydrogens in meta-dichlorobenzene still fall into three classes, while those of ortho- fall into two, and those of para- are all equivalent again. Still, some of these 3 + 2 + 1 = 6 substitutions end up yielding the same structure, so there are only three structurally distinct trichlorobenzenes: 1,2,3-, 1,2,4-, and 1,3,5-.

1,2,3-Trichlorobenzene 1,2,4-Trichlorobenzene 1,3,5-Trichlorobenzene

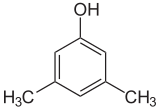
If the substituents at each step are different, there will usually be more structural isomers. Xylenol, which is benzene with one hydroxyl substituent and two methyl substituents, has a total of 6 isomers:

2,3-Xylenol 2,4-Xylenol 2,5-Xylenol
2,6-Xylenol 3,4-Xylenol 3,5-Xylenol

Isomer enumeration and counting

[edit]

Enumerating or counting structural isomers in general is a difficult problem, since one must take into account several bond types (including delocalized ones), cyclic structures, and structures that cannot possibly be realized due to valence or geometric constraints, and non-separable tautomers.

For example, there are nine structural isomers with molecular formula C3H6O having different bond connectivities. Seven of them are air-stable at room temperature, and these are given in the table below.

Compounds with molecular formula C3H6O
Name Molecular structure Melting
point (°C)		 Boiling
point (°C)		 Comment
Allyl alcohol –129 97
Cyclopropanol 101–102
Propionaldehyde –81 48 Tautomeric with prop-1-en-1-ol, which has both cis and trans stereoisomeric forms
Acetone 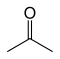–94.9 56.53 Tautomeric with propen-2-ol
Oxetane –97 48
Propylene oxide –112 34 Has two enantiomeric forms
Methyl vinyl ether –122 6

Two structural isomers are the enol tautomers of the carbonyl isomers (propionaldehyde and acetone), but these are not stable.[13]

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Structural isomer

View on Grokipedia
from Grokipedia
Structural isomers, also known as constitutional isomers, are molecules that share the same molecular formula but exhibit different connectivity between their atoms, resulting in distinct structural arrangements. This form of isomerism contrasts with , where connectivity is identical but spatial arrangements vary. Structural isomerism encompasses several subtypes based on the nature of the structural differences. Chain isomers feature variations in the carbon skeleton, such as straight-chain versus branched configurations, as seen in n-butane and isobutane, both with the formula C₄H₁₀. Position isomers have the same carbon chain and functional groups but differ in the placement of these groups along the chain, for example, 1-propanol and 2-propanol (C₃H₈O). Functional group isomers involve compounds with the same formula but belonging to different functional group classes, such as ethanol (an alcohol) and dimethyl ether (an ether), both C₂H₆O. These isomers typically display markedly different physical and chemical properties, including boiling points, melting points, , and reactivity, due to their unique structures. The phenomenon is particularly prevalent in , where increasing molecular complexity leads to a rapid rise in the number of possible structural isomers, influencing fields like pharmaceuticals, , and biochemistry.

Fundamentals

Definition and Scope

Structural isomers, also known as constitutional isomers, are molecules that possess the same molecular formula but differ in the connectivity of their atoms, resulting in distinct structural arrangements described by different line formulae. This form of isomerism arises from variations in how atoms are bonded together, leading to compounds with potentially different physical and chemical properties despite sharing the same elemental composition. The scope of structural isomerism is primarily confined to constitutional variants in both organic and , where the focus is on differences in atomic rather than spatial orientation. It excludes stereoisomers, which maintain the same connectivity but vary in three-dimensional arrangement, and tautomers, which are rapidly interconverting constitutional forms typically not classified as stable structural isomers unless explicitly noted. This distinction ensures that structural isomerism emphasizes fixed bonding differences, applicable across diverse chemical contexts from simple hydrocarbons to complex coordination compounds. The recognition of structural isomerism emerged in the mid-19th century as part of the development of structural organic theory, pioneered by chemists like , who in 1857-1858 proposed that carbon's tetravalency enables varied atomic linkages to explain observed molecular diversity. A classic early example involves the C₄H₁₀ isomers n-butane and (2-methylpropane), first isolated and characterized in the 1860s from , illustrating how linear and branched carbon chains yield distinct compounds with the same formula. The structural formulas are:
  • n-Butane: CH₃-CH₂-CH₂-CH₃
  • Isobutane: (CH₃)₂CH-CH₃
These cases highlighted isomerism's role in expanding the understanding of chemical variety beyond mere composition. Understanding structural isomerism requires familiarity with molecular formula notation, such as the general CₙH₂ₙ₊₂ for acyclic alkanes, which predicts the hydrogen count based on carbon atoms and saturation, serving as a prerequisite for identifying potential isomeric structures.

Comparison to Other Isomer Types

Structural isomers, also known as constitutional isomers, are distinguished from other types of isomers primarily by differences in the connectivity of atoms, while sharing the same molecular . According to IUPAC recommendations, isomers are with identical atomic composition but differing line formulae (indicating connectivity) or stereochemical formulae (indicating spatial arrangement), leading to distinct properties. Structural isomers specifically exhibit different line formulae, meaning the atoms are bonded in different sequences or arrangements, whereas stereoisomers maintain the same connectivity but differ in the three-dimensional orientation of atoms or groups. This classification is based on IUPAC criteria requiring distinct constitutional diagrams for structural isomers, ensuring they cannot be superimposed by or reflection without altering bond connections. In contrast, stereoisomers include categories such as enantiomers (non-superimposable mirror images due to ) and diastereomers (stereoisomers that are not mirror images, often arising from geometric isomerism). For example, cis-trans isomers in alkenes like 2-butene represent stereoisomers because the carbon-carbon restricts , resulting in different spatial arrangements around the without changing atom connectivity; these are not structural isomers. Atropisomers, such as certain biaryl compounds with bulky substituents, are another form of stereoisomers classified as stable conformers due to hindered about a , allowing isolation as separate entities, but they still share the same connectivity and thus differ from structural isomers. Tautomers are a subset of structural isomers characterized by rapid interconversion, typically via proton transfer, as seen in keto-enol tautomerism where a compound like acetone equilibrates with its form; this mobility distinguishes them from typical structural isomers that do not interconvert easily under standard conditions. Unlike stereoisomers, which require energy barriers like double bonds or chiral centers for stability, tautomers involve constitutional changes but are dynamically linked. The following table summarizes key differences:
AspectStructural IsomersStereoisomersTautomers
Atom ConnectivityDifferent (e.g., branched vs. straight chain)SameDifferent, but interconvertible
Spatial ArrangementMay vary, but not the defining featureDifferent (e.g., cis vs. trans, vs. S)Varies with interconversion
InterconversionRequires bond breaking/reformationRequires rotation or reconfiguration without bond breakingRapid, often via proton shift
Examplen-Pentane vs. (E)-2-butene vs. (Z)-2-buteneAcetone (keto) vs. enol form
StabilityGenerally stable and isolableStable if barrier high (e.g., geometric)Equilibrium mixture, not always isolable
A common misconception is that conformers—different spatial arrangements arising from rotation about single bonds—are isomers; however, unless the rotation is sufficiently hindered to allow isolation (as in atropisomers), conformers are not classified as stereoisomers because they interconvert rapidly at without breaking bonds. This distinction emphasizes that true isomerism implies more persistent structural or spatial differences.

Types of Constitutional Isomerism

Skeletal Isomerism

Skeletal isomerism arises from variations in the connectivity of the carbon atoms forming the molecular backbone, resulting in different chain lengths or branching patterns while preserving the overall molecular formula and functional groups. This type of constitutional isomerism is prevalent in hydrocarbons and other compounds where the carbon framework can adopt straight-chain, branched, or even cyclic arrangements, though cycles are often classified separately. The differences in skeletal influence molecular shape, packing efficiency, and interactions, leading to distinct physical and chemical properties. A representative set of skeletal isomers is found among the alkanes with the formula C₅H₁₂, which includes three distinct structures: n-pentane, (also known as 2-methylbutane), and (2,2-dimethylpropane). In n-pentane, the carbon skeleton forms a straight chain of five atoms, depicted as CH₃–CH₂–CH₂–CH₂–CH₃. features a four-carbon chain with a methyl at the second carbon, shown as (CH₃)₂CH–CH₂–CH₃. has a highly compact skeleton with a central carbon bonded to four methyl groups, represented as C(CH₃)₄. These variations illustrate how branching alters the overall geometry from linear to increasingly spherical. The International Union of Pure and Applied Chemistry (IUPAC) nomenclature for skeletal isomers emphasizes identifying the longest continuous carbon chain as the parent structure, to which substituents are added based on their positions. For instance, in isopentane, the longest chain is butane (four carbons), and the methyl group attached to carbon 2 yields the name 2-methylbutane; numbering starts from the end that gives the lowest locant to the branch. In neopentane, the parent chain is propane with two methyl groups on carbon 2, but it is systematically named 2,2-dimethylpropane to reflect the longest chain rule. This systematic approach ensures unique names for each skeletal variant, facilitating identification in synthesis and analysis. Skeletal differences significantly affect physical properties, particularly points, due to changes in molecular surface area and intermolecular forces. Straight-chain isomers like n-pentane exhibit higher points from greater van der Waals interactions along their extended shape, at 36.1°C, compared to the more compact branched at 27.8°C and at 9.5°C. The spherical nature of highly branched structures reduces contact points between molecules, lowering points and volatility. Analogous skeletal isomerism appears in inorganic compounds such as silanes, where atoms form chain frameworks similar to carbon. For tetrasilane (Si₄H₁₀), n-tetrasilane adopts a linear H₃Si–SiH₂–SiH₂–SiH₃ structure, while the branched isotetrasilane (silyltrisilane) features a central bonded to three SiH₃ groups, H₃Si–SiH(SiH₃)₂. These isomers differ in stability and reactivity, with the branched form often more accessible via catalytic rearrangement.

Positional Isomerism

Positional isomerism, also known as regioisomerism, refers to a type of constitutional isomerism in which molecules possess the same carbon skeleton and identical functional groups but differ in the positions where those functional groups or substituents are attached to the skeleton. This variation in attachment points leads to distinct molecular structures while maintaining the overall formula and connectivity framework. A classic example of positional isomerism is observed in the alcohols with the molecular formula , where (CH₃CH₂CH₂OH) has the hydroxyl group attached to a terminal carbon, while 2-propanol (CH₃CH(OH)CH₃) features it on the central carbon. In aromatic systems, disubstituted s exemplify this, with ortho-, meta-, and para-xylenes representing positional isomers of C₈H₁₀ where two methyl groups occupy adjacent (1,2-), separated by one carbon (1,3-), or opposite (1,4-) positions on the benzene ring. Positional isomers often exhibit distinct reactivity profiles due to differences in the local environment around the . For instance, in alkyl halides, primary positional isomers like 1-chloropropane undergo primarily via the SN2 mechanism because of minimal steric hindrance, whereas secondary isomers such as 2-chloropropane can proceed through either SN1 or SN2 pathways, with SN1 favored under conditions promoting formation due to greater stability at the secondary position. Tertiary positional variants, if applicable, further accelerate SN1 reactions owing to enhanced stabilization through . Nuclear magnetic resonance (NMR) serves as a key tool for identifying positional isomers through variations in chemical shifts and resonance multiplicities that reflect the unique electronic and spatial environments of protons or carbons. For example, the proton NMR spectrum of shows distinct signals for the CH₂OH methylene (around 3.5 ppm, triplet) compared to the CH₃CH(OH) methine in 2-propanol (around 3.8 ppm, septet), allowing unambiguous differentiation. In aromatic positional isomers, such as the ortho-, meta-, and para- isomers of , the coupling patterns and shifts of ring protons (e.g., symmetric doublets in para vs. complex multiplets in ortho) provide diagnostic signatures. In aromatic compounds, positional isomerism is particularly prominent, and follow IUPAC guidelines using numerical locants or traditional prefixes to specify positions relative to a reference group. For disubstituted benzenes, the ortho (o-, 1,2-), meta (m-, 1,3-), and para (p-, 1,4-) designations are standard, with the lowest possible numbers assigned to substituents in when multiple options exist. These regioisomers often display property differences, such as varying boiling points or reactivity in , influenced by the relative positions of electron-donating or withdrawing groups.

Functional Group Isomerism

Functional group isomerism refers to a type of constitutional isomerism in which compounds share the same molecular formula but differ in the nature of their functional groups or the specific bonding patterns that define those groups, leading to membership in different chemical families. This variation arises from rearrangements in atom connectivity that alter the primary reactive site of the molecule, such as converting an alcohol to an ether or an aldehyde to a ketone. Unlike other forms of structural isomerism, the focus here is on the identity and type of the functional group rather than its position or the carbon skeleton. A classic example is the molecular formula C₂H₆O, which can represent (CH₃CH₂OH), an alcohol with a hydroxyl group, or (CH₃OCH₃), an with an oxygen atom bridging two alkyl groups. Another illustrative case is C₃H₆O, manifesting as propanal (CH₃CH₂CHO), an featuring a at the end of the chain, or acetone (CH₃COCH₃), a with the carbonyl between two methyl groups. For C₃H₆, isomers include (CH₃CH=CH₂), an with a carbon-carbon ; (a three-carbon ring). These examples highlight how redistributing bonds can shift the molecule from one functional class to another, such as from unsaturated hydrocarbons to cyclic structures. Tautomerism represents a dynamic subset of functional group isomerism, where stable forms differ in identity and interconvert rapidly via proton shifts, as seen in keto-enol tautomers like acetone and its form (CH₂=C(OH)CH₃). Such cases emphasize structural differences in bonding patterns, though the equilibrium favors one tautomer under standard conditions. These isomers often exhibit stark contrasts in physical and chemical properties due to the distinct reactivity of their functional groups. For instance, in the C₄H₈O₂ isomers, acetic acid (CH₃COOH), a , is highly soluble in , acidic (pKₐ ≈ 4.76), and capable of hydrogen bonding, whereas its ester isomer, (CH₃COOCH₃), has lower solubility, is neutral, and boils at a lower (57°C vs. 118°C for acetic acid). Similarly, ethanol's ability to form intermolecular hydrogen bonds results in a higher (78°C) and greater polarity compared to dimethyl ether ( -24°C). In , isomerism appears in coordination compounds through variations in bonding modes, akin to , where the same coordinates via different donor atoms, effectively altering the functional group's attachment. A prominent example is the (III) complex [Co(NH₃)₅(NO₂)]²⁺, which exists as the nitro isomer (N-bound, -NO₂) or the nitrito isomer (O-bound, -ONO), displaying differences in color, reactivity, and stability due to the changed bonding pattern. These s highlight how arrangement influences electronic properties and geometry in metal complexes.

Isotopic Structural Variants

Structural Isotopomers

Structural isotopomers refer to molecules that share the identical atomic connectivity and molecular as their compound but differ in the specific positions occupied by isotopic variants of the atoms, thereby creating positional distinctions that parallel those in structural isomers. These differences arise from the placement of heavier isotopes, such as (2^{2}H or D) or 13^{13}C, at distinct sites within the scaffold, without altering the covalent framework. This emphasizes how isotopic substitution can lead to measurable variations in physical properties, such as bond lengths or vibrational modes, due to the increased mass of the affecting local dynamics. A representative example involves tritiated ethane derivatives, where 3^{3}H (T) replaces a hydrogen atom at different positions: CH3_{3}-CH2_{2}-T (1-tritioethane) versus CH3_{3}-CHT-H (2-tritioethane). Although ethane's symmetry renders these equivalent in practice, the illustration highlights the conceptual difference in isotopic positioning for molecules with nonequivalent sites, such as in propane where CH3_{3}CH2_{2}CH2_{2}D and CH3_{3}CHDCH3_{3} represent distinct structural isotopomers with deuterium at terminal versus central positions. Another common case is in ethanol, where 13^{13}C substitution at the methyl carbon (CH3_{3}-13^{13}CH2_{2}OH) differs from that at the methylene carbon (13^{13}CH3_{3}CH2_{2}OH), both having one 13^{13}C atom but in varied locations. Notation for structural isotopomers employs standard conventions, using superscripts for mass numbers (e.g., 13^{13}C or 2^{2}H) integrated into the to denote position, such as 13^{13}CH3_{3}-CH3_{3} for 13^{13}C-labeled at one carbon. These labels facilitate precise identification in experimental contexts, distinguishing variants like CH2_{2}DCHO (deuterium on the aldehydic carbon) from CH3_{3}CDO ( on the ) in . In , structural isotopomers play a crucial role in elucidating molecular architectures. (NMR) exploits the positional dependence of chemical shifts and scalar couplings; for instance, a 2^{2}H label at different sites in a produces distinct frequencies, enabling mapping of isotopic distributions and conformational analysis in complex mixtures. complements this by revealing isotopic peak clusters from isotopomers, where identical nominal masses yield overlapping molecular ions, but fragmentation patterns differ based on position, aiding structural confirmation under high-resolution conditions. The key distinction from constitutional isomers lies in the preservation of bonding connectivity: while constitutional variants rearrange atoms into different scaffolds (e.g., altering chain branching), structural isotopomers maintain the exact same , with isotopic effects primarily influencing kinetic isotope effects or spectroscopic observables rather than fundamentally changing reactivity or stability. This subtle mimicry of structural diversity makes them invaluable for studies requiring minimal perturbation to the parent molecule's . Isotopologues are molecular entities that differ only in their isotopic composition, specifically the number of isotopic substitutions, while maintaining the same connectivity of atoms. For instance, (C₆H₆) and fully deuterated (C₆D₆) represent isotopologues, as the latter has all atoms replaced by without altering the molecular structure. In contrast to isotopomers, which are isomers with the same total number and type of isotopic atoms but differing in their specific positions—such as ortho-, meta-, and para-dideuterated —isotopologues focus solely on the overall isotopic content rather than positional arrangements. This distinction highlights that isotopologues represent broader variants in isotopic enrichment, whereas isotopomers emphasize stereospecific labeling within the same isotopic total. In the context of structural isomerism, isotopologues extend the concept by introducing isotopic differences that do not change atomic connectivity, yet they can influence physical properties and reactivity in ways analogous to constitutional isomers. Related terms include isotopically substituted compounds, which are essentially pure in the specified at designated positions, meaning nearly all contain only the indicated without . Isotopically labeled compounds, however, are of an unmodified compound with one or more isotopically substituted analogs, often used in tracing experiments. Isotopic scrambling refers to the process achieving an equilibrium distribution of isotopes among a set of atoms in a or reaction , commonly observed in dynamic equilibria or catalytic processes. Isotopologues find significant applications in studying reaction mechanisms through kinetic isotope effects (KIEs), where the substitution of isotopes alters reaction rates due to differences in zero-point energies and vibrational frequencies. For example, a primary KIE in hydrogen-to-deuterium substitution can indicate if a C-H bond cleavage is rate-determining, providing insights into transition states and pathways. These effects are particularly valuable in organic and for elucidating mechanisms, as reviewed in studies on isotope-sensitive steps.

Symmetry and Structural Equivalence

Defining Structural Equivalence

Structural equivalence in molecules refers to the indistinguishability of atoms or groups under the symmetry operations of the molecular structure, meaning one can be superimposed on the other through rotations, reflections, or other transformations that leave the molecule unchanged. This concept is fundamental in organic chemistry for identifying positions that are chemically identical, ensuring that substitutions at equivalent sites yield the same product. In terms of criteria, structural equivalence is rigorously defined using , where the molecule is represented as a graph with atoms as vertices and bonds as edges. Two atoms are equivalent if there exists a —a bijective mapping of vertices to vertices that preserves adjacency—such that one atom maps to the other while maintaining the graph's structure. This approach allows for precise determination of equivalence classes without relying solely on geometric visualization. A classic example is (CH₄), where all four hydrogen atoms are structurally equivalent due to the of the carbon atom, allowing any hydrogen to be superimposed on another via . Similarly, in (C(CH₃)₄), the four methyl groups attached to the central carbon are equivalent, as the molecule's high permutes them indistinguishably. To test for structural equivalence, one method involves relabeling the atoms in the molecular graph and verifying if the resulting structure is isomorphic to the original, meaning it can be mapped onto it without altering connectivity. This relabeling checks whether permuting labels preserves the graph's properties, confirming equivalence if the structures match. The importance of structural equivalence lies in its role as the foundation for simplifying isomer enumeration, where symmetry reduces the number of distinct configurations by accounting for indistinguishable substitutions, as applied in Pólya's enumeration theorem for counting molecular isomers. Additionally, it is essential for nuclear magnetic resonance (NMR) analysis, where structurally equivalent atoms produce identical signals, enabling the interpretation of spectra to reveal molecular symmetry.

Molecular Symmetry and Atom Equivalence

Molecular symmetry plays a crucial role in determining the equivalence of atoms within a molecule, particularly in the context of structural isomers where connectivity is fixed but spatial arrangement influences symmetry properties. Symmetry elements, such as rotation axes, mirror planes, and inversion centers, define the point group of a molecule, which classifies its overall symmetry. For instance, the water molecule (H₂O) belongs to the C_{2v} point group, featuring a principal C_2 rotation axis bisecting the H-O-H angle and two vertical mirror planes (σ_v). These elements interchange the two hydrogen atoms under symmetry operations, rendering them equivalent. This equivalence arises because operations like the C_2 rotation map one hydrogen onto the other while leaving the molecular framework unchanged, a fundamental principle in assessing atomic indistinguishability. Atom equivalence is directly tied to these symmetry operations: atoms are considered equivalent if there exists a symmetry element that permutes them into identical environments. In (CH₂Cl₂), which also adopts C_{2v} symmetry with the C_2 axis along the Cl-C-Cl bisector, the two atoms are and equivalent, as the C_2 and mirror planes interchange them without altering the structure. In contrast, structural isomers with chiral centers, such as those lacking a plane of symmetry (e.g., C_1 ), exhibit nonequivalent atoms due to the absence of such interchanging operations; however, for structural isomerism, the focus remains on constitutional connectivity rather than stereochemical distinctions unless explicitly breaks potential . Tools like groups formalize this by representing symmetry operations as permutations of atomic positions, where the acts as a of the full on the atoms, identifying orbits of equivalent sites. Similarly, -adapted orbitals, constructed as linear combinations of atomic orbitals that transform according to irreducible representations of the , highlight equivalence by grouping orbitals from symmetric atoms (e.g., the A_1 and B_2 combinations of 1s orbitals in H₂O). Illustrative examples underscore these concepts in organic structural isomers. In (C₆H₆), the D_{6h} , with its six-fold rotation axis and multiple mirror planes, renders all six carbon atoms equivalent, as any carbon can be mapped to any other via operations. This high distinguishes from its structural isomer, (C₆H₅CH₃), where the methyl substituent reduces the to C_{2v}, making the ring carbons nonequivalent: the ipso and para carbons differ from the equivalent ortho pairs and meta pairs. These limitations of symmetry analysis apply primarily to structural isomers by considering averaged or idealized geometries, without delving into ; equivalence holds only for atoms interchanged by the 's operations, and perturbations like isotopic substitution can reveal underlying nonequivalences if they break .

Symmetry in Positional Isomerism

In positional isomerism, plays a crucial role in determining the number of distinct isomers by identifying equivalent substitution sites, thereby reducing the total count of unique structures compared to what might be expected from a simple linear arrangement. High , such as in molecules with point groups featuring multiple rotation axes and mirror planes, renders certain positions indistinguishable under symmetry operations, leading to fewer positional variants. A classic example is , which possesses D_{6h} , making all six carbon atoms equivalent for monosubstitution; thus, only one unique monosubstituted product exists, regardless of which position is chosen. For disubstitution, this results in three distinct positional isomers—ortho (1,2), meta (1,3), and para (1,4)—as the two ortho sites relative to a fixed are equivalent, as are the two meta sites, while the para site is unique. Similarly, , with its D_{5d} in the staggered conformation, exhibits ten equivalent carbon positions across its two cyclopentadienyl rings, yielding just one monosubstituted isomer and limiting disubstituted variants to symmetric and asymmetric forms based on intra- or inter-ring placement. Symmetry enables the prediction of distinct regioisomers by applying to classify atom equivalence classes within the parent molecule's , allowing chemists to forecast viable substitution patterns without exhaustive . For instance, in (D_{2h} ), the eight hydrogen atoms fall into two equivalence classes: the alpha positions (1,4,5,8) and beta positions (2,3,6,7), resulting in only two monosubstituted isomers rather than eight potential ones. This equivalence arises from operations like the C_2 axis and mirror planes that interchange positions within each class. Positions deemed symmetric by these operations exhibit identical physical and chemical properties, such as equivalent (NMR) signals or reactivity profiles in , simplifying spectroscopic identification and synthetic targeting. In , for example, alpha-substituted derivatives display higher reactivity and distinct UV absorption compared to beta isomers due to these symmetry-defined differences, influencing applications in dyes and pharmaceuticals.

Symmetry Breaking by Substitutions

Chemical substitutions in symmetric molecules often reduce the overall by altering the equivalence of atoms or functional groups, thereby lowering the point group and introducing structural distinctions that were not present in the parent compound. This process, known as , occurs because the substituting group disrupts the original operations, such as rotations or reflections, that leave the molecule indistinguishable from its original form. For instance, in (NH₃), which possesses C_{3v} due to its trigonal pyramidal structure with three equivalent atoms, replacement of one with yields chloramine (NH₂Cl), reducing the to C_s, characterized by a single mirror plane bisecting the H-N-H angle and passing through the nitrogen- bond./04%3A__Some_Important_Tools_of_Theory/4.04%3A_Point_Group_Symmetry) In aromatic systems like , which exhibits D_{6h} with all carbon atoms equivalent, monosubstitution with a group such as a methyl () or fluoro () lowers the to C_{2v}, retaining a C_2 rotation axis through the substituent and the opposite carbon, along with two mirror planes: one containing the ring and the other perpendicular to it bisecting the ring. Further disubstitution can exacerbate this breaking; for example, ortho- or para-disubstituted benzenes maintain C_{2v} if the substituents are identical, while meta-disubstitution reduces it to C_s, with only a single mirror plane. These reductions arise because the substituents eliminate higher-order rotations and multiple mirror planes inherent to the unsubstituted ring./15%3A_Benzene_and_Aromaticity%3A_Electrophilic_Aromatic_Substitution/15.04%3A_Spectral__Characteristics_of_the__Benzene__Ring) The consequences of such include the creation of nonequivalent atomic positions, which increases the number of possible positional isomers. In symmetric parents like , all positions are equivalent, yielding only one monosubstituted product; however, after monosubstitution, the ring carbons become distinct (e.g., ipso, ortho, meta, para), allowing disubstitution to produce three isomers (ortho, meta, para) due to the lowered . This effect extends to spectroscopic properties, where nonequivalent atoms lead to distinct signals in NMR or IR spectra, aiding isomer identification./15%3A_Benzene_and_Aromaticity%3A_Electrophilic_Aromatic_Substitution/15.04%3A_Spectral__Characteristics_of_the__Benzene__Ring) Group theory provides a systematic framework to predict these symmetry reductions by analyzing how substitution transforms the character table of the original into a . The original symmetry operations are evaluated to determine which are preserved; for example, in NH₃ (C_{3v}), the C_3 and multiple σ_v planes are lost in NH₂Cl, leaving only one σ plane, as confirmed by applying the group's irreducible representations to the substituted . This theoretical approach, rooted in the of symmetry groups, allows chemists to anticipate the resulting without exhaustive computation. In applications, deliberate symmetry breaking via substitutions is crucial for designing molecular precursors in asymmetric catalysis, where reduced symmetry creates chiral environments that favor enantioselective reactions. For example, substituting symmetric ligands with chiral groups breaks mirror symmetry, enabling catalysts like those in the Soai autocatalytic system to amplify small enantiomeric excesses into high optical purity products, facilitating the synthesis of enantiomerically pure compounds essential for pharmaceuticals.

Isomer Enumeration and Counting

Principles of Isomer Counting

The enumeration of structural begins with the systematic of all possible molecular connectivities that satisfy a given molecular formula while adhering to chemical valence rules. This process involves constructing molecular graphs where atoms are vertices and bonds are edges, ensuring that the graph represents a valid without violating atomic valences or stability constraints. To avoid generating duplicate structures, canonical labeling is employed, which assigns a unique representation to each distinct connectivity by selecting the minimal lexicographic labeling among all possible permutations of atom labels. This method, rooted in orderly principles, ensures exhaustive coverage without redundancy. For small molecules, manual enumeration can be performed by systematically categorizing possible carbon skeletons, functional group positions, and branching patterns. Consider the formula C₄H₈O, which has one ; isomers are enumerated by first identifying possible s (e.g., carbonyls, unsaturated alcohols, or cyclic ethers) and then placing them on straight-chain or branched scaffolds while checking for duplicates. Examples of constitutional isomers include two aldehydes (butanal and 2-methylpropanal), one (butan-2-one), several unsaturated alcohols (e.g., but-2-en-1-ol, 2-methylprop-2-en-1-ol, and but-3-en-2-ol), and cyclic ethers such as . This approach relies on exhaustive listing but becomes impractical beyond a few dozen atoms due to . In cases involving , Pólya's enumeration theorem provides a foundational rule for counting distinct isomers by accounting for group actions on equivalent positions. The theorem uses the of the of a molecular skeleton to compute the number of unique substitutions via generating functions, where the average number of fixed points under group permutations yields the count. For example, it predicts three isomers from benzene's D₆ₕ symmetry by substituting two hydrogens. This method is essential for symmetric cases like substitution patterns in rings or branched chains. A key historical advancement in manual counting came from Henze and Blair, who in developed a method for alkanes, using a unique to label structures and enumerate up to C₂₀ (366,319 isomers). Their approach systematically divides carbon chains into substructures, summing possibilities while avoiding overcounting. Challenges in isomer counting include the in the number of possible structures with increasing molecular size; for alkanes, the count rises from 18 for C₁₀ to over 10⁹ for C₃₀, overwhelming manual methods. Undercounting can occur if alternative skeletons (e.g., overlooked rings or branches) or equivalences are missed, necessitating rigorous validation.

Graph-Theoretic Methods

In chemical , structural isomers are enumerated by representing molecules as undirected graphs, where vertices correspond to atoms and edges to chemical bonds, often using hydrogen-suppressed graphs that focus on the carbon skeleton for hydrocarbons. This approach abstracts the three-dimensional structure into a combinatorial problem, allowing systematic generation and counting of distinct connectivity patterns. Graph isomorphism plays a central role in identifying unique structural isomers, as two molecular graphs are considered identical if there exists a bijective mapping between their vertices that preserves adjacency relations, ensuring that relabeling atoms does not produce new structures. Algorithms for isomer generation typically construct graphs via adjacency matrices, which encode vertex connections as binary entries, and employ exhaustive search techniques to build all possible matrices satisfying valence and connectivity constraints while discarding isomorphic duplicates through canonical labeling. One prominent method involves canonical augmentation paths, where intermediate graphs are grown by adding bonds incrementally, with checks at each step to maintain uniqueness; similar approaches use orderly generation principles from algorithmic to produce non-redundant structures. For example, these algorithms have been applied to count constitutional isomers of alkanes, yielding 75 distinct structures for (C10_{10}H22_{22}), encompassing branched and unbranched chains. Extensions handle rings by incorporating cycle constraints and functional groups by assigning heteroatoms or multiple bond types to vertices, enabling enumeration for more complex systems like polycyclic aromatic hydrocarbons. Modern implementations include the Chemical Algorithmic Graph Enumerator (CaGe), which generates exhaustive lists of mathematical graphs modeling chemical molecules, and the Open Molecule Generator (OMG), an open-source tool that produces all non-isomorphic structures for a given elemental composition using modified augmentation paths. Another is MAYGEN, which applies the orderly generation algorithm to enumerate constitutional isomers efficiently, supporting constraints like maximum ring size. These graph-theoretic methods offer significant advantages over manual counting by automatically accounting for molecular symmetry through isomorphism testing or orbit-stabilizer theorems in group theory, reducing redundancy and enabling scalable computation for large formulas where basic principles alone falter.

References

  1. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Supplemental_Modules_%28Organic_Chemistry%29/Fundamentals/Isomerism_in_Organic_Compounds/Structural_Isomerism_in_Organic_Molecules
  2. https://chem.libretexts.org/Courses/Brevard_College/CHE_201%253A_Organic_Chemistry_I/01%253A_Introduction_to_Organic_Chemistry/1.05%253A_Structural_Isomerism_in_Organic_Molecules
  3. https://goldbook.iupac.org/terms/view/C01285
  4. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Supplemental_Modules_(Organic_Chemistry)/Fundamentals/Isomerism_in_Organic_Compounds/Structural_Isomerism_in_Organic_Molecules
  5. https://www.masterorganicchemistry.com/2018/09/10/types-of-isomers/
  6. https://goldbook.iupac.org/terms/view/I03289
  7. https://goldbook.iupac.org/terms/view/I03294
  8. https://goldbook.iupac.org/terms/view/A00511
  9. https://goldbook.iupac.org/terms/view/T06252
  10. https://goldbook.iupac.org/terms/view/T06253
  11. https://www.sas.upenn.edu/~badoyle/Conformation.html
  12. https://goldbook.iupac.org/terms/view/C01258
  13. https://courses.lumenlearning.com/suny-potsdam-organicchemistry/chapter/3-4-isomers/
  14. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Supplemental_Modules_%28Organic_Chemistry%29/Alkanes/Nomenclature_of_Alkanes
  15. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_General_Chemistry_%28Petrucci_et_al.%29/12%253A_Intermolecular_Forces%253A_Liquids_And_Solids/12.1%253A_Intermolecular_Forces
  16. https://www.sciencedirect.com/science/article/pii/S0022024818301362
  17. https://chem.libretexts.org/Ancillary_Materials/Reference/Organic_Chemistry_Glossary/Positional_Isomers
  18. https://www.creative-chemistry.org.uk/molecules/isomers/positional
  19. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_%28Morsch_et_al.%29/15%253A_Benzene_and_Aromaticity/15.01%253A_Naming_Aromatic_Compounds
  20. https://www.masterorganicchemistry.com/2012/08/08/comparing-the-sn1-and-sn2-reactions/
  21. https://pubs.acs.org/doi/10.1021/ed062p260
  22. https://chem.libretexts.org/Ancillary_Materials/Reference/Organic_Chemistry_Glossary/Functional_Isomers
  23. https://chem.libretexts.org/Bookshelves/General_Chemistry/Book%253A_Structure_and_Reactivity_in_Organic_Biological_and_Inorganic_Chemistry_%28Schaller%29/I%253A__Chemical_Structure_and_Properties/07%253A_Structure-Property_Relationships/7.08%253A_Comparing_Properties_of_Isomers
  24. https://chem.libretexts.org/Courses/Purdue/Purdue_Chem_26100%253A_Organic_Chemistry_I_%28Wenthold%29/Chapter_09%253A_Alkynes/9.4_Electrophilic_Addition_to_Alkynes/9.4.2._Tautomers
  25. https://www.sciencedirect.com/topics/chemistry/tautomerization
  26. https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_and_Websites_%28Inorganic_Chemistry%29/Coordination_Chemistry/Structure_and_Nomenclature_of_Coordination_Compounds/Isomers/Structural_Isomers%253A_Linkage_Isomerism_in_Transition_Metal_Complexes
  27. https://www.spectroscopyonline.com/view/role-naturally-occurring-stable-isotopes-mass-spectrometry-part-i-theory
  28. https://depts.washington.edu/stollgrp/publication/2007_stoll/2007_stoll.pdf
  29. https://pmc.ncbi.nlm.nih.gov/articles/PMC9539636/
  30. https://goldbook.iupac.org/terms/view/I03351
  31. https://goldbook.iupac.org/terms/view/I03338
  32. https://www.acdlabs.com/iupac/nomenclature/93/r93_655.htm
  33. https://iupac.qmul.ac.uk/gtpoc/I.html
  34. https://goldbook.iupac.org/terms/view/K03405
  35. https://xingweili.snnu.edu.cn/KIE_mechanism_review.pdf
  36. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/intro3.htm
  37. https://pubs.acs.org/doi/10.1021/jp049300j
  38. https://www.khanacademy.org/science/organic-chemistry/spectroscopy-jay/proton-nmr/v/chemical-equivalence
  39. https://pmc.ncbi.nlm.nih.gov/articles/PMC7745470/
  40. https://match.pmf.kg.ac.rs/electronic_versions/Match01/match1_11-31.pdf
  41. http://web.mit.edu/5.03/www/readings/symmetry_mo/06_mo_intro.pdf
  42. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/symmetry/symmtry.htm
  43. http://chem.wisc.edu/deptfiles/genchem/Chm346/pdf/nmr.pdf
  44. https://troglerlab.ucsd.edu/GroupTheory224/Chap2B.pdf
  45. https://www.auburn.edu/~deruija/pda1_aromatics.pdf
  46. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/chapt15.htm
  47. https://pubs.acs.org/doi/10.1021/acs.organomet.8b00514
  48. https://www.sciencedirect.com/science/article/abs/pii/S0022231315003622
  49. https://www.chm.uri.edu/weuler/chm401/studyaids/symmetrypracticeproblems_answers.html
  50. https://pmc.ncbi.nlm.nih.gov/articles/PMC8279645/
  51. https://vallance.chem.ox.ac.uk/pdfs/SymmetryLectureNotes.pdf
  52. https://pubs.acs.org/doi/10.1021/ar5003208
  53. https://molgen.de/download/pubs/StructEnumHandbookChemInfAlgo.pdf
  54. https://people.unipmn.it/fragnelli/dispense/Chimica/Balaban.pdf
  55. https://pubs.acs.org/doi/10.1021/ed065p661
  56. https://jcheminf.biomedcentral.com/articles/10.1186/s13321-022-00677-6
  57. https://jcheminf.biomedcentral.com/articles/10.1186/1758-2946-4-21
  58. https://www.sciencedirect.com/science/article/abs/pii/S1540748920301358
  59. https://www.math.uni-bielefeld.de/~CaGe/
  60. https://jcheminf.biomedcentral.com/articles/10.1186/s13321-021-00529-9
Add your contribution
Related Hubs
User Avatar
No comments yet.