Recent from talks
Nothing was collected or created yet.
Deferent and epicycle
View on Wikipedia

In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle (from Ancient Greek ἐπίκυκλος (epíkuklos) 'upon the circle', meaning "circle moving on another circle")[1] was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth.
It was first proposed by Apollonius of Perga at the end of the 3rd century BC. It was developed by Apollonius of Perga and Hipparchus of Rhodes, who used it extensively, during the 2nd century BC, then formalized and extensively used by Ptolemy in his 2nd century AD astronomical treatise the Almagest.
Epicyclical motion is used in the Antikythera mechanism,[citation needed] an ancient Greek astronomical device, for compensating for the elliptical orbit of the Moon, moving faster at perigee and slower at apogee than circular orbits would, using four gears, two of them engaged in an eccentric way that quite closely approximates Kepler's second law.
Epicycles worked very well and were highly accurate, because, as Fourier analysis later showed, any smooth curve can be approximated to arbitrary accuracy with a sufficient number of epicycles. However, they fell out of favor with the discovery that planetary motions were largely elliptical from a heliocentric frame of reference, which led to the discovery that gravity obeying a simple inverse square law could better explain all planetary motions.
Introduction
[edit]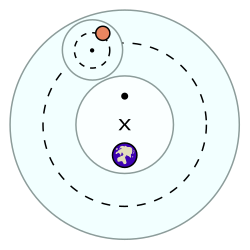
In both Hipparchian and Ptolemaic systems, the planets are assumed to move in a small circle called an epicycle, which in turn moves along a larger circle called a deferent (Ptolemy himself described the point but did not give it a name[2]). Both circles rotate eastward and are roughly parallel to the plane of the Sun's apparent orbit under those systems (ecliptic). Despite the fact that the system is considered geocentric, neither of the circles were centered on the earth, rather each planet's motion was centered at a planet-specific point slightly away from the Earth called the eccentric. The orbits of planets in this system are similar to epitrochoids, but are not exactly epitrochoids because the angle of the epicycle is not a linear function of the angle of the deferent.
In the Hipparchian system the epicycle rotated and revolved along the deferent with uniform motion. However, Ptolemy found that he could not reconcile that with the Babylonian observational data available to him; in particular, the shape and size of the apparent retrogrades differed. The angular rate at which the epicycle traveled was not constant unless he measured it from another point which is now called the equant (Ptolemy did not give it a name). It was the angular rate at which the deferent moved around the point midway between the equant and the Earth (the eccentric) that was constant; the epicycle center swept out equal angles over equal times only when viewed from the equant. It was the use of equants to decouple uniform motion from the center of the circular deferents that distinguished the Ptolemaic system. For the outer planets, the angle between the center of the epicycle and the planet was the same as the angle between the Earth and the Sun.
Ptolemy did not predict the relative sizes of the planetary deferents in the Almagest. All of his calculations were done with respect to a normalized deferent, considering a single case at a time. This is not to say that he believed the planets were all equidistant, but he had no basis on which to measure distances, except for the Moon. He generally ordered the planets outward from the Earth based on their orbit periods. Later he calculated their distances in the Planetary Hypotheses and summarized them in the first column of this table:[3]
| Body | Mean size (in Earth radii) |
Modern value (semimajor axis, in Earth radii) |
Ratio (modern/Ptolemy) |
Ratio (modern/Ptolemy, normalized to Sun = 1) |
|---|---|---|---|---|
| Moon | 48 | 60.3 | 1.26 | 0.065 |
| Mercury | 115 | 9,090 | 79.0 | 4.1 |
| Venus | 622.5 | 16,980 | 27.3 | 1.4 |
| Sun | 1,210 | 23,480 | 19.4 | 1 |
| Mars | 5,040 | 35,780 | 7.10 | 0.37 |
| Jupiter | 11,504 | 122,200 | 10.6 | 0.55 |
| Saturn | 17,026 | 225,000 | 13.2 | 0.68 |
| Star shell | 20,000 | — | — | — |
Had his values for deferent radii relative to the Earth–Sun distance been more accurate, the epicycle sizes would have all approached the Earth–Sun distance. Although all the planets are considered separately, in one peculiar way they were all linked: the lines drawn from the body through the epicentric center of all the planets were all parallel, along with the line drawn from the Sun to the Earth along which Mercury and Venus were situated. That means that all the bodies revolve in their epicycles in lockstep with Ptolemy's Sun (that is, they all have exactly a one-year period).[citation needed]
Babylonian observations showed that for superior planets the planet would typically move through in the night sky slower than the stars. Each night the planet appeared to lag a little behind the stars, in what is called prograde motion. Near opposition, the planet would appear to reverse and move through the night sky faster than the stars for a time in retrograde motion before reversing again and resuming prograde. Epicyclic theory, in part, sought to explain this behavior.
The inferior planets were always observed to be near the Sun, appearing only shortly before sunrise or shortly after sunset. Their apparent retrograde motion occurs during the transition between evening star into morning star, as they pass between the Earth and the Sun.
History
[edit]When ancient astronomers viewed the sky, they saw the Sun, Moon, and stars moving overhead in a regular fashion. Babylonians did celestial observations, mainly of the Sun and Moon as a means of recalibrating and preserving timekeeping for religious ceremonies.[4] Other early civilizations such as the Greeks had thinkers like Thales of Miletus, the first to document and predict a solar eclipse (585 BC),[5] or Heraclides Ponticus. They also saw the "wanderers" or "planetai" (our planets). The regularity in the motions of the wandering bodies suggested that their positions might be predictable.

The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions.[6] The introduction of better celestial measurement instruments, such as the introduction of the gnomon by Anaximander,[7] allowed the Greeks to have a better understanding of the passage of time, such as the number of days in a year and the length of seasons,[8] which are indispensable for astronomic measurements.
The ancients worked from a geocentric perspective for the simple reason that the Earth was where they stood and observed the sky, and it is the sky which appears to move while the ground seems still and steady underfoot. Some Greek astronomers (e.g., Aristarchus of Samos) speculated that the planets (Earth included) orbited the Sun, but the optics (and the specific mathematics – Isaac Newton's law of gravitation for example) necessary to provide data that would convincingly support the heliocentric model did not exist in Ptolemy's time and would not come around for over fifteen hundred years after his time. Furthermore, Aristotelian physics was not designed with these sorts of calculations in mind, and Aristotle's philosophy regarding the heavens was entirely at odds with the concept of heliocentrism. It was not until Galileo Galilei observed the moons of Jupiter on 7 January 1610, and the phases of Venus in September 1610, that the heliocentric model began to receive broad support among astronomers, who also came to accept the notion that the planets are individual worlds orbiting the Sun (that is, that the Earth is a planet, too). Johannes Kepler formulated his three laws of planetary motion, which describe the orbits of the planets in the Solar System to a remarkable degree of accuracy utilizing a system that employs elliptical rather than circular orbits. Kepler's three laws are still taught today in university physics and astronomy classes, and the wording of these laws has not changed since Kepler first formulated them four hundred years ago.
The apparent motion of the heavenly bodies with respect to time is cyclical in nature. Apollonius of Perga (3rd century BC) realized that this cyclical variation could be represented visually by small circular orbits, or epicycles, revolving on larger circular orbits, or deferents. Hipparchus (2nd century BC) calculated the required orbits. Deferents and epicycles in the ancient models did not represent orbits in the modern sense, but rather a complex set of circular paths whose centers are separated by a specific distance in order to approximate the observed movement of the celestial bodies.
Claudius Ptolemy refined the deferent-and-epicycle concept and introduced the equant as a mechanism that accounts for velocity variations in the motions of the planets. The empirical methodology he developed proved to be extraordinarily accurate for its day and was still in use at the time of Copernicus and Kepler. A heliocentric model is not necessarily more accurate as a system to track and predict the movements of celestial bodies than a geocentric one when considering strictly circular orbits. A heliocentric system would require more intricate systems to compensate for the shift in reference point. It was not until Kepler's proposal of elliptical orbits that such a system became increasingly more accurate than a mere epicyclical geocentric model.[9]

Owen Gingerich[10] describes a planetary conjunction that occurred in 1504 and was apparently observed by Copernicus. In notes bound with his copy of the Alfonsine Tables, Copernicus commented that "Mars surpasses the numbers by more than two degrees. Saturn is surpassed by the numbers by one and a half degrees." Using modern computer programs, Gingerich discovered that, at the time of the conjunction, Saturn indeed lagged behind the tables by a degree and a half and Mars led the predictions by nearly two degrees. Moreover, he found that Ptolemy's predictions for Jupiter at the same time were quite accurate. Copernicus and his contemporaries were therefore using Ptolemy's methods and finding them trustworthy well over a thousand years after Ptolemy's original work was published.
When Copernicus transformed Earth-based observations to heliocentric coordinates,[11] he was confronted with an entirely new problem. The Sun-centered positions displayed a cyclical motion with respect to time but without retrograde loops in the case of the outer planets.[dubious – discuss] In principle, the heliocentric motion was simpler but with new subtleties due to the yet-to-be-discovered elliptical shape of the orbits. Another complication was caused by a problem that Copernicus never solved: correctly accounting for the motion of the Earth in the coordinate transformation.[12]: 267 In keeping with past practice, Copernicus used the deferent/epicycle model in his theory but his epicycles were small and were called "epicyclets".
In the Ptolemaic system the models for each of the planets were different, and so it was with Copernicus' initial models. As he worked through the mathematics, however, Copernicus discovered that his models could be combined in a unified system. Furthermore, if they were scaled so that the Earth's orbit was the same in all of them, the ordering of the planets we recognize today easily followed from the math. Mercury orbited closest to the Sun and the rest of the planets fell into place in order outward, arranged in distance by their periods of revolution.[12]: 54
Although Copernicus' models reduced the magnitude of the epicycles considerably, whether they were simpler than Ptolemy's is moot. Copernicus eliminated Ptolemy's somewhat-maligned equant but at a cost of additional epicycles. Various 16th-century books based on Ptolemy and Copernicus use about equal numbers of epicycles.[13][14][15] The idea that Copernicus used only 34 circles in his system comes from his own statement in a preliminary unpublished sketch called the Commentariolus. By the time he published De revolutionibus orbium coelestium, he had added more circles. Counting the total number is difficult, but estimates are that he created a system just as complicated, or even more so.[16] Koestler, in his history of man's vision of the universe, equates the number of epicycles used by Copernicus at 48.[17] The popular total of about 80 circles for the Ptolemaic system seems to have appeared in 1898. It may have been inspired by the non-Ptolemaic system of Girolamo Fracastoro, who used either 77 or 79 orbs in his system inspired by Eudoxus of Cnidus.[18] Copernicus in his works exaggerated the number of epicycles used in the Ptolemaic system; although original counts ranged to 80 circles, by Copernicus's time the Ptolemaic system had been updated by Peurbach toward the similar number of 40; hence Copernicus effectively replaced the problem of retrograde with further epicycles.[19]
Copernicus' theory was at least as accurate as Ptolemy's but never achieved the stature and recognition of Ptolemy's theory. What was needed was Kepler's elliptical-orbit theory, not published until 1609 and 1619. Copernicus' work provided explanations for phenomena like retrograde motion, but really did not prove that the planets actually orbited the Sun.

Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today had Gottfried Wilhelm Leibniz and Isaac Newton not invented calculus.[20]
According to Maimonides, the now-lost astronomical system of Ibn Bajjah in 12th century Andalusian Spain lacked epicycles. Gersonides of 14th century France also eliminated epicycles, arguing that they did not align with his observations.[21] Despite these alternative models, epicycles were not eliminated until the 17th century, when Johannes Kepler's model of elliptical orbits gradually replaced Copernicus' model based on perfect circles.
Newtonian or classical mechanics eliminated the need for deferent/epicycle methods altogether and produced more accurate theories. By treating the Sun and planets as point masses and using Newton's law of universal gravitation, equations of motion were derived that could be solved by various means to compute predictions of planetary orbital velocities and positions. If approximated as simple two-body problems, for example, they could be solved analytically, while the more realistic n-body problem required numerical methods for solution.
The power of Newtonian mechanics to solve problems in orbital mechanics is illustrated by the discovery of Neptune. Analysis of observed perturbations in the orbit of Uranus produced estimates of the suspected planet's position within a degree of where it was found. This could not have been accomplished with deferent/epicycle methods. Still, Newton in 1702 published Theory of the Moon's Motion which employed an epicycle and remained in use in China into the nineteenth century. Subsequent tables based on Newton's Theory could have approached arcminute accuracy.[22]
The number of epicycles
[edit]According to one school of thought in the history of astronomy, minor imperfections in the original Ptolemaic system were discovered through observations accumulated over time. It was mistakenly believed that more levels of epicycles (circles within circles) were added to the models to match more accurately the observed planetary motions. The multiplication of epicycles is believed to have led to a nearly unworkable system by the 16th century, and that Copernicus created his heliocentric system in order to simplify the Ptolemaic astronomy of his day, thus succeeding in drastically reducing the number of circles.
With better observations additional epicycles and eccentrics were used to represent the newly observed phenomena till in the later Middle Ages the universe became a 'Sphere/With Centric and Eccentric scribbled o'er,/Cycle and Epicycle, Orb in Orb'.
— Dorothy Stimson, The Gradual Acceptance of the Copernican Theory of the Universe, 1917[23]
As a measure of complexity, the number of circles is given as 80 for Ptolemy, versus a mere 34 for Copernicus.[24] The highest number appeared in the Encyclopædia Britannica on Astronomy during the 1960s, in a discussion of King Alfonso X of Castile's interest in astronomy during the 13th century. (Alfonso is credited with commissioning the Alfonsine Tables.)
By this time each planet had been provided with from 40 to 60 epicycles to represent after a fashion its complex movement among the stars. Amazed at the difficulty of the project, Alfonso is credited with the remark that had he been present at the Creation he might have given excellent advice.
— Encyclopædia Britannica, 1968[25]
As it turns out, a major difficulty with this epicycles-on-epicycles theory is that historians examining books on Ptolemaic astronomy from the Middle Ages and the Renaissance have found absolutely no trace of multiple epicycles being used for each planet. The Alfonsine Tables, for instance, were apparently computed using Ptolemy's original unadorned methods.[12]: 57
Another problem is that the models themselves discouraged tinkering. In a deferent-and-epicycle model, the parts of the whole are interrelated. A change in a parameter to improve the fit in one place would throw off the fit somewhere else. Ptolemy's model is probably optimal in this regard. On the whole it gave good results but missed a little here and there. Experienced astronomers would have recognized these shortcomings and allowed for them.
In fact, in Ptolemy's Almagest the Sun has one cycle and the Moon has three: the deferent, an epicycle, and an inner small circle or "epicyclet". Each outer planet has four: deferent, epicycle, equant, and latitude wheel. Venus has two more latitude wheels than the outer planets, so six. Mercury has all of Venus’s cycles plus an epicyclet, or seven. If we include the sphere of the fixed stars, and another sphere to account for the precession of the equinoxes, the total number of cycles and spheres comes to 31.[26]
Mathematical formalism
[edit]According to the historian of science Norwood Russell Hanson:
There is no bilaterally-symmetrical, nor eccentrically-periodic curve used in any branch of astrophysics or observational astronomy which could not be smoothly plotted as the resultant motion of a point turning within a constellation of epicycles, finite in number, revolving around a fixed deferent.
— Norwood Russell Hanson, "The Mathematical Power of Epicyclical Astronomy", 1960[27]
Any path—periodic or not, closed or open—can be represented with an infinite number of epicycles. This is because epicycles can be represented as a complex Fourier series; therefore, with a large number of epicycles, very complex paths can be represented in the complex plane.[28]
Let the complex number
where a0 and k0 are constants, is the imaginary unit, and t is time, correspond to a deferent centered on the origin of the complex plane and revolving with a radius a0 and angular velocity
where T is the period.
If z1 is the path of an epicycle, then the deferent plus epicycle is represented as the sum
This is an almost periodic function, and is a periodic function just when the ratio of the constants kj is rational. Generalizing to N epicycles yields the almost periodic function
which is periodic just when every pair of kj is rationally related. Finding the coefficients aj to represent a time-dependent path in the complex plane, z = f(t), is the goal of reproducing an orbit with deferent and epicycles, and this is a way of "saving the phenomena" (σώζειν τα φαινόμενα).[29]
This parallel was noted by Giovanni Schiaparelli.[30][31] Pertinent to the Copernican Revolution's debate about "saving the phenomena" versus offering explanations, one can understand why Thomas Aquinas, in the 13th century, wrote:
Reason may be employed in two ways to establish a point: firstly, for the purpose of furnishing sufficient proof of some principle [...]. Reason is employed in another way, not as furnishing a sufficient proof of a principle, but as confirming an already established principle, by showing the congruity of its results, as in astronomy the theory of eccentrics and epicycles is considered as established, because thereby the sensible appearances of the heavenly movements can be explained; not, however, as if this proof were sufficient, forasmuch as some other theory might explain them.
Epicycles and the Catholic Church
[edit]Being a system that was for the most part used to justify the geocentric model, with the exception of Copernicus' cosmos, the deferent and epicycle model was favored over the heliocentric ideas that Kepler and Galileo proposed. Later adopters of the epicyclic model such as Tycho Brahe, who considered the Church's scriptures when creating his model,[33] were seen even more favorably. The Tychonic model was a hybrid model that blended the geocentric and heliocentric characteristics, with a still Earth that has the sun and moon surrounding it, and the planets orbiting the Sun. To Brahe, the idea of a revolving and moving Earth was impossible, and the scripture should be always paramount and respected.[34] When Galileo tried to challenge Tycho Brahe's system, the church was dissatisfied with their views being challenged. Galileo's publication did not aid his case in his trial.
As an example of bad science
[edit]"Adding epicycles" has come to be used as a derogatory comment in modern scientific discussion. The term might be used, for example, to describe continuing to try to adjust a theory to make its predictions match the facts. There is a generally accepted idea that extra epicycles were invented to alleviate the growing errors that the Ptolemaic system noted as measurements became more accurate, particularly for Mars. According to this notion, epicycles are regarded by some as the paradigmatic example of bad science.[35]
Copernicus added an extra epicycle to his planets, but that was only in an effort to eliminate Ptolemy's equant, which he considered a philosophical break away from Aristotle's perfection of the heavens. Mathematically, the second epicycle and the equant produce nearly the same results, and many Copernican astronomers before Kepler continued using the equant, as the mathematical calculations were easier. Copernicus' epicycles were also much smaller than Ptolemy's, and were required because the planets in his model moved in perfect circles. Johannes Kepler would later show that the planets move in ellipses, which removed the need for Copernicus' epicycles as well.[36]
See also
[edit]Notes
[edit]- ^ Harper, Douglas. "epicycle". Online Etymology Dictionary.
- ^ See page 21 of the Introduction in Ptolemy's Almagest (PDF). Translated by Toomer, Gerald J. 1984.
- ^ Andrea, Murschel (1995). "The Structure and Function of Ptolemy's Physical Hypotheses of Planetary Motion". Journal for the History of Astronomy. 26 (xxvii): 33–61. Bibcode:1995JHA....26...33M. doi:10.1177/002182869502600102. S2CID 116006562. Retrieved 2 August 2014.
- ^ Olmstead, A. T. (1938). "Babylonian Astronomy: Historical Sketch". The American Journal of Semitic Languages and Literatures. 55 (2): 113–129. doi:10.1086/amerjsemilanglit.55.2.3088090. ISSN 1062-0516. JSTOR 3088090. S2CID 170628425.
- ^ Mosshammer, Alden A. (1981). "Thales' Eclipse". Transactions of the American Philological Association. 111: 145–155. doi:10.2307/284125. ISSN 0360-5949. JSTOR 284125.
- ^ For an example of the complexity of the problem, see Owen Gingerich (2004). 'The Book Nobody Read'. Arrow. p. 50. ISBN 978-0099476443.
- ^ Diogenes Laertius (September 2013). The lives and opinions of eminent philosophers. General Books. ISBN 978-1-230-21699-7. OCLC 881385989.
- ^ Pedersen, Olaf (1993). Early physics and astronomy: a historical introduction (Rev. ed.). Cambridge, UK: Cambridge University Press. ISBN 0-521-40340-5. OCLC 24173447.
- ^ Evans, James (1998). The history and practice of ancient astronomy. New York: Oxford University Press. ISBN 978-0-19-987445-3. OCLC 729872798.
- ^ Owen Gingerich (2004). "4". 'The Book Nobody Read'. Arrow. ISBN 978-0099476443.
- ^ One volume of De Revolutionibus was devoted to a description of the trigonometry used to make the transformation between geocentric and heliocentric coordinates.
- ^ a b c Owen Gingerich (2004). 'The Book Nobody Read'. Arrow. ISBN 978-0099476443.
- ^ Palter, Robert (1970). "Approach to the History of Astronomy". Studies in the History and Philosophy of Science. 1: 94. doi:10.1016/0039-3681(70)90001-4.
- ^ Owen Gingerich, "Alfonso X as a Patron of Astronomy", in The Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics, 1993), p. 125.
- ^ Gingerich, "Crisis versus Aesthetic in the Copernican Revolution", in Eye of Heaven, pp. 193–204.
- ^ "The popular belief that Copernicus's heliocentric system constitutes a significant simplification of the Ptolemaic system is obviously wrong ... [T]he Copernican models themselves require about twice as many circles as the Ptolemaic models and are far less elegant and adaptable." Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 ed.). Dover Publications. ISBN 978-0-486-22332-2., p. 204. This is an extreme estimate in favor of Ptolemy.
- ^ Koestler, Arthur (1989) [1959]. The Sleepwalkers. Arkana, Penguin Books., p. 195
- ^ Palter, Approach to the History of Astronomy, pp. 113–114.
- ^ Koestler, Arthur (1989) [1959]. The Sleepwalkers. Arkana, Penguin Books., pp. 194–195.
- ^ A deferent/epicycle model is in fact used to compute Lunar positions needed to define modern Hindu calendars. See Nachum Dershovitz and Edward M. Reingold: Calendrical Calculations, Cambridge University Press, 1997, Chapter 14. (ISBN 0-521-56474-3)
- ^ Goldstein, Bernard R. (1972). "Theory and Observation in Medieval Astronomy". Isis. 63 (1): 39–47 [40–41]. doi:10.1086/350839. S2CID 120700705.
- ^ Kollerstrom, Nicholas (2000). Newton's Forgotten Lunar Theory. Green Lion Press. ISBN 1-888009-08-X.
- ^ Dorothy Stimson,
 The Gradual Acceptance of the Copernican Theory of the Universe. (New York, 1917),
The Gradual Acceptance of the Copernican Theory of the Universe. (New York, 1917),  p. 14.. The quotation is from John Milton's Paradise Lost, Book 8, 11.82–85.
p. 14.. The quotation is from John Milton's Paradise Lost, Book 8, 11.82–85.
- ^ Robert Palter, An Approach to the History of Early Astronomy
- ^ Encyclopædia Britannica, 1968, vol. 2, p. 645. This is identified as the highest number in Owen Gingerich, Alfonso X. Gingerich also expressed doubt about the quotation attributed to Alfonso. In The Book Nobody Read (p. 56), however, Gingerich relates that he challenged Encyclopædia Britannica about the number of epicycles. Their response was that the original author of the entry had died and its source couldn't be verified.
- ^ Weiss, Michael (20 May 2025). "From Kepler to Ptolemy 15". Diagonal Argument. Retrieved 20 May 2025.
- ^ Hanson, Norwood Russell (1 June 1960). "The Mathematical Power of Epicyclical Astronomy" (PDF). Isis. 51 (2): 150–158. doi:10.1086/348869. ISSN 0021-1753. JSTOR 226846. S2CID 33083254. Archived from the original (PDF) on 1 November 2020. Retrieved 21 October 2011.
- ^ See, e.g., this animation made by Christián Carman and Ramiro Serra, which uses 1000 epicycles to retrace the cartoon character Homer Simpson; see also Christián Carman's "Deferentes, epiciclos y adaptaciones." and "La refutabilidad del Sistema de Epiciclos y Deferentes de Ptolomeo".
- ^ Duhem, Pierre (1969). To save the phenomena, an essay on the idea of physical theory from Plato to Galileo. Chicago: University of Chicago Press. OCLC 681213472. (excerpt).
- ^ Giovanni Gallavotti: "Quasi periodic motions from Hipparchus to Kolmogorov". In: Rendiconti Lincei – Matematica e Applicazioni. Series 9, Band 12, No. 2, 2001, p. 125–152. (PDF; 205 KB)
- ^ Lucio Russo: The forgotten revolution. How science was born in 300 BC and why it had to be reborn. Springer, Berlin. 2004, ISBN 3-540-20068-1, p. 91.
- ^ Summa Theologica, I q. 32 a. 1 ad 2.
- ^ Håkansson, Håkan (2007), "Tycho the Prophet: History, Astrology and the Apocalypse in Early Modern Science", The Word and the World, London: Palgrave Macmillan UK, pp. 137–156, doi:10.1057/9780230206472_8, ISBN 978-1-349-35338-5, retrieved 6 December 2021.
- ^ Repcheck, Jack (2008). Copernicus' secret: how the scientific revolution began. New York: Simon & Schuster Paperbacks. ISBN 978-0-7432-8952-8. OCLC 209693599.
- ^ See e.g., Kolb, Rocky, Blind Watchers of the Sky, Addison–Wesley, 1996. p. 299. (ISBN 0-201-48992-9)
- ^ "Whose Revolution? Copernicus, Brahe & Kepler | Modeling the Cosmos | Articles and Essays | Finding Our Place in the Cosmos: From Galileo to Sagan and Beyond | Digital Collections | Library of Congress". Library of Congress, Washington, D.C. Retrieved 6 December 2021.
External links
[edit]- Ptolemaic System – at Rice University's Galileo Project
- Eccentrics, Deferents, Epicycles, and Equants at MathPages
Animated illustrations
[edit]- Ptolemaic System Simulator, interactive, Foothill College.
- Orbits with Epicycles on a Deferent, interactive, Wolfram Demonstrations.
- ANIMATE: Epicycles, interactive JavaScript coding example, Khan Academy.
- Ptolemy and Homer (Simpson) Reconstruction of a planet's bizarre orbit with Ptolemy's system of epicycles and deferents.
Deferent and epicycle
View on GrokipediaConceptual Foundations
Definition and Geometric Principles
In the geocentric models of ancient astronomy, particularly as systematized by Claudius Ptolemy in the 2nd century CE, the deferent constitutes the primary circular orbit, a large circle whose center is positioned at or near the Earth, along which the center of a secondary circle known as the epicycle travels with uniform angular velocity. The epicycle, in turn, is a smaller circle upon which the planet or celestial body executes its own uniform circular motion around the epicycle's center. This dual-circle geometry forms the foundational mechanism for representing the positions of planets, the Sun, and the Moon relative to a stationary Earth.[8][9] Geometrically, the position of the celestial body results from the vector composition of two independent circular displacements: the displacement from the deferent's center to the epicycle's center, determined by the deferent's radius and the mean anomaly angle , and the displacement from the epicycle's center to the body, governed by the epicycle's radius and the angle relative to the line connecting the deferent center to the epicycle center. In Ptolemy's framework, both angular velocities are constant, with the deferent motion corresponding to the sidereal period of the body and the epicycle motion adjusted to account for observed irregularities. The radii and are empirically derived ratios, typically with on the order of 0.1 to 0.3 for superior planets, ensuring the model's predictive alignment with tabulated observations.[8][4] This epicycle-deferent construct adheres to the principle of uniform circular motion, a core tenet inherited from Aristotelian cosmology and earlier Hellenistic astronomers like Apollonius of Perga around 200 BCE, who demonstrated its mathematical equivalence to certain eccentric models for generating the same locus of points. The geometry permits the apparent path of the body to deviate from perfect circularity around Earth, manifesting as loops or stations in the sky, without violating the axiom of circular orbits central to pre-Copernican celestial mechanics. Empirical validation involved chord tables and spherical trigonometry to compute longitudes and latitudes, with the model's parameters fitted to Babylonian and Greek eclipse and planetary opposition data spanning centuries.[9][4]Role in Explaining Planetary Motion
The deferent and epicycle mechanism provided a geometric solution to the observed irregularities in planetary motion within the geocentric framework, particularly the retrograde loops exhibited by superior planets against the background of fixed stars. Each planet was modeled as traversing a small circular path, termed the epicycle, at uniform angular speed, while the center of this epicycle simultaneously orbited the Earth along a larger circular path, the deferent, also at uniform angular speed. This dual motion resulted in the planet's apparent position tracing a cycloidal path relative to Earth, where periods of eastward (prograde) motion alternated with brief westward (retrograde) excursions when the planet's epicycle position aligned such that its tangential velocity opposed the deferent's direction.[10][11] For superior planets like Mars, Jupiter, and Saturn, retrograde motion occurred near opposition, when the planet was closest to Earth, aligning with empirical observations of increased brightness during these intervals due to reduced distance. The epicycle's radius was calibrated to match the angular extent of the observed retrograde loops, typically spanning 10-20 degrees for Mars, while the deferent's period corresponded to the synodic cycle relative to the Sun's position. This setup maintained the axiom of uniform circular motion for celestial bodies, avoiding ad hoc accelerations or non-circular trajectories that contradicted prevailing Aristotelian physics.[10][12] Inferior planets, such as Venus and Mercury, exhibited similar but more frequent retrograde motions, explained by larger epicycles relative to their deferents, with the deferent centers offset to synchronize with solar elongations. The model extended to the Sun and Moon with adjusted parameters, though lunar anomalies required additional refinements. Overall, the deferent-epicycle system reconciled geocentric assumptions with positional data from Babylonian and Greek observations, enabling predictive ephemerides for up to a millennium before significant heliocentric alternatives emerged.[1][13]Historical Development
Ancient Greek Origins
The deferent and epicycle model originated in Hellenistic Greek astronomy as a geometric solution to the observed irregularities in planetary motion, such as retrograde loops, while adhering to the principle of uniform circular motion centered on Earth. Apollonius of Perga (c. 262–190 BC) first proposed the core mechanism, in which a planet executes uniform motion along a small circle, the epicycle, whose center in turn moves uniformly along a larger circle, the deferent, around the Earth. This configuration allowed for the synthesis of prograde and retrograde components of planetary paths, demonstrating mathematical equivalence to the earlier eccentric circle model.[14][15] Preceding this, Eudoxus of Cnidus (c. 408–355 BC) had developed a system of nested homocentric spheres to account for planetary positions under Plato's stipulation of circular uniformity, employing up to 27 spheres per planet to approximate motions without epicycles. However, this spherical framework proved inadequate for precise quantitative predictions and variations in planetary brightness or distance. Apollonius's planar epicycle-deferent approach marked a shift toward more flexible two-dimensional modeling, enabling better fits to empirical data through adjustable radii and speeds.[16][17] Hipparchus of Nicaea (c. 190–120 BC) advanced the model by integrating it with systematic observations, applying epicycles to describe the Moon's anomalous motion and extending it to planets to explain synodic periods and elongations. His work, though fragmentary and preserved mainly through later syntheses, established the deferent-epicycle as a predictive tool, with the epicycle radius and angular velocities tuned to match recorded positions from Babylonian and Greek catalogs dating back centuries. This empirical refinement distinguished the model from purely philosophical constructs, prioritizing causal alignment with visible celestial anomalies over idealized symmetry.[18][19][16]Ptolemy's Synthesis in the Almagest
In the Almagest, composed circa 150 CE, Claudius Ptolemy developed a comprehensive geocentric model integrating deferents and epicycles to replicate observed celestial motions with quantitative precision. Drawing on Hipparchus's observations from around 127 BCE and his own measurements, Ptolemy employed geometric constructions and trigonometric computations to parameterize the models, prioritizing empirical agreement over purely philosophical constraints like perfect uniformity centered on Earth.[20] His synthesis demonstrated the mathematical equivalence of simple eccentric orbits and epicycle-deferent combinations, opting for epicycles to handle the "anomaly" in planetary longitudes while using offsets for directional irregularities.[21] For superior planets such as Mars, Jupiter, and Saturn, the core configuration features the planet moving uniformly on an epicycle, with the epicycle's center traversing a deferent circle displaced from Earth by an eccentricity e. Ptolemy introduced the equant point Q, positioned such that the deferent's geometric center C lies midway between Earth E and Q, making EC = CQ. Uniform circular motion is enforced with respect to Q: the line from Q to the epicycle center sweeps equal angles in equal times, accounting for the observed acceleration near opposition and deceleration elsewhere without additional circles.[5][22] This equant mechanism, justified by its fit to longitudinal data from multiple apparitions, marked a key innovation, deviating from strict Aristotelian principles but enabling predictions within roughly 1° accuracy using parameters derived iteratively from oppositions and stations.[23] Ptolemy calculated the epicycle radius relative to the deferent (normalized to 60 parts) from maximum elongations at quadrature or opposition; for Mars, this ratio is approximately 39;30 parts, reflecting its pronounced retrograde loop, while for Saturn it is smaller at 6;30 parts.[5] Eccentricities were bisection-adjusted using differences in opposition longitudes over cycles, with values like 6 parts for Mars' deferent. For inferior planets, Venus and Mercury, the deferents are aligned near the Sun's mean path, with larger epicycles (e.g., Mercury's at 22;30 parts) to model their inferior conjunctions and greatest elongations up to 47°.[3] Additional small epicycles or crank mechanisms addressed latitudinal variations and prosneuses (apogee shifts).[21] This framework, detailed in Books IX–XIII of the Almagest, required only one epicycle per planet plus the equant adjustment, synthesizing prior ad hoc refinements into a predictive system validated against centuries of data, though it implicitly relaxed centered uniformity to achieve causal fidelity to appearances.[20]Medieval Refinements and Islamic Contributions
The Ptolemaic geocentric model, incorporating deferents and epicycles, was preserved and refined by Islamic astronomers during the 9th to 14th centuries through translations of Greek texts at centers like the House of Wisdom in Baghdad, enabling systematic parameter adjustments and theoretical critiques.[24] These scholars, building on Ptolemy's Almagest, conducted precise observations to update epicycle radii, deferent eccentricities, and angular velocities, achieving predictive accuracies rivaling or surpassing Ptolemy's for planets like Mars and Jupiter.[25] Nasir al-Din al-Tusi (1201–1274), founder of the Maragha Observatory in Persia around 1259, introduced the "Tusi couple"—a geometric device using two linked circular motions to produce linear oscillation from uniform circles, allowing reformulation of planetary anomalies without Ptolemy's equant point, which violated Aristotelian uniform circularity.[26] In his Tadhkira fi 'ilm al-hay'a (Memoir on the Science of Astronomy, c. 1260), al-Tusi retained deferents and primary epicycles but modified their interactions via the Tusi couple to model latitudinal and longitudinal variations, influencing subsequent geocentric models by restoring physical realism to celestial kinematics.[25] This Maragha school's approach, involving al-Tusi and collaborators like Qutb al-Din al-Shirazi, emphasized empirical verification against observations, critiquing Ptolemy's ad hoc equant while preserving the deferent-epicycle framework for predictive fidelity.[27] Further advancements came from Ibn al-Shatir (1304–1375), a Damascene astronomer, whose Nihayat al-Sul fi Taysir al-Usul (Final Quest Concerning the Simplification of the Principles, c. 1340s) eliminated both the equant and eccentric deferents entirely through a system of secondary epicycles and Tusi-couple variants, achieving equivalent retrograde motion and first-station effects using only uniform circular paths.[28] For Mercury and Venus, Ibn al-Shatir adjusted epicycle-deferent ratios based on Syrian observations, reducing model complexity while matching Ptolemaic predictions to within 0.5 degrees for superior conjunctions; his lunar model employed dual epicycles to account for evection without Ptolemy's crank mechanism.[29] These innovations, grounded in rejecting non-uniform motion as unphysical, represented a causal refinement prioritizing geometric purity over Ptolemy's empirical expedients, though they retained geocentrism.[30] In medieval Europe, from the 12th century onward, Arabic transmissions of Ptolemaic and Islamic refinements—via translations by figures like Gerard of Cremona (c. 1114–1187)—facilitated incremental adjustments, such as refined trigonometric tables for epicycle calculations in works by John of Sacrobosco's Tractatus de Sphaera (c. 1230).[31] Late medieval scholars, including Georg von Peuerbach and Johannes Regiomontanus in their Epitome of the Almagest (1450–1464), incorporated Islamic parameter tweaks, like updated solar epicycle sizes from al-Battani's observations (d. 929), to improve almanac predictions, but focused more on computational aids than radical geometric overhauls.[24] These efforts bridged to Renaissance critiques, underscoring Islamic works' role in sustaining the model's empirical viability amid growing observational demands.[25]Mathematical Framework
Deferent and Epicycle Geometry
In the basic deferent and epicycle geometry of ancient astronomy, a planet's position is modeled as uniform circular motion around the center of a small circle, termed the epicycle, whose own center traces uniform circular motion on a larger circle, the deferent, centered at Earth. The deferent has radius , typically standardized to 60 units in Ptolemaic calculations for computational convenience with chord tables approximating trigonometric functions.[32] The epicycle radius is significantly smaller, determined empirically for each planet to match observed elongations and retrograde arcs, such as for Mars based on third-century BCE observations refined by Ptolemy around 150 CE.[32][33] The parametric equations for the planet's coordinates in the ecliptic plane, assuming coplanar motion for simplicity, are given by: where is the angular speed of the epicycle center on the deferent ( the deferent period), and is the angular speed of the planet on the epicycle ( the epicycle period).[32] For superior planets, approximates the sidereal period, while matches Earth's orbital period in the equivalent heliocentric frame, with often negative relative to to generate westward retrograde loops when the planet is near opposition.[33] This composition yields a path resembling an epicycloid, with cusps corresponding to retrograde stations if .[32] To compute the geocentric longitude and latitude (often negligible for basic models), astronomers applied the law of sines in the triangle formed by Earth, the epicycle center, and the planet. The true longitude is the deferent angle plus a correction , approximated as for small , where is the angular position on the epicycle (anomaly).[33] Exact computation used Ptolemy's table of chords, equivalent to , to resolve distances and angles via the cosine rule: for epicycle center at distance and angle , the planet's offset vector of length at angle relative to the line of apsides yields radial distance and position angle adjustments.[34] This framework allowed prediction of maximum elongations and retrograde durations, with for inferior planets like Venus, reaching 47 degrees historically.[33]The Equant and Angular Velocity Adjustments
In Ptolemy's planetary models, the equant point serves as the reference for uniform angular motion of the epicycle's center around the deferent, addressing discrepancies in observed planetary velocities that uniform motion around the deferent's geometric center could not accommodate.[23] Positioned such that the deferent's center lies midway between Earth and the equant, with the equant offset from Earth by twice the Earth-deferent center distance in the opposite direction, this configuration ensures the epicycle center sweeps equal angles in equal times relative to the equant.[22] Ptolemy introduced this adjustment in Almagest Book IX.5 to reconcile empirical data showing planets' angular speeds varying systematically—faster near opposition for superior planets and slower at quadrature—with the commitment to circular orbits.[23] The equant's effect modulates the apparent angular velocity as viewed from Earth: when the epicycle center aligns such that the line from equant to epicycle center passes near Earth, the planet's motion accelerates relative to the geocentric frame, mimicking observed elongations and retrogrades more accurately without additional epicycles.[5] Mathematically, the longitude calculation involves computing the mean motion angle θ from the equant, then deriving the true anomaly via the deferent's eccentricity, using trigonometric identities like the chord theorem for positions.[35] This yields predictions aligning with Hipparchan observations to within about 0.5 degrees for Mars' opposition longitudes, a marked improvement over eccentric-only models.[23] Critics like Ibn al-Haytham later noted the equant deviated from strict uniform circular motion, as the epicycle center's path around the deferent center exhibits variable speed, prompting medieval astronomers to seek equant-free equivalents through compounded epicycles, though Ptolemy justified it philosophically as preserving uniformity about a single point consistent with natural circularity.[4] Empirical validation relied on Ptolemy's tables, derived from adjusted parameters fitting Babylonian and Greek eclipse and planetary data spanning centuries, underscoring the model's pragmatic adaptation to causal observations over pure geometric ideals.[5]Trigonometric and Computational Models
The position of a planet in the deferent-epicycle model is computed as the vector sum of the deferent displacement and the epicycle displacement relative to Earth at the model's center. In rectangular coordinates centered on Earth, this yieldswhere is the deferent radius (normalized to 60 parts in Ptolemaic tables), the epicycle radius, the mean longitude of the epicycle center (adjusted for equant nonuniformity), and the anomaly (angle from epicycle apogee).[36] These parametric equations derive from the geometry of uniform circular motions, with longitude and latitude obtained via spherical projections for celestial coordinates.[3] Ptolemy implemented these calculations using chord tables in the Almagest (ca. 150 CE), which tabulated chord lengths in a circle of radius 60 for angles in 0.5° increments, equivalent to .[36] Chords facilitated addition and subtraction of angles without explicit sines or cosines: for instance, Ptolemy's difference formula computes from products of chords and supplements, enabling resolution of the epicycle triangle via the law of cosines analog.[36] Ratios were determined trigonometrically from observed retrograde arcs, applying the law of sines in the triangle formed by Earth, epicycle center, and planet at maximum elongation: , where angles derive from half the retrograde period times sidereal and synodic rates (e.g., yielding for Mars).[37] ![z_N = \sum_{j=0}^N a_j e^{i k_j t}}[center] Modern computational models represent deferent-epicyle motions in the complex plane as , evaluated numerically for simulations or visualizations.[7] Stacked epicycles generalize to finite trigonometric polynomials, or Fourier series:
with coefficients fitted to data via least squares or discrete Fourier transform, approximating any continuous periodic orbit within error for sufficient .[7] This harmonic decomposition underscores the model's capacity to fit empirical paths through superposed circular components, though it requires iterative parameter tuning for accuracy beyond first-order anomalies.[7]
Empirical Performance
Predictive Accuracy for Known Planets
The Ptolemaic deferent-epicycle model, as detailed in the Almagest (circa 150 CE), yielded predictive accuracies for planetary ecliptic longitudes that were adequate for contemporary observational needs but revealed systematic deviations when assessed against modern ephemerides. Maximum errors, stemming from imprecise mean motion rates and geometric parameters, reached approximately 1.0° for Mercury, 1.5° for Venus, 3.5° for Mars, 1.0° for Jupiter, and 0.5° for Saturn.[38] These discrepancies accumulated over time due to unmodeled precession and long-term orbital perturbations, rendering unadjusted predictions less reliable beyond a few centuries without recalibration. For epochs proximate to Ptolemy's data sources—primarily Hipparchus' observations from around 127 BCE—the model's short-term forecasts matched recorded positions to within 1–2 arcminutes, aligning with the practical limits of unaided visual astronomy or basic instruments like the astrolabe.[13] Superior planets (Mars, Jupiter, Saturn) benefited from the equant's adjustment for variable angular speeds, reducing residuals during oppositions, while inferior planets (Mercury, Venus) required additional epicycle refinements to account for their proximity to the Sun and rapid elongations. Mars exhibited the largest inconsistencies, with errors occasionally exceeding 2° in retrograde phases, as the single epicycle struggled to fully replicate the observed loop geometry without further ad hoc modifications.| Planet | Maximum Ecliptic Longitude Error (°) |
|---|---|
| Mercury | 1.0[38] |
| Venus | 1.5[38] |
| Mars | 3.5[38] |
| Jupiter | 1.0[38] |
| Saturn | 0.5[38] |






