Mach number

The Mach number is named after the physicist and philosopher Ernst Mach,^[3] in honour of his achievements, according to a proposal by the aeronautical engineer Jakob Ackeret in 1929.^[4] The word Mach is always capitalized since it derives from a proper name and since the Mach number is a dimensionless quantity rather than a unit of measure. This is also why the number comes after the word Mach. It was also known as Mach's number by Lockheed when reporting the effects of compressibility on the P-38 aircraft in 1942.^[5]

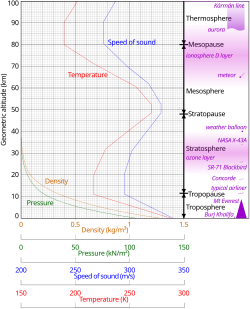
Mach number is a measure of the compressibility characteristics of fluid flow: the fluid (air) behaves under the influence of compressibility in a similar manner at a given Mach number, regardless of other variables.^[6] As modeled in the International Standard Atmosphere, dry air at mean sea level, standard temperature of 15 °C (59 °F), the speed of sound is 340.3 meters per second (1,116.5 ft/s; 761.23 mph; 1,225.1 km/h; 661.49 kn).^[7] The speed of sound is not a constant; in a gas, it increases proportionally to the square root of the absolute temperature, and since atmospheric temperature generally decreases with increasing altitude between sea level and 11,000 meters (36,089 ft), the speed of sound also decreases. For example, the standard atmosphere model lapses temperature to −56.5 °C (−69.7 °F) at 11,000 meters (36,089 ft) altitude, with a corresponding speed of sound (Mach 1) of 295.0 meters per second (967.8 ft/s; 659.9 mph; 1,062 km/h; 573.4 kn), 86.7% of the sea level value.

The Mach number arises naturally when the continuity equation is nondimensionalized for compressible flows. If density variations are related to pressure through the isentropic relation ${\displaystyle dp=c^{2}\,d\rho }$, the nondimensionalized continuity equation contains a prefactor ${\displaystyle (u/c)^{2}=M^{2}}$. This shows that the Mach number directly measures the importance of compressibility effects in a flow. In the limit ${\displaystyle M\to 0}$, the equation reduces to the incompressibility condition ${\displaystyle \nabla \cdot \mathbf {u} =0}$.^[8]

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2025) (Learn how and when to remove this message)

The terms subsonic and supersonic are used to refer to speeds below and above the local speed of sound, and to particular ranges of Mach values. This occurs because of the presence of a transonic regime around flight (free stream) M = 1 where approximations of the Navier-Stokes equations used for subsonic design no longer apply; the simplest explanation is that the flow around an airframe locally begins to exceed M = 1 even though the free stream Mach number is below this value.

Meanwhile, the supersonic regime is usually used to talk about the set of Mach numbers for which linearised theory may be used, where for example the (air) flow is not chemically reacting, and where heat-transfer between air and vehicle may be reasonably neglected in calculations.

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2025) (Learn how and when to remove this message)

Flight can be roughly classified in six categories:^{[citation needed]}

At transonic speeds, the flow field around the object includes both sub- and supersonic parts. The transonic period begins when first zones of M > 1 flow appear around the object. In case of an airfoil (such as an aircraft's wing), this typically happens above the wing. Supersonic flow can decelerate back to subsonic only in a normal shock; this typically happens before the trailing edge. (Fig.1a)

As the speed increases, the zone of M > 1 flow increases towards both leading and trailing edges. As M = 1 is reached and passed, the normal shock reaches the trailing edge and becomes a weak oblique shock: the flow decelerates over the shock, but remains supersonic. A normal shock is created ahead of the object, and the only subsonic zone in the flow field is a small area around the object's leading edge. (Fig.1b)

(a)

(b)

Fig. 1. Mach number in transonic airflow around an airfoil; M < 1 (a) and M > 1 (b).

When an aircraft exceeds Mach 1 (i.e. the sound barrier), a large pressure difference is created just in front of the aircraft. This abrupt pressure difference, called a shock wave, spreads backward and outward from the aircraft in a cone shape (a so-called Mach cone). It is this shock wave that causes the sonic boom heard as a fast moving aircraft travels overhead. A person inside the aircraft will not hear this. The higher the speed, the more narrow the cone; at just over M = 1 it is hardly a cone at all, but closer to a slightly concave plane.

At fully supersonic speed, the shock wave starts to take its cone shape and flow is either completely supersonic, or (in case of a blunt object), only a very small subsonic flow area remains between the object's nose and the shock wave it creates ahead of itself. (In the case of a sharp object, there is no air between the nose and the shock wave: the shock wave starts from the nose.)

As the Mach number increases, so does the strength of the shock wave and the Mach cone becomes increasingly narrow. As the fluid flow crosses the shock wave, its speed is reduced and temperature, pressure, and density increase. The stronger the shock, the greater the changes. At high enough Mach numbers the temperature increases so much over the shock that ionization and dissociation of gas molecules behind the shock wave begin.

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (August 2025) (Learn how and when to remove this message)

As a flow in a channel becomes supersonic, one significant change takes place. The conservation of mass flow rate leads one to expect that contracting the flow channel would increase the flow speed (i.e. making the channel narrower results in faster air flow) and at subsonic speeds this holds true. However, once the flow becomes supersonic, the relationship of flow area and speed is reversed: expanding the channel actually increases the speed.

When the speed of sound is known, the Mach number at which an aircraft is flying can be calculated by $${\displaystyle \mathrm {M} ={\frac {u}{c}}}$$

where:

• M is the Mach number
• u is velocity of the moving aircraft and
• c is the speed of sound at the given altitude (more properly temperature)

and the speed of sound varies with the thermodynamic temperature as:

$${\displaystyle c={\sqrt {\gamma \cdot R_{*}\cdot T}},}$$

where:

• ${\displaystyle \gamma \,}$ is the ratio of specific heat of a gas at a constant pressure to heat at a constant volume (1.4 for air)
• ${\displaystyle R_{*}}$ is the specific gas constant for air.
• ${\displaystyle T,}$ is the static air temperature.

If the speed of sound is not known, Mach number may be determined by measuring the various air pressures (static and dynamic) and using the following formula that is derived from Bernoulli's equation for Mach numbers less than 1.0. Assuming air to be an ideal gas, the formula to compute Mach number in a subsonic compressible flow is:^[9]

$${\displaystyle \mathrm {M} ={\sqrt {{\frac {2}{\gamma -1}}\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {\gamma -1}{\gamma }}-1\right]}}\,}$$

where:

• q_c is impact pressure (dynamic pressure) and
• p is static pressure
• ${\displaystyle \gamma \,}$ is the ratio of specific heat of a gas at a constant pressure to heat at a constant volume (1.4 for air)

The formula to compute Mach number in a supersonic compressible flow is derived from the Rayleigh supersonic pitot equation:

$${\displaystyle {\frac {p_{t}}{p}}=\left[{\frac {\gamma +1}{2}}\mathrm {M} ^{2}\right]^{\frac {\gamma }{\gamma -1}}\cdot \left[{\frac {\gamma +1}{1-\gamma +2\gamma \,\mathrm {M} ^{2}}}\right]^{\frac {1}{\gamma -1}}}$$

Mach number is a function of temperature and true airspeed. Aircraft flight instruments, however, operate using pressure differential to compute Mach number, not temperature.

Assuming air to be an ideal gas, the formula to compute Mach number in a subsonic compressible flow is found from Bernoulli's equation for M < 1 (above):^[9] $${\displaystyle \mathrm {M} ={\sqrt {5\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {2}{7}}-1\right]}}\,}$$

The formula to compute Mach number in a supersonic compressible flow can be found from the Rayleigh supersonic pitot equation (above) using parameters for air:

$${\displaystyle \mathrm {M} \approx 0.88128485{\sqrt {\left({\frac {q_{c}}{p}}+1\right)\left(1-{\frac {1}{7\,\mathrm {M} ^{2}}}\right)^{2.5}}}}$$

where:

• q_c is the dynamic pressure measured behind a normal shock.

As can be seen, M appears on both sides of the equation, and for practical purposes a root-finding algorithm must be used for a numerical solution (the equation is a septic equation in M² and, though some of these may be solved explicitly, the Abel–Ruffini theorem guarantees that there exists no general form for the roots of these polynomials). It is first determined whether M is indeed greater than 1.0 by calculating M from the subsonic equation. If M is greater than 1.0 at that point, then the value of M from the subsonic equation is used as the initial condition for fixed point iteration of the supersonic equation, which usually converges very rapidly.^[9] Alternatively, Newton's method can also be used.

• Critical Mach number – Concept in aerodynamics
• Machmeter – Flight instrument
• Ramjet – Supersonic atmospheric jet engine
• Scramjet – Jet engine where combustion takes place in supersonic airflow
• Speed of sound – Speed of sound wave through elastic medium
• True airspeed – Speed of an aircraft relative to the air mass through which it is flying
• Orders of magnitude (speed) – Comparison of a wide range of speeds
• Fujita scale – Used to estimate wind speeds and bridges the Beaufort scale and the Mach scale