Hubbry Logo
Minor scaleMinor scaleMain
Open search
Minor scale
Community hub
Minor scale
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Minor scale
Minor scale
Minor scale
View on Wikipedia
from Wikipedia

In Western classical music theory, the minor scale refers to three scale patterns – the natural minor scale (or Aeolian mode), the harmonic minor scale, and the melodic minor scale (ascending or descending).[1]

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { C natural minor scale } d es f g aes bes c2 } }
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { C harmonic minor scale } d es f g aes b!? c2 } }
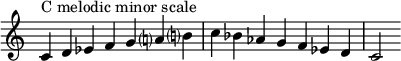
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { C melodic minor scale } d es f g a!? b!? c bes aes g f es d c2 } }

These scales contain all three notes of a minor triad: the root, a minor third (rather than the major third, as in a major triad or major scale), and a perfect fifth (rather than the diminished fifth, as in a diminished scale or half diminished scale).

Minor scale is also used to refer to other scales with this property,[2] such as the Dorian mode or the minor pentatonic scale (see other minor scales below).

Natural minor scale

[edit]

Relationship to relative major

[edit]

A natural minor scale (or Aeolian mode) is a diatonic scale that is built by starting on the sixth degree of its relative major scale. For instance, the A natural minor scale can be built by starting on the 6th degree of the C major scale:

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { C major scale } d e f g \override NoteHead.color = #red a \override NoteHead.color = #black b c2 \bar "||" \time 9/4 \override NoteHead.color = #red a,4^\markup { A natural minor scale } \override NoteHead.color = #black b c d e f g a2 } }

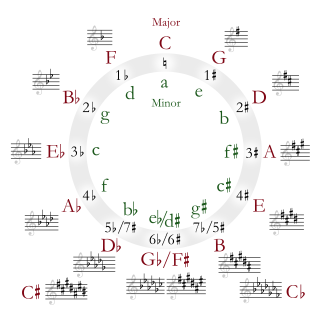
Because of this, the key of A minor is called the relative minor of C major. Every major key has a relative minor, which starts on the 6th scale degree or step. For instance, since the 6th degree of F major is D, the relative minor of F major is D minor.

Relationship to parallel major

[edit]

A natural minor scale can also be constructed by altering a major scale with accidentals. In this way, a natural minor scale is represented by the following notation:

1, 2, ♭3, 4, 5, ♭6, ♭7, 8

This notation is based on the major scale, and represents each degree (each note in the scale) by a number, starting with the tonic (the first, lowest note of the scale). By making use of flat symbols (♭) this notation thus represents notes by how they deviate from the notes in the major scale. Because of this, we say that a number without a flat represents a major (or perfect) interval, while a number with a flat represents a minor interval. In this example, the numbers mean:

Thus, for instance, the A natural minor scale can be built by lowering the third, sixth, and seventh degrees of the A major scale by one semitone:

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 a4^\markup { A major scale } b \override NoteHead.color = #red cis \override NoteHead.color = #black d e \override NoteHead.color = #red fis gis \override NoteHead.color = #black a2 \bar "||" \time 9/4 a,4^\markup { A natural minor scale } b \override NoteHead.color = #red c! \override NoteHead.color = #black d e \override NoteHead.color = #red f! g! \override NoteHead.color = #black a2 } }

Because they share the same tonic note of A, the key of A minor is called the parallel minor of A major.

Intervals

[edit]
This pattern of whole and half steps characterizes the natural minor scales.

The intervals between the notes of a natural minor scale follow the sequence below:

whole, half, whole, whole, half, whole, whole

where "whole" stands for a whole tone (a red u-shaped curve in the figure), and "half" stands for a semitone (a red angled line in the figure).

The natural minor scale is maximally even.

Harmonic minor scale

[edit]
Main article: Harmonic minor scale

Construction

[edit]
\relative c { \clef bass \time 2/2 \key g \minor \tempo "Allegro" g2 a bes4 c2 d4 es2 fis g1 }
Theme in harmonic minor from the opening of Schumann's First Symphony (1841)[3]

The harmonic minor scale (or Aeolian ♮7 scale) has the same notes as the natural minor scale except that the seventh degree is raised by one semitone, creating an augmented second between the sixth and seventh degrees.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 a4^\markup { A harmonic minor scale } b c d e f gis a2 } }

Thus, a harmonic minor scale is represented by the following notation:

1, 2, ♭3, 4, 5, ♭6, 7, 8

A harmonic minor scale can be built by lowering the 3rd and 6th degrees of the parallel major scale by one semitone.

Because of this construction, the 7th degree of the harmonic minor scale functions as a leading tone to the tonic because it is a semitone lower than the tonic, rather than a whole tone lower than the tonic as it is in natural minor scales.

Intervals

[edit]

The intervals between the notes of a harmonic minor scale follow the sequence below:

whole, half, whole, whole, half, augmented second, half

Uses

[edit]

While it evolved primarily as a basis for chords, the harmonic minor with its augmented second is sometimes used melodically. Instances can be found in Mozart, Beethoven (for example, the finale of his String Quartet No. 14), and Schubert (for example, in the first movement of the Death and the Maiden Quartet). In this role, it is used while descending far more often than while ascending. A familiar example of the descending scale is heard in a ring of bells. A ring of twelve is sometimes augmented with a 5♯ and 6♭ to make a 10 note harmonic minor scale from bell 2 to bell 11 (for example, Worcester Cathedral).[4]

The Hungarian minor scale is similar to the harmonic minor scale but with a raised 4th degree. This scale is sometimes also referred to as "Gypsy Run", or alternatively "Egyptian Minor Scale", as mentioned by Miles Davis who describes it in his autobiography as "something that I'd learned at Juilliard".[5]

In popular music, examples of songs in harmonic minor include Katy B's "Easy Please Me", Bobby Brown's "My Prerogative", and Jazmine Sullivan's "Bust Your Windows". The scale also had a notable influence on heavy metal, spawning a sub-genre known as neoclassical metal, with guitarists such as Chuck Schuldiner, Yngwie Malmsteen, Ritchie Blackmore, and Randy Rhoads employing it in their music.[6]

Melodic minor scale

[edit]
Further information: Jazz minor scale

Construction

[edit]

The distinctive sound of the harmonic minor scale comes from the augmented second between its sixth and seventh scale degrees. While some composers have used this interval to advantage in melodic composition, others felt it to be an awkward leap, particularly in vocal music, and preferred a whole step between these scale degrees for smooth melody writing. To eliminate the augmented second, these composers either raised the sixth degree by a semitone or lowered the seventh by a semitone.

The melodic minor scale is formed by using both of these solutions. In particular, the raised sixth appears in the ascending form of the scale, while the lowered seventh appears in the descending form of the scale. Traditionally, these two forms are referred to as:

  • the ascending melodic minor scale or jazz minor scale (also known as the Ionian ♭3 or Dorian ♮7): this form of the scale is also the 5th mode of the acoustic scale.
  • the descending melodic minor scale: this form is identical to the natural minor scale .

The ascending and descending forms of the A melodic minor scale are shown below:

{ \override Score.TimeSignature #'stencil = ##f\relative c' { \clef treble \time 7/4 \hide Staff.TimeSignature \override Voice.TextScript.font-size = #-2 a4^\markup { Ascending melodic minor } b c d e fis gis a^\markup { Descending melodic minor } g! f! e d c b a2 } }

The ascending melodic minor scale can be notated as

1, 2, ♭3, 4, 5, 6, 7, 8

while the descending melodic minor scale is

8, ♭7, ♭6, 5, 4, ♭3, 2, 1

Using these notations, the two melodic minor scales can be built by altering the parallel major scale.

Intervals

[edit]

The intervals between the notes of an ascending melodic minor scale follow the sequence below:

whole, half, whole, whole, whole, whole, half

The intervals between the notes of a descending melodic minor scale are the same as those of a descending natural minor scale.

Uses

[edit]
\relative c''' { \set Staff.midiInstrument = #"violin" \set Score.tempoHideNote = ##t \tempo 4 = 120 \key g \dorian \time 4/4 g8^\markup \bold "Allegro" f16 es d c bes a g a bes c d e fis g fis8[ d] }
Theme in G melodic minor from the opening of the second concerto in Vivaldi's L'estro armonico (1711)[3] Although the piece is in G minor, the key signature is for G Dorian (one flat). By convention, in modern notation (and for tonal music written since the common-practice period), key signatures are typically only based on a major (Ionian mode) or minor (natural minor or Aeolian mode) key, not on modes like the Dorian mode.

Composers have not been consistent in using the two forms of the melodic minor scale. Composers frequently require the lowered 7th degree found in the natural minor in order to avoid the augmented triad (III+) that arises in the ascending form of the scale.

Examples of the use of melodic minor in rock and popular music include Elton John's "Sorry Seems to Be the Hardest Word", which makes, "a nod to the common practice... by the use of F♯ [the leading tone in G minor] as the penultimate note of the final cadence."[7] The Beatles' "Yesterday" also partly uses the melodic minor scale.[citation needed]

Other minor scales

[edit]

Other scales with a minor third and a perfect fifth (i.e. containing a minor triad) are also commonly referred to as minor scales.

Within the diatonic modes of the major scale, in addition to the Aeolian mode (which is the natural minor scale), the Dorian mode and the Phrygian mode also fall under this definition. Conversely, the Locrian mode has a minor third, but a diminished fifth (thus containing a diminished triad), and is therefore not commonly referred to as a minor scale.

The Hungarian minor scale is another heptatonic (7-note) scale referred to as minor.

The Jazz minor scale is a name for the melodic minor scale when only the "ascending form" is used.

Non-heptatonic scales may also be called "minor", such as the minor pentatonic scale.[8]

Limits of terminology

[edit]

While any other scale containing a minor triad could be defined as a "minor scale", the terminology is less commonly used for some scales, especially those further outside the Western classical tradition.

The hexatonic (6-note) blues scale is similar to the minor pentatonic scale and fits the above definition. However, the flat fifth is present as a passing tone along with the perfect fifth, and the scale is often played with microtonal mixing of the major and minor thirds – thus making it harder to classify as a "major" or "minor" scale.

The two Neapolitan scales are both "minor scales" following the above definition, but were historically referred to as the "Neapolitan Major" or "Neapolitan Minor" based rather on the quality of their sixth degree.

Key signature

[edit]

In modern notation, the key signature for music in a minor key is typically based on the accidentals of the natural minor scale, not on those of the harmonic or melodic minor scales. For example, a piece in E minor will have one sharp in its key signature because the E natural minor scale has one sharp (F♯).

Major and minor keys that share the same key signature are relative to each other. For instance, F major is the relative major of D minor since both have key signatures with one flat. Since the natural minor scale is built on the 6th degree of the major scale, the tonic of the relative minor is a major sixth above the tonic of the major scale. For instance, B minor is the relative minor of D major because the note B is a major sixth above D. As a result, the key signatures of B minor and D major both have two sharps (F♯ and C♯).

Other notations and usage

[edit]

When expressing the names of minor scale keys as abbreviations, the alphabet of the corresponding tonic note name can be written in lower case letters to indicate only the tonic note name. For example, when expressing the English notation of A minor, it can be abbreviated as 'a'. Plus, when expressing the names of major scale keys as abbreviations, the Roman alphabet of the corresponding tonic note is sometimes upper case to indicate only the tonic note name. For example, when expressing the English notation of C major, it is abbreviated as 'C'.[9]

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Minor scale

View on Grokipedia
from Grokipedia
In Western music theory, the minor scale is a seven-note diatonic scale that forms the basis of minor keys, featuring a lowered third scale degree—a minor third interval from the tonic—compared to the major scale, which creates its signature somber or melancholic sound. There are three primary variants: the natural minor (also known as Aeolian mode), the harmonic minor, and the melodic minor, each with distinct interval patterns to suit melodic and harmonic contexts. The natural minor scale follows the interval pattern of whole step, half step, whole step, whole step, half step, whole step, whole step (W-H-W-W-H-W-W), sharing the same as its relative , which begins a minor third above the minor tonic. In contrast, the harmonic minor raises the seventh degree by a half step (W-H-W-W-H-Aug2-H), introducing a leading tone for stronger resolution in cadences, such as the dominant V chord to tonic i. The melodic minor adjusts both the sixth and seventh degrees ascending (W-H-W-W-W-W-H) to avoid the awkward augmented second interval and provide a leading tone, while descending it reverts to the natural minor form for smoother stepwise motion. Historically, the minor scale evolved from the modal system, where the natural minor corresponds to the , one of the eight church modes used in medieval and before the standardization of tonality in the era. These scales underpin a wide range of compositions across genres, from classical symphonies to modern and , enabling expressive harmonic progressions and emotional depth through parallel and relationships.

Fundamentals

Definition and characteristics

The minor scale is a foundational seven-note diatonic scale in Western music theory, characterized by a minor third interval above the tonic, which sets it apart from the major scale and typically evokes a somber or melancholic mood. This defining feature contributes to its emotional depth, often associated with sadness, introspection, or tension in musical expression. As one of the two primary tonal scales alongside the major, it forms the basis for minor keys and is constructed from the natural minor pattern, influencing harmony, melody, and overall tonality in compositions. The minor scale's prominence emerged in Western classical music during the era (approximately 1600–1750), when major and minor tonalities fully developed as structural pillars, allowing composers to convey complex emotions through key choices. Johann Sebastian Bach, a key figure of this period, frequently employed minor scales in works like to explore harmonic progressions and affective contrasts. Beyond classical traditions, the scale's cultural associations with melancholy persist in and modern genres such as , where it underscores themes of longing and resilience.

Scale degrees and basic intervals

In the minor scale, the seven scale degrees are identified by numbers from 1 to 7, each with a traditional name that reflects its position relative to the tonic: the first degree (1) is the tonic, the second (2) is the , the third (3) is the , the fourth (4) is the , the fifth (5) is the dominant, the sixth (6) is the , and the seventh (7) is the subtonic. These names are consistent across diatonic scales, though the subtonic specifically denotes the lowered seventh degree in minor, which lies a whole step below the tonic rather than a half step. The basic intervals from the tonic to each scale degree define the scale's structure: to the (2) is a major second (two s), to the (3) is a minor third (three semitones), to the (4) is a (five semitones), to the dominant (5) is a (seven semitones), to the (6) is a minor sixth (eight semitones), and to the subtonic (7) is a minor seventh (ten semitones). These intervals arise from the cumulative semitone positions: 0 (tonic), 2, 3, 5, 7, 8, and 10. The stepwise interval pattern of the , measured in whole steps (W, two s) and half steps (H, one ), is W-H-W-W-H-W-W, progressing from the tonic through the . This pattern distinguishes the from the (W-W-H-W-W-W-H) primarily through the positions of the half steps, resulting in lowered third, sixth, and seventh degrees relative to the parallel (e.g., E♭, A♭, and B♭ instead of E, A, and B in C minor). Scale degrees are notated using with carets (e.g., 1^\hat{1}, 3^\hat{3}) or for chords, often incorporating to indicate the flattened third (3^\hat{3}), sixth (6^\hat{6}), and seventh (7^\hat{7}) degrees that characterize the minor quality. For instance, in the key of , the scale is A-B-C-D-E-F-G, with C (♭3^\hat{3}), F (♭6^\hat{6}), and G (♭7^\hat{7}) marked relative to the major. While the natural uses these lowered degrees, the sixth and seventh may be raised in and melodic minor forms to create different interval relationships.
Scale DegreeNameInterval from TonicSemitones
1Tonic0
22
33
45
5Dominant7
68
7Subtonic10

Natural minor scale

Construction

The natural minor scale is constructed by beginning with the tonic (root) note and ascending through seven diatonic notes using the fixed interval pattern of whole step (W), half step (H), whole step (W), whole step (W), half step (H), whole step (W), whole step (W), before returning to the above the tonic. This sequence, denoted as W-H-W-W-H-W-W, ensures the scale's characteristic interval from the tonic to the third degree, distinguishing it from the . To build the scale in any key, apply this pattern sequentially from the chosen root note, adjusting for the key's as needed. A practical example is the A natural , which contains no sharps or flats and thus serves as an accessible starting point for beginners. Starting on A, the notes are A (tonic), B (whole step above A), C (half step above B), D (whole step above C), E (whole step above D), F (half step above E), G (whole step above F), and A (whole step above G, completing the ). This scale can be represented on a musical staff in the treble clef as follows: the tonic A on the second space from the bottom, ascending to B in the third space, C on the ledger line below the staff, D on the middle line, E in the space above, F on the top line, G in the space above, and back to A. The natural minor scale derives from the , the sixth of the seven diatonic modes of the , formed by taking the same pitches as a but starting and ending on its sixth degree. For instance, the A natural minor scale uses the exact notes of the scale (its relative major, a minor third above the tonic), but reoriented around A as the tonal center. On a piano keyboard, the A natural minor scale is particularly straightforward, as it employs only the white keys, starting from the A nearest the center of the keyboard and moving rightward through the consecutive white notes: A, B, C, D, E, F, G, A. This white-key configuration highlights the scale's diatonic purity without requiring any black keys.

Relationships to major scales

The natural minor scale maintains a close relationship with its relative , sharing all seven pitches and thus the same . The relative major is derived by starting on the sixth scale degree of the natural minor; for instance, the A natural minor scale (A-B-C-D-E-F-G) is the relative minor of (C-D-E-F-G-A-B), both employing no sharps or flats. This equivalence in pitch content facilitates seamless theoretical and practical connections between the two keys. In contrast, the parallel shares the same tonic note as the natural but alters three scale degrees: the third, sixth, and seventh are raised by a half step to form major intervals relative to the tonic. For example, A natural (A-B-C-D-E-F-G) contrasts with (A-B-C♯-D-E-F♯-G♯), resulting in different key signatures—the parallel typically has three fewer flats or three more sharps than the natural . This difference introduces chromatic elements when transitioning between parallel keys, though the shared tonic provides a point of tonal stability. These relationships have significant practical implications in composition and , particularly for modulation and chord usage between relative keys. Modulation from a natural minor to its relative major (or vice versa) is common due to the identical pitch sets, often achieved through pivot chords that function diatonically in both keys, such as the subdominant chord in minor becoming the mediant in major. For example, in , a pivot from the IV chord () to exploits this overlap for smooth key changes without introducing accidentals. Chord borrowing between relative keys leverages their shared diatonic collection, allowing composers to introduce color by reinterpreting chords under a shifted tonic without altering the . In a natural minor context, chords from the relative major can be incorporated to evoke a brighter tonal quality, such as using the relative major's dominant as a borrowed leading-tone chord for resolution, enhancing expressiveness in progressions while maintaining structural unity.

Harmonic minor scale

Construction and intervals

The harmonic minor scale is derived from the natural minor scale by raising the seventh scale degree by a semitone, creating a leading tone that strengthens resolution to the tonic. This alteration maintains the first six notes of the natural minor while sharpening the seventh, resulting in a scale pattern of whole step, half step, whole step, whole step, half step, augmented second (three semitones), and half step. For example, the consists of the notes A, B, C, D, E, F, and G♯, ascending and descending identically since it lacks variable forms. From the tonic, the intervals are to the second degree, to the third, to the fourth, to the fifth, to the sixth, and to the seventh. The defining feature of this scale is the augmented second interval between the sixth and seventh degrees, which introduces a distinctive, exotic tension compared to the natural minor's whole step in that position. This interval pattern distinguishes the harmonic minor from the natural minor, where the sixth-to-seventh step is a whole step and the seventh-to-tonic is also a whole step.

Harmonic applications

The harmonic minor scale's primary application in Western tonal harmony lies in its provision of a leading tone through the raised seventh degree, enabling a stronger half-step resolution from the dominant (V) chord to the tonic (i) in minor keys. This alteration addresses the natural minor scale's subtonic (♭7), which produces a weaker whole-step approach to the tonic, thus enhancing the sense of resolution in cadences. In practice, this facilitates the authentic cadence (V-i), a cornerstone of tonal progressions, by incorporating the major third and leading tone within the V chord. Common chords derived from the harmonic minor scale include the tonic i (minor triad), the mediant III (augmented triad), the dominant V (major triad), and the submediant VI (major triad). These chords support typical progressions such as i-V-i or i-VI-III-V, which reinforce the key's tonal center while exploiting the scale's augmented second interval for expressive tension. In , such appear frequently; for instance, employs the V-i resolution using the harmonic minor in his Piano Sonata No. 8 in , K. 310, to heighten dramatic closure at phrase ends. Similarly, Beethoven utilizes it in the first movement of No. 5 in C minor, where the leading tone B resolves emphatically to C in the V-i , underscoring the work's fateful intensity. In and , the harmonic minor scale's raised seventh ensures proper resolution of tendency tones, with the leading tone ascending to the tonic and avoiding parallel fifths or octaves that might arise from the natural minor's ♭7. This adherence to strict voice-leading rules strengthens coherence in polyphonic textures, as seen in the contrapuntal lines of Mozart's and Beethoven's chamber works.

Melodic minor scale

Construction and forms

The melodic minor scale is constructed by altering the natural minor scale, specifically by raising the sixth and seventh scale degrees in its ascending form. This modification starts from the natural minor and sharpens the (6th) and leading tone (7th), creating a scale that facilitates smoother melodic progression upward. For example, the A melodic minor scale ascending is A–B–C–D–E–F♯–G♯–A. The interval pattern for the ascending melodic minor follows whole (W) and half (H) steps as W–H–W–W–W–W–H, which differs from the natural minor's W–H–W–W–H–W–W by incorporating consecutive whole steps between the fifth, sixth, and seventh degrees. This pattern overlaps partially with the harmonic minor scale's raised seventh but adds the raised sixth for melodic purposes. In contrast, the descending form of the melodic minor scale reverts to the natural minor scale, using the unaltered sixth and seventh degrees. For the same key, the A melodic minor descending is A–G–F–E–D–C–B–A, with the interval pattern mirroring the natural minor's descending sequence of W–W–H–W–W–H–W. This dual-form structure arises from theory practices, where the ascending alterations provide smoother stepwise motion by eliminating the augmented second interval present between the sixth and seventh in the , while the descending form preserves a characteristic minor sound and aligns with harmonic expectations.

Melodic applications

The melodic minor scale, particularly its ascending form, is employed in melodic contexts to facilitate smooth ascending lines over minor-major seventh chords, where the raised sixth and seventh degrees provide a major sixth and seventh that enhance tension resolution without the dissonance of an augmented second. This form allows performers to create fluid scalar passages that align with the chord's natural thirteenth and leading tone, promoting a sense of directed motion in solos. Unlike the , the melodic minor produces a less exotic, more diatonic sound due to its even step pattern, avoiding the jarring interval that can disrupt linear flow. In , the melodic minor scale serves as the parent scale for several modes, such as the (seventh mode), which is applied over altered dominant chords to introduce tensions like the flat , sharp , and flat thirteenth for expressive melodic development. Modern compositions often derive modal lines from it, enabling improvisers to navigate complex progressions with varied color, as seen in transcriptions of trumpet solos by on tunes like "Daahoud," where scalar runs build and release tension over minor and dominant harmonies. Examples of its application include guitar solos in standards such as "Autumn Leaves," where ascending melodic minor patterns over minor-major seventh chords create lyrical ascents, and violin passages in classical repertoire that employ the scale for dramatic, unbroken melodic contours in film scores, contributing to emotional intensity without harmonic disruption. In , the dual forms of the scale—ascending with raised sixth and seventh, descending as natural minor—allow flexibility, while in , the ascending form with raised sixth and seventh is typically used in both directions.

Additional minor scales

Diatonic modes as minor scales

The diatonic modes derived from the major scale that exhibit minor qualities are the Aeolian, Dorian, and Phrygian modes, all characterized by a minor third interval from the tonic, which imparts a fundamentally somber or introspective tonal color. These modes differ primarily in their sixth and seventh scale degrees relative to the natural minor, allowing for varied emotional expressions within modal music traditions such as Renaissance polyphony and modern rock compositions. The Aeolian mode serves as the foundation, identical to the natural minor scale, with the interval pattern whole-half-whole-whole-half-whole-whole (e.g., A Aeolian: A-B-C-D-E-F-G-A). The , starting on the second degree of the , features a raised sixth degree compared to the Aeolian, creating a brighter yet still minor tonality with the pattern whole-half-whole-whole-whole-half-whole (e.g., D Dorian: D-E-F-G-A-B-C-D). This mode's subtle lift from the natural minor's flattened sixth evokes a brooding or thoughtful mood, making it prevalent in , as in the English "Scarborough Fair," and in , where it often outlines the in ii-V-I progressions, exemplified by Miles Davis's "So What." In contrast, the , derived from the third degree of the , includes a flattened second degree, yielding a tense, exotic flavor through the half-step pattern half-whole-whole-whole-half-whole-whole (e.g., E Phrygian: E-F-G-A-B-C-D-E). Its distinctive minor second interval contributes to a mysterious or intense quality, commonly associated with Spanish traditions, where it underpins the , and appears in rock for evocative effects, such as in certain heavy metal riffs emphasizing modal ambiguity. These minor modes were integral to vocal and instrumental works, where composers like employed Dorian and Phrygian for their expressive ranges in sacred and secular contexts, predating the dominance of major-minor . In contemporary rock, they provide alternatives to the natural minor, enhancing modal interchange, as seen in the Dorian-inflected progressions of songs like ' "."

Non-diatonic variants

Non-diatonic variants of the incorporate chromatic alterations that deviate from the standard , , and melodic forms, often drawing from ethnic or genre-specific traditions to create distinctive tonal colors. These scales introduce additional raised or lowered notes, resulting in augmented seconds or other intervals not found in purely diatonic structures. The , also known as the Gypsy minor, is derived from the minor by raising the fourth scale degree, producing the interval pattern of whole, half, augmented second, half, half, augmented second, half (e.g., in A: A–B–C–D♯–E–F–G♯–A). This alteration creates a tense, exotic sound characterized by two augmented seconds between the third-to-fourth and sixth-to-seventh degrees. It emerged in 19th-century Hungarian dance music and was popularized by Gypsy ensembles, influencing composers such as in his and in his Hungarian Dances. The scale remains prevalent in Eastern European folk traditions and has been adapted in Western for its dramatic effect. The double harmonic minor scale, sometimes called the Byzantine or Arabic scale, features a flattened second degree alongside the raised seventh of the harmonic minor, yielding the pattern of half, augmented second, half, whole, half, augmented second, half (e.g., in A: A–B♭–C♯–D–E–F–G♯–A). This configuration produces a highly dissonant profile with two augmented seconds, evoking intense emotional depth. Originating from Middle Eastern maqam systems, it has influenced music in and appears in Western compositions seeking orientalist flavors, such as in Nikolai Rimsky-Korsakov's works. Its use highlights cultural exchanges in global . Other non-diatonic variants include the , which applies the ascending melodic minor form bidirectionally (e.g., in A: A–B–C–D–E–F♯–G♯–A), providing a brighter minor for over dominant and minor-major seventh chords in . Similarly, the extends the minor pentatonic by adding a flattened fifth (e.g., in A: A–C–D–D♯–E–G–A), introducing a "" for expressive and tension in and related genres. These scales illustrate the synthetic nature of non-diatonic minors, which often blend diatonic foundations with chromatic elements tailored to specific musical idioms rather than adhering to strict Western modal categories.

Notation and usage

Key signatures

The key signatures for natural minor scales are identical to those of their relative major scales, which begin on the sixth degree of the minor scale. For instance, uses the same three sharps (F♯, C♯, G♯) as its relative , . Similarly, has no sharps or flats, matching , while features one flat (B♭), corresponding to . In compositions using harmonic or melodic minor scales, the key signature remains that of the natural minor, with adjustments made through added accidentals. For the harmonic minor, the seventh scale degree is raised by a half step (e.g., in A harmonic minor, the natural A minor key signature is used, but G is sharpened to G♯). The melodic minor similarly employs accidentals to raise the sixth and seventh degrees in the ascending form (e.g., F to F♯ and G to G♯ in A melodic minor), reverting to the natural minor descending, all within the base key signature. Minor keys are positioned on the circle of fifths inside the major keys, with each minor key serving as the relative minor to the major key three fifths clockwise from it. This arrangement progresses by perfect fifths, adding one sharp clockwise or one flat counterclockwise, facilitating quick identification of signatures (e.g., shares one sharp (F♯) with its relative ). Enharmonic equivalents exist for certain minor keys, such as and , which sound identical but use different notations. G♯ minor employs five sharps (F♯, C♯, G♯, D♯, A♯), while A♭ minor uses seven flats (B♭, E♭, A♭, D♭, G♭, C♭, F♭); in practice, A♭ minor is often preferred to minimize complex sharps in harmonic contexts or for instrumental readability.

Alternative notations

In the movable-do solfège system, the la-based minor assigns syllables to the degrees relative to its relative major, starting the tonic as la, followed by , do, re, mi, fa, sol, and returning to la. This approach, used in methods like Kodály training, facilitates recognition by treating the minor tonic as the sixth degree of the . Chord notations for typically append "m" to the root note to indicate a minor triad or , such as Cm for or Cm7 for , with a (-) serving as an alternative for minor seventh chords like C-. For alterations derived from harmonic or melodic minor, such as the minor-major seventh chord (minor triad with ), symbols include m(maj7) or mΔ7, while modal variants may use superscripts like those in the () or Phrygian dominant (harmonic minor-based). In jazz lead sheets and real books, melodic scales are often implied through chord symbols like A-Δ or A-Δ7, denoting A minor with a major seventh, which draws from the ascending melodic 's raised sixth and seventh degrees for harmonic tension and resolution. Slash chords, such as Am/G#, further specify bass notes or inversions in minor contexts, common in improvisational settings to guide scalar choices. Pre-20th century treatises described minor scales through modal distinctions rather than fixed diatonic structures, with Jean-Philippe Rameau's Traité de l'harmonie () emphasizing the mode's raised seventh for dominant (resembling modern harmonic minor) while noting separate ascending and descending melodic forms to avoid the augmented second. Earlier French theorists like Jean Rousseau and François Campion notated variants as Dorian (e.g., D without full flats) or Aeolian (e.g., A with complete signatures), using "réyennes" and "layennes" labels to reflect incomplete key signatures and mediant inflections differing from later standardized natural minor.

References

  1. https://pressbooks.nebraska.edu/openmusictheory/chapter/minor-scales/
  2. https://musictheory.pugetsound.edu/mt21c/MinorScales.html
  3. https://online.berklee.edu/takenote/music-modes-major-and-minor/
  4. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/16-minor-scale-variants/
  5. https://ojs.library.osu.edu/index.php/EMR/article/view/3731
  6. https://scholarworks.iu.edu/journals/index.php/iujur/article/download/24524/32031/62300
  7. https://www.potsdam.edu/sites/default/files/documents/academics/Crane/MusicTheory/Historical-periods.pdf
  8. https://digitalcommons.cedarville.edu/cgi/viewcontent.cgi?article=1032&context=musicalofferings
  9. https://musictheory.pugetsound.edu/mt21c/ScaleDegreeNames.html
  10. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/9-minor-keys-and-key-signatures-2/
  11. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/7-minor-scales/
  12. https://musictheorymaterials.utk.edu/wp-content/uploads/2018/09/Major-and-Minor-scales-small.pdf
  13. https://www.musictheoryacademy.com/understanding-music/the-minor-scales/
  14. https://viva.pressbooks.pub/openmusictheory/chapter/minor-scales/
  15. https://www.piano-keyboard-guide.com/a-minor-scale.html
  16. https://www.pianoscales.org/minor.html
  17. https://www.jazz-guitar-licks.com/pages/guitar-scales-modes/modes-of-the-major-scale/the-aeolian-mode.html
  18. https://www.guitarorb.com/natural-minor-scale/
  19. https://www.musiccrashcourses.com/lessons/scales_minor.html
  20. https://musictheory.pugetsound.edu/mt21c/MinorKeySignatures.html
  21. https://www.studybass.com/lessons/harmony/parallel-major-and-minor-scales/
  22. https://musictheorymaterials.utk.edu/wp-content/uploads/2018/09/Modulation.pdf
  23. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/28-modulation/
  24. https://musictheory.pugetsound.edu/mt21c/KeyRelationships.html
  25. https://www.studybass.com/lessons/harmony/the-harmonic-minor-scale/
  26. https://study.com/learn/lesson/harmonic-minor-scale-formula-modes.html
  27. https://appliedguitartheory.com/lessons/harmonic-minor-scale/
  28. https://www.jazz-guitar-licks.com/pages/guitar-scales-modes/modes-of-the-harmonic-minor-scale/harmonic-minor-scale-guitar-positions.html
  29. https://m.basicmusictheory.com/b-harmonic-minor-scale
  30. https://www.learnjazzstandards.com/blog/harmonic-minor-scale-guitar-piano/
  31. https://production.cbts.edu/Textbook/64dg2r/418142/Minor_Key_Scale_Degrees.pdf
  32. https://www.guitar-chords.org.uk/a-harmonic-minor-chords.html
  33. https://dmitri.mycpanel.princeton.edu/mozart.pdf
  34. https://www.hoffmanacademy.com/blog/cadence-in-music
  35. https://digitalcollections.lipscomb.edu/cgi/viewcontent.cgi?article=1382&context=jmtp
  36. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/17-the-viio-chord/
  37. https://mymusictheory.com/scales-and-keys/melodic-minor-scales/
  38. https://www.studybass.com/lessons/harmony/the-melodic-minor-scale/
  39. https://www.jazzadvice.com/lessons/4-ways-to-use-the-melodic-minor-scale/
  40. https://www.learnjazzstandards.com/blog/melodic-minor-scale/
  41. https://www.skoove.com/blog/the-melodic-minor-scale/
  42. https://www.masterclass.com/articles/learn-the-melodic-minor-scale
  43. https://academics.ysu.edu/percussion/diatonic-modes
  44. https://pressbooks.uiowa.edu/twentieth-and-twenty-first-century-music/chapter/mode/
  45. https://www.exhibit.xavier.edu/cgi/viewcontent.cgi?article=1033&context=hab
  46. https://jjs.libraries.rutgers.edu/index.php/jjs/article/download/113/89/444
  47. https://scholarworks.sfasu.edu/context/etds/article/1586/viewcontent/Modes_In_Heavy_Metal_Music.pdf
  48. https://digitalcommons.liberty.edu/cgi/viewcontent.cgi?article=1675&context=masters
  49. https://content.ucpress.edu/pages/10347/10347.ch01.pdf
  50. https://www.pianoscales.org/hungarian.html
  51. https://read.dukeupress.edu/journal-of-music-theory/article/69/1/1/401399/Modal-Color-Theory
  52. https://www.granthaalayahpublication.org/Arts-Journal/ShodhKosh/article/download/5668/5167/29968
  53. https://www.jazz-guitar-licks.com/pages/guitar-scales-modes/double-harmonic-scale/double-harmonic-major-byzantine-scale.html
  54. https://www.jazzguitar.be/blog/melodic-minor-modes/
  55. https://viva.pressbooks.pub/openmusictheory/chapter/blues-melodies-and-the-blues-scale/
  56. https://www.masterclass.com/articles/minor-scale-guide
  57. https://www.libertyparkmusic.com/the-circle-of-fifths/
  58. https://study.com/learn/lesson/enharmonic-scale-notes-equivalents.html
  59. https://www.piano-lessons-info.com/minor-key-signatures.html
  60. https://www.myeartraining.net/article_solfege
  61. https://jazz-library.com/articles/chord-symbols/
  62. https://www.jazzbooks.com/mm5/download/FREE-nomenclature.pdf
  63. https://mtosmt.org/issues/mto.17.23.1/mto.17.23.1.pedneault.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.