Recent from talks
Nothing was collected or created yet.
Water (data page)
View on WikipediaThis page provides supplementary data to the article properties of water.
Further comprehensive authoritative data can be found at the NIST Chemistry WebBook page on thermophysical properties of fluids.[1]
Structure and properties
[edit]| Structure and properties | |
|---|---|
| Index of refraction, nD | 1.333 at 20 °C |
| Dielectric constant[2] |
88.00 at 0 °C |
| Bond strength | 492.215 kJ/mol O–H bond dissociation energy[3] |
| Bond length | 95.87 pm (equilibrium)[4] |
| Bond angle | 104.48° (equilibrium) [5][6] |
| Magnetic susceptibility | −9.04 × 10−6 volume SI units[7] |
Thermodynamic properties
[edit]| Phase behavior | |
|---|---|
| Triple point | 273.16 K (0.01 °C), 611.73 Pa |
| Critical point | 647 K (374 °C), 22.1 MPa |
| Enthalpy change of fusion at 273.15 K, ΔfusH |
6.01 kJ/mol |
| Entropy change of fusion at 273.15 K, 1 bar, ΔfusS |
22.0 J/(mol·K) |
| Std enthalpy change of vaporization, ΔvapH |
44.0 kJ/mol |
| Enthalpy change of vaporization at 373.15 K, ΔvapH |
40.68 kJ/mol |
| Std entropy change of vaporization, ΔvapS |
118.89 J/(mol·K) |
| Entropy change of vaporization at 373.15 K, ΔvapS |
109.02 J/(mol·K) |
| Enthalpy change of sublimation at 273.15 K, ΔsubH |
51.1 kJ/mol |
| Std entropy change of sublimation at 273.15 K, 1 bar, ΔsubS |
~144 J/(mol·K) |
| Molal freezing point constant | −1.858 °C kg/mol |
| Molal boiling point constant | 0.512 °C kg/mol |
| Solid properties | |
| Std enthalpy change of formation, ΔfH |
−291.83 kJ/mol |
| Standard molar entropy, S |
41 J/(mol K) |
| Heat capacity, cp | 12.2 J/(mol K) at −200 °C 15.0 J/(mol K) at −180 °C 17.3 J/(mol K) at −160 °C 19.8 J/(mol K) at −140 °C 24.8 J/(mol K) at −100 °C 29.6 J/(mol K) at −60 °C 32.77 J/(mol K) at −38.3 °C 33.84 J/(mol K) at −30.6 °C 35.20 J/(mol K) at −20.8 °C 36.66 J/(mol K) at −11.0 °C 37.19 J/(mol K) at −4.9 °C 37.84 J/(mol K) at −2.2 °C |
| Liquid properties | |
| Std enthalpy change of formation, ΔfH |
−285.83 kJ/mol |
| Standard molar entropy, S |
69.95 J/(mol K) |
| Heat capacity, cp | 75.97 J/(mol K) and 4.2176 J/(g·K) at 0 °C 75.52 J/(mol K) and 4.1921 J/(g·K) at 10 °C 75.33 J/(mol K) and 4.1818 J/(g·K) at 20 °C 75.28 J/(mol K) and 4.1787 J/(g·K) at 25 °C 75.26 J/(mol K) and 4.1784 J/(g·K) at 30 °C 75.26 J/(mol K) and 4.1785 J/(g·K) at 40 °C 75.30 J/(mol K) and 4.1806 J/(g·K) at 50 °C 75.37 J/(mol K) and 4.1843 J/(g·K) at 60 °C 75.46 J/(mol K) and 4.1895 J/(g·K) at 70 °C 75.58 J/(mol K) and 4.1963 J/(g·K) at 80 °C 75.74 J/(mol K) and 4.2050 J/(g·K) at 90 °C 75.94 J/(mol K) and 4.2159 J/(g·K) at 100 °C |
| Gas properties | |
| Std enthalpy change of formation, ΔfH |
−241.83 kJ/mol |
| Standard molar entropy, S |
188.84 J/(mol K) |
| Heat capacity, cp | 36.5 J/(mol K) at 100 °C 36.1 J/(mol K) at 200 °C 36.2 J/(mol K) at 400 °C 37.9 J/(mol K) at 700 °C 41.4 J/(mol K) at 1000 °C |
| Heat capacity, cv | 27.5 J/(mol K) at 100 °C 27.6 J/(mol K) at 200 °C 27.8 J/(mol K) at 400 °C 29.5 J/(mol K) at 700 °C 33.1 J/(mol K) at 1000 °C |
| Heat capacity ratio, γ = cp/cv |
1.324 at 100 °C 1.310 at 200 °C 1.301 at 400 °C 1.282 at 700 °C 1.252 at 1000 °C |
| van der Waals' constants | a = 553.6 L2 kPa/mol2 b = 0.03049 L/mol |
Liquid physical properties
[edit]
| Velocity of sound in water | |
|---|---|
| c in distilled water at 25 °C | 1498 m/s |
| c at other temperatures[8] | 1403 m/s at 0 °C 1427 m/s at 5 °C 1447 m/s at 10 °C 1481 m/s at 20 °C 1507 m/s at 30 °C 1526 m/s at 40 °C 1541 m/s at 50 °C 1552 m/s at 60 °C 1555 m/s at 70 °C 1555 m/s at 80 °C 1550 m/s at 90 °C 1543 m/s at 100 °C |
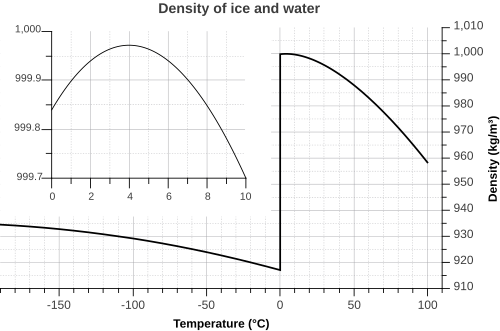
| Density[9][2][page needed] | |
| 0.983854 g/cm3 at −30 °C | 0.99221 g/cm3 at 40 °C |
| 0.993547 g/cm3 at −20 °C | 0.99022 g/cm3 at 45 °C |
| 0.998117 g/cm3 at −10 °C | 0.98804 g/cm3 at 50 °C |
| 0.9998395 g/cm3 at 0 °C | 0.98570 g/cm3 at 55 °C |
| 0.999972 g/cm3 at 3.984 °C[10] | |
| 0.9999720 g/cm3 at 4 °C | 0.98321 g/cm3 at 60 °C |
| 0.99996 g/cm3 at 5 °C | 0.98056 g/cm3 at 65 °C |
| 0.9997026 g/cm3 at 10 °C | 0.97778 g/cm3 at 70 °C |
| 0.9991026 g/cm3 at 15 °C | 0.97486 g/cm3 at 75 °C |
| 0.9982071 g/cm3 at 20 °C | 0.97180 g/cm3 at 80 °C |
| 0.9977735 g/cm3 at 22 °C | 0.96862 g/cm3 at 85 °C |
| 0.9970479 g/cm3 at 25 °C | 0.96531 g/cm3 at 90 °C |
| 0.9956502 g/cm3 at 30 °C | 0.96189 g/cm3 at 95 °C |
| 0.99403 g/cm3 at 35 °C | 0.95835 g/cm3 at 100 °C |
| The values below 0 °C refer to supercooled water. | |
| Viscosity[11] | |
| 1.7921 mPa·s (cP) at 0 °C | 0.5494 mPa·s at 50 °C |
| 1.5188 mPa·s at 5 °C | 0.5064 mPa·s at 55 °C |
| 1.3077 mPa·s at 10 °C | 0.4688 mPa·s at 60 °C |
| 1.1404 mPa·s at 15 °C | 0.4355 mPa·s at 65 °C |
| 1.0050 mPa·s at 20 °C | 0.4061 mPa·s at 70 °C |
| 0.8937 mPa·s at 25 °C | 0.3799 mPa·s at 75 °C |
| 0.8007 mPa·s at 30 °C | 0.3635 mPa·s at 80 °C |
| 0.7225 mPa·s at 35 °C | 0.3355 mPa·s at 85 °C |
| 0.6560 mPa·s at 40 °C | 0.3165 mPa·s at 90 °C |
| 0.5988 mPa·s at 45 °C | 0.2994 mPa·s at 95 °C |
| 0.2838 mPa·s at 100 °C | |
| Surface tension[12] | |
| 75.64 dyn/cm at 0 °C | 69.56 dyn/cm at 40 °C |
| 74.92 dyn/cm at 5 °C | 68.74 dyn/cm at 45 °C |
| 74.22 dyn/cm at 10 °C | 67.91 dyn/cm at 50 °C |
| 73.49 dyn/cm at 15 °C | 66.18 dyn/cm at 60 °C |
| 72.75 dyn/cm at 20 °C | 64.42 dyn/cm at 70 °C |
| 71.97 dyn/cm at 25 °C | 62.61 dyn/cm at 80 °C |
| 71.18 dyn/cm at 30 °C | 60.75 dyn/cm at 90 °C |
| 70.38 dyn/cm at 35 °C | 58.85 dyn/cm at 100 °C |
| Temperature, °C | Conductivity, μS/m |
|---|---|
| 0.01 | 1.15 |
| 25 | 5.50 |
| 100 | 76.5 |
| 200 | 299 |
| 300 | 241 |
Water/steam equilibrium properties
[edit]Vapor pressure formula for steam in equilibrium with liquid water:[14]
where P is equilibrium vapor pressure in kPa, and T is temperature in kelvins.
For T = 273 K to 333 K: A = 7.2326; B = 1750.286; C = 38.1.
For T = 333 K to 423 K: A = 7.0917; B = 1668.21; C = 45.1.
| Steam table[15] | |||||
|---|---|---|---|---|---|
| Temperature (°C) |
Pressure (kPa) |
H of liquid (J/g) |
ΔvapH (J/g) |
Wvap (J/g) |
ρ of vapor (kg/m3) |
| 0 | 0.612 | 0.00 | 2496.5 | 126.0 | 0.004855 |
| 10 | 1.227 | 42.0 | 2473.5 | 130.5 | 0.009498 |
| 20 | 2.336 | 83.8 | 2450.9 | 135.1 | 0.01728 |
| 30 | 4.242 | 125.6 | 2427.9 | 139.7 | 0.03037 |
| 40 | 7.370 | 167.2 | 2404.9 | 144.2 | 0.05107 |
| 50 | 12.33 | 209.0 | 2381.4 | 148.7 | 0.08275 |
| 60 | 19.90 | 250.8 | 2357.6 | 153.0 | 0.1300 |
| 70 | 31.15 | 292.7 | 2332.9 | 157.3 | 0.1979 |
| 80 | 46.12 | 334.6 | 2307.7 | 161.5 | 0.2930 |
| 90 | 70.10 | 376.6 | 2282.6 | 165.5 | 0.4232 |
| 100 | 101.32 | 419.0 | 2256.3 | 169.4 | 0.5974 |
| 110 | 143.27 | 460.8 | 2229.5 | 173.1 | 0.8264 |
| 120 | 198.50 | 503.2 | 2201.4 | 176.7 | 1.121 |
| 130 | 270.13 | 545.8 | 2172.5 | 180.2 | 1.497 |
| 140 | 361.4 | 588.5 | 2142.8 | 183.2 | 1.967 |
| 150 | 476.0 | 631.5 | 2111.8 | 186.1 | 2.548 |
| 160 | 618.1 | 674.7 | 2080.0 | 188.7 | 3.263 |
| 170 | 792.0 | 718.5 | 2047.0 | 190.6 | 4.023 |
| 180 | 1002.7 | 762.5 | 2012.2 | 192.8 | 5.165 |
| 190 | 1254.9 | 807.0 | 1975.8 | 194.5 | 6.402 |
| 200 | 1554.3 | 851.9 | 1937.3 | 195.6 | 7.868 |
| 210 | 1907.9 | 897.5 | 1897.5 | 196.3 | 9.606 |
| 221.1 | 2369.8 | 948.5 | 1850.2 | 196.6 | 11.88 |
| 229.4 | 2769.6 | 987.9 | 1812.5 | 196.2 | 13.87 |
| 240.6 | 3381.1 | 1040.6 | 1759.4 | 195.1 | 16.96 |
| 248.9 | 3904.1 | 1080.3 | 1715.8 | 193.7 | 19.66 |
| 260.0 | 4695.9 | 1134.8 | 1653.9 | 190.8 | 23.84 |
| 271.1 | 5603.4 | 1195.9 | 1586.5 | 186.9 | 28.83 |
| 279.4 | 6366.5 | 1240.7 | 1532.5 | 183.3 | 33.18 |
| 290.6 | 7506.2 | 1302.3 | 1456.3 | 177.4 | 39.95 |
| 298.9 | 8463.9 | 1350.0 | 1394.8 | 172.2 | 45.93 |
| 310.0 | 9878.0 | 1415.7 | 1307.7 | 164.2 | 55.25 |
| 321.1 | 11461 | 1483.9 | 1212.7 | 154.5 | 66.58 |
| 329.4 | 12785 | 1537.9 | 1133.2 | 145.6 | 76.92 |
| 340.6 | 14727 | 1617.9 | 1007.6 | 130.9 | 94.25 |
| 348.9 | 16331 | 1687.0 | 892.0 | 117.0 | 111.5 |
| 360.0 | 18682 | 1797.0 | 694.0 | 91.0 | 145.3 |
| 371.1 | 21349 | 1968.3 | 365.0 | 47.0 | 214.5 |
| 374.4 | 22242 | 2151.2 | 0 | 0 | 306.8 |
| Temperature (°C) |
Pressure (kPa) |
H of liquid (J/g) |
ΔvapH (J/g) |
Wvap (J/g) |
ρ of vapor (kg/m3) |
Data in the table above is given for water–steam equilibria at various temperatures over the entire temperature range at which liquid water can exist. Pressure of the equilibrium is given in the second column in kPa. The third column is the heat content of each gram of the liquid phase relative to water at 0 °C. The fourth column is the heat of vaporization of each gram of liquid that changes to vapor. The fifth column is the work PΔV done by each gram of liquid that changes to vapor. The sixth column is the density of the vapor.
Melting point of ice at various pressures
[edit]Data obtained from CRC Handbook of Chemistry and Physics 44th ed., p. 2390.
| Pressure kPa | Temp. °C |
| 101.325 | 0.0 |
| 32950 | −2.5 |
| 60311 | −5.0 |
| 87279 | −7.5 |
| 113267 | −10.0 |
| 138274 | −12.5 |
| 159358 | −15.0 |
| 179952 | −17.5 |
| 200251 | −20.0 |
| 215746 | −22.1 |
Table of various forms of ice
[edit]| Properties of various forms of ice[16] | |||||
|---|---|---|---|---|---|
| Ice form |
Density g/cm3 |
Crystal structure |
Triple points |
TP temp °C | TP pressure MPa |
| Ih | 0.92 | hexagonal | Lq, Vap, Ih | 0.01 | 0.000612 |
| Lq, Ih, III | −22.0 | 207.5 | |||
| Ih, II, III | −34.7 | 212.9 | |||
| Ic | 0.92 | cubic | |||
| II | 1.17 | rhombohedral | Ih, II, III | −34.7 | 212.9 |
| II, III, V | −24.3 | 344.3 | |||
| II, V, VI | −55 (est) | 620 | |||
| III | 1.14 | tetragonal | Lq, Ih, III | −22.0 | 207.5 |
| Lq, III, V | −17 | 346.3 | |||
| Ih, II, III | −34.7 | 212.9 | |||
| II, III, V | −24.3 | 344.3 | |||
| IV | 1.27 | rhombohedral | |||
| V | 1.23 | monoclinic | Lq, III, V | −17 | 346.3 |
| Lq, V, VI | 0.16 | 625.9 | |||
| II, III, V | −24.3 | 344.3 | |||
| II, V, VI | −55 (est) | 620 | |||
| VI | 1.31 | tetragonal | Lq, V, VI | 0.16 | 625.9 |
| Lq, VI, VII | 81.6 | 2200 | |||
| II, V, VI | −55 (est) | 620 | |||
| VI, VII, VIII | ≈5 | 2100 | |||
| VII | 1.50 | cubic | Lq, VI, VII | 81.6 | 2200 |
| VI, VII, VIII | ≈5 | 2100 | |||
| VII, VIII, X | −173 | 62000 | |||
| VIII | 1.46 | tetragonal | VI, VII, VIII | ≈5 | 2100 |
| VII, VIII, X | −173 | 62000 | |||
| IX | 1.16 | tetragonal | |||
| X | 2.46 | cubic | VII, VIII, X | −173 | 62000 |
| XI‡ | 0.92 | orthorhombic | Vap, Ih, XI | −201.5 | 0 (expected) |
| XII | 1.29 | tetragonal | |||
| XIII | 1.23 | monoclinic | |||
| XIV | 1.29 | orthorhombic | |||
‡Ice XI triple point is theoretical and has never been obtained
Phase diagram
[edit]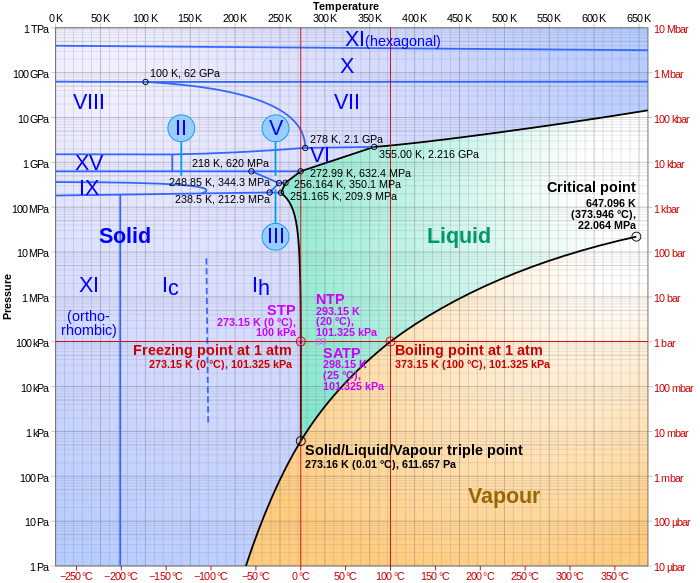
Water with dissolved NaCl
[edit]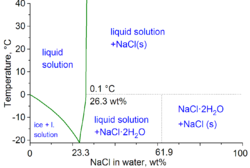
| NaCl, wt% | Teq, °C | ρ, g/cm3 | n | η, mPa·s |
|---|---|---|---|---|
| 0 | 0 | 0.99984 | 1.333 | 1.002 |
| 0.5 | −0.3 | 1.0018 | 1.3339 | 1.011 |
| 1 | −0.59 | 1.0053 | 1.3347 | 1.02 |
| 2 | −1.19 | 1.0125 | 1.3365 | 1.036 |
| 3 | −1.79 | 1.0196 | 1.3383 | 1.052 |
| 4 | −2.41 | 1.0268 | 1.34 | 1.068 |
| 5 | −3.05 | 1.034 | 1.3418 | 1.085 |
| 6 | −3.7 | 1.0413 | 1.3435 | 1.104 |
| 7 | −4.38 | 1.0486 | 1.3453 | 1.124 |
| 8 | −5.08 | 1.0559 | 1.347 | 1.145 |
| 9 | −5.81 | 1.0633 | 1.3488 | 1.168 |
| 10 | −6.56 | 1.0707 | 1.3505 | 1.193 |
| 12 | −8.18 | 1.0857 | 1.3541 | 1.25 |
| 14 | −9.94 | 1.1008 | 1.3576 | 1.317 |
| 16 | −11.89 | 1.1162 | 1.3612 | 1.388 |
| 18 | −14.04 | 1.1319 | 1.3648 | 1.463 |
| 20 | −16.46 | 1.1478 | 1.3684 | 1.557 |
| 22 | −19.18 | 1.164 | 1.3721 | 1.676 |
| 23.3 | −21.1 | |||
| 23.7 | −17.3 | |||
| 24.9 | −11.1 | |||
| 26.1 | −2.7 | |||
| 26.28 | 0 | |||
| 26.32 | 10 | |||
| 26.41 | 20 | |||
| 26.45 | 25 | |||
| 26.52 | 30 | |||
| 26.67 | 40 | |||
| 26.84 | 50 | |||
| 27.03 | 60 | |||
| 27.25 | 70 | |||
| 27.5 | 80 | |||
| 27.78 | 90 | |||
| 28.05 | 100 |
Note: ρ is density, n is refractive index at 589 nm,[clarification needed] and η is viscosity, all at 20 °C; Teq is the equilibrium temperature between two phases: ice/liquid solution for Teq < 0–0.1 °C and NaCl/liquid solution for Teq above 0.1 °C.
Self-ionization
[edit]Spectral data
[edit]| UV-Vis | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λmax | ? nm | |||||||||||||||
| Extinction coefficient, ε | ? | |||||||||||||||
| IR | ||||||||||||||||
| Major absorption bands[19] |
| |||||||||||||||
| NMR | ||||||||||||||||
| Proton NMR | 4.79 ppm in D2O ; 1.56 ppm in CDCl3 ; 0.40 ppm in C6D6 ; 4.87 in CD3OD[20] | |||||||||||||||
| Carbon-13 NMR | N/A | |||||||||||||||
| Other NMR data | ||||||||||||||||
| MS | ||||||||||||||||
| Masses of main fragments |
||||||||||||||||
Self-diffusion coefficients
[edit]| Experimental self-diffusion coefficients at various temperatures[21] | ||||||||||
| Temperature in °C | Coefficients in 10−9 m2/s | |||||||||
| 0 | 1.099 | |||||||||
| 1 | 1.138 | |||||||||
| 4 | 1.261 | |||||||||
| 5 | 1.303 | |||||||||
| 10 | 1.525 | |||||||||
| 15 | 1.765 | |||||||||
| 20 | 2.023 | |||||||||
| 25 | 2.299 | |||||||||
| 30 | 2.594 | |||||||||
| 35 | 2.907 | |||||||||
| 40 | 3.238 | |||||||||
| 45 | 3.588 | |||||||||
| 50 | 3.956 | |||||||||
| 56 | 4.423 | |||||||||
| 60 | 4.748 | |||||||||
| 70 | 5.615 | |||||||||
| 80 | 6.557 | |||||||||
| 90 | 7.574 | |||||||||
| 100 | 8.667 | |||||||||
Additional data translated from German "Wasser (Stoffdaten)" page
[edit]The data that follows was copied and translated from the German language Wikipedia version of this page (which has moved to here). It provides supplementary physical, thermodynamic, and vapor pressure data, some of which is redundant with data in the tables above, and some of which is additional.
Physical and thermodynamic tables
[edit]In the following tables, values are temperature-dependent and to a lesser degree pressure-dependent, and are arranged by state of aggregation (s = solid, lq = liquid, g = gas), which are clearly a function of temperature and pressure. All of the data were computed from data given in "Formulation of the Thermodynamic Properties of Ordinary Water Substance for Scientific and General Use" (IAPWS , 1984) (obsolete as of 1995).[22] This applies to:
- T – temperature in degrees Celsius
- V – specific volume in cubic decimeters per kilogram (1 dm3 is equivalent to 1 liter)
- H – specific enthalpy in kilojoules per kilogram
- U – specific internal energy in kilojoules per kilogram
- S – specific entropy in kilojoules per kilogram-kelvin
- cp – specific heat capacity at constant pressure in kilojoules per kilogram-kelvin
- γ – Thermal expansion coefficient as 10−3 per kelvin
- λ – Heat conductivity in milliwatts per meter-kelvin
- η – Viscosity in micropascal-seconds (1 cP = 1000 μPa·s)
- σ – surface tension in millinewtons per meter (equivalent to dyn/cm)
Standard conditions
[edit]In the following table, material data are given for standard pressure of 0.1 MPa (equivalent to 1 bar). Up to 99.63 °C (the boiling point of water at 0.1 MPa), at this pressure water exists as a liquid. Above that, it exists as water vapor. Note that the boiling point of 100.0 °C is at a pressure of 0.101325 MPa (1 atm), which is the average atmospheric pressure.
| Water/steam data table at standard pressure (0.1 MPa) | ||||||||||
| T °C | V dm3/kg |
H kJ/kg |
U kJ/kg |
S kJ/(kg·K) |
cp kJ/(kg·K) |
γ 10−3/K |
λ mW / (m·K) |
η μPa·s |
σ ‡ mN/m | |
| 0 | lq | 1.0002 | 0.06 | −0.04 | −0.0001 | 4.228 | −0.080 | 561.0 | 1792 | 75.65 |
| 5 | 1.0000 | 21.1 | 21.0 | 0.076 | 4.200 | 0.011 | 570.6 | 1518 | 74.95 | |
| 10 | 1.0003 | 42.1 | 42.0 | 0.151 | 4.188 | 0.087 | 580.0 | 1306 | 74.22 | |
| 15 | 1.0009 | 63.0 | 62.9 | 0.224 | 4.184 | 0.152 | 589.4 | 1137 | 73.49 | |
| 20 | 1.0018 | 83.9 | 83.8 | 0.296 | 4.183 | 0.209 | 598.4 | 1001 | 72.74 | |
| 25 | 1.0029 | 104.8 | 104.7 | 0.367 | 4.183 | 0.259 | 607.2 | 890.4 | 71.98 | |
| 30 | 1.0044 | 125.8 | 125.7 | 0.437 | 4.183 | 0.305 | 615.5 | 797.7 | 71.20 | |
| 35 | 1.0060 | 146.7 | 146.6 | 0.505 | 4.183 | 0.347 | 623.3 | 719.6 | 70.41 | |
| 40 | 1.0079 | 167.6 | 167.5 | 0.572 | 4.182 | 0.386 | 630.6 | 653.3 | 69.60 | |
| 45 | 1.0099 | 188.5 | 188.4 | 0.638 | 4.182 | 0.423 | 637.3 | 596.3 | 68.78 | |
| 50 | 1.0121 | 209.4 | 209.3 | 0.704 | 4.181 | 0.457 | 643.6 | 547.1 | 67.95 | |
| 60 | 1.0171 | 251.2 | 251.1 | 0.831 | 4.183 | 0.522 | 654.4 | 466.6 | 66.24 | |
| 70 | 1.0227 | 293.1 | 293.0 | 0.955 | 4.187 | 0.583 | 663.1 | 404.1 | 64.49 | |
| 80 | 1.0290 | 335.0 | 334.9 | 1.075 | 4.194 | 0.640 | 670.0 | 354.5 | 62.68 | |
| 90 | 1.0359 | 377.0 | 376.9 | 1.193 | 4.204 | 0.696 | 675.3 | 314.6 | 60.82 | |
| 99.63 | lq | 1.0431 | 417.5 | 417.4 | 1.303 | 4.217 | 0.748 | 679.0 | 283.0 | 58.99 |
| g | 1694.3 | 2675 | 2505 | 7.359 | 2.043 | 2.885 | 25.05 | 12.26 | – | |
| 100 | g | 1696.1 | 2675 | 2506 | 7.361 | 2.042 | 2.881 | 25.08 | 12.27 | 58.92 |
| 200 | 2172.3 | 2874 | 2657 | 7.833 | 1.975 | 2.100 | 33.28 | 16.18 | 37.68 | |
| 300 | 2638.8 | 3073 | 2810 | 8.215 | 2.013 | 1.761 | 43.42 | 20.29 | 14.37 | |
| 500 | 3565.5 | 3488 | 3131 | 8.834 | 2.135 | 1.297 | 66.970 | 28.57 | – | |
| 750 | 4721.0 | 4043 | 3571 | 9.455 | 2.308 | 0.978 | 100.30 | 38.48 | – | |
| 1000 | 5875.5 | 4642 | 4054 | 9.978 | 2.478 | 0.786 | 136.3 | 47.66 | – | |
| ‡ The values for surface tension for the liquid section of the table are for a liquid/air interface. Values for the gas section of the table are for a liquid/saturated steam interface. | ||||||||||
Triple point
[edit]In the following table, material data are given with a pressure of 611.7 Pa (equivalent to 0.006117 bar). Up to a temperature of 0.01 °C, the triple point of water, water normally exists as ice, except for supercooled water, for which one data point is tabulated here. At the triple point, ice can exist together with both liquid water and vapor. At higher temperatures, the data are for water vapor only.
| Water/steam data table at triple point pressure (0.0006117 MPa) | |||||||||
| T °C | V dm3/kg |
H kJ/kg |
U kJ/kg |
S kJ/(kg·K) |
cp kJ/(kg·K) |
γ 10−3/K |
λ mW / (m·K) |
η μPa·s | |
| 0 | lq | 1.0002 | −0.04 | −0.04 | −0.0002 | 4.339 | −0.081 | 561.0 | 1792 |
| 0.01 | s | 1.0908 | −333.4 | −333.4 | −1.221 | 1.93 | 0.1 | 2180 | – |
| lq | 1.0002 | 0.0 | 0 | 0 | 4.229 | −0.080 | 561.0 | 1791 | |
| g | 205986 | 2500 | 2374 | 9.154 | 1.868 | 3.672 | 17.07 | 9.22 | |
| 5 | g | 209913 | 2509 | 2381 | 9.188 | 1.867 | 3.605 | 17.33 | 9.34 |
| 10 | 213695 | 2519 | 2388 | 9.222 | 1.867 | 3.540 | 17.60 | 9.46 | |
| 15 | 217477 | 2528 | 2395 | 9.254 | 1.868 | 3.478 | 17.88 | 9.59 | |
| 20 | 221258 | 2537 | 2402 | 9.286 | 1.868 | 3.417 | 18.17 | 9.73 | |
| 25 | 225039 | 2547 | 2409 | 9.318 | 1.869 | 3.359 | 18.47 | 9.87 | |
| 30 | 228819 | 2556 | 2416 | 9.349 | 1.869 | 3.304 | 18.78 | 10.02 | |
| 35 | 232598 | 2565 | 2423 | 9.380 | 1.870 | 3.249 | 19.10 | 10.17 | |
| 40 | 236377 | 2575 | 2430 | 9.410 | 1.871 | 3.197 | 19.43 | 10.32 | |
| 45 | 240155 | 2584 | 2437 | 9.439 | 1.872 | 3.147 | 19.77 | 10.47 | |
| 50 | 243933 | 2593 | 2444 | 9.469 | 1.874 | 3.098 | 20.11 | 10.63 | |
| 60 | 251489 | 2612 | 2459 | 9.526 | 1.876 | 3.004 | 20.82 | 10.96 | |
| 70 | 259043 | 2631 | 2473 | 9.581 | 1.880 | 2.916 | 21.56 | 11.29 | |
| 80 | 266597 | 2650 | 2487 | 9.635 | 1.883 | 2.833 | 22.31 | 11.64 | |
| 90 | 274150 | 2669 | 2501 | 9.688 | 1.887 | 2.755 | 23.10 | 11.99 | |
| 100 | 281703 | 2688 | 2515 | 9.739 | 1.891 | 2.681 | 23.90 | 12.53 | |
| 200 | 357216 | 2879 | 2661 | 10.194 | 1.940 | 2.114 | 32.89 | 16.21 | |
| 300 | 432721 | 3076 | 2811 | 10.571 | 2.000 | 1.745 | 43.26 | 20.30 | |
| 500 | 583725 | 3489 | 3132 | 11.188 | 2.131 | 1.293 | 66.90 | 28.57 | |
| 750 | 772477 | 4043 | 3571 | 11.808 | 2.307 | 0.977 | 100.20 | 38.47 | |
| 1000 | 961227 | 4642 | 4054 | 12.331 | 2.478 | 0.785 | 136.30 | 47.66 | |
Saturated vapor pressure
[edit]The following table is based on different, complementary sources and approximation formulas, whose values are of various quality and accuracy. The values in the temperature range of −100 °C to 100 °C were inferred from D. Sunday (1982) and are quite uniform and exact. The values in the temperature range of the boiling point of water up to the critical point (100 °C to 374 °C) are drawn from different sources and are substantially less accurate; hence they should be used only as approximate values.[23][24][25][26]
To use the values correctly, consider the following points:
- The values apply only to smooth interfaces and in the absence other gases or gas mixtures such as air. Hence they apply only to pure phases and need a correction factor for systems in which air is present.
- The values were not computed according formulas widely used in the US, but using somewhat more exact formulas (see below), which can also be used to compute further values in the appropriate temperature ranges.
- The saturated vapor pressure over water in the temperature range of −100 °C to −50 °C is only extrapolated [Translator's note: Supercooled liquid water is not known to exist below −42 °C].
- The values have various units (Pa, hPa or bar), which must be considered when reading them.
Formulas
[edit]The table values for −100 °C to 100 °C were computed by the following formulas, where T is in kelvins and vapor pressures, Pw and Pi, are in pascals.
Over liquid water
- loge(Pw) = −6094.4642 T−1 + 21.1249952 − 2.724552×10−2 T + 1.6853396×10−5 T2 + 2.4575506 loge(T)
For temperature range: 173.15 K to 373.15 K or equivalently −100 °C to 100 °C
Over ice
- loge(Pi) = −5504.4088 T−1 − 3.5704628 − 1.7337458×10−2 T + 6.5204209×10−6 T2 + 6.1295027 loge(T)
For temperature range: 173.15 K to 273.15 K or equivalently −100 °C to 0 °C
At triple point
An important basic value, which is not registered in the table, is the saturated vapor pressure at the triple point of water. The internationally accepted value according to measurements of Guildner, Johnson and Jones (1976) amounts to:
| Values of saturated vapor pressure of water | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp. T in °C |
Pi(T) over ice in Pa |
Pw(T) over water in Pa |
Temp. T in °C |
Pw(T) over water in hPa |
Temp. T in °C |
P(T) in bar |
Temp. T in °C |
P(T) in bar |
Temp. T in °C |
P(T) in bar | ||||
| −100 | 0.0013957 | 0.0036309 | 0 | 6.11213 | 100 | 1.01 | 200 | 15.55 | 300 | 85.88 | ||||
| −99 | 0.0017094 | 0.0044121 | 1 | 6.57069 | 101 | 1.05 | 201 | 15.88 | 301 | 87.09 | ||||
| −98 | 0.0020889 | 0.0053487 | 2 | 7.05949 | 102 | 1.09 | 202 | 16.21 | 302 | 88.32 | ||||
| −97 | 0.0025470 | 0.0064692 | 3 | 7.58023 | 103 | 1.13 | 203 | 16.55 | 303 | 89.57 | ||||
| −96 | 0.0030987 | 0.0078067 | 4 | 8.13467 | 104 | 1.17 | 204 | 16.89 | 304 | 90.82 | ||||
| −95 | 0.0037617 | 0.0093996 | 5 | 8.72469 | 105 | 1.21 | 205 | 17.24 | 305 | 92.09 | ||||
| −94 | 0.0045569 | 0.011293 | 6 | 9.35222 | 106 | 1.25 | 206 | 17.60 | 306 | 93.38 | ||||
| −93 | 0.0055087 | 0.013538 | 7 | 10.0193 | 107 | 1.30 | 207 | 17.96 | 307 | 94.67 | ||||
| −92 | 0.0066455 | 0.016195 | 8 | 10.7280 | 108 | 1.34 | 208 | 18.32 | 308 | 95.98 | ||||
| −91 | 0.0080008 | 0.019333 | 9 | 11.4806 | 109 | 1.39 | 209 | 18.70 | 309 | 97.31 | ||||
| −90 | 0.0096132 | 0.023031 | 10 | 12.2794 | 110 | 1.43 | 210 | 19.07 | 310 | 98.65 | ||||
| −89 | 0.011528 | 0.027381 | 11 | 13.1267 | 111 | 1.48 | 211 | 19.46 | 311 | 100.00 | ||||
| −88 | 0.013797 | 0.032489 | 12 | 14.0251 | 112 | 1.53 | 212 | 19.85 | 312 | 101.37 | ||||
| −87 | 0.016482 | 0.038474 | 13 | 14.9772 | 113 | 1.58 | 213 | 20.25 | 313 | 102.75 | ||||
| −86 | 0.019653 | 0.045473 | 14 | 15.9856 | 114 | 1.64 | 214 | 20.65 | 314 | 104.15 | ||||
| −85 | 0.02339 | 0.053645 | 15 | 17.0532 | 115 | 1.69 | 215 | 21.06 | 315 | 105.56 | ||||
| −84 | 0.027788 | 0.063166 | 16 | 18.1829 | 116 | 1.75 | 216 | 21.47 | 316 | 106.98 | ||||
| −83 | 0.032954 | 0.074241 | 17 | 19.3778 | 117 | 1.81 | 217 | 21.89 | 317 | 108.43 | ||||
| −82 | 0.039011 | 0.087101 | 18 | 20.6409 | 118 | 1.86 | 218 | 22.32 | 318 | 109.88 | ||||
| −81 | 0.046102 | 0.10201 | 19 | 21.9757 | 119 | 1.93 | 219 | 22.75 | 319 | 111.35 | ||||
| −80 | 0.054388 | 0.11925 | 20 | 23.3854 | 120 | 1.99 | 220 | 23.19 | 320 | 112.84 | ||||
| −79 | 0.064057 | 0.13918 | 21 | 24.8737 | 121 | 2.05 | 221 | 23.64 | 321 | 114.34 | ||||
| −78 | 0.075320 | 0.16215 | 22 | 26.4442 | 122 | 2.12 | 222 | 24.09 | 322 | 115.86 | ||||
| −77 | 0.088419 | 0.18860 | 23 | 28.1006 | 123 | 2.18 | 223 | 24.55 | 323 | 117.39 | ||||
| −76 | 0.10363 | 0.21901 | 24 | 29.8470 | 124 | 2.25 | 224 | 25.02 | 324 | 118.94 | ||||
| −75 | 0.12127 | 0.25391 | 25 | 31.6874 | 125 | 2.32 | 225 | 25.49 | 325 | 120.51 | ||||
| −74 | 0.14168 | 0.29390 | 26 | 33.6260 | 126 | 2.40 | 226 | 25.98 | 326 | 122.09 | ||||
| −73 | 0.16528 | 0.33966 | 27 | 35.6671 | 127 | 2.47 | 227 | 26.46 | 327 | 123.68 | ||||
| −72 | 0.19252 | 0.39193 | 28 | 37.8154 | 128 | 2.55 | 228 | 26.96 | 328 | 125.30 | ||||
| −71 | 0.22391 | 0.45156 | 29 | 40.0754 | 129 | 2.62 | 229 | 27.46 | 329 | 126.93 | ||||
| −70 | 0.26004 | 0.51948 | 30 | 42.4520 | 130 | 2.70 | 230 | 27.97 | 330 | 128.58 | ||||
| −69 | 0.30156 | 0.59672 | 31 | 44.9502 | 131 | 2.78 | 231 | 28.48 | 331 | 130.24 | ||||
| −68 | 0.34921 | 0.68446 | 32 | 47.5752 | 132 | 2.87 | 232 | 29.01 | 332 | 131.92 | ||||
| −67 | 0.40383 | 0.78397 | 33 | 50.3322 | 133 | 2.95 | 233 | 29.54 | 333 | 133.62 | ||||
| −66 | 0.46633 | 0.89668 | 34 | 53.2267 | 134 | 3.04 | 234 | 30.08 | 334 | 135.33 | ||||
| −65 | 0.53778 | 1.0242 | 35 | 56.2645 | 135 | 3.13 | 235 | 30.62 | 335 | 137.07 | ||||
| −64 | 0.61933 | 1.1682 | 36 | 59.4513 | 136 | 3.22 | 236 | 31.18 | 336 | 138.82 | ||||
| −63 | 0.71231 | 1.3306 | 37 | 62.7933 | 137 | 3.32 | 237 | 31.74 | 337 | 140.59 | ||||
| −62 | 0.81817 | 1.5136 | 38 | 66.2956 | 138 | 3.42 | 238 | 32.31 | 338 | 142.37 | ||||
| −61 | 0.93854 | 1.7195 | 39 | 69.9675 | 139 | 3.51 | 239 | 32.88 | 339 | 144.18 | ||||
| −60 | 1.0753 | 1.9509 | 40 | 73.8127 | 140 | 3.62 | 240 | 33.47 | 340 | 146.00 | ||||
| −59 | 1.2303 | 2.2106 | 41 | 77.8319 | 141 | 3.72 | 241 | 34.06 | 341 | 147.84 | ||||
| −58 | 1.4060 | 2.5018 | 42 | 82.0536 | 142 | 3.82 | 242 | 34.66 | 342 | 149.71 | ||||
| −57 | 1.6049 | 2.8277 | 43 | 86.4633 | 143 | 3.93 | 243 | 35.27 | 343 | 151.58 | ||||
| −56 | 1.8296 | 3.1922 | 44 | 91.0757 | 144 | 4.04 | 244 | 35.88 | 344 | 153.48 | ||||
| −55 | 2.0833 | 3.5993 | 45 | 95.8984 | 145 | 4.16 | 245 | 36.51 | 345 | 155.40 | ||||
| −54 | 2.3694 | 4.0535 | 46 | 100.939 | 146 | 4.27 | 246 | 37.14 | 346 | 157.34 | ||||
| −53 | 2.6917 | 4.5597 | 47 | 106.206 | 147 | 4.39 | 247 | 37.78 | 347 | 159.30 | ||||
| −52 | 3.0542 | 5.1231 | 48 | 111.708 | 148 | 4.51 | 248 | 38.43 | 348 | 161.28 | ||||
| −51 | 3.4618 | 5.7496 | 49 | 117.452 | 149 | 4.64 | 249 | 39.09 | 349 | 163.27 | ||||
| −50 | 3.9193 | 6.4454 | 50 | 123.4478 | 150 | 4.76 | 250 | 39.76 | 350 | 165.29 | ||||
| −49 | 4.4324 | 7.2174 | 51 | 129.7042 | 151 | 4.89 | 251 | 40.44 | 351 | 167.33 | ||||
| −48 | 5.0073 | 8.0729 | 52 | 136.2304 | 152 | 5.02 | 252 | 41.12 | 352 | 169.39 | ||||
| −47 | 5.6506 | 9.0201 | 53 | 143.0357 | 153 | 5.16 | 253 | 41.81 | 353 | 171.47 | ||||
| −46 | 6.3699 | 10.068 | 54 | 150.1298 | 154 | 5.29 | 254 | 42.52 | 354 | 173.58 | ||||
| −45 | 7.1732 | 11.225 | 55 | 157.5226 | 155 | 5.43 | 255 | 43.23 | 355 | 175.70 | ||||
| −44 | 8.0695 | 12.503 | 56 | 165.2243 | 156 | 5.58 | 256 | 43.95 | 356 | 177.85 | ||||
| −43 | 9.0685 | 13.911 | 57 | 173.2451 | 157 | 5.72 | 257 | 44.68 | 357 | 180.02 | ||||
| −42 | 10.181 | 15.463 | 58 | 181.5959 | 158 | 5.87 | 258 | 45.42 | 358 | 182.21 | ||||
| −41 | 11.419 | 17.170 | 59 | 190.2874 | 159 | 6.03 | 259 | 46.16 | 359 | 184.43 | ||||
| −40 | 12.794 | 19.048 | 60 | 199.3309 | 160 | 6.18 | 260 | 46.92 | 360 | 186.66 | ||||
| −39 | 14.321 | 21.110 | 61 | 208.7378 | 161 | 6.34 | 261 | 47.69 | 361 | 188.93 | ||||
| −38 | 16.016 | 23.372 | 62 | 218.5198 | 162 | 6.50 | 262 | 48.46 | 362 | 191.21 | ||||
| −37 | 17.893 | 25.853 | 63 | 228.6888 | 163 | 6.67 | 263 | 49.25 | 363 | 193.52 | ||||
| −36 | 19.973 | 28.570 | 64 | 239.2572 | 164 | 6.84 | 264 | 50.05 | 364 | 195.86 | ||||
| −35 | 22.273 | 31.544 | 65 | 250.2373 | 165 | 7.01 | 265 | 50.85 | 365 | 198.22 | ||||
| −34 | 24.816 | 34.795 | 66 | 261.6421 | 166 | 7.18 | 266 | 51.67 | 366 | 200.61 | ||||
| −33 | 27.624 | 38.347 | 67 | 273.4845 | 167 | 7.36 | 267 | 52.49 | 367 | 203.02 | ||||
| −32 | 30.723 | 42.225 | 68 | 285.7781 | 168 | 7.55 | 268 | 53.33 | 368 | 205.47 | ||||
| −31 | 34.140 | 46.453 | 69 | 298.5363 | 169 | 7.73 | 269 | 54.17 | 369 | 207.93 | ||||
| −30 | 37.903 | 51.060 | 70 | 311.7731 | 170 | 7.92 | 270 | 55.03 | 370 | 210.43 | ||||
| −29 | 42.046 | 56.077 | 71 | 325.5029 | 171 | 8.11 | 271 | 55.89 | 371 | 212.96 | ||||
| −28 | 46.601 | 61.534 | 72 | 339.7401 | 172 | 8.31 | 272 | 56.77 | 372 | 215.53 | ||||
| −27 | 51.607 | 67.466 | 73 | 354.4995 | 173 | 8.51 | 273 | 57.66 | 373 | 218.13 | ||||
| −26 | 57.104 | 73.909 | 74 | 369.7963 | 174 | 8.72 | 274 | 58.56 | 374 | 220.64 | ||||
| −25 | 63.134 | 80.902 | 75 | 385.6459 | 175 | 8.92 | 275 | 59.46 | 374.15 | 221.20 | ||||
| −24 | 69.745 | 88.485 | 76 | 402.0641 | 176 | 9.14 | 276 | 60.38 | ||||||
| −23 | 76.987 | 96.701 | 77 | 419.0669 | 177 | 9.35 | 277 | 61.31 | ||||||
| −22 | 84.914 | 105.60 | 78 | 436.6708 | 178 | 9.57 | 278 | 62.25 | ||||||
| −21 | 93.584 | 115.22 | 79 | 454.8923 | 179 | 9.80 | 279 | 63.20 | ||||||
| −20 | 103.06 | 125.63 | 80 | 473.7485 | 180 | 10.03 | 280 | 64.17 | ||||||
| −19 | 113.41 | 136.88 | 81 | 493.2567 | 181 | 10.26 | 281 | 65.14 | ||||||
| −18 | 124.70 | 149.01 | 82 | 513.4345 | 182 | 10.50 | 282 | 66.12 | ||||||
| −17 | 137.02 | 162.11 | 83 | 534.3000 | 183 | 10.74 | 283 | 67.12 | ||||||
| −16 | 150.44 | 176.23 | 84 | 555.8714 | 184 | 10.98 | 284 | 68.13 | ||||||
| −15 | 165.06 | 191.44 | 85 | 578.1673 | 185 | 11.23 | 285 | 69.15 | ||||||
| −14 | 180.97 | 207.81 | 86 | 601.2068 | 186 | 11.49 | 286 | 70.18 | ||||||
| −13 | 198.27 | 225.43 | 87 | 625.0090 | 187 | 11.75 | 287 | 71.22 | ||||||
| −12 | 217.07 | 244.37 | 88 | 649.5936 | 188 | 12.01 | 288 | 72.27 | ||||||
| −11 | 237.49 | 264.72 | 89 | 674.9806 | 189 | 12.28 | 289 | 73.34 | ||||||
| −10 | 259.66 | 286.57 | 90 | 701.1904 | 190 | 12.55 | 290 | 74.42 | ||||||
| −9 | 283.69 | 310.02 | 91 | 728.2434 | 191 | 12.83 | 291 | 75.51 | ||||||
| −8 | 309.75 | 335.16 | 92 | 756.1608 | 192 | 13.11 | 292 | 76.61 | ||||||
| −7 | 337.97 | 362.10 | 93 | 784.9639 | 193 | 13.40 | 293 | 77.72 | ||||||
| −6 | 368.52 | 390.95 | 94 | 814.6743 | 194 | 13.69 | 294 | 78.85 | ||||||
| −5 | 401.58 | 421.84 | 95 | 845.3141 | 195 | 13.99 | 295 | 79.99 | ||||||
| −4 | 437.31 | 454.88 | 96 | 876.9057 | 196 | 14.29 | 296 | 81.14 | ||||||
| −3 | 475.92 | 490.19 | 97 | 909.4718 | 197 | 14.60 | 297 | 82.31 | ||||||
| −2 | 517.62 | 527.93 | 98 | 943.0355 | 198 | 14.91 | 298 | 83.48 | ||||||
| −1 | 562.62 | 568.22 | 99 | 977.6203 | 199 | 15.22 | 299 | 84.67 | ||||||
| 0 | 611.153 | 611.213 | 100 | 1013.25 | 200 | 15.55 | 300 | 85.88 | ||||||
| Temp. T in °C |
Pi(T) over ice in Pa |
Pw(T) over water in Pa |
Temp. T in °C |
Pw(T) over water in hPa |
Temp. T in °C |
P(T) in bar |
Temp. T in °C |
P(T) in bar |
Temp. T in °C |
P(T) in bar | ||||
Magnetic susceptibility
[edit]Accepted standardized value of the magnetic susceptibility of water at 20 °C (room temperature) is −12.97 cm3/mol.[27]
Accepted standardized value of the magnetic susceptibility of water at 20 °C (room temperature) is −0.702 cm3/g.[27]
| Isotopolog, state |
Temperature in K |
Magnetic susceptibiliy in cm3/mol |
|---|---|---|
| H2O(g) | >373 | −13.1 |
| H2O(l) | 373 | −13.09 |
| H2O(l) | 293 | −12.97 |
| H2O(l) | 273 | −12.93 |
| H2O(s) | 273 | −12.65 |
| H2O(s) | 223 | −12.31 |
| DHO(l) | 302 | −12.97 |
| D2O(l) | 293 | −12.76 |
| D2O(l) | 276.8 | −12.66 |
| D2O(s) | 276.8 | −12.54 |
| D2O(s) | 213 | −12.41 |
- Except where noted otherwise, data relate to Standard temperature and pressure.
- Reliability of data general note.
See also
[edit]References
[edit]- ^ "Thermophysical Properties of Fluid Systems". NIST Chemistry WebBook. National Institute of Standards and Technology. doi:10.18434/T4D303. NIST Standard Reference Database Number 69.
- ^ a b Lide 2004, p. 6-15.
- ^ Maksyutenko, Pavlo; Rizzo, Thomas R.; Boyarkin, Oleg V. (2006). "A direct measurement of the dissociation energy of water". The Journal of Chemical Physics. 125 (18): 181101. Bibcode:2006JChPh.125r1101M. doi:10.1063/1.2387163. PMID 17115729.
- ^ Cook, R; Delucia, F; Helminger, P (1974). "Molecular force field and structure of water: Recent microwave results". Journal of Molecular Spectroscopy. 53 (1): 62–76. Bibcode:1974JMoSp..53...62C. doi:10.1016/0022-2852(74)90261-6.
- ^ Hoy, AR; Bunker, PR (1979). "A precise solution of the rotation bending Schrödinger equation for a triatomic molecule with application to the water molecule". Journal of Molecular Spectroscopy. 74 (1): 1–8. Bibcode:1979JMoSp..74....1H. doi:10.1016/0022-2852(79)90019-5.
- ^ "List of experimental bond angles of type aHOH". Computational Chemistry Comparison and Benchmark DataBase. Archived from the original on 2014-09-03. Retrieved 2014-08-27.
- ^ Griffiths, David Jeffery (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. p. 275. ISBN 978-0-13-919960-8.
- ^ "Water and the Speed of Sound". www.engineeringtoolbox.com. Retrieved 2008-04-29.
- ^ Dean & Lange 1999, p. 1199: Due to the old definition of liter used at the time, the data from the Handbook was converted from old g/ml to g/cm3, by multiplying by 0.999973
- ^ Franks 2012, p. 376.
- ^ Lide 2004, p. 6-201.
- ^ Dean & Lange 1999, p. 1663.
- ^ Revised Release on Viscosity and Thermal Conductivity of Heavy Water Substance Archived 2017-01-01 at the Wayback Machine, The International Association for the Properties of Water and Steam Lucerne, Switzerland, August 2007.
- ^ Dean & Lange 1999, p. 1436.
- ^ Dean & Lange 1999, p. 1476.
- ^ Martin Chaplin. "Water Phase Diagram". London South Bank University. Retrieved 2022-05-27.
- ^ Lide, D. R., ed. (2005). CRC Handbook of Chemistry and Physics (86th ed.). Boca Raton, Florida: CRC Press. pp. 8–71, 8–116. ISBN 0-8493-0486-5.
- ^ Martin Chaplin. "Water ionization". London South Bank University. Retrieved 2022-05-27.
- ^ Martin Chaplin. "Water Absorption Spectrum". London South Bank University. Retrieved 2022-05-27.
- ^ Fulmer, Gregory R.; Miller, Alexander J. M.; Sherden, Nathaniel H.; Gottlieb, Hugo E.; Nudelman, Abraham; Stoltz, Brian M.; Bercaw, John E.; Goldberg, Karen I. (2010). "NMR Chemical Shifts of Trace Impurities: Common Laboratory Solvents, Organics, and Gases in Deuterated Solvents Relevant to the Organometallic Chemist" (PDF). Organometallics. 29 (9): 2176–2179. doi:10.1021/om100106e. ISSN 0276-7333.
- ^ Holz, Manfred; Heil, Stefan R.; Sacco, Antonio (2000). "Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1
H NMR PFG measurements". Physical Chemistry Chemical Physics. 2 (20): 4740–4742. Bibcode:2000PCCP....2.4740H. doi:10.1039/b005319h. ISSN 1463-9084. - ^ "IAPWS". Main IAPWS Thermodynamic Property Formulations. Retrieved 4 May 2023.
In 1995, IAPWS approved a new formulation of the thermodynamic properties of water and steam for general and scientific use. This replaced the 1984 formulation of Haar, Gallagher and Kell, and now serves as the international standard for water's thermodynamic properties.
- ^ Guildner, L. A.; Johnson, D. P.; Jones, F. E. (1976). "Vapor Pressure of Water at Its Triple Point: Highly Accurate Value". Science. 191 (4233): 1261. Bibcode:1976Sci...191.1261G. doi:10.1126/science.191.4233.1261. PMID 17737716. S2CID 37399612.
- ^ Klaus Scheffler (1981): Wasserdampftafeln: thermodynam. Eigenschaften von Wasser u. Wasserdampf bis 800°C u. 800 bar (Water Vapor Tables: Thermodynamic Characteristics of Water and Water Vapor to 800°C and 800 bar), Berlin [u.a.] ISBN 3-540-10930-7
- ^ D. Sonntag und D. Heinze (1982): Sättigungsdampfdruck- und Sättigungsdampfdichtetafeln für Wasser und Eis. (Saturated Vapor Pressure and Saturated Vapor Density Tables for Water and Ice)(1. Aufl.), VEB Deutscher Verlag für Grundstoffindustrie
- ^ Ulrich Grigull, Johannes Staub, Peter Schiebener (1990): Steam Tables in SI-Units – Wasserdampftafeln. Springer-Verlagdima gmbh
- ^ a b c Weast, Robert (1983–1984). CRC, Handbook of Chemistry and Physics 64th edition. Boca Raton, Florida: CRC publishing. pp. E-119. ISBN 0-8493-0464-4.
Bibliography
[edit]- Dean, John Aurie; Lange, Norbert Adolph (1999). Lange's Handbook of Chemistry (15th ed.). McGraw-Hill. ISBN 978-0-07-016384-3.
- Franks, Felix (2012). The Physics and Physical Chemistry of Water. Springer. ISBN 978-1-4684-8334-5.
- Linstrom, Peter J.; Mallard, William G. (eds.); NIST Chemistry WebBook, NIST Standard Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg (MD)
- Lide, David R. (2004). CRC Handbook of Chemistry and Physics (85th ed.). CRC Press. ISBN 978-0-8493-0485-9.
External links
[edit]- Microwave Spectrum (by NIST)
- Water properties by Martin Chaplin, London South Bank University.
Water (data page)
View on GrokipediaMolecular Structure and Basic Properties
Molecular Geometry
The water molecule in its ground state exhibits a bent (V-shaped) geometry in the gas phase, with each O-H bond having a length of 95.87 pm and the H-O-H bond angle measuring 104.48° []. These structural parameters arise from the sp³ hybridization of the oxygen atom's valence orbitals, distorted by the repulsion of the two lone electron pairs on oxygen, which compress the angle from the ideal tetrahedral value of 109.5° []. The O-H bonds are strong polar covalent linkages, characterized by a bond dissociation energy of 492.215 kJ/mol at 0 K for breaking one O-H bond to form OH and H radicals []. This polarity imparts a permanent molecular dipole moment of 1.85 D to the isolated water molecule, with the negative end centered on the oxygen atom []. In the liquid phase, intermolecular hydrogen bonds dominate, creating a dynamic, disordered network where each water molecule participates in an average of about 3.5 to 4 hydrogen bonds, resulting in local geometries that approximate but deviate from tetrahedral arrangements due to thermal fluctuations and bond bending []. By contrast, the solid phase (ice Ih, the common form at atmospheric pressure) forms a rigid, open hexagonal lattice in which every water molecule achieves perfect tetrahedral coordination, donating two hydrogen bonds and accepting two from neighboring molecules at O···O distances of approximately 276 pm []. This extended tetrahedral structure in ice contrasts sharply with the monomeric bent form in the gas phase and the partially coordinated, fluxional network in the liquid, influencing water's unique phase behaviors such as the density maximum at 4°C in the liquid state [].Optical and Electrical Properties
The refractive index of liquid water, a measure of its optical density, is 1.3330 at 20 °C for the sodium D-line wavelength of 589 nm.[6] This value reflects the bulk medium's response to visible light and arises from the polarizability of water molecules, influenced by their permanent dipole moment.[7] The static permittivity, or relative dielectric constant, of water quantifies its ability to store electrical energy in an electric field and is exceptionally high due to strong hydrogen bonding and orientational polarization. At 20 °C, this value is 80.36.[8] The dielectric constant decreases with increasing temperature, as thermal agitation disrupts dipole alignment, with values tabulated below for atmospheric pressure up to 100 °C (data interpolated at 5 °C intervals where necessary).[9]| Temperature (°C) | Dielectric Constant |
|---|---|
| 0 | 88.00 |
| 5 | 86.04 |
| 10 | 84.11 |
| 15 | 82.22 |
| 20 | 80.36 |
| 25 | 78.54 |
| 30 | 76.75 |
| 35 | 75.00 |
| 40 | 73.28 |
| 45 | 71.60 |
| 50 | 69.95 |
| 55 | 68.34 |
| 60 | 66.76 |
| 65 | 65.21 |
| 70 | 63.68 |
| 75 | 62.18 |
| 80 | 60.78 |
| 85 | 59.40 |
| 90 | 58.04 |
| 95 | 56.71 |
| 100 | 55.40 |
| Temperature (°C) | Magnetic Susceptibility (× 10^{-6}, SI) |
|---|---|
| 0 | -9.035 |
| 20 | -9.040 |
| 40 | -9.045 |
| 60 | -9.050 |
| 80 | -9.055 |
| 100 | -9.060 |
Thermodynamic Properties
Phase Transitions
The phase transitions of water define the boundaries between its solid, liquid, and vapor phases under varying temperature and pressure conditions, governed by thermodynamic equilibrium. These transitions are fundamental to understanding water's behavior in natural and industrial processes, with key invariant points marking coexistence of multiple phases. The triple point of water occurs at a temperature of 273.16 K and a pressure of 611.657 Pa, where solid ice (Ih), liquid water, and water vapor coexist in equilibrium. This point serves as a primary fixed point for temperature calibration in the International Temperature Scale and represents the lower limit of the liquid-vapor equilibrium curve.[13] At standard atmospheric pressure of 1 atm (101.325 kPa), the normal melting point of water is 273.15 K, slightly below the triple point temperature due to the positive slope of the solid-liquid equilibrium line. Similarly, the normal boiling point, where liquid water transitions to vapor, is 373.124 K under the same pressure, establishing the upper temperature for the liquid phase at ambient conditions. These normal points are widely used as reference states in thermophysical data compilations.[14] The critical point of water, beyond which the liquid and vapor phases become indistinguishable, is located at 647.096 K and 22.064 MPa. At this supercritical state, water exhibits unique properties such as high diffusivity and low viscosity, relevant to applications in power generation and geochemistry.[14] The vapor pressure curve separating the liquid and vapor phases can be approximated using the Clausius-Clapeyron equation in its basic integrated form: , where is the vapor pressure, is the enthalpy of vaporization, is the gas constant, is temperature, and is a constant. This relation provides a conceptual framework for estimating phase boundaries near the normal boiling point, though more precise equations-of-state are used for quantitative predictions.[2]Solid Phase Data
The solid phase of water, primarily in the form of hexagonal ice Ih under ambient conditions, exhibits distinct thermodynamic properties that govern its stability and behavior below the melting point. These properties include key state functions such as enthalpy of formation, heat capacity, and density, which are essential for understanding energy changes in freezing and sublimation processes. Data for ice Ih are derived from high-precision measurements and formulations recommended by international standards organizations. The standard enthalpy of formation (ΔH_f°) for ice Ih at 298 K is -291.83 kJ/mol, representing the hypothetical value for the solid phase at this temperature above its stability limit, calculated by adjusting the liquid water value for the enthalpy of fusion and heat capacity differences.[15] The molar heat capacity at constant pressure (C_p) for ice Ih is 37.84 J/(mol·K) at -2.2 °C, reflecting its vibrational contributions in the solid lattice and increasing nearly linearly with temperature in the high-temperature limit.[16] The enthalpy of fusion at the triple point (273.15 K) is 6.00678 kJ/mol, corresponding to the energy required to transition from ice Ih to liquid water at standard pressure.[17] The density of ice Ih at 0 °C and 1 atm is 0.9167 g/cm³, lower than that of liquid water due to the open hexagonal structure, leading to the characteristic buoyancy of ice.[18] Thermodynamic data for ice Ih, including heat capacity and enthalpy as functions of temperature, are tabulated below for selected points from 0 K to 273 K. These values are based on adiabatic calorimetry measurements and the IAPWS equation of state for ice Ih, with enthalpy referenced to zero at 0 K (H° - H°(0)). Heat capacity rises from near-zero at absolute zero, following the Debye T³ law at low temperatures, to a Dulong-Petit-like value near the melting point. Enthalpy accumulates as the integral of C_p dT, providing context for total energy storage in the solid phase.| Temperature (K) | Heat Capacity, C_p (J/mol·K) | Enthalpy, H° - H°(0) (kJ/mol) |
|---|---|---|
| 10 | 0.65 | 0.002 |
| 50 | 9.8 | 0.12 |
| 100 | 20.5 | 0.85 |
| 150 | 28.7 | 2.45 |
| 200 | 34.2 | 5.12 |
| 250 | 37.1 | 8.76 |
| 273 | 38.1 | 11.05 |
Liquid Phase Data
The standard enthalpy of formation of liquid water at 298 K and standard pressure is Δ_f H° = -285.83 kJ/mol.[20] The corresponding standard Gibbs free energy of formation is Δ_f G° = -237.14 kJ/mol.[20] These values reflect the thermodynamic stability of liquid water relative to its elements in their standard states and are derived from critically evaluated experimental data.[20] The isobaric molar heat capacity of liquid water at 25 °C (298.15 K) and 1 bar is C_p = 75.291 J/(mol·K), which characterizes its ability to store thermal energy and contributes to its high specific heat relative to other liquids.[20] This value is obtained from calorimetric measurements and is nearly constant over a wide temperature range near ambient conditions, facilitating accurate modeling of heat transfer processes involving water.[20] The enthalpy of vaporization at the normal boiling point of 373.15 K (100 °C) and 1 atm is Δ_vap H = 40.657 kJ/mol, representing the energy required to transition one mole of liquid water to vapor at equilibrium.[21] This quantity decreases with increasing temperature due to intermolecular forces weakening near the critical point but remains significant at standard boiling conditions.[21] Thermodynamic potentials for saturated liquid water vary with temperature, as shown in the following table derived from the IAPWS-95 formulation. The table presents values at 10 °C intervals from 0 °C to 100 °C (273.15 K to 373.15 K), with specific properties converted to molar basis using the molar mass of 18.015 g/mol. Molar enthalpy (H) and entropy (S) are relative to the reference state at the triple point (273.16 K, 611.657 Pa), where H = 0 kJ/mol and S = 0 J/mol·K. The molar Gibbs free energy (G = H - TS) is computed accordingly for the liquid phase at saturation pressure.| T (K) | Molar Enthalpy H (kJ/mol) | Molar Entropy S (J/mol·K) | Molar Gibbs Free Energy G (kJ/mol) |
|---|---|---|---|
| 273.15 | 0.000 | 0.000 | 0.000 |
| 283.15 | 0.757 | 2.723 | -0.014 |
| 293.15 | 1.512 | 5.342 | -0.054 |
| 303.15 | 2.265 | 7.870 | -0.121 |
| 313.15 | 3.016 | 10.302 | -0.211 |
| 323.15 | 3.766 | 12.644 | -0.320 |
| 333.15 | 4.514 | 14.900 | -0.451 |
| 343.15 | 5.261 | 17.074 | -0.598 |
| 353.15 | 6.006 | 19.167 | -0.764 |
| 363.15 | 6.750 | 21.180 | -0.940 |
| 373.15 | 7.493 | 23.115 | -1.133 |
Vapor Phase Data
The thermodynamic properties of water in the vapor phase are primarily described using models for ideal gases at low pressures and densities, with deviations accounted for by real gas equations near higher pressures or the critical region. These properties include key state functions such as enthalpy, heat capacity, and entropy, which are essential for understanding energy changes in processes involving water vapor, such as combustion or humidification. Data for water vapor are often derived from high-precision formulations like the Shomate equation or JANAF thermochemical tables, providing polynomial representations suitable for computational use across temperature ranges relevant to atmospheric and industrial conditions.[23] The standard enthalpy of formation of water vapor (Δ_f H°) at 298.15 K and 1 bar is -241.83 kJ/mol, reflecting the energy released when gaseous H₂ and ½ O₂ combine to form H₂O(g). This value is based on experimental thermochemical measurements and is a reference point for calculating reaction enthalpies involving water vapor.[23] The corresponding standard molar entropy (S°) at the same conditions is 188.84 J/(mol·K), indicating the disorder of the gaseous molecules compared to the elements in their standard states.[23] The molar heat capacity at constant pressure (C_p) for ideal water vapor increases with temperature due to vibrational contributions becoming significant above room temperature. At 373.15 K (100 °C), C_p is approximately 34.2 J/(mol·K). Over the range 300–2000 K, C_p can be accurately fitted using the Shomate polynomial equation:where t = T/1000 (with T in K), and the parameters (valid for 500–1700 K but commonly extrapolated) are A = 30.09200, B = 6.832514, C = 6.793435, D = -2.534480, and E = 0.082139; enthalpy and entropy can also be computed from integrated forms of this equation.[24] This fit enables precise evaluation of thermal properties for engineering applications like steam cycles. The entropy change associated with vaporization at the normal boiling point (373.15 K) is 109 J/(mol·K), calculated as Δ_vap S = Δ_vap H / T_b, where the enthalpy of vaporization Δ_vap H = 40.66 kJ/mol at this temperature. This value quantifies the increase in disorder upon transitioning from liquid to vapor at equilibrium and is consistent with Trouton's rule for non-associated liquids.[25] Near the critical point (647.096 K, 22.064 MPa), water vapor deviates significantly from ideal gas behavior, with the compressibility factor Z = PV/(RT) dropping to 0.229 at the critical isotherm. This low Z reflects strong intermolecular forces and density fluctuations, impacting transport and phase properties in supercritical applications. Representative thermodynamic data for superheated water vapor (approximating ideal gas behavior at low pressure) are tabulated below as a function of temperature, showing C_p, the enthalpy change relative to 298.15 K (H° - H°_{298.15}), and absolute entropy (S°). These values are derived from JANAF thermochemical tables and are useful for isobaric processes.[26]
| Temperature (K) | C_p (J/mol·K) | H° - H°_{298.15} (kJ/mol) | S° (J/mol·K) |
|---|---|---|---|
| 500 | 35.22 | 6.92 | 206.5 |
| 600 | 36.32 | 10.50 | 213.1 |
| 700 | 37.50 | 14.19 | 218.7 |
| 800 | 38.74 | 18.00 | 223.8 |
| 900 | 40.00 | 21.94 | 228.5 |
| 1000 | 41.27 | 26.00 | 232.7 |
| 1100 | 42.52 | 30.19 | 236.7 |
| 1200 | 43.75 | 34.51 | 240.5 |
| 1300 | 44.94 | 38.94 | 244.0 |
| 1400 | 46.06 | 43.49 | 247.4 |
| 1500 | 47.11 | 48.15 | 250.6 |
| 1600 | 48.07 | 52.91 | 253.7 |
| 1700 | 48.92 | 57.76 | 256.6 |
| 1800 | 49.75 | 62.69 | 259.4 |
| 1900 | 50.51 | 67.70 | 262.2 |
| 2000 | 51.20 | 72.79 | 264.8 |
Physical Properties of Liquid Water
Density and Volumetric Properties
Liquid water exhibits a unique density maximum near 4 °C under standard atmospheric pressure, a property arising from the anomalous thermal expansion behavior due to hydrogen bonding. The maximum density of liquid water is 0.999975 g/cm³ (999.975 kg/m³) at 3.98 °C and 1 atm (101.325 kPa).[27] This anomaly ensures that lakes and oceans freeze from the top down, preserving aquatic life beneath the ice surface. The volumetric thermal expansion coefficient, α, quantifies the relative volume change with temperature at constant pressure. For liquid water at 20 °C and 1 atm, α = 2.07 × 10^{-4} K^{-1}.[28] This coefficient is negative below approximately 4 °C, leading to the density maximum, and becomes positive above that temperature, causing density to decrease as temperature rises. The isothermal compressibility, κ_T, measures the relative volume change with pressure at constant temperature. At 25 °C and 1 atm, κ_T = 4.59 × 10^{-5} bar^{-1} for liquid water. This low compressibility indicates that water is relatively incompressible compared to gases, with only minor density increases under moderate pressures. The International Association for the Properties of Water and Steam (IAPWS) provides the definitive equation of state for thermodynamic properties of water via the IAPWS-95 formulation. This Helmholtz free energy-based model, expressed as a dimensionless function α(τ, δ) where τ = T_c / T and δ = ρ / ρ_c (with critical temperature T_c = 647.096 K and critical density ρ_c = 322 kg/m³), allows computation of density ρ(T, P) by solving for δ given τ and the pressure term involving the ideal and residual parts of the free energy. The formulation achieves uncertainties below 0.0001% in density for liquid water at ambient conditions. The following table presents representative densities of liquid water at 1 atm across a range of temperatures from 0 °C to 100 °C, illustrating the variation and the peak near 4 °C:| Temperature (°C) | Density (kg/m³) |
|---|---|
| 0 | 999.82 |
| 4 | 1000.00 |
| 10 | 999.77 |
| 20 | 998.29 |
| 25 | 997.13 |
| 30 | 995.71 |
| 40 | 992.25 |
| 50 | 988.02 |
| 60 | 983.13 |
| 70 | 977.63 |
| 80 | 971.60 |
| 90 | 965.06 |
| 100 | 958.05 |
Rheological Properties
Liquid water exhibits rheological properties characterized primarily by its viscosity, which quantifies resistance to shear flow, and surface tension, which determines the cohesive forces at the liquid-air interface. These properties are crucial for understanding fluid dynamics, capillary action, and wetting behaviors in aqueous systems. Viscosity decreases with increasing temperature, reflecting reduced intermolecular hydrogen bonding, while surface tension follows a similar trend due to thermal disruption of surface molecules.[30] The dynamic viscosity (μ) of water at 20 °C and standard atmospheric pressure is 1.0016 mPa·s.[31] The kinematic viscosity (ν), obtained by dividing the dynamic viscosity by the fluid density (ρ ≈ 998.2 kg/m³ at 20 °C), is 1.0037 × 10⁻⁶ m²/s.[32] Surface tension (σ) at the water-air interface under the same conditions is 72.75 mN/m.[33] The temperature dependence of dynamic viscosity can be approximated using the Andrade equation, an empirical model for liquids: where μ is in Pa·s, T is the absolute temperature in K, A = 1.732 × 10⁻⁶ Pa·s, and B = 1863 K; this form captures the exponential decrease in viscosity over typical temperature ranges. For surface tension, the International Association for the Properties of Water and Steam (IAPWS) recommends the following correlation valid from the triple point to the critical point: with T in K; this equation provides accuracy within 0.2% for liquid water.[34] The following table summarizes selected values of dynamic viscosity and surface tension for pure water at atmospheric pressure across 0–100 °C:| Temperature (°C) | Dynamic Viscosity (mPa·s) | Surface Tension (mN/m) |
|---|---|---|
| 0 | 1.791 | 75.64 |
| 10 | 1.306 | 74.22 |
| 20 | 1.002 | 72.75 |
| 30 | 0.797 | 71.18 |
| 40 | 0.653 | 69.56 |
| 50 | 0.547 | 67.94 |
| 60 | 0.466 | 66.24 |
| 70 | 0.404 | 64.48 |
| 80 | 0.354 | 62.67 |
| 90 | 0.314 | 60.85 |
| 100 | 0.282 | 58.91 |
Thermal and Acoustic Properties
The thermal conductivity of liquid water, a measure of its ability to transfer heat through conduction, is 0.598 W/(m·K) at 20 °C and atmospheric pressure. This value reflects the molecular interactions in the liquid phase, enabling efficient heat dissipation in aqueous systems. Thermal conductivity increases modestly with temperature at constant pressure due to enhanced molecular motion, but remains relatively stable compared to gases. The following table presents thermal conductivity values for liquid water at selected temperatures up to 100 °C and near-atmospheric pressure (1 bar):| Temperature (°C) | Thermal Conductivity [W/(m·K)] |
|---|---|
| 0 | 0.561 |
| 20 | 0.598 |
| 40 | 0.629 |
| 60 | 0.651 |
| 80 | 0.668 |
| 100 | 0.680 |
| Temperature (°C) | Speed of Sound [m/s] |
|---|---|
| 0 | 1403 |
| 20 | 1481 |
| 40 | 1526 |
| 60 | 1552 |
| 80 | 1555 |
| 100 | 1543 |
Vapor-Liquid Equilibrium
Saturation Properties
The saturation properties of water characterize the equilibrium between its liquid and vapor phases along the coexistence curve. The saturation temperature at standard atmospheric pressure of 1 atm (101.325 kPa) is precisely 99.974 °C, as defined by the International Temperature Scale of 1990 (ITS-90) for Vienna Standard Mean Ocean Water (VSMOW).[27] This value reflects the temperature at which the vapor pressure equals 101.325 kPa under equilibrium conditions.[2] At the triple point (0.01 °C, 611.657 Pa), where liquid, solid, and vapor phases coexist, the molar latent heat of vaporization is 45.054 kJ/mol.[2] This enthalpy change decreases with increasing temperature along the saturation curve, reaching approximately 40.657 kJ/mol at the normal boiling point.[2] The specific volume of saturated liquid () remains nearly constant due to the incompressibility of liquid water, varying slightly from about 0.001000 m³/kg near 0 °C to 0.001043 m³/kg at 100 °C, reflecting thermal expansion.[21] In contrast, the specific volume of saturated vapor () decreases sharply with rising temperature as the vapor density increases under higher saturation pressures, from over 200 m³/kg at low temperatures to about 1.67 m³/kg at 100 °C. This behavior is evident in the following representative data points along the saturation curve (specific volumes in m³/kg, calculated from the IAPWS-95 formulation):[21]| Temperature (°C) | (×10⁻³) | |
|---|---|---|
| 0 | 1.000 | 205.8 |
| 20 | 1.002 | 57.76 |
| 40 | 1.008 | 19.52 |
| 60 | 1.017 | 7.671 |
| 80 | 1.029 | 3.408 |
| 100 | 1.043 | 1.673 |
| Temperature (°C) | (kPa) |
|---|---|
| 0 | 0.6113 |
| 10 | 1.2276 |
| 20 | 2.3378 |
| 30 | 4.2436 |
| 40 | 7.3814 |
| 50 | 12.349 |
| 60 | 19.932 |
| 70 | 31.186 |
| 80 | 47.373 |
| 90 | 70.117 |
| 100 | 101.325 |
Steam Table Data
Steam table data for water-steam mixtures in equilibrium are provided by the IAPWS Industrial Formulation 1997 (IAPWS-IF97), which enables calculation of key thermodynamic properties such as specific volume, enthalpy, and entropy for saturated liquid, saturated vapor, and superheated steam across a wide range of conditions up to the critical point.[42] This formulation is divided into regions to optimize accuracy and computational efficiency for industrial applications, including the two-phase region where properties depend on the vapor quality x (the mass fraction of vapor phase, 0 ≤ x ≤ 1). In the two-phase region, mixture properties are linearly interpolated between saturated liquid (subscript f) and saturated vapor (subscript g) values: where v is specific volume (m³/kg), h is specific enthalpy (kJ/kg), and s is specific entropy (kJ/kg·K). For instance, at 100 °C (saturation pressure ≈ 0.1013 MPa), h_f = 419.04 kJ/kg and h_g = 2676.1 kJ/kg; for x = 0.5, the mixture enthalpy is h = 2047.57 kJ/kg.[42] The following table excerpts saturated properties at selected pressures from 0.01 MPa to 22 MPa, based on IAPWS-IF97. Data approach the critical point at 22.064 MPa and 373.946 °C, where liquid and vapor phases become indistinguishable (v_c = 0.003155 m³/kg, h_c = 2084.3 kJ/kg, s_c = 4.412 kJ/kg·K).[42]| Pressure (MPa) | T (°C) | v_f (×10^{-3} m³/kg) | v_g (m³/kg) | h_f (kJ/kg) | h_g (kJ/kg) | s_f (kJ/kg·K) | s_g (kJ/kg·K) |
|---|---|---|---|---|---|---|---|
| 0.01 | 45.81 | 1.000 | 14.674 | 191.83 | 2584.7 | 0.6493 | 8.3166 |
| 0.1 | 99.63 | 1.043 | 1.694 | 417.46 | 2675.5 | 1.3026 | 7.3594 |
| 1.0 | 179.91 | 1.127 | 0.1944 | 762.81 | 2776.2 | 2.1386 | 6.5859 |
| 5.0 | 263.99 | 1.286 | 0.03944 | 1154.5 | 2792.2 | 2.9206 | 5.9734 |
| 10.0 | 311.00 | 1.452 | 0.01803 | 1407.6 | 2725.3 | 3.3603 | 5.6141 |
| 15.0 | 342.2 | 1.555 | 0.01050 | 1610.5 | 2610.5 | 3.6844 | 5.3117 |
| 20.0 | 365.8 | 1.652 | 0.007084 | 1823.0 | 2609.9 | 4.0277 | 5.4125 |
| 22.064 (crit.) | 373.95 | 3.155 | 3.155 | 2084.3 | 2084.3 | 4.412 | 4.412 |
| Pressure (MPa) | T (°C) | v (m³/kg) | h (kJ/kg) | s (kJ/kg·K) |
|---|---|---|---|---|
| 1.0 | 200 | 0.2060 | 2827.9 | 6.6940 |
| 1.0 | 300 | 0.2579 | 3051.2 | 7.1228 |
Vapor Pressure Formulas
The saturation vapor pressure over liquid water is described by the Wagner equation, recommended by the International Association for the Properties of Water and Steam (IAPWS) for temperatures from 273.16 K to 647.096 K. This equation takes the form where is the vapor pressure in MPa, MPa is the critical pressure, K is the critical temperature, , and the coefficients are , , , , , .[44] This formulation ensures consistency with the IAPWS-95 thermodynamic equation of state and achieves relative deviations from experimental data of less than 0.1% across its validity range.[44] For meteorological and engineering applications limited to 0–100 °C, the simplified Buck equation provides a computationally efficient alternative with comparable precision. It is expressed as where is in Pa and is in °C; the equation yields relative errors below 0.2% in this range, making it suitable for routine calculations of humidity and dew point.[45] The sublimation pressure over ice Ih, relevant below the triple point, is given by the IAPWS equation valid from 50 K to 273.16 K: where (with in Pa), (with in K), and the coefficients are , ; , ; , .[46] This correlation maintains consistency with the IAPWS-95 fluid properties and ice Ih equation of state, with relative uncertainties under 0.1% for temperatures above 130 K and increasing modestly at lower temperatures due to sparse experimental data.[46]Solid Phase Behavior
Pressure-Dependent Melting
The melting point of ice Ih exhibits a negative dependence on pressure, a consequence of the larger molar volume of ice compared to liquid water, leading to a depression in the melting temperature as pressure increases. This behavior is governed by the Clapeyron equation, which yields an initial slope of the melting curve dT/dP ≈ -0.074 K/MPa near atmospheric conditions.[47] At 0.1 MPa, the melting point is 0 °C, decreasing to approximately -22 °C at 200 MPa.[47] The pressure dependence is described by empirical equations recommended by the International Association for the Properties of Water and Steam (IAPWS), valid along the ice Ih-liquid equilibrium curve from the triple point (0.01 °C, 0.000611657 MPa) to the ice Ih-ice III-liquid triple point.[47] Selected values of the melting temperature as a function of pressure are tabulated below, based on IAPWS formulations.| Pressure (MPa) | Melting Temperature (°C) |
|---|---|
| 0.1 | 0.00 |
| 1 | -0.06 |
| 10 | -0.75 |
| 50 | -4.09 |
| 100 | -8.94 |
| 200 | -20.83 |
| 209.2 | -21.99 |
Ice Polymorphs
Water ice exists in numerous crystalline polymorphs, each characterized by distinct molecular arrangements and stable under specific pressure and temperature conditions. As of November 2025, 21 crystalline phases have been experimentally confirmed, spanning low-density forms like Ice Ih to high-density, high-pressure structures such as Ice VII and superionic Ice XVIII. These polymorphs are classified based on whether their hydrogen (proton) positions are disordered—allowing multiple configurations consistent with the Bernal-Fowler ice rules—or ordered, where protons occupy fixed lattice sites, often achieved by cooling or doping to lower symmetry and energy. Proton ordering typically enhances stability at low temperatures and influences properties like dielectric response and entropy. High-pressure ices, exemplified by the cubic Ice VII with a body-centered structure and density around 1.50 g/cm³, form above approximately 2 GPa and feature more compact hydrogen-bond networks, enabling them to persist up to extreme conditions relevant to planetary interiors.[48] Recent discoveries include Ice XV (2016), a proton-ordered variant of Ice VI stable below 103 K at ~0.8 GPa; Ice XVIII (2019), a superionic phase with mobile protons in a body-centered cubic oxygen lattice at pressures exceeding 100 GPa and temperatures above 2000 K; Ice XIX (2021), a partially proton-ordered orthorhombic phase related to Ice VI, thermodynamically stable between 1.0 and 1.5 GPa below 103 K; Ice XX (2021), a high-temperature phase derived from Ice VII stable at 20-60 GPa and 900-1800 K; and Ice XXI (2025), a metastable body-centered tetragonal phase (space group I4̄2d) forming at ~2 GPa and room temperature via rapid compression pathways. These additions highlight ongoing exploration of water's phase diagram, with gaps in intermediate pressures and temperatures still under investigation.[49][50][51] The following table summarizes the 21 known ice polymorphs, including representative densities at ambient or typical conditions, crystal systems, proton ordering, and approximate stability ranges (pressure in GPa, temperature in K). Densities increase with pressure, and exact values vary; stability ranges indicate primary domains but overlap at transitions. Note: Details for Ice XX and Ice XXI are approximate based on recent reports.| Phase | Crystal System | Proton Order | Density (g/cm³) | Stability Range (P, T) |
|---|---|---|---|---|
| Ice Ih | Hexagonal | Disordered | 0.92 | <0.2 GPa, 0–273 K |
| Ice Ic | Cubic | Disordered | 0.92 | <0.2 GPa, <140 K (metastable) |
| Ice II | Rhombohedral | Ordered | 1.19 | 0.2–0.35 GPa, <253 K |
| Ice III | Tetragonal | Disordered | 1.16 | 0.2–0.35 GPa, >253 K |
| Ice V | Monoclinic | Disordered | 1.23 | 0.35–0.6 GPa, 253–350 K |
| Ice VI | Tetragonal | Disordered | 1.31 | 0.6–2.2 GPa, >273 K |
| Ice VII | Cubic | Disordered | 1.50 | >2.2 GPa, >273 K |
| Ice VIII | Tetragonal | Ordered | 1.50 | >2.2 GPa, <273 K |
| Ice IX | Tetragonal | Ordered | 1.27 | 0.2–0.6 GPa, <140 K |
| Ice X | ? (body-centered) | Symmetric | ~1.8 | >60 GPa, room T (predicted) |
| Ice XI | Orthorhombic | Ordered | 0.92 | <0.2 GPa, <72 K (doped) |
| Ice XII | Orthorhombic | Disordered | 1.12 | ~0.6 GPa, <260 K (metastable) |
| Ice XIII | Monoclinic | Ordered | 1.18 | ~0.15 GPa, <130 K |
| Ice XIV | Monoclinic | Ordered | 1.27 | ~0.1 GPa, <110 K |
| Ice XV | Tetragonal | Ordered | 1.33 | ~0.8 GPa, <103 K |
| Ice XVI | Cubic | Ordered | 0.81 | <0.1 GPa, <127 K (clathrate) |
| Ice XVII | Orthorhombic | Ordered | 0.97 | <0.1 GPa, <62 K (from filled) |
| Ice XVIII | Cubic | Superionic | ~2.0 | >100 GPa, >2000 K |
| Ice XIX | Orthorhombic | Partially ordered | 1.26 | 1.0–1.5 GPa, <103 K |
| Ice XX | Unknown | Disordered | ~1.5 | 20–60 GPa, 900–1800 K |
| Ice XXI | Tetragonal | Disordered | ~1.3 | ~2 GPa, ~300 K (metastable) |
Pressure-Temperature Phase Diagram
The pressure-temperature (P-T) phase diagram of water provides a comprehensive map of its thermodynamic phases across a wide range of conditions, typically presented with logarithmic pressure (log P) on the vertical axis versus linear temperature (T) on the horizontal axis to effectively span the extensive variability in pressure from low vacuum to high terrestrial extremes. This representation accommodates the diagram's coverage from approximately 100 K to 1000 K in temperature and 10^{-3} MPa to 10^{2} MPa in pressure, encompassing ambient conditions to those relevant for geophysical and industrial applications.[52][53] The diagram delineates distinct phase fields, with the low-temperature, low-pressure region dominated by the vapor (gas) phase transitioning to the liquid phase along the vaporization curve, which terminates at the critical point (647.096 K, 22.064 MPa). Beyond this point, the supercritical fluid region emerges, characterized by fluid-like properties without a distinct liquid-vapor boundary. Solid phases occupy the lower-temperature sectors, including the stable hexagonal Ice Ih at ambient pressures, transitioning to denser polymorphs such as Ice III, Ice V, Ice VI, Ice VII, and extending to Ice X at the higher end of the pressure range, where proton delocalization begins to occur. These regions are clearly labeled, illustrating water's polymorphism driven by hydrogen bonding under compression.[53] Notable features include the anomalous expansion line, representing the locus of maximum density in the liquid phase, which originates near the melting curve of Ice Ih around 277 K at 0.1 MPa and curves upward into the liquid field, underscoring water's unique density inversion where it expands upon freezing and exhibits a density maximum upon slight heating at low temperatures. The critical isochore, a vertical line extending from the critical point at the critical density (322 kg/m³), demarcates regions of differing compressibility in the supercritical domain, influencing properties like thermal expansion and sound speed. These lines highlight water's deviations from typical fluid behavior, rooted in its tetrahedral hydrogen-bond network.[54][52] Key intersections define phase coexistence: the liquid-Ih-vapor triple point at 273.16 K and 6.11657 × 10^{-4} MPa marks the boundary where all three phases equilibrate under standard conditions, while the Ih-III-liquid triple point at 251.165 K and 209.2 MPa signals the onset of high-pressure ice transitions, beyond which the melting curve slopes positively due to the density increase in higher ice phases. These points anchor the diagram's topology, guiding predictions of phase stability in diverse environments from Earth's interior to engineering processes.[53]Aqueous Solutions and Ionization
NaCl Solutions
Dissolved sodium chloride (NaCl) in water significantly alters the solvent's colligative properties, including freezing point depression, boiling point elevation, and vapor pressure lowering, due to the dissociation of NaCl into Na⁺ and Cl⁻ ions, which reduces the mole fraction of water molecules available at the surface. These effects are proportional to the molality of the solution and follow van't Hoff's factor for electrolytes, where the effective particle count is approximately 1.85–2 for NaCl depending on concentration and ion pairing. Additionally, physical properties like density and viscosity increase with NaCl concentration owing to stronger intermolecular interactions and hydration shells around the ions.[55] The freezing point of water is depressed by approximately 2.8 °C in a 5 wt% NaCl solution at atmospheric pressure, allowing such mixtures to remain liquid at subzero temperatures useful for applications like de-icing. Boiling point elevation is smaller but notable; for instance, a 10 wt% NaCl solution boils at about 101.5 °C, an increase of roughly 1.5 °C over pure water, calculated via the ebullioscopic constant Kb = 0.512 °C/m for water and the effective molality. Vapor pressure lowering follows Raoult's law, with the partial pressure of water reduced by the mole fraction of NaCl; at 5 wt% (≈0.9 molal), the vapor pressure at 25 °C drops from 23.8 mmHg for pure water to about 23.3 mmHg, enhancing osmotic effects in biological and industrial contexts. Density increases to 1.034 g/cm³ for a 5 wt% solution at 20 °C, reflecting the added mass and partial molar volume of the solute.[55][56][57] The following table summarizes key properties of aqueous NaCl solutions across concentrations from 0 to 25 wt% at standard conditions, illustrating the progressive changes (freezing points from ice liquidus; for >23.3 wt%, initial freezing involves hydrohalite at higher temperature, but eutectic given for complete solidification reference; viscosity at 20 °C):| NaCl Concentration (wt%) | Freezing Point (°C) | Density (g/cm³ at 20 °C) | Dynamic Viscosity (mPa·s at 20 °C) |
|---|---|---|---|
| 0 | 0.0 | 0.998 | 1.002 |
| 5 | -2.8 | 1.034 | 1.015 |
| 10 | -6.2 | 1.071 | 1.045 |
| 15 | -10.0 | 1.108 | 1.090 |
| 20 | -16.0 | 1.145 | 1.150 |
| 25 | -21.1 (eutectic) | 1.183 | 1.230 |
Autoionization Constants
The autoionization of water refers to the equilibrium reaction , characterized by the ion product constant . At 25 °C and standard pressure, (mol/kg), corresponding to , where .[59] The value of increases with temperature, reflecting the endothermic nature of the autoionization process, which shifts the equilibrium toward greater ionization at higher temperatures and results in a lower . Representative values include at 0 °C and at 50 °C. This temperature dependence is described by the empirical equation valid from 0 to 1000 °C and 1 to 10,000 bar, where is in K, is the density of water in g/cm³, and the parameters are , K, K², K³, , K, K². At low pressures where g/cm³, the density term vanishes, simplifying the expression. The equation fits experimental data with an accuracy of ±0.01 log units at saturation vapor pressure.[59] The following table presents , , and the neutral pH (equal to ) for pure water at selected temperatures from 0 to 100 °C under saturation conditions:| Temperature (°C) | (mol/kg) | Neutral pH | |
|---|---|---|---|
| 0 | 1.13 × 10^{-15} | 14.95 | 7.47 |
| 10 | 2.91 × 10^{-15} | 14.54 | 7.27 |
| 20 | 6.82 × 10^{-15} | 14.17 | 7.08 |
| 25 | 1.01 × 10^{-14} | 14.00 | 7.00 |
| 30 | 1.47 × 10^{-14} | 13.83 | 6.92 |
| 40 | 2.92 × 10^{-14} | 13.53 | 6.77 |
| 50 | 5.47 × 10^{-14} | 13.26 | 6.63 |
| 60 | 9.61 × 10^{-14} | 13.02 | 6.51 |
| 70 | 1.64 × 10^{-13} | 12.79 | 6.39 |
| 80 | 2.71 × 10^{-13} | 12.57 | 6.28 |
| 90 | 4.36 × 10^{-13} | 12.36 | 6.18 |
| 100 | 6.81 × 10^{-13} | 12.17 | 6.08 |
Spectroscopic Properties
Electronic Spectra
Water's electronic spectrum is dominated by ultraviolet absorption arising from transitions involving promotion of electrons from occupied molecular orbitals to antibonding or Rydberg orbitals. In the gas phase, the lowest-energy allowed transition is the n→σ* excitation from the oxygen lone pair (1b₁ orbital) to a σ* antibonding orbital, peaking at approximately 165 nm with a molar extinction coefficient of ~12,000 M⁻¹ cm⁻¹.[60] This band exhibits vibronic structure due to coupling with bending and stretching modes. Strong absorption continues below ~140 nm, involving higher-energy valence transitions and Rydberg series converging to the first ionization potential at 12.62 eV (98.2 nm).[61] In the liquid phase, hydrogen bonding broadens and blue-shifts the n→σ* band to ~150-160 nm, with reduced peak intensity (~1,500-1,600 M⁻¹ cm⁻¹) owing to delocalization of the lone pair across the network.[62] The onset of significant absorption occurs below 200 nm, marking the practical UV cutoff for transmission in aqueous media. No discrete bands appear in the visible spectrum (400-800 nm), conferring transparency essential for optical applications; absorption coefficients remain below 0.02 cm⁻¹ across this range, increasing gradually toward the near-IR due to overtone contributions (not detailed here).[63] Data on higher Rydberg states remain limited experimentally in the condensed phase, but recent ab initio quantum calculations have characterized series such as 3s, 3p, and 3d states up to ~20 eV, aiding assignment of diffuse VUV features and photodissociation pathways.| Wavelength (nm) | Gas Phase (ε, M⁻¹ cm⁻¹) | Liquid Phase (α, cm⁻¹) |
|---|---|---|
| 165 | 12,000 | >100 (strong absorption) |
| 180 | ~5,000 | ~5 |
| 200 | ~1,000 | 0.007 |
| 300 | <100 | 0.0017 |
| 400 | <10 | 0.00045 |
| 600 | <1 | 0.0006 |
| 800 | <1 | 0.003 |
Vibrational Spectra
The vibrational spectrum of water arises from the molecular vibrations of the H₂O molecule, which has three fundamental modes due to its nonlinear structure: the symmetric stretch (ν₁), the bending mode (ν₂), and the asymmetric stretch (ν₃). In the gas phase, these modes appear as sharp, well-resolved bands because isolated water molecules experience minimal intermolecular interactions. The symmetric stretch ν₁ occurs at 3657 cm⁻¹, the bending mode ν₂ at 1595 cm⁻¹, and the asymmetric stretch ν₃ at 3756 cm⁻¹.[66] These frequencies are derived from high-resolution IR and Raman spectroscopy, with the gas-phase values serving as benchmarks for understanding shifts in condensed phases.[67] In the liquid phase, hydrogen bonding causes significant broadening and red-shifting of the vibrational bands, as water molecules form dynamic networks that couple the local modes into delocalized excitations. The symmetric and asymmetric stretches merge into a broad, asymmetric band centered around 3280 cm⁻¹, reflecting the distribution of hydrogen bond strengths and leading to a pronounced shoulder near 3400 cm⁻¹ from weaker or broken bonds. The bending mode ν₂ appears as a narrower band at approximately 1640 cm⁻¹, with its intensity enhanced relative to the gas phase due to the polar nature of the liquid environment.[68][69] These effects highlight how hydrogen bonding averages the vibrational frequencies and increases the spectral width, typically spanning 200–300 cm⁻¹ for the OH stretch region. For ice Ih, the hexagonal form of ice at ambient pressure, the ordered hydrogen-bonded lattice further modifies the spectrum compared to the liquid, resulting in sharper but still broadened bands due to the tetrahedral coordination. The OH stretching modes (ν₁ and ν₃) form a broad envelope from 3170 to 3400 cm⁻¹, deconvoluted into sub-bands corresponding to different hydrogen-bond configurations, such as single-donor double-acceptor bonds around 3150 cm⁻¹. The bending mode ν₂ is observed near 1600 cm⁻¹, with reduced IR intensity compared to liquid water owing to the more symmetric environment that diminishes dipole changes during vibration.[70] Hydrogen bonding in ice Ih enforces a narrower distribution of bond lengths and angles, leading to less broadening than in the liquid but persistent coupling effects that split the stretching region. Infrared (IR) and Raman spectroscopy probe different aspects of these modes based on selection rules: IR activity requires a change in dipole moment, while Raman activity requires a change in polarizability. For isolated gas-phase water (C_{2v} symmetry), all three modes are both IR- and Raman-active, though ν₁ and ν₃ dominate IR spectra due to stronger dipole variations, whereas ν₂ is more prominent in Raman. In liquid and solid phases, hydrogen bonding relaxes strict symmetry, making most features active in both techniques, but collective excitations (e.g., resonant modes in the stretch region) can enhance Raman intensities for isotropic components, while IR emphasizes anisotropic or charged fluctuations.[68] This complementarity allows comprehensive analysis, with IR often showing stronger bending mode absorption in the liquid due to its sensitivity to local dipoles.| Phase | Mode | Frequency (cm⁻¹) | IR Intensity | Raman Intensity | Notes on Hydrogen Bonding Effects |
|---|---|---|---|---|---|
| Gas | Symmetric stretch (ν₁) | 3657 | Strong | Strong | Sharp; no H-bonding |
| Gas | Bend (ν₂) | 1595 | Medium | Medium | Sharp; no H-bonding |
| Gas | Asymmetric stretch (ν₃) | 3756 | Strong | Weak | Sharp; no H-bonding |
| Liquid | OH stretches (ν₁/ν₃ combined) | ~3280 (broad, 3000–3700) | Very strong (peak ~3400) | Strong (shoulder ~3250) | Broadened by dynamic H-bonds; red-shift ~400 cm⁻¹ |
| Liquid | Bend (ν₂) | ~1640 | Strong | Medium | Moderate broadening; enhanced coupling |
| Ice Ih | OH stretches (ν₁/ν₃) | 3170–3400 (multipeak) | Strong | Strong | Lattice-induced splitting; tetrahedral H-bonds narrow range |
| Ice Ih | Bend (ν₂) | ~1600 | Weak | Medium | Reduced IR due to symmetry; static H-bonds |
Nuclear Magnetic Resonance
Nuclear magnetic resonance (NMR) spectroscopy provides insights into the local electronic environment and dynamics of water molecules through the measurement of chemical shifts, coupling constants, and relaxation times for its constituent nuclei, primarily ¹H and ¹⁷O. In liquid water at 25 °C, the ¹H NMR chemical shift is 4.80 ppm relative to tetramethylsilane (TMS) when referenced via the HOD signal in D₂O solutions, though values up to 5.0 ppm are reported for pure H₂O under similar conditions.[71] This shift exhibits a temperature dependence of approximately -0.01 ppm/K, arising from changes in hydrogen bonding and molecular reorientation that alter the magnetic shielding.[72] For ¹⁷O NMR in liquid water, the chemical shift is set to 0 ppm as an internal reference in D₂O, while in H₂O it appears at +3.3 ppm due to isotopic differences in vibrational averaging and bonding.[73] The ¹⁷O nucleus, with spin I = 5/2, experiences quadrupolar interactions, leading to a quadrupolar coupling constant (C_Q) of approximately 6.9 MHz in liquid water at 300 K, which increases slightly upon cooling as molecular motion slows and electric field gradients become more pronounced.[74] Isotope effects are evident in ¹H NMR, where the residual HOD signal in D₂O shifts upfield by about 0.2 ppm compared to pure H₂O protons, reflecting stronger hydrogen bonds and altered zero-point vibrations in the deuterated form.[75][76] Chemical shifts vary significantly across phases and temperatures due to differences in condensation and hydrogen bonding networks. The table below summarizes representative ¹H and ¹⁷O chemical shifts (in ppm, relative to gas-phase values set at 0 ppm for each nucleus) for water in gas, liquid, and ice Ih phases, along with temperature-dependent values in the liquid state.| Phase/Temperature | ¹H Chemical Shift (ppm) | ¹⁷O Chemical Shift (ppm) |
|---|---|---|
| Gas (isolated molecule) | 0 | 0 |
| Liquid (25 °C) | -5.8 | -36.6 |
| Liquid (0 °C) | -6.5 (extrapolated) | -37.5 (extrapolated) |
| Ice Ih (low temperature) | -8.0 | -48.6 |
Transport and Magnetic Properties
Diffusion Coefficients
The self-diffusion coefficient of liquid water quantifies the translational mobility of water molecules, typically measured using nuclear magnetic resonance (NMR) techniques or isotopic tracers such as tritium or deuterium. At 25 °C and ambient pressure, the self-diffusion coefficient is m²/s.[81] This value reflects the average distance a water molecule travels in one second under Brownian motion, providing insight into the liquid's microscopic dynamics. The temperature dependence of follows an Arrhenius form, , where is the pre-exponential factor, is the activation energy, is the gas constant, and is the absolute temperature. For liquid water, kJ/mol over the range 15–45 °C.[82] This activation energy corresponds to the energy barrier for molecular hopping, influenced by hydrogen bonding networks. The following table summarizes self-diffusion coefficients for liquid water at atmospheric pressure across temperatures from 0 °C to 100 °C, compiled from NMR and tracer measurements:| Temperature (°C) | (10⁻⁹ m²/s) |
|---|---|
| 0 | 1.130 |
| 10 | 1.536 |
| 20 | 2.022 |
| 25 | 2.299 |
| 30 | 2.590 |
| 40 | 3.240 |
| 50 | 3.968 |
| 60 | 4.772 |
| 70 | 5.646 |
| 80 | 6.582 |
| 90 | 7.578 |
| 100 | 8.623 |
Magnetic Susceptibility
Water exhibits diamagnetic behavior, meaning it is weakly repelled by magnetic fields, with a volume magnetic susceptibility (SI units) at 20 °C.[89] The corresponding molar magnetic susceptibility is cm³/mol (cgs units).[90] These negative values indicate that water's magnetization opposes the applied field, a property arising primarily from the orbital motion of electrons in its molecular structure. The magnetic susceptibility of liquid water shows a linear temperature dependence, becoming slightly more negative (increasing in magnitude) with rising temperature due to subtle changes in molecular interactions, such as hydrogen bonding.[11] This variation is small, with the magnitude increasing by approximately 1% from 0 °C to 80 °C.[91] Theoretical calculations attribute the diamagnetic response to contributions from molecular orbitals, computed using Gaussian atomic orbital basis sets for the ground-state wavefunction of the H₂O molecule. Across phases, water maintains its diamagnetic character, with comparable susceptibility values:| Phase | Temperature (°C) | (×10⁻⁶ cm³/mol, cgs) |
|---|---|---|
| Ice Ih (solid) | 0 | -12.63 |
| Liquid | 20 | -12.96 |
| Liquid | 100 | -13.09 |
| Vapor (gas) | 100 | -13.1 |
Supplementary Thermodynamic Data
Standard State Values
The standard state for water is defined as the pure liquid at a temperature of 298.15 K and a pressure of 1 bar. In this reference state, the standard enthalpy of formation (Δ_f H°) of liquid water is -285.830 kJ/mol.[20] The standard molar entropy (S°) is 69.91 J/(mol·K).[20] The standard Gibbs energy of formation (Δ_f G°) is -237.140 kJ/mol.[92] The isobaric heat capacity (C_p) is 75.3 J/(mol·K).[20] These values serve as fundamental reference points for thermodynamic calculations involving water in aqueous systems and phase changes. They are derived from high-precision calorimetric and equilibrium measurements, ensuring consistency with international standards for thermochemical data. The following table summarizes the standard thermodynamic properties for water in its solid (ice Ih, extrapolated), liquid, and gas (ideal) phases at 298.15 K and 1 bar, compiled from evaluated data in thermochemical references.| Phase | Δ_f H° (kJ/mol) | S° (J/mol·K) | Δ_f G° (kJ/mol) | C_p (J/mol·K) |
|---|---|---|---|---|
| Solid | -291.84 | 44.7 | -236.59 | 38 |
| Liquid | -285.830 | 69.91 | -237.140 | 75.3 |
| Gas | -241.826 | 188.83 | -228.572 | 33.6 |
Triple Point Specifications
The triple point of water marks the unique condition where its solid (ice Ih), liquid, and vapor phases coexist in thermodynamic equilibrium, serving as a fundamental reference state in thermodynamics and the basis for the International Temperature Scale of 1990 (ITS-90). By international convention, this occurs at a temperature of exactly 273.16 K (0.01 °C) and a pressure of 611.657 Pa. These values are precisely defined and adopted by the International Association for the Properties of Water and Steam (IAPWS) for consistency in scientific and engineering applications.[93] At this triple point, the coexisting phases exhibit distinct physical properties reflective of their phase boundaries. The liquid phase has a density of 0.99984 g/cm³, the solid ice Ih phase has a density of 0.91671 g/cm³, and the vapor phase has a density of 4.85 × 10^{-3} g/cm³. These densities highlight the volume expansion upon freezing, as ice is less dense than liquid water, contributing to water's anomalous behavior. The phase changes at this point involve specific enthalpies: the enthalpy of fusion (solid to liquid) is 333.55 J/g, and the enthalpy of vaporization (liquid to vapor) is 2500.8 J/g. These values are derived from the IAPWS-95 formulation for thermodynamic properties and the equation of state for ice Ih.[14][94] The following table summarizes key thermodynamic and physical properties of the coexisting phases at the triple point, based on IAPWS standards:| Property | Liquid Phase | Solid Phase (Ice Ih) | Vapor Phase |
|---|---|---|---|
| Temperature (K) | 273.16 | 273.16 | 273.16 |
| Pressure (Pa) | 611.657 | 611.657 | 611.657 |
| Density (g/cm³) | 0.99984 | 0.91671 | 4.85 × 10^{-3} |
| Specific Enthalpy (J/g) | 0 (reference) | -333.55 | 2500.8 |
| Specific Internal Energy (J/g) | 0 (reference) | -333.46 | 2500.5 |
| Specific Entropy (J/g·K) | 0 (reference) | -1.222 | 9.155 |


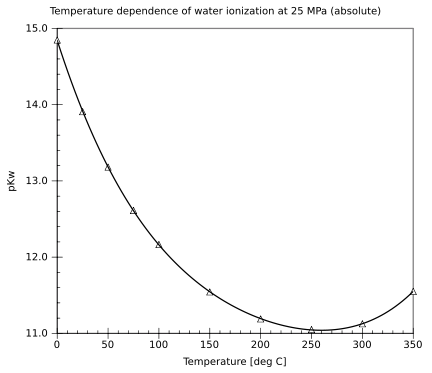
![{\displaystyle pK_{w}=-\log([\mathrm {H} ^{+}][\mathrm {OH} ^{-}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dba46e853cb413eb22ac014a23a7f9b9fbceb56)