Hubbry Logo
Celestial navigationCelestial navigationMain
Open search
Celestial navigation
Community hub
Celestial navigation
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Celestial navigation
Celestial navigation
Celestial navigation
View on Wikipedia
from Wikipedia
A diagram of a typical nautical sextant, a tool used in celestial navigation to measure the angle between two objects viewed by means of its optical sight

Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface of the Earth without relying solely on estimated positional calculations, commonly known as dead reckoning. Celestial navigation is performed without using satellite navigation or other similar modern electronic or digital positioning means.

Celestial navigation uses "sights," or timed angular measurements, taken typically between a celestial body (e.g., the Sun, the Moon, a planet, or a star) and the visible horizon. Celestial navigation can also take advantage of measurements between celestial bodies without reference to the Earth's horizon, such as when the Moon and other selected bodies are used in the practice called "lunars" or the lunar distance method, used for determining precise time when time is unknown.

Celestial navigation by taking sights of the Sun and the horizon whilst on the surface of the Earth is commonly used, providing various methods of determining position, one of which is the popular and simple method called "noon sight navigation"—being a single observation of the exact altitude of the Sun and the exact time of that altitude (known as "local noon")—the highest point of the Sun above the horizon from the position of the observer in any single day. This angular observation, combined with knowing its simultaneous precise time, referred to as the time at the prime meridian, directly renders a latitude and longitude fix at the time and place of the observation by simple mathematical reduction. The Moon, a planet, Polaris, or one of the 57 other navigational stars whose coordinates are tabulated in any of the published nautical or air almanacs can also accomplish this same goal.

Celestial navigation accomplishes its purpose by using angular measurements (sights) between celestial bodies and the visible horizon to locate one's position on the Earth, whether on land, in the air, or at sea. In addition, observations between stars and other celestial bodies accomplished the same results while in space, – used in the Apollo space program and is still used on many contemporary satellites. Equally, celestial navigation may be used while on other planetary bodies to determine position on their surface, using their local horizon and suitable celestial bodies with matching reduction tables and knowledge of local time.

For navigation by celestial means, when on the surface of the Earth at any given instant in time, a celestial body is located directly over a single point on the Earth's surface. The latitude and longitude of that point are known as the celestial body's geographic position (GP), the location of which can be determined from tables in the nautical or air almanac for that year. The measured angle between the celestial body and the visible horizon is directly related to the distance between the celestial body's GP and the observer's position. After some computations, referred to as "sight reduction," this measurement is used to plot a line of position (LOP) on a navigational chart or plotting worksheet, with the observer's position being somewhere on that line. The LOP is actually a short segment of a very large circle on Earth that surrounds the GP of the observed celestial body. (An observer located anywhere on the circumference of this circle on Earth, measuring the angle of the same celestial body above the horizon at that instant of time, would observe that body to be at the same angle above the horizon.) Sights on two celestial bodies give two such lines on the chart, intersecting at the observer's position (actually, the two circles would result in two points of intersection arising from sights on two stars described above, but one can be discarded since it will be far from the estimated position—see the figure at the example below). Most navigators will use sights of three to five stars, if available, since that will result in only one common intersection and minimize the chance of error. That premise is the basis for the most commonly used method of celestial navigation, referred to as the "altitude-intercept method." At least three points must be plotted. The plot intersection will usually provide a triangle where the exact position is inside of it. The accuracy of the sights is indicated by the size of the triangle.

Joshua Slocum used both noon sight and star sight navigation to determine his current position during his voyage, the first recorded single-handed circumnavigation of the world. In addition, he used the lunar distance method (or "lunars") to determine and maintain known time at Greenwich (the prime meridian), thereby keeping his "tin clock" reasonably accurate and therefore his position fixes accurate.

Celestial navigation can only determine longitude when the time at the prime meridian is accurately known. The more accurately time at the prime meridian (0° longitude) is known, the more accurate the fix; – indeed, every four seconds of time source (commonly a chronometer or, in aircraft, an accurate "hack watch") error can lead to a positional error of one nautical mile. When time is unknown or not trusted, the lunar distance method can be used as a method of determining time at the prime meridian. A functioning timepiece with a second hand or digit, an almanac with lunar corrections, and a sextant are used. With no knowledge of time at all, a lunar calculation (given an observable Moon of respectable altitude) can provide time accurate to within a second or two with about 15 to 30 minutes of observations and mathematical reduction from the almanac tables. After practice, an observer can regularly derive and prove time using this method to within about one second, or one nautical mile, of navigational error due to errors ascribed to the time source.

Example

[edit]

An example illustrating the concept behind the intercept method for determining position is shown to the right. (Two other common methods for determining one's position using celestial navigation are longitude by chronometer and ex-meridian methods.) In the adjacent image, the two circles on the map represent lines of position for the Sun and Moon at 12:00 GMT on October 29, 2005. At this time, a navigator on a ship at sea measured the Moon to be 56° above the horizon using a sextant. Ten minutes later, the Sun was observed to be 40° above the horizon. Lines of position were then calculated and plotted for each of these observations. Since both the Sun and Moon were observed at their respective angles from the same location, the navigator would have to be located at one of the two locations where the circles cross.

In this case, the navigator is either located on the Atlantic Ocean, about 350 nautical miles (650 km) west of Madeira, or in South America, about 90 nautical miles (170 km) southwest of Asunción, Paraguay. In most cases, determining which of the two intersections is the correct one is obvious to the observer because they are often thousands of miles apart. As it is unlikely that the ship is sailing across South America, the position in the Atlantic is the correct one. Note that the lines of position in the figure are distorted because of the map's projection; they would be circular if plotted on a globe.

An observer at the Gran Chaco point would see the Moon at the left of the Sun, and an observer at the Madeira point would see the Moon at the right of the Sun.

Angular measurement

[edit]
Using a marine sextant to measure the altitude of the Sun above the horizon

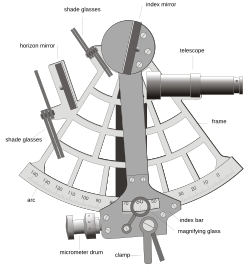
Accurate angle measurement has evolved over the years. One simple method is to hold the hand above the horizon with one's arm stretched out. The angular width of the little finger is just over 1.5 degrees at extended arm's length and can be used to estimate the elevation of the Sun from the horizon plane and therefore estimate the time until sunset. The need for more accurate measurements led to the development of a number of increasingly accurate instruments, including the kamal, astrolabe, octant, and sextant. The sextant and octant are most accurate because they measure angles from the horizon, eliminating errors caused by the placement of an instrument's pointers, and because their dual-mirror system cancels relative motions of the instrument, showing a steady view of the object and horizon.

Navigators measure distance on the Earth in degrees, arcminutes, and arcseconds. A nautical mile is defined as 1,852 meters but is also (not accidentally) one arc minute of angle along a meridian on the Earth. Sextants can be read accurately to within 0.1 arcminutes, so the observer's position can be determined within (theoretically) 0.1 nautical miles (185.2 meters, or about 203 yards). Most ocean navigators, measuring from a moving platform under fair conditions, can achieve a practical accuracy of approximately 1.5 nautical miles (2.8 km), enough to navigate safely when out of sight of land or other hazards.[1]

Practical navigation

[edit]
Ships Marine Chronometer giving an accuracy of less than ±5 seconds per year, French Navy issued, 1980
U.S. Navy quartermaster 3rd class, practices using a sextant as part of a navigation training aboard the amphibious assault ship USS Bonhomme Richard, 2018.

Practical celestial navigation usually requires a marine chronometer to measure time, a sextant to measure the angles, an almanac[2] giving schedules of the coordinates of celestial objects, a set of sight reduction tables to help perform the height and azimuth computations, and a chart of the region.[3] With sight reduction tables, the only calculations required are addition and subtraction.[4] Small handheld computers, laptops and even scientific calculators enable modern navigators to "reduce" sextant sights in minutes, by automating all the calculation and/or data lookup steps.[5] Most people can master simpler celestial navigation procedures after a day or two of instruction and practice, even using manual calculation methods.

Modern practical navigators usually use celestial navigation in combination with satellite navigation to correct a dead reckoning track, that is, a course estimated from a vessel's position, course, and speed. Using multiple methods helps the navigator detect errors and simplifies procedures. When used this way, a navigator, from time to time, measures the Sun's altitude with a sextant, then compares that with a precalculated altitude based on the exact time and estimated position of the observation. On the chart, the straight edge of a plotter can mark each position line. If the position line indicates a location more than a few miles from the estimated position, more observations can be taken to restart the dead-reckoning track.[6]

In the event of equipment or electrical failure, taking Sun lines a few times a day and advancing them by dead reckoning allows a vessel to get a crude running fix sufficient to return to port. One can also use the Moon, a planet, Polaris, or one of 57 other navigational stars to track celestial positioning.

Latitude

[edit]
Main article: Meridian altitude
See also: Latitude determination
Two ship's officers "shoot" a morning sight with sextants, the Sun altitude (1963).

Latitude was measured in the past either by measuring the altitude of the Sun at noon (the "noon sight") or by measuring the altitudes of any other celestial body when crossing the meridian (reaching its maximum altitude when due north or south), and frequently by measuring the altitude of Polaris, the north star (assuming it is sufficiently visible above the horizon, which it is not in the Southern Hemisphere). Polaris always stays within 1 degree of the celestial north pole. If a navigator measures the angle to Polaris and finds it to be 10 degrees from the horizon, then he is about 10 degrees north of the equator. This approximate latitude is then corrected using simple tables or almanac corrections to determine a latitude that is theoretically accurate to within a fraction of a mile. Angles are measured from the horizon because locating the point directly overhead, the zenith, is not normally possible. When haze obscures the horizon, navigators use artificial horizons, which are horizontal mirrors or pans of reflective fluid, especially mercury. In the latter case, the angle between the reflected image in the mirror and the actual image of the object in the sky is exactly twice the required altitude.

Longitude

[edit]
See also: Longitude determination
The relative longitude to a position (for example Greenwich) can be calculated with the position of the Sun and the reference time (for example, UTC/GMT).

If the angle to Polaris can be accurately measured, a similar measurement of a star near the eastern or western horizons would provide the longitude. The problem is that the Earth turns 15 degrees per hour, making such measurements dependent on time. A measure a few minutes before or after the same measure the day before creates serious navigation errors. Before good chronometers were available, longitude measurements were based on the transit of the moon or the positions of the moons of Jupiter. For the most part, these were too difficult to be used by anyone except professional astronomers. The invention of the modern chronometer by John Harrison in 1761 vastly simplified longitudinal calculation.

The longitude problem took centuries to solve and was dependent on the construction of a non-pendulum clock (as pendulum clocks cannot function accurately on a tilting ship, or indeed a moving vehicle of any kind). Two useful methods evolved during the 18th century and are still practiced today: lunar distance, which does not involve the use of a chronometer, and the use of an accurate timepiece or chronometer.

Presently, layperson calculations of longitude can be made by noting the exact local time (leaving out any reference for daylight saving time) when the Sun is at its highest point in Earth's sky. The calculation of noon can be made more easily and accurately with a small, exactly vertical rod driven into level ground—take the time reading when the shadow is pointing due north (in the northern hemisphere). Then take your local time reading and subtract it from GMT (Greenwich Mean Time), or the time in London, England. For example, a noon reading (12:00) near central Canada or the US would occur at approximately 6 p.m. (18:00) in London. The 6-hour difference is one quarter of a 24-hour day, or 90 degrees of a 360-degree circle (the Earth). The calculation can also be made by taking the number of hours (use decimals for fractions of an hour) multiplied by 15, the number of degrees in one hour. Either way, it can be demonstrated that much of central North America is at or near 90 degrees west longitude. Eastern longitudes can be determined by adding the local time to GMT, with similar calculations.

Lunar distance

[edit]
Main article: Lunar distance

An older but still useful and practical method of determining accurate time at sea before the advent of precise timekeeping and satellite-based time systems is called "lunar distances," or "lunars," which was used extensively for a short period and refined for daily use on board ships in the 18th century. Use declined through the middle of the 19th century as better and better timepieces (chronometers) became available to the average vessel at sea. Although most recently only used by sextant hobbyists and historians, it is now becoming more common in celestial navigation courses to reduce total dependence on GNSS systems as potentially the only accurate time source aboard a vessel. Designed for use when an accurate timepiece is not available or timepiece accuracy is suspect during a long sea voyage, the navigator precisely measures the angle between the Moon and the Sun or between the Moon and one of several stars near the ecliptic. The observed angle must be corrected for the effects of refraction and parallax, like any celestial sight. To make this correction, the navigator measures the altitudes of the Moon and Sun (or another star) at about the same time as the lunar distance angle. Only rough values for the altitudes are required. A calculation with suitable published tables (or longhand with logarithms and graphical tables) requires about 10 to 15 minutes' work to convert the observed angle(s) to a geocentric lunar distance. The navigator then compares the corrected angle against those listed in the appropriate almanac pages for every three hours of Greenwich time, using interpolation tables to derive intermediate values. The result is a difference in time between the time source (of unknown time) used for the observations and the actual prime meridian time (that of the "Zero Meridian" at Greenwich, also known as UTC or GMT). Knowing UTC/GMT, a further set of sights can be taken and reduced by the navigator to calculate their exact position on the Earth as a local latitude and longitude.

Use of time

[edit]
Main articles: Longitude by chronometer and Marine chronometer

The considerably more popular method was (and still is) to use an accurate timepiece to directly measure the time of a sextant sight. The need for accurate navigation led to the development of progressively more accurate chronometers in the 18th century (see John Harrison). Today, time is measured with a chronometer, a quartz watch, a shortwave radio time signal broadcast from an atomic clock, or the time displayed on a satellite time signal receiver.[7] A quartz wristwatch normally keeps time within a half-second per day. If it is worn constantly, keeping it near body heat, its rate of drift can be measured with the radio, and by compensating for this drift, a navigator can keep time to better than a second per month. When time at the prime meridian (or another starting point) is accurately known, celestial navigation can determine longitude, and the more accurately latitude and time are known, the more accurate the longitude determination. The angular speed of the Earth is latitude-dependent. At the poles, or latitude 90°, the rotation velocity of the Earth reaches zero. At 45° latitude, one second of time is equivalent in longitude to 1,077.8 ft (328.51 m), or one-tenth of a second means 107.8 ft (32.86 m)[8] At the slightly bulged-out equator, or latitude 0°, the rotation velocity of Earth or its equivalent in longitude reaches its maximum at 465.10 m/s (1,525.9 ft/s).[9]

Traditionally, a navigator checked their chronometer(s) with their sextant at a geographic marker surveyed by a professional astronomer. This is now a rare skill, and most harbormasters cannot locate their harbor's marker. Ships often carried more than one chronometer. Chronometers were kept on gimbals in a dry room near the center of the ship. They were used to set a hack watch for the actual sight, so that no chronometers were ever exposed to the wind and salt water on deck. Winding and comparing the chronometers was a crucial duty of the navigator. Even today, it is still logged daily in the ship's deck log and reported to the captain before eight bells on the forenoon watch (shipboard noon). Navigators also set the ship's clocks and calendar. Two chronometers provided dual modular redundancy, allowing a backup if one ceases to work but not allowing any error correction if the two displayed a different time, since in case of contradiction between the two chronometers, it would be impossible to know which one was wrong (the error detection obtained would be the same as having only one chronometer and checking it periodically: every day at noon against dead reckoning). Three chronometers provided triple modular redundancy, allowing error correction if one of the three was wrong, so the pilot would take the average of the two with closer readings (average precision vote). There is an old adage to this effect, stating: "Never go to sea with two chronometers; take one or three."[10] Vessels engaged in survey work generally carried many more than three chronometers – for example, HMS Beagle carried 22 chronometers.[11]

Modern celestial navigation

[edit]

The celestial line of position concept was discovered in 1837 by Thomas Hubbard Sumner when, after one observation, he computed and plotted his longitude at more than one trial latitude in his vicinity and noticed that the positions lay along a line. Using this method with two bodies, navigators were finally able to cross two position lines and obtain their position, in effect determining both latitude and longitude. Later in the 19th century came the development of the modern (Marcq St. Hilaire) intercept method; with this method, the body height and azimuth are calculated for a convenient trial position and compared with the observed height. The difference in arcminutes is the nautical mile "intercept" distance that the position line needs to be shifted toward or away from the direction of the body's subpoint. (The intercept method uses the concept illustrated in the example in the "How it works" section above.) Two other methods of reducing sights are the longitude by chronometer and the ex-meridian method.

While celestial navigation is becoming increasingly redundant with the advent of inexpensive and highly accurate satellite navigation receivers (GNSS), it was used extensively in aviation until the 1960s and marine navigation until quite recently. However, since a prudent mariner never relies on any sole means of fixing their position, many national maritime authorities still require deck officers to show knowledge of celestial navigation in examinations, primarily as a backup for electronic or satellite navigation. One of the most common current uses of celestial navigation aboard large merchant vessels is for compass calibration and error checking at sea when no terrestrial references are available.

In 1980, French Navy regulations still required an independently operated timepiece on board so that, in combination with a sextant, a ship's position could be determined by celestial navigation.[12]

The U.S. Air Force and U.S. Navy continued instructing military aviators on celestial navigation use until 1997, because:

  • celestial navigation can be used independently of ground aids.
  • celestial navigation has global coverage.
  • celestial navigation cannot be jammed (although it can be obscured by clouds).
  • celestial navigation does not give off any signals that could be detected by an enemy.[13]

The United States Naval Academy (USNA) announced that it was discontinuing its course on celestial navigation (considered to be one of its most demanding non-engineering courses) from the formal curriculum in the spring of 1998.[14] In October 2015, citing concerns about the reliability of GNSS systems in the face of potential hostile hacking, the USNA reinstated instruction in celestial navigation in the 2015 to 2016 academic year.[15][16]

At another federal service academy, the US Merchant Marine Academy, there was no break in instruction in celestial navigation as it is required to pass the US Coast Guard License Exam to enter the Merchant Marine. It is also taught at Harvard, most recently as Astronomy 2.[17]

Celestial navigation continues to be used by private yachtsmen, and particularly by long-distance cruising yachts around the world. For small cruising boat crews, celestial navigation is generally considered an essential skill when venturing beyond visual range of land. Although satellite navigation technology is reliable, offshore yachtsmen use celestial navigation as either a primary navigational tool or as a backup.

Celestial navigation was used in commercial aviation up until the early part of the jet age; early Boeing 747s had a "sextant port" in the roof of the cockpit.[18] It was only phased out in the 1960s with the advent of inertial navigation and Doppler navigation systems, and today's satellite-based systems which can locate the aircraft's position accurate to a 3-meter sphere with several updates per second.

A variation on terrestrial celestial navigation was used to help orient the Apollo spacecraft en route to and from the Moon. To this day, space missions such as the Mars Exploration Rover use star trackers to determine the attitude of the spacecraft.

As early as the mid-1960s, advanced electronic and computer systems had evolved enabling navigators to obtain automated celestial sight fixes. These systems were used aboard both ships and US Air Force aircraft, and were highly accurate, able to lock onto up to 11 stars (even in daytime) and resolve the craft's position to less than 300 feet (91 m). The SR-71 high-speed reconnaissance aircraft was one example of an aircraft that used a combination of automated celestial and inertial navigation. These rare systems were expensive, however, and the few that remain in use today are regarded as backups to more reliable satellite positioning systems.

Intercontinental ballistic missiles use celestial navigation to check and correct their course (initially set using internal gyroscopes) while flying outside the Earth's atmosphere. The immunity to jamming signals is the main driver behind this seemingly archaic technique.

X-ray pulsar-based navigation and timing (XNAV) is an experimental navigation technique for space whereby the periodic X-ray signals emitted from pulsars are used to determine the location of a vehicle, such as a spacecraft in deep space. A vehicle using XNAV would compare received X-ray signals with a database of known pulsar frequencies and locations. Similar to GNSS, this comparison would allow the vehicle to triangulate its position accurately (±5 km). The advantage of using X-ray signals over radio waves is that X-ray telescopes can be made smaller and lighter.[19][20][21] On 9 November 2016 the Chinese Academy of Sciences launched an experimental pulsar navigation satellite called XPNAV 1.[22][23] SEXTANT (Station Explorer for X-ray Timing and Navigation Technology) is a NASA-funded project developed at the Goddard Space Flight Center that is testing XNAV on-orbit aboard the International Space Station in connection with the NICER project, launched on 3 June 2017 on the SpaceX CRS-11 ISS resupply mission.[24]

Training

[edit]

Celestial navigation training equipment for aircraft crews combine a simple flight simulator with a planetarium.

An early example is the Link Celestial Navigation Trainer, used in the Second World War.[25][26] Housed in a 45-foot (14 m) high building, it featured a cockpit accommodating a whole bomber crew (pilot, navigator, and bombardier). The cockpit offered a full array of instruments, which the pilot used to fly the simulated airplane. Fixed to a dome above the cockpit was an arrangement of lights, some collimated, simulating constellations, from which the navigator determined the plane's position. The dome's movement simulated the changing positions of the stars with the passage of time and the movement of the plane around the Earth. The navigator also received simulated radio signals from various positions on the ground. Below the cockpit moved "terrain plates"—large, movable aerial photographs of the land below—which gave the crew the impression of flight and enabled the bomber to practice lining up bombing targets. A team of operators sat at a control booth on the ground below the machine, from which they could simulate weather conditions such as wind or clouds. This team also tracked the airplane's position by moving a "crab" (a marker) on a paper map.

The Link Celestial Navigation Trainer was developed in response to a request made by the Royal Air Force (RAF) in 1939. The RAF ordered 60 of these machines, and the first one was built in 1941. The RAF used only a few of these, leasing the rest back to the US, where eventually hundreds were in use.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Celestial navigation

View on Grokipedia
from Grokipedia
Celestial navigation is the process of determining a craft's geographic position on by measuring the altitudes of celestial bodies—such as the Sun, , planets, and stars—above the horizon and applying , precise timekeeping, and astronomical data to calculate . This method relies on the geometry of the and , forming a navigational triangle between the observer's , the , and the observed body to derive lines of position (LOPs). The practice traces its origins to ancient civilizations, including the Minoans, , and Phoenicians around 1500 BCE, who used the Sun and stars for coastal in the Mediterranean, with Phoenicians achieving feats like circumnavigating circa 600 BCE. Significant advancements occurred during the Age of Exploration in the , spurred by Portugal's , who established a navigation school and promoted instruments like the and quadrant for determination. The marked a breakthrough with John Harrison's (tested successfully in 1761), solving the longitude problem, alongside the independent invention of the reflecting sextant by John Hadley and Thomas Godfrey in the 1730s. Further refinements included Thomas Sumner's line-of-position method (1843) and Marcq St. Hilaire's (1875), which simplified computations, while Nathaniel Bowditch's The New American Practical Navigator (1802) popularized accessible tables and techniques. Key methods involve sight reduction, where observed altitudes are corrected for atmospheric refraction, index error, and height of eye (dip), then compared to computed altitudes using the and sight reduction tables like Publication No. 229 to plot LOPs or fixes. is found via meridian altitudes or polaris sightings, while longitude requires Greenwich Mean Time from a chronometer and local hour angle calculations. Essential instruments include the for angle measurements (accurate to 0.1 minutes of arc), the chronometer for universal time, and aids like the star finder for identifying bodies. Early tools evolved from the , which measured star angles against the horizon, to the for sun observations without direct viewing. Despite the dominance of satellite systems like GPS since the late , celestial navigation endures as a vital for maritime and , offering redundancy in electronic-denied environments and achieving positional accuracy within 2 miles under optimal conditions. It continues to be taught in naval training, with resources like the annual providing ephemerides for bodies' positions. Modern adaptations include automated sextants and software for , preserving its role in exploration and emergency navigation.

Principles and Theory

Celestial Sphere and Coordinates

The celestial sphere is an imaginary sphere of arbitrarily large radius centered at the observer on , onto which the positions of celestial bodies such as , the Sun, , and are projected for the purpose of locating them in the sky. This model simplifies the vast distances of space by treating all objects as if they lie on the inner surface of a dome surrounding the , allowing navigators to track apparent motions without needing to account for actual stellar distances. Key features of the celestial sphere include the celestial equator, a great circle projected from Earth's equator onto the sphere, which divides the sky into northern and southern hemispheres at 0° declination. The north and south celestial poles are the points where Earth's rotational axis extended intersects the sphere, at +90° and -90° declination respectively, around which the stars appear to rotate daily due to Earth's spin. The celestial horizon is the great circle representing the boundary between Earth and sky from the observer's viewpoint, perpendicular to the local (the point directly overhead). To specify positions on the celestial sphere, the equatorial coordinate system is used, analogous to latitude and longitude on Earth but aligned with the celestial equator and poles. Declination (Dec) measures the angular distance north or south of the celestial equator, in degrees from 0° at the equator to +90° at the north pole and -90° at the south pole, with subdivisions in arcminutes (′) and arcseconds (″); it remains fixed for stars due to their great distance. Right ascension (RA) measures the eastward angular distance along the celestial equator from a reference point, expressed in hours, minutes, and seconds of time (0h to 24h, where 1h equals 15°), reflecting the daily rotation of the sphere as Earth turns. The reference for RA is the vernal equinox, the point where the (apparent path of the Sun) intersects the in spring, defining the 0h hour circle that passes through the celestial poles. Hour circles are great circles connecting the celestial poles and running through specific points on the equator, serving as meridians for measuring RA eastward from the vernal equinox. Basic conversions between celestial and terrestrial coordinates involve adjusting for the observer's and local , which aligns the equatorial system with the horizon system by accounting for relative to the stars. A prominent example is , the North Star, with a of approximately +89° 16′, positioning it very near the north celestial pole and making its altitude roughly equal to the observer's in the . In celestial navigation, —based on relative to distant stars and measuring 23 hours 56 minutes 4 seconds per day—differs from , which is 24 hours based on the Sun's position and includes Earth's orbital motion around the Sun. This distinction is crucial for timing observations, as local equals the RA of objects crossing the meridian.

Angular Measurement Fundamentals

In celestial navigation, altitude is defined as the vertical of a celestial body above the observer's horizon, measured along the vertical circle passing through the body and the , ranging from 0° at the horizon to 90° at the . is the horizontal angular direction of the body, measured clockwise from (0°) to 360°, indicating the bearing relative to the observer's meridian. Zenith distance, denoted as z, is the complementary angle to altitude, calculated as z = 90° − altitude, representing the angular separation from the point directly overhead to the body. Several corrections are essential to adjust the raw measurement of altitude for observational inaccuracies. Dip correction accounts for the observer's eye height above , which causes the visible horizon to dip below the true celestial horizon; this correction subtracts an amount approximately equal to 0.97 × √(height in feet) arcminutes from the measured altitude. Index error arises from misalignment in the sextant's optical components, a constant instrumental bias determined by (e.g., sighting the horizon) and subtracted or added accordingly to the sextant reading. correction addresses the bending of light rays by the Earth's atmosphere, which elevates the apparent position of the body; the correction value, tabulated in the , decreases from about 34 arcminutes at the horizon to near zero at higher altitudes and is subtracted from the apparent altitude. Parallax correction applies primarily to nearby celestial bodies like the Sun and , arising from the observer's position on Earth's surface relative to the planet's center; it adds a value equal to the horizontal parallax (e.g., ~8.8 arcminutes for the Sun, ~57 arcminutes for the Moon) multiplied by cos(altitude) to the apparent altitude. Semi-diameter correction compensates for the finite angular size of the Sun and , equivalent to their apparent radius (~16 arcminutes for the Sun, ~15.5 arcminutes for the Moon); it is added when observing the lower limb or subtracted for the upper limb to refer to the body's center. The relationship between observed and true altitude incorporates these effects through the equation: Ho=Ht+dip+[refraction](/page/Refraction)+[parallax](/page/Parallax)+semi-diameterH_o = H_t + \text{dip} + \text{[refraction](/page/Refraction)} + \text{[parallax](/page/Parallax)} + \text{semi-diameter} where HoH_o is the observed (apparent) altitude after instrumental corrections, and HtH_t is the true geometric altitude. This derives from geometric principles: refraction bends incoming rays toward the normal, increasing apparent altitude; dip geometrically lowers the reference horizon; parallax shifts nearby bodies' positions topocentrically; and semi-diameter adjusts for the offset from the limb to the center, with signs depending on observation specifics (e.g., negative for refraction and dip in standard application). Early angular measurements in celestial navigation relied on instruments like the astrolabe, originating in ancient Greece around 120 BCE and credited to Hipparchus, with adaptations by Islamic astronomers in the 9th century for measuring the altitudes of stars and the Sun to determine latitude.

Instruments and Equipment

Sextants and Optical Tools

The sextant is a doubly reflecting optical instrument designed to measure the angular distance between two visible objects, primarily the horizon and a celestial body, for celestial navigation. Its core principle relies on the reflection of light from two mirrors to double the observed angle, allowing measurements up to 120 degrees despite a typical arc of 60 degrees. The instrument consists of a sturdy frame, usually made of brass for corrosion resistance at sea or aluminum in modern versions for lighter weight, which supports the graduated arc, index arm, mirrors, and telescope. The arc is engraved with fine graduations in degrees and minutes, enabling readings to a precision of 0.1 arcminute under ideal conditions, though typical hand-held observations achieve about 1 arcminute accuracy due to observer motion. The index arm, a movable bar pivoting at the arc's center of curvature, carries the fully silvered index mirror, while the horizon glass—half-silvered and fixed to the frame—allows direct and reflected views to coincide. A telescope, often erect-image for horizon sights or inverting for stars, attaches via an adjustable collar to magnify the field of view, and interchangeable shade filters of colored glass reduce glare during solar or bright-body observations. To operate the sextant, the navigator holds it vertically by the handle, directing the telescope toward the horizon through the unsilvered portion of the horizon glass. The index arm is then adjusted via a tangent screw or micrometer drum until the reflected image of the celestial body, viewed through the index mirror, aligns precisely with the direct horizon image, forming a single straight line via double reflection. The instrument is rocked side-to-side to ensure the line of sight is perpendicular to the horizon, minimizing dip errors, and the reading is taken from the arc scale using a vernier for minutes and seconds. This process captures the body's altitude, with index error—a common angular correction arising from non-parallel mirrors at zero—verified and applied by observing the horizon alone or a star pair. Predecessors to the include the quadrant, a wooden quarter-circle instrument with a 90-degree arc and , used from the mid-1400s for by sighting celestial bodies against a plumb line. The octant, developed by English instrument maker John Hadley and independently by American glazier Thomas Godfrey, and presented to the Royal Society in 1731, marked a significant advancement with its reflecting mirrors and 45-degree arc, improving accuracy over earlier backstaves and quadrants to within a few nautical miles. The evolved from the octant in the late 1750s, with the first instruments produced by John Bird in 1757-1759, extending the arc to 60 degrees for broader measurements while retaining the double-reflection design, and became standard after modifications for marine durability post-1770. These early tools, often constructed from wood, brass, and glass, laid the foundation for precise angle measurement at sea. Modern marine sextants incorporate enhancements like LED illumination for low-light scale reading and robust coatings on for reduced distortion, maintaining the traditional or aluminum construction for durability against saltwater exposure. Recent developments as of 2024 include digital star trackers and automated celestial navigation systems for unmanned aerial vehicles (UAVs), providing GPS-independent positioning. In , where a natural horizon is unavailable, bubble sextants provide an artificial horizon via a liquid-filled level, enabling aerial celestial fixes as used in early transatlantic flights. involves storing the instrument in a padded case to protect against dampness and , cleaning mirrors with lens tissue and alcohol, and lubricating the tangent lightly; collimation errors, where the axis deviates from the frame, are adjusted by the manufacturer using specialized screws to ensure parallelism. Shade filters must be checked for prismatic effects from non-parallel faces, which can introduce errors during solar sights, and periodic against a certified standard prevents cumulative inaccuracies.

Timekeeping Devices

Accurate timekeeping is essential in celestial navigation, particularly for determining , as it allows navigators to compare —derived from celestial observations—with a fixed reference time, such as (GMT). Without precise , errors in positioning could accumulate rapidly at sea, where environmental factors like and motion challenge clock stability. Marine chronometers emerged as the solution, providing a reliable means to maintain GMT aboard ships. Marine chronometers are specialized, constant-rate timepieces designed for maritime use, featuring a and spiral spring to regulate oscillations, typically at a high frequency for stability. They incorporate temperature compensation mechanisms, such as bimetallic rims on the that adjust for and contraction, ensuring minimal rate variation across temperature ranges encountered at sea, from freezing decks to tropical cabins. These devices are housed in gimbaled wooden boxes to isolate them from a vessel's rolling motion, maintaining a level position and thus consistent performance. The development of the marine chronometer culminated in John Harrison's H4, completed in 1759 and first tested at sea in 1761, which revolutionized by solving the longstanding problem. This pocket-watch-sized instrument achieved an accuracy of better than one second per month during trials, far surpassing prior mechanical clocks and meeting the British Longitude Act's requirements for errors under half a degree of . In modern practice, quartz watches serve as equivalents, oscillating via a at 32,768 Hz and offering accuracies of 15 to 20 seconds per month, sufficient for most celestial fixes when rated for drift. Operationally, marine chronometers require daily winding—typically once every 24 hours at a consistent time—to maintain tension in the via a fusee mechanism that delivers even power. Navigators monitor error rates, defined as the daily gain or loss in seconds relative to GMT, and compute the chronometer's overall rate (average variation over days) to apply during sights. High-quality chronometers receive rating certificates from testing authorities, verifying positional and thermal stability, such as mean daily rates within -4 to +6 seconds under controlled conditions. As backups, radio time signals from stations like NIST's WWV broadcast UTC on shortwave frequencies (2.5, 5, 10, 15, 20 MHz), allowing with accuracies better than 1 when conditions permit. Celestial navigation distinguishes between sidereal clocks, which track relative to distant and gain approximately 3 minutes 56 seconds per solar day, and solar clocks aligned to the Sun's apparent motion. Standard marine chronometers use mean (GMT), but for precise stellar observations, conversions to are applied via nautical almanacs. Additionally, the equation of time correction accounts for the up to 16-minute discrepancy between mean and apparent solar time due to Earth's elliptical orbit and , ensuring alignment during solar sights. In contemporary celestial navigation, GPS satellites provide UTC—synchronized to within nanoseconds of atomic standards—directly via messages, offering high reliability for timekeeping. However, emphasis remains on standalone mechanical or devices for , as can be jammed or unavailable, preserving the chronometer's role in independent positioning.

Determining Latitude

Determining in celestial navigation relies on measuring the altitude of a celestial body at its meridian passage, when it crosses the observer's meridian, providing a direct vertical alignment independent of . This method has been fundamental since ancient times, allowing navigators to establish their north-south position relative to the . The two primary bodies used are the Sun, observed at local noon, and (the North Star) in the , each offering a straightforward once the observed altitude is corrected and combined with the body's known from a . For the Sun, the procedure involves taking morning and evening sights with a to bracket the time of meridian passage, ensuring the observation captures the Sun's highest altitude (local noon). The (d), which is the Sun's angular distance north or south of the , is obtained from the for the date of observation. The corrected observed altitude (Ho) is then used to compute the zenith distance ZD = 90° - Ho. If the observer's and the have the same name (both north or both south), the L = ZD + d, taking the name of d. If they have contrary names, L is the difference between ZD and |d|, taking the name of the larger value. This yields without requiring precise timekeeping, as the meridian alignment inherently provides the fix. Observed altitudes require brief corrections for factors like and dip. For Polaris, the method is simpler in the Northern Hemisphere due to its proximity to the north celestial pole (declination ≈ +89°). The latitude approximates the corrected altitude (Ho) of Polaris above the horizon, measured at any time since its position remains nearly fixed: L≈HoL \approx H_o. This direct relation stems from the pole's alignment, making it ideal for quick checks, though a small correction table from the Nautical Almanac refines the result to within 1° accuracy. In the , can be determined using the meridian altitude of the Sun in the same manner as in the north, or by sighting southern circumpolar stars such as , though it is fainter (magnitude 5.5) and requires more precise measurements and tables for accuracy comparable to . Special cases include the noon sight for the Sun, which eliminates the need for time and is particularly useful for standalone fixes during voyages. In polar regions, however, errors can arise from horizon dip—the apparent depression of the visible horizon due to the observer's eye height and atmospheric conditions—exacerbated by low solar altitudes, ice mirages, or extreme , potentially requiring additional adjustments from tables.

Determining Longitude

Determining longitude in celestial navigation relies on measuring the time difference between the local apparent time at the observer's position and (GMT), as the rotates 360° in 24 hours, equivalent to 15° of per hour of time. Local apparent time is derived from the of a celestial body's position, such as its (meridian transit), using instruments like a to note the instant when the body crosses the local meridian. This temporal discrepancy, when converted to angular measure, yields the east-west position relative to the Greenwich meridian: positions east of Greenwich have local time ahead of GMT, while those west are behind. The fundamental equation for longitude (Lo), expressed in degrees with west longitude positive, is given by: Lo=(GMT−LHA)×15∘\text{Lo} = (\text{GMT} - \text{LHA}) \times 15^\circ where GMT is the Greenwich Mean Time of the observation in hours, and LHA is the local hour angle of the celestial body in hours, derived from the body's right ascension (RA) and the local sidereal time. The LHA represents the angular distance from the local meridian to the body's hour circle, measured westward; signs are adjusted for east/west longitude (negative for east). For the Sun, at local apparent noon (LHA = 0 hours), this simplifies to Lo = 15° × (GMT - 12 hours). Accurate timekeeping, typically via a marine chronometer, is essential to obtain GMT, as even a four-minute error equates to one degree of longitude. Before reliable chronometers became widespread in the late , the method provided an alternative for determining GMT without a timepiece. This technique involves measuring the angular separation () between the and a fixed celestial body, such as a star or the Sun, using a ; the Moon's rapid motion relative to the —approximately 13.2° per day or 33 arcminutes per hour—allows this distance to serve as a "clock" when compared to precomputed data. Observations are taken in sets, cleared for , , semi-diameter, and instrument index error to obtain the true geocentric distance, then matched against tables of "clearance" angles (precalculated distances at three-hour GMT intervals) via or to derive GMT. The resulting GMT is then used in the equation above, enabling positions accurate to about 0.5° under ideal conditions. The lunar method's viability hinged on precise lunar tables, with German astronomer Tobias Mayer developing highly accurate ones in the 1750s based on extensive observations and error corrections for . Mayer's tables, sent to the British Board of Longitude in 1755, allowed longitude determinations within half a degree and were posthumously refined and published in 1770. These tables formed the basis for the first , published in 1767 under Nevil , which included three-hourly lunar clearances to facilitate the method at sea; the almanac's instructions emphasized use and table interpolation for practical application. Despite initial complexity in calculations, the method was tested successfully on voyages, though it was gradually supplanted by chronometers after John Harrison's designs proved reliable. In modern celestial navigation, longitude determination via these time-based methods serves primarily as a backup to satellite systems like GPS, mandated by regulations such as SOLAS Chapter V for vessels without redundant positioning. The U.S. Navy, for instance, reinstituted training in 2016 to counter GPS spoofing and jamming threats, using chronometer-assisted sights for lines of position that yield fixes within 0.1 to 10 nautical miles depending on conditions. Error sources include inaccuracies from unmodeled perturbations (typically under 1 arcsecond but cumulative over long intervals), chronometer drift (up to 1.5 minutes over days), and observational factors like horizon dip or , emphasizing the need for multiple sights and rigorous corrections. While GPS dominates routine use, celestial techniques ensure resilience in contested environments.

Sight Reduction Techniques

Sight reduction is the process of deriving a line of position (LOP) from an observed celestial altitude, typically obtained with a , by applying corrections for , instrument errors, and other factors to compute the body's true altitude and then using to determine the observer's position relative to the celestial body's geographic position. This involves the assumed position method, where an approximate position near the dead reckoning location is selected—often with rounded to the nearest whole minute and adjusted to make the local a multiple of 30° for tabular convenience—and used to calculate the expected altitude and of the body from that point. The difference between the computed and observed altitudes, known as the intercept, defines the perpendicular distance from the assumed position to the LOP, along with the angle. Key methods for sight reduction rely on precomputed tables to avoid direct trigonometric calculations. The 's sight reduction tables (Pub. No. 229), published by the U.S. Naval Observatory and the , provide values for the calculated altitude and based on , , and local , covering latitudes from 0° to 60° in six volumes and enabling the intercept method for . H.O. 208, a compact set of tables known as the "Dead Reckoning Altitude and Azimuth Tables," offers a self-contained alternative for emergency use, requiring only the for body data and providing solutions accurate to 0.1 minutes in altitude with entries for hour angles in 10-minute increments. Ageton's tables (H.O. 211) provide a concise trigonometric method using haversine functions and a single-page table for solving the navigational triangle, suitable for quick manual reductions with an average altitude error of less than 0.5 minutes. The core equation for sight reduction derives from the applied to the spherical navigational triangle formed by the , the elevated pole, and the celestial body, where the zenith distance c=90∘−hc = 90^\circ - h (with hh as the observed altitude) satisfies: cos⁡c=sin⁡ϕsin⁡δ+cos⁡ϕcos⁡δcos⁡t\cos c = \sin \phi \sin \delta + \cos \phi \cos \delta \cos t Here, ϕ\phi is the observer's , δ\delta is the body's , and tt is the local ; is then found using the or cosines for the triangle. This formula allows computation of the expected zenith distance from the assumed position, with the intercept measured along the azimuth from that position to the actual LOP. To obtain a position fix, multiple LOPs from different bodies or times are plotted on a universal plotting sheet, with the fix at their intersection; for a single sight, the LOP is drawn perpendicular to the through point relative to the assumed position. In cases of ship motion between sights, a running fix advances the earlier LOP forward by the estimated distance run (course and speed over ground) to intersect with the later LOP, providing an updated position without simultaneous observations. Modern software and electronic calculators have largely supplanted manual tables, performing sight reductions in seconds using built-in almanacs and algorithms based on the same . Programs like StarPilot and mobile apps such as Celestial Navigation integrate GPS for assumed positions while preserving traditional methods as backups, ensuring accuracy to within 0.1 nautical miles for properly corrected sights.

Historical Development

Ancient and Early Methods

Celestial navigation originated in ancient cultures through qualitative observations of stars and natural phenomena, enabling early seafarers to maintain direction and estimate position without mechanical aids. Polynesian wayfinders, as early as 1500 BCE, traversed the Pacific using memorized star paths, where specific constellations guided routes to islands, supplemented by wave swells and bird behaviors to detect landfalls. In around 3000 BCE, astronomers tracked the of Sirius to predict the Nile's annual flooding, aligning agricultural calendars with celestial events. Greek scholars advanced these practices by systematizing stellar positions in the 2nd century BCE, with compiling the first comprehensive star catalog of over 850 entries, providing coordinates that formed the basis for later positional astronomy essential to navigation. built on this in his 2nd-century CE Almagest, incorporating tables of latitudes derived from distances and angles, which allowed mariners to estimate their position relative to known stellar references. During the medieval period, Islamic astronomers refined instruments for practical use, with al-Sufi in the authoring a detailed on astrolabes that outlined over 1,000 applications, including determination from star altitudes for overland and maritime travel. In China, from the onward (circa 200 BCE–200 CE), navigators employed stellar observations of to gauge during coastal voyages. The south-pointing device, used from the for divination, later aided navigation in subsequent dynasties. Viking seafarers around the 9th–11th centuries reportedly used crystals, known as sunstones, to detect skylight polarization and locate the sun's position through overcast skies, aiding transatlantic routes. These early methods, however, were constrained by the inability to measure accurately without precise timekeeping, forcing reliance on —estimating position via speed, direction, and elapsed time—which accumulated errors over long voyages and limited open-ocean precision. This qualitative approach persisted until the , when explorers on caravels adapted simple quadrants for star altitude measurements, bridging ancient traditions toward more systematic exploration.

Age of Sail and Exploration

During the and from the 16th to the 19th centuries, celestial navigation advanced dramatically, enabling European mariners to undertake transoceanic voyages that expanded routes, empires, and scientific . Instruments and methods refined during this addressed critical challenges in determining position at sea, particularly through solar and stellar observations and the more elusive via time-based calculations. These innovations were spurred by the demands of exploration, where accurate positioning could mean the difference between success and disaster in uncharted waters. Key developments included the log and line, a device for estimating a ship's speed over ground by trailing a wooden chip attached to a knotted line from the stern, allowing navigators to compute distance traveled when combined with bearings. This tool, widely adopted in the , complemented celestial fixes by providing essential data. The cross-staff, developed in the and refined for maritime use by the , measured the angular altitude of celestial bodies above the horizon by aligning a sliding crosspiece against the eye, though it required the observer to sight both the horizon and the object simultaneously, often uncomfortably. To mitigate the hazards of direct sun observation, the was invented in 1594 by English navigator John Davis; it allowed measurements by casting a shadow from a vane onto a horizon-aligned scale, enabling safer solar sights without blinding the user. The longitude problem—determining east-west position—remained a profound obstacle until legislative and inventive breakthroughs in the . In 1714, the British established a prize of up to £20,000 (equivalent to millions today) for a method accurate to within 30 nautical miles at the , prompting intense innovation. carpenter John Harrison's marine chronometers, culminating in the H4 model of 1761, provided reliable timekeeping to compare local with Greenwich mean time, thus calculating via Earth's rotation. These chronometers proved their worth on Captain James Cook's voyages in the 1760s and 1770s, where a copy of H4 enabled precise charting of the Pacific, demonstrating accuracies of mere seconds over months at sea and facilitating safer, more efficient exploration. Prominent navigators exemplified both the triumphs and limitations of these techniques. , on his 1492 voyage, relied on celestial observations with a quadrant for but committed significant errors in and distance estimation due to miscalculations from outdated almanacs and geographical tables, such as those derived from , leading him to believe he had reached rather than the after sailing only about two-thirds the intended distance. Similarly, Ferdinand Magellan's 1519–1522 employed early methods—observing the moon's angular separation from fixed stars to infer time and —under the guidance of cosmographer Rui Faleiro and pilot Andrés de San Martín, achieving remarkably accurate fixes despite rudimentary tables and instruments. These efforts highlighted celestial navigation's role in historic feats while underscoring its reliance on precise ephemerides. Institutional advancements further standardized celestial practices. The Royal Observatory at Greenwich, founded in 1675 by King Charles II, served as a hub for astronomical observations to support , with its meridian line emerging as a global reference for calculations by the . Complementing this, the first , published in 1767 under Nevil , provided tabulated positions of the sun, , and , essential for computations and marking a shift toward reliable, annual data for mariners worldwide. By the late 19th century, celestial navigation's primacy waned as transformed maritime operations; submarine cables and emerging systems from the enabled ships to receive real-time time signals and positional updates from shore stations, diminishing the need for onboard chronometers and lunar observations in routine voyages.

Modern Applications

Current Uses in Maritime and

In maritime operations, celestial navigation serves primarily as a reliable to electronic systems like GPS, mandated by international regulations to ensure in case of failures. The International Convention on Standards of Training, Certification and Watchkeeping for Seafarers (STCW) requires deck officers to demonstrate proficiency in celestial navigation, including the use of sextants for position fixes, as part of the competencies for Officers in Charge of a Navigational Watch (OICNW) on vessels of 500 gross tons or more. Under the Chapter V, ships must maintain navigational capabilities with backups to primary electronic aids; celestial tools such as sextants, chronometers, and nautical almanacs are commonly carried to support observations when primary navigation aids are unavailable. This is particularly critical in environments prone to GPS jamming or denial, such as contested waters, where celestial methods provide an independent means of determining position. In naval contexts, including , celestial navigation is employed through periscope-based observations or emerging automated star trackers to maintain positioning in GPS-denied scenarios. In , celestial navigation functions as a non-electronic contingency for long-range overwater flights, though modern reliance on inertial and systems has diminished its routine use. The (FAA) mandates dual independent navigation systems for extended overwater operations beyond 100 nautical miles, which historically included celestial capabilities as a , especially for transoceanic routes. Today, while not a primary requirement, celestial training persists in and some commercial pilot certifications to address potential disruptions in -based . As of 2025, regulatory and operational emphases on celestial navigation have intensified due to growing GPS vulnerabilities, including jamming, spoofing, and disruptions from solar flares that can degrade signals. For instance, heightened solar activity in the current cycle has prompted maritime authorities to recommend more frequent celestial practice drills, while aviation regulators highlight the need for resilient backups in oceanic airspace. Hybrid systems are emerging that integrate celestial observations with satellite-derived data, such as electronic almanacs from GNSS constellations, to enhance accuracy and automate without full reliance on vulnerable GPS. A key advantage of celestial navigation lies in its complete independence from electronic , allowing fixes using only optical tools and manual computations, which proves invaluable during electronic warfare or natural disruptions. Under optimal conditions with clear skies and skilled observation, it achieves positional accuracy of 1-2 nautical miles, sufficient for safe routing in open seas or airspace. However, contemporary challenges persist, including urban light pollution that obscures faint stars and planets essential for sightings, particularly in coastal or near-shore operations. Additionally, the prevalence of automated systems has eroded manual proficiency among crews, necessitating renewed to maintain competence.

Training and Preservation

Celestial navigation remains a required competency in maritime programs worldwide, governed by the International Maritime Organization's (IMO) Standards of Training, Certification and Watchkeeping for Seafarers (STCW) Convention. Under STCW Chapter II, which addresses for masters and deck officers, candidates for officers in charge of a navigational watch must demonstrate knowledge of celestial navigation principles, including observations, timekeeping, and position fixing using heavenly bodies. This ensures proficiency in backup navigation methods amid potential electronic failures. Nautical academies integrate practical celestial navigation into their curricula, often combining theoretical instruction with hands-on exercises. At the U.S. Merchant Marine Academy (USMMA), midshipmen in the Marine Transportation program study celestial navigation alongside terrestrial methods, utilizing simulators to replicate sight-taking scenarios and prepare for U.S. Coast Guard licensing exams. These programs emphasize the integration of celestial fixes with modern tools, fostering skills for ocean voyages. In , celestial navigation training has diminished but persists in specialized contexts, such as or long-haul flight preparation, where provides navigation manuals that cover foundational celestial concepts as backups to GPS. For pilots holding certain instrument ratings, (FAA) regulations mandate recurrent training every 12 months, which may include navigation refreshers, though celestial methods are typically supplementary rather than core. The widespread adoption of GPS in the led to a significant decline in celestial navigation proficiency among navigators, with many institutions phasing out dedicated courses by the due to reliance on systems. However, by 2025, concerns over GPS vulnerabilities—such as jamming and spoofing—have spurred a resurgence, evidenced by increased interest in celestial methods for resilient positioning. Mobile applications now enable virtual practice of sights and reductions, democratizing access for amateurs and professionals alike. Preservation efforts focus on educational outreach and resources to sustain the skill. Amateur organizations offer workshops and forums for enthusiasts, while updated textbooks provide modern interpretations of traditional techniques. Non-Western programs, such as those in the , incorporate celestial navigation into officer training to complement electronic systems, addressing regional gaps in global curricula. Challenges to training include the cost of equipment, with quality sextants priced from approximately $400 upward, limiting accessibility for individual learners. Emerging technologies like (AR) and (VR) simulators are being explored to provide cost-effective virtual sight-taking experiences, reducing the need for physical horizons and instruments during instruction.

References

  1. https://www.dco.uscg.mil/Portals/9/NMC/pdfs/examinations/bowditch_Vol_2_2019.pdf
  2. https://ufdcimages.uflib.ufl.edu/AA/00/03/71/98/00001/analysisofdevelo00mors.pdf
  3. https://timeandnavigation.si.edu/navigating-at-sea/navigating-without-a-clock/celestial-navigation
  4. https://science.nasa.gov/learn/basics-of-space-flight/chapter2-2/
  5. https://www.sciencelearn.org.nz/resources/623-the-celestial-sphere
  6. https://skyandtelescope.org/astronomy-resources/right-ascension-declination-celestial-coordinates/
  7. https://astro.unl.edu/naap/motion1/cec_units.html
  8. https://lco.global/spacebook/sky/sidereal-time/
  9. https://astronavigationdemystified.com/the-role-of-altitude-azimuth-and-zenith-distance-in-astro-navigation/
  10. https://www.hughes38.com/wp-content/uploads/2016/03/astro.pdf
  11. https://aa.usno.navy.mil/data/celnav
  12. https://exploration.marinersmuseum.org/object/astrolabe/
  13. https://thenauticalalmanac.com/2019_Bowditch-_American_Practical_Navigator/Volume-_1/05-%20Part%203-%20Celestial%20Navigation/Chapter%2014-%20Instruments%20For%20Celestial%20Navigation.pdf
  14. https://ntrs.nasa.gov/api/citations/19680004089/downloads/19680004089.pdf
  15. https://aa.usno.navy.mil/downloads/reports/ghk_posmo.pdf
  16. https://www.backbearing.com/files/The_Sextant_Simplified_O_M_Watts.pdf
  17. https://www.boem.gov/sites/default/files/documents/regions/gulf-mexico-ocs-region/office-environment/TR-BOEM-2021-057.pdf
  18. https://highways.today/2024/12/03/celestial-uav-drone/
  19. https://www.history.navy.mil/about-us/leadership/director/directors-corner/h-grams/h-gram-030/h-030-2.html
  20. https://www.rmg.co.uk/stories/time/greenwich-mean-time-gmt
  21. https://timeandnavigation.si.edu/multimedia-asset/what-makes-a-sea-chronometer-so-precise
  22. https://www.hodinkee.com/watch101/compensating-balance
  23. https://www.rmg.co.uk/stories/time/harrisons-clocks-longitude-problem
  24. http://davidburchnavigation.blogspot.com/2018/05/ways-to-get-accurate-gmt-utc.html
  25. https://www.cultofsea.com/bridge-equipment/the-marine-chronometer/
  26. https://www.crawfordnautical.com/2018/09/14/chronometer-error-and-chronometer-rate/
  27. https://barringtonwatchwinders.com/pages/chronometer
  28. https://www.nist.gov/blogs/taking-measure/nist-radio-station-wwv-celebrates-century-service
  29. https://aa.usno.navy.mil/faq/eqtime
  30. https://upcommons.upc.edu/bitstreams/02f8ec53-a2a1-4f08-93a1-67b8de209a86/download
  31. https://people.umass.edu/wqd/strobel/nakedeye/nakedeya.htm
  32. https://teachersinstitute.yale.edu/curriculum/units/files/07.03.09.pdf
  33. https://www.aoc.nrao.edu/~smyers/courses/astrolabs/navigation.html
  34. https://www.ion.org/publications/upload/celestialnavtoc.pdf
  35. https://thenauticalalmanac.com/2017_Bowditch-_American_Practical_Navigator/Volume-_1/Bowditch_Vol_1_LoRes.pdf
  36. https://astrolabesailing.com/2016/10/27/celestial-navigation-local-hour-angle/
  37. https://www.cambridge.org/core/journals/journal-of-navigation/article/gmt-and-longitude-by-lunar-distance-two-methods-compared-from-a-practitioners-point-of-view/264D429197D6182A7D04193FD95FDD7E
  38. https://mathshistory.st-andrews.ac.uk/Biographies/Mayer_Tobias/
  39. https://www.royalobservatorygreenwich.org/articles.php?article=935
  40. https://www.usni.org/magazines/proceedings/2021/december/bring-celestial-navigation-21st-century
  41. https://thenauticalalmanac.com/2024_Bowditch-_American_Practical_Navigator/Volume_2/09_Volume_2_Calculations_For_Navigation/Chapter_8_Sight_Reduction.pdf
  42. https://www.dco.uscg.mil/Portals/9/NMC/pdfs/examinations/03_sight_reduction_tables_pub_229_vol_2.pdf
  43. http://www.devill.net/Infos/Astro/0-Celestial-navigation-with-HO208.pdf
  44. https://www.starpath.com/cgi-bin/web_card/courses/glossary.pl?show_def=70&cat=Celestial_Navigation
  45. https://www.starpilotllc.com/products/pc.htm
  46. https://manoa.hawaii.edu/exploringourfluidearth/physical/navigation-and-transportation/wayfinding-and-navigation
  47. https://press.uchicago.edu/books/hoc/HOC_V2_B3/HOC_VOLUME2_Book3_chapter13.pdf
  48. https://www.researchgate.net/publication/234348473_The_Heliacal_Rise_of_Sirius_and_Ancient_Egyptian_Chronology
  49. https://link.springer.com/article/10.1007/s10816-025-09724-6
  50. https://journals.sagepub.com/doi/10.1177/00218286221128289
  51. https://skyandtelescope.org/astronomy-news/lost-star-catalog-of-ancient-times-comes-to-light/
  52. https://ojs.library.okstate.edu/osu/index.php/OAS/article/view/4324/3997
  53. https://jonvoisey.net/blog/2019/05/almagest-book-ii-table-of-zenith-distances-and-ecliptic-angles/
  54. https://www.bibalex.org/SCIplanet/en/Article/Details.aspx?id=5198
  55. https://legacy.geog.ucsb.edu/the-astrolabe-a-mathematical-jewel/
  56. https://link.springer.com/chapter/10.1007/978-981-16-4079-7_8
  57. https://pmc.ncbi.nlm.nih.gov/articles/PMC3049005/
  58. https://royalsocietypublishing.org/doi/10.1098/rsos.150406
  59. https://arxiv.org/pdf/2209.02371
  60. https://sciencescholar.us/journal/index.php/ijhs/article/download/13034/9695/9800
  61. https://press.uchicago.edu/books/hoc/HOC_V3_Pt1/HOC_VOLUME3_Part1_chapter20.pdf
  62. https://journals.openedition.org/cahierscfv/752
  63. https://www.usni.org/magazines/proceedings/1936/november/evolution-sextant
  64. https://www.nps.gov/fora/learn/education/navigation-and-related-instruments-in-16th-century-england.htm
  65. https://exploration.marinersmuseum.org/object/cross-staff/
  66. https://www.history.com/articles/navigational-tools-ships-age-exploration
  67. https://www.usni.org/magazines/naval-history-magazine/2019/october/john-harrison-and-longitude-problem
  68. https://www.americanscientist.org/article/the-british-longitude-act-reconsidered
  69. https://www.usni.org/magazines/proceedings/1926/april/navigation-columbus
  70. https://www.cambridge.org/core/journals/journal-of-navigation/article/san-martins-accurate-longitude-measurements-on-magellans-circumnavigation-luck-or-mastery/71D9A5328195AE41A9B926B27038128D
  71. https://www.royalobservatorygreenwich.org/articles.php?article=1
  72. https://ethw.org/The_Sea_and_Early_Electrical_Technology
  73. https://www.ecfr.gov/current/title-46/chapter-I/subchapter-B/part-11/subpart-C/section-11.309
  74. https://www.usni.org/magazines/proceedings/2021/october/navigate-stars-beneath-waves
  75. https://www.law.cornell.edu/cfr/text/14/91.511
  76. https://www.usni.org/magazines/proceedings/2025/january/ships-must-practice-celestial-navigation
  77. https://www.gpsworld.com/solar-storm-may-impact-gps/
  78. https://aerospace.honeywell.com/us/en/products-and-services/products/navigation-and-sensors/navigation-systems/celestial-aided-navigation
  79. https://astronavigationdemystified.com/the-accuracy-of-astronomical-celestial-navigation/
  80. https://www.imo.org/en/OurWork/HumanElement/Pages/STCW-Convention.aspx
  81. https://www.usmma.edu/academics/curriculum/marine-transportation
  82. https://ww2.jeppesen.com/training-and-pilot-supplies/courseware/
  83. https://skybrary.aero/articles/celestial-navigation
  84. https://www.researchgate.net/publication/341479107_21_st_century_Celestial_navigation_systems
  85. https://www.unmannedairspace.info/uncategorized/researchers-develop-celestial-navigation-system-as-a-gps-alternative-for-drones/
  86. https://digitalcommons.odu.edu/cgi/viewcontent.cgi?article=1040&context=ots_masters_projects
  87. https://www.landfallnavigation.com/navigation/celestial-navigation/sextants.html
Add your contribution
Related Hubs
User Avatar
No comments yet.