Area of a triangle

Heron of Alexandria found what is known as Heron's formula for the area of a triangle in terms of its sides, and a proof can be found in his book, Metrica, written around 60 CE. It has been suggested that Archimedes knew the formula over two centuries earlier,^[4] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.^[5] In 300 BCE Greek mathematician Euclid proved that the area of a triangle is half that of a parallelogram with the same base and height in his book Elements of Geometry.^[6]

In 499 Aryabhata, a great mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, expressed the area of a triangle as one-half the base times the height in the Aryabhatiya.^[7]

A formula equivalent to Heron's was discovered by the Chinese independently of the Greeks. It was published in 1247 in Shushu Jiuzhang ("Mathematical Treatise in Nine Sections"), written by Qin Jiushao.^[8]

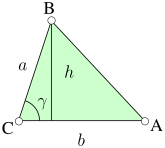
The area ${\displaystyle T}$ of a triangle can be found through the application of trigonometry.

Using the labels in the image on the right, the height or altitude is ${\displaystyle h=a\sin \gamma }$. Substituting this in the area formula ${\displaystyle T={\tfrac {1}{2}}bh}$ derived above, the area of the triangle can be expressed as:

${\displaystyle T={\tfrac {1}{2}}ab\sin \gamma ={\tfrac {1}{2}}bc\sin \alpha ={\tfrac {1}{2}}ca\sin \beta }$

Where ${\displaystyle a}$ is the line BC, ${\displaystyle b}$ is the line AC, ${\displaystyle c}$ is the line AB, ${\displaystyle \alpha }$ is the interior angle at A, ${\displaystyle \beta }$ is the interior angle at B, ${\displaystyle \gamma }$ is the interior angle at C.

Furthermore, since ${\displaystyle \sin \alpha =\sin(\pi -\alpha )=\sin(\beta +\gamma )}$, and similarly for the other two angles:

${\displaystyle T={\tfrac {1}{2}}ab\sin(\alpha +\beta )={\tfrac {1}{2}}bc\sin(\beta +\gamma )={\tfrac {1}{2}}ca\sin(\gamma +\alpha )}$

Since ${\displaystyle \cot \gamma =-\cot(\pi -\gamma )=-\cot(\alpha +\beta )}$, and similarly for the other two angles:

${\displaystyle T={\frac {b^{2}}{2(\cot \alpha -\cot(\alpha +\beta ))}}={\frac {b^{2}\sin \alpha \sin(\alpha +\beta )}{2\sin \beta }},}$

and analogously if the known side is ${\displaystyle a}$ or ${\displaystyle c}$.

${\displaystyle T={\frac {a^{2}}{2(\cot \beta +\cot \gamma )}}={\frac {a^{2}\sin \beta \sin \gamma }{2\sin(\beta +\gamma )}},}$

and analogously if the known side is ${\displaystyle b}$ or ${\displaystyle c}$.^[9]

A triangle's shape is uniquely determined by the lengths of the sides, so its metrical properties, including area, can be described in terms of those lengths. By Heron's formula,

${\displaystyle T={\sqrt {s(s-a)(s-b)(s-c)}}}$

where ${\textstyle s={\tfrac {1}{2}}(a+b+c)}$ is the semiperimeter, or half of the triangle's perimeter.

Three other equivalent ways of writing Heron's formula are

${\displaystyle {\begin{aligned}T&={\tfrac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}\\[5mu]&={\tfrac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}\\[5mu]&={\tfrac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}.\end{aligned}}}$

Three formulas have the same structure as Heron's formula but are expressed in terms of different variables. First, denoting the medians from sides ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ respectively as ${\displaystyle m_{a}}$, ${\displaystyle m_{b}}$, and ${\displaystyle m_{c}}$ and their semi-sum ${\displaystyle \sigma =(m_{a}+m_{b}+m_{c})/2}$, we have^[10]

${\displaystyle T={\tfrac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}.}$

Next, denoting the altitudes from sides ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ respectively as ${\displaystyle h_{a}}$, ${\displaystyle h_{b}}$, and ${\displaystyle h_{c}}$, and denoting the semi-sum of the reciprocals of the altitudes as ${\displaystyle H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2}$ we have^[11]

${\displaystyle T^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}.}$

And denoting the semi-sum of the angles' sines as ${\displaystyle S=(\sin \alpha +\sin \beta +\sin \gamma )/2}$, we have^[12]

${\displaystyle T=D^{2}{\sqrt {S(S-\sin \alpha )(S-\sin \beta )(S-\sin \gamma )}}}$

where ${\displaystyle D}$ is the diameter of the circumcircle: ${\displaystyle D={\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}.}$

The area of triangle ABC is half of the area of a parallelogram:

${\displaystyle T={\tfrac {1}{2}}{\bigl \|}(\mathbf {b} -\mathbf {a} )\wedge (\mathbf {c} -\mathbf {a} ){\bigr \|}={\tfrac {1}{2}}{\bigl \|}\mathbf {a} \wedge \mathbf {b} +\mathbf {b} \wedge \mathbf {c} +\mathbf {c} \wedge \mathbf {a} {\bigr \|},}$

where ⁠${\displaystyle \mathbf {a} }$⁠, ⁠${\displaystyle \mathbf {b} }$⁠, and ⁠${\displaystyle \mathbf {c} }$⁠ are vectors to the triangle's vertices from any arbitrary origin point, so that ⁠${\displaystyle \mathbf {b} -\mathbf {a} }$⁠ and ⁠${\displaystyle \mathbf {c} -\mathbf {a} }$⁠ are the translation vectors from vertex ⁠${\displaystyle A}$⁠ to each of the others, and ⁠${\displaystyle \wedge }$⁠ is the wedge product. If vertex ⁠${\displaystyle A}$⁠ is taken to be the origin, this simplifies to ${\displaystyle {\tfrac {1}{2}}\|\mathbf {b} \wedge \mathbf {c} \|}$.

The oriented relative area of a parallelogram in any affine space, a type of bivector, is defined as ⁠${\displaystyle \mathbf {u} \wedge \mathbf {v} }$⁠ where ⁠${\displaystyle \mathbf {u} }$⁠ and ⁠${\displaystyle \mathbf {v} }$⁠ are translation vectors from one vertex of the parallelogram to each of the two adjacent vertices. In Euclidean space, the magnitude of this bivector is a well-defined scalar number representing the area of the parallelogram. (For vectors in three-dimensional space, the bivector-valued wedge product has the same magnitude as the vector-valued cross product, but unlike the cross product, which is only defined in three-dimensional Euclidean space, the wedge product is well-defined in an affine space of any dimension.)

The area of triangle ABC can also be expressed in terms of dot products. Taking vertex ⁠${\displaystyle A}$⁠ to be the origin and calling translation vectors to the other vertices ⁠${\displaystyle \mathbf {b} }$⁠ and ⁠${\displaystyle \mathbf {c} }$⁠,

${\displaystyle T={\tfrac {1}{2}}{\sqrt {\mathbf {b} ^{2}\mathbf {c} ^{2}-(\mathbf {b} \cdot \mathbf {c} )^{2}}},}$

where for any Euclidean vector ${\displaystyle \mathbf {v} ^{2}=\|\mathbf {v} \|^{2}=\mathbf {v} \cdot \mathbf {v} }$.^[13] This area formula can be derived from the previous one using the elementary vector identity ${\displaystyle \mathbf {u} ^{2}\mathbf {v} ^{2}=(\mathbf {u} \cdot \mathbf {v} )^{2}+\|\mathbf {u} \wedge \mathbf {v} \|^{2}}$.

In two-dimensional Euclidean space, for a vector ⁠${\displaystyle \mathbf {b} }$⁠ with coordinates ⁠${\displaystyle (x_{B},y_{B})}$⁠ and vector ⁠${\displaystyle \mathbf {c} }$⁠ with coordinates ⁠${\displaystyle (x_{C},y_{C})}$⁠, the magnitude of the wedge product is

${\displaystyle \|\mathbf {b} \wedge \mathbf {c} \|=|x_{B}y_{C}-x_{C}y_{B}|.}$

(See the following section.)

If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (x_B, y_B) and C = (x_C, y_C), then the area can be computed as 1⁄2 times the absolute value of the determinant

${\displaystyle T={\tfrac {1}{2}}\left|\det {\begin{pmatrix}x_{B}&x_{C}\\y_{B}&y_{C}\end{pmatrix}}\right|={\tfrac {1}{2}}|x_{B}y_{C}-x_{C}y_{B}|.}$

For three general vertices, the equation is:

${\displaystyle T={\tfrac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right|={\tfrac {1}{2}}{\big |}x_{A}y_{B}-x_{A}y_{C}+x_{B}y_{C}-x_{B}y_{A}+x_{C}y_{A}-x_{C}y_{B}{\big |},}$

which can be written as

${\displaystyle T={\tfrac {1}{2}}{\big |}(x_{A}-x_{C})(y_{B}-y_{A})-(x_{A}-x_{B})(y_{C}-y_{A}){\big |}.}$

If the points are labeled sequentially in the counterclockwise direction, the above determinant expressions are positive and the absolute value signs can be omitted.^[14] The above formula is known as the shoelace formula or the surveyor's formula.

If we locate the vertices in the complex plane and denote them in counterclockwise sequence as a = x_A + y_Ai, b = x_B + y_Bi, and c = x_C + y_Ci, and denote their complex conjugates as ${\displaystyle {\bar {a}}}$, ${\displaystyle {\bar {b}}}$, and ${\displaystyle {\bar {c}}}$, then the formula

${\displaystyle T={\frac {i}{4}}{\begin{vmatrix}a&{\bar {a}}&1\\b&{\bar {b}}&1\\c&{\bar {c}}&1\end{vmatrix}}}$

is equivalent to the shoelace formula.

In three dimensions, the area of a general triangle A = (x_A, y_A, z_A), B = (x_B, y_B, z_B) and C = (x_C, y_C, z_C) is the Pythagorean sum of the areas of the respective projections on the three principal planes (i.e. x = 0, y = 0 and z = 0):

${\displaystyle T={\tfrac {1}{2}}{\sqrt {{\begin{vmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{vmatrix}}^{2}+{\begin{vmatrix}y_{A}&y_{B}&y_{C}\\z_{A}&z_{B}&z_{C}\\1&1&1\end{vmatrix}}^{2}+{\begin{vmatrix}z_{A}&z_{B}&z_{C}\\x_{A}&x_{B}&x_{C}\\1&1&1\end{vmatrix}}^{2}}}.}$

The area within any closed curve, such as a triangle, is given by the line integral around the curve of the algebraic or signed distance of a point on the curve from an arbitrary oriented straight line L. Points to the right of L as oriented are taken to be at negative distance from L, while the weight for the integral is taken to be the component of arc length parallel to L rather than arc length itself.

This method is well suited to computation of the area of an arbitrary polygon. Taking L to be the x-axis, the line integral between consecutive vertices (x_i,y_i) and (x_i+1,y_i+1) is given by the base times the mean height, namely (x_i+1 − x_i)(y_i + y_i+1)/2. The sign of the area is an overall indicator of the direction of traversal, with negative area indicating counterclockwise traversal. The area of a triangle then falls out as the case of a polygon with three sides.

While the line integral method has in common with other coordinate-based methods the arbitrary choice of a coordinate system, unlike the others it makes no arbitrary choice of vertex of the triangle as origin or of side as base. Furthermore, the choice of coordinate system defined by L commits to only two degrees of freedom rather than the usual three, since the weight is a local distance (e.g. x_i+1 − x_i in the above) whence the method does not require choosing an axis normal to L.

When working in polar coordinates it is not necessary to convert to Cartesian coordinates to use line integration, since the line integral between consecutive vertices (r_i,θ_i) and (r_i+1,θ_i+1) of a polygon is given directly by r_ir_i+1sin(θ_i+1 − θ_i)/2. This is valid for all values of θ, with some decrease in numerical accuracy when |θ| is many orders of magnitude greater than π. With this formulation negative area indicates clockwise traversal, which should be kept in mind when mixing polar and cartesian coordinates. Just as the choice of y-axis (x = 0) is immaterial for line integration in cartesian coordinates, so is the choice of zero heading (θ = 0) immaterial here.

See Pick's theorem for a technique for finding the area of any arbitrary lattice polygon (one drawn on a grid with vertically and horizontally adjacent lattice points at equal distances, and with vertices on lattice points).

The theorem states:

${\displaystyle T=I+{\tfrac {1}{2}}B-1}$

where ${\displaystyle I}$ is the number of internal lattice points and B is the number of lattice points lying on the border of the polygon.

Numerous other area formulas exist, such as

${\displaystyle T=r\cdot s,}$

where r is the inradius, and s is the semiperimeter (in fact, this formula holds for all tangential polygons), and^{[15]: Lemma 2}

${\displaystyle T=r_{a}(s-a)=r_{b}(s-b)=r_{c}(s-c)}$

where ${\displaystyle r_{a},\,r_{b},\,r_{c}}$ are the radii of the excircles tangent to sides a, b, c respectively.

We also have

${\displaystyle T={\tfrac {1}{2}}D^{2}(\sin \alpha )(\sin \beta )(\sin \gamma )}$

and^[16]

${\displaystyle T={\frac {abc}{2D}}={\frac {abc}{4R}}}$

for circumdiameter D; and^[17]

${\displaystyle T={\tfrac {1}{4}}(\tan \alpha )(b^{2}+c^{2}-a^{2})}$

for angle α ≠ 90°.

The area can also be expressed as^[18]

${\displaystyle T={\sqrt {rr_{a}r_{b}r_{c}}}.}$

In 1885, Baker^[19] gave a collection of over a hundred distinct area formulas for the triangle. These include:

${\displaystyle T={\tfrac {1}{2}}{\sqrt[{3}]{abch_{a}h_{b}h_{c}}},}$

${\displaystyle T={\tfrac {1}{2}}{\sqrt {abh_{a}h_{b}}},}$

${\displaystyle T={\frac {a+b}{2(h_{a}^{-1}+h_{b}^{-1})}},}$

${\displaystyle T={\frac {Rh_{b}h_{c}}{a}}}$

for circumradius (radius of the circumcircle) R, and

${\displaystyle T={\frac {h_{a}h_{b}}{2\sin \gamma }}.}$

The area T of any triangle with perimeter p satisfies

${\displaystyle T\leq {\tfrac {p^{2}}{12{\sqrt {3}}}},}$

with equality holding if and only if the triangle is equilateral.^{[20][21]: 657}

Other upper bounds on the area T are given by^{[22]: p.290}

${\displaystyle 4{\sqrt {3}}T\leq a^{2}+b^{2}+c^{2}}$

and

${\displaystyle 4{\sqrt {3}}T\leq {\frac {9abc}{a+b+c}},}$

both again holding if and only if the triangle is equilateral.

There are infinitely many lines that bisect the area of a triangle.^[23] Three of them are the medians, which are the only area bisectors that go through the centroid. Three other area bisectors are parallel to the triangle's sides.

Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter. There can be one, two, or three of these for any given triangle.

• Area of a circle
• Congruence of triangles