String vibration

The velocity of propagation of a wave in a string (${\displaystyle v}$) is proportional to the square root of the force of tension of the string (${\displaystyle T}$) and inversely proportional to the square root of the linear density (${\displaystyle \mu }$) of the string:

${\displaystyle v={\sqrt {T \over \mu }}.}$

This relationship was discovered by Vincenzo Galilei in the late 1500s. ^{[citation needed]}

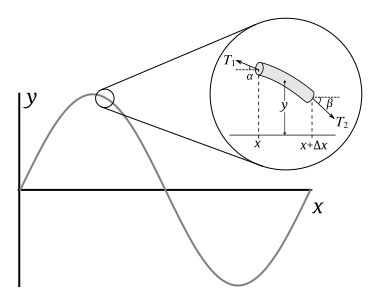
Source:^[1]

Let ${\displaystyle \Delta x}$ be the length of a piece of string, ${\displaystyle m}$ its mass, and ${\displaystyle \mu }$ its linear density. If angles ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are small, then the horizontal components of tension on either side can both be approximated by a constant ${\displaystyle T}$, for which the net horizontal force is zero. Accordingly, using the small angle approximation, the horizontal tensions acting on both sides of the string segment are given by

${\displaystyle T_{1x}=T_{1}\cos(\alpha )\approx T.}$

${\displaystyle T_{2x}=T_{2}\cos(\beta )\approx T.}$

From Newton's second law for the vertical component, the mass (which is the product of its linear density and length) of this piece times its acceleration, ${\displaystyle a}$, will be equal to the net force on the piece:

${\displaystyle \Sigma F_{y}=T_{1y}-T_{2y}=-T_{2}\sin(\beta )+T_{1}\sin(\alpha )=\Delta ma\approx \mu \Delta x{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Dividing this expression by ${\displaystyle T}$ and substituting the first and second equations obtains (we can choose either the first or the second equation for ${\displaystyle T}$, so we conveniently choose each one with the matching angle ${\displaystyle \beta }$ and ${\displaystyle \alpha }$)

${\displaystyle -{\frac {T_{2}\sin(\beta )}{T_{2}\cos(\beta )}}+{\frac {T_{1}\sin(\alpha )}{T_{1}\cos(\alpha )}}=-\tan(\beta )+\tan(\alpha )={\frac {\mu \Delta x}{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

According to the small-angle approximation, the tangents of the angles at the ends of the string piece are equal to the slopes at the ends, with an additional minus sign due to the definition of ${\displaystyle \alpha }$ and ${\displaystyle \beta }$. Using this fact and rearranging provides

${\displaystyle {\frac {1}{\Delta x}}\left(\left.{\frac {\partial y}{\partial x}}\right|^{x+\Delta x}-\left.{\frac {\partial y}{\partial x}}\right|^{x}\right)={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

In the limit that ${\displaystyle \Delta x}$ approaches zero, the left hand side is the definition of the second derivative of ${\displaystyle y}$,

${\displaystyle {\frac {\partial ^{2}y}{\partial x^{2}}}={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

this equation is known as the wave equation, and the coefficient of the second time derivative term is equal to ${\displaystyle {\frac {1}{v^{2}}}}$; thus

${\displaystyle v={\sqrt {T \over \mu }},}$

Where ${\displaystyle v}$ is the speed of propagation of the wave in the string. However, this derivation is only valid for small amplitude vibrations; for those of large amplitude, ${\displaystyle \Delta x}$ is not a good approximation for the length of the string piece, the horizontal component of tension is not necessarily constant. The horizontal tensions are not well approximated by ${\displaystyle T}$.

Once the speed of propagation is known, the frequency of the sound produced by the string can be calculated. The speed of propagation of a wave is equal to the wavelength ${\displaystyle \lambda }$ divided by the period ${\displaystyle \tau }$, or multiplied by the frequency ${\displaystyle f}$:

${\displaystyle v={\frac {\lambda }{\tau }}=\lambda f.}$

If the length of the string is ${\displaystyle L}$, the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so ${\displaystyle L}$ is half of the wavelength of the fundamental harmonic. Hence one obtains Mersenne's laws:

${\displaystyle f={\frac {v}{2L}}={1 \over 2L}{\sqrt {T \over \mu }}}$

where ${\displaystyle T}$ is the tension (in Newtons), ${\displaystyle \mu }$ is the linear density (that is, the mass per unit length), and ${\displaystyle L}$ is the length of the vibrating part of the string. Therefore:

• the shorter the string, the higher the frequency of the fundamental
• the higher the tension, the higher the frequency of the fundamental
• the lighter the string, the higher the frequency of the fundamental

Moreover, if we take the nth harmonic as having a wavelength given by ${\displaystyle \lambda _{n}=2L/n}$, then we easily get an expression for the frequency of the nth harmonic:

${\displaystyle f_{n}={\frac {nv}{2L}}}$

And for a string under a tension T with linear density ${\displaystyle \mu }$, then

${\displaystyle f_{n}={\frac {n}{2L}}{\sqrt {\frac {T}{\mu }}}}$

One can see the waveforms on a vibrating string if the frequency is low enough and the vibrating string is held in front of a CRT screen such as one of a television or a computer (not of an analog oscilloscope). This effect is called the stroboscopic effect, and the rate at which the string seems to vibrate is the difference between the frequency of the string and the refresh rate of the screen. The same can happen with a fluorescent lamp, at a rate that is the difference between the frequency of the string and the frequency of the alternating current. (If the refresh rate of the screen equals the frequency of the string or an integer multiple thereof, the string will appear still but deformed.) In daylight and other non-oscillating light sources, this effect does not occur and the string appears still but thicker, and lighter or blurred, due to persistence of vision.

A similar but more controllable effect can be obtained using a stroboscope. This device allows matching the frequency of the xenon flash lamp to the frequency of vibration of the string. In a dark room, this clearly shows the waveform. Otherwise, one can use bending or, perhaps more easily, by adjusting the machine heads, to obtain the same, or a multiple, of the AC frequency to achieve the same effect. For example, in the case of a guitar, the 6th (lowest pitched) string pressed to the third fret gives a G at 97.999 Hz. A slight adjustment can alter it to 100 Hz, exactly one octave above the alternating current frequency in Europe and most countries in Africa and Asia, 50 Hz. In most countries of the Americas—where the AC frequency is 60 Hz—altering A# on the fifth string, first fret from 116.54 Hz to 120 Hz produces a similar effect.

• Fretted instruments
• Musical acoustics
• Vibrations of a circular drum
• Melde's experiment
• 3rd bridge (harmonic resonance based on equal string divisions)
• String resonance
• Reflection phase change
• Hilbert space