Hubbry Logo
Curved mirrorCurved mirrorMain
Open search
Curved mirror
Community hub
Curved mirror
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Curved mirror
Curved mirror
Curved mirror
View on Wikipedia
from Wikipedia
Reflections in a convex mirror. The photographer is seen reflected at top right

A curved mirror is a mirror with a curved reflecting surface. The surface may be either convex (bulging outward) or concave (recessed inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems, like spherical lenses, suffer from spherical aberration. Distorting mirrors are used for entertainment. They have convex and concave regions that produce deliberately distorted images. They also provide highly magnified or highly diminished (smaller) images when the object is placed at certain distances. Convex mirrors are often used for security and safety in shops and parking lots.

Convex mirrors

[edit]
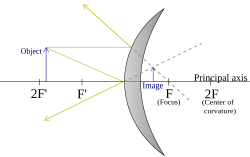
A convex mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc.

A convex mirror or diverging mirror is a curved mirror in which the reflective surface bulges towards the light source.[1] Convex mirrors reflect light outwards, therefore they are not used to focus light. Such mirrors always form a virtual image, since the focal point (F) and the centre of curvature (2F) are both imaginary points "inside" the mirror, that cannot be reached. As a result, images formed by these mirrors cannot be projected on a screen, since the image is inside the mirror. The image is smaller than the object, but gets larger as the object approaches the mirror.

A collimated (parallel) beam of light diverges (spreads out) after reflection from a convex mirror, since the normal to the surface differs at each spot on the mirror.

Uses

[edit]
Convex mirror lets motorists see around a corner.
Detail of the convex mirror in the Arnolfini Portrait

The passenger-side mirror on a car is typically a convex mirror. In some countries, these are labeled with the safety warning "Objects in mirror are closer than they appear", to warn the driver of the convex mirror's distorting effects on distance perception. Convex mirrors are preferred in vehicles because they give an upright (not inverted), though diminished (smaller), image and because they provide a wider field of view as they are curved outwards.

These mirrors are often found in the hallways of various buildings (commonly known as "hallway safety mirrors"), including hospitals, hotels, schools, stores, and apartment buildings. They are usually mounted on a wall or ceiling where hallways intersect each other, or where they make sharp turns. They are useful for people to look at any obstruction they will face on the next hallway or after the next turn. They are also used on roads, driveways, and alleys to provide safety for road users where there is a lack of visibility, especially at curves and turns.[2]

Convex mirrors are used in some automated teller machines as a simple and handy security feature, allowing the users to see what is happening behind them. Similar devices are sold to be attached to ordinary computer monitors. Convex mirrors make everything seem smaller but cover a larger area of surveillance.

Round convex mirrors called Oeil de Sorcière (French for "sorcerer's eye") were a popular luxury item from the 15th century onwards, shown in many depictions of interiors from that time.[3] With 15th century technology, it was easier to make a regular curved mirror (from blown glass) than a perfectly flat one. They were also known as "bankers' eyes" because their wide field of vision was useful for security. Famous examples in art include the Arnolfini Portrait by Jan van Eyck and the left wing of the Werl Altarpiece by Robert Campin.[4]

Image

[edit]
A virtual image in a Christmas bauble.

The image on a convex mirror is always virtual (rays haven't actually passed through the image; their extensions do, like in a regular mirror), diminished (smaller), and upright (not inverted). As the object gets closer to the mirror, the image gets larger, until approximately the size of the object, when it touches the mirror. As the object moves away, the image diminishes in size and gets gradually closer to the focus, until it is reduced to a point in the focus when the object is at an infinite distance. These features make convex mirrors very useful: since everything appears smaller in the mirror, they cover a wider field of view than a normal plane mirror, so useful for looking at cars behind a driver's car on a road, watching a wider area for surveillance, etc.

Effect on image of object's position relative to mirror focal point (convex)
Object's position (S),
focal point (F) 		Image Diagram
  • Virtual
  • Upright
  • Reduced (diminished/smaller)

Concave mirrors

[edit]
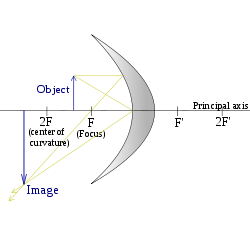
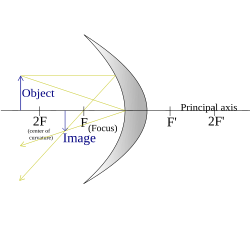
A concave mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc.

A concave mirror, or converging mirror, has a reflecting surface that is recessed inward (away from the incident light). Concave mirrors reflect light inward to one focal point. They are used to focus light. Unlike convex mirrors, concave mirrors show different image types depending on the distance between the object and the mirror.

The mirrors are called "converging mirrors" because they tend to collect light that falls on them, refocusing parallel incoming rays toward a focus. This is because the light is reflected at different angles at different spots on the mirror as the normal to the mirror surface differs at each spot.

Uses

[edit]

Concave mirrors are used in reflecting telescopes.[5] They are also used to provide a magnified image of the face for applying make-up or shaving.[6] In illumination applications, concave mirrors are used to gather light from a small source and direct it outward in a beam as in torches, headlamps and spotlights, or to collect light from a large area and focus it into a small spot, as in concentrated solar power. Concave mirrors are used to form optical cavities, which are important in laser construction. Some dental mirrors use a concave surface to provide a magnified image. The mirror landing aid system of modern aircraft carriers also uses a concave mirror.

Image

[edit]
Effect on image of object's position relative to mirror focal point (concave)
Object's position (S),
focal point (F) 		Nature of Image Diagram

(Object between focal point and mirror)
  • Virtual
  • Upright
  • Magnified (larger)

(Object at focal point)
  • Reflected rays are parallel and never meet, so no image is formed.
  • In the limit where S approaches F, the image distance approaches infinity, and the image can be either real or virtual and either upright or inverted depending on whether S approaches F from its left or right side.

(Object between focus and centre of curvature)
  • Real image
  • Inverted (vertically)
  • Magnified (larger)

(Object at centre of curvature)
  • Real image
  • Inverted (vertically)
  • Same size
  • Image formed at centre of curvature

(Object beyond centre of curvature)
  • Real image
  • Inverted (vertically)
  • Reduced (diminished/smaller)
  • As the distance of the object increases, the image asymptotically approaches the focal point
  • In the limit where S approaches infinity, the image size approaches zero as the image approaches F

Mirror shape

[edit]

Most curved mirrors have a spherical profile.[7] These are the simplest to make, and it is the best shape for general-purpose use. Spherical mirrors, however, suffer from spherical aberration—parallel rays reflected from such mirrors do not focus to a single point. For parallel rays, such as those coming from a very distant object, a parabolic reflector can do a better job. Such a mirror can focus incoming parallel rays to a much smaller spot than a spherical mirror can. A toroidal reflector is a form of parabolic reflector which has a different focal distance depending on the angle of the mirror.

Analysis

[edit]

Mirror equation, magnification, and focal length

[edit]

The Gaussian mirror equation, also known as the mirror and lens equation, relates the object distance and image distance to the focal length :[2]

.

The sign convention used here is that the focal length is positive for concave mirrors and negative for convex ones, and and are positive when the object and image are in front of the mirror, respectively. (They are positive when the object or image is real.)[2]

For convex mirrors, if one moves the term to the right side of the equation to solve for , then the result is always a negative number, meaning that the image distance is negative—the image is virtual, located "behind" the mirror. This is consistent with the behavior described above.

For concave mirrors, whether the image is virtual or real depends on how large the object distance is compared to the focal length. If the term is larger than the term, then is positive and the image is real. Otherwise, the term is negative and the image is virtual. Again, this validates the behavior described above.

The magnification of a mirror is defined as the height of the image divided by the height of the object:

.

By convention, if the resulting magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down).

Ray tracing

[edit]
Main article: Ray tracing (physics)

The image location and size can also be found by graphical ray tracing, as illustrated in the figures above. A ray drawn from the top of the object to the mirror surface vertex (where the optical axis meets the mirror) will form an angle with the optical axis. The reflected ray has the same angle to the axis, but on the opposite side (See Specular reflection).

A second ray can be drawn from the top of the object, parallel to the optical axis. This ray is reflected by the mirror and passes through its focal point. The point at which these two rays meet is the image point corresponding to the top of the object. Its distance from the optical axis defines the height of the image, and its location along the axis is the image location. The mirror equation and magnification equation can be derived geometrically by considering these two rays. A ray that goes from the top of the object through the focal point can be considered instead. Such a ray reflects parallel to the optical axis and also passes through the image point corresponding to the top of the object.

Ray transfer matrix of spherical mirrors

[edit]
Further information: Ray transfer matrix analysis

The mathematical treatment is done under the paraxial approximation, meaning that under the first approximation a spherical mirror is a parabolic reflector. The ray matrix of a concave spherical mirror is shown here. The element of the matrix is , where is the focal point of the optical device.

Boxes 1 and 3 feature summing the angles of a triangle and comparing to π radians (or 180°). Box 2 shows the Maclaurin series of up to order 1. The derivations of the ray matrices of a convex spherical mirror and a thin lens are very similar.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Curved mirror

View on Grokipedia
from Grokipedia
A curved mirror is a reflecting surface with a curvature, typically spherical, that deviates from the flat plane of a standard mirror, enabling it to focus or diverge light rays according to the laws of reflection. These mirrors are classified into two primary types: concave mirrors, which curve inward like the inside of a sphere and converge parallel rays to a focal point, and convex mirrors, which curve outward like the outside of a sphere and cause parallel rays to diverge as if emanating from a virtual focal point behind the surface. The focal length ff of a curved mirror is determined by half the radius of curvature RR, given by the formula f=R/2f = R/2, with concave mirrors having a positive focal length and convex mirrors a negative one./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.03%3A_Spherical_Mirrors) In , curved mirrors form through ray tracing, where principal rays—such as those parallel to the or passing through the focal point—follow predictable paths to locate the position and determine its nature as real (formed by actual ray convergence) or virtual (formed by apparent ray ). For concave mirrors, can be real and inverted when the object is beyond the focal point, or virtual and upright when closer, allowing greater than one; convex mirrors always produce virtual, upright, and diminished , providing a wider ./University_Physics_III_-Optics_and_Modern_Physics()/02%3A_Geometric_Optics_and_Image_Formation/2.03%3A_Spherical_Mirrors) The mirror equation, 1f=1do+1di\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}, where dod_o is the object distance and did_i the distance, quantifies these relationships, while m=−didom = -\frac{d_i}{d_o} describes size and orientation. Curved mirrors find extensive applications across scientific, industrial, and everyday contexts due to their light-manipulating properties. Concave mirrors are used in telescopes and microscopes to gather and focus light for magnified observation, in solar concentrators to harness sunlight for generation, and in devices like dental mirrors for detailed examination. Convex mirrors, valued for their broad viewing angle, appear in rearview and side mirrors to enhance visibility, as well as in systems for monitoring large areas in stores and hallways. Additionally, specialized curved mirrors, such as parabolic ones, minimize in high-precision like dishes and headlights.

Fundamentals of Curved Mirrors

Definition and Basic Principles

A curved mirror is a reflective surface with a that deviates from flatness, causing incident rays to converge or diverge upon reflection, unlike the parallel reflection produced by a . These mirrors are typically portions of a , with the reflecting surface either on the inner (concave) or outer (convex) side, enabling applications in by altering the paths of rays based on the surface's . The legend attributes early use of curved mirrors to in the BCE, who reportedly employed concave mirrors as burning devices to focus sunlight during the siege of Syracuse by concentrating solar rays to ignite invading ships. Significant advancements occurred in the 17th century, particularly through Isaac Newton's development of the in 1668, which utilized a concave mirror to gather and focus light, addressing issues in refractive telescopes. The fundamental principle governing reflection in curved mirrors is the law of reflection, which states that the incident ray, the reflected ray, and to the surface at the point of incidence all lie in the same plane, with of incidence equaling of reflection. In curved mirrors, this law applies locally at each point on the surface, where the normal is to the at that point; the curvature causes rays parallel to the principal axis—a line passing through the of and the mirror's vertex (or pole, the geometric where the axis meets the surface)—to reflect toward or away from a common focal point, qualitatively bending the ray paths to either converge (in concave mirrors) or diverge (in convex mirrors). The of is the central point of from which the mirror is derived, defining the mirror's overall shape. In contrast to plane mirrors, which produce virtual, upright images of the same size as the object and located at an equal distance behind the mirror, curved mirrors modify image properties such that the size, orientation, and position vary depending on the object's distance and the mirror's curvature radius. This deviation arises because the non-uniform normals across the curved surface redirect rays non-parallelly, allowing for focused or spread-out reflections that plane mirrors cannot achieve.

Spherical Mirror Geometry

A spherical mirror consists of a portion of a sphere's surface that acts as a reflector, approximating the behavior of more complex curved mirrors in basic optical analysis. The reflecting surface can face inward toward the center of the sphere, forming a concave mirror, or outward away from the center, forming a convex mirror. The RR is defined as the distance from the mirror's vertex—the point where the mirror intersects the principal axis—to the center of curvature, which is the center of the sphere from which the mirror segment is derived. In the standard Cartesian for , RR is positive when the center of curvature lies on the same side as the incident light (for concave mirrors) and negative when it lies on the opposite side (for convex mirrors). The focal length ff, which locates the focal point where parallel rays along the principal axis converge or appear to diverge after reflection, is related to the by the equation f=R2.f = \frac{R}{2}. This relationship arises from the geometry of reflection on a spherical surface: for rays parallel to the principal axis, the law of reflection ensures they intersect at a point halfway between the vertex and the center of curvature. Analysis of spherical mirrors relies on the paraxial approximation, which assumes incident rays make small angles with the principal axis, enabling simplified trigonometric relations and the neglect of higher-order terms in the reflection equations. A key limitation of this approximation in spherical mirrors is spherical aberration, where rays farther from the principal axis focus at different points than paraxial rays, resulting in imperfect image formation.

Types of Curved Mirrors

Convex Mirrors

A convex mirror features a reflective surface that curves outward, bulging toward the incoming and thereby acting as a diverging mirror. This outward distinguishes it from concave mirrors, where the surface indents inward, and results in the reflection of light rays away from a common point. The mirror's is characterized by a positive measured from the vertex to the center of curvature behind the surface. Upon reflection from a convex mirror, parallel incident rays diverge in directions that, when traced backward, appear to originate from a virtual focal point situated behind the mirror. This diverging behavior contrasts with the converging action of concave mirrors and ensures that no can form in front of the mirror. The focal point lies at half the from the mirror's vertex. In standard Cartesian sign conventions for , the focal length ff and RR of a convex mirror are assigned negative values, reflecting the virtual nature of the focal point relative to incident light from the left. This convention facilitates consistent calculations across mirror types, where f=R/2f = R/2. Convex mirrors offer a wider of reflection compared to flat mirrors, enabling over a broader field without the need for head movement and thereby minimizing obscured areas in the view. They are commonly constructed using silvered substrates with protective coatings or polished metal surfaces to ensure durability and high reflectivity, with typical radii of ranging from 10 to 50 cm for and applications.

Concave Mirrors

A concave mirror possesses an inward-curving reflective surface that faces toward the incident , enabling it to act as a converging optical element. This causes incoming rays to bend inward upon reflection, distinguishing it from flat or outward-curving mirrors. The reflective coating is applied to the inner, concave side of the surface, which is typically spherical in basic designs. In a concave mirror, rays of light incident parallel to the principal axis—the line passing through the mirror's center and perpendicular to its surface—converge after reflection to a real focal point situated in front of the mirror. This focal point lies midway along the radius to the center of , the point on the principal axis where of which the mirror is a segment would have its center. The converging nature arises from the of the curved surface, which directs parallel rays toward a common intersection. Concave mirrors can produce enlarged real images under specific object placements, such as when the object is positioned between the focal point and the center of . In standard sign conventions, the and for concave mirrors are assigned positive values, reflecting their converging behavior relative to the incident light direction. This convention facilitates consistent calculations in optical analysis, treating the mirror's front side as the reference for positive distances. For many optical instruments and setups, the of concave mirrors typically ranges from 20 to 100 cm, which proportionally influences the since it is half the radius. Such dimensions are common in educational kits and small-scale devices, balancing compactness with effective light convergence.

Non-Spherical Mirrors

Spherical mirrors suffer from , where peripheral rays parallel to the focus at different points from paraxial rays, leading to blurred images and reduced sharpness for extended objects. This limitation arises because the spherical surface approximates a only near the axis, causing off-axis rays to converge short of the paraxial focal point. To address these issues, non-spherical mirrors employ conic section profiles that eliminate for specific ray configurations. Parabolic mirrors, formed as paraboloids of revolution, direct all parallel incident rays—such as those from distant sources—precisely to a single focal point without aberration, making them superior for applications requiring sharp focus. This property stems from the parabola's , where the reflective surface ensures equal path lengths for rays to the focus after reflection. Elliptical mirrors, shaped from ellipsoid segments, possess two foci and reflect rays originating from one focus directly to the other, enabling efficient transfer in compact systems without for that configuration. Hyperbolic mirrors, conversely, focus diverging rays from a virtual focus to a real one, often used as secondary elements to correct off-axis aberrations in composite designs like Cassegrain telescopes. The development of parabolic mirrors traces to the 17th century, when James Gregory proposed a with a parabolic primary to avoid , predating practical implementations. Laurent Cassegrain later described a configuration pairing a parabolic primary with a hyperbolic secondary, advancing folded optical paths for telescopes. In modern contexts, parabolic mirrors underpin satellite dishes, where they concentrate microwave signals from geostationary satellites onto a receiver at the focal point for amplified reception.
Mirror TypeSpherical Aberration for Parallel Incident RaysKey Advantage
SphericalPresent; peripheral rays focus short of paraxial pointSimple fabrication
ParabolicAbsent; all rays converge at single focal pointAberration-free focusing for collimated light

Image Formation

Images in Convex Mirrors

Convex mirrors, being diverging mirrors, produce images by spreading out reflected rays, resulting in the appearance of an behind the reflecting surface. The images formed are always virtual, meaning the reflected rays do not actually converge but appear to diverge from a point behind the mirror, and they cannot be projected onto a screen. Regardless of the object's position, the image location remains behind the mirror and between the mirror surface and the focal point, providing a consistent virtual placement. These images exhibit specific properties: they are upright, maintaining the same orientation as the object, and reduced in size, or demagnified, compared to the actual object. This demagnification contributes to a wider field of view, allowing observation of a broader area than with a flat mirror. No real images are possible in convex mirrors, as the diverging reflection prevents ray convergence in front of the mirror. The characteristics of the image vary qualitatively with object position. For an object at , such as a distant source, the image forms at the focal point behind the mirror. As the object moves closer to the mirror, the virtual shifts nearer to the mirror surface while remaining smaller and upright, though the size reduction becomes less pronounced for very close objects. To locate the image qualitatively, ray diagrams employ two principal rays originating from the top of the object. The first ray travels parallel to the principal axis and reflects such that it appears to come from the focal point behind the mirror. The second ray heads toward the center of curvature and reflects back along the same path due to the normal incidence at that point. The point where these reflected rays (or their extensions) intersect behind the mirror determines the image position, illustrating its virtual, upright, and diminished nature. In modern applications like security mirrors used in retail stores, the minified images from convex mirrors enable broader coverage, allowing monitors to view larger areas with the inherent providing a panoramic but scaled-down perspective.

Images in Concave Mirrors

In concave mirrors, which converge parallel rays of to a focal point, the nature of the formed image depends on the object's position relative to the focal point (F) and the center of curvature (C), where the is half the . When the object is placed beyond C, the image is real, inverted, and diminished, located between F and C. As the object moves closer between C and F, the image becomes real, inverted, and magnified, positioned beyond C. Specific cases illustrate this variability further. If the object is at C, the image forms at the same position, real, inverted, and the same size as the object. For an object at F, the reflected rays become parallel, forming a at . When the object is between F and the mirror's pole (vertex), the image is virtual, upright, and enlarged, appearing behind the mirror. For example, for a concave mirror with focal length f = 15 cm and object distance d_o = 10 cm (between the mirror and focal point), using the mirror equation 1/d_i = 1/f - 1/d_o yields d_i = -30 cm, indicating a virtual, upright, and magnified image behind the mirror. This uses the sign convention where f is positive for concave mirrors and negative d_i indicates a virtual image. Ray diagrams are constructed using principal rays to locate the image for these positions. A ray parallel to the principal axis reflects through F; a ray passing through F reflects parallel to the axis; and a ray through C reflects back along the same path, undeviated. These rays intersect at the image point for objects in different zones, confirming the image's position, size, and orientation without relying on equations. Despite ideal formation, concave mirrors suffer from aberrations that degrade image quality. Spherical aberration affects on-axis points, causing rays farther from the to focus closer to the mirror than paraxial rays, resulting in a blurred rather than point-like . Off-axis aberrations such as cause point sources off the to appear as asymmetric, comet-like blurs, with the streak directed away from the axis, increasing with field angle. results in elliptical or line-like images for off-axis points, as rays in meridional and sagittal planes focus at different distances along the axis. These aberrations, inherent to spherical surfaces, limit the mirror's performance for wide fields.

Applications

Uses of Convex Mirrors

Convex mirrors are widely employed in traffic and vehicle safety applications due to their ability to provide a broad , which helps eliminate blind spots and enhances driver awareness. In automobiles, the passenger-side exterior mirror is typically convex to offer a wider rearward view, a requirement under Federal Motor Vehicle Safety Standard (FMVSS) No. 111, which requires a convex passenger-side exterior mirror when the interior mirror does not provide sufficient , to ensure visibility along the vehicle's sides. This standard has been in place since the , with refinements in the emphasizing convex designs for improved during lane changes and merging. Additionally, aftermarket blind-spot mirrors—small convex attachments placed on side mirrors—further reduce hidden areas by expanding the observable area behind and beside the . Modern designs may incorporate aspheric sections to minimize distortion while maintaining wide fields of view. In and , convex mirrors serve as cost-effective tools for monitoring large areas without significant distortion, particularly in retail environments. These mirrors are commonly installed at the ends of aisles in stores to allow staff to observe customer activity across multiple sections, providing a near-360-degree view that deters by eliminating concealed spots. Their diverging properties produce virtual, upright images that maintain recognizability of shapes and movements, making them ideal for anti-theft purposes in and boutiques where quick visual checks are essential. Industrial applications leverage convex mirrors for detection in confined or high-traffic spaces, such as parking garages and driveways, where they help prevent collisions by revealing approaching vehicles or pedestrians in blind corners. For instance, mirrors positioned at garage entrances or driveway junctions allow safe navigation, significantly lowering rates in multi-level parking structures. In certain optical devices, convex mirrors contribute to expanded viewing capabilities. They are incorporated into simple designs to widen the field of view, enabling observation around obstacles with minimal image inversion. Despite these advantages, convex mirrors have limitations stemming from their production of diminished, virtual images, which appear smaller and farther away than . This requires users to adjust their perception and distance judgment, making them unsuitable for applications needing precise sizing or detailed , such as close-range identification.

Uses of Concave Mirrors

Concave mirrors serve as primary optical elements in reflecting telescopes, where a large concave mirror collects and focuses incoming light from distant celestial objects onto a secondary optic, forming a without the inherent in refracting lenses. This design, pioneered by in 1668, revolutionized astronomy by enabling larger apertures and sharper images across all wavelengths of light. In the Newtonian configuration, the primary concave mirror is positioned at the base of the telescope tube, reflecting light to a flat secondary mirror that redirects it to the for . In automotive headlights, concave reflectors, often parabolic in shape, surround the light source—typically positioned at the focal point—to collimate the emitted rays into a parallel beam that projects forward efficiently, illuminating the road ahead while minimizing scatter. This setup ensures a directed, high-intensity distribution essential for nighttime . Similarly, in slide projectors, a concave mirror positioned behind the lamp collects divergent rays and directs them toward the transparency slide, enhancing brightness and uniformity before the light passes through condensing lenses to form a focused, enlarged image on a screen. Concave mirrors, particularly in parabolic trough or dish configurations, are integral to solar concentrators, where they focus onto a receiver tube or point to achieve high temperatures for generation in concentrating (CSP) systems. Parabolic trough collectors can reach operating temperatures up to 400°C by tracking the sun and concentrating its rays along a linear absorber, driving turbines for production. Modern CSP plants, such as the Ivanpah Solar Electric Generating commissioned in , employ large arrays of mirrors to , generating up to 392 MW of power through similar focusing principles, though utilizing fields in a tower setup. In medical and cosmetic applications, concave mirrors provide magnified, real images for detailed viewing. Makeup mirrors with concave surfaces, held close to the face, produce enlarged upright images (up to 3x magnification) of facial features, facilitating precise application of by converging reflected light to create a behind the mirror. In , concave mouth mirrors offer indirect illumination and slight magnification (typically 2x) to visualize hard-to-reach oral areas, such as posterior teeth, by reflecting ambient light into shadowed regions while minimizing distortion for clinical accuracy. Recent advancements in astronomy incorporate adaptive concave mirrors in reflecting telescopes to dynamically correct atmospheric distortions, enhancing for ground-based observations. These deformable mirrors, adjusted in real-time using sensors and actuators, compensate for turbulence-induced aberrations, achieving near-diffraction-limited performance equivalent to space telescopes; for instance, systems at facilities like the Keck Observatory have improved Strehl ratios to over 0.5 in the near-infrared since the 1990s, with ongoing innovations in faster control algorithms and larger mirror segments.

Mathematical Analysis

Mirror Equation and Magnification

The mirror equation provides a quantitative relationship between the object dod_o, the image did_i, and the focal ff for a spherical mirror under the paraxial , which assumes rays are close to the principal axis. The equation is given by 1f=1do+1di,\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}, where distances are measured from the mirror surface along the principal axis. This equation can be derived geometrically using ray diagrams and the similarity of triangles formed by principal rays. Consider a concave spherical mirror with an object of hoh_o at distance dod_o from the mirror vertex. Two principal rays are drawn: one parallel to the axis, reflecting through the focal point FF at distance ff from the vertex; and another passing through FF, reflecting parallel to the axis. These rays intersect at the point, forming two similar triangles: a larger one with base dod_o and hoh_o, and a smaller one with base did_i and hih_i. The similarity yields hodo=hidi\frac{h_o}{d_o} = \frac{h_i}{d_i}. A second pair of similar triangles—one with base do−fd_o - f and hoh_o, the other with base ff and hih_i—gives hodo−f=hif\frac{h_o}{d_o - f} = \frac{h_i}{f}. Dividing these proportions and substituting leads to dido=fd0−f\frac{d_i}{d_o} = \frac{f}{d_0 - f}, which rearranges to the mirror equation. The standard sign convention for the mirror equation treats distances as positive in the direction of incident (from left to right). The object dod_o is positive for real objects in front of the mirror. The ff is positive for concave mirrors (converging) and negative for convex mirrors (diverging). The image did_i is positive for real images (formed in front of the mirror) and negative for virtual images (formed behind the mirror). This convention ensures consistency in calculations for both mirror types. The linear magnification mm quantifies the size and orientation of the image relative to the object, given by m=−dido=hiho,m = -\frac{d_i}{d_o} = \frac{h_i}{h_o}, where hih_i and hoh_o are the image and object heights, respectively. The negative sign indicates that real images are inverted (m<0m < 0), while virtual images are upright (m>0m > 0); the absolute value ∣m∣|m| gives the size ratio. For example, if ∣m∣>1|m| > 1, the image is enlarged; if ∣m∣<1|m| < 1, it is reduced. The focal length relates to the radius of curvature RR of the spherical surface by f=R/2f = R/2, where RR is positive for concave mirrors and negative for convex mirrors. This follows from the geometry of parallel rays reflecting to the focal point, with the center of curvature CC at distance RR from the vertex, and FF midway between the vertex and CC. For a concave mirror, parallel incident rays converge at f=+R/2f = +R/2; for convex, they diverge as if from f=−R/2f = -R/2. As an illustrative calculation for a concave mirror with f=10f = 10 cm (R=20R = 20 cm), place an object at do=20d_o = 20 cm (twice the focal length). Substituting into the mirror equation gives 1di=110−120=120\frac{1}{d_i} = \frac{1}{10} - \frac{1}{20} = \frac{1}{20}, so di=20d_i = 20 cm (real image). The magnification is m=−2020=−1m = -\frac{20}{20} = -1, indicating an inverted image of the same size. For a convex mirror with the same ∣R∣=20|R| = 20 cm (f=−10f = -10 cm) and do=20d_o = 20 cm, 1di=−110−120=−320\frac{1}{d_i} = -\frac{1}{10} - \frac{1}{20} = -\frac{3}{20}, so di=−6.67d_i = -6.67 cm (virtual image), and m=−(−6.67)/20=+0.333m = -(-6.67)/20 = +0.333 (upright, reduced image). Another example for a concave mirror with f=15f = 15 cm and do=10d_o = 10 cm (object inside the focal point) yields 1di=115−110=−130\frac{1}{d_i} = \frac{1}{15} - \frac{1}{10} = -\frac{1}{30}, so di=−30d_i = -30 cm (virtual image behind the mirror). The magnification is m=−−3010=+3m = -\frac{-30}{10} = +3, indicating an upright and magnified image.

Ray Tracing

Ray tracing provides a graphical technique to determine the position, orientation, and size of images formed by curved mirrors through the application of the law of reflection, without relying on algebraic equations. This method visualizes how light rays from an object interact with the mirror surface, using a set of principal rays to locate the image at their intersection point after reflection. The standard procedure begins by drawing the mirror's principal axis, indicating the mirror's vertex, focal point (at half the radius of curvature), and center of curvature. The object is positioned along the axis, typically represented as an arrow perpendicular to it. Three principal rays are then traced from the object's tip: one parallel to the principal axis, which reflects through the focal point in concave mirrors or appears to diverge from it in convex mirrors; one passing through the focal point, which reflects parallel to the axis; and one passing through the , which reflects back along the same path due to normal incidence. The reflected paths of any two of these rays intersect at the image point, with the third serving as verification. In convex mirrors, all reflected rays diverge outward, requiring backward extension of these rays to find their virtual intersection behind the mirror. This always produces an upright, diminished virtual image, regardless of object position, as the focal point lies behind the mirror. For concave mirrors, the behavior depends on the object's distance from the mirror. When the object is beyond the center of curvature, the rays converge to form a real, inverted, and diminished image between the focal point and center of curvature. If the object is between the focal point and center, a real, inverted, magnified image appears beyond the center. For objects inside the focal point, rays diverge after reflection, yielding an upright, magnified virtual image behind the mirror. Paraxial ray tracing, which limits rays to small angles near the axis, neglects optical aberrations but provides accurate predictions for narrow beams. Spherical aberration arises in spherical mirrors when marginal rays—those farther from the axis—focus closer to the mirror than paraxial rays, resulting in a blurred or diffuse image rather than a sharp point. Qualitative diagrams illustrate this as a series of focal points along the axis, with the effect worsening for wider apertures relative to the radius of curvature. Practical implementation often employs graph paper or pre-printed ray-tracing sheets to ensure proportional scaling and accuracy in manual drawings. Modern optical design software automates these traces for complex systems, building on historical graphical methods developed in 17th-century optics to analyze reflection in curved surfaces.

Ray Transfer Matrix Analysis

The ray transfer matrix analysis, also known as the ABCD matrix formalism, provides a linear algebraic method to describe the propagation of paraxial rays through optical systems, including curved mirrors. In this approach, a ray is characterized by its position rr (transverse distance from the optical axis) and angle θ\theta (paraxial slope, approximately the angle with the axis), forming a vector (rθ)\begin{pmatrix} r \\ \theta \end{pmatrix}. The effect of an optical element transforms the input vector to the output vector via a 2×2 matrix (ABCD)\begin{pmatrix} A & B \\ C & D \end{pmatrix}, such that (routθout)=(ABCD)(rinθin)\begin{pmatrix} r_{\text{out}} \\ \theta_{\text{out}} \end{pmatrix} = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} r_{\text{in}} \\ \theta_{\text{in}} \end{pmatrix}. This formalism assumes the paraxial approximation, where rays are close to the axis and angles are small. For a spherical mirror, the ray transfer matrix is (10−2/R1)\begin{pmatrix} 1 & 0 \\ -2/R & 1 \end{pmatrix}, where [R](/page/R)[R](/page/R) is the radius of curvature (positive for a concave mirror facing the incident light). This matrix accounts for the reflection at the curved surface, altering the ray's angle based on its position while preserving the position at the mirror surface. For complex systems involving multiple elements, such as a mirror followed by a lens or propagation through free space, the overall transfer matrix is obtained by multiplying the individual matrices in reverse order of traversal (from output to input). The effective focal length of the system can then be determined from the matrix elements; for instance, if the B element is zero (as in a focused system), the focal length f=−1/Cf = -1/C. This method offers advantages over basic ray tracing techniques by enabling systematic analysis of multi-element systems, including those with thick mirrors or multiple reflections, through straightforward matrix multiplication. It remains invariant under the paraxial approximation, facilitating computations for stability and beam parameters without graphical constructions. As an example, consider a single concave mirror with radius R>0R > 0. The transfer matrix is (10−2/R1)\begin{pmatrix} 1 & 0 \\ -2/R & 1 \end{pmatrix}, yielding an effective f=R/2f = R/2, consistent with the mirror equation for paraxial rays. Extensions of the ABCD formalism to non-spherical mirrors incorporate generalized matrices that account for arbitrary aberrations, allowing modeling of aspheric surfaces beyond simple quadratic curvature. These advanced matrices are particularly useful in designing cavities, where stability depends on round-trip matrix eigenvalues, and in fiber optic systems for precise beam control.

References

  1. https://pressbooks.online.ucf.edu/phy2053bc/chapter/image-formation-by-mirrors/
  2. https://micro.magnet.fsu.edu/primer/lightandcolor/mirrorsintro.html
  3. https://www.physicsclassroom.com/class/refln/Lesson-3/The-Anatomy-of-a-Curved-Mirror
  4. https://math.nyu.edu/Archimedes/Mirrors/legend/legend.html
  5. https://ecuip.lib.uchicago.edu/multiwavelength-astronomy/optical/history/04.html
  6. https://www.asc.ohio-state.edu/humanic.1/p1201lecture15.pdf
  7. https://www.physicsbootcamp.org/curved-mirrors.html
  8. https://farside.ph.utexas.edu/teaching/316/lectures/node136.html
  9. https://pages.physics.ua.edu/staff/fabi/ph102/classnotes/9mirrorlens102.pdf
  10. http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/mireq.html
  11. https://faculty.uml.edu/chandrika_narayan/Teaching/documents/Lecture_Ch-23_000.pdf
  12. https://pressbooks.online.ucf.edu/osuniversityphysics3/chapter/spherical-mirrors/
  13. https://www.sjsu.edu/people/ignacio.mosqueira/courses/c2/s1/CH-23rev.pdf
  14. http://physics.bu.edu/~duffy/PY106/Reflection.html
  15. https://faculty.etsu.edu/lutter/courses/phys2021/OPTC_5_Mirrors_Lenses.pdf
  16. https://digitalcommons.unl.edu/context/physicskatz/article/1173/viewcontent/38__Mirros_and_Lenses.pdf
  17. http://homepage.physics.uiowa.edu/~rmerlino/6Spring09/29006_L33.pdf
  18. https://www.edmundoptics.com/f/convex-mirrors/14829/
  19. https://micro.magnet.fsu.edu/primer/java/mirrors/concavemirrors/index.html
  20. http://physics.bu.edu/~duffy/sc528_notes10/sign_convention.html
  21. https://www.arborsci.com/products/concave-convex-mirror-set
  22. https://www.amazon.com/Round-Concave-Glass-Mirror-Diameter/dp/B079836VBW
  23. http://scipp.ucsc.edu/~haber/ph5B/parabolic09.pdf
  24. https://www.meetoptics.com/academy/ellipsoidal-mirrors
  25. https://www.osti.gov/pages/biblio/2533557
  26. https://mathshistory.st-andrews.ac.uk/Extras/Schmidt-Cassegrain/
  27. https://history.aip.org/exhibits/cosmology/tools/tools-early-reflectors.htm
  28. https://spacemath.gsfc.nasa.gov/IRAD/IRAD-4.pdf
  29. https://pressbooks.uiowa.edu/clonedbook/chapter/image-formation-by-mirrors/
  30. https://irc.rice.edu/?movies=convex-side-mirror
  31. https://farside.ph.utexas.edu/teaching/316/lectures/node137.html
  32. https://people.ohio.edu/elster/psc1051/c7d/Mirror-Equation-concave.pdf
  33. http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/mirray.html
  34. https://vikdhillon.staff.shef.ac.uk/teaching/phy217/telescopes/phy217_tel_reflectors.html
  35. http://labman.phys.utk.edu/phys136core/modules/m10/aberrations.html
  36. https://www.ecfr.gov/current/title-49/subtitle-B/chapter-V/part-571/subpart-B/section-571.111
  37. https://www.federalregister.gov/documents/2003/01/22/03-1353/new-rearview-technology-and-federal-motor-vehicle-safety-standard-no-111-rearview-mirrors
  38. https://www.securitymirror.net/
  39. https://www.americantheftprevention.com/Security-Mirrors-c5/
  40. https://safetyxpress.co.za/the-essential-role-convex-mirrors-in-traffic-road-safety/
  41. https://www.convexmirrors.co.uk/convex-mirrors-in-scientific-instruments/
  42. https://ethos.lps.library.cmu.edu/article/id/480/
  43. https://www.physics.udel.edu/~jlp/classweb2/directory/powerpoint/telescopes.pdf
  44. https://www.mtwilson.edu/wp-content/uploads/2018/03/Reflections_March_2018_Rev.pdf
  45. https://van.physics.illinois.edu/ask/listing/1976
  46. https://americacomesalive.com/the-magic-lantern-early-form-of-slide-projector/
  47. https://www.ucs.org/resources/concentrating-solar-power-plants
  48. https://www.energy.gov/sites/prod/files/2014/10/f18/CSP-report-final-web.pdf
  49. https://hayeshandpiece.com/dental-resources/post/mouth-mirror-types-uses-smart-tools
  50. https://www.makeupmirror.com.au/blogs/tips-articles/a-guide-to-using-magnifying-makeup-mirrors
  51. https://heritageproject.caltech.edu/interviews-updates/peter-wizinowich
  52. https://pmc.ncbi.nlm.nih.gov/articles/PMC8892592/
  53. https://www.physics.utah.edu/~woolf/2020_Jui/apr03.pdf
  54. https://www.phys.uconn.edu/~rcote/Courses/PHY1202/Spring2018/lec17-pdf.pdf
  55. https://phys.libretexts.org/Bookshelves/University_Physics/University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.03%3A_Spherical_Mirrors
  56. https://www.usna.edu/Users/physics/mungan/_files/documents/Scholarship/RayTracing.pdf
  57. https://www.edmundoptics.com/knowledge-center/application-notes/optics/geometrical-optics-101-paraxial-ray-tracing-calculations/
  58. https://www.cambridge.org/core/books/introduction-to-lens-design/ray-tracing/560E2991F5E4391DF31E728F97F67F9A
  59. https://www.rp-photonics.com/abcd_matrix.html
  60. https://arxiv.org/pdf/2205.09746
  61. http://users.ntua.gr/eglytsis/EO/Ray_Matrices_p.pdf
  62. https://pubs.aip.org/aapt/ajp/article/91/6/449/2891435/Beyond-the-ABCDs-A-better-matrix-method-for
Add your contribution
Related Hubs
User Avatar
No comments yet.