Hubbry Logo
Reflecting telescopeReflecting telescopeMain
Open search
Reflecting telescope
Community hub
Reflecting telescope
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Reflecting telescope
Reflecting telescope
Reflecting telescope
View on Wikipedia
from Wikipedia
Stratospheric Observatory for Infrared Astronomy
24-inch convertible Newtonian/Cassegrain reflecting telescope on display at the Franklin Institute

A reflecting telescope (also called a reflector) is a telescope that uses a single or a combination of curved mirrors that reflect light and form an image. The reflecting telescope was invented in the 17th century by Isaac Newton as an alternative to the refracting telescope which, at that time, was a design that suffered from severe chromatic aberration. Although reflecting telescopes produce other types of optical aberrations, it is a design that allows for very large diameter objectives. Almost all of the major telescopes used in astronomy research are reflectors. Many variant forms are in use and some employ extra optical elements to improve image quality or place the image in a mechanically advantageous position. Since reflecting telescopes use mirrors, the design is sometimes referred to as a catoptric telescope.[1]

From the time of Newton to the 19th century, the mirror itself was made of metal – usually speculum metal. This type included Newton's first designs and the largest telescope of the 19th century, the Leviathan of Parsonstown with a 6 feet (1.8 m) wide metal mirror. In the 19th century a new method using a block of glass coated with very thin layer of silver began to become more popular by the turn of the century. Common telescopes which led to the Crossley and Harvard reflecting telescopes, which helped establish a better reputation for reflecting telescopes as the metal mirror designs were noted for their drawbacks. Chiefly the metal mirrors only reflected about 2⁄3 of the light and the metal would tarnish. After multiple polishings and tarnishings, the mirror could lose its precise figuring needed.

Reflecting telescopes became extraordinarily popular for astronomy and many famous telescopes, such as the Hubble Space Telescope, and popular amateur models use this design. In addition, the reflection telescope principle was applied to other electromagnetic wavelengths, and for example, X-ray telescopes also use the reflection principle to make image-forming optics.

History

[edit]
Main article: History of the telescope
A replica of Newton's second reflecting telescope which was presented to the Royal Society in 1672.[2]
The great telescope of Birr Castle, the Leviathan of Parsonstown. Modern day remnants of the mirror and support structure.

The idea that curved mirrors behave like lenses dates back at least to Alhazen's 11th century treatise on optics, works that had been widely disseminated in Latin translations in early modern Europe.[3] Soon after the invention of the refracting telescope, Galileo Galilei, Giovanni Francesco Sagredo, and others, spurred on by their knowledge of the principles of curved mirrors, discussed the idea of building a telescope using a mirror as the image forming objective.[4] There were reports that the Bolognese Cesare Caravaggi had constructed one around 1626 and the Italian professor Niccolò Zucchi, in a later work, wrote that he had experimented with a concave bronze mirror in 1616, but said it did not produce a satisfactory image.[4] The potential advantages of using parabolic mirrors, primarily reduction of spherical aberration with no chromatic aberration, led to many proposed designs for reflecting telescopes. These included one by James Gregory, published in 1663. In 1673, experimental scientist Robert Hooke was able to build this type of telescope, which became known as the Gregorian telescope.[5][6][7]

Five years after Gregory designed his telescope and five years before Hooke built the first such Gregorian telescope, Isaac Newton in 1668 built his own reflecting telescope, which is considered the first reflecting telescope, as previous designs were never put into practice or ended in failure when attempted.[6][8][9] Newton's telescope used a spherically ground metal primary mirror and a small diagonal mirror in an optical configuration that has come to be known as the Newtonian telescope.

Despite the theoretical advantages of the reflector design, the difficulty of construction and the poor performance of the speculum metal mirrors being used at the time meant it took over 100 years for them to become popular. Many of the advances in reflecting telescopes included the perfection of parabolic mirror fabrication in the 18th century,[10] silver coated glass mirrors in the 19th century (built by Léon Foucault in 1858),[11] long-lasting aluminum coatings in the 20th century,[12] segmented mirrors to allow larger diameters, and active optics to compensate for gravitational deformation. A mid-20th century innovation was catadioptric telescopes such as the Schmidt camera, which use both a spherical mirror and a lens (called a corrector plate) as primary optical elements, mainly used for wide-field imaging without spherical aberration.

The late 20th century has seen the development of adaptive optics and lucky imaging to overcome the problems of seeing, and reflecting telescopes are ubiquitous on space telescopes and many types of spacecraft imaging devices.

Technical considerations

[edit]
Gran Telescopio Canarias

A curved primary mirror is the reflector telescope's basic optical element that creates an image at the focal plane. The distance from the mirror to the focal plane is called the focal length. Film or a digital sensor may be located here to record the image, or a secondary mirror may be added to modify the optical characteristics and/or redirect the light to film, digital sensors, or an eyepiece for visual observation.

The primary mirror in most modern telescopes is composed of a solid glass cylinder whose front surface has been ground to a spherical or parabolic shape. A thin layer of aluminum is vacuum deposited onto the mirror, forming a highly reflective first surface mirror.

Some telescopes use primary mirrors which are made differently. Molten glass is rotated to make its surface paraboloidal, and is kept rotating while it cools and solidifies. (See Rotating furnace.) The resulting mirror shape approximates a desired paraboloid shape that requires minimal grinding and polishing to reach the exact figure needed.[13]

Optical errors

[edit]

Reflecting telescopes, just like any other optical system, do not produce "perfect" images. The need to image objects at distances up to infinity, view them at different wavelengths of light, along with the requirement to have some way to view the image the primary mirror produces, means there is always some compromise in a reflecting telescope's optical design.

An image of Sirius A and Sirius B by the Hubble Space Telescope, showing diffraction spikes and concentric diffraction rings.

Because the primary mirror focuses light to a common point in front of its own reflecting surface almost all reflecting telescope designs have a secondary mirror, film holder, or detector near that focal point partially obstructing the light from reaching the primary mirror. Not only does this cause some reduction in the amount of light the system collects, it also causes a loss in contrast in the image due to diffraction effects of the obstruction as well as diffraction spikes caused by most secondary support structures.[14][15]

The use of mirrors avoids chromatic aberration but they produce other types of aberrations. A simple spherical mirror cannot bring light from a distant object to a common focus since the reflection of light rays striking the mirror near its edge do not converge with those that reflect from nearer the center of the mirror, a defect called spherical aberration. To avoid this problem most reflecting telescopes use parabolic shaped mirrors, a shape that can focus all the light to a common focus. Parabolic mirrors work well with objects near the center of the image they produce, (light traveling parallel to the mirror's optical axis), but towards the edge of that same field of view they suffer from off axis aberrations:[16][17]

  • Coma – an aberration where point sources (stars) at the center of the image are focused to a point but typically appears as "comet-like" radial smudges that get worse towards the edges of the image.
  • Field curvature – The best image plane is in general curved, which may not correspond to the detector's shape and leads to a focus error across the field. It is sometimes corrected by a field flattening lens.
  • Astigmatism – an azimuthal variation of focus around the aperture causing point source images off-axis to appear elliptical. Astigmatism is not usually a problem in a narrow field of view, but in a wide field image it gets rapidly worse and varies quadratically with field angle.
  • Distortion – Distortion does not affect image quality (sharpness) but does affect object shapes. It is sometimes corrected by image processing.

There are reflecting telescope designs that use modified mirror surfaces (such as the Ritchey–Chrétien telescope) or some form of correcting lens (such as catadioptric telescopes) that correct some of these aberrations.

Use in astronomical research

[edit]
Main mirror of James Webb Space Telescope assembled at Goddard Space Flight Center, May 2016.

Nearly all large research-grade astronomical telescopes are reflectors. There are several reasons for this:

  • Reflectors work in a wider spectrum of light since certain wavelengths are absorbed when passing through glass elements like those found in a refractor or in a catadioptric telescope.
  • In a lens the entire volume of material has to be free of imperfection and inhomogeneities, whereas in a mirror, only one surface has to be perfectly polished.
  • Light of different wavelengths travels through a medium other than vacuum at different speeds. This causes chromatic aberration. Reducing this to acceptable levels usually involves a combination of two or three aperture sized lenses (see achromat and apochromat for more details). The cost of such systems therefore scales significantly with aperture size. An image obtained from a mirror does not suffer from chromatic aberration to begin with, and the cost of the mirror scales much more modestly with its size.
  • There are structural problems involved in manufacturing and manipulating large-aperture lenses. Since a lens can only be held in place by its edge, the center of a large lens will sag due to gravity, distorting the image it produces. The largest practical lens size in a refracting telescope is around 1 meter.[18] In contrast, a mirror can be supported by the whole side opposite its reflecting face, allowing for reflecting telescope designs that can overcome gravitational sag. The largest reflector designs currently exceed 10 meters in diameter.

Reflecting telescope designs

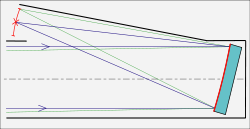
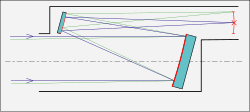
[edit]

Gregorian

[edit]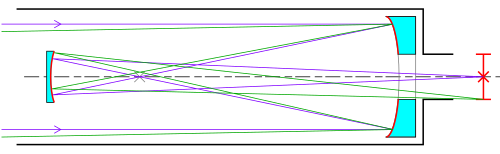
Main article: Gregorian telescope
Light path in a Gregorian telescope.

The Gregorian telescope, described by Scottish astronomer and mathematician James Gregory in his 1663 book Optica Promota, employs a concave secondary mirror that reflects the image back through a hole in the primary mirror. This produces an upright image, useful for terrestrial observations. Some small spotting scopes are still built this way. There are several large modern telescopes that use a Gregorian configuration such as the Vatican Advanced Technology Telescope, the Magellan telescopes, the Large Binocular Telescope, and the Giant Magellan Telescope.

Newtonian

[edit]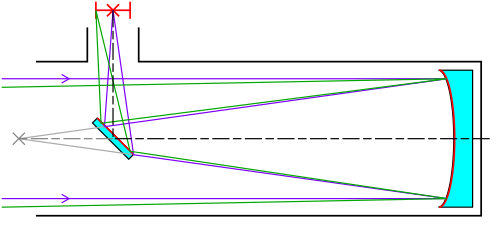
Light path in a Newtonian telescope.
Main article: Newtonian telescope
See also: Schmidt–Newton telescope

The Newtonian telescope was the first successful reflecting telescope, completed by Isaac Newton in 1668. It usually has a paraboloid primary mirror but at focal ratios of about f/10 or longer a spherical primary mirror can be sufficient for high visual resolution. A flat secondary mirror reflects the light to a focal plane at the side of the top of the telescope tube. It is one of the simplest and least expensive designs for a given size of primary, and is popular with amateur telescope makers as a home-build project.

The Cassegrain design and its variations

[edit]
Light path in a Cassegrain telescope.
Main article: Cassegrain reflector

The Cassegrain telescope (sometimes called the "Classic Cassegrain") was first published in a 1672 design attributed to Laurent Cassegrain. It has a parabolic primary mirror, and a hyperbolic secondary mirror that reflects the light back down through a hole in the primary. The folding and diverging effect of the secondary mirror creates a telescope with a long focal length while having a short tube length.

Ritchey–Chrétien

[edit]
Main article: Ritchey–Chrétien telescope

The Ritchey–Chrétien telescope, invented by George Willis Ritchey and Henri Chrétien in the early 1910s, is a specialized Cassegrain reflector which has two hyperbolic mirrors (instead of a parabolic primary). It is free of coma and spherical aberration at a nearly flat focal plane if the primary and secondary curvature are properly figured, making it well suited for wide field and photographic observations.[19] Almost every professional reflector telescope in the world is of the Ritchey–Chrétien design.

Three-mirror anastigmat

[edit]
Main article: Three-mirror anastigmat

Including a third curved mirror allows correction of the remaining distortion, astigmatism, from the Ritchey–Chrétien design. This allows much larger fields of view.

Dall–Kirkham

[edit]
See also: Modified Dall–Kirkham telescope
Dall-Kirkham reflecting telescope, built by Horace Edward Dall

The Dall–Kirkham Cassegrain telescope's design was created by Horace Dall in 1928 and took on the name in an article published in Scientific American in 1930 following discussion between amateur astronomer Allan Kirkham and Albert G. Ingalls, the magazine editor at the time. It uses a concave elliptical primary mirror and a convex spherical secondary. While this system is easier to grind than a classic Cassegrain or Ritchey–Chrétien system, it does not correct for off-axis coma. Field curvature is actually less than a classical Cassegrain. Because this is less noticeable at longer focal ratios, Dall–Kirkhams are seldom faster than f/15.

Off-axis designs

[edit]

There are several designs that try to avoid obstructing the incoming light by eliminating the secondary or moving any secondary element off the primary mirror's optical axis, commonly called off-axis optical systems.

Herschelian

[edit]
Light paths
Herschelian telescope
Schiefspiegler telescope

The Herschelian reflector is named after William Herschel, who used this design to build very large telescopes including the 40-foot telescope in 1789. In the Herschelian reflector the primary mirror is tilted so the observer's head does not block the incoming light. Although this introduces geometrical aberrations, Herschel employed this design to avoid the use of a Newtonian secondary mirror since the speculum metal mirrors of that time tarnished quickly and could only achieve 60% reflectivity.[20]

Schiefspiegler

[edit]
Main article: Schiefspiegler

A variant of the Cassegrain, the Schiefspiegler telescope ("skewed" or "oblique reflector") uses tilted mirrors to avoid the secondary mirror casting a shadow on the primary. However, while eliminating diffraction patterns this leads to an increase in coma and astigmatism. These defects become manageable at large focal ratios — most Schiefspieglers use f/15 or longer, which tends to restrict useful observations to objects which fit in a moderate field of view. A 6" (150mm) f/15 telescope offers a maximum 0.75 degree field of view using 1.25" eyepieces. A number of variations are common, with varying numbers of mirrors of different types. The Kutter (named after its inventor Anton Kutter) style uses a single concave primary, a convex secondary and a plano-convex lens between the secondary mirror and the focal plane, when needed (this is the case of the catadioptric Schiefspiegler). One variation of a multi-schiefspiegler uses a concave primary, convex secondary and a parabolic tertiary. One of the interesting aspects of some Schiefspieglers is that one of the mirrors can be involved in the light path twice — each light path reflects along a different meridional path.

Stevick-Paul

[edit]

Stevick-Paul telescopes[21] are off-axis versions of Paul 3-mirror systems[22] with an added flat diagonal mirror. A convex secondary mirror is placed just to the side of the light entering the telescope, and positioned afocally so as to send parallel light on to the tertiary. The concave tertiary mirror is positioned exactly twice as far to the side of the entering beam as was the convex secondary, and its own radius of curvature distant from the secondary. Because the tertiary mirror receives parallel light from the secondary, it forms an image at its focus. The focal plane lies within the system of mirrors, but is accessible to the eye with the inclusion of a flat diagonal. The Stevick-Paul configuration results in all optical aberrations totaling zero to the third-order, except for the Petzval surface which is gently curved.

Yolo

[edit]

The Yolo was developed by Arthur S. Leonard in the mid-1960s.[23] Like the Schiefspiegler, it is an unobstructed, tilted reflector telescope. The original Yolo consists of a primary and secondary concave mirror, with the same curvature, and the same tilt to the main axis. Most Yolos use toroidal reflectors. The Yolo design eliminates coma, but leaves significant astigmatism, which is reduced by deformation of the secondary mirror by some form of warping harness, or alternatively, polishing a toroidal figure into the secondary. Like Schiefspieglers, many Yolo variations have been pursued. The needed amount of toroidal shape can be transferred entirely or partially to the primary mirror. In large focal ratios optical assemblies, both primary and secondary mirror can be left spherical and a spectacle correcting lens is added between the secondary mirror and the focal plane (catadioptric Yolo). The addition of a convex, long focus tertiary mirror leads to Leonard's Solano configuration. The Solano telescope doesn't contain any toric surfaces.

Liquid-mirror telescopes

[edit]
Main article: Liquid-mirror telescope

One design of telescope uses a rotating mirror consisting of a liquid metal in a tray that is spun at constant speed. As the tray spins, the liquid forms a paraboloidal surface of essentially unlimited size. This allows making very big telescope mirrors (over 6 metres), but they are limited to use by zenith telescopes.

Focal planes

[edit]

Prime focus

[edit]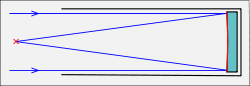
A prime focus telescope design. The observer/camera is at the focal point (shown as a red X).

In a prime focus design no secondary optics are used, the image is accessed at the focal point of the primary mirror. At the focal point is some type of structure for holding a film plate or electronic detector. In the past, in very large telescopes, an observer would sit inside the telescope in an "observing cage" to directly view the image or operate a camera.[24] Nowadays CCD cameras allow for remote operation of the telescope from almost anywhere in the world. The space available at prime focus is severely limited by the need to avoid obstructing the incoming light.[25]

Radio telescopes often have a prime focus design. The mirror is replaced by a metal surface for reflecting radio waves, and the observer is an antenna.

See also: Schmidt camera

Cassegrain focus

[edit]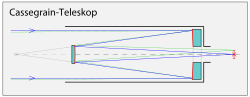
Cassegrain design

For telescopes built to the Cassegrain design or other related designs, the image is formed behind the primary mirror, at the focal point of the secondary mirror. An observer views through the rear of the telescope, or a camera or other instrument is mounted on the rear. Cassegrain focus is commonly used for amateur telescopes or smaller research telescopes. However, for large telescopes with correspondingly large instruments, an instrument at Cassegrain focus must move with the telescope as it slews; this places additional requirements on the strength of the instrument support structure, and potentially limits the movement of the telescope in order to avoid collision with obstacles such as walls or equipment inside the observatory.

Nasmyth and coudé focus

[edit]
Nasmyth/coudé light path.

Nasmyth

[edit]
Main article: Nasmyth telescope

The Nasmyth design is similar to the Cassegrain except the light is not directed through a hole in the primary mirror; instead, a third mirror reflects the light to the side of the telescope to allow for the mounting of heavy instruments. This is a very common design in large research telescopes.[26]

Coudé

[edit]

Adding further optics to a Nasmyth-style telescope to deliver the light (usually through the declination axis) to a fixed focus point that does not move as the telescope is reoriented gives a coudé focus (from the French word for elbow).[27] The coudé focus gives a narrower field of view than a Nasmyth focus[27] and is used with very heavy instruments that do not need a wide field of view. One such application is high-resolution spectrographs that have large collimating mirrors (ideally with the same diameter as the telescope's primary mirror) and very long focal lengths. Such instruments could not withstand being moved, and adding mirrors to the light path to form a coudé train, diverting the light to a fixed position to such an instrument housed on or below the observing floor (and usually built as an unmoving integral part of the observatory building) was the only option. The 60-inch Hale telescope (1.5 m), Hooker Telescope, 200-inch Hale Telescope, Shane Telescope, and Harlan J. Smith Telescope all were built with coudé foci instrumentation. The development of echelle spectrometers allowed high-resolution spectroscopy with a much more compact instrument, one which can sometimes be successfully mounted on the Cassegrain focus. Since inexpensive and adequately stable computer-controlled alt-az telescope mounts were developed in the 1980s, the Nasmyth design has generally supplanted the coudé focus for large telescopes.

Fibre-fed spectrographs

[edit]

For instruments requiring very high stability, or that are very large and cumbersome, it is desirable to mount the instrument on a rigid structure, rather than moving it with the telescope. Whilst transmission of the full field of view would require a standard coudé focus, spectroscopy typically involves the measurement of only a few discrete objects, such as stars or galaxies. It is therefore feasible to collect light from these objects with optical fibers at the telescope, placing the instrument at an arbitrary distance from the telescope. Examples of fiber-fed spectrographs include the planet-hunting spectrographs HARPS[28] or ESPRESSO.[29]

Additionally, the flexibility of optical fibers allow light to be collected from any focal plane; for example, the HARPS spectrograph utilises the Cassegrain focus of the ESO 3.6 m Telescope,[28] whilst the Prime Focus Spectrograph is connected to the prime focus of the Subaru telescope.[30]

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Reflecting telescope

View on Grokipedia
from Grokipedia
A is an that uses one or more curved mirrors to collect and focus incoming rays, forming an without the use of lenses as the primary optical elements. This design reflects off the mirrors to produce a magnified view of distant objects, such as celestial bodies, and operates as an afocal system when paired with an , projecting the at for the observer. The concept of the reflecting telescope was first proposed by Scottish mathematician James Gregory in 1663, who described a design using a parabolic primary mirror and an ellipsoidal secondary mirror in his work Optica Promota, though he never constructed it. English Isaac built and demonstrated the first practical reflecting telescope in 1668, presenting a 6-inch model to the Royal Society in 1672; his motivation was to overcome the inherent in refracting telescopes, where different wavelengths of light focus at different points due to lens dispersion. Subsequent improvements, such as better mirror parabolization by John Hadley in the 1720s, enabled wider adoption for astronomical observations. Reflecting telescopes come in several designs, each optimizing for factors like focal length, field of view, and mechanical simplicity. The Newtonian design, invented by Newton, features a concave parabolic primary mirror that focuses light onto a flat secondary mirror angled at 45 degrees to redirect the beam to an eyepiece on the side of the tube, making it popular for amateur astronomy due to its straightforward construction. The Cassegrain configuration, proposed by Guillaume Cassegrain in 1672, uses a convex secondary mirror to reflect light back through a hole in the primary mirror, resulting in a compact tube length ideal for professional instruments but with a narrower field of view. The Gregorian telescope, based on Gregory's original idea from 1663, employs a concave ellipsoidal secondary mirror placed beyond the primary focus to produce a longer effective focal length, offering reduced aberrations for certain applications like solar observations. Later variants, such as the catadioptric Schmidt-Cassegrain (developed by Bernhard Schmidt in 1930) and Maksutov-Cassegrain (1944), incorporate corrective lenses to widen the field of view and correct for spherical aberration. Key advantages of reflecting telescopes include the absence of , as mirrors reflect all wavelengths equally without dispersing them, and the ability to fabricate large primary mirrors that are thinner, lighter, and less expensive than equivalent lenses, facilitating the construction of massive instruments for deep-space imaging. These benefits have made reflectors dominant in modern astronomy, powering observatories like the 8.2-meter (Cassegrain focus) and space-based missions including the (Ritchey-Chrétien variant) and the , whose 6.5-meter gold-coated primary mirror captures light from the early universe.

Principles and Advantages

Basic Optical Principles

Reflecting telescopes utilize curved mirrors to gather and focus incoming rays from distant objects, forming real images at the focal plane through the principles of . The core component is a concave primary mirror, which reflects parallel rays—approximating from astronomical sources at —to converge at a single focal point. This reflection-based imaging avoids the need for transmissive elements like lenses, relying instead on the law of reflection where the angle of incidence equals the angle of reflection relative to the surface normal at each point of incidence./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation) The primary mirror, often shaped as a paraboloid of revolution, collects light over its entire aperture and directs it to the focus without chromatic dispersion, since reflection occurs identically for all wavelengths of visible and near-infrared light. Unlike refractive systems, where varying refractive indices cause different colors to focus at different distances, mirrors maintain a consistent focal position across the spectrum, enabling broadband imaging. This property stems from the wavelength-independent nature of specular reflection governed by Maxwell's equations in the geometric optics limit. The focal length ff of a parabolic mirror is derived from its geometric form using ray tracing and the reflection law. Consider the mirror surface defined by y=Ax2y = A x^2, with the vertex at the origin and the optical axis along the x-direction. For an incident ray parallel to the axis striking at point (x,y)(x, y), the surface slope gives the incidence angle θ\theta via tan⁡θ=2Ax\tan \theta = 2 A x. Applying reflection, the outgoing ray direction ensures convergence at f=14Af = \frac{1}{4A}, independent of the impact point, confirming the focus location. Equivalently, this focal length equals half the radius of curvature RR at the vertex, f=R2f = \frac{R}{2}, where R=12AR = \frac{1}{2A} from curvature calculations. In basic on-axis ray tracing, all parallel incident rays reflect to intersect precisely at this focal point, forming a point image for an infinitely distant on-axis source; off-axis rays follow similar paths but shifted to the focal plane./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.03%3A_Spherical_Mirrors) The aperture size of the primary mirror fundamentally determines the telescope's light-gathering power, as the total collected flux scales with the mirror area π(D/2)2\pi (D/2)^2, where DD is the diameter—doubling DD quadruples the power. This enables detection of fainter objects compared to smaller apertures. The system's speed is further characterized by the f-ratio, f/Df/D, which sets the beam convergence angle and thus the image brightness and scale at the focal plane; lower f-ratios yield faster systems with brighter but smaller-scale images. Étendue, the product of aperture area and solid angle, quantifies the conserved light throughput, underscoring why larger apertures enhance overall performance.

Comparison with Refracting Telescopes

Reflecting telescopes eliminate , a significant limitation in refracting telescopes, because reflection occurs independently of , directing all colors to the same focal point. In contrast, refracting telescopes suffer from due to the dispersion of in lenses, where different wavelengths refract at varying angles, resulting in colored fringes around images that require complex multi-element lenses to mitigate. This inherent advantage of reflectors allows for sharper, color-true images without the need for corrective optics that add bulk and cost to refractors. Reflecting telescopes offer substantial cost and scalability benefits over refractors, primarily because mirrors can be supported across their entire back surface or at the edges, preventing the gravitational sagging that distorts large lenses. Refractors are practically limited to apertures around 1 meter, as exemplified by the Yerkes Observatory's 40-inch (1-meter) refractor, the largest ever built, due to the weight-induced deformation of unsupported lens interiors. In comparison, reflecting telescopes routinely achieve apertures exceeding 8 meters, such as the 8- to 12-meter class instruments at major observatories, enabling far greater light-gathering power at lower relative costs since mirrors require polishing on only one surface. While reflectors provide these advantages, they exhibit more pronounced off-axis aberrations, such as , which degrade image quality away from the , though these can be corrected through specialized mirror configurations. Refractors, by contrast, generally support wider fields of view with less in compact designs, but achieving large sizes incurs exponentially higher expenses due to material and fabrication challenges. Following the , when refractors dominated professional astronomy, reflectors became the standard for large-scale telescopes owing to their superior scalability and performance in deep-sky observations. In terms of light transmission efficiency, reflecting telescopes typically achieve about 90% reflectivity per mirror surface with modern aluminum coatings, and while multiple reflections reduce overall throughput, the design often involves fewer optical elements than refractors. Refracting telescopes transmit around 95% of light per lens surface but suffer greater cumulative losses from absorption and multiple refractions in thicker, multi-lens objectives, making reflectors more efficient for faint object detection in large apertures.

Historical Development

Early Inventions and Pioneers

The earliest recorded attempt to construct a reflecting telescope dates to , when Italian Jesuit priest Niccolò Zucchi experimented with a parabolic mirror paired with a concave lens to form an image. Zucchi's design aimed to reflect light onto the lens but produced unsatisfactory results due to imperfections in the mirror's curvature and surface quality, rendering it non-functional as a practical instrument. This effort, detailed in Zucchi's later writings, highlighted the potential of mirrors to avoid the plaguing refracting telescopes but underscored the technical hurdles in mirror fabrication at the time. In 1663, Scottish mathematician James Gregory advanced the concept theoretically in his treatise Optica Promota, proposing a design with a parabolic primary mirror and an ellipsoidal secondary mirror to reflect light back through a hole in the primary, forming an image free of spherical aberration. Gregory's configuration, later known as the Gregorian telescope, predated any successful practical implementation and relied on precise mirror shapes that were beyond contemporary manufacturing capabilities. Although Gregory attempted to commission a prototype, these efforts failed, leaving the design as an influential blueprint rather than a realized instrument. The first functional reflecting telescope emerged in 1668 from the work of , who constructed a device using a spherical primary mirror about 1 inch in diameter and a flat secondary mirror to redirect the light to an at the side of the tube. Motivated by his experiments demonstrating in refracting lenses—where different wavelengths of light focus at varying points—Newton sought a reflector to achieve sharper images without color fringing. Newton's handmade instrument, presented to the Royal Society in 1672, magnified objects about 38 times and marked the practical inception of reflecting telescopes, though its small size limited observational use. Shortly thereafter, in 1672, French priest and inventor Laurent Cassegrain proposed an alternative configuration in a letter published in the , featuring a parabolic primary mirror and a convex hyperbolic secondary mirror placed beyond the primary's focal point to reflect light out through an in the primary. This design aimed to produce a compact with a longer effective , addressing some limitations of Newton's side-viewing setup. Like Gregory's, Cassegrain's proposal faced immediate implementation challenges and was not built until the 18th century. Early reflecting telescopes encountered significant obstacles, particularly in achieving the precise parabolic curvature required for aberration-free performance, as spherical mirrors introduced coma and other distortions. Craftsmen relied on hand-polishing speculum metal alloys—high-tin bronzes—using rudimentary tools like pitch laps and abrasives, a labor-intensive process prone to errors that limited aperture sizes to a few inches in the 17th and early 18th centuries. These technological constraints, persisting into the 18th century, delayed widespread adoption until innovations in figuring techniques emerged around 1720.

Evolution and Key Milestones

The development of reflecting telescopes advanced significantly in the through the efforts of , who constructed a series of increasingly large instruments between 1774 and 1789 to pursue deep-sky observations. His early reflectors featured mirrors up to 20 inches in aperture, but his most ambitious project was the , with a 48-inch (1.2-meter) primary mirror and a of 40 feet, completed in 1789 after first light in 1787. This instrument, funded by King George III, represented the largest telescope in the world for over 50 years and introduced the use of alt-azimuth mounts for stable tracking of celestial objects, enabling Herschel's discoveries of numerous nebulae and galaxies. In the 19th century, key improvements focused on mirror fabrication techniques to achieve more precise parabolic figures, overcoming the limitations of spherical aberrations in larger reflectors. William Parsons, the Third Earl of Rosse, pioneered these advancements with his Leviathan telescope at Birr Castle, Ireland, which featured a 72-inch (1.83-meter) speculum metal primary mirror cast and figured into a near-perfect paraboloid between 1842 and 1845. Rosse's innovative casting methods, involving multiple alloy compositions and annealing processes, allowed for the production of durable, high-reflectivity mirrors that maintained figure under their own weight, setting a benchmark for future large-scale reflectors. Subsequent refinements, such as Léon Foucault's development of the foucault test in the 1850s for verifying parabolic surfaces and Carl August von Steinheil's introduction of silvered glass mirrors in 1856, further enhanced reflectivity and reduced weight, making reflecting telescopes more practical for observatory use. The 20th century marked a shift toward monumental ground-based observatories, exemplified by the 100-inch (2.5-meter) Hooker telescope at , which achieved first light on November 2, 1917, and remained the world's largest until 1949. Constructed under George Ellery Hale's direction, its mirror enabled Edwin Hubble's groundbreaking observations in the 1920s, including the identification of Cepheid variables in the Andromeda Nebula, confirming the existence of extragalactic "island universes" and establishing the expanding universe model. A pivotal space-based milestone came with the , a 2.4-meter launched on April 24, 1990, which provided unprecedented and high-resolution imaging free from atmospheric interference despite an initial mirror flaw corrected in 1993. The late 20th century introduced segmented mirror designs to surpass the manufacturing limits of monolithic primaries, with the W. M. Keck Observatory's 10-meter telescopes on pioneering this approach. Keck I, comprising 36 hexagonal segments actively aligned using edge sensors and wavefront sensors for piston, tip, and tilt corrections, captured first light on November 24, 1990, followed by full operations in 1993. This active optics system maintained the mirror's parabolic figure to within a of a , enabling light-gathering power equivalent to a single 10-meter mirror and facilitating discoveries in exoplanets and distant quasars. Post-2000 developments emphasize even larger apertures to probe cosmic origins, with the European Southern Observatory's Extremely Large Telescope (ELT) representing the forefront. Under construction in Chile's Atacama Desert, the ELT features a 39-meter primary mirror composed of 798 actively controlled segments, planned for first light in 2029, paired with advanced adaptive optics to compensate for atmospheric distortions. This design builds on Keck's segmentation legacy while integrating a deformable secondary mirror (M4) that adjusts shape up to 1,000 times per second, promising 10-16 times the resolution of Hubble for studies of exoplanet atmospheres and early universe structures.

Optical Design Fundamentals

Aberrations and Error Corrections

Reflecting telescopes, like all optical systems, are susceptible to various aberrations that degrade image quality by deviating rays from their ideal paths. Spherical aberration occurs when parallel rays incident on the mirror at different heights from the optical axis converge to different focal points, resulting in a blurred central image that worsens with faster focal ratios (smaller f-numbers). This on-axis error is inherent in spherical mirrors but can be eliminated by shaping the primary mirror as a paraboloid, which ensures all parallel rays focus to a single point regardless of height. Off-axis, coma introduces asymmetric distortion, where point sources appear as comet-like tails due to unequal magnification of rays from different zones of the , with the effect scaling with the cube of the field . further complicates off-axis imaging by causing rays in the tangential and sagittal planes to focus at separate points, producing line-like images rather than points, and its severity increases quadratically with field . Field curvature manifests as a warped focal surface resembling a (Petzval surface), where peripheral rays focus closer to the mirror than axial ones, requiring compromises in focus position across the field. To quantify coma in a parabolic primary mirror, the transverse coma can be approximated using Seidel theory as Δy≈θ3f16F2\Delta y \approx \frac{\theta^3 f}{16 F^2}, where θ\theta is the field angle in radians, ff is the , and FF is the ; this derives from the third-order Seidel coma coefficient SIII=h34f2tan⁡θS_{III} = \frac{h^3}{4 f^2} \tan \theta, with wavefront aberration W=12SIIIρ2sin⁡θW = \frac{1}{2} S_{III} \rho^2 \sin \theta (normalized radial coordinate ρ\rho) leading to the transverse displacement after ray tracing. Correction of coma, alongside residual , often employs a hyperbolic secondary mirror in designs like the Ritchey-Chrétien, which balances the coefficients to reduce off-axis errors over a wider field. Aplanatic surfaces, free from and , play a crucial role in multi-mirror systems by enabling diffraction-limited performance across modest fields, as seen in classical two-mirror aplanats where conic constants are optimized to minimize these primary Seidel errors. Beyond optical design, non-optical errors such as thermal distortions from uneven heating and gravitational sagging in large mirrors degrade quality, but active optics mitigates these through low-frequency adjustments to deformable mirrors, maintaining near-diffraction-limited in facilities like the ESO .

Mirror Fabrication and Materials

Early reflecting telescopes relied on speculum metal, a copper-tin alloy often incorporating for enhanced luster, as the primary mirror material. This brittle, white metal alloy, pioneered by in the late , could be polished to achieve moderate reflectivity of around 65%, but it was highly susceptible to tarnishing from atmospheric exposure, requiring frequent repolishing. By the mid-19th century, advancements shifted toward glass substrates coated with thin metallic layers, beginning with silver deposition developed by in 1835, which offered superior reflectivity of up to 95% across the compared to . Aluminum coatings emerged later in the century, providing durable alternatives with around 90% reflectivity and better resistance to , enabling larger and more stable mirrors for astronomical use. Contemporary mirror substrates prioritize thermal stability to minimize distortions from temperature fluctuations, with low-expansion glasses such as (a glass-ceramic from Schott) and ULE (ultra-low expansion titania-silica glass from Corning) featuring coefficients of near zero (approximately 0.05 ppm/K for Zerodur). These materials ensure dimensional stability under varying environmental conditions, critical for large ground-based telescopes. For extremely large telescopes (ELTs), lightweight carbon-fiber reinforced polymer (CFRP) composites are increasingly employed in segmented mirror designs, offering high stiffness-to-weight ratios and reduced areal density to support massive apertures without excessive structural demands. Fabrication of primary mirrors involves precise grinding and to achieve parabolic or hyperbolic aspheric figures, typically using computer-controlled machines that automate the process for sub-wavelength accuracy. The stressed-lap technique, developed for large aspheres, employs a flexible tool that conforms to the mirror's changing curvature under controlled stress, enabling efficient figuring of mirrors up to several meters in diameter while correcting for aberrations like those from imperfect surface figures. Testing occurs iteratively via methods such as the for qualitative wavefront assessment and (e.g., Fizeau or phase-shifting setups) for quantitative surface error measurement down to nanometers, ensuring optical performance meets specifications. Mirror coatings consist of vacuum-deposited aluminum layers, often enhanced with dielectric overcoats (e.g., silicon dioxide or magnesium fluoride multilayers), achieving average reflectivities exceeding 95% across the ultraviolet-to-visible range (300-700 nm) while providing protection against oxidation and abrasion. Aluminum's broad-spectrum performance makes it ideal for multi-wavelength observations, though it degrades over time due to environmental factors like humidity-induced oxidation, necessitating recoating intervals of 1-5 years for large mirrors to maintain optimal throughput. Segmented mirror technology addresses the challenges of fabricating monolithic mirrors beyond 8 meters by dividing the primary into numerous hexagonal segments, as exemplified by the W.M. Keck Observatory's 10-meter telescopes, each with 36 segments actively aligned using edge sensors and actuators to co-phase the surface to within 10 nm RMS. Recent advancements for next-generation ELTs, such as the (TMT) with its 492 off-axis segments, incorporate improved polishing via ion-beam figuring and real-time metrology, enabling a 30-meter effective with unprecedented and control.

Primary Reflector Designs

Newtonian Configuration

The Newtonian configuration represents the simplest form of reflecting telescope, utilizing a single concave parabolic primary mirror to collect and focus incoming parallel light rays onto a focal plane, with a flat diagonal secondary mirror positioned to redirect the light at a 90-degree angle for observation via an placed on the side of the tube. This design, originally developed by around 1668, relies on the reflective properties of the parabolic primary mirror, which approximates the ideal shape for focusing distant light sources without on-axis, as established in basic optical principles. In the light path of a , incoming travels down the open tube and strikes the primary mirror at the base, where it reflects back toward the tube's upper end to converge at the primary focal plane; the flat secondary mirror, mounted at a 45-degree near the tube's top end, intercepts this converging beam and reflects it perpendicularly to the side, allowing the to form a for the observer without obstructing the incoming path. The secondary mirror introduces a central obstruction, typically with a sized to 10-20% of the primary mirror's , balancing field illumination and effects while fully illuminating the focal plane, ensuring the obstruction ratio remains low enough to preserve image quality. This configuration offers several advantages, including a minimal number of optical components—just two mirrors—which reduces manufacturing complexity and cost, making it particularly accessible for astronomers. Newtonian telescopes typically feature f-ratios between 4 and 8, providing a balance of wide suitable for visual observations of extended celestial objects like star clusters and galaxies, while maintaining sufficient for planetary details. The design's simplicity also contributes to its portability and ease of alignment, with the side-mounted allowing comfortable viewing without the observer's head interfering with the light path. Practically, the tube length of a equals the of the primary mirror, which for common amateur apertures up to 0.5 meters (20 inches) results in manageable sizes for tabletop or alt-azimuth mounts, though longer s in larger instruments can make them cumbersome to handle and store. These telescopes are widely employed in for their affordability and performance in visual observing, with many hobbyists constructing their own using commercially available mirrors. A primary limitation arises from the secondary mirror's central obstruction, which causes a minor loss in contrast due to , though this effect is negligible for most visual applications and can be further minimized by keeping the obstruction below 20%.

Cassegrain and Its Variants

The classical Cassegrain design features a concave paraboloidal primary mirror and a convex hyperboloidal secondary mirror positioned just inside the primary's focal point, which reflects incoming light back through a central hole in the primary to form a final at a focus behind the primary. This configuration effectively doubles the while significantly shortening the physical tube length compared to an equivalent , making it ideal for compact professional instruments where space is limited. The design, first proposed in the but first practically implemented in the late 18th century by Jesse Ramsden, allows for f-ratios typically between f/8 and f/13, facilitating stable mountings and easier access to the focal plane. A prominent variant, the Ritchey-Chrétien telescope, modifies the classical form by employing hyperbolic surfaces for both the primary and secondary mirrors to correct for and , enabling a wider with minimal off-axis . Developed in the early 1910s by astronomers George Willis Ritchey and Henri Chrétien, patented in 1928, and first built in 1930, this design gained widespread adoption in the 1930s and is used in major observatories, such as the 2.4-meter , where the primary mirror collects light and directs it to the secondary for reflection back through the primary's . Hyperbolic corrections in the Ritchey-Chrétien, as addressed in discussions of optical aberrations, enhance performance for precision imaging over fields up to 1 degree. The system's popularity stems from its balance of aberration control and manufacturability for large apertures exceeding 1 meter. The Dall-Kirkham variant simplifies fabrication by using an ellipsoidal primary mirror paired with a spherical secondary, eliminating on-axis while retaining the folded light path of the Cassegrain. This design, introduced in by Dall and Allan Kirkham, reduces production costs and misalignment sensitivity compared to the classical Cassegrain, as the spherical secondary is easier to polish to high precision. However, it introduces more off-axis, limiting its field to narrow applications like planetary , though is reduced relative to the classical form. For even broader fields and lower distortion, the (TMA) extends the Cassegrain by adding a tertiary mirror after the secondary, achieving aplanatic correction across a wider angular extent suitable for advanced imaging. The anastigmatic condition requires the sum of the Petzval curvatures of the three mirrors to equal zero; in a typical configuration, 2R1−2R2+2R3=0\frac{2}{R_1} - \frac{2}{R_2} + \frac{2}{R_3} = 0 where R1,R2,R3R_1, R_2, R_3 are the signed radii of curvature of the primary, secondary, and tertiary mirrors, respectively, ensuring a flat focal surface with minimal field curvature. This configuration maintains the compact envelope of the Cassegrain while supporting low-distortion views over fields exceeding 2 degrees, commonly employed in modern survey telescopes. Central obstructions in Cassegrain designs, arising from the secondary mirror and its supports blocking the primary's , typically reduce throughput by 10-20% depending on the obstruction ratio (e.g., a 30-45% linear obstruction yields 9-20% area loss), though actual impacts vary with specific geometries. This loss is proportional to the square of the obstruction relative to the primary, but the design's compactness—enabling f/8 to f/13 ratios—outweighs the penalty for many professional applications, as the obstruction also slightly sharpens the point spread function at high spatial frequencies while mildly degrading low-contrast resolution.

Specialized Reflector Configurations

Off-Axis Designs

Off-axis designs in reflecting telescopes eliminate the central obstruction typically introduced by secondary mirrors in conventional configurations, allowing for full utilization of the primary mirror's and thereby enhancing contrast and resolution, particularly for high-contrast observations such as planetary or solar . These designs achieve this by tilting or offsetting the optical components, which redirects the light path away from the central axis, though this introduces challenges like increased field curvature and alignment sensitivities. The Herschelian telescope, developed by in the late 18th century, represents one of the earliest off-axis configurations, employing a single tilted paraboloidal primary mirror without a secondary optic. In this setup, the observer views the image directly through an positioned above the tilted mirror, which reflects light from an off-axis portion of the incoming beam, producing a wedge-shaped that is simple to construct but limited in angular coverage due to inherent at the edges. This design's obstruction-free path provides unobscured access to the full , making it suitable for early astronomical observations where compactness was secondary to image clarity. The Schiefspiegler, or oblique telescope, extends the off-axis principle to a two-mirror system, with both the primary paraboloidal mirror and a convex secondary tilted and offset to correct for introduced by the decentering. Pioneered by Anton Kutter in the , this configuration balances the aberrations from tilting, enabling a coma-free point at the field center while maintaining an unobscured , and has found application in solar telescopes where high contrast is essential for resolving fine details in the Sun's atmosphere. Alignment precision is critical, as small misalignments can exacerbate , but the design's compactness and lack of obstruction make it advantageous for specialized, high-resolution solar monitoring. Catadioptric off-axis variants like the Stevick-Paul and Yolo designs incorporate lens correctors to widen the field while preserving the obstruction-free benefits. The Stevick-Paul system, an evolution of Maurice Paul's , uses off-axis sections of spherical mirrors with a flat diagonal to fold the path, achieving low distortion and a flat field suitable for , though it requires precise computational optimization for beam paths. The Yolo, developed by Arthur Leonard, employs a Mangin mirror—a meniscus lens with a reflective rear surface—as the secondary to correct and in its off-axis Cassegrain-like arrangement, enabling wider fields for amateur applications while utilizing spherical surfaces for easier fabrication. Both designs enhance contrast for planetary and solar viewing by avoiding central obstructions but face challenges in field curvature management and complex alignment. In modern contexts, off-axis designs remain niche, particularly among amateur astronomers for solar scopes, where recent 2020s prototypes leverage for custom mounts and corrector holders to simplify assembly and reduce costs, though these remain experimental and limited by material thermal stability.

Liquid Mirror Telescopes

Liquid mirror telescopes utilize a rotating pool of reflective , typically mercury, to form the primary mirror, leveraging to shape the liquid surface into a suitable for focusing . The paraboloidal profile arises from the balance between gravitational and centrifugal forces, with the surface height zz at radial distance rr from the axis given by z=ω2r22gz = \frac{\omega^2 r^2}{2g}, where ω\omega is the and gg is the acceleration due to gravity; this yields a f=g2ω2f = \frac{g}{2 \omega^2}, independent of the mirror radius. The rotation rate is precisely controlled to achieve the desired , typically around 7 for large mirrors, ensuring the surface remains stable and reflective. The concept dates to the mid-19th century, when Italian astronomer Ernesto Capocci proposed using a rotating liquid mercury surface as a telescope mirror in 1850, building on Isaac Newton's earlier observation of rotating fluids forming paraboloids. Practical demonstrations followed in the late 19th and early 20th centuries, but modern development began in the 1980s, leading to the first 3-meter liquid mirror telescope constructed in the early 1990s at NASA's Orbital Debris Observatory in for tracking . The largest ground-based example, the 6-meter Large Zenith Telescope at the , operated from 2003 to 2016 and demonstrated high-resolution imaging capabilities for zenith-pointing observations. A key advantage of liquid mirrors is their low cost relative to solid glass or metal optics, enabling large apertures at a fraction of the expense—potentially up to 100 in for ground- or space-based systems—due to the of pouring and rotating the rather than polishing a rigid surface. However, their fixed zenith-pointing orientation severely limits sky coverage to approximately 2% of the , as the parabolic shape distorts if tilted away from vertical. This constraint suits them for drift-scan surveys of narrow zenith strips but precludes tracking individual objects across the sky. Challenges include the toxicity of mercury vapor, which requires enclosed operations and constant air monitoring to mitigate health risks, as well as sensitivity to that can ripple the surface and degrade image quality. The inability to tilt the mirror for off-zenith observations further restricts versatility, though these telescopes have proven effective for continuous monitoring surveys, such as wide-field astronomical imaging and detection. Recent advancements as of 2025 focus on safer alternatives to mercury, including gallium-based alloys and ferrofluidic ionic liquids, which maintain reflectivity while reducing toxicity and enabling potential magnetic control for shape adjustment in experimental setups. A notable operational example is the 4-meter at Devasthal Observatory in , inaugurated in 2023 and conducting photometric and astrometric surveys of the sky strip since 2023. NASA's explores liquid mirrors in space, where microgravity allows for larger, spherical configurations up to 50 meters, bypassing Earth's tilting limitations. DARPA's program, initiated in 2023, investigates nanoengineered coatings on low-toxicity liquids to enhance durability and adaptability for both ground and orbital applications.

Focal System Arrangements

Prime and Cassegrain Foci

In reflecting telescopes, the prime focus represents the simplest optical arrangement, where incoming light reflects directly off the primary mirror and converges at its focal plane without intervention from a secondary optic. This configuration positions instruments, such as cameras or spectrographs, at the top of the , near the converging point. The design yields a wide with minimal optical obstructions or , making it ideal for large-scale sky surveys that require capturing extensive areas of the sky in a single exposure. However, the prime focus demands a long tube length equal to the primary mirror's , which can complicate and instrument placement due to the elevated position and added weight at the telescope's apex. A prominent example of prime focus application is the , an 8.2-meter instrument operated by the National Astronomical Observatory of Japan, which employs this arrangement for wide-field imaging and . Instruments like the Hyper Suprime-Cam mosaic imager and the Prime Focus Spectrograph utilize the prime focus to achieve a 1.3-degree , enabling efficient mapping of billions of galaxies for cosmological studies. This setup minimizes light loss from additional reflections, preserving photon efficiency for faint object detection in survey programs. The Cassegrain focus introduces a secondary convex mirror to redirect light after the primary reflection, folding the back through a central hole in the primary mirror to a final convergence point behind it. This compact design shortens the overall tube length while increasing the effective through secondary , typically achieving f-ratios of f/10 or higher for enhanced resolution in detailed observations. Accessibility is a key benefit, as instruments mount directly behind the primary mirror, facilitating easier integration with modern detectors like CCD cameras and spectrographs. However, the secondary introduces a central obstruction, which shadows 10-20% of the incoming light depending on its size relative to the primary (e.g., a 1/3 linear obstruction blocks about 11% of the light-gathering area). In the Cassegrain configuration, the effective focal length FF extends beyond the primary's focal length fpf_p by the magnification factor mm of the secondary, given by F=mfp,m=fsfs−fp,F = m f_p, \quad m = \frac{f_s}{f_s - f_p}, where fsf_s is the focal length of the secondary mirror. This geometric path lengthening supports high-resolution applications, such as spectrographs that benefit from the elongated focus for dispersing light across detectors, though it incurs minor additional losses from the two reflections (typically 5-10% reflectivity reduction per surface with modern coatings). Prime and Cassegrain foci present distinct trade-offs in reflector design: the prime focus excels in unobstructed, wide-field performance but burdens the telescope with instrument mass high in the structure, potentially requiring specialized correctors to mitigate aberrations like over larger fields. Conversely, the Cassegrain offers operational convenience and scalability for heavy but suffers from the central obstruction's impact on contrast and throughput, particularly for point sources where diffraction effects from the secondary shadow become noticeable. These arrangements are often selected based on scientific priorities, with prime focus favoring survey efficiency and Cassegrain suiting precision follow-up observations.

Nasmyth, Coudé, and Advanced Foci

The Nasmyth focus configuration in reflecting telescopes directs the light path from the secondary mirror to a flat tertiary mirror positioned at the intersection of the and the axis of the mount. This setup brings the focal plane to a position on the side of the mount, allowing instruments to rotate with the as it tracks celestial objects, thereby maintaining orientation without field rotation. This stability is particularly advantageous for mounting heavy instruments like large spectrographs, as the rotating platform supports their weight directly on the mount's bearings rather than the telescope tube. For instance, the (VLT) at the employs Nasmyth foci for its Unit Telescopes, accommodating instruments such as the UVES spectrograph and the MUSE integral field unit. In contrast, the Coudé focus uses a series of additional flat mirrors to redirect the light path from the telescope tube to a fixed location, typically in a room below or adjacent to the mount, independent of the telescope's motion. This stationary arrangement provides exceptional mechanical stability for precision instruments, as the focal plane does not rotate or move with the telescope, eliminating field rotation entirely and facilitating long-exposure observations. Historically, Coudé foci have been implemented in meter-class telescopes for high-precision radial velocity measurements, such as in the 1-meter telescopes at observatories like the Dominion Astrophysical Observatory, where the fixed setup supported early stellar spectroscopy efforts. Advanced foci build on these principles by incorporating fiber-optic feeds from Nasmyth or Coudé positions to remote locations, such as underground laboratories, enabling the separation of heavy instrumentation from the telescope while minimizing light losses along extended paths up to 100 meters. Each reflection in these systems incurs a typical loss of about 5% due to imperfect mirror reflectivity, with overall throughput calculated as η=(1−R)n\eta = (1 - R)^n, where RR is the fractional reflectivity loss per mirror and nn is the number of additional mirrors in the path; for example, with R=0.05R = 0.05 and n=4n = 4, η≈0.82\eta \approx 0.82, highlighting the need for high-reflectivity coatings. This configuration enhances instrument stability by isolating sensitive detectors from mount vibrations and allows for multi-instrument facilities. In modern implementations post-2010, such as the fiber-fed multi-object spectrograph at a Nasmyth focus of the , these systems integrate adaptive optics-corrected light feeds to support high-resolution and imaging without compromising efficiency.

Modern Applications and Instrumentation

Use in Ground-Based Astronomy

Reflecting telescopes dominate ground-based astronomy due to their ability to collect large amounts of over wide fields, enabling detailed studies of distant cosmic structures despite atmospheric distortions. These instruments, often 4-10 meters in , facilitate deep imaging, high-precision , and time-domain monitoring, with and corrective technologies mitigating seeing effects to achieve resolutions as fine as 0.5 arcseconds. In deep imaging, large reflecting telescopes like the twin 8-meter instruments capture faint light from remote galaxies, probing their evolution across cosmic time. For instance, Gemini's systems enable resolutions approaching 0.1 arcseconds in near-infrared wavelengths, allowing astronomers to resolve structural details in galaxies at redshifts greater than 1, as demonstrated in surveys of the . These capabilities have revealed morphological changes in galaxy populations, from early mergers to mature disk formations, providing key data on influence and histories. Spectroscopy with reflecting telescopes employs multi-object fiber systems to simultaneously measure spectra and redshifts for thousands of objects per exposure on 4-10 meter class scopes. The (SDSS), utilizing a 2.5-meter reflector upgraded with fiber-fed spectrographs, has cataloged redshifts for nearly 3 million , enabling mapping of large-scale cosmic structures and constraints on cosmological parameters. Similar systems on larger telescopes, such as those at the 4-meter Blanco, extend this to denser fields, yielding velocity dispersions and chemical abundances for galaxy clusters. For , robotic 2-meter class reflecting telescopes excel in detecting transients like through automated imaging sequences. The 2-meter Liverpool Telescope, a fully robotic facility, has followed up thousands of candidates, providing rapid photometry to classify events and measure light curves within hours of discovery. These systems trigger alerts for larger telescopes, contributing to surveys that track supernova rates and probes. Atmospheric corrections are essential for ground-based reflecting telescopes, with site selection in dry, high-altitude regions like the yielding median seeing of 0.6-0.8 arcseconds, improvable to 0.5 arcseconds via tip-tilt stabilization. Telescopes at sites such as Cerro Pachón employ wavefront sensors to correct low-order aberrations, enhancing image stability for long exposures. As of 2025, the Vera C. Rubin Observatory's 8.4-meter reflecting telescope inaugurates the Legacy Survey of and Time (LSST), imaging the entire visible southern sky every few nights to detect billions of transient events and variable sources. Its data processing integrates for real-time and classification, handling petabytes of imagery to advance studies in solar system dynamics and cosmology. Upcoming facilities like the 39-meter European Extremely Large Telescope (ELT, first light expected ~2028) and the 25.4-meter (GMT) will further advance segmented reflector designs with integrated for imaging and cosmology.

Role in Space Telescopes and Adaptive Optics

Reflecting telescopes have played a pivotal role in space-based astronomy, enabling high-resolution observations free from atmospheric interference. The (HST) employs a 2.4-meter Ritchey-Chrétien primary mirror, optimized for () and across a broad spectral range from the far- to the near-. This design allows HST to capture detailed images of distant galaxies and stellar phenomena that are obscured by Earth's atmosphere. Similarly, the () features a 6.5-meter primary mirror composed of 18 gold-coated segments, which unfolds after launch to form a lightweight, cryogenic structure capable of observations. The segmented, folded design accommodates the constraints of rocket fairings while providing unprecedented sensitivity for studying the early . Operating in the vacuum of space, reflecting telescopes achieve diffraction-limited performance, unhindered by atmospheric turbulence. For a visible wavelength of approximately 500 nm and a 2.4-meter aperture like HST's, the theoretical is about 0.05 arcseconds, determined by the θ≈1.22λD\theta \approx 1.22 \frac{\lambda}{D}, where λ\lambda is the and DD is the diameter. This resolution enables the detection of fine details in celestial objects, such as planetary disks and jets, far surpassing ground-based capabilities without correction. On the ground, (AO) systems enhance reflecting telescopes by compensating for atmospheric distortions in real time, using deformable mirrors to adjust errors. These systems employ laser guide stars to create artificial reference points when natural stars are unavailable, allowing correction across wider fields. aberrations are decomposed into for phase correction, with the deformable mirror actuators responding via a servo loop to minimize residual errors; typical systems feature delays under 1 ms and up to 1000 actuators for high-order corrections. High-performance AO can achieve Strehl ratios exceeding 0.8 in the near-infrared, approaching diffraction-limited imaging on large-aperture telescopes. Hybrid approaches combine ground-based AO with space-like precision, as demonstrated by the Keck Observatory's AO system, which enables high-resolution exoplanet spectroscopy by injecting light into spectrographs like NIRSPEC for atmospheric characterization. As of 2025, advancements in multi-conjugate AO (MCAO) have expanded corrected fields to several arcminutes, using multiple deformable mirrors to address layered atmospheric turbulence, thereby supporting wide-field surveys on operational facilities and planned ones like the (TMT, under construction with first light in the 2030s).

References

  1. https://science.nasa.gov/universe/telescopes-101/
  2. https://wp.optics.arizona.edu/mnofziger/wp-content/uploads/sites/31/2016/05/OPTI202L-Lab7-Reflective-Telescopes-SP16.pdf
  3. https://web.njit.edu/~cao/Phys320_L6.pdf
  4. https://pages.uoregon.edu/jschombe/glossary/reflecting_telescope.html
  5. https://people.umass.edu/wqd/strobel/telescop/telescpa.htm
  6. http://scipp.ucsc.edu/~haber/ph5B/parabolic09.pdf
  7. https://courses.ems.psu.edu/astro801/content/l3_p7.html
  8. https://www.physics.udel.edu/~jlp/classweb2/directory/powerpoint/telescopes.pdf
  9. http://www.as.utexas.edu/astronomy/education/fall01/ast103l/labpdfs/telescope.pdf
  10. https://sceweb.uhcl.edu/blanford/04Telescopes.pdf
  11. http://www.physics.smu.edu/~jcotton/ph1311/ch03a.htm
  12. https://wi101.wisc.edu/object-history-yerkes-telescope/
  13. https://www.astro.caltech.edu/~george/ay20/reflecting-telescopes.pdf
  14. https://open.maricopa.edu/asttemp/chapter/telescopes/
  15. https://pages.astronomy.ua.edu/keel/techniques/telescopes.html
  16. https://secwww.jhuapl.edu/techdigest/content/techdigest/pdf/V10-N01/10-01-Peacock.pdf
  17. https://micro.magnet.fsu.edu/primer/lightandcolor/mirrorsintro.html
  18. http://www.astro.gsu.edu/~ryle/Lecture11.pdf
  19. https://www.vaticanobservatory.org/education/many-great-minds-take-invent-telescope/
  20. https://www.scientus.org/Reflecting-Telescope-History-2.html
  21. https://thonyc.wordpress.com/2011/11/07/james-gregory-did-not-invent-the-reflecting-telescope/
  22. https://adsabs.harvard.edu/full/1992JHA....23...77S
  23. https://collection.sciencemuseumgroup.org.uk/people/cp43378/james-gregory
  24. https://scienceworld.wolfram.com/astronomy/GregorianTelescope.html
  25. https://history.aip.org/exhibits/cosmology/tools/tools-early-reflectors.htm
  26. https://www.cambridge.org/core/books/an-amateurs-guide-to-observing-and-imaging-the-heavens/newtonian-telescope-and-its-derivatives/729392E965D8D4BC3FCCB42D940E8E17
  27. https://www.omegon.eu/advice/telescope/telescope-knowledge/telescope-different-types/the-newtonian-reflector/c%2C8687
  28. https://www.lindahall.org/about/news/scientist-of-the-day/laurent-cassegrain/
  29. https://royalsociety.org/blog/2020/05/object-lessons/
  30. https://blog.sciencemuseum.org.uk/looking-at-the-mirror/
  31. https://galileo.library.rice.edu/sci/instruments/telescope.html
  32. https://adsabs.harvard.edu/full/1987JBAA...98....8W
  33. https://www.rmg.co.uk/collections/objects/rmgc-object-11109
  34. https://web.astronomicalheritage.net/show-entity?identity=198&idsubentity=1
  35. https://adsabs.harvard.edu/full/1977JBAA...87..472H
  36. https://www.researchgate.net/publication/308696652_EVOLUTION_OF_THE_FOUCAULT-SECRETAN_REFLECTING_TELESCOPE
  37. https://www.mtwilson.edu/discovering-mount-wilson-chapter-7-first-light-on-the-100-inch-telescope/
  38. https://www.mtwilson.edu/building-the-100-inch-telescope/
  39. https://carnegiescience.edu/about/history/universe-edwin-hubble
  40. https://science.nasa.gov/mission/hubble/overview/the-history-of-hubble/
  41. https://science.nasa.gov/mission/hubble/observatory/design/optics/
  42. https://magazine.caltech.edu/post/building-keck-an-oral-history
  43. https://keckobservatory.org/our-story/telescopes/
  44. https://www2.lbl.gov/Science-Articles/Archive/keck-telescope.html
  45. https://elt.eso.org/mirror/
  46. https://www.eso.org/public/news/eso2310/
  47. https://www.eso.org/public/announcements/ann25001/
  48. https://www.handprint.com/ASTRO/ae4.html
  49. https://www.telescope-optics.net/spherical1.htm
  50. https://www.telescope-optics.net/coma.htm
  51. https://www.rp-photonics.com/optical_aberrations.html
  52. https://www.telescope-optics.net/Seidel_aberrations.htm
  53. https://www.telescope-optics.net/classical_and_aplanatic.htm
  54. https://www.eso.org/sci/facilities/develop/ao/what_ao.html
  55. https://collection.sciencemuseumgroup.org.uk/objects/co56770/original-mirror-for-william-herschels-forty-foot-telescope-1785
  56. https://www.brlsi.org/a-mirror-of-the-past-herschel-and-the-james-webb-space-telescope
  57. https://www.britannica.com/science/primary-mirror
  58. https://opticaorgdev.blob.core.windows.net/%24web/optica/media/osa.history/century_of_optics/1941-1959/68.pdf
  59. https://ntrs.nasa.gov/api/citations/20180006385/downloads/20180006385.pdf
  60. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/11180/1118017/ZERODUR-as-a-dimensionally-stable-mirror-substrate-material-for-spaceborne/10.1117/12.2535962.full
  61. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10567/2308098/An-ultra-lightweight-large-aperture-deployable-telescope-for-advanced-lidar/10.1117/12.2308098.full
  62. https://opg.optica.org/abstract.cfm?uri=OAM-1991-WC5
  63. https://ntrs.nasa.gov/api/citations/20130009019/downloads/20130009019.pdf
  64. https://www.astroreflect.com/optical-tests/
  65. https://www.edmundoptics.com/knowledge-center/application-notes/optics/metallic-mirror-coatings/
  66. https://www.band-optics.com/blog/coating-telescope-mirror.html
  67. https://news.ucsc.edu/2017/09/mirror-coating/
  68. https://www2.keck.hawaii.edu/observing/kecktelgde/ktelinstupdate.pdf
  69. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/12182/121821B/Thirty-Meter-Telescope-TMT-project-status/10.1117/12.2631546.full
  70. https://www.coherent.com/news/press-releases/100th-roundel-for-thirty-meter-telescope-project-delivered
  71. https://www.montana.edu/jshaw/documents/17a%20EELE582_S15_TelescopeDesign.pdf
  72. https://skyandtelescope.org/wp-content/uploads/GS-Adler-Secondary.pdf
  73. https://faculty.up.edu/lulay/EGR491/Optics4-TelescopeSpecifications.pdf
  74. https://srmastro.uvacreate.virginia.edu/astr1230/LECTURES/LECTURE3/lecture3C-s13.html
  75. https://collection.sciencemuseumgroup.org.uk/objects/co56491/cassegrain-reflecting-telescope-1762-1774
  76. https://www.astronomy.com/observing/the-history-of-the-ritchey-chretien-telescope/
  77. https://science.nasa.gov/mission/hubble/observatory/design/
  78. https://adsabs.harvard.edu/full/1998BASI...26..353B
  79. https://www.telescope-optics.net/dall_kirkham_telescope.htm
  80. https://www.telescope-optics.net/three-mirror.htm
  81. https://www.telescope-optics.net/obstruction.htm
  82. http://www.astrophoto.fr/obstruction.html
  83. https://spie.org/Publications/Proceedings/Paper/10.1117/12.857310
  84. https://ntrs.nasa.gov/api/citations/19680001637/downloads/19680001637.pdf
  85. https://adsabs.harvard.edu/full/2009JRASC.103...18G
  86. https://spie.org/Publications/Proceedings/Paper/10.1117/12.2279782
  87. https://ui.adsabs.harvard.edu/abs/2020SPIE11478E..0BW/abstract
  88. https://www.telescope-optics.net/TCT_2.htm
  89. https://adsabs.harvard.edu/full/1986JRASC..80..128O
  90. https://www.americanscientist.org/article/liquid-mirror-telescopes
  91. https://adsabs.harvard.edu/full/1991JRASC..85..158G
  92. https://www.astro.ubc.ca/LMT/Nodo/index.html
  93. https://ui.adsabs.harvard.edu/abs/2007PASP..119..444H/abstract
  94. https://www.aanda.org/articles/aa/pdf/2006/04/aa3880-05.pdf
  95. https://adsabs.harvard.edu/full/1987PASP...99.1229B
  96. https://adsabs.harvard.edu/full/1985PASP...97..454B
  97. https://ui.adsabs.harvard.edu/abs/1998HiA....11..464H/abstract
  98. https://www.researchgate.net/publication/383459024_Development_of_a_self-assembling_ferrofluidic_ionic_liquid_mirror
  99. https://www.aanda.org/articles/aa/full_html/2025/02/aa52667-24/aa52667-24.html
  100. https://www.nasa.gov/science-research/astrophysics/what-is-the-fluidic-telescope/
  101. https://www.darpa.mil/news/2023/liquid-mirror-telescope-designs
  102. https://www.pas.rochester.edu/~blackman/ast104/reflecting.html
  103. https://celt.ucolick.org/greenbook/ch03.pdf
  104. https://subarutelescope.org/en/news/topics/2025/01/09/3499.html
  105. https://spie.org/news/1203-advanced-instruments-for-the-subaru-telescope
  106. https://www.telescope-optics.net/two-mirror.htm
  107. https://www.cloudynights.com/topic/666494-percentage-of-light-loss-from-secondary-obstruction/
  108. https://library.nrao.edu/public/memos/misc/MISC_UNUM_1064.pdf
  109. https://ccdsh.konkoly.hu/wiki/Cassegrain_Optics
  110. https://subarutelescope.org/en/about/instrument/fmos/index.html
  111. https://arxiv.org/abs/astro-ph/0012443
  112. https://noirlab.edu/public/announcements/geminiann04002/
  113. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/13097/130970M/Adaptive-optics-at-Gemini-observatories-past-present-and-future/10.1117/12.3019127.full
  114. https://www.sdss.org/dr18/
  115. http://ui.adsabs.harvard.edu/abs/2013AJ....146...32S/abstract
  116. https://academic.oup.com/mnras/article/508/4/5138/6385772
  117. https://amsdottorato.unibo.it/id/eprint/2031/1/lombardi_gianluca_tesi.pdf
  118. https://spectrum.ieee.org/vera-rubin-observatory-first-images
  119. https://ntrs.nasa.gov/api/citations/19920008265/downloads/19920008265.pdf
  120. https://science.nasa.gov/mission/webb/webbs-mirrors/
  121. https://www.eoportal.org/satellite-missions/jwst
  122. https://esahubble.org/about/faq/
  123. https://www.eso.org/sci/facilities/eelt/owl/Blue_Book/8_Adaptive_optics.pdf
  124. https://arxiv.org/pdf/2103.07566
  125. https://pmc.ncbi.nlm.nih.gov/articles/PMC8892592/
  126. https://www.tmt.org/page/instruments-adaptive-optics
Add your contribution
Related Hubs
User Avatar
No comments yet.