Hubbry Logo
DodecagramDodecagramMain
Open search
Dodecagram
Community hub
Dodecagram
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Dodecagram
Dodecagram
Dodecagram
View on Wikipedia
from Wikipedia
Regular dodecagram
A regular dodecagram
TypeRegular star polygon
Edges and vertices12
Schläfli symbol{12/5}
t{6/5}
Coxeter–Dynkin diagrams
Symmetry groupDihedral (D12)
Internal angle (degrees)30°
Propertiesstar, cyclic, equilateral, isogonal, isotoxal
Dual polygonself

In geometry, a dodecagram (from Greek δώδεκα (dṓdeka) 'twelve' and γραμμῆς (grammēs) 'line'[1]) is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon (with Schläfli symbol {12/5} and a turning number of 5). There are also 4 regular compounds {12/2}, {12/3}, {12/4}, and {12/6}.

Regular dodecagram

[edit]

There is one regular form: {12/5}, containing 12 vertices, with a turning number of 5. A regular dodecagram has the same vertex arrangement as a regular dodecagon, which may be regarded as {12/1}.

Dodecagrams as regular compounds

[edit]

There are four regular dodecagram star figures: {12/2}=2{6}, {12/3}=3{4}, {12/4}=4{3}, and {12/6}=6{2}. The first is a compound of two hexagons, the second is a compound of three squares, the third is a compound of four triangles, and the fourth is a compound of six straight-sided digons. The last two can be considered compounds of two compound hexagrams and the last as three compound tetragrams.

  • 2{6}
    2{6}
  • 3{4}
    3{4}
  • 4{3}
    4{3}
  • 6{2}
    6{2}

Dodecagrams as isotoxal figures

[edit]

An isotoxal polygon has two vertices and one edge type within its symmetry class. There are 5 isotoxal dodecagram star with a degree of freedom of angles, which alternates vertices at two radii, one simple, 3 compounds, and 1 unicursal star.

Isotoxal dodecagrams
Type Simple Compounds Star
Density 1 2 3 4 5
Image
{(6)α}
2{3α}
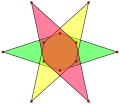3{2α}
2{(3/2)α}
{(6/5)α}

Dodecagrams as isogonal figures

[edit]

A regular dodecagram can be seen as a quasitruncated hexagon, t{6/5}={12/5}. Other isogonal (vertex-transitive) variations with equally spaced vertices can be constructed with two edge lengths.


t{6}
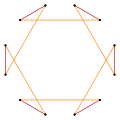
t{6/5}={12/5}

Complete graph

[edit]

Superimposing all the dodecagons and dodecagrams on each other – including the degenerate compound of six digons (line segments), {12/6} – produces the complete graph K12.

K12
black: the twelve corner points (nodes)

red: {12} regular dodecagon
green: {12/2}=2{6} two hexagons
blue: {12/3}=3{4} three squares
cyan: {12/4}=4{3} four triangles
magenta: {12/5} regular dodecagram
yellow: {12/6}=6{2} six digons

Regular dodecagrams in polyhedra

[edit]

Dodecagrams can also be incorporated into uniform polyhedra. Below are the three prismatic uniform polyhedra containing regular dodecagrams (there are no other dodecagram-containing uniform polyhedra).

  • Dodecagrammic prism
    Dodecagrammic prism
  • Dodecagrammic antiprism
    Dodecagrammic antiprism
  • Dodecagrammic crossed-antiprism
    Dodecagrammic crossed-antiprism

Dodecagrams can also be incorporated into star tessellations of the Euclidean plane.

Dodecagram Symbolism

[edit]
The twelve-pointed star is a prominent feature on the ancient Vietnamese Dong Son drums

Dodecagrams or twelve-pointed stars have been used as symbols for the following:

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Dodecagram

View on Grokipedia
from Grokipedia
A dodecagram is a regular with twelve vertices, denoted by the {12/5}, formed by connecting every fifth point among twelve equally spaced points on a . This geometric figure is a type of , characterized by its intersecting edges that create a star-like with a of 5, meaning the polygon winds around the center five times before closing. Unlike the convex regular {12}, which has no intersecting sides, the dodecagram {12/5} is non-convex and represents one of the distinct star polygons possible for twelve vertices, equivalent to {12/7} due to . It can be constructed using compass and , as twelve is a , and its vertices lie on a common . The is notable as the sole non-compound of the regular , obtained by extending the sides of the until they intersect to form the . In the broader context of uniform and tilings, it relates to other polygons through shared symmetry groups, specifically the D_{12} with 24 elements. While compounds involving twelve vertices exist—such as {12/2} (two regular hexagons) or {12/3} (three squares)—the term "dodecagram" typically refers to the simple {12/5} form in geometric literature.

Definition and Properties

Star Polygons and Schläfli Symbols

A dodecagram is a or compound polygon with 12 vertices, derived from prefix dōdeka- meaning "twelve" and the -gramma meaning "that which is drawn" or "line." are non-convex constructed by connecting every k-th vertex among n equally spaced points on a , where k > 1 and k < n/2 to avoid redundancy. This process traces a single closed path that intersects itself, forming the characteristic star shape, unlike the convex boundary of a simple regular . Regular star polygons, including dodecagrams, are denoted using Schläfli symbols of the form {n/m}\{n/m\}, where n is the number of vertices and m (the density) indicates the step size or number of edges crossed between connected vertices. For dodecagrams, n = 12, and m ranges from 1 to 5, as {12/m}={12/(12−m)}\{12/m\} = \{12/(12-m)\} due to rotational symmetry, with {12/7}\{12/7\} equivalent to {12/5}\{12/5\} in the opposite direction. The density m measures the number of polygon edges enclosed within the figure; for example, {12/5}\{12/5\} is the primary regular dodecagram with density 5, producing a simple star with five intersecting layers. Regular dodecagrams are classified as simple or compound based on whether the greatest common divisor of 12 and m is 1. The convex form {12/1}\{12/1\} is the regular dodecagon, a simple polygon with no intersections. {12/5}\{12/5\} and {12/7}\{12/7\} are simple star polygons, each forming a single connected component. In contrast, {12/2}\{12/2\}, {12/3}\{12/3\}, {12/4}\{12/4\}, and {12/6}\{12/6\} are compounds, consisting of multiple intertwined due to a greatest common divisor greater than 1 between 12 and m. All dodecagrams share the same vertex arrangement as the regular , with vertices equally spaced on a common circumcircle.

Geometric Properties

A dodecagram is a regular star polygon inscribed in a circle, sharing the same 12 equally spaced vertices as a regular , with edges connecting every k-th vertex according to its {12/k}. This inscription ensures that all vertices lie on the circumcircle of the enclosing , maintaining rotational symmetry while allowing the star form to intersect itself. The density of a dodecagram {12/k} is defined as k, representing the minimum number of edges crossed by a ray extending from the center to the exterior of the polygon. For example, the dodecagram {12/5} has a density of 5, indicating that such a ray intersects five edges before exiting. This measure quantifies the winding complexity of the figure around its center. The turning number, equivalent to the density in this context, is also 5 for {12/5}, signifying the number of complete rotations the boundary makes around the center during traversal. The interior angle at each vertex of a regular dodecagram {n/m} is given by the formula (n−2m)×180∘n\frac{(n - 2m) \times 180^\circ}{n}, where m is the density. For the {12/5} dodecagram, this yields (12−10)×180∘12=30∘\frac{(12 - 10) \times 180^\circ}{12} = 30^\circ, the acute angle at the points of the star. This calculation generalizes the interior angle formula for convex polygons by accounting for the increased intersections due to density. The dodecagrams {12/5} and {12/7} are retrogrades of each other, meaning they share the same vertex set and edge connections but are traversed in opposite directions, forming mirror images or isogonal conjugates in the context of star polygon symmetry. This relationship highlights the orientational duality inherent in regular star polygons with densities summing to the number of sides.

Types of Dodecagrams

Simple Regular Dodecagrams

Simple regular dodecagrams refer to the non-compound, unicursal star polygons constructed from 12 equally spaced vertices on a circle, where the connections form a single continuous path without separate components. These are denoted using Schläfli symbols 12/k{12/k}, where kk is coprime to 12 and 1<k<61 < k < 6, yielding the distinct star form 12/5{12/5}, with 12/7{12/7} as its enantiomorph obtained by reversing the connection direction (equivalent to k=12−5=7k=12-5=7). Unlike compound variants, their edges intersect internally to create a cohesive star outline, emphasizing rotational symmetry and uniform side lengths. The primary simple regular dodecagram, 12/5{12/5}, consists of 12 vertices and 12 equal-length edges that link every fifth point in the vertex set. This configuration produces a five-pointed star-like appearance with multiple intersection points, where each edge crosses others to enclose a central pentagonal region surrounded by triangular and other polygonal areas. As a unicursal figure, it can be drawn in one continuous stroke, highlighting its connected, non-degenerate structure. The form 12/7{12/7} serves as the enantiomorph of 12/5{12/5}, achieved by connecting every seventh vertex, which mirrors the original by reversing the connection direction. This results in opposite chirality—left-handed versus right-handed—while maintaining the same geometric density and overall topology, including 12 vertices and 12 edges. Visually, it exhibits analogous intersections and internal divisions, distinguishable only by orientation. In terms of density, simple regular dodecagrams 12/5{12/5} and 12/7{12/7} have density 5, measuring the winding number, or how many times the polygon's boundary encircles the center before closing, providing a measure of the figure's "starriness" and intersection complexity.

Compound Dodecagrams

Compound dodecagrams are regular compounds formed by superimposing multiple regular polygons that share the same twelve vertices arranged on a circle, exhibiting full rotational symmetry of the . These compounds arise when the Schläfli symbol {12/k} has k sharing a common divisor greater than 1 with 12, resulting in disconnected components rather than a single connected star polygon. Unlike simple dodecagrams, which form a single continuous path connecting all vertices, compound dodecagrams consist of multiple independent polygons overlaid with precise rotational offsets. There are four regular compound dodecagrams, each decomposing into identical regular polygons. The compound {12/2}, also denoted as 2{6/1}, comprises two regular hexagons rotated by 30 degrees relative to each other, sharing the twelve vertices. Similarly, {12/3} or 3{4/1} consists of three regular squares offset by 30 degrees. The {12/4} compound, written as 4{3/1}, is made of four equilateral triangles rotated by 15 degrees apart. Finally, {12/6} or 6{2/1} involves six digons, which are degenerate line segments connecting antipodal vertices, arranged with 15-degree rotations. These formations ensure that the overall figure maintains the dihedral symmetry of order 24. The density of a compound dodecagram is calculated as the sum of the densities of its component polygons, where each convex component like a or has density 1. For instance, {12/2} has density 2 from its two , {12/3} density 3 from the three , {12/4} density 4 from the four , and {12/6} density 6 from the six . This additive density measures the total winding or enclosure within the vertex arrangement, distinguishing compounds by their multi-layered coverage compared to the singular density of simple stars.
CompoundSchläfli SymbolComponentsNumber of ComponentsDensity
Two hexagons{12/2} or 2{6/1}Regular hexagons22
Three squares{12/3} or 3{4/1}33
Four triangles{12/4} or 4{3/1}44
Six digons{12/6} or 6{2/1} (line segments)66
These compounds are constructed by connecting every k-th vertex among the twelve, but due to the common divisor, the path closes after fewer steps, repeating to form the separate .

Symmetry and Variations

Isotoxal Dodecagrams

An isotoxal dodecagram is defined as a 12-sided polygonal figure, either simple or compound, where all edges are of equal length and the symmetry group acts transitively on the edges, ensuring identical vertex figures up to symmetry. This property distinguishes isotoxal figures from more general equilateral polygons by emphasizing edge uniformity under the full symmetry operations. There are five regular isotoxal dodecagrams, classified by their densities: density 1 corresponds to the convex dodecagon {12/1}; density 2 to the compound {12/2} consisting of two regular hexagons; density 3 to the compound {12/3} of three squares; density 4 to the compound {12/4} of four equilateral triangles; and density 5 to the simple great dodecagon {12/5}. These figures share the vertex set of a regular 12-gon but connect vertices differently according to the Schläfli symbol {12/k}, where k determines the density and connection step. The compounds for k=2,3,4 arise because gcd(12,k)>1, resulting in multiple interwoven regular polygons that together form an isotoxal structure. Irregular isotoxal dodecagrams also exist, featuring equal edge lengths but non-regular interior angles, often with two alternating vertex types under the symmetry group. Examples include rhombidodecagrams, which maintain edge transitivity while allowing variations in angle measures, providing flexibility beyond the regular cases. For the regular isotoxal dodecagrams, the symmetry group is the full dihedral group D_{12}, of order 24, which acts transitively on both edges and vertices. This group includes rotations by multiples of 30° and reflections, preserving the equilateral and uniform vertex figure properties across all five variants.

Isogonal Dodecagrams

Isogonal dodecagrams are star polygons with 12 vertices that exhibit vertex-transitivity under their , ensuring all vertices are equivalent and thus feature equal angles at each vertex, though edge lengths may vary. This property distinguishes them from regular dodecagrams, where both edges and angles are uniform, allowing for more flexible geometric configurations while preserving angular uniformity. These figures form part of continuous families of isogonal 12-gons that morph between convex and configurations, such as transitioning from the regular {12/1} to the dodecagram {12/5}, with edge lengths adjusting continuously to maintain equal vertex angles throughout the metamorphosis. In such families, the polygons remain equiangular, often featuring alternating edge lengths that reflect the underlying , typically reduced to dihedral order n/2 for even-sided forms. A prominent example is the quasitruncated hexagon, symbolized as t{6/5} and equivalent to {12/5} in its uniform realization, where isogonal variants incorporate two alternating edge lengths to achieve the star topology while upholding vertex-transitive symmetry. Other variants, such as alternated forms derived from snubbing operations, introduce chiral symmetry, resulting in enantiomorphic pairs with equal angles but non-superimposable mirror images. These isogonal dodecagrams occasionally serve as faces or equatorial girdles in uniform star polyhedra, linking planar symmetry to higher-dimensional structures.

Representations and Constructions

Complete Graph Representation

The complete graph representation of dodecagrams conceptualizes the superposition of all distinct regular star polygons and their compounds inscribed in a regular dodecagon. By overlaying the edge sets of {12/k} for k=1 to 6—where {12/1} is the convex , {12/2} is a compound of two hexagons, {12/3} is a compound of three squares, {12/4} is a compound of four triangles, {12/5} is the simple star dodecagram, and {12/6} is six diameters—the resulting figure encompasses every possible connection between the 12 vertices. This union forms the , consisting of 12 vertices and \binom{12}{2} = 66 edges, as each {12/k} contributes chords spanning k steps, collectively covering all pairwise links without omission or duplication beyond multiplicity in compounds. In this visualization, the vertices lie equally spaced on a , and each edge type in the superposition corresponds to a unique chord length determined by the angular separation in the . The full overlay produces a intricate, symmetric of intersecting lines that densely fills the interior, illustrating the exhaustive connectivity among the points; shorter chords from smaller k values form near-peripheral connections, while larger k yield more central crossings. This graphical embedding highlights the combinatorial richness of dodecagrams, treating them as subgraphs of the maximal connection network. From a perspective, is non-planar, containing minors of the forbidden K_5 or K_{3,3} subgraphs, and possesses a chromatic number of 12, requiring one color per vertex to avoid adjacent monochromatic pairs. This representation aids in enumerating edges across dodecagram variants by providing a universal framework: individual {12/k} edge counts (e.g., 12 edges for simple cases, multiples for compounds) sum toward the total 66, facilitating analysis of densities and intersections.

Construction Methods

One common method for constructing a dodecagram using and begins with the creation of a regular , followed by connecting specific vertices to form the star pattern. To construct the regular inscribed in a , first draw the and inscribe a regular hexagon within it by marking six equally spaced points using the set to the 's radius. Then, for each side of the hexagon, draw two circles centered at the endpoints of the side and passing through the 's center; the intersection points of these circles (other than the center) lie on the original and bisect the arcs between hexagon vertices, yielding the 12 equally spaced vertices of the . For the simple regular dodecagram {12/5}, connect every fifth vertex around the using the , starting from any vertex and proceeding sequentially until the figure closes after traversing all 12 points. In coordinate geometry, the vertices of a regular dodecagram {12/5} can be placed on the unit circle centered at the origin, with coordinates given by (cos⁡2πk12,sin⁡2πk12)\left( \cos \frac{2\pi k}{12}, \sin \frac{2\pi k}{12} \right) for k=0,1,…,11k = 0, 1, \dots, 11. The edges are then drawn between vertex kk and vertex (k+5)mod  12(k+5) \mod 12, producing the intersecting star pattern. This parametric representation allows for precise plotting in Cartesian coordinates, where the angles correspond to increments of 30∘30^\circ around the circle. For digital or parametric constructions, particularly in computational , a dodecagram {12/5} can be generated using polar coordinates with a fixed r=1r=1 and angular steps of 150∘150^\circ (equivalent to 5×30∘5 \times 30^\circ), starting from θ=0∘\theta=0^\circ and incrementing θk=k×150∘\theta_k = k \times 150^\circ for k=0k=0 to $11,thenconnectingconsecutivepointstoformthestar.[](https://mathworld.wolfram.com/StarPolygon.html)Theverticesarecomputedas, then connecting consecutive points to form the star.[](https://mathworld.wolfram.com/StarPolygon.html) The vertices are computed as (r \cos \theta_k, r \sin \theta_k)$, and the path closes after 12 steps due to the density of the . Compound dodecagrams, such as {12/3} (a compound of three squares) or {12/4} (a compound of four equilateral triangles), are constructed by separately building each component inscribed in the same circle using the above methods, then superimposing the figures by drawing all edges together.

Applications

In Polyhedra and Tessellations

Dodecagrams appear as bases in three uniform prismatic polyhedra, each constructed by connecting parallel faces with rectangular or triangular lateral faces. The dodecagrammic consists of two dodecagrams and twelve squares, with each vertex incident to one dodecagram and two squares, resulting in a central of 5. The dodecagrammic antiprism features two dodecagrams connected by twenty-four equilateral triangles, where each vertex meets one dodecagram and three triangles, maintaining uniform symmetry under the . The dodecagrammic retroprism, also known as the crossed antiprism variant, similarly includes two dodecagrams and twenty-four triangles, but with a twisted configuration that enhances its nonconvex star properties while preserving vertex-transitivity. Beyond prisms, dodecagrams do not form faces in the Kepler–Poinsot polyhedra, which instead use pentagrams, though isogonal dodecagrammic forms can be adapted for faces in certain nonconvex polyhedra. In s, dodecagrams enable patterns with greater than 1, particularly in . By replacing dodecagons in the {12,12,3} hyperbolic with {12/5} dodecagrams—aligning vertices to the original lattice—three distinct uniform tilings emerge, such as the {12/5,6,12/5,∞} pattern combining dodecagrams, hexagons, and infinite apeirogons, illustrating how polygons facilitate non-Euclidean edge-to-edge coverings.

Symbolism and Historical Context

The dodecagram, or twelve-pointed star, appears as a central motif on many ancient Vietnamese Đông Sơn bronze drums, dating from approximately 1000 BCE to 300 CE, where it is often interpreted as a celestial or associated with rituals and ancestral protection. These drums, produced by the Đông Sơn culture in the , feature the star encircled by concentric bands of motifs such as water birds and geometric patterns, signifying between the earthly and divine realms. The emblem's prominence underscores its role in Southeast Asian cosmology, evoking protective energies against misfortune. In medieval Islamic geometric art, particularly from and between the 13th and 15th centuries, twelve-pointed stars were integral to intricate tilework and architectural ornamentation, symbolizing divine order and multiplicity through interlocking polygons. These patterns, often constructed using compass and methods, represented the infinite nature of creation and appeared in mosques and madrasas as compounded forms evoking . During the in , similar compounded star motifs emerged in , where twelve-pointed variants denoted noble lineages or celestial multiplicity, though less common than simpler . Such designs reflected a broader revival of classical , blending symbolic depth with aesthetic complexity. In modern contexts, the dodecagram holds significance in occult traditions, frequently symbolizing the twelve zodiac signs and the cyclical harmony of the cosmos. It appears in esoteric practices as a of wholeness and spiritual integration, drawing on ancient astrological associations. Variations also feature in national emblems, such as Namibia's flag, where a twelve-pointed golden star represents the country's twelve ethnic regions and unity post-independence. In the 20th century, mathematician H.S.M. Coxeter advanced systematic analysis of the dodecagram {12/5} within regular polytopes and star configurations, emphasizing its topological properties in modern geometry.

References

  1. https://mathworld.wolfram.com/Dodecagram.html
  2. https://mathworld.wolfram.com/StarPolygon.html
  3. https://mathworld.wolfram.com/RegularPolygon.html
  4. https://polytope.miraheze.org/wiki/Dodecagon
  5. https://www.etymonline.com/word/dodeca-
  6. https://www.etymonline.com/word/-gram
  7. https://encyclopediaofmath.org/wiki/Polygon
  8. https://mathworld.wolfram.com/SchlaefliSymbol.html
  9. http://www.mapleprimes.com/posts/219833-Regular-Polyhedra-And-Schlfli-Symbols
  10. https://ospi.k12.wa.us/sites/default/files/2023-08/star-polygons-ada.pdf
  11. https://walser-h-m.ch/hans/Miniaturen/S/Star-Polygons/Star-Polygons.pdf
  12. https://jasoncantarella.com/downloads/coxeter-chapter-3.pdf
  13. https://www.bendwavy.org/polytile/polytile-notation-intro-A4-revision1.pdf
  14. https://mathworld.wolfram.com/RegularDodecagon.html
  15. http://faculty.washington.edu/moishe/branko/BG201.Metamorphoses.pdf
  16. https://ejmt.mathandtech.org/Contents/eJMT_v15n3p2.pdf
  17. https://bendwavy.org/klitzing/explain/isogonal.htm
  18. https://polytope.miraheze.org/wiki/Dodecagram
  19. http://www.polytope.net/hedrondude/sym.htm
  20. https://mathworld.wolfram.com/UniformPolyhedron.html
  21. https://mathworld.wolfram.com/CompleteGraph.html
  22. https://www.math.brown.edu/tbanchof/Beyond3d.new/chapter5/s5_1.html
  23. https://mathworld.wolfram.com/deMoivreNumber.html
  24. https://polytope.miraheze.org/wiki/Dodecagrammic_prism
  25. https://polytope.miraheze.org/wiki/Dodecagrammic_antiprism
  26. https://polytope.miraheze.org/wiki/Dodecagrammic_retroprism
  27. http://www.orchidpalms.com/polyhedra/tessellations/type3.htm
  28. https://www.roots.gov.sg/Collection-Landing/listing/1038527
  29. https://mim.org/wp-content/uploads/2022/08/CGC-2022-Vietnam-Tool-Kit.pdf
  30. https://vietnamnet.vn/en/national-treasure-sao-vang-bronze-drum-insured-for-1-million-2289470.html
  31. https://archive.bridgesmathart.org/2015/bridges2015-45.pdf
  32. https://www.aramcoworld.com/articles/2022/art-of-islamic-patterns-a-moorish-star
  33. https://escholarship.org/uc/item/4pp65378
  34. https://www.lucistrust.org/blog_triangles/12_pointed_star_and_the_new_age_symbol
  35. https://www.outofstress.com/12-pointed-star-meaning/
  36. https://worldpopulationreview.com/country-rankings/country-with-stars-on-flag
  37. https://projecteuclid.org/journals/bulletin-of-the-american-mathematical-society/volume-56/issue-5/Self-dual-configurations-and-regular-graphs/bams/1183514923.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.