Hubbry Logo
OctagramOctagramMain
Open search
Octagram
Community hub
Octagram
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Octagram
Octagram
Octagram
View on Wikipedia
from Wikipedia
Regular octagram
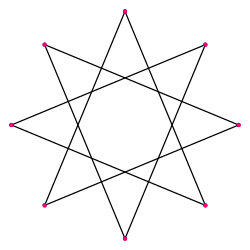A regular octagram
TypeRegular star polygon
Edges and vertices8
Schläfli symbol{8/3}
t{4/3}
Coxeter–Dynkin diagrams
Symmetry groupDihedral (D8)
Internal angle (degrees)45°
Propertiesstar, cyclic, equilateral, isogonal, isotoxal
Dual polygonself
Star polygons

In geometry, an octagram is an eight-angled star polygon.

The name octagram combine a Greek numeral prefix, octa-, with the Greek suffix -gram. The -gram suffix derives from γραμμή (grammḗ) meaning "line".[1]

Detail

[edit]
A regular octagram with each side length equal to 1

In general, an octagram is any self-intersecting octagon (8-sided polygon).

The regular octagram is labeled by the Schläfli symbol {8/3}, which means an 8-sided star, connected by every third point.

Variations

[edit]

These variations have a lower dihedral, Dih4, symmetry:


Narrow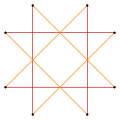

Wide
(45 degree rotation)

Isotoxal
An old Flag of Chile contained this octagonal star geometry with edges removed (the Guñelve).
The regular octagonal star is very popular as a symbol of rowing clubs in the Cologne Lowland, as seen on the club flag of the Cologne Rowing Association.
The geometry can be adjusted so 3 edges cross at a single point, like the Auseklis symbol
An 8-point compass rose can be seen as an octagonal star, with 4 primary points, and 4 secondary points.

The symbol Rub el Hizb is a Unicode glyph ۞  at U+06DE.

As a quasitruncated square

[edit]

Deeper truncations of the square can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated square is an octagon, t{4}={8}. A quasitruncated square, inverted as {4/3}, is an octagram, t{4/3}={8/3}.[2]

The uniform star polyhedron stellated truncated hexahedron, t'{4,3}=t{4/3,3} has octagram faces constructed from the cube in this way. It may be considered for this reason as a three-dimensional analogue of the octagram.

Isogonal truncations of square and cube
Regular Quasiregular Isogonal Quasiregular

{4}
t{4}={8}
t'{4}=t{4/3}={8/3}
Regular Uniform Isogonal Uniform

{4,3}
t{4,3}
t'{4,3}=t{4/3,3}

Another three-dimensional version of the octagram is the nonconvex great rhombicuboctahedron (quasirhombicuboctahedron), which can be thought of as a quasicantellated (quasiexpanded) cube, t0,2{4/3,3}.

Star polygon compounds

[edit]

There are two regular octagrammic star figures (compounds) of the form {8/k}, the first constructed as two squares {8/2}=2{4}, and second as four degenerate digons, {8/4}=4{2}. There are other isogonal and isotoxal compounds including rectangular and rhombic forms.

Regular Isogonal Isotoxal

a{8}={8/2}=2{4}
{8/4}=4{2}

{8/2} or 2{4}, like Coxeter diagrams + , can be seen as the 2D equivalent of the 3D compound of cube and octahedron, + , 4D compound of tesseract and 16-cell, + and 5D compound of 5-cube and 5-orthoplex; that is, the compound of a n-cube and cross-polytope in their respective dual positions.

Other presentations of an octagonal star

[edit]

An octagonal star can be seen as a concave hexadecagon, with internal intersecting geometry erased. It can also be dissected by radial lines.

star polygon Concave Central dissections

Compound 2{4}
|8/2|

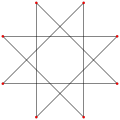Regular {8/3}
|8/3|

Isogonal

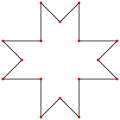
Isotoxal

Other uses

[edit]
  • In Unicode, the "Eight Spoked Asterisk" symbol ✳ is U+2733.
A big round white circle with faint rays around on a brown background. A black irregular shape stands on its left border. A black spot to its left issues six white spikes separated by 60 degrees and two fainter spikes in vertical.
The spikes are specially visible around Jupiter's moon Europa (on the left) in this NIRCam image.
Edges of the JWST primary mirror segments and spider colour-coded with their corresponding diffraction spikes
  • The 8-pointed diffraction spikes of the star images from the James Webb Space Telescope are due to the diffraction caused by the hexagonal shape of the mirror sections and the struts holding the secondary mirror.[3]
  • Used as a parol or star for the 2010 ABS-CBN Christmas Station ID Ngayong Pasko Magniningning Ang Pilipino (lit. 'This Christmas, the Filipinos will Shine') due to the usage of a sun from the Philippine flag, making it also a nationalism and patriotism-themed song aside from being a Christmas song.

See also

[edit]
Wikimedia Commons has media related to Octagrams.
Usage
Stars generally
Others

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Octagram

View on Grokipedia
from Grokipedia
An octagram is a regular star polygon consisting of eight sides and eight vertices, denoted by the {8/3}, formed by connecting every third point among eight equally spaced points on a , resulting in a self-intersecting, non-convex figure. It possesses octagonal dihedral symmetry (D8), a central of 3, and an interior angle of 45°, with its area given by 2(√2 - 1) for a side length of 1. The can be constructed as the second of a regular or as a uniform quasitruncation of a square, and its is the enantiomorphic form {8/5}. Unlike compound eight-pointed stars such as the Star of ({8/2}, formed by two overlapping squares), the is a single, simple . In higher dimensions, it relates to uniform , appearing as faces in certain 5D and higher figures. Historically, the octagram has held significant symbolic meaning across cultures, often representing celestial bodies, deities, and cosmic order due to its geometric elegance and constructibility with compass and straightedge. In ancient , it symbolized the Sumerian goddess (later Ishtar in Semitic traditions), associated with , , and the planet , appearing in from the third millennium BCE. This motif influenced later artistic traditions, including medieval Islamic tessellations in architecture—such as those in the Alcazar of —where it contributed to intricate geometric patterns emphasizing harmony and infinity, evolving from simpler forms in the 9th century to more complex star designs by the 16th century.

Definition and Basic Properties

Geometric Definition

An octagram is an eight-vertex {8/3} formed by connecting every third point on the vertices of a regular . This self-intersecting figure exhibits the rotational and reflectional symmetries of the underlying while creating a star-like shape through its overlapping sides. The construction begins with a regular inscribed in a circle of circumradius RR, where the eight vertices are positioned at equal angular intervals of 45∘45^\circ. To form the octagram, connect successive vertices by skipping two intervening points (connecting every third point overall), yielding line segments that each subtend a of 135∘135^\circ. In this case, the side length ss of each edge is the chord corresponding to this , calculated as
s=2Rsin⁡(135∘2)=2Rsin⁡(67.5∘).s = 2 R \sin\left( \frac{135^\circ}{2} \right) = 2 R \sin(67.5^\circ).
At each vertex, the angle between adjacent sides, known as the vertex angle, measures 45∘45^\circ, derived from the generalized interior angle sum for star polygons divided equally among the vertices. The possesses isogonal symmetry under the D8D_8, which includes 16 transformations preserving the figure's rotational order of eight and reflections across eight axes passing through opposite vertices or midpoints of opposite sides. From the center, eight radial rays extend to the vertices, dividing the into equal sectors. The sides intersect at additional points, forming a smaller regular at the core bounded by these intersection segments. The of the octagram, also termed the , quantifies its topological complexity and can be illustrated as the number of edges a ray from the interior must cross to reach the exterior boundary when traversing the polygon's outline. This measure reflects how the path winds around the center multiple times, enclosing regions with varying enclosure levels.

Schläfli Symbol and

The {n/k} provides a concise notation for regular star polygons, where n denotes the number of vertices and edges, and k represents the step or parameter indicating how many vertices are skipped when connecting successive points on a . For the octagram, n=8 and k=3 (coprime), yielding {8/3} for the simple form. The enantiomorphic form is {8/5}, the of {8/3}. When gcd(n, k) > 1, the figure is a compound rather than a single simple ; for example, {8/2} is a compound of two squares (gcd=2), while {8/4} is a compound of four digons (gcd=4), consisting of four diameters intersecting at the center. The density d of a star polygon, which measures the or the number of times its edges encircle the center, is given by d = k for simple star polygons {n/k} where gcd(n, k) = 1 and k < n/2. In the case of {8/3}, the density is 3, meaning the edges wind around the center three times, creating a more interlaced and centrally filled appearance compared to lower-density stars like the pentagram {5/2} with d=2. For compounds like {8/4}, the density is 4, reflecting the multiple components. Higher density values in octagrams enhance the "filled" visual effect by increasing internal intersections and reducing the prominence of the central void, as the path revisits interior regions more frequently before closing. Octagrams relate to regular polygons as stellations of the , where the {8/3} form arises as the second stellation by extending the octagon's sides until they intersect to form the star.

Variations and Types

Simple Octagram {8/3}

The simple octagram, denoted by the Schläfli symbol {8/3}, is a unicursal star polygon formed by connecting every third vertex of a regular octagon, resulting in a single continuous line that winds around the center with a density of 3, completing three full turns before closing after eight edges. This configuration distinguishes it as the primary non-compound regular octagram, exhibiting self-intersections that create a star-shaped figure with eight equilateral sides. The symmetry group of the {8/3} octagram is the full dihedral group D8D_8, which consists of 16 elements: eight rotations (by multiples of 45∘45^\circ) and eight reflections across axes passing through opposite vertices or midpoints of opposite sides. The vertex angle at each point is 45∘45^\circ. In the complex plane, assuming a unit circumradius, the vertices of the {8/3} octagram can be represented as e2πi⋅3k/8e^{2\pi i \cdot 3k / 8} for k=0,1,…,7k = 0, 1, \dots, 7, which traces the points in the order of connection. The side length ss for this unit circumradius is given by s=2sin⁡(3π/8)s = 2 \sin(3\pi / 8). For plotting the star parametrically, the coordinates are x(t)=cos⁡(6πt8),y(t)=sin⁡(6πt8),x(t) = \cos\left(\frac{6\pi t}{8}\right), \quad y(t) = \sin\left(\frac{6\pi t}{8}\right), where tt increments in steps of 1 from 0 to 7 (discretized) or continuously for the envelope curve. The {8/5} octagram is equivalent to {8/3}, as the connection step of 5 is congruent to -3 modulo 8, producing the same figure but traversed in the reverse direction.

Compound Octagram {8/2}

The compound octagram denoted by the Schläfli symbol {8/2}, equivalently 2{4}, is a regular star polygon compound consisting of two interlocked squares rotated relative to each other by 45 degrees. This figure arises as the first stellation of a regular and represents a multicursal structure where the two square components share the same eight vertices on a common circumcircle. Unlike simple star polygons, which form a single connected path, the {8/2} is a uniform compound composed of distinct polygonal elements. Key properties include a central density of 2, reflecting the twofold overlap in the interior regions covered by the squares, with the density derived from the indicating the number of component polygons. The eight vertices are shared among the components, and the edges intersect to form a regular at the center where the squares overlap. Topologically, it is not a single connected polygon but a discrete compound maintaining uniformity through its regular construction. This compound can be constructed by overlapping two regular squares inscribed in the unit circle, with one square having vertices at (1,0), (0,1), (-1,0), and (0,-1), and the other rotated by 45 degrees with vertices at (22,22)\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.