Fundamental group

Start with a space (for example, a surface), and some point in it, and all the loops both starting and ending at this point—paths that start at this point, wander around and eventually return to the starting point. Two loops can be combined in an obvious way: travel along the first loop, then along the second. Two loops are considered equivalent if one can be deformed into the other without breaking. The set of all such loops with this method of combining and this equivalence between them is the fundamental group for that particular space.

Henri Poincaré defined the fundamental group in 1895 in his paper "Analysis situs".^[1] The concept emerged in the theory of Riemann surfaces, in the work of Bernhard Riemann, Poincaré, and Felix Klein. It describes the monodromy properties of complex-valued functions, as well as providing a complete topological classification of closed surfaces.

Throughout this article, ${\displaystyle X}$ is a topological space. A typical example is a surface such as the one depicted at the right. Moreover, ${\displaystyle x_{0}}$ is a point in ${\displaystyle X}$ called the base-point. (As is explained below, its role is rather auxiliary.) The idea of the definition of the homotopy group is to measure how many (broadly speaking) curves on ${\displaystyle X}$ can be deformed into each other. The precise definition depends on the notion of the homotopy of loops, which is explained first.

Given a topological space ${\displaystyle X}$, a loop based at ${\displaystyle x_{0}}$ is defined to be a continuous function (also known as a continuous map)

${\displaystyle \gamma \colon [0,1]\to X}$

such that the starting point ${\displaystyle \gamma (0)}$ and the end point ${\displaystyle \gamma (1)}$ are both equal to ${\displaystyle x_{0}}$.

A homotopy is a continuous interpolation between two loops. More precisely, a homotopy between two loops ${\displaystyle \gamma ,\gamma '\colon [0,1]\to X}$ (based at the same point ${\displaystyle x_{0}}$) is a continuous map

${\displaystyle h\colon [0,1]\times [0,1]\to X,}$

such that

• ${\displaystyle h(0,t)=x_{0}}$ for all ${\displaystyle t\in [0,1],}$ that is, the starting point of the homotopy is ${\displaystyle x_{0}}$ for all ${\displaystyle t}$ (which is often thought of as a time parameter).
• ${\displaystyle h(1,t)=x_{0}}$ for all ${\displaystyle t\in [0,1],}$ that is, similarly the end point stays at ${\displaystyle x_{0}}$ for all t.
• ${\displaystyle h(r,0)=\gamma (r),\,h(r,1)=\gamma '(r)}$ for all ${\displaystyle r\in [0,1]}$.

If such a homotopy ${\displaystyle h}$ exists, ${\displaystyle \gamma }$ and ${\displaystyle \gamma '}$ are said to be homotopic. The relation "${\displaystyle \gamma }$ is homotopic to ${\displaystyle \gamma '}$" is an equivalence relation so that the set of equivalence classes can be considered:

${\displaystyle \pi _{1}(X,x_{0}):=\{{\text{all loops }}\gamma {\text{ based at }}x_{0}\}/{\text{homotopy}}}$.

This set (with the group structure described below) is called the fundamental group of the topological space ${\displaystyle X}$ at the base point ${\displaystyle x_{0}}$. The purpose of considering the equivalence classes of loops up to homotopy, as opposed to the set of all loops (the so-called loop space of ${\displaystyle X}$) is that the latter, while being useful for various purposes, is a rather big and unwieldy object. By contrast the above quotient is, in many cases, more manageable and computable.

By the above definition, ${\displaystyle \pi _{1}(X,x_{0})}$ is just a set. It becomes a group (and therefore deserves the name fundamental group) using the concatenation of loops. More precisely, given two loops ${\displaystyle \gamma _{0},\gamma _{1}}$, their product is defined as the loop

${\displaystyle \gamma _{0}\cdot \gamma _{1}\colon [0,1]\to X}$

${\displaystyle (\gamma _{0}\cdot \gamma _{1})(t)={\begin{cases}\gamma _{0}(2t)&0\leq t\leq {\tfrac {1}{2}}\\\gamma _{1}(2t-1)&{\tfrac {1}{2}}\leq t\leq 1.\end{cases}}}$

Thus the loop ${\displaystyle \gamma _{0}\cdot \gamma _{1}}$ first follows the loop ${\displaystyle \gamma _{0}}$ with "twice the speed" and then follows ${\displaystyle \gamma _{1}}$ with "twice the speed".

The product of two homotopy classes of loops ${\displaystyle [\gamma _{0}]}$ and ${\displaystyle [\gamma _{1}]}$ is then defined as ${\displaystyle [\gamma _{0}\cdot \gamma _{1}]}$. It can be shown that this product does not depend on the choice of representatives and therefore gives a well-defined operation on the set ${\displaystyle \pi _{1}(X,x_{0})}$. This operation turns ${\displaystyle \pi _{1}(X,x_{0})}$ into a group. Its neutral element is the equivalence (homotopy) class of the constant loop, which stays at ${\displaystyle x_{0}}$ for all times ${\displaystyle t}$ (i.e. this class consists of all loops that can be continuously deformed into the constant loop; intuitively speaking of all the loops that do not "wrap around a hole"). The inverse of a (homotopy class of a) loop is the same loop, but traversed in the opposite direction (which is in a different homotopy class). More formally,

${\displaystyle \gamma ^{-1}(t):=\gamma (1-t).}$

Given three based loops ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2},}$ the product

${\displaystyle (\gamma _{0}\cdot \gamma _{1})\cdot \gamma _{2}}$

is the concatenation of these loops, traversing ${\displaystyle \gamma _{0}}$ and then ${\displaystyle \gamma _{1}}$ with quadruple speed, and then ${\displaystyle \gamma _{2}}$ with double speed. By comparison,

${\displaystyle \gamma _{0}\cdot (\gamma _{1}\cdot \gamma _{2})}$

traverses the same paths (in the same order), but ${\displaystyle \gamma _{0}}$ with double speed, and ${\displaystyle \gamma _{1},\gamma _{2}}$ with quadruple speed. Thus, because of the differing speeds, the two paths are not identical. The associativity axiom

${\displaystyle [\gamma _{0}]\cdot \left([\gamma _{1}]\cdot [\gamma _{2}]\right)=\left([\gamma _{0}]\cdot [\gamma _{1}]\right)\cdot [\gamma _{2}]}$

therefore crucially depends on the fact that paths are considered up to homotopy. Indeed, both above composites are homotopic, for example, to the loop that traverses all three loops ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2}}$ with triple speed. The set of based loops up to homotopy, equipped with the above operation therefore does turn ${\displaystyle \pi _{1}(X,x_{0})}$ into a group.

Although the fundamental group in general depends on the choice of base point, it turns out that, up to isomorphism, this choice makes no difference as long as the space ${\displaystyle X}$ is path-connected: more precisely, one obtains an isomorphism by pre- and post-concatenating with a path between the two basepoints. This isomorphism is, in general, not unique: it depends on the choice of path up to homotopy. However changing the path results in changing the isomorphism between the two fundamental groups only by composition with an inner automorphism. It is therefore customary to write ${\displaystyle \pi _{1}(X)}$ instead of ${\displaystyle \pi _{1}(X,x_{0})}$ when the choice of basepoint does not matter.

This section lists some basic examples of fundamental groups. To begin with, in Euclidean space (${\displaystyle \mathbb {R} ^{n}}$) or any convex subset of ${\displaystyle \mathbb {R} ^{n},}$ there is only one homotopy class of loops, and the fundamental group is therefore the trivial group with one element. More generally, any star domain – and yet more generally, any contractible space – has a trivial fundamental group. Thus, the fundamental group does not distinguish between such spaces.

A path-connected space whose fundamental group is trivial is called simply connected. For example, the 2-sphere ${\displaystyle S^{2}=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}}$ depicted on the right, and also all the higher-dimensional spheres, are simply-connected. The figure illustrates a homotopy contracting one particular loop to the constant loop. This idea can be adapted to all loops ${\displaystyle \gamma }$ such that there is a point ${\displaystyle (x,y,z)\in S^{2}}$ that is not in the image of ${\displaystyle \gamma .}$ However, since there are loops such that ${\displaystyle \gamma ([0,1])=S^{2}}$ (constructed from the Peano curve, for example), a complete proof requires more careful analysis with tools from algebraic topology, such as the Seifert–van Kampen theorem or the cellular approximation theorem.

The circle (also known as the 1-sphere)

${\displaystyle S^{1}=\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}$

is not simply connected. Instead, each homotopy class consists of all loops that wind around the circle a given number of times (which can be positive or negative, depending on the direction of winding). The product of a loop that winds around ${\displaystyle m}$ times and another that winds around ${\displaystyle n}$ times is a loop that winds around ${\displaystyle m+n}$ times. Therefore, the fundamental group of the circle is isomorphic to ${\displaystyle (\mathbb {Z} ,+),}$ the additive group of integers. This fact can be used to give proofs of the Brouwer fixed point theorem^[2] and the Borsuk–Ulam theorem in dimension 2.^[3]

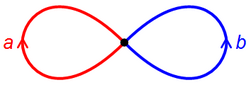
The fundamental group of the figure eight is the free group on two letters. The idea to prove this is as follows: choosing the base point to be the point where the two circles meet (dotted in black in the picture at the right), any loop ${\displaystyle \gamma }$ can be decomposed as

${\displaystyle \gamma =a^{n_{1}}b^{m_{1}}\cdots a^{n_{k}}b^{m_{k}}}$

where a and b are the two loops winding around each half of the figure as depicted, and the exponents ${\displaystyle n_{1},\dots ,n_{k},m_{1},\dots ,m_{k}}$ are integers. Unlike ${\displaystyle \pi _{1}(S^{1}),}$ the fundamental group of the figure eight is not abelian: the two ways of composing ${\displaystyle a}$ and ${\displaystyle b}$ are not homotopic to each other:

${\displaystyle [a]\cdot [b]\neq [b]\cdot [a].}$

More generally, the fundamental group of a bouquet of ${\displaystyle r}$ circles is the free group on ${\displaystyle r}$ letters.

The fundamental group of a wedge sum of two path connected spaces ${\displaystyle X}$ and ${\displaystyle Y}$ can be computed as the free product of the individual fundamental groups:

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

This generalizes the above observations since the figure eight is the wedge sum of two circles.

The fundamental group of the plane punctured at ${\displaystyle n}$ points is also the free group with ${\displaystyle n}$ generators. The ${\displaystyle i}$-th generator is the class of the loop that goes around the ${\displaystyle i}$-th puncture without going around any other punctures.

The fundamental group can be defined for discrete structures too. In particular, consider a connected graph ${\displaystyle G=(V,E)}$, with a designated vertex ${\displaystyle v_{0}}$ in ${\displaystyle V}$. The loops in ${\displaystyle G}$ are the cycles that start and end at ${\displaystyle v_{0}}$.^[4] Let ${\displaystyle T}$ be a spanning tree of ${\displaystyle G}$. Every simple loop in ${\displaystyle G}$ contains exactly one edge in ${\displaystyle E\setminus T}$; every loop in ${\displaystyle G}$ is a concatenation of such simple loops. Therefore, the fundamental group of a graph is a free group, in which the number of generators is exactly the number of edges in ${\displaystyle E\setminus T}$. This number equals ${\displaystyle |E|-|V|+1}$.^[5]

For example, suppose ${\displaystyle G}$ has 16 vertices arranged in 4 rows of 4 vertices each, with edges connecting vertices that are adjacent horizontally or vertically. Then ${\displaystyle G}$ has 24 edges overall, and the number of edges in each spanning tree is 16 − 1 = 15, so the fundamental group of ${\displaystyle G}$ is the free group with 9 generators.^[6] Note that ${\displaystyle G}$ has 9 "holes", similarly to a bouquet of 9 circles, which has the same fundamental group.

Knot groups are by definition the fundamental group of the complement of a knot ${\displaystyle K}$ embedded in ${\displaystyle \mathbb {R} ^{3}.}$ For example, the knot group of the trefoil knot is known to be the braid group ${\displaystyle B_{3},}$ which gives another example of a non-abelian fundamental group. The Wirtinger presentation explicitly describes knot groups in terms of generators and relations based on a diagram of the knot. Therefore, knot groups have some usage in knot theory to distinguish between knots: if ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K)}$ is not isomorphic to some other knot group ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K')}$ of another knot ${\displaystyle K'}$, then ${\displaystyle K}$ can not be transformed into ${\displaystyle K'}$. Thus the trefoil knot can not be continuously transformed into the circle (also known as the unknot), since the latter has knot group ${\displaystyle \mathbb {Z} }$. There are, however, knots that can not be deformed into each other, but have isomorphic knot groups.

The fundamental group of a genus-n orientable surface can be computed in terms of generators and relations as

${\displaystyle \left\langle A_{1},B_{1},\ldots ,A_{n},B_{n}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\right.\right\rangle .}$

This includes the torus, being the case of genus 1, whose fundamental group is

${\displaystyle \left\langle A_{1},B_{1}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\right.\right\rangle \cong \mathbb {Z} ^{2}.}$

The fundamental group of a topological group ${\displaystyle X}$ (with respect to the base point being the neutral element) is always commutative. In particular, the fundamental group of a Lie group is commutative. In fact, the group structure on ${\displaystyle X}$ endows ${\displaystyle \pi _{1}(X)}$ with another group structure: given two loops ${\displaystyle \gamma }$ and ${\displaystyle \gamma '}$ in ${\displaystyle X}$, another loop ${\displaystyle \gamma \star \gamma '}$ can defined by using the group multiplication in ${\displaystyle X}$:

${\displaystyle (\gamma \star \gamma ')(x)=\gamma (x)\cdot \gamma '(x).}$

This binary operation ${\displaystyle \star }$ on the set of all loops is a priori independent from the one described above. However, the Eckmann–Hilton argument shows that it does in fact agree with the above concatenation of loops, and moreover that the resulting group structure is abelian.^[7][8]

An inspection of the proof shows that, more generally, ${\displaystyle \pi _{1}(X)}$ is abelian for any H-space ${\displaystyle X}$, i.e., the multiplication need not have an inverse, nor does it have to be associative. For example, this shows that the fundamental group of a loop space of another topological space ${\displaystyle Y}$, ${\displaystyle X=\Omega (Y),}$ is abelian. Related ideas lead to Heinz Hopf's computation of the cohomology of a Lie group.

If ${\displaystyle f\colon X\to Y}$ is a continuous map, ${\displaystyle x_{0}\in X}$ and ${\displaystyle y_{0}\in Y}$ with ${\displaystyle f(x_{0})=y_{0},}$ then every loop in ${\displaystyle X}$ with base point ${\displaystyle x_{0}}$ can be composed with ${\displaystyle f}$ to yield a loop in ${\displaystyle Y}$ with base point ${\displaystyle y_{0}.}$ This operation is compatible with the homotopy equivalence relation and with composition of loops. The resulting group homomorphism, called the induced homomorphism, is written as ${\displaystyle \pi (f)}$ or, more commonly,

${\displaystyle f_{*}\colon \pi _{1}(X,x_{0})\to \pi _{1}(Y,y_{0}).}$

This mapping from continuous maps to group homomorphisms is compatible with composition of maps and identity morphisms. In the parlance of category theory, the formation of associating to a topological space its fundamental group is therefore a functor

${\displaystyle {\begin{aligned}\pi _{1}\colon \mathbf {Top} _{*}&\to \mathbf {Grp} \\(X,x_{0})&\mapsto \pi _{1}(X,x_{0})\end{aligned}}}$

from the category of topological spaces together with a base point to the category of groups. It turns out that this functor does not distinguish maps that are homotopic relative to the base point: if ${\displaystyle f,g:X\to Y}$ are continuous maps with ${\displaystyle f(x_{0})=g(x_{0})=y_{0}}$, and ${\displaystyle f}$ and ${\displaystyle g}$ are homotopic relative to ${\displaystyle \{x_{0}\}}$, then ${\displaystyle f_{*}=g_{*}}$. As a consequence, two homotopy equivalent path-connected spaces have isomorphic fundamental groups:

${\displaystyle X\simeq Y\implies \pi _{1}(X,x_{0})\cong \pi _{1}(Y,y_{0}).}$

For example, the inclusion of the circle in the punctured plane

${\displaystyle S^{1}\subset \mathbb {R} ^{2}\setminus \{0\}}$

is a homotopy equivalence and therefore yields an isomorphism of their fundamental groups.

The fundamental group functor takes products to products and coproducts to coproducts. That is, if ${\displaystyle X}$ and ${\displaystyle Y}$ are path connected, then

${\displaystyle \pi _{1}(X\times Y,(x_{0},y_{0}))\cong \pi _{1}(X,x_{0})\times \pi _{1}(Y,y_{0})}$

and if they are also locally contractible, then

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

(In the latter formula, ${\displaystyle \vee }$ denotes the wedge sum of pointed topological spaces, and ${\displaystyle *}$ the free product of groups.) The latter formula is a special case of the Seifert–van Kampen theorem, which states that the fundamental group functor takes pushouts along inclusions to pushouts.

As was mentioned above, computing the fundamental group of even relatively simple topological spaces tends to be not entirely trivial, but requires some methods of algebraic topology.

The abelianization of the fundamental group can be identified with the first homology group of the space.

A special case of the Hurewicz theorem asserts that the first singular homology group ${\displaystyle H_{1}(X)}$ is, colloquially speaking, the closest approximation to the fundamental group by means of an abelian group. In more detail, mapping the homotopy class of each loop to the homology class of the loop gives a group homomorphism

${\displaystyle \pi _{1}(X)\to H_{1}(X)}$

from the fundamental group of a topological space ${\displaystyle X}$ to its first singular homology group ${\displaystyle H_{1}(X).}$ This homomorphism is not in general an isomorphism since the fundamental group may be non-abelian, but the homology group is, by definition, always abelian. This difference is, however, the only one: if ${\displaystyle X}$ is path-connected, this homomorphism is surjective and its kernel is the commutator subgroup of the fundamental group, so that ${\displaystyle H_{1}(X)}$ is isomorphic to the abelianization of the fundamental group.^[9]

Generalizing the statement above, for a family of path connected spaces ${\displaystyle X_{i},}$ the fundamental group ${\textstyle \pi _{1}\left(\bigvee _{i\in I}X_{i}\right)}$ is the free product of the fundamental groups of the ${\displaystyle X_{i}.}$^[10] This fact is a special case of the Seifert–van Kampen theorem, which allows to compute, more generally, fundamental groups of spaces that are glued together from other spaces. For example, the 2-sphere ${\displaystyle S^{2}}$ can be obtained by gluing two copies of slightly overlapping half-spheres along a neighborhood of the equator. In this case the theorem yields ${\displaystyle \pi _{1}(S^{2})}$ is trivial, since the two half-spheres are contractible and therefore have trivial fundamental group. The fundamental groups of surfaces, as mentioned above, can also be computed using this theorem.

In the parlance of category theory, the theorem can be concisely stated by saying that the fundamental group functor takes pushouts (in the category of topological spaces) along inclusions to pushouts (in the category of groups).^[11]

Given a topological space ${\displaystyle B}$, a continuous map

${\displaystyle f:E\to B}$

is called a covering or ${\displaystyle E}$ is called a covering space of ${\displaystyle B}$ if every point ${\displaystyle b}$ in ${\displaystyle B}$ admits an open neighborhood ${\displaystyle U}$ such that there is a homeomorphism between the preimage of ${\displaystyle U}$ and a disjoint union of copies of ${\displaystyle U}$ (indexed by some set ${\displaystyle I}$),

${\displaystyle \varphi :\bigsqcup _{i\in I}U\to f^{-1}(U)}$

in such a way that ${\displaystyle \pi \circ \varphi }$ is the standard projection map ${\displaystyle \bigsqcup _{i\in I}U\to U.}$^[12]

A covering is called a universal covering if ${\displaystyle E}$ is, in addition to the preceding condition, simply connected.^[13] It is universal in the sense that all other coverings can be constructed by suitably identifying points in ${\displaystyle E}$. Knowing a universal covering

${\displaystyle p:{\widetilde {X}}\to X}$

of a topological space ${\displaystyle X}$ is helpful in understanding its fundamental group in several ways: first, ${\displaystyle \pi _{1}(X)}$ identifies with the group of deck transformations, i.e., the group of homeomorphisms ${\displaystyle \varphi :{\widetilde {X}}\to {\widetilde {X}}}$ that commute with the map to ${\displaystyle X}$, i.e., ${\displaystyle p\circ \varphi =p.}$ Another relation to the fundamental group is that ${\displaystyle \pi _{1}(X,x)}$ can be identified with the fiber ${\displaystyle p^{-1}(x).}$ For example, the map

${\displaystyle p:\mathbb {R} \to S^{1},\,t\mapsto \exp(2\pi it)}$

(or, equivalently, ${\displaystyle \pi :\mathbb {R} \to \mathbb {R} /\mathbb {Z} ,\ t\mapsto [t]}$) is a universal covering. The deck transformations are the maps ${\displaystyle t\mapsto t+n}$ for ${\displaystyle n\in \mathbb {Z} .}$ This is in line with the identification ${\displaystyle p^{-1}(1)=\mathbb {Z} ,}$ in particular this proves the above claim ${\displaystyle \pi _{1}(S^{1})\cong \mathbb {Z} .}$

Any path connected, locally path connected and locally simply connected topological space ${\displaystyle X}$ admits a universal covering.^[14] An abstract construction proceeds analogously to the fundamental group by taking pairs ${\displaystyle (x,\gamma )}$, where ${\displaystyle x}$ is a point in ${\displaystyle X}$ and ${\displaystyle \gamma }$ is a homotopy class of paths from ${\displaystyle x_{0}}$ to ${\displaystyle x}$. The passage from a topological space to its universal covering can be used in understanding the geometry of ${\displaystyle X}$. For example, the uniformization theorem shows that any simply connected Riemann surface is (isomorphic to) either ${\displaystyle S^{2},}$ ${\displaystyle \mathbb {C} ,}$ or the upper half-plane.^[15] General Riemann surfaces then arise as quotients of group actions on these three surfaces.

The quotient of a free action of a discrete group ${\displaystyle G}$ on a simply connected space ${\displaystyle Y}$ has fundamental group

${\displaystyle \pi _{1}(Y/G)\cong G.}$

As an example, the real ${\displaystyle n}$-dimensional real projective space ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ is obtained as the quotient of the ${\displaystyle n}$-dimensional unit sphere ${\displaystyle S^{n}}$ by the antipodal action of the group ${\displaystyle \mathbb {Z} /2}$ sending ${\displaystyle x\in S^{n}}$ to ${\displaystyle -x.}$ As ${\displaystyle S^{n}}$ is simply connected for ${\displaystyle n\geq 2}$, it is a universal cover of ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ in these cases, which implies ${\displaystyle \pi _{1}(\mathbb {R} \mathrm {P} ^{n})\cong \mathbb {Z} /2}$ for ${\displaystyle n\geq 2}$.

Let ${\displaystyle G}$ be a connected, simply connected compact Lie group, for example, the special unitary group ${\displaystyle {\text{SU}}(n)}$, and let ${\displaystyle \Gamma }$ be a finite subgroup of ${\displaystyle G}$. Then the homogeneous space ${\displaystyle X=G/\Gamma }$ has fundamental group ${\displaystyle \Gamma }$, which acts by right multiplication on the universal covering space ${\displaystyle G}$. Among the many variants of this construction, one of the most important is given by locally symmetric spaces ${\displaystyle X=\Gamma \setminus G/K}$, where

• ${\displaystyle G}$ is a non-compact simply connected, connected Lie group (often semisimple),
• ${\displaystyle K}$ is a maximal compact subgroup of ${\displaystyle G}$
• ${\displaystyle \Gamma }$ is a discrete countable torsion-free subgroup of ${\displaystyle G}$.

In this case the fundamental group is ${\displaystyle \Gamma }$ and the universal covering space ${\displaystyle G/K}$ is actually contractible (by the Cartan decomposition for Lie groups).

As an example take ${\displaystyle G={\text{SL}}(2,\mathbb {R} )}$, ${\displaystyle K={\text{SO}}(2)}$ and ${\displaystyle \Gamma }$ any torsion-free congruence subgroup of the modular group ${\displaystyle {\text{SL}}(2,\mathbb {Z} )}$.

From the explicit realization, it also follows that the universal covering space of a path connected topological group ${\displaystyle H}$ is again a path connected topological group ${\displaystyle G}$. Moreover, the covering map is a continuous open homomorphism of ${\displaystyle G}$ onto ${\displaystyle H}$ with kernel ${\displaystyle \Gamma }$, a closed discrete normal subgroup of ${\displaystyle G}$:

${\displaystyle 1\to \Gamma \to G\to H\to 1.}$

Since ${\displaystyle G}$ is a connected group with a continuous action by conjugation on a discrete group ${\displaystyle \Gamma }$, it must act trivially, so that ${\displaystyle \Gamma }$ has to be a subgroup of the center of ${\displaystyle G}$. In particular ${\displaystyle \pi _{1}(H)=\Gamma }$ is an abelian group; this can also easily be seen directly without using covering spaces. The group ${\displaystyle G}$ is called the universal covering group of ${\displaystyle H}$.

As the universal covering group suggests, there is an analogy between the fundamental group of a topological group and the center of a group; this is elaborated at Lattice of covering groups.

Fibrations provide a very powerful means to compute homotopy groups. A fibration ${\displaystyle f}$ the so-called total space, and the base space ${\displaystyle B}$ has, in particular, the property that all its fibers ${\displaystyle f^{-1}(b)}$ are homotopy equivalent and therefore can not be distinguished using fundamental groups (and higher homotopy groups), provided that ${\displaystyle B}$ is path-connected.^[16] Therefore, the space ${\displaystyle E}$ can be regarded as a "twisted product" of the base space ${\displaystyle B}$ and the fiber ${\displaystyle F=f^{-1}(b).}$ The great importance of fibrations to the computation of homotopy groups stems from a long exact sequence

${\displaystyle \dots \to \pi _{2}(B)\to \pi _{1}(F)\to \pi _{1}(E)\to \pi _{1}(B)\to \pi _{0}(F)\to \pi _{0}(E)}$

provided that ${\displaystyle B}$ is path-connected.^[17] The term ${\displaystyle \pi _{2}(B)}$ is the second homotopy group of ${\displaystyle B}$, which is defined to be the set of homotopy classes of maps from ${\displaystyle S^{2}}$ to ${\displaystyle B}$, in direct analogy with the definition of ${\displaystyle \pi _{1}.}$

If ${\displaystyle E}$ happens to be path-connected and simply connected, this sequence reduces to an isomorphism

${\displaystyle \pi _{1}(B)\cong \pi _{0}(F)}$

which generalizes the above fact about the universal covering (which amounts to the case where the fiber ${\displaystyle F}$ is also discrete). If instead ${\displaystyle F}$ happens to be connected and simply connected, it reduces to an isomorphism

${\displaystyle \pi _{1}(E)\cong \pi _{1}(B).}$

What is more, the sequence can be continued at the left with the higher homotopy groups ${\displaystyle \pi _{n}}$ of the three spaces, which gives some access to computing such groups in the same vein.

Such fiber sequences can be used to inductively compute fundamental groups of compact classical Lie groups such as the special unitary group ${\displaystyle \mathrm {SU} (n),}$ with ${\displaystyle n\geq 2.}$ This group acts transitively on the unit sphere ${\displaystyle S^{2n-1}}$ inside ${\displaystyle \mathbb {C} ^{n}=\mathbb {R} ^{2n}.}$ The stabilizer of a point in the sphere is isomorphic to ${\displaystyle \mathrm {SU} (n-1).}$ It then can be shown^[18] that this yields a fiber sequence

${\displaystyle \mathrm {SU} (n-1)\to \mathrm {SU} (n)\to S^{2n-1}.}$

Since ${\displaystyle n\geq 2,}$ the sphere ${\displaystyle S^{2n-1}}$ has dimension at least 3, which implies

${\displaystyle \pi _{1}(S^{2n-1})\cong \pi _{2}(S^{2n-1})=1.}$

The long exact sequence then shows an isomorphism

${\displaystyle \pi _{1}(\mathrm {SU} (n))\cong \pi _{1}(\mathrm {SU} (n-1)).}$

Since ${\displaystyle \mathrm {SU} (1)}$ is a single point, so that ${\displaystyle \pi _{1}(\mathrm {SU} (1))}$ is trivial, this shows that ${\displaystyle \mathrm {SU} (n)}$ is simply connected for all ${\displaystyle n.}$

The fundamental group of noncompact Lie groups can be reduced to the compact case, since such a group is homotopic to its maximal compact subgroup.^[19] These methods give the following results:^[20]

Compact classical Lie group G	Non-compact Lie group	${\displaystyle \pi _{1}}$
special unitary group ${\displaystyle \mathrm {SU} (n)}$	${\displaystyle \mathrm {SL} (n,\mathbb {C} )}$	1
unitary group ${\displaystyle \mathrm {U} (n)}$	${\displaystyle \mathrm {GL} (n,\mathbb {C} ),\mathrm {Sp} (n,\mathbb {R} )}$	${\displaystyle \mathbb {Z} }$
special orthogonal group ${\displaystyle \mathrm {SO} (n)}$	${\displaystyle \mathrm {SO} (n,\mathbb {C} )}$	${\displaystyle \mathbb {Z} /2}$ for ${\displaystyle n\geq 3}$ and ${\displaystyle \mathbb {Z} }$ for ${\displaystyle n=2}$
compact symplectic group ${\displaystyle \mathrm {Sp} (n)}$	${\displaystyle \mathrm {Sp} (n,\mathbb {C} )}$	1

A second method of computing fundamental groups applies to all connected compact Lie groups and uses the machinery of the maximal torus and the associated root system. Specifically, let ${\displaystyle T}$ be a maximal torus in a connected compact Lie group ${\displaystyle K,}$ and let ${\displaystyle {\mathfrak {t}}}$ be the Lie algebra of ${\displaystyle T.}$ The exponential map

${\displaystyle \exp :{\mathfrak {t}}\to T}$

is a fibration and therefore its kernel ${\displaystyle \Gamma \subset {\mathfrak {t}}}$ identifies with ${\displaystyle \pi _{1}(T).}$ The map

${\displaystyle \pi _{1}(T)\to \pi _{1}(K)}$

can be shown to be surjective^[21] with kernel given by the set ${\displaystyle I}$ of integer linear combination of coroots. This leads to the computation

${\displaystyle \pi _{1}(K)\cong \Gamma /I.}$^[22]

This method shows, for example, that any connected compact Lie group for which the associated root system is of type ${\displaystyle G_{2}}$ is simply connected.^[23] Thus, there is (up to isomorphism) only one connected compact Lie group having Lie algebra of type ${\displaystyle G_{2}}$; this group is simply connected and has trivial center.

When the topological space is homeomorphic to a simplicial complex, its fundamental group can be described explicitly in terms of generators and relations.

If ${\displaystyle X}$ is a connected simplicial complex, an edge-path in ${\displaystyle X}$ is defined to be a chain of vertices connected by edges in ${\displaystyle X}$. Two edge-paths are said to be edge-equivalent if one can be obtained from the other by successively switching between an edge and the two opposite edges of a triangle in ${\displaystyle X}$. If ${\displaystyle v}$ is a fixed vertex in ${\displaystyle X}$, an edge-loop at ${\displaystyle v}$ is an edge-path starting and ending at ${\displaystyle v}$. The edge-path group ${\displaystyle E(X,v)}$ is defined to be the set of edge-equivalence classes of edge-loops at ${\displaystyle v}$, with product and inverse defined by concatenation and reversal of edge-loops.

The edge-path group is naturally isomorphic to ${\displaystyle \pi _{1}(|X|,v)}$, the fundamental group of the geometric realisation ${\displaystyle |X|}$ of ${\displaystyle X}$.^[24] Since it depends only on the 2-skeleton ${\displaystyle X^{2}}$ of ${\displaystyle X}$ (that is, the vertices, edges, and triangles of ${\displaystyle X}$), the groups ${\displaystyle \pi _{1}(|X|,v)}$ and ${\displaystyle \pi _{1}(|X^{2}|,v)}$ are isomorphic.

The edge-path group can be described explicitly in terms of generators and relations. If ${\displaystyle T}$ is a maximal spanning tree in the 1-skeleton of ${\displaystyle X}$, then '${\displaystyle E(X,v)}$ is canonically isomorphic to the group with generators (the oriented edge-paths of ${\displaystyle X}$ not occurring in ${\displaystyle T}$) and relations (the edge-equivalences corresponding to triangles in ${\displaystyle X}$). A similar result holds if ${\displaystyle T}$ is replaced by any simply connected—in particular contractible—subcomplex of ${\displaystyle X}$. This often gives a practical way of computing fundamental groups and can be used to show that every finitely presented group arises as the fundamental group of a finite simplicial complex. It is also one of the classical methods used for topological surfaces, which are classified by their fundamental groups.

The universal covering space of a finite connected simplicial complex ${\displaystyle X}$ can also be described directly as a simplicial complex using edge-paths. Its vertices are pairs ${\displaystyle (w,\gamma )}$ where ${\displaystyle w}$ is a vertex of ${\displaystyle X}$ and γ is an edge-equivalence class of paths from ${\displaystyle v}$ to ${\displaystyle w}$. The ${\displaystyle k}$-simplices containing ${\displaystyle (w,\gamma )}$ correspond naturally to the ${\displaystyle k}$-simplices containing ${\displaystyle w}$. Each new vertex ${\displaystyle u}$ of the ${\displaystyle k}$-simplex gives an edge ${\displaystyle wu}$ and hence, by concatenation, a new path ${\displaystyle \gamma _{u}}$ from ${\displaystyle v}$ to ${\displaystyle u}$. The points ${\displaystyle (w,\gamma )}$ and ${\displaystyle (u,\gamma _{u})}$ are the vertices of the "transported" simplex in the universal covering space. The edge-path group acts naturally by concatenation, preserving the simplicial structure, and the quotient space is just ${\displaystyle X}$.

It is well known that this method can also be used to compute the fundamental group of an arbitrary topological space. This was doubtless known to Eduard Čech and Jean Leray and explicitly appeared as a remark in a paper by André Weil;^[25] various other authors such as Lorenzo Calabi, Wu Wen-tsün, and Nodar Berikashvili have also published proofs. In the simplest case of a compact space ${\displaystyle X}$ with a finite open covering in which all non-empty finite intersections of open sets in the covering are contractible, the fundamental group can be identified with the edge-path group of the simplicial complex corresponding to the nerve of the covering.

• Every group can be realized as the fundamental group of a connected CW-complex of dimension 2 (or higher). As noted above, though, only free groups can occur as fundamental groups of 1-dimensional CW-complexes (that is, graphs).
• Every finitely presented group can be realized as the fundamental group of a compact, connected, smooth manifold of dimension 4 (or higher). But there are severe restrictions on which groups occur as fundamental groups of low-dimensional manifolds. For example, no free abelian group of rank 4 or higher can be realized as the fundamental group of a manifold of dimension 3 or less. It can be proved that every group can be realized as the fundamental group of a compact Hausdorff space if and only if there is no measurable cardinal.^[26]

Roughly speaking, the fundamental group detects the 1-dimensional hole structure of a space, but not higher-dimensional holes such as for the 2-sphere. Such "higher-dimensional holes" can be detected using the higher homotopy groups ${\displaystyle \pi _{n}(X)}$, which are defined to consist of homotopy classes of (basepoint-preserving) maps from ${\displaystyle S^{n}}$ to ${\displaystyle X}$. For example, the Hurewicz theorem implies that for all ${\displaystyle n\geq 1}$ the ${\displaystyle n}$-th homotopy group of the n-sphere is

${\displaystyle \pi _{n}(S^{n})=\mathbb {Z} .}$^[27]

As was mentioned in the above computation of ${\displaystyle \pi _{1}}$ of classical Lie groups, higher homotopy groups can be relevant even for computing fundamental groups.

The set of based loops (as is, i.e. not taken up to homotopy) in a pointed space ${\displaystyle X}$, endowed with the compact open topology, is known as the loop space, denoted ${\displaystyle \Omega X.}$ The fundamental group of ${\displaystyle X}$ is in bijection with the set of path components of its loop space:^[28]

${\displaystyle \pi _{1}(X)\cong \pi _{0}(\Omega X).}$

The fundamental groupoid is a variant of the fundamental group that is useful in situations where the choice of a base point ${\displaystyle x_{0}\in X}$ is undesirable. It is defined by first considering the category of paths in ${\displaystyle X,}$ i.e., continuous functions

${\displaystyle \gamma \colon [0,r]\to X}$,

where ${\displaystyle r}$ is an arbitrary non-negative real number. Since the length ${\displaystyle r}$ is variable in this approach, such paths can be concatenated as is (i.e., not up to homotopy) and therefore yield a category.^[29] Two such paths ${\displaystyle \gamma ,\gamma '}$ with the same endpoints and length ${\displaystyle r}$, resp. ${\displaystyle r}$' are considered equivalent if there exist real numbers ${\displaystyle u,v\geqslant 0}$ such that ${\displaystyle r+u=r'+v}$ and ${\displaystyle \gamma _{u},\gamma '_{v}\colon [0,r+u]\to X}$ are homotopic relative to their end points, where ${\displaystyle \gamma _{u}(t)={\begin{cases}\gamma (t),&t\in [0,r]\\\gamma (r),&t\in [r,r+u].\end{cases}}}$^[30][31]

The category of paths up to this equivalence relation is denoted ${\displaystyle \Pi (X).}$ Each morphism in ${\displaystyle \Pi (X)}$ is an isomorphism, with inverse given by the same path traversed in the opposite direction. Such a category is called a groupoid. It reproduces the fundamental group since

${\displaystyle \pi _{1}(X,x_{0})=\mathrm {Hom} _{\Pi (X)}(x_{0},x_{0})}$.

More generally, one can consider the fundamental groupoid on a set ${\displaystyle A}$ of base points, chosen according to the geometry of the situation; for example, in the case of the circle, which can be represented as the union of two connected open sets whose intersection has two components, one can choose one base point in each component. The van Kampen theorem admits a version for fundamental groupoids which gives, for example, another way to compute the fundamental group(oid) of ${\displaystyle S^{1}.}$^[32]

Generally speaking, representations may serve to exhibit features of a group by its actions on other mathematical objects, often vector spaces. Representations of the fundamental group have a very geometric significance: any local system (i.e., a sheaf ${\displaystyle {\mathcal {F}}}$ on ${\displaystyle X}$ with the property that locally in a sufficiently small neighborhood ${\displaystyle U}$ of any point on ${\displaystyle X}$, the restriction of ${\displaystyle F}$ is a constant sheaf of the form ${\displaystyle {\mathcal {F}}|_{U}=\mathbb {Q} ^{n}}$) gives rise to the so-called monodromy representation, a representation of the fundamental group on an ${\displaystyle n}$-dimensional ${\displaystyle \mathbb {Q} }$-vector space. Conversely, any such representation on a path-connected space ${\displaystyle X}$ arises in this manner.^[33] This equivalence of categories between representations of ${\displaystyle \pi _{1}(X)}$ and local systems is used, for example, in the study of differential equations, such as the Knizhnik–Zamolodchikov equations.

In algebraic geometry, the so-called étale fundamental group is used as a replacement for the fundamental group.^[34] Since the Zariski topology on an algebraic variety or scheme ${\displaystyle X}$ is much coarser than, say, the topology of open subsets in ${\displaystyle \mathbb {R} ^{n},}$ it is no longer meaningful to consider continuous maps from an interval to ${\displaystyle X}$. Instead, the approach developed by Grothendieck consists in constructing ${\displaystyle \pi _{1}^{\text{et}}}$ by considering all finite étale covers of ${\displaystyle X}$. These serve as an algebro-geometric analogue of coverings with finite fibers.

This yields a theory applicable in situations where no great generality classical topological intuition whatsoever is available, for example for varieties defined over a finite field. Also, the étale fundamental group of a field is its (absolute) Galois group. On the other hand, for smooth varieties ${\displaystyle X}$ over the complex numbers, the étale fundamental group retains much of the information inherent in the classical fundamental group: the former is the profinite completion of the latter.^[35]

The fundamental group of a root system is defined in analogy to the computation for Lie groups.^[36] This allows to define and use the fundamental group of a semisimple linear algebraic group ${\displaystyle G}$, which is a useful basic tool in the classification of linear algebraic groups.^[37]

The homotopy relation between 1-simplices of a simplicial set ${\displaystyle X}$ is an equivalence relation if ${\displaystyle X}$ is a Kan complex but not necessarily so in general.^[38] Thus, ${\displaystyle \pi _{1}}$ of a Kan complex can be defined as the set of homotopy classes of 1-simplices. The fundamental group of an arbitrary simplicial set ${\displaystyle X}$ are defined to be the homotopy group of its topological realization, ${\displaystyle |X|,}$ i.e., the topological space obtained by gluing topological simplices as prescribed by the simplicial set structure of ${\displaystyle X}$.^[39]

• Orbifold fundamental group
• Fundamental group scheme