Recent from talks
Nothing was collected or created yet.
Hubble's law
View on Wikipedia
| Part of a series on |
| Physical cosmology |
|---|
 |
Hubble's law, also known as the Hubble–Lemaître law,[1] is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther a galaxy is from the Earth, the faster it moves away. A galaxy's recessional velocity is typically determined by measuring its redshift, a shift in the frequency of light emitted by the galaxy.
The discovery of Hubble's law is attributed to work published by Edwin Hubble in 1929,[2][3][4] but the notion of the universe expanding at a calculable rate was first derived from general relativity equations in 1922 by Alexander Friedmann. The Friedmann equations showed the universe might be expanding, and presented the expansion speed if that were the case.[5] Before Hubble, astronomer Carl Wilhelm Wirtz had, in 1922[6] and 1924,[7] deduced with his own data that galaxies that appeared smaller and dimmer had larger redshifts and thus that more distant galaxies recede faster from the observer. In 1927, Georges Lemaître concluded that the universe might be expanding by noting the proportionality of the recessional velocity of distant bodies to their respective distances. He estimated a value for this ratio, which—after Hubble confirmed cosmic expansion and determined a more precise value for it two years later—became known as the Hubble constant.[8][9][10][11][12] Hubble inferred the recession velocity of the objects from their redshifts, many of which were earlier measured and related to velocity by Vesto Slipher in 1917.[13][14][15] Combining Slipher's velocities with Henrietta Swan Leavitt's intergalactic distance calculations and methodology allowed Hubble to better calculate an expansion rate for the universe.[16]
Hubble's law is considered the first observational basis for the expansion of the universe, and is one of the pieces of evidence most often cited in support of the Big Bang model.[8][17] The motion of astronomical objects due solely to this expansion is known as the Hubble flow.[18] It is described by the equation v = H0D, with H0 the constant of proportionality—the Hubble constant—between the "proper distance" D to a galaxy (which can change over time, unlike the comoving distance) and its speed of separation v, i.e. the derivative of proper distance with respect to the cosmic time coordinate.[a] Though the Hubble constant H0 is constant at any given moment in time, the Hubble parameter H, of which the Hubble constant is the current value, varies with time, so the term constant is sometimes thought of as somewhat of a misnomer.[19][20]
The Hubble constant is most frequently quoted in km/s/Mpc, which gives the speed of a galaxy 1 megaparsec (3.09×1019 km) away as 70 km/s. Simplifying the units of the generalized form reveals that H0 specifies a frequency (SI unit: s−1), leading the reciprocal of H0 to be known as the Hubble time (14.4 billion years). The Hubble constant can also be stated as a relative rate of expansion. In this form H0 = 7%/Gyr, meaning that, at the current rate of expansion, it takes one billion years for an unbound structure to grow by 7%.
Discovery
[edit]
A decade before Hubble made his observations, a number of physicists and mathematicians had established a consistent theory of an expanding universe by using Einstein field equations of general relativity. Applying the most general principles to the nature of the universe yielded a dynamic solution that conflicted with the then-prevalent notion of a static universe.
Slipher's observations
[edit]In 1912, Vesto M. Slipher measured the first Doppler shift of a "spiral nebula" (the obsolete term for spiral galaxies) and soon discovered that almost all such objects were receding from Earth. He did not grasp the cosmological implications of this fact, and indeed at the time it was highly controversial whether or not these nebulae were "island universes" outside the Milky Way galaxy.[22][23]
FLRW equations
[edit]In 1922, Alexander Friedmann derived his Friedmann equations from Einstein field equations, showing that the universe might expand at a rate calculable by the equations.[24] The parameter used by Friedmann is known today as the scale factor and can be considered as a scale invariant form of the proportionality constant of Hubble's law. Georges Lemaître independently found a similar solution in his 1927 paper discussed in the following section. The Friedmann equations are derived by inserting the metric for a homogeneous and isotropic universe into Einstein's field equations for a fluid with a given density and pressure. This idea of an expanding spacetime would eventually lead to the Big Bang and Steady State theories of cosmology.
Lemaître's equation
[edit]In 1927, two years before Hubble published his own article, the Belgian priest and astronomer Georges Lemaître was the first to publish research deriving what is now known as Hubble's law. According to the Canadian astronomer Sidney van den Bergh, "the 1927 discovery of the expansion of the universe by Lemaître was published in French in a low-impact journal. In the 1931 high-impact English translation of this article, a critical equation was changed by omitting reference to what is now known as the Hubble constant."[25] It is now known that the alterations in the translated paper were carried out by Lemaître himself.[10][26]
Shape of the universe
[edit]Before the advent of modern cosmology, there was considerable talk about the size and shape of the universe. In 1920, the Shapley–Curtis debate took place between Harlow Shapley and Heber D. Curtis over this issue. Shapley argued for a small universe the size of the Milky Way galaxy, and Curtis argued that the universe was much larger. The issue was resolved in the coming decade with Hubble's improved observations.
Cepheid variable stars outside the Milky Way
[edit]Edwin Hubble did most of his professional astronomical observing work at Mount Wilson Observatory,[27] home to the world's most powerful telescope at the time. His observations of Cepheid variable stars in "spiral nebulae" enabled him to calculate the distances to these objects. Surprisingly, these objects were discovered to be at distances which placed them well outside the Milky Way. They continued to be called nebulae, and it was only gradually that the term galaxies replaced it.
Combining redshifts with distance measurements
[edit]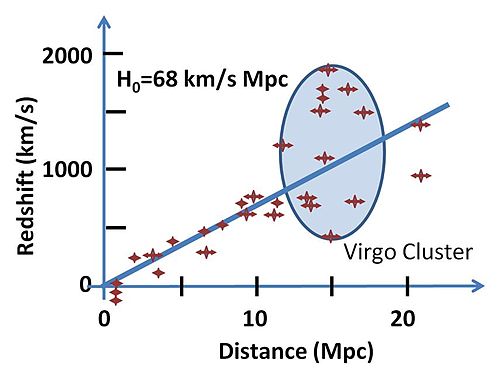
The velocities and distances that appear in Hubble's law are not directly measured. The velocities are inferred from the redshift z = ∆λ/λ of radiation and distance is inferred from brightness. Hubble sought to correlate brightness with parameter z.
Combining his measurements of galaxy distances with Vesto Slipher and Milton Humason's measurements of the redshifts associated with the galaxies, Hubble discovered a rough proportionality between redshift of an object and its distance. Though there was considerable scatter (now known to be caused by peculiar velocities—the 'Hubble flow' is used to refer to the region of space far enough out that the recession velocity is larger than local peculiar velocities), Hubble was able to plot a trend line from the 46 galaxies he studied and obtain a value for the Hubble constant of 500 (km/s)/Mpc (much higher than the currently accepted value due to errors in his distance calibrations; see cosmic distance ladder for details).[29]
Hubble diagram
[edit]Hubble's law can be easily depicted in a "Hubble diagram" in which the velocity (assumed approximately proportional to the redshift) of an object is plotted with respect to its distance from the observer.[30] A straight line of positive slope on this diagram is the visual depiction of Hubble's law.
Cosmological constant abandoned
[edit]After Hubble's discovery was published, Albert Einstein abandoned his work on the cosmological constant, a term he had inserted into his equations of general relativity to coerce them into producing the static solution he previously considered the correct state of the universe. The Einstein equations in their simplest form model either an expanding or contracting universe, so Einstein introduced the constant to counter expansion or contraction and lead to a static and flat universe.[31] After Hubble's discovery that the universe was, in fact, expanding, Einstein called his faulty assumption that the universe is static his "greatest mistake".[31] On its own, general relativity could predict the expansion of the universe, which (through observations such as the bending of light by large masses, or the precession of the orbit of Mercury) could be experimentally observed and compared to his theoretical calculations using particular solutions of the equations he had originally formulated.
In 1931, Einstein went to Mount Wilson Observatory to thank Hubble for providing the observational basis for modern cosmology.[32]
The cosmological constant has regained attention in recent decades as a hypothetical explanation for dark energy.[33]
Interpretation
[edit]
The discovery of the linear relationship between redshift and distance, coupled with a supposed linear relation between recessional velocity and redshift, yields a straightforward mathematical expression for Hubble's law as follows:
where
- v is the recessional velocity, typically expressed in km/s.
- H0 is Hubble's constant and corresponds to the value of H (often termed the Hubble parameter which is a value that is time dependent and which can be expressed in terms of the scale factor) in the Friedmann equations taken at the time of observation denoted by the subscript 0. This value is the same throughout the universe for a given comoving time.
- D is the proper distance (which can change over time, unlike the comoving distance, which is constant) from the galaxy to the observer, measured in mega parsecs (Mpc), in the 3-space defined by given cosmological time. (Recession velocity is just v = dD/dt).
Hubble's law is considered a fundamental relation between recessional velocity and distance. However, the relation between recessional velocity and redshift depends on the cosmological model adopted and is not established except for small redshifts.
For distances D larger than the radius of the Hubble sphere rHS, objects recede at a rate faster than the speed of light (See Uses of the proper distance for a discussion of the significance of this):
Since the Hubble "constant" is a constant only in space, not in time, the radius of the Hubble sphere may increase or decrease over various time intervals. The subscript '0' indicates the value of the Hubble constant today.[28] Current evidence suggests that the expansion of the universe is accelerating (see Accelerating universe), meaning that for any given galaxy, the recession velocity dD/dt is increasing over time as the galaxy moves to greater and greater distances; however, the Hubble parameter is actually thought to be decreasing with time, meaning that if we were to look at some fixed distance D and watch a series of different galaxies pass that distance, later galaxies would pass that distance at a smaller velocity than earlier ones.[35]
Redshift velocity and recessional velocity
[edit]Redshift can be measured by determining the wavelength of a known transition, such as hydrogen α-lines for distant quasars, and finding the fractional shift compared to a stationary reference. Thus, redshift is a quantity unambiguously acquired from observation. Care is required, however, in translating these to recessional velocities: for small redshift values, a linear relation of redshift to recessional velocity applies, but more generally the redshift-distance law is nonlinear, meaning the co-relation must be derived specifically for each given model and epoch.[36]
Redshift velocity
[edit]The redshift z is often described as a redshift velocity, which is the recessional velocity that would produce the same redshift if it were caused by a linear Doppler effect (which, however, is not the case, as the velocities involved are too large to use a non-relativistic formula for Doppler shift). This redshift velocity can easily exceed the speed of light.[37] In other words, to determine the redshift velocity vrs, the relation:
is used.[38][39] That is, there is no fundamental difference between redshift velocity and redshift: they are rigidly proportional, and not related by any theoretical reasoning. The motivation behind the "redshift velocity" terminology is that the redshift velocity agrees with the velocity from a low-velocity simplification of the so-called Fizeau–Doppler formula[40]
Here, λo, λe are the observed and emitted wavelengths respectively. The "redshift velocity" vrs is not so simply related to real velocity at larger velocities, however, and this terminology leads to confusion if interpreted as a real velocity. Next, the connection between redshift or redshift velocity and recessional velocity is discussed.[41]
Recessional velocity
[edit]Suppose R(t) is called the scale factor of the universe, and increases as the universe expands in a manner that depends upon the cosmological model selected. Its meaning is that all measured proper distances D(t) between co-moving points increase proportionally to R. (The co-moving points are not moving relative to their local environments.) In other words:
where t0 is some reference time.[42] If light is emitted from a galaxy at time te and received by us at t0, it is redshifted due to the expansion of the universe, and this redshift z is simply:
Suppose a galaxy is at distance D, and this distance changes with time at a rate dtD. We call this rate of recession the "recession velocity" vr:
We now define the Hubble constant as
and discover the Hubble law:
From this perspective, Hubble's law is a fundamental relation between (i) the recessional velocity associated with the expansion of the universe and (ii) the distance to an object; the connection between redshift and distance is a crutch used to connect Hubble's law with observations. This law can be related to redshift z approximately by making a Taylor series expansion:
If the distance is not too large, all other complications of the model become small corrections, and the time interval is simply the distance divided by the speed of light:
or
According to this approach, the relation cz = vr is an approximation valid at low redshifts, to be replaced by a relation at large redshifts that is model-dependent. See velocity-redshift figure.
Observability of parameters
[edit]Strictly speaking, neither v nor D in the formula are directly observable, because they are properties now of a galaxy, whereas our observations refer to the galaxy in the past, at the time that the light we currently see left it.
For relatively nearby galaxies (redshift z much less than one), v and D will not have changed much, and v can be estimated using the formula v = zc where c is the speed of light. This gives the empirical relation found by Hubble.
For distant galaxies, v (or D) cannot be calculated from z without specifying a detailed model for how H changes with time. The redshift is not even directly related to the recession velocity at the time the light set out, but it does have a simple interpretation: (1 + z) is the factor by which the universe has expanded while the photon was traveling towards the observer.
Expansion velocity vs. peculiar velocity
[edit]In using Hubble's law to determine distances, only the velocity due to the expansion of the universe can be used. Since gravitationally interacting galaxies move relative to each other independent of the expansion of the universe,[43] these relative velocities, called peculiar velocities, need to be accounted for in the application of Hubble's law. Such peculiar velocities give rise to redshift-space distortions.
Time-dependence of Hubble parameter
[edit]The parameter H is commonly called the "Hubble constant", but that is a misnomer since it is constant in space only at a fixed time; it varies with time in nearly all cosmological models, and all observations of far distant objects are also observations into the distant past, when the "constant" had a different value. "Hubble parameter" is a more correct term, with H0 denoting the present-day value.
Another common source of confusion is that the accelerating universe does not imply that the Hubble parameter is actually increasing with time; since , in most accelerating models increases relatively faster than , so H decreases with time. (The recession velocity of one chosen galaxy does increase, but different galaxies passing a sphere of fixed radius cross the sphere more slowly at later times.)
On defining the dimensionless deceleration parameter , it follows that
From this it is seen that the Hubble parameter is decreasing with time, unless q < -1; the latter can only occur if the universe contains phantom energy, regarded as theoretically somewhat improbable.
However, in the standard Lambda cold dark matter model (Lambda-CDM or ΛCDM model), q will tend to −1 from above in the distant future as the cosmological constant becomes increasingly dominant over matter; this implies that H will approach from above to a constant value of ≈ 57 (km/s)/Mpc, and the scale factor of the universe will then grow exponentially in time.
Idealized Hubble's law
[edit]The mathematical derivation of an idealized Hubble's law for a uniformly expanding universe is a fairly elementary theorem of geometry in 3-dimensional Cartesian/Newtonian coordinate space, which, considered as a metric space, is entirely homogeneous and isotropic (properties do not vary with location or direction). Simply stated, the theorem is this:
Any two points which are moving away from the origin, each along straight lines and with speed proportional to distance from the origin, will be moving away from each other with a speed proportional to their distance apart.
In fact, this applies to non-Cartesian spaces as long as they are locally homogeneous and isotropic, specifically to the negatively and positively curved spaces frequently considered as cosmological models (see shape of the universe).
An observation stemming from this theorem is that seeing objects recede from us on Earth is not an indication that Earth is near to a center from which the expansion is occurring, but rather that every observer in an expanding universe will see objects receding from them.
Ultimate fate and age of the universe
[edit]
A closed universe with ΩM > 1 and ΩΛ = 0 comes to an end in a Big Crunch and is considerably younger than its Hubble age.
An open universe with ΩM ≤ 1 and ΩΛ = 0 expands forever and has an age that is closer to its Hubble age. For the accelerating universe with nonzero ΩΛ that we inhabit, the age of the universe is coincidentally very close to the Hubble age.
The value of the Hubble parameter changes over time, either increasing or decreasing depending on the value of the so-called deceleration parameter q, which is defined by
In a universe with a deceleration parameter equal to zero, it follows that H = 1/t, where t is the time since the Big Bang. A non-zero, time-dependent value of q simply requires integration of the Friedmann equations backwards from the present time to the time when the comoving horizon size was zero.
It was long thought that q was positive, indicating that the expansion is slowing down due to gravitational attraction. This would imply an age of the universe less than 1/H (which is about 14 billion years). For instance, a value for q of 1/2 (once favoured by most theorists) would give the age of the universe as 2/(3H). The discovery in 1998 that q is apparently negative means that the universe could actually be older than 1/H. However, estimates of the age of the universe are very close to 1/H.
Olbers' paradox
[edit]The expansion of space summarized by the Big Bang interpretation of Hubble's law is relevant to the old conundrum known as Olbers' paradox: If the universe were infinite in size, static, and filled with a uniform distribution of stars, then every line of sight in the sky would end on a star, and the sky would be as bright as the surface of a star. However, the night sky is largely dark.[44][45]
Since the 17th century, astronomers and other thinkers have proposed many possible ways to resolve this paradox, but the currently accepted resolution depends in part on the Big Bang theory, and in part on the Hubble expansion: in a universe that existed for a finite amount of time, only the light of a finite number of stars has had enough time to reach us, and the paradox is resolved. Additionally, in an expanding universe, distant objects recede from us, which causes the light emanated from them to be redshifted and diminished in brightness by the time we see it.[44][45]
Dimensionless Hubble constant
[edit]Instead of working with Hubble's constant, a common practice is to introduce the dimensionless Hubble constant, usually denoted by h and commonly referred to as "little h",[29] then to write Hubble's constant H0 as h × 100 km⋅s−1⋅Mpc−1, all the relative uncertainty of the true value of H0 being then relegated to h.[46] The dimensionless Hubble constant is often used when giving distances that are calculated from redshift z using the formula d ≈ c/H0 × z. Since H0 is not precisely known, the distance is expressed as:
In other words, one calculates 2998 × z and one gives the units as Mpc h-1 or h-1 Mpc.
Occasionally a reference value other than 100 may be chosen, in which case a subscript is presented after h to avoid confusion; e.g. h70 denotes H0 = 70 h70 (km/s)/Mpc, which implies h70 = h / 0.7.
This should not be confused with the dimensionless value of Hubble's constant, usually expressed in terms of Planck units, obtained by multiplying H0 by 1.75×10−63 (from definitions of parsec and tP), for example for H0 = 70, a Planck unit version of 1.2×10−61 is obtained.
Acceleration of the expansion
[edit]A value for q measured from standard candle observations of Type Ia supernovae, which was determined in 1998 to be negative, surprised many astronomers with the implication that the expansion of the universe is currently "accelerating"[47] (although the Hubble factor is still decreasing with time, as mentioned above in the Interpretation section; see the articles on dark energy and the ΛCDM model).
Derivation of the Hubble parameter
[edit]This section needs additional citations for verification. (March 2014) |
Start with the Friedmann equation:
where H is the Hubble parameter, a is the scale factor, G is the gravitational constant, k is the normalised spatial curvature of the universe and equal to −1, 0, or 1, and Λ is the cosmological constant.
Matter-dominated universe (with a cosmological constant)
[edit]If the universe is matter-dominated, then the mass density of the universe ρ should be taken to include just matter so
where ρm0 is the density of matter today. From the Friedmann equation and thermodynamic principles we know for non-relativistic particles that their mass density decreases proportional to the inverse volume of the universe, so the equation above must be true. We can also define (see density parameter for Ωm)
therefore:
Also, by definition,
where the subscript 0 refers to the values today, and a0 = 1. Substituting all of this into the Friedmann equation at the start of this section and replacing a with a = 1/(1+z) gives
Matter- and dark energy-dominated universe
[edit]If the universe is both matter-dominated and dark energy-dominated, then the above equation for the Hubble parameter will also be a function of the equation of state of dark energy. So now:
where ρde is the mass density of the dark energy. By definition, an equation of state in cosmology is P = wρc2, and if this is substituted into the fluid equation, which describes how the mass density of the universe evolves with time, then
If w is constant, then
implying:
Therefore, for dark energy with a constant equation of state w, . If this is substituted into the Friedman equation in a similar way as before, but this time set k = 0, which assumes a spatially flat universe, then (see shape of the universe)
If the dark energy derives from a cosmological constant such as that introduced by Einstein, it can be shown that w = −1. The equation then reduces to the last equation in the matter-dominated universe section, with Ωk set to zero. In that case the initial dark energy density ρde0 is given by[48]
If dark energy does not have a constant equation-of-state w, then
and to solve this, w(a) must be parametrized, for example if w(a) = w0 + wa(1−a), giving[49]
Units derived from the Hubble constant
[edit]Hubble time
[edit]The Hubble constant H0 has units of inverse time; the Hubble time tH is simply defined as the inverse of the Hubble constant,[50] i.e.
This is slightly different from the age of the universe, which is approximately 13.8 billion years. The Hubble time is the age it would have had if the expansion had been linear,[51] and it is different from the real age of the universe because the expansion is not linear; it depends on the energy content of the universe (see § Derivation of the Hubble parameter).
We currently appear to be approaching a period where the expansion of the universe is exponential due to the increasing dominance of vacuum energy. In this regime, the Hubble parameter is constant, and the universe grows by a factor e each Hubble time:
Likewise, the generally accepted value of 2.27 Es−1 means that (at the current rate) the universe would grow by a factor of e2.27 in one exasecond.
Over long periods of time, the dynamics are complicated by general relativity, dark energy, inflation, etc., as explained above.
Hubble length
[edit]The Hubble length or Hubble distance is a unit of distance in cosmology, defined as cH−1 — the speed of light multiplied by the Hubble time. It is equivalent to 4,420 million parsecs or 14.4 billion light years. (The numerical value of the Hubble length in light years is, by definition, equal to that of the Hubble time in years.) Substituting D = cH−1 into the equation for Hubble's law, v = H0D reveals that the Hubble distance specifies the distance from our location to those galaxies which are currently receding from us at the speed of light.
Hubble volume
[edit]The Hubble volume is sometimes defined as a volume of the universe with a comoving size of cH−1. The exact definition varies: it is sometimes defined as the volume of a sphere with radius cH−1, or alternatively, a cube of side cH−1. Some cosmologists even use the term Hubble volume to refer to the volume of the observable universe, although this has a radius approximately three times larger.
Determining the Hubble constant
[edit]
The value of the Hubble constant, H0, cannot be measured directly, but is derived from a combination of astronomical observations and model-dependent assumptions. Increasingly accurate observations and new models over many decades have led to two sets of highly precise values which do not agree. This difference is known as the "Hubble tension".[8][53]
Earlier measurements
[edit]For the original 1929 estimate of the constant now bearing his name, Hubble used observations of Cepheid variable stars as "standard candles" to measure distance.[54] The result he obtained was 500 (km/s)/Mpc, much larger than the value astronomers currently calculate. Later observations by astronomer Walter Baade led him to realize that there were distinct "populations" for stars (Population I and Population II) in a galaxy. The same observations led him to discover that there are two types of Cepheid variable stars with different luminosities. Using this discovery, he recalculated Hubble constant and the size of the known universe, doubling the previous calculation made by Hubble in 1929.[55][56][54] He announced this finding to considerable astonishment at the 1952 meeting of the International Astronomical Union in Rome.
For most of the second half of the 20th century, the value of H0 was estimated to be between 50 and 90 (km/s)/Mpc.
The value of the Hubble constant was the topic of a long and rather bitter controversy between Gérard de Vaucouleurs, who claimed the value was around 100, and Allan Sandage, who claimed the value was near 50.[57] In one demonstration of vitriol between the parties, when Sandage and his colleague Gustav Andreas Tammann formally acknowledged the shortcomings of confirming the systematic error of their method in 1975, Vaucouleurs responded: "It is unfortunate that this sober warning was so soon forgotten and ignored by most astronomers and textbook writers".[58] In 1996, a debate moderated by John Bahcall between Sidney van den Bergh and Gustav Tammann was held in similar fashion to the earlier Shapley–Curtis debate over these two competing values.
This previously wide variance in estimates was partially resolved with the introduction of the ΛCDM model of the universe in the late 1990s. Incorporating the ΛCDM model, observations of high-redshift clusters at X-ray and microwave wavelengths using the Sunyaev–Zel'dovich effect, measurements of anisotropies in the cosmic microwave background radiation, and optical surveys all gave a value of around 50–70 km/s/Mpc for the constant.[59]
Precision cosmology and the Hubble tension
[edit]By the late 1990s, advances in ideas and technology allowed higher precision measurements.[60] However, two major categories of methods, each with high precision, fail to agree. "Late universe" measurements using calibrated distance ladder techniques have converged on a value of approximately 73 (km/s)/Mpc. Since 2000, "early universe" techniques based on measurements of the cosmic microwave background have become available, and these agree on a value near 67.7 (km/s)/Mpc.[61] (This accounts for the change in the expansion rate since the early universe, so is comparable to the first number.) Initially, this discrepancy was within the estimated measurement uncertainties and thus no cause for concern. However, as techniques have improved, the estimated measurement uncertainties have shrunk, but the discrepancies have not, to the point that the disagreement is now highly statistically significant. This discrepancy is called the Hubble tension.[62][63]
An example of an "early" measurement, the Planck mission published in 2018 gives a value for H0 = of 67.4±0.5 (km/s)/Mpc.[64] In the "late" camp is the higher value of 74.03±1.42 (km/s)/Mpc determined by the Hubble Space Telescope[65] and confirmed by the James Webb Space Telescope in 2023.[66][67] The "early" and "late" measurements disagree at the >5 σ level, beyond a plausible level of chance.[68][69] The resolution to this disagreement is an ongoing area of active research.[70]

Reducing systematic errors
[edit]Since 2013, extensive checks for possible systematic errors and improvements in reproducibility have been undertaken.[53]
The "late universe" or distance ladder measurements typically employ three stages or "rungs". In the first rung, distances to Cepheids are determined while trying to reduce luminosity errors from dust and correlations of metallicity with luminosity. The second rung uses Type Ia supernova, explosions of almost constant amounts of mass. Thusly, these produce very similar amounts of light; the primary systematic error in this case is the limited number of objects that can be observed. The third rung of the distance ladder measures the red-shift of supernovae to extract the Hubble flow, and from that the constant. At this rung, corrections due to motion other than expansion are applied.[53]: 2.1 As an example of the kind of work needed to reduce systematic errors, photometry on observations from the James Webb Space Telescope of extra-galactic Cepheids confirm the findings from the HST. The higher resolution avoided confusion from crowding of stars in the field of view but came to the same value for H0.[71][53]
The "early universe" or inverse distance ladder measures the observable consequences of spherical sound waves on primordial plasma density. These pressure waves – called baryon acoustic oscillations (BAO) – ceased once the universe cooled enough for electrons to stay bound to nuclei, ending the plasma and allowing the photons trapped by interaction with the plasma to escape. The subsequent pressure waves are evident in very small perturbations in the density imprinted on the cosmic microwave background, and on the large-scale density of galaxies across the sky. Detailed structure in high-precision measurements of the CMB can be matched to physics models of the oscillations. These models depend upon the Hubble constant such that a match reveals a value for the constant. Similarly, the BAO affects the statistical distribution of matter, observed as distant galaxies across the sky.
These two independent measurements produce similar values for the constant from the current models, giving strong evidence that systematic errors in the measurements themselves do not affect the result.[53]: Sup. B
Other kinds of measurements
[edit]In addition to measurements based on calibrated distance ladder techniques or measurements of the CMB, other methods have been used to determine the Hubble constant.
One alternative method for constraining the Hubble constant involves transient events seen in multiple images of a strongly lensed object. A transient event, such as a supernova, is seen at different times in each of the lensed images, and if this time delay between each image can be measured, it can be used to constrain the Hubble constant. This method is commonly known as "time-delay cosmography", and was first proposed by Refsdal in 1964,[72] years before the first strongly lensed object was observed. The first strongly lensed supernova to be discovered was named SN Refsdal in his honor. While Refsdal suggested this could be done with supernovae, he also noted that extremely luminous and distant star-like objects could also be used. These objects were later named quasars, and to date (April 2025) the majority of time-delay cosmography measurements have been done with strongly lensed quasars. This is because current samples of lensed quasars vastly outnumber known lensed supernovae, of which <10 are known. This is expected to change dramatically in the next few years, with surveys such as LSST expected to discover ~10 lensed SNe in the first three years of observation.[73] For example time-delay constraints on H0, see the results from STRIDES and H0LiCOW in the table below.
In October 2018, scientists used information from gravitational wave events (especially those involving the merger of neutron stars, like GW170817), of determining the Hubble constant.[74][75]
In July 2019, astronomers reported that a new method to determine the Hubble constant, and resolve the discrepancy of earlier methods, has been proposed based on the mergers of pairs of neutron stars, following the detection of the neutron star merger of GW170817, an event known as a dark siren.[76][77] Their measurement of the Hubble constant is 73.3+5.3
−5.0 (km/s)/Mpc.[78]
Also in July 2019, astronomers reported another new method, using data from the Hubble Space Telescope and based on distances to red giant stars calculated using the tip of the red-giant branch (TRGB) distance indicator. Their measurement of the Hubble constant is 69.8+1.9
−1.9 (km/s)/Mpc.[79][80][81]
In February 2020, the Megamaser Cosmology Project published independent results based on astrophysical masers visible at cosmological distances and which do not require multi-step calibration. That work confirmed the distance ladder results and differed from the early-universe results at a statistical significance level of 95%.[82]
In July 2020, measurements of the cosmic background radiation by the Atacama Cosmology Telescope predict that the Universe should be expanding more slowly than is currently observed.[83]
In July 2023, an independent estimate of the Hubble constant was derived from a kilonova, the optical afterglow of a neutron star merger, using the expanding photosphere method.[84] Due to the blackbody nature of early kilonova spectra,[85] such systems provide strongly constraining estimators of cosmic distance. Using the kilonova AT2017gfo (the aftermath of, once again, GW170817), these measurements indicate a local-estimate of the Hubble constant of 67.0±3.6 (km/s)/Mpc.[86][84]

Possible resolutions of the Hubble tension
[edit]The cause of the Hubble tension is unknown,[87] and there are many possible proposed solutions. The most conservative is that there is an unknown systematic error affecting either early-universe or late-universe observations. Although intuitively appealing, this explanation requires multiple unrelated effects regardless of whether early-universe or late-universe observations are incorrect, and there are no obvious candidates. Furthermore, any such systematic error would need to affect multiple different instruments, since both the early-universe and late-universe observations come from several different telescopes.[53]
Alternatively, it could be that the observations are correct, but some unaccounted-for effect is causing the discrepancy. If the cosmological principle fails (see Lambda-CDM model § Violations of the cosmological principle), then the existing interpretations of the Hubble constant and the Hubble tension have to be revised, which might resolve the Hubble tension.[88] In particular, we would need to be located within a very large void, up to about a redshift of 0.5, for such an explanation to conflate with supernovae and baryon acoustic oscillation observations.[63] Yet another possibility is that the uncertainties in the measurements could have been underestimated, but given the internal agreements this is neither likely, nor resolves the overall tension.[53]
Finally, another possibility is new physics beyond the currently accepted cosmological model of the universe, the ΛCDM model.[63][89] There are very many theories in this category, for example, replacing general relativity with a modified theory of gravity could potentially resolve the tension,[90][91] as can a dark energy component in the early universe,[b][92] dark energy with a time-varying equation of state,[c][93] or dark matter that decays into dark radiation.[94] A problem faced by all these theories is that both early-universe and late-universe measurements rely on multiple independent lines of physics, and it is difficult to modify any of those lines while preserving their successes elsewhere. The scale of the challenge can be seen from how some authors have argued that new early-universe physics alone is not sufficient;[95][96] while other authors argue that new late-universe physics alone is also not sufficient.[97] Nonetheless, astronomers are trying, with interest in the Hubble tension growing strongly since the mid 2010s.[63]
Measurements of the Hubble constant
[edit]| Date published | Hubble constant (km/s)/Mpc |
Observer | Citation | Remarks / methodology |
|---|---|---|---|---|
| 2025-05-27 | 70.39±1.94 | W. Freedman et al | [98] | Tip of the Red Giant Branch (TRGB) method (values from J-Region Asymptotic Giant Branch (JAGB) and Cepheids also reported)(JWST and HST data)[99] |
| 2025-01-14 | 75.7+8.1 −5.5 |
Pascale et al. | [100] | Timing delay of gravitationally lensed images of Supernova H0pe. Independent of cosmic distance ladder or the CMB. JWST data. (2023-05-11 cell and this one are the only 2 values with this method so far) |
| 2024-12-01 | 72.6±2.0 | SH0ES+CCHP JWST | [101] | JWST, 3 methods, Cepheids, TRGB, JAGB, 2 groups data |
| 2023-07-19 | 67.0±3.6 | Sneppen et al. | [86][84] | Due to the blackbody spectra of the optical counterpart of neutron-star mergers, these systems provide strongly constraining estimators of cosmic distance. |
| 2023-07-13 | 68.3±1.5 | SPT-3G | [102] | CMB TT/TE/EE power spectrum. Less than 1σ discrepancy with Planck. |
| 2023-05-11 | 66.6+4.1 −3.3 |
P. L. Kelly et al. | [103] | Timing delay of gravitationally lensed images of Supernova Refsdal. Independent of cosmic distance ladder or the CMB. |
| 2022-12-14 | 67.3+10.0 −9.1 |
S. Contarini et al. | [104] | Statistics of cosmic voids using BOSS DR12 data set.[105] |
| 2022-02-08 | 73.4+0.99 −1.22 |
Pantheon+ | [106] | SN Ia distance ladder (+SH0ES) |
| 2022-06-17 | 75.4+3.8 −3.7 |
T. de Jaeger et al. | [107] | Use Type II supernovae as standardisable candles to obtain an independent measurement of the Hubble constant—13 SNe II with host-galaxy distances measured from Cepheid variables, the tip of the red giant branch, and geometric distance (NGC 4258). |
| 2021-12-08 | 73.04±1.04 | SH0ES | [108] | Cepheids-SN Ia distance ladder (HST+Gaia EDR3+"Pantheon+"). 5σ discrepancy with planck. |
| 2021-09-17 | 69.8±1.7 | W. Freedman | [109] | Tip of the red-giant branch (TRGB) distance indicator (HST+Gaia EDR3) |
| 2020-12-16 | 72.1±2.0 | Hubble Space Telescope and Gaia EDR3 | [110] | Combining earlier work on red giant stars, using the tip of the red-giant branch (TRGB) distance indicator, with parallax measurements of Omega Centauri from Gaia EDR3. |
| 2020-12-15 | 73.2±1.3 | Hubble Space Telescope and Gaia EDR3 | [111] | Combination of HST photometry and Gaia EDR3 parallaxes for Milky Way Cepheids, reducing the uncertainty in calibration of Cepheid luminosities to 1.0%. Overall uncertainty in the value for H0 is 1.8%, which is expected to be reduced to 1.3% with a larger sample of type Ia supernovae in galaxies that are known Cepheid hosts. Continuation of a collaboration known as Supernovae, H0, for the Equation of State of Dark Energy (SHoES). |
| 2020-12-04 | 73.5±5.3 | E. J. Baxter, B. D. Sherwin | [112] | Gravitational lensing in the CMB is used to estimate H0 without referring to the sound horizon scale, providing an alternative method to analyze the Planck data. |
| 2020-11-25 | 71.8+3.9 −3.3 |
P. Denzel et al. | [113] | Eight quadruply lensed galaxy systems are used to determine H0 to a precision of 5%, in agreement with both "early" and "late" universe estimates. Independent of distance ladders and the cosmic microwave background. |
| 2020-11-07 | 67.4±1.0 | T. Sedgwick et al. | [114] | Derived from 88 0.02 < z < 0.05 Type Ia supernovae used as standard candle distance indicators. The H0 estimate is corrected for the effects of peculiar velocities in the supernova environments, as estimated from the galaxy density field. The result assumes Ωm = 0.3, ΩΛ = 0.7 and a sound horizon of 149.3 Mpc, a value taken from Anderson et al. (2014).[115] |
| 2020-09-29 | 67.6+4.3 −4.2 |
S. Mukherjee et al. | [116] | Gravitational waves, assuming that the transient ZTF19abanrh found by the Zwicky Transient Facility is the optical counterpart to GW190521. Independent of distance ladders and the cosmic microwave background. |
| 2020-06-18 | 75.8+5.2 −4.9 |
T. de Jaeger et al. | [117] | Use Type II supernovae as standardisable candles to obtain an independent measurement of the Hubble constant—7 SNe II with host-galaxy distances measured from Cepheid variables or the tip of the red giant branch. |
| 2020-02-26 | 73.9±3.0 | Megamaser Cosmology Project | [82] | Geometric distance measurements to megamaser-hosting galaxies. Independent of distance ladders and the cosmic microwave background. |
| 2019-10-14 | 74.2+2.7 −3.0 |
STRIDES | [118] | Modelling the mass distribution & time delay of the lensed quasar DES J0408-5354. |
| 2019-09-12 | 76.8±2.6 | SHARP/H0LiCOW | [119] | Modelling three galactically lensed objects and their lenses using ground-based adaptive optics and the Hubble Space Telescope. |
| 2019-08-20 | 73.3+1.36 −1.35 |
K. Dutta et al. | [120] | This is obtained analysing low-redshift cosmological data within ΛCDM model. The datasets used are type-Ia supernovae, baryon acoustic oscillations, time-delay measurements using strong-lensing, H(z) measurements using cosmic chronometers and growth measurements from large scale structure observations. |
| 2019-08-15 | 73.5±1.4 | M. J. Reid, D. W. Pesce, A. G. Riess | [121] | Measuring the distance to Messier 106 using its supermassive black hole, combined with measurements of eclipsing binaries in the Large Magellanic Cloud. |
| 2019-07-16 | 69.8±1.9 | Hubble Space Telescope | [79][80][81] | Distances to red giant stars are calculated using the tip of the red-giant branch (TRGB) distance indicator. |
| 2019-07-10 | 73.3+1.7 −1.8 |
H0LiCOW collaboration | [122] | Updated observations of multiply imaged quasars, now using six quasars, independent of the cosmic distance ladder and independent of the cosmic microwave background measurements. |
| 2019-07-08 | 70.3+5.3 −5.0 |
The LIGO Scientific Collaboration and The Virgo Collaboration | [78] | Uses radio counterpart of GW170817, combined with earlier gravitational wave (GW) and electromagnetic (EM) data. |
| 2019-03-28 | 68.0+4.2 −4.1 |
Fermi-LAT | [123] | Gamma ray attenuation due to extragalactic light. Independent of the cosmic distance ladder and the cosmic microwave background. |
| 2019-03-18 | 74.03±1.42 | Hubble Space Telescope | [68] | Precision HST photometry of Cepheids in the Large Magellanic Cloud (LMC) reduce the uncertainty in the distance to the LMC from 2.5% to 1.3%. The revision increases the tension with CMB measurements to the 4.4σ level (P=99.999% for Gaussian errors), raising the discrepancy beyond a plausible level of chance. Continuation of a collaboration known as Supernovae, H0, for the Equation of State of Dark Energy (SHoES). |
| 2019-02-08 | 67.78+0.91 −0.87 |
Joseph Ryan et al. | [124] | Quasar angular size and baryon acoustic oscillations, assuming a flat ΛCDM model. Alternative models result in different (generally lower) values for the Hubble constant. |
| 2018-11-06 | 67.77±1.30 | Dark Energy Survey | [125] | Supernova measurements using the inverse distance ladder method based on baryon acoustic oscillations. |
| 2018-09-05 | 72.5+2.1 −2.3 |
H0LiCOW collaboration | [126] | Observations of multiply imaged quasars, independent of the cosmic distance ladder and independent of the cosmic microwave background measurements. |
| 2018-07-18 | 67.66±0.42 | Planck Mission | [64] | Final Planck 2018 results. |
| 2018-04-27 | 73.52±1.62 | Hubble Space Telescope and Gaia | [127][128] | Additional HST photometry of galactic Cepheids with early Gaia parallax measurements. The revised value increases tension with CMB measurements at the 3.8σ level. Continuation of the SHoES collaboration. |
| 2018-02-22 | 73.45±1.66 | Hubble Space Telescope | [129][130] | Parallax measurements of galactic Cepheids for enhanced calibration of the distance ladder; the value suggests a discrepancy with CMB measurements at the 3.7σ level. The uncertainty is expected to be reduced to below 1% with the final release of the Gaia catalog. SHoES collaboration. |
| 2017-10-16 | 70.0+12.0 −8.0 |
The LIGO Scientific Collaboration and The Virgo Collaboration | [131] | Standard siren measurement independent of normal "standard candle" techniques; the gravitational wave analysis of a binary neutron star (BNS) merger GW170817 directly estimated the luminosity distance out to cosmological scales. An estimate of fifty similar detections in the next decade may arbitrate tension of other methodologies.[132] Detection and analysis of a neutron star-black hole merger (NSBH) may provide greater precision than BNS could allow.[133] |
| 2016-11-22 | 71.9+2.4 −3.0 |
Hubble Space Telescope | [134] | Uses time delays between multiple images of distant variable sources produced by strong gravitational lensing. Collaboration known as H0 Lenses in COSMOGRAIL's Wellspring (H0LiCOW). |
| 2016-08-04 | 76.2+3.4 −2.7 |
Cosmicflows-3 | [135] | Comparing redshift to other distance methods, including Tully–Fisher, Cepheid variable, and Type Ia supernovae. A restrictive estimate from the data implies a more precise value of 75±2. |
| 2016-07-13 | 67.6+0.7 −0.6 |
SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS) | [136] | Baryon acoustic oscillations. An extended survey (eBOSS) began in 2014 and is expected to run through 2020. The extended survey is designed to explore the time when the universe was transitioning away from the deceleration effects of gravity from 3 to 8 billion years after the Big Bang.[137] |
| 2016-05-17 | 73.24±1.74 | Hubble Space Telescope | [138] | Type Ia supernova, the uncertainty is expected to go down by a factor of more than two with upcoming Gaia measurements and other improvements. SHoES collaboration. |
| 2015-02 | 67.74±0.46 | Planck Mission | [139][140] | Results from an analysis of Planck's full mission were made public on 1 December 2014 at a conference in Ferrara, Italy. A full set of papers detailing the mission results were released in February 2015. |
| 2013-10-01 | 74.4±3.0 | Cosmicflows-2 | [141] | Comparing redshift to other distance methods, including Tully–Fisher, Cepheid variable, and Type Ia supernovae. |
| 2013-03-21 | 67.80±0.77 | Planck Mission | [52][142][143][144][145] | The ESA Planck Surveyor was launched in May 2009. Over a four-year period, it performed a significantly more detailed investigation of cosmic microwave radiation than earlier investigations using HEMT radiometers and bolometer technology to measure the CMB at a smaller scale than WMAP. On 21 March 2013, the European-led research team behind the Planck cosmology probe released the mission's data including a new CMB all-sky map and their determination of the Hubble constant. |
| 2012-12-20 | 69.32±0.80 | WMAP (9 years), combined with other measurements | [146] | |
| 2010 | 70.4+1.3 −1.4 |
WMAP (7 years), combined with other measurements | [147] | These values arise from fitting a combination of WMAP and other cosmological data to the simplest version of the ΛCDM model. If the data are fit with more general versions, H0 tends to be smaller and more uncertain: typically around 67±4 (km/s)/Mpc although some models allow values near 63 (km/s)/Mpc.[148] |
| 2010 | 71.0±2.5 | WMAP only (7 years). | [147] | |
| 2009-02 | 70.5±1.3 | WMAP (5 years), combined with other measurements | [149] | |
| 2009-02 | 71.9+2.6 −2.7 |
WMAP only (5 years) | [149] | |
| 2007 | 70.4+1.5 −1.6 |
WMAP (3 years), combined with other measurements | [150] | |
| 2006-08 | 76.9+10.7 −8.7 |
Chandra X-ray Observatory | [151] | Combined Sunyaev–Zeldovich effect and Chandra X-ray observations of galaxy clusters. Adjusted uncertainty in table from Planck Collaboration 2013.[152] |
| 2003 | 72±5 | WMAP (First year) only | [153] | |
| 2001-05 | 72±8 | Hubble Space Telescope Key Project | [154] | This project established the most precise optical determination, consistent with a measurement of H0 based upon Sunyaev–Zel'dovich effect observations of many galaxy clusters having a similar accuracy. |
| before 1996 | 50 — 90 (est.) | [57] | ||
| 1994 | 67±7 | Supernova 1a Light Curve Shapes | [155] | Determined relationship between luminosity of SN 1a's and their Light Curve Shapes. Riess et al. used this ratio of the light curve of SN 1972E and the Cepheid distance to NGC 5253 to determine the constant. |
| mid 1970's | 100±10 | Gérard de Vaucouleurs | [58] | De Vaucouleurs believed he had improved the accuracy of Hubble's constant from Sandage's because he used 5x more primary indicators, 10× more calibration methods, 2× more secondary indicators, and 3× as many galaxy data points to derive his 100±10. |
| early 1970s | 55 (est.) | Allan Sandage and Gustav Tammann | [156] | |
| 1958 | 75 (est.) | Allan Sandage | [157] | This was the first good estimate of H0, but it would be decades before a consensus was achieved. |
| 1956 | 180 | Humason, Mayall and Sandage | [156] | |
| 1929 | 500 | Edwin Hubble, Hooker telescope | [158][156][159] | |
| 1927 | 625 | Georges Lemaître | [160] | First measurement and interpretation as a sign of the expansion of the universe. |
See also
[edit]- List of scientists whose names are used in physical constants
- S8 tension- a similar problem from another parameter of the ΛCDM model.
- Tests of general relativity
Notes
[edit]- ^ See Comoving and proper distances § Uses of the proper distance for discussion of the subtleties of this definition of velocity.
- ^ In standard ΛCDM, dark energy only comes into play in the late universe – its effect in the early universe is too small to have an effect.
- ^ In standard ΛCDM, dark energy has a constant equation of state w = −1.
References
[edit]- ^ "IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law" (Press release). IAU. 29 October 2018. Archived from the original on 2019-03-30. Retrieved 2018-10-29.
- ^ van den Bergh, S. (August 2011). "The Curious Case of Lemaitre's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.
- ^ Nussbaumer, H.; Bieri, L. (2011). "Who discovered the expanding universe?". The Observatory. 131 (6): 394–398. arXiv:1107.2281. Bibcode:2011Obs...131..394N.
- ^ Way, M.J. (2013). "Dismantling Hubble's Legacy?" (PDF). In Michael J. Way; Deidre Hunter (eds.). Origins of the Expanding Universe: 1912-1932. ASP Conference Series. Vol. 471. Astronomical Society of the Pacific. pp. 97–132. arXiv:1301.7294. Bibcode:2013ASPC..471...97W.
- ^ Friedman, A. (December 1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902.. (English translation in Friedman, A. (December 1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.)
- ^ Wirtz, C. W. (April 1922). "Einiges zur Statistik der Radialbewegungen von Spiralnebeln und Kugelsternhaufen". Astronomische Nachrichten. 215 (17): 349–354. Bibcode:1922AN....215..349W. doi:10.1002/asna.19212151703.
- ^ Wirtz, C. W. (1924). "De Sitters Kosmologie und die Radialbewegungen der Spiralnebel". Astronomische Nachrichten. 222 (5306): 21–26. Bibcode:1924AN....222...21W. doi:10.1002/asna.19242220203.
- ^ a b c Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". New York Times. Retrieved 21 February 2017.
- ^ Lemaître, G. (1927). "Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles A (in French). 47: 49–59. Bibcode:1927ASSB...47...49L. Partially translated to English in Lemaître, G. (1931). "Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae". Monthly Notices of the Royal Astronomical Society. 91 (5): 483–490. Bibcode:1931MNRAS..91..483L. doi:10.1093/mnras/91.5.483.
- ^ a b Livio, M. (2011). "Lost in translation: Mystery of the missing text solved". Nature. 479 (7372): 171–173. Bibcode:2011Natur.479..171L. doi:10.1038/479171a. PMID 22071745. S2CID 203468083.
- ^ Livio, M.; Riess, A. (2013). "Measuring the Hubble constant". Physics Today. 66 (10): 41–47. Bibcode:2013PhT....66j..41L. doi:10.1063/PT.3.2148.
- ^ Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
- ^ Slipher, V.M. (1917). "Radial velocity observations of spiral nebulae". The Observatory. 40: 304–306. Bibcode:1917Obs....40..304S.
- ^ Longair, M. S. (2006). The Cosmic Century. Cambridge University Press. p. 109. ISBN 978-0-521-47436-8.
- ^ Nussbaumer, Harry (2013). "Slipher's redshifts as support for de Sitter's model and the discovery of the dynamic universe" (PDF). In Michael J. Way; Deidre Hunter (eds.). Origins of the Expanding Universe: 1912–1932. ASP Conference Series. Vol. 471. Astronomical Society of the Pacific. pp. 25–38. arXiv:1303.1814.
- ^ "1912: Henrietta Leavitt Discovers the Distance Key". Everyday Cosmology. Retrieved 18 February 2024.
- ^ Coles, P., ed. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202. ISBN 978-0-203-16457-0.
- ^ "Hubble Flow". The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology. Retrieved 2013-05-14.
- ^ Overbye, Dennis (25 February 2019). "Have Dark Forces Been Messing With the Cosmos? – Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process". The New York Times. Retrieved 26 February 2019.
- ^ O'Raifeartaigh, Cormac (2013). "The Contribution of V.M. Slipher to the discovery of the expanding universe" (PDF). Origins of the Expanding Universe: 1912-1932. ASP Conference Series. Vol. 471. Astronomical Society of the Pacific. pp. 49–62. arXiv:1212.5499.
- ^ "Three steps to the Hubble constant". www.spacetelescope.org. Retrieved 26 February 2018.
- ^ Slipher, V. M. (1913). "The Radial Velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1 (8): 56–57. Bibcode:1913LowOB...2...56S.
- ^ Slipher, V. M. (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S.
- ^ Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik (in German). 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902. Translated to English in Friedmann, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.
- ^ van den Bergh, Sydney (2011). "The Curious Case of Lemaître's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195. Bibcode:2011JRASC.105..151V.
- ^ Block, David (2012). 'Georges Lemaitre and Stigler's law of eponymy' in Georges Lemaître: Life, Science and Legacy (Holder and Mitton ed.). Springer. pp. 89–96.
- ^ Sandage, Allan (December 1989). "Edwin Hubble 1889–1953". Journal of the Royal Astronomical Society of Canada. 83 (6): 351–362. Bibcode:1989JRASC..83..351S.
- ^ a b Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8. ISBN 978-3-540-72534-3.
- ^ a b Croton, Darren J. (14 October 2013). "Damn You, Little h! (Or, Real-World Applications of the Hubble Constant Using Observed and Simulated Data)". Publications of the Astronomical Society of Australia. 30 e052. arXiv:1308.4150. Bibcode:2013PASA...30...52C. doi:10.1017/pasa.2013.31. S2CID 119257465. Retrieved 8 December 2021.
- ^ Kirshner, R. P. (2003). "Hubble's diagram and cosmic expansion". Proceedings of the National Academy of Sciences. 101 (1): 8–13. Bibcode:2004PNAS..101....8K. doi:10.1073/pnas.2536799100. PMC 314128. PMID 14695886.
- ^ a b "What is a Cosmological Constant?". Goddard Space Flight Center. Retrieved 2013-10-17.
- ^ Isaacson, W. (2007). Einstein: His Life and Universe. Simon & Schuster. p. 354. ISBN 978-0-7432-6473-0.
- ^ "Einstein's Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant". Science Daily. 28 November 2007. Retrieved 2013-06-02.
- ^ Davis, T. M.; Lineweaver, C. H. (2001). "Superluminal Recessional Velocities". AIP Conference Proceedings. 555: 348–351. arXiv:astro-ph/0011070. Bibcode:2001AIPC..555..348D. CiteSeerX 10.1.1.254.1810. doi:10.1063/1.1363540. S2CID 118876362.
- ^ "Is the universe expanding faster than the speed of light?". Ask an Astronomer at Cornell University. Archived from the original on 23 November 2003. Retrieved 5 June 2015.
- ^ Harrison, E. (1992). "The redshift-distance and velocity-distance laws". The Astrophysical Journal. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.
- ^ Madsen, M. S. (1995). The Dynamic Cosmos. CRC Press. p. 35. ISBN 978-0-412-62300-4.
- ^ Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164. ISBN 978-0-521-58632-0.
- ^ Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. p. 58. ISBN 978-0-521-42486-8.
- ^ Sartori, L. (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B. ISBN 978-0-520-20029-6.
- ^ Sartori, L. (1996). Understanding Relativity. University of California Press. pp. 304–305. ISBN 978-0-520-20029-6.
- ^ Matts Roos, Introduction to Cosmology
- ^ Scharping, Nathaniel (18 October 2017). "Gravitational Waves Show How Fast The Universe is Expanding". Astronomy. Retrieved 18 October 2017.
- ^ a b Chase, S. I.; Baez, J. C. (2004). "Olbers' Paradox". The Original Usenet Physics FAQ. Retrieved 2013-10-17.
- ^ a b Asimov, I. (1974). "The Black of Night". Asimov on Astronomy. Doubleday. ISBN 978-0-385-04111-9.
- ^ Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press. ISBN 978-0-691-07428-3.
- ^ Perlmutter, S. (2003). "Supernovae, Dark Energy, and the Accelerating Universe" (PDF). Physics Today. 56 (4): 53–60. Bibcode:2003PhT....56d..53P. CiteSeerX 10.1.1.77.7990. doi:10.1063/1.1580050. OSTI 1032838. Archived (PDF) from the original on 2022-10-09.
- ^ Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). San Francisco: Addison-Wesley. p. 328. ISBN 978-0-8053-8732-2.
- ^ Heneka, C.; Amendola, L. (2018). "General modified gravity with 21cm intensity mapping: simulations and forecast". Journal of Cosmology and Astroparticle Physics. 2018 (10): 004. arXiv:1805.03629. Bibcode:2018JCAP...10..004H. doi:10.1088/1475-7516/2018/10/004. S2CID 119224326.
- ^ Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford [u.a.]: Oxford University Press. p. 304. ISBN 978-0-19-853096-1.
- ^ Ridpath, Ian (2012). A Dictionary of Astronomy (2nd ed.). Oxford University Press. p. 225. doi:10.1093/acref/9780199609055.001.0001. ISBN 978-0-19-960905-5.
- ^ a b Bucher, P. A. R.; et al. (Planck Collaboration) (2013). "Planck 2013 results. I. Overview of products and scientific Results". Astronomy & Astrophysics. 571: A1. arXiv:1303.5062. Bibcode:2014A&A...571A...1P. doi:10.1051/0004-6361/201321529. S2CID 218716838.
- ^ a b c d e f g Verde, Licia; Schöneberg, Nils; Gil-Marín, Héctor (2024-09-13). "A Tale of Many H0". Annual Review of Astronomy and Astrophysics. 62: 287–331. doi:10.1146/annurev-astro-052622-033813. ISSN 0066-4146.
- ^ a b Allen, Nick. "Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade". The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007. Retrieved 19 November 2011.
- ^ Baade, W. (1944) The resolution of Messier 32, NGC 205, and the central region of the Andromeda nebula. ApJ 100 137–146
- ^ Baade, W. (1956) The period-luminosity relation of the Cepheids. PASP 68 5–16
- ^ a b Overbye, D. (1999). "Prologue". Lonely Hearts of the Cosmos (2nd ed.). HarperCollins. p. 1ff. ISBN 978-0-316-64896-7.
- ^ a b de Vaucouleurs, G. (1982). The cosmic distance scale and the Hubble constant. Mount Stromlo and Siding Spring Observatories, Australian National University.
- ^ Myers, S. T. (1999). "Scaling the universe: Gravitational lenses and the Hubble constant". Proceedings of the National Academy of Sciences of the United States of America. 96 (8): 4236–4239. Bibcode:1999PNAS...96.4236M. doi:10.1073/pnas.96.8.4236. PMC 33560. PMID 10200245.
- ^ Turner, Michael S. (2022-09-26). "The Road to Precision Cosmology". Annual Review of Nuclear and Particle Science. 72: 1–35. arXiv:2201.04741. Bibcode:2022ARNPS..72....1T. doi:10.1146/annurev-nucl-111119-041046. ISSN 0163-8998.
- ^ Freedman, Wendy L.; Madore, Barry F. (2023-11-01). "Progress in direct measurements of the Hubble constant". Journal of Cosmology and Astroparticle Physics. 2023 (11) 050. arXiv:2309.05618. Bibcode:2023JCAP...11..050F. doi:10.1088/1475-7516/2023/11/050. ISSN 1475-7516.
- ^ Mann, Adam (26 August 2019). "One Number Shows Something Is Fundamentally Wrong with Our Conception of the Universe – This fight has universal implications". Live Science. Retrieved 26 August 2019.
- ^ a b c d e di Valentino, Eleonora; et al. (2021). "In the realm of the Hubble tension—a review of solutions". Classical and Quantum Gravity. 38 (15) 153001. arXiv:2103.01183. Bibcode:2021CQGra..38o3001D. doi:10.1088/1361-6382/ac086d. S2CID 232092525.
- ^ a b Planck Collaboration; Aghanim, N.; et al. (2018). "Planck 2018 results. VI. Cosmological parameters". Astronomy and Astrophysics. 641 A6. arXiv:1807.06209. Bibcode:2020A&A...641A...6P. doi:10.1051/0004-6361/201833910.
- ^ Ananthaswamy, Anil (22 March 2019). "Best-Yet Measurements Deepen Cosmological Crisis". Scientific American. Retrieved 23 March 2019.
- ^ Riess, Adam G.; Anand, Gagandeep S.; Yuan, Wenlong; Casertano, Stefano; Dolphin, Andrew; Macri, Lucas M.; Breuval, Louise; Scolnic, Dan; Perrin, Marshall (2023-07-28), "Crowded No More: The Accuracy of the Hubble Constant Tested with High Resolution Observations of Cepheids by JWST", The Astrophysical Journal, 956 (1) L18, arXiv:2307.15806, Bibcode:2023ApJ...956L..18R, doi:10.3847/2041-8213/acf769
- ^ "Webb Confirms Accuracy of Universe's Expansion Rate Measured by Hubble, Deepens Mystery of Hubble Constant Tension – James Webb Space Telescope". blogs.nasa.gov. 2023-09-12. Retrieved 2024-02-15.
- ^ a b Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan (18 March 2019). "Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM". The Astrophysical Journal. 876 (1) 85. arXiv:1903.07603. Bibcode:2019ApJ...876...85R. doi:10.3847/1538-4357/ab1422. S2CID 85528549.
- ^ Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Anand, Gagandeep S.; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V.; Hoffmann, Samantha; Jha, Saurabh W.; Kenworthy, W. D'arcy (July 2022). "A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team". The Astrophysical Journal Letters. 934 (1): L7. arXiv:2112.04510. Bibcode:2022ApJ...934L...7R. doi:10.3847/2041-8213/ac5c5b. ISSN 2041-8205.
- ^ Millea, Marius; Knox, Lloyd (2019-08-10). "Hubble constant hunter's guide". Physical Review D. 101 (4) 043533. arXiv:1908.03663. doi:10.1103/PhysRevD.101.043533.
- ^ Riess, Adam G.; Anand, Gagandeep S.; Yuan, Wenlong; Casertano, Stefano; Dolphin, Andrew; Macri, Lucas M.; Breuval, Louise; Scolnic, Dan; Perrin, Marshall; Anderson, Richard I. (2023-10-01). "Crowded No More: The Accuracy of the Hubble Constant Tested with High-resolution Observations of Cepheids by JWST". The Astrophysical Journal Letters. 956 (1): L18. arXiv:2307.15806. Bibcode:2023ApJ...956L..18R. doi:10.3847/2041-8213/acf769. ISSN 2041-8205.
- ^ Refsdal, S. (1 September 1964). "On the Possibility of Determining Hubble's Parameter and the Masses of Galaxies from the Gravitational Lens Effect". Monthly Notices of the Royal Astronomical Society. 128 (4): 307–310. doi:10.1093/mnras/128.4.307.
- ^ Bronikowski, M.; Petrushevska, T.; Pierel, J. D. R.; Acebron, A.; Donevski, D.; Apostolova, B.; Blagorodnova, N.; Jankovič, T. (2025). "Cluster-lensed supernova yields from the Vera C. Rubin Observatory and Nancy Grace Roman Space Telescope". Astronomy & Astrophysics. 697: A146. arXiv:2504.01068. Bibcode:2025A&A...697A.146B. doi:10.1051/0004-6361/202451457.
- ^ Lerner, Louise (22 October 2018). "Gravitational waves could soon provide measure of universe's expansion". Phys.org. Retrieved 22 October 2018.
- ^ Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). "A two per cent Hubble constant measurement from standard sirens within five years". Nature. 562 (7728): 545–547. arXiv:1712.06531. Bibcode:2018Natur.562..545C. doi:10.1038/s41586-018-0606-0. PMID 30333628. S2CID 52987203.
- ^ National Radio Astronomy Observatory (8 July 2019). "New method may resolve difficulty in measuring universe's expansion – Neutron star mergers can provide new 'cosmic ruler'". EurekAlert!. Archived from the original on 8 July 2019. Retrieved 8 July 2019.
- ^ Finley, Dave (8 July 2019). "New Method May Resolve Difficulty in Measuring Universe's Expansion". National Radio Astronomy Observatory. Retrieved 8 July 2019.
- ^ a b Hotokezaka, K.; et al. (8 July 2019). "A Hubble constant measurement from superluminal motion of the jet in GW170817". Nature Astronomy. 3 (10): 940–944. arXiv:1806.10596. Bibcode:2019NatAs...3..940H. doi:10.1038/s41550-019-0820-1. S2CID 119547153.
- ^ a b Carnegie Institution of Science (16 July 2019). "New measurement of universe's expansion rate is 'stuck in the middle' – Red giant stars observed by Hubble Space Telescope used to make an entirely new measurement of how fast the universe is expanding". EurekAlert!. Retrieved 16 July 2019.
- ^ a b Sokol, Joshua (19 July 2019). "Debate intensifies over speed of expanding universe". Science. doi:10.1126/science.aay8123. S2CID 200021863. Retrieved 20 July 2019.
- ^ a b Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; et al. (2019). "The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch". The Astrophysical Journal. 882 (1) 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. S2CID 196623652.
- ^ a b Pesce, D. W.; Braatz, J. A.; Reid, M. J.; Riess, A. G.; et al. (26 February 2020). "The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints". The Astrophysical Journal. 891 (1) L1. arXiv:2001.09213. Bibcode:2020ApJ...891L...1P. doi:10.3847/2041-8213/ab75f0. S2CID 210920444.
- ^ Castelvecchi, Davide (2020-07-15). "Mystery over Universe's expansion deepens with fresh data". Nature. 583 (7817): 500–501. Bibcode:2020Natur.583..500C. doi:10.1038/d41586-020-02126-6. PMID 32669728. S2CID 220583383.
- ^ a b c Sneppen, Albert; Watson, Darach; Poznanski, Dovi; Just, Oliver; Bauswein, Andreas; Wojtak, Radosław (2023-10-01). "Measuring the Hubble constant with kilonovae using the expanding photosphere method". Astronomy & Astrophysics. 678 A14. arXiv:2306.12468. Bibcode:2023A&A...678A..14S. doi:10.1051/0004-6361/202346306. ISSN 0004-6361.
- ^ Sneppen, Albert (2023-09-01). "On the Blackbody Spectrum of Kilonovae". The Astrophysical Journal. 955 (1) 44. arXiv:2306.05452. Bibcode:2023ApJ...955...44S. doi:10.3847/1538-4357/acf200. ISSN 0004-637X.
- ^ a b Sneppen, Albert; Watson, Darach; Bauswein, Andreas; Just, Oliver; Kotak, Rubina; Nakar, Ehud; Poznanski, Dovi; Sim, Stuart (February 2023). "Spherical symmetry in the kilonova AT2017gfo/GW170817". Nature. 614 (7948): 436–439. arXiv:2302.06621. Bibcode:2023Natur.614..436S. doi:10.1038/s41586-022-05616-x. ISSN 1476-4687. PMID 36792736. S2CID 256846834.
- ^ Gresko, Michael (17 December 2021). "The universe is expanding faster than it should be". National Geographic. Archived from the original on December 17, 2021. Retrieved 21 December 2021.
- ^ Abdalla, Elcio; Abellán, Guillermo Franco; Aboubrahim, Amin (11 Mar 2022), "Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies", Journal of High Energy Astrophysics, 34: 49, arXiv:2203.06142, Bibcode:2022JHEAp..34...49A, doi:10.1016/j.jheap.2022.04.002, S2CID 247411131
- ^ Vagnozzi, Sunny (2020-07-10). "New physics in light of the H0 tension: An alternative view". Physical Review D. 102 (2) 023518. arXiv:1907.07569. Bibcode:2020PhRvD.102b3518V. doi:10.1103/PhysRevD.102.023518. S2CID 197430820.
- ^ Haslbauer, M.; Banik, I.; Kroupa, P. (2020-12-21). "The KBC void and Hubble tension contradict LCDM on a Gpc scale – Milgromian dynamics as a possible solution". Monthly Notices of the Royal Astronomical Society. 499 (2): 2845–2883. arXiv:2009.11292. Bibcode:2020MNRAS.499.2845H. doi:10.1093/mnras/staa2348. ISSN 0035-8711.
- ^ Mazurenko, S.; Banik, I.; Kroupa, P.; Haslbauer, M. (2024-01-21). "A simultaneous solution to the Hubble tension and observed bulk flow within 250/h Mpc". Monthly Notices of the Royal Astronomical Society. 527 (3): 4388–4396. arXiv:2311.17988. Bibcode:2024MNRAS.527.4388M. doi:10.1093/mnras/stad3357. ISSN 0035-8711.
- ^ Poulin, Vivian; Smith, Tristan L.; Karwal, Tanvi; Kamionkowski, Marc (2019-06-04). "Early Dark Energy can Resolve the Hubble Tension". Physical Review Letters. 122 (22) 221301. arXiv:1811.04083. Bibcode:2019PhRvL.122v1301P. doi:10.1103/PhysRevLett.122.221301. PMID 31283280. S2CID 119233243.
- ^ Zhao, Gong-Bo; Raveri, Marco; Pogosian, Levon; Wang, Yuting; Crittenden, Robert G.; Handley, Will J.; Percival, Will J.; Beutler, Florian; Brinkmann, Jonathan; Chuang, Chia-Hsun; Cuesta, Antonio J.; Eisenstein, Daniel J.; Kitaura, Francisco-Shu; Koyama, Kazuya; l'Huillier, Benjamin; Nichol, Robert C.; Pieri, Matthew M.; Rodriguez-Torres, Sergio; Ross, Ashley J.; Rossi, Graziano; Sánchez, Ariel G.; Shafieloo, Arman; Tinker, Jeremy L.; Tojeiro, Rita; Vazquez, Jose A.; Zhang, Hanyu (2017). "Dynamical dark energy in light of the latest observations". Nature Astronomy. 1 (9): 627–632. arXiv:1701.08165. Bibcode:2017NatAs...1..627Z. doi:10.1038/s41550-017-0216-z. S2CID 256705070.
- ^ Berezhiani, Zurab; Dolgov, A. D.; Tkachev, I. I. (2015). "Reconciling Planck results with low redshift astronomical measurements". Physical Review D. 92 (6) 061303. arXiv:1505.03644. Bibcode:2015PhRvD..92f1303B. doi:10.1103/PhysRevD.92.061303. S2CID 118169478.
- ^ Laila Linke (17 May 2021). "Solving the Hubble tension might require more than changing the early Universe". Astrobites.
- ^ Vagnozzi, Sunny (2023-08-30). "Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension". Universe. 9 (9) 393. arXiv:2308.16628. Bibcode:2023Univ....9..393V. doi:10.3390/universe9090393.
- ^ Ryan E. Keeley and Arman Shafieloo (August 2023). "Ruling Out New Physics at Low Redshift as a Solution to the H0 Tension". Physical Review Letters. 131 (11) 111002. arXiv:2206.08440. Bibcode:2023PhRvL.131k1002K. doi:10.1103/PhysRevLett.131.111002. PMID 37774270. S2CID 249848075.
- ^ Freedman, Wendy L.; Madore, Barry F.; Hoyt, Taylor J.; Jang, In Sung; Lee, Abigail J.; Owens, Kayla A. (2025-06-01). "Status Report on the Chicago-Carnegie Hubble Program (CCHP): Measurement of the Hubble Constant Using the Hubble and James Webb Space Telescopes". The Astrophysical Journal. 985 (2): 203. arXiv:2408.06153. Bibcode:2025ApJ...985..203F. doi:10.3847/1538-4357/adce78. ISSN 0004-637X.
- ^ Kruesi, Liz (2024-08-13). "The Webb Telescope Further Deepens the Biggest Controversy in Cosmology". Quanta Magazine. Retrieved 2024-08-17.
- ^ Pascale, Massimo; Frye, Brenda L.; Pierel, Justin D.R.; Chen, Wenlei; Kelly, Patrick L.; Cohen, Seth H.; Windhorst, Rogier A.; Riess, Adam G.; Kamieneski, Patrick S.; Diego, Jos'e M.; Meena, Ashish K.; Cha, Sangjun; Oguri, Masamune; Zitrin, Adi; Jee, M. James (2025-01-14). "SN H0pe: The First Measurement of H0 from a Multiply Imaged Type Ia Supernova, Discovered by JWST". The Astrophysical Journal. 979 (1): 13. arXiv:2403.18902. Bibcode:2025ApJ...979...13P. doi:10.3847/1538-4357/ad9928. ISSN 0004-637X.
- ^ Riess, Adam G.; Scolnic, Dan; Anand, Gagandeep S.; Breuval, Louise; Casertano, Stefano; Macri, Lucas M.; Li, Siyang; Yuan, Wenlong; Huang, Caroline D.; Jha, Saurabh; Murakami, Yukei S.; Beaton, Rachael; Brout, Dillon; Wu, Tianrui; Addison, Graeme E.; Bennett, Charles; Anderson, Richard I.; Filippenko, Alexei V.; Carr, Anthony (2024). "JWST Validates HST Distance Measurements: Selection of Supernova Subsample Explains Differences in JWST Estimates of Local H 0". The Astrophysical Journal. 977 (1): 120. arXiv:2408.11770. Bibcode:2024ApJ...977..120R. doi:10.3847/1538-4357/ad8c21.
- ^ Balkenhol, L.; Dutcher, D.; Spurio Mancini, A.; Doussot, A.; Benabed, K.; Galli, S.; et al. (SPT-3G Collaboration) (2023-07-13). "Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 T T, T E, and E E dataset". Physical Review D. 108 (2) 023510. arXiv:2212.05642. Bibcode:2023PhRvD.108b3510B. doi:10.1103/PhysRevD.108.023510. ISSN 2470-0010.
- ^ Kelly, P. L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitri, A.; et al. (2023-05-11). "Constraints on the Hubble constant from Supernova Refsdal's reappearance". Science. 380 (6649) eabh1322. arXiv:2305.06367. Bibcode:2023Sci...380.1322K. doi:10.1126/science.abh1322. PMID 37167351. S2CID 258615332.
- ^ Contarini, Sofia; Pisani, Alice; Hamaus, Nico; Marulli, Federico; Moscardini, Lauro; Baldi, Marco (2024). "The perspective of voids on rising cosmology tensions". Astronomy & Astrophysics. 682 A20. arXiv:2212.07438. Bibcode:2024A&A...682A..20C. doi:10.1051/0004-6361/202347572.
- ^ Chiou, Lyndie (2023-07-25). "How (Nearly) Nothing Might Solve Cosmology's Biggest Questions". Quanta Magazine. Retrieved 2023-07-31.
- ^ Brout, Dillon; Scolnic, Dan; Popovic, Brodie; Riess, Adam G.; Carr, Anthony; Zuntz, Joe; Kessler, Rick; Davis, Tamara M.; Hinton, Samuel; Jones, David; Kenworthy, W. D'Arcy; Peterson, Erik R.; Said, Khaled; Taylor, Georgie; Ali, Noor; Armstrong, Patrick; Charvu, Pranav; Dwomoh, Arianna; Meldorf, Cole; Palmese, Antonella; Qu, Helen; Rose, Benjamin M.; Sanchez, Bruno; Stubbs, Christopher W.; Vincenzi, Maria; Wood, Charlotte M.; Brown, Peter J.; Chen, Rebecca; Chambers, Ken; Coulter, David A.; Dai, Mi; Dimitriadis, Georgios; Filippenko, Alexi V.; Foley, Ryan J.; Jha, Saurabh W.; Kelsey, Lisa; Kirshner, Robert P.; Möller, Anais; Muir, Jessie; Nadathur, Seshadri; Pan, Yen-Chen; Rest, Armin; Rojas-Bravo, Cesar; Sako, Masao; Siebert, Matthew R.; Smith, Mat; Stahl, Benjamin E.; Wiseman, Phil (2022-02-08). "The Pantheon+ Analysis: Cosmological Constraints". The Astrophysical Journal. 938 (2): 110. arXiv:2202.04077. Bibcode:2022ApJ...938..110B. doi:10.3847/1538-4357/ac8e04. S2CID 246679941.
- ^ de Jaeger, T.; Galbany, L.; Riess, A. G.; Stahl, Ben E.; et al. (17 June 2022). "A 5 per cent measurement of the Hubble–Lemaître constant from Type II supernovae". MNRAS. 514 (3): 4620–4628. arXiv:2203.08974. doi:10.1093/mnras/stac1661.
- ^ Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V. (2021-12-08). "A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team". The Astrophysical Journal. 934 (1). arXiv:2112.04510. Bibcode:2022ApJ...934L...7R. doi:10.3847/2041-8213/ac5c5b. S2CID 245005861.
- ^ Freedman, Wendy L. (2021-09-01). "Measurements of the Hubble Constant: Tensions in Perspective*". The Astrophysical Journal. 919 (1) 16. arXiv:2106.15656. Bibcode:2021ApJ...919...16F. doi:10.3847/1538-4357/ac0e95. ISSN 0004-637X. S2CID 235683396.
- ^ Soltis, J.; Casertano, S.; Riess, A. G. (2021). "The Parallax of Omega Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant". The Astrophysical Journal. 908 (1) L5. arXiv:2012.09196. Bibcode:2021ApJ...908L...5S. doi:10.3847/2041-8213/abdbad. S2CID 229297709.
- ^ Riess, A. G.; Casertano, S.; Yuan, W.; Bowers, J. B.; et al. (2021). "Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM". The Astrophysical Journal. 908 (1) L6. arXiv:2012.08534. Bibcode:2021ApJ...908L...6R. doi:10.3847/2041-8213/abdbaf. S2CID 229213131.
- ^ Baxter, E. J.; Sherwin, B. D. (February 2021). "Determining the Hubble constant without the sound horizon scale: measurements from CMB lensing". Monthly Notices of the Royal Astronomical Society. 501 (2): 1823–1835. arXiv:2007.04007. Bibcode:2021MNRAS.501.1823B. doi:10.1093/mnras/staa3706. S2CID 220404332.
- ^ Denzel, P.; Coles, J. P.; Saha, P.; Williams, L. L. R. (February 2021). "The Hubble constant from eight time-delay galaxy lenses". Monthly Notices of the Royal Astronomical Society. 501 (1): 784–801. arXiv:2007.14398. Bibcode:2021MNRAS.501..784D. doi:10.1093/mnras/staa3603. S2CID 220845622.
- ^ Sedgwick, Thomas M; Collins, Chris A; Baldry, Ivan K; James, Philip A (2020-11-07). "The effects of peculiar velocities in SN Ia environments on the local H0 measurement". Monthly Notices of the Royal Astronomical Society. 500 (3): 3728–3742. arXiv:1911.03155. doi:10.1093/mnras/staa3456. ISSN 0035-8711.
- ^ Anderson, Lauren; Aubourg, Éric; Bailey, Stephen; Beutler, Florian; Bhardwaj, Vaishali; Blanton, Michael; Bolton, Adam S.; Brinkmann, J.; Brownstein, Joel R.; Burden, Angela; Chuang, Chia-Hsun (2014-04-21). "The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples". Monthly Notices of the Royal Astronomical Society. 441 (1): 24–62. arXiv:1312.4877. doi:10.1093/mnras/stu523. hdl:2445/101758. ISSN 1365-2966.
- ^ Mukherjee, S.; Ghosh, A.; Graham, M. J.; Karathanasis, C.; et al. (29 September 2020). "First measurement of the Hubble parameter from bright binary black hole GW190521". arXiv:2009.14199 [astro-ph.CO].
- ^ de Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.V.; et al. (18 June 2020). "A measurement of the Hubble constant from Type II supernovae". MNRAS. 496 (3): 3402–3411. arXiv:2006.03412. doi:10.1093/mnras/staa1801.
- ^ Shajib, A. J.; Birrer, S.; Treu, T.; Agnello, A.; et al. (14 October 2019). "STRIDES: A 3.9 per cent measurement of the Hubble constant from the strongly lensed system DES J0408-5354". Monthly Notices of the Royal Astronomical Society. 494 (4). arXiv:1910.06306. doi:10.1093/mnras/staa828. S2CID 204509190.
- ^ Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; et al. (12 September 2019). "A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging". Monthly Notices of the Royal Astronomical Society. 490 (2): 1743–1773. arXiv:1907.02533. Bibcode:2019MNRAS.490.1743C. doi:10.1093/mnras/stz2547. S2CID 195820422.
- ^ Dutta, Koushik; Roy, Anirban; Ruchika, Ruchika; Sen, Anjan A.; Sheikh-Jabbari, M. M. (20 August 2019). "Cosmology With Low-Redshift Observations: No Signal For New Physics". Phys. Rev. D. 100 (10) 103501. arXiv:1908.07267. Bibcode:2019PhRvD.100j3501D. doi:10.1103/PhysRevD.100.103501. S2CID 201107151.
- ^ Reid, M. J.; Pesce, D. W.; Riess, A. G. (15 August 2019). "An Improved Distance to NGC 4258 and its Implications for the Hubble Constant". The Astrophysical Journal. 886 (2) L27. arXiv:1908.05625. Bibcode:2019ApJ...886L..27R. doi:10.3847/2041-8213/ab552d. S2CID 199668809.
- ^ Kenneth C. Wong (2020). "H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes". Monthly Notices of the Royal Astronomical Society. 498 (1). arXiv:1907.04869. doi:10.1093/mnras/stz3094. S2CID 195886279.
- ^ Domínguez, Alberto; et al. (28 March 2019). "A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation". The Astrophysical Journal. 885 (2) 137. arXiv:1903.12097. Bibcode:2019ApJ...885..137D. doi:10.3847/1538-4357/ab4a0e. S2CID 85543845.
- ^ Ryan, Joseph; Chen, Yun; Ratra, Bharat (8 February 2019). "Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature". Monthly Notices of the Royal Astronomical Society. 488 (3): 3844–3856. arXiv:1902.03196. Bibcode:2019MNRAS.488.3844R. doi:10.1093/mnras/stz1966. S2CID 119226802.
- ^ Macaulay, E; et al. (DES collaboration) (2018). "First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant". Monthly Notices of the Royal Astronomical Society. 486 (2): 2184–2196. arXiv:1811.02376. doi:10.1093/mnras/stz978. S2CID 119310644.
- ^ Birrer, S.; Treu, T.; Rusu, C. E.; Bonvin, V.; Fassnacht, C. D.; Chan, J. H. H.; et al. (2018). "H0LiCOW – IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant". Monthly Notices of the Royal Astronomical Society. 484 (4): 4726–4753. arXiv:1809.01274. Bibcode:2019MNRAS.484.4726B. doi:10.1093/mnras/stz200. S2CID 119053798.
- ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (2018). "Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant". The Astrophysical Journal. 861 (2) 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 0004-637X. S2CID 55643027.
- ^ Devlin, Hannah (10 May 2018). "The answer to life, the universe and everything might be 73. Or 67". the Guardian. Retrieved 13 May 2018.
- ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; et al. (22 February 2018). "New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: Implications for the Hubble constant". The Astrophysical Journal. 855 (2) 136. arXiv:1801.01120. Bibcode:2018ApJ...855..136R. doi:10.3847/1538-4357/aaadb7. S2CID 67808349.
- ^ Weaver, Donna; Villard, Ray; Hille, Karl (22 February 2018). "Improved Hubble Yardstick Gives Fresh Evidence for New Physics in the Universe". NASA. Retrieved 24 February 2018.
- ^ Foley, R. J.; Annis, J.; Tanvir, N. R. T; et al. (The LIGO Scientific Collaboration and The Virgo Collaboration, The 1M2H Collaboration, The Dark Energy Camera GW-EM Collaboration and the DES Collaboration, The DLT40 Collaboration, The Las Cumbres Observatory Collaboration, The VINROUGE Collaboration & The MASTER Collaboration) (2017-10-16). "A gravitational-wave standard siren measurement of the Hubble constant". Nature. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551...85A. doi:10.1038/nature24471. ISSN 0028-0836. PMID 29094696.
- ^ Feeney, Stephen M; Peiris, Hiranya V; Williamson, Andrew R; Nissanke, Samaya M; et al. (2019). "Prospects for resolving the Hubble constant tension with standard sirens". Physical Review Letters. 122 (6) 061105. arXiv:1802.03404. Bibcode:2019PhRvL.122f1105F. doi:10.1103/PhysRevLett.122.061105. hdl:2066/201510. PMID 30822066. S2CID 73493934.
- ^ Vitale, Salvatore; Chen, Hsin-Yu (12 July 2018). "Measuring the Hubble Constant with Neutron Star Black Hole Mergers". Physical Review Letters. 121 (2) 021303. arXiv:1804.07337. Bibcode:2018PhRvL.121b1303V. doi:10.1103/PhysRevLett.121.021303. hdl:1721.1/117110. PMID 30085719. S2CID 51940146.
- ^ Bonvin, Vivien; Courbin, Frédéric; Suyu, Sherry H.; et al. (2016-11-22). "H0LiCOW – V. New COSMOGRAIL time delays of HE 0435−1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model". MNRAS. 465 (4): 4914–4930. arXiv:1607.01790. Bibcode:2017MNRAS.465.4914B. doi:10.1093/mnras/stw3006. S2CID 109934944.
- ^ Tully, R. Brent; Courtois, Hélène M.; Sorce, Jenny G. (3 August 2016). "COSMICFLOWS-3". The Astronomical Journal. 152 (2) 50. arXiv:1605.01765. Bibcode:2016AJ....152...50T. doi:10.3847/0004-6256/152/2/50. S2CID 250737862.
- ^ Grieb, Jan N.; Sánchez, Ariel G.; Salazar-Albornoz, Salvador (2016-07-13). "The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the Fourier space wedges of the final sample". Monthly Notices of the Royal Astronomical Society. 467 (2): 2085–2112. arXiv:1607.03143. Bibcode:2017MNRAS.467.2085G. doi:10.1093/mnras/stw3384. S2CID 55888085.
- ^ "The Extended Baryon Oscillation Spectroscopic Survey (eBOSS)". SDSS. Retrieved 13 May 2018.
- ^ Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; et al. (2016-04-05). "A 2.4% Determination of the Local Value of the Hubble Constant". The Astrophysical Journal. 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ...826...56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.
- ^ "Planck Publications: Planck 2015 Results". European Space Agency. February 2015. Retrieved 9 February 2015.
- ^ Cowen, Ron; Castelvecchi, Davide (2 December 2014). "European probe shoots down dark-matter claims". Nature. doi:10.1038/nature.2014.16462. Retrieved 6 December 2014.
- ^ Tully, R. Brent; Courtois, Helene M.; Dolphin, Andrew E.; Fisher, J. Richard; et al. (5 September 2013). "Cosmicflows-2: The Data". The Astronomical Journal. 146 (4) 86. arXiv:1307.7213. Bibcode:2013AJ....146...86T. doi:10.1088/0004-6256/146/4/86. ISSN 0004-6256. S2CID 118494842.
- ^ "Planck reveals an almost perfect universe". ESA. 21 March 2013. Retrieved 2013-03-21.
- ^ "Planck Mission Brings Universe Into Sharp Focus". JPL. 21 March 2013. Retrieved 2013-03-21.
- ^ Overbye, D. (21 March 2013). "An infant universe, born before we knew". New York Times. Retrieved 2013-03-21.
- ^ Boyle, A. (21 March 2013). "Planck probe's cosmic 'baby picture' revises universe's vital statistics". NBC News. Archived from the original on 2013-03-23. Retrieved 2013-03-21.
- ^ Bennett, C. L.; et al. (2013). "Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results". The Astrophysical Journal Supplement Series. 208 (2) 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
- ^ a b Jarosik, N.; et al. (2011). "Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results". The Astrophysical Journal Supplement Series. 192 (2) 14. arXiv:1001.4744. Bibcode:2011ApJS..192...14J. doi:10.1088/0067-0049/192/2/14. S2CID 46171526.
- ^ Results for H0 and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website Archived 2014-07-09 at the Wayback Machine.
- ^ a b Hinshaw, G.; et al. (WMAP Collaboration) (2009). "Five-year Wilkinson Microwave Anisotropy Probe observations: Data processing, sky maps, and basic results". The Astrophysical Journal Supplement. 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.
- ^ Spergel, D. N.; et al. (WMAP Collaboration) (2007). "Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology". The Astrophysical Journal Supplement Series. 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode:2007ApJS..170..377S. doi:10.1086/513700. S2CID 1386346.
- ^ Bonamente, M.; Joy, M. K.; Laroque, S. J.; Carlstrom, J. E.; et al. (2006). "Determination of the cosmic distance scale from Sunyaev–Zel'dovich effect and Chandra X-ray measurements of high-redshift galaxy clusters". The Astrophysical Journal. 647 (1) 25. arXiv:astro-ph/0512349. Bibcode:2006ApJ...647...25B. doi:10.1086/505291. S2CID 15723115.
- ^ Planck Collaboration (2013). "Planck 2013 results. XVI. Cosmological parameters". Astronomy & Astrophysics. 571: A16. arXiv:1303.5076. Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID 118349591.
- ^ Spergel, D.N. (September 2003). "First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
- ^ Freedman, W. L.; et al. (2001). "Final results from the Hubble Space Telescope Key Project to measure the Hubble constant". The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376. Bibcode:2001ApJ...553...47F. doi:10.1086/320638. S2CID 119097691.
- ^ Riess, Adam G. (January 1995). "Using SN Ia Light Curve Shapes to Measure The Hubble Constant". The Astrophysical Journal. 438 (L17). arXiv:astro-ph/9410054. Bibcode:1995ApJ...438L..17R. doi:10.1086/187704. S2CID 118938423.
- ^ a b c John P. Huchra (2008). "The Hubble Constant". Harvard Center for Astrophysics.
- ^ Sandage, A. R. (1958). "Current problems in the extragalactic distance scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
- ^ Edwin Hubble, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences, vol. 15, no. 3, pp. 168-173, March 1929
- ^ "Hubble's Constant". Skywise Unlimited – Western Washington University.
- ^ Lemaître, Georges (1927). "Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles (in French). A47: 49–59. Bibcode:1927ASSB...47...49L.
Bibliography
[edit]- Hubble, E. P. (1937). The Observational Approach to Cosmology. Clarendon Press. LCCN 38011865.
- Kutner, M. (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 978-0-521-52927-3.
- Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). John Wiley & Sons. ISBN 978-0-470-84835-7.
External links
[edit]- NASA's WMAP B ig Bang Expansion: the Hubble Constant
- The Hubble Key Project
- The Hubble Diagram Project
- Coming to terms with different Hubble Constants (Forbes; 3 May 2019)
- Merrifield, Michael (2009). "Hubble Constant". Sixty Symbols. Brady Haran for the University of Nottingham.
Hubble's law
View on GrokipediaHistorical Development
Early Spectroscopic Observations
The pioneering spectroscopic observations of spiral nebulae, which laid the empirical groundwork for understanding galactic motions, were conducted by Vesto Slipher at the Lowell Observatory in Flagstaff, Arizona. Beginning in 1912, Slipher utilized a 24-inch refractor telescope equipped with a custom spectrograph to measure the radial velocities of these faint objects through Doppler shifts in their spectral lines. His first success came on September 17, 1912, with the Andromeda nebula (M31), yielding a blueshift corresponding to an approach velocity of approximately 300 km/s, the largest such motion recorded at the time.[4] Slipher's subsequent observations between 1913 and 1925 revealed striking patterns: while Andromeda approached, the majority of the 40 or so spiral nebulae he studied exhibited redshifts indicative of recession, with velocities ranging from a few hundred to as high as 1,800 km/s, such as the 1,800 km/s measured for NGC 584 in 1918. He interpreted these shifts as true Doppler effects due to the nebulae moving away from the Milky Way, attributing the faint, broad emission lines in their spectra to rapid internal motions that broadened the features but allowed velocity measurements relative to our galaxy. By 1917, Slipher had compiled velocities for 25 nebulae, noting an average recession of about 570 km/s—roughly 30 times the typical stellar velocities within the Milky Way—and emphasizing the unexpected uniformity in direction away from the Sun.[5][6] These findings gained prominence when Slipher presented them at the August 1914 meeting of the American Astronomical Society in Evanston, Illinois, reporting on 15 nebulae where 12 showed recessions up to 1,100 km/s, eliciting widespread astonishment among astronomers for the implied high speeds of these "island universes." By 1925, his comprehensive compilation of radial velocities for over 35 spiral nebulae demonstrated a clear preponderance of recessions, with an average velocity of around 600 km/s, underscoring a systematic outward motion that challenged static models of the cosmos. This dataset profoundly influenced subsequent surveys, notably those by Milton Humason at Mount Wilson Observatory starting in 1923, who built on Slipher's techniques to probe fainter, more distant nebulae with even greater velocities.[6]Theoretical Precursors in General Relativity
In 1917, Albert Einstein applied general relativity to cosmology by proposing a static, homogeneous, and isotropic universe model, which required the introduction of a cosmological constant in his field equations to balance gravitational attraction and prevent collapse or expansion.[7] This static solution assumed a closed universe with positive spatial curvature, where the radius and matter density satisfied , with as the gravitational coupling constant.[8] In 1922, Alexander Friedmann derived dynamic solutions to Einstein's field equations for a homogeneous and isotropic universe, demonstrating that it could expand or contract over time rather than remain static.[9] Friedmann's work introduced the Friedmann–Lemaître–Robertson–Walker (FLRW) metric as the foundational framework, incorporating a curvature parameter that determines the universe's geometry: for a flat universe, for closed (spherical), and for open (hyperbolic).[10] These solutions showed that without the cosmological constant, the universe's scale factor evolves according to the Friedmann equations, allowing for expanding models from an initial singularity.[11] Independently in 1927, Georges Lemaître developed similar expanding universe models from general relativity, deriving the linear relation between recession velocity and distance as , where is the time-dependent expansion rate and is the scale factor.[12] Lemaître's analysis also explored the role of the cosmological constant and curvature, predicting an expanding universe that could originate from a "primeval atom"—a singular, superdense state serving as a precursor to the Big Bang theory.[13] Following Edwin Hubble's 1929 confirmation of galactic redshifts as evidence of expansion, Einstein abandoned the cosmological constant in 1931, acknowledging it as unnecessary for a dynamic universe.[14]Hubble's Distance-Redshift Correlation
In the early 1920s, Edwin Hubble leveraged Henrietta Swan Leavitt's 1912 discovery of the period-luminosity relation for Cepheid variable stars to calibrate distances to nearby galaxies. Leavitt had identified a correlation between the pulsation periods of Cepheids in the Small Magellanic Cloud and their apparent brightness, enabling the determination of their intrinsic luminosity and thus absolute distances when observed in other systems. Hubble applied this "standard candle" method by identifying Cepheids in the Andromeda nebula (M31), confirming its status as a separate galaxy far beyond the Milky Way. His observations from 1923 to 1924, using the 100-inch Hooker telescope at Mount Wilson Observatory, revealed multiple Cepheids, yielding a distance estimate of approximately 900,000 light-years (about 280,000 parsecs) for Andromeda.[15] Building on this, Hubble extended distance measurements to 24 extra-galactic nebulae using Cepheid variables where possible, supplemented by apparent magnitudes of brightest stars and nebular luminosities for more distant objects. He combined these distances with radial velocity data primarily from Vesto Slipher's earlier spectroscopic surveys, augmented by new measurements from his collaborator Milton Humason, who obtained spectra for fainter galaxies using the same telescope. Humason's contributions included velocities for objects like NGC 7619 at +3,779 km/s, extending the sample to velocities up to several thousand km/s.[16] In his seminal 1929 paper published in the Proceedings of the National Academy of Sciences, Hubble presented a scatter plot—now known as the Hubble diagram—of recession velocities against distances for these 24 galaxies, revealing an approximate linear correlation. The relation was expressed as , where is the radial velocity, is the distance in megaparsecs, and the proportionality constant corresponds to an initial Hubble parameter .[16] This empirical finding suggested that galaxies recede proportionally to their distance, though Hubble noted the scatter and proposed it as a first approximation. Hubble initially interpreted the correlation cautiously, suggesting it might reflect the de Sitter effect predicted by Willem de Sitter's static cosmological model, where apparent recessions arise from light propagation in a relativistic universe rather than true expansion. He also accounted for local perturbations, such as the peculiar motions of four nebulae in the Virgo cluster at about 2 million parsecs, which deviated from the linear trend due to their proximity and gravitational influences, adjusting the constant accordingly.[16] This observational breakthrough laid the empirical foundation for understanding the universe's large-scale structure, though its full implications as evidence for cosmic expansion emerged later.Refinement and Initial Interpretations
In 1931, Georges Lemaître published an English translation and expansion of his 1927 paper, reconciling Edwin Hubble's recent observational data on galaxy redshifts with his earlier theoretical model of an expanding universe. Lemaître emphasized that the observed recessional velocities were evidence of dynamic expansion rather than a static universe, aligning the empirical velocity-distance relation with solutions to Einstein's field equations that permitted a growing radius for a homogeneous cosmos. This integration shifted interpretations away from static models, portraying the universe as evolving from a "primeval atom" state, though Lemaître's full primeval hypothesis gained traction later.[17] Following Hubble's confirmation of expansion, Albert Einstein abandoned his cosmological constant in 1931, which he had introduced in 1917 to stabilize a static universe model.[18] During a visit to Mount Wilson Observatory, Einstein acknowledged that the redshift data rendered the constant unnecessary, later collaborating on expanding models without it.[19] Concurrently, Richard C. Tolman developed observational tests in the 1930s to verify expansion, including the surface brightness test proposed in 1930, which predicted a (1+z)^4 dimming of galaxy surface brightness with redshift in an expanding space. Tolman, in collaboration with Hubble, applied this and angular size tests in 1935, analyzing data from 12 bright galaxies to confirm the expected dimming and size effects, supporting the cosmological interpretation of redshifts over alternatives like gravitational effects. Observational refinements began promptly with Milton L. Humason's 1931 collaboration with Hubble, extending redshift measurements to fainter, more distant galaxies using the 100-inch Hooker telescope at Mount Wilson.[20] This effort measured velocities up to approximately 20,000 km/s for nebulae in clusters like Virgo and Coma, nearly quadrupling the redshift range from Hubble's 1929 sample and strengthening the linear velocity-distance correlation across a broader volume.[20] By 1936, Humason, Hubble, and Tolman conducted a comprehensive survey of over 800 extra-galactic nebulae, compiling redshifts up to cz ≈ 30,000 km/s and apparent magnitudes to assess distribution effects under expansion. Their analysis, published in multiple papers, incorporated redshift distortions into nebula counts, confirming the law's applicability while noting apparent magnitude limits due to observational constraints. A significant theoretical refinement came in 1952 when Walter Baade revised the Cepheid variable star calibration, distinguishing between classical (Population I) and Type II Cepheids; the classical Cepheids in external galaxies proved 1.5 magnitudes brighter than previously assumed based on Type II calibrations. This correction doubled the estimated distances to galaxies like M31 and M33, thereby reducing Hubble's constant from around 500 km/s/Mpc to approximately 250 km/s/Mpc, reshaping early estimates of the universe's expansion rate. Initial interpretations in the 1930s also sparked debates on whether the galaxy distribution was uniform and homogeneous—as assumed in expanding models—or hierarchical and clustered, potentially mimicking expansion through local velocities.[21] Hubble and Tolman's 1936 work addressed this by modeling redshift effects on nebula distributions, finding that uniform expansion better explained the observed uniformity in counts at faint magnitudes, though hierarchical clustering hypotheses persisted among some astronomers like Harlow Shapley. These discussions underscored the need for deeper surveys to distinguish global expansion from local structure.[21]Formulation and Interpretation
Statement of the Law
Hubble's law, in its idealized modern formulation, states that the recessional velocity of a distant galaxy is directly proportional to its proper distance from an observer, expressed as where is the Hubble parameter, a time-dependent quantity that characterizes the expansion rate of the universe at cosmic time . The proper distance refers to the distance measured at a fixed time in the expanding universe, while comoving coordinates fix the relative positions of galaxies, with proper distances scaling according to the cosmic scale factor. The present-day value of the Hubble parameter, denoted , quantifies the current expansion rate.[22][23][24] The recessional velocity is inferred from the observed redshift of the galaxy's spectral lines, where for low redshifts (), corresponding to (with the speed of light), the approximation holds. This low-redshift regime applies to nearby galaxies within hundreds of megaparsecs, where the linear relationship in Hubble's law is most accurate. The cosmological redshift arises from the stretching of space during photon travel, distinct from the special relativistic Doppler effect, though the low-velocity approximation mimics the Doppler formula.[25][22] The Hubble parameter is conventionally expressed in units of km/s/Mpc, indicating the recession speed in kilometers per second for every megaparsec of distance. At higher redshifts (), relativistic effects in general relativity cause the simple linear form to break down, as recession velocities can exceed without violating causality, and the redshift-velocity relation becomes nonlinear. This idealized law assumes a homogeneous, isotropic expansion, providing the foundational relation for probing cosmic structure on large scales.[26][27][28]Redshift as Recessional Velocity
In cosmology, the redshift observed in the spectra of distant galaxies provides a measure of the universe's expansion. Spectroscopic observations reveal shifts in the positions of absorption and emission lines toward longer wavelengths, quantified by the redshift parameter , where is the change in wavelength and is the rest-frame wavelength.[29] This phenomenon is detectable through instruments that resolve spectral features, such as the hydrogen Balmer lines or calcium H and K lines, allowing astronomers to determine for objects across cosmic distances.[29] The cosmological redshift arises from the expansion of space itself, rather than the motion of sources through space. As photons propagate from their emission at time to observation at , their wavelengths stretch in proportion to the increase in the cosmic scale factor , which describes the relative size of the universe over time (normalized such that ). The precise relation is given by or equivalently, derived from the fact that the photon's frequency (and thus inverse wavelength) scales inversely with the scale factor along null geodesics in the Friedmann–Lemaître–Robertson–Walker metric.[29] This stretching occurs continuously as the photon travels through expanding space, accumulating the effect over the light's path. In contrast, the classical Doppler redshift results from the relative velocity of the source and observer, with for non-relativistic speeds , or the relativistic form accounting for time dilation; the cosmological case lacks a direct "source velocity" and instead reflects the global metric evolution.[30] For nearby galaxies where , the cosmological redshift approximates the Doppler form, such that , with interpreted as the recessional velocity. This velocity represents the apparent rate at which a galaxy recedes due to expansion, given by , where is the time derivative of the scale factor, is the Hubble parameter (currently km/s/Mpc), and is the proper distance. This linear relation underpins Hubble's law and allows redshift to serve as a distance indicator, though the full cosmological interpretation extends beyond the low- approximation.Distinguishing Expansion from Local Motions
In observations of distant galaxies, the redshift is interpreted as primarily arising from the uniform cosmic expansion described by Hubble's law, but local peculiar velocities—deviations from this isotropic Hubble flow caused by gravitational interactions—introduce significant scatter in the Hubble diagram, which plots recession velocity against distance. These peculiar motions, typically on the order of hundreds of km/s, arise from attractions toward massive structures like galaxy clusters and can either add to or subtract from the expansion signal, leading to apparent deviations of up to 20-30% in velocity estimates at low redshifts. For instance, the Local Group experiences an infall toward the Virgo Cluster at approximately 220 km/s due to the cluster's gravitational pull, contributing to this scatter and necessitating corrections to isolate the pure expansion component.[31] The Hubble flow becomes reliably observable only beyond distances where peculiar velocities are dwarfed by the expansion velocity, generally limited to about 100 Mpc, as closer in, local gravitational effects dominate and obscure the linear velocity-distance relation. Within this volume, the velocity field is reconstructed using large-scale surveys that measure distances independently of redshift, allowing subtraction of peculiar components to reveal the underlying isotropic expansion. A prominent example is the Cosmicflows program, which compiles distances and infers peculiar velocities for thousands of galaxies through methods like the fundamental plane and surface brightness fluctuations, enabling detailed mapping of velocity fields and corrections for Hubble constant measurements.[32][33] Our own position in this velocity field is evidenced by the cosmic microwave background (CMB) dipole anisotropy, which reflects the Solar System's peculiar velocity of about 370 km/s relative to the CMB rest frame, directed toward the constellation Hydra (galactic coordinates l ≈ 264°, b ≈ 48°). This motion, measured precisely by the Planck satellite, modulates the observed CMB temperature and must be accounted for in galaxy surveys to avoid biasing the expansion signal. To derive velocity-independent distances essential for these corrections, relations like the Tully-Fisher empirical correlation between a spiral galaxy's rotational velocity and its infrared luminosity are employed, providing distances accurate to 10-20% without relying on redshift, thus helping to disentangle local motions from cosmic expansion.[34]Time Evolution of the Hubble Parameter
The Hubble parameter, denoted , where is the scale factor describing the relative size of the universe at cosmic time , quantifies the expansion rate at any epoch.[26] In an expanding universe, decreases over time as the scale factor grows, contrasting with the low-redshift approximation where the present-day value is treated as constant for nearby observations. This time dependence arises from the evolving energy content of the universe, with currently estimated at approximately 70 km/s/Mpc based on multiple observational datasets.[23] In a flat, matter-dominated cosmological model, the Hubble parameter evolves as , specifically , reflecting the deceleration driven by gravitational attraction of matter.[35] This proportionality allows integration of to compute lookback time, the duration light has traveled from a given redshift to the present, providing a direct link between expansion history and observable timelines. For convenience in cosmological calculations, the present Hubble constant is often expressed in dimensionless form as , facilitating comparisons across models and datasets.[36] The time evolution of is probed observationally through methods that access different cosmic epochs, such as Type Ia supernova light curves, which measure luminosity distances and thus infer via the distance-redshift relation at redshifts .[37] Baryon acoustic oscillations (BAO) in the cosmic microwave background and large-scale structure further constrain by providing standard rulers for angular diameter distances across a broad range of up to several. In the current accelerating phase, dominated by dark energy, deviates from the matter-only decline, approaching a slower decrease or even stabilization at late times, as evidenced by these probes showing reduced deceleration since .Theoretical Derivations
Friedmann–Lemaître–Robertson–Walker Framework
The Friedmann–Lemaître–Robertson–Walker (FLRW) framework provides the general relativistic foundation for modeling the large-scale structure and evolution of the universe, assuming it adheres to the cosmological principle of spatial homogeneity and isotropy on sufficiently large scales. This principle implies that the universe appears the same from any location and in any direction, leading to a metric that describes a spacetime with uniform expansion. The FLRW metric, first derived by Alexander Friedmann in 1922, takes the form where is the time-dependent scale factor, is a comoving radial coordinate, is the metric on the unit sphere, is the speed of light, and is the curvature parameter ( for closed, flat, or open geometries, respectively). Independently, Georges Lemaître proposed a similar form in 1927, emphasizing its application to an expanding universe with constant mass. Howard P. Robertson and Arthur Geoffrey Walker later proved in 1935–1936 that this metric is the unique solution satisfying the cosmological principle for homogeneous and isotropic spacetimes. The Hubble parameter, , quantifies the relative rate of expansion at time , with the overdot denoting differentiation with respect to cosmic time . For objects at rest in the comoving coordinate system, such as distant galaxies, the recession velocity arises from the stretching of space itself rather than peculiar motions. The proper distance to a comoving observer at coordinate is . The physical recession velocity is then the time derivative of this distance, yielding in the low-redshift limit where distances are small compared to the curvature radius and velocities are non-relativistic. This relation emerges directly from the geodesic motion of test particles in the expanding metric, confirming that the observed redshift-distance correlation reflects global metric expansion. To derive the dynamical equations governing , the FLRW metric is substituted into Einstein's field equations, , assuming a perfect fluid stress-energy tensor with energy density and isotropic pressure , where is the cosmological constant, is the gravitational constant, and , are the Ricci tensor and scalar, respectively.[38] This yields the Friedmann equations, first obtained by Friedmann without but generalized to include it: These equations relate the expansion history to the contents of the universe, with the first governing the evolution of and the second describing its acceleration. Friedmann's derivation demonstrated that non-static solutions are permitted, resolving earlier assumptions of a static cosmos.[38]Matter-Dominated Cosmology
In a matter-dominated cosmology, the universe is filled with non-relativistic matter (dust) characterized by an equation of state parameter , leading to a specific form of the Friedmann equation derived from general relativity.[11] For a flat universe without a cosmological constant (, ), the first Friedmann equation simplifies to where is the Hubble parameter, is the scale factor, is the gravitational constant, and is the matter density.[39] The matter density evolves as due to the conservation of mass in an expanding volume, implying . Integrating this relation yields the scale factor evolution and for a flat, matter-dominated universe.[40] The critical density, which separates open and closed universes in the Friedmann framework, is defined as , providing a benchmark for the matter density parameter .[39] In the Einstein-de Sitter model, a flat universe with and no cosmological constant, the expansion is purely matter-driven, recovering the above parametric solutions and representing an early-universe approximation where matter dominance holds.[41] When including a cosmological constant in a flat matter-dominated universe, the Friedmann equation generalizes to where is the present-day Hubble constant, is the redshift, and .[42] This form allows for parametric solutions that interpolate between matter and vacuum energy dominance. The present-day deceleration parameter, quantifying the second derivative of the scale factor, is given by , which is positive () in the pure matter case (), indicating decelerating expansion.[43]Inclusion of Dark Energy and Acceleration
The inclusion of dark energy in cosmological models extends the Friedmann equations to account for the observed acceleration of the universe's expansion at late times. Dark energy is typically modeled as a cosmological constant Λ with an equation of state parameter w ≈ -1, or more generally as a dynamic component like quintessence with w close to -1. In the Friedmann equation, this component contributes a constant energy density term, leading to the modified form where H is the Hubble parameter at redshift z, H_0 is the present-day Hubble constant, Ω_m is the present-day matter density parameter, and Ω_Λ is the present-day dark energy density parameter. For a flat universe, spatial curvature is negligible (Ω_k = 0), so Ω_m + Ω_Λ = 1. This equation shows that dark energy dominates at low redshifts (z ≲ 1), causing the expansion to accelerate if Ω_Λ > 0, as the Λ term grows relative to the matter term which dilutes as (1+z)^3. The acceleration of the universe is quantified by the second Friedmann equation, which governs the time derivative of the scale factor a (with ȧ/a = H): where ρ_i and p_i are the energy density and pressure of component i. For matter (w_m = 0), the term is positive and decelerating; for dark energy with w_Λ = -1, ρ_Λ + 3p_Λ/c² = -2ρ_Λ < 0, yielding net acceleration (ä > 0) when dark energy density exceeds half the total energy density. In the ΛCDM model—the standard concordance model incorporating cold dark matter, baryons, and a cosmological constant—the universe transitions from matter-dominated deceleration at high redshifts (z > 0.7) to dark energy-driven acceleration at low redshifts (z < 0.7). This transition redshift z_t ≈ 0.7 marks the point where the deceleration parameter q(z) = (1 + 3w_{eff}(z))/2 changes sign, with q_0 ≈ -0.55 today. Observational evidence for this acceleration and the need for dark energy came from type Ia supernova measurements in 1998, which showed that distant supernovae are fainter than expected in a decelerating universe, implying faster past expansion consistent with current acceleration. The High-Z Supernova Search Team (Riess et al.) analyzed 10 high-redshift supernovae (0.16 ≤ z ≤ 0.62) and found Ω_Λ ≈ 0.7 at high significance, favoring a flat universe with positive Λ. Independently, the Supernova Cosmology Project (Perlmutter et al., building on 1998 announcements) used 42 supernovae to measure Ω_m ≈ 0.28 and Ω_Λ ≈ 0.72, confirming acceleration with >99% confidence. These results established dark energy as essential to explain the data within the Friedmann framework.[44] In the flat ΛCDM model, the Hubble parameter's evolution is derived directly from the Friedmann equation by integrating the density contributions: assuming Ω_Λ = 1 - Ω_m. This functional form predicts H(z) decreasing from high values at early times (matter domination) to approaching a constant H_∞ = H_0 √Ω_Λ in the far future (de Sitter phase). The equation of state w(z) for dark energy, generalized beyond Λ as w ≈ -1 but potentially varying, parameterizes deviations. As of 2025, constraints from datasets including DESI, Planck, supernovae, and baryon acoustic oscillations favor models with w close to -1 but provide evidence for time variation in the dark energy equation of state, with a ~4.2 sigma preference for evolving dark energy over a cosmological constant (DESI DR2). Recent observations, including the DESI DR2 results from 2025, provide evidence for dynamical dark energy models, challenging the strict cosmological constant interpretation within ΛCDM.[45] This inclusion resolves tensions in Hubble's law interpretations by linking redshift-distance relations to late-time acceleration driven by dark energy.Cosmological Implications
Derived Units and Scales
The Hubble time, denoted as , is defined as the reciprocal of the Hubble constant, , providing a characteristic timescale for the expansion of the universe.[46] This quantity serves as a natural unit in cosmology, offering an order-of-magnitude estimate for the age of the universe in a simple, empty (matter-free) model where expansion proceeds at a constant rate.[47] For the currently favored value of km/s/Mpc, the Hubble time is approximately 14 billion years.[48] In the conventional parameterization where km/s/Mpc with , the Hubble time converts to Gyr.[46] The Hubble length, or Hubble distance, , where is the speed of light, represents a characteristic length scale associated with the current expansion rate, marking the distance over which recession velocities approach the speed of light.[46] This scale, approximately 4.4 Gpc for km/s/Mpc, defines a natural unit for cosmological distances and approximates the radius of the observable universe's horizon in simplified models.[49] The corresponding Hubble volume, , delineates a spherical region centered on an observer within which the universe's expansion is subluminal, serving as a key volume scale in cosmological analyses of structure and causality.[46] These derived units—Hubble time, length, and volume—act as fundamental benchmarks in cosmology, normalizing distances, times, and volumes relative to the expansion rate without invoking additional model parameters.[50] In particular, the Hubble length relates to the particle horizon, the maximum proper distance light could have traveled since the Big Bang, which in general is given by the integral over the scale factor ; in an empty universe, this coincides exactly with , underscoring the Hubble scale's role as a zeroth-order estimate for causal connectivity.Age, Size, and Fate of the Universe
Hubble's law, through the time evolution of the expansion rate, enables the computation of the universe's current age by integrating the inverse of the Hubble parameter over the scale factor. The age is given by the formula where is the cosmic scale factor (normalized to today) and is the Hubble parameter as a function of . This integral accounts for the varying expansion history, with depending on the composition of the universe, including the matter density parameter and the dark energy density parameter . In the standard CDM model, higher shortens the age by accelerating early deceleration, while higher lengthens it by driving late-time acceleration. Using cosmic microwave background data, the Planck Collaboration estimates the age at billion years for and .[51] The observable universe's size is determined by the particle horizon, the maximum comoving distance from which light could have reached us since the Big Bang, closely tied to the lookback time—the duration light has traveled from distant sources. Lookback time to an object at redshift is , where is the cosmic time at emission, and it increases with distance due to the finite speed of light and expansion. In CDM, the comoving radius of the observable universe is approximately 46 billion light-years, corresponding to the light-travel distance integrated over the expansion history; this sphere has a diameter of about 93 billion light-years. The Hubble time provides a rough upper bound estimate of this scale, but the full integral yields the precise horizon.[51] The fate of the universe follows from the long-term behavior of the expansion under Hubble's law. In CDM with , dark energy dominates, driving eternal acceleration and leading to a "heat death" where the universe expands indefinitely, stars exhaust fuel, and matter dilutes to a cold, uniform state with maximum entropy. If dark energy exhibits phantom behavior with equation-of-state parameter , acceleration could intensify, culminating in a Big Rip where expansion tears apart galaxies, stars, planets, and atoms in finite time, ending spacetime itself. Hubble's law also resolves Olbers' paradox—the expectation of an infinitely bright night sky in a static, infinite universe—by implying a finite age that limits visible sources and expansion that redshifts and dilutes incoming light, preventing total brightness saturation.Dimensionless Parameters and Paradox Resolutions
In cosmology, the Hubble constant is often expressed in a dimensionless form as , which normalizes the expansion rate relative to a reference value and facilitates comparisons across datasets.[36] This parameterization encapsulates uncertainties in without altering the physical predictions of the model.[52] The density parameters provide another set of dimensionless quantities, defined as the ratio of the actual energy density of a component to the critical density , where is the gravitational constant.[53] These include the matter density parameter , the dark energy density parameter , the radiation density parameter , and the curvature density parameter . In a flat universe, the total density parameter satisfies , implying zero spatial curvature and consistency with general relativity's Friedmann equations.[53] Observations of the cosmic microwave background (CMB) from the Planck satellite confirm near-flatness, with to within 0.4% precision.[54] The evolution of the Hubble parameter with redshift is captured dimensionlessly by , assuming a flat universe dominated by matter and dark energy (neglecting radiation at low ). This form arises from the Friedmann equation, where matter density scales as due to volume dilution and dark energy remains constant.[23] It enables model-independent scaling of expansion history without specifying . Cosmic expansion resolves classical paradoxes like Olbers' paradox, which posits that an infinite, static universe filled with stars of uniform density would produce an infinitely bright night sky, as every line of sight intersects a star surface.[55] In an expanding universe with finite age, light from distant sources has finite travel time, limiting the observable volume and preventing infinite stellar contributions; additionally, redshift stretches photon wavelengths, dimming distant light.[55] Expansion also averts infinite density accumulation by diluting matter over time, ensuring the universe's energy density decreases rather than building to infinity in a static scenario.[53]Measurement Techniques
Distance Ladder Methods
The cosmic distance ladder constructs measurements of the Hubble constant by establishing a chain of calibrated distance indicators, beginning with geometric methods and extending to standard candles observable in distant galaxies. This local approach pairs distance estimates with redshift observations to infer the expansion rate in the nearby universe, typically within a few hundred megaparsecs. Successive calibrations propagate accuracy outward: trigonometric parallax measures distances to nearby stars, which anchor the luminosities of variable stars like Cepheids; these, in turn, calibrate secondary indicators such as the Tully-Fisher relation for spiral galaxies or Type Ia supernovae, enabling broader application.[56] Cepheid variables form the foundational rung of the ladder due to their period-luminosity relation, which correlates a Cepheid's pulsation period with its intrinsic brightness, allowing distances to be derived from apparent magnitude and period alone. Discovered by Henrietta Swan Leavitt in 1912 using Cepheids in the Small Magellanic Cloud, this relation has been refined through modern calibrations.[57] Trigonometric parallaxes from the Gaia mission, particularly Data Release 3, provide direct geometric distances to Milky Way Cepheids, yielding a precise zero-point for the period-luminosity-metallicity relation in near-infrared bands at ~0.9% precision.[58] Independent anchoring comes from the tip of the red giant branch (TRGB) method, which identifies the luminosity of the brightest red giant stars in nearby galaxies to calibrate Cepheid distances, achieving consistency at the percent level with Gaia results.[59] The Hubble Space Telescope (HST) and James Webb Space Telescope (JWST) have observed Cepheids in over 50 galaxies to extend this calibration, measuring periods and magnitudes in hosts of other distance indicators. In the SH0ES (Supernovae, , for the Equation of State) project, HST photometry of more than 1,000 Cepheids across 40+ galaxies calibrates distances to supernova host galaxies, with JWST's infrared imaging resolving potential crowding and confirming the HST scale to within 1-2%. As of December 2024, JWST observations of additional galaxies yield km/s/Mpc, consistent with prior HST results.[60][61] Cepheids also calibrate the Tully-Fisher relation, an empirical scaling between a spiral galaxy's infrared luminosity and its neutral hydrogen rotation velocity, using Cepheid distances to about two dozen nearby spirals to set the zero-point and extend measurements to fainter systems up to 100 Mpc.[62] Type Ia supernovae serve as the ladder's capstone, acting as standardized candles after corrections for intrinsic variations. The Phillips relation, derived in 1993, links a supernova's peak absolute magnitude to its light-curve decline rate (the "stretch" parameter), homogenizing luminosities to an effective absolute magnitude of about -19.3 in the B-band.[63] Calibrated via Cepheid distances to their host galaxies, these supernovae probe volumes up to thousands of megaparsecs. The SH0ES project integrates this chain, yielding km/s/Mpc from 42 supernova hosts with Cepheid-calibrated distances.[64] Systematic uncertainties in the ladder arise primarily from the Cepheid rung, including metallicity effects that may brighten low-metallicity Cepheids by up to 0.2 magnitudes, potentially underestimating distances in metal-poor environments. Theoretical period-luminosity models incorporating opacities and pulsation hydrodynamics quantify this slope as -0.08 mag/dex in oxygen abundance, with observations in the Large Magellanic Cloud supporting a mild dependence.[65] Other errors, such as interstellar extinction and photometric crowding, are minimized through multi-wavelength observations, but residual biases at the 1-2% level persist in linking rungs.Early Universe Probes
Probes of the early universe offer independent determinations of the Hubble constant by examining physical processes that occurred shortly after the Big Bang, providing insights into the expansion rate at high redshifts. These methods rely on the standard Friedmann–Lemaître–Robertson–Walker (FLRW) framework to connect early-time dynamics to the present-day value of . Unlike local measurements, they integrate information over cosmic history, yielding model-dependent estimates typically lower than direct distance ladder results.[51] The cosmic microwave background (CMB) serves as a primary early universe probe for , capturing photons from recombination at approximately 380,000 years after the Big Bang (redshift ). The positions of acoustic peaks in the CMB temperature and polarization power spectra encode the sound horizon at last scattering—a comoving scale set by plasma oscillations in the early universe—and the angular diameter distance to the last scattering surface. In the CDM model, the angular diameter distance to this epoch is inversely sensitive to , as slower present-day expansion stretches the observed angular scale of the sound horizon. The Planck satellite's 2018 analysis, fitting the full-mission CMB data to CDM, constrains km/s/Mpc through these acoustic features, assuming a flat universe with standard relativistic degrees of freedom.[51] This value arises from the multipole moments of the power spectrum, where the first peak's position fixes the geometry via , with the sound horizon calibrated by early-universe physics largely independent of late-time details.[51] Big Bang nucleosynthesis (BBN), occurring roughly 1 to 20 minutes after the Big Bang, provides another constraint on the early expansion rate through the primordial abundances of light elements, particularly helium-4 (He). The He mass fraction is highly sensitive to the neutron-to-proton ratio at freeze-out, which depends on the expansion rate during BBN; faster expansion freezes out more neutrons, increasing . Observations of from extragalactic H II regions, combined with standard weak interaction rates, limit the effective number of relativistic species and thus the expansion rate at temperatures MeV.[66] Extrapolating this limit forward in a standard CDM cosmology yields an indirect upper bound on km/s/Mpc, as higher present-day expansion would imply excessively rapid early expansion inconsistent with observed . BBN complements CMB constraints by probing an earlier epoch, though its sensitivity is weaker and primarily acts through correlations with the baryon density .[66] Baryon acoustic oscillations (BAO) in the large-scale structure of the universe also trace early universe physics, using the sound horizon at the drag epoch (shortly after recombination) as a standard ruler. The comoving scale of this horizon, Mpc in CDM, imprints oscillations in the galaxy correlation function and power spectrum, observed at low redshifts () by surveys like SDSS and DESI. To infer , the observed angular scale of BAO features requires calibration of from early universe data, such as CMB measurements of integrated from recombination.[51] This combination yields values consistent with CMB results, around 67 km/s/Mpc, by measuring the ratio (where is the volume-averaged distance) and using the early-universe to fix the ruler's length. Recent DESI 2024 results provide km/s/Mpc. BAO thus bridges early and late universe probes, reinforcing the angular diameter distance sensitivity seen in CMB analyses.[67][51]Alternative Observational Approaches
Alternative observational approaches to measuring the Hubble constant leverage direct geometric or wave-based methods that bypass traditional distance ladders, providing independent constraints on the expansion rate. These techniques include gravitational wave standard sirens, which use binary neutron star mergers to infer luminosity distances, gravitational lensing time delays from quasar images, and geometric distances derived from megamaser disks in active galactic nuclei. Each method combines distance estimates with spectroscopic redshifts to probe , offering model-independent insights into late-universe cosmology. Gravitational wave standard sirens exploit the fact that the amplitude of a gravitational wave signal encodes the luminosity distance to the source directly, without reliance on intermediate calibrations. For events with electromagnetic counterparts, the redshift is obtained from host galaxy spectroscopy, enabling inference via the relation , approximated locally as . The pioneering event GW170817, detected by LIGO and Virgo on August 17, 2017, involved a binary neutron star merger with a kilonova counterpart in NGC 4993 at , yielding Mpc and km s Mpc. Subsequent analyses using multiple events from GWTC-3 provide statistical constraints on around 70 km/s/Mpc with ~10% precision. This measurement demonstrated the potential of multi-messenger astronomy for cosmology. Future detections by advanced LIGO, Virgo, and KAGRA are expected to yield dozens of standard sirens per year, potentially constraining to sub-5% precision through statistical samples, even for "dark sirens" without direct counterparts via galaxy catalog matching.[68] Gravitational lensing time delays provide another geometric probe, where light from a background quasar takes different paths around a foreground lens galaxy, producing multiple images with measurable arrival time differences . The time delay distance , derived from , lens mass modeling, and angular separations, relates to inversely in a flat CDM cosmology via . The H0LiCOW collaboration pioneered this with quadruply imaged quasars like RXJ1131-1231, achieving early precisions of ~8%. Building on this, the TDCOSMO collaboration analyzed six lenses, incorporating refined mass models and external priors on lens properties, to obtain km s Mpc from time delays alone. The 2025 TDCOSMO sample of eight lenses, combined with external data, yields km/s/Mpc with 4.6% precision in CDM. Ongoing efforts with telescopes like the Vera C. Rubin Observatory aim to expand the sample to dozens of lenses, reducing uncertainties to ~2%.[69] Megamaser disks offer precise geometric distances through very long baseline interferometry (VLBI) observations of water vapor masers orbiting supermassive black holes in galaxies. The maser velocities and angular positions trace Keplerian orbits in edge-on accretion disks, yielding the distance from the geometric relation , where is the angular size and the acceleration or velocity gradient. NGC 4258, the archetypal megamaser galaxy at 7.58 ± 0.08 Mpc, serves as a primary calibrator due to its well-resolved disk, anchoring the cosmic distance scale. The Megamaser Cosmology Project (MCP) has measured distances to five additional galaxies in the Hubble flow (e.g., NGC 5765b, Mrk 1029), combining them with Cepheid-calibrated supernovae to derive km s Mpc. Future MCP targets with the Next Generation Very Large Array could double the sample, enhancing precision to ~2%.Current Challenges and Measurements
Historical and Recent Values
The measurement of the Hubble constant, , began with Edwin Hubble's seminal 1929 observation of the recession of galaxies, yielding an initial estimate of approximately 500 km/s/Mpc based on Cepheid variable calibrations and limited distance data.[70] Subsequent refinements in the mid-20th century addressed systematic errors in distance indicators, such as the recognition of Population II stars' impact on Cepheid luminosities. Allan Sandage's 1958 analysis revised the value to around 75 km/s/Mpc, incorporating improved spectroscopic redshifts and nearby galaxy samples.[70] By the 1970s, Gérard de Vaucouleurs synthesized multiple datasets, including brightest cluster galaxies and supernova observations, to arrive at an estimate near 100 km/s/Mpc, reflecting broader surveys but still hampered by calibration uncertainties.[70] The Hubble Space Telescope's Key Project in 2001 marked a pivotal advancement, using Cepheid distances to 18 galaxies and supernova Type Ia standard candles to determine km/s/Mpc, achieving a 10% precision level and establishing a benchmark for local measurements.[71]| Era | Key Measurement | Value (km/s/Mpc) | Primary Method/Source |
|---|---|---|---|
| 1929 | Hubble | ~500 | Cepheids and galaxy redshifts[70] |
| 1958 | Sandage | ~75 | Improved Cepheid calibrations[70] |
| 1970s | de Vaucouleurs | ~100 | Cluster galaxies and supernovae[70] |
| 2001 | HST Key Project | 72 ± 8 | Cepheids and Type Ia supernovae[71] |