Heliocentric orbit

Heliocentric orbitMain

Community hub

Heliocentric orbit

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Heliocentric orbit

View on Wikipedia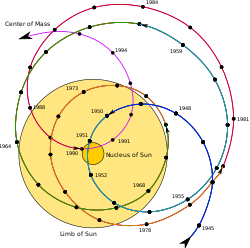

from Wikipedia

A heliocentric orbit (also called circumsolar orbit) is an orbit around the barycenter of the Solar System, which is usually located within or very near the surface of the Sun. All planets, comets, and asteroids in the Solar System, and the Sun itself are in such orbits, as are many artificial probes and pieces of debris. The moons of planets in the Solar System, by contrast, are not in heliocentric orbits, as they orbit their respective planet (although the Moon has a convex orbit around the Sun).

The barycenter of the Solar System, while always very near the Sun, moves through space as time passes, depending on where other large bodies in the Solar System, such as Jupiter and other large gas giants, are located at that time. A similar phenomenon allows the detection of exoplanets by way of the radial-velocity method.

The helio- prefix is derived from the Greek word "ἥλιος", meaning "Sun", and also Helios, the personification of the Sun in Greek mythology.^[1]

The first spacecraft to be put in a heliocentric orbit was Luna 1 in 1959. An incorrectly timed upper-stage burn caused it to miss its planned impact on the Moon.^[2]

Trans-Mars injection

[edit]

A trans-Mars injection (TMI) is a heliocentric orbit in which a propulsive maneuver is used to set a spacecraft on a trajectory, also known as Mars transfer orbit, which will place it as far as Mars orbit.

Every two years, low-energy transfer windows open up, which allow movement between the two planets with the lowest possible energy requirements. Transfer injections can place spacecraft into either a Hohmann transfer orbit or bi-elliptic transfer orbit. Trans-Mars injections can be either a single maneuver burn, such as that used by the NASA MAVEN orbiter in 2013, or a series of perigee kicks, such as that used by the ISRO Mars Orbiter Mission in 2013.^[3]^[4]

References

[edit]

^ "helio-". Dictionary.com Unabridged (v 1.1). Random House. 2006. Retrieved 2009-02-12.
^ "NASA – NSSDCA – Spacecraft – Details". nssdc.gsfc.nasa.gov. Archived from the original on 2019-06-02. Retrieved 2022-01-04.
^ ISRO successfully sends Mars orbiter into sun-centric orbit.
^ Orbiter successfully placed in Mars Transfer Trajectory.

Gravitational orbits

Types

General	Box Circular Elliptical / Highly elliptical Horseshoe Hyperbolic trajectory Inclined / Non-inclined Kepler Lagrange point Osculating Parabolic / Escape / Capture Parking Prograde / Retrograde Radial Synchronous semi sub Transfer orbit
Geocentric	Geosynchronous Geostationary Geostationary transfer Graveyard High Earth Low Earth Medium Earth Molniya Near-equatorial Orbit of the Moon Polar Sun-synchronous Transatmospheric Tundra Very low Earth
About other points	Mars Areocentric Areosynchronous Areostationary Lagrange points Distant retrograde Halo Lissajous Libration Lunar Sun Heliocentric Earth's orbit Mars cycler Heliosynchronous Other Lunar cycler

Parameters

Shape Size	$e$ Eccentricity $a$ Semi-major axis $b$ Semi-minor axis $Q$ , $q$ Apsides
Orientation	$i$ Inclination $Ω$ Longitude of the ascending node $ω$ Argument of periapsis $ϖ$ Longitude of the periapsis
Position	$M$ Mean anomaly $ν$ , $θ$ , $f$ True anomaly $E$ Eccentric anomaly $L$ Mean longitude $l$ True longitude
Variation	$T$ Orbital period $n$ Mean motion $v$ Orbital speed $t 0$ Epoch

Maneuvers

Orbital
mechanics

List of orbits

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

A heliocentric orbit is an orbit around the barycenter of the Solar System, which serves as the center of mass and is located within or very near the center of the Sun due to its overwhelming mass compared to other bodies.^[1] These orbits are followed by planets, dwarf planets, asteroids, comets, and various spacecraft, distinguishing them from geocentric orbits around Earth or other planetary systems.^[2]^[3] The concept of heliocentric orbits emerged from the heliocentric model proposed by Nicolaus Copernicus in 1543, which posited the Sun as the center of the Solar System rather than Earth, challenging the long-dominant geocentric view.^[4] This model gained empirical support through observations by Galileo Galilei in 1610, who noted the phases of Venus and the moons of Jupiter, providing evidence that not all celestial bodies revolved around Earth.^[4] Johannes Kepler further refined the understanding in the early 17th century by formulating three laws of planetary motion based on precise data from Tycho Brahe, describing how bodies in heliocentric orbits behave.^[5] Kepler's first law states that planets orbit the Sun in elliptical paths with the Sun at one focus, rather than perfect circles, explaining variations in orbital speed and distance.^[5] The second law, known as the law of equal areas, indicates that a line connecting a planet to the Sun sweeps out equal areas in equal intervals of time, meaning planets move faster when closer to the Sun (at perihelion) and slower when farther away (at aphelion).^[5] The third law relates the orbital period to the semi-major axis, asserting that the square of the orbital period is proportional to the cube of the average distance from the Sun, allowing predictions of orbital durations for different bodies—such as Mercury's 88-day orbit versus Saturn's approximately 29-year orbit.^[5] In the modern era, heliocentric orbits are crucial for interplanetary exploration, with spacecraft achieving them by reaching escape velocity from Earth to follow independent paths around the Sun.^[3] Notable examples include the ESA's Solar Orbiter, which studies the Sun from distances as close as 42 million kilometers and is planned to reach inclinations up to 33 degrees relative to the solar equator during its extended mission, and the Rosetta mission, which used a heliocentric trajectory to rendezvous with comet 67P/Churyumov-Gerasimenko.^[3]^[6] These orbits enable detailed observations of solar system dynamics, from planetary formation to comet behavior, underscoring their role in advancing astronomical and space science.^[3]

Fundamentals

Definition

A heliocentric orbit is the path followed by a celestial body or spacecraft as it revolves around the Sun under the influence of its gravitational attraction, with the orbit described in a reference frame centered at the Sun's center.^[2] This coordinate system positions the Sun at the origin, allowing positions and velocities to be expressed relative to the central star. Key characteristics of heliocentric orbits include their shapes—either closed (elliptical) or open (parabolic or hyperbolic)—which are primarily determined by the Sun's gravity, following qualitative principles such as Kepler's laws of planetary motion.^[5] In first-order approximations, perturbations from other solar system bodies are considered negligible, making the two-body Sun-object interaction a valid model for most dynamics within the system.^[7] This simplifies analysis for scales typical of planetary and interplanetary trajectories. Heliocentric orbits differ from geocentric orbits, which center on Earth, and barycentric frames, which use the solar system's center of mass as the origin; the heliocentric approximation is sufficiently accurate for most solar system applications due to the Sun's dominant mass. The type of orbit—bound or unbound—is determined by the total specific mechanical energy

\epsilon

, given by

\epsilon = \frac{v^2}{2} - \frac{\mu}{r},

where

v

is the speed relative to the Sun,

r

is the heliocentric distance, and

\mu

is the Sun's gravitational parameter (

\mu = GM_\odot \approx 1.327 \times 10^{20}

m³ s⁻²).^[8] Negative

\epsilon

indicates a bound (closed) orbit, while positive

\epsilon

signifies an unbound (open) trajectory.^[9]

Historical Context

The concept of a heliocentric universe, with celestial bodies orbiting the Sun, traces its earliest known articulation to the ancient Greek astronomer Aristarchus of Samos in the 3rd century BCE, who proposed a model placing the Sun at the center of the cosmos and the Earth in motion around it. This idea, however, was overshadowed by the prevailing geocentric model, which positioned Earth at the universe's center and dominated astronomical thought for centuries due to philosophical and observational preferences of the time.^[10]^[11] The heliocentric model gained renewed prominence during the Copernican revolution in the 16th century, when Nicolaus Copernicus published De revolutionibus orbium coelestium in 1543, systematically describing a Sun-centered system where planets, including Earth, follow circular paths around the Sun. Copernicus's work revived and formalized the heliocentric hypothesis, arguing it simplified explanations of planetary retrogrades and seasonal variations compared to geocentric alternatives.^[12]^[13] Building on this foundation, Johannes Kepler advanced the theory in the early 17th century by analyzing precise observations from Tycho Brahe, publishing his first two laws of planetary motion in Astronomia nova in 1609 and the third in Harmonices mundi in 1619. Kepler's first law specifically established that planets trace elliptical orbits with the Sun at one focus, departing from Copernicus's circular assumptions and providing a more accurate description of heliocentric paths.^[14]^[13] Isaac Newton's Philosophiæ Naturalis Principia Mathematica in 1687 synthesized these developments by introducing the law of universal gravitation as an inverse-square force, offering a physical mechanism that explained and unified heliocentric motion under a single mathematical framework applicable to all celestial bodies.^[15] In the 18th and 19th centuries, refinements addressed perturbations—small deviations in orbits caused by mutual gravitational influences among bodies—with Joseph-Louis Lagrange's work in the late 1700s developing analytical methods to model these effects in celestial mechanics, enabling more precise predictions of heliocentric trajectories. The 20th century brought empirical confirmations through space-age missions, as spacecraft like Voyager followed predicted heliocentric orbits with high accuracy, validating the model's foundational principles against direct observational data.^[16]^[17]

Orbital Mechanics

Keplerian Elements

The six classical Keplerian elements fully specify the orientation, shape, and size of a heliocentric orbit in the two-body approximation, where the Sun is treated as the central mass and the orbiting body follows an elliptical path governed by Kepler's first law.^[18] These elements are derived from observations and provide a standardized framework for describing orbits relative to a reference plane, typically the ecliptic, which is the plane of Earth's orbit around the Sun.^[19] The elements consist of the semi-major axis (a), eccentricity (e), inclination (i), longitude of the ascending node (Ω), argument of perihelion (ω), and true anomaly (ν). The semi-major axis (a) measures the size of the orbit, defined as half the length of the major axis of the ellipse; it relates directly to the orbital period via Kepler's third law.^[18] The eccentricity (e) describes the shape, with e = 0 indicating a circular orbit and 0 < e < 1 for bound elliptical orbits, where e approaches 1 for highly elongated paths.^[19] The inclination (i) quantifies the tilt of the orbital plane relative to the ecliptic, ranging from 0° for coplanar orbits to values up to 180° for retrograde motion.^[20] The longitude of the ascending node (Ω) specifies the orientation of the orbital plane by giving the angle from the vernal equinox to the point where the orbit crosses the ecliptic from south to north, measured along the ecliptic.^[18] The argument of perihelion (ω) locates the perihelion (closest point to the Sun) within the orbital plane, measured eastward from the ascending node to the perihelion.^[21] Finally, the true anomaly (ν) indicates the instantaneous angular position of the body along the orbit, measured from the perihelion to the current position.^[18] Geometrically, these elements define the ellipse's position and orientation in three-dimensional space relative to the Sun and the ecliptic reference. The semi-major axis and eccentricity establish the ellipse's scale and elongation, with the focus at the Sun. Inclination and the longitude of the ascending node rotate the orbital plane about the ecliptic's north pole and around the Sun, respectively, while the argument of perihelion further orients the major axis within that plane; the true anomaly then pinpoints the body's location on the ellipse at a given time.^[22] This configuration allows visualization of the orbit as an inclined, rotated ellipse centered on the Sun, with the reference frame aligned to the vernal equinox and ecliptic pole. Orbital elements are determined from astronomical observations, such as right ascension and declination, using methods like Gauss's preliminary orbit determination, which requires at least three observations to compute an initial set of elements, or least-squares fitting for refined estimates from multiple data points.^[23] Gauss's method involves solving for the heliocentric distances and positions that best match the observed angular separations, often iteratively to minimize residuals.^[24] Least-squares optimization adjusts the elements to achieve the closest fit to all observations, accounting for measurement uncertainties.^[25] Standard units and conventions ensure consistency across astronomical applications: the semi-major axis is expressed in astronomical units (AU), where 1 AU is the mean Earth-Sun distance of approximately 149.6 million kilometers; angular elements (i, Ω, ω, ν) are measured in degrees; and elements are typically referenced to the J2000.0 epoch, corresponding to January 1, 2000, at 12:00 Terrestrial Time, to account for precession and other secular changes.^[26]^[27]

Equations of Motion

In the two-body problem central to heliocentric orbits, the motion of a smaller body around the Sun is governed by the gravitational parameter μ = GM, where G is the gravitational constant and M is the Sun's mass. The vis-viva equation provides the speed v at any radial distance r from the Sun, derived from the conservation of total mechanical energy in the system. The specific total energy ε is constant and given by ε = v²/2 - μ/r, which equals -μ/(2a) for elliptical orbits, where a is the semi-major axis. Substituting and solving for v yields the vis-viva equation:

v = \sqrt{\mu \left( \frac{2}{r} - \frac{1}{a} \right)}

v=μ(r2−a1)

This equation holds for all conic sections in the two-body approximation, with a interpreted as positive for ellipses, negative for hyperbolas, and infinite for parabolas.^[28]^[29] To propagate the position in an elliptical heliocentric orbit, the mean anomaly M = n(t - τ) is first computed, where n = √(μ/a³) is the mean motion and τ is the time of perihelion passage. Kepler's equation relates M to the eccentric anomaly E via: $M = E - e \sin E$ where e is the eccentricity. This transcendental equation lacks a closed-form solution and is typically solved iteratively using methods like Newton-Raphson, which converges quadratically for e < 1. The iteration starts with an initial guess E₀ ≈ M and updates E_{k+1} = E_k - (E_k - e sin E_k - M)/(1 - e cos E_k) until convergence within a specified tolerance. Once E is obtained, the heliocentric distance r = a(1 - e cos E) and true anomaly ν = 2 arctan[√((1+e)/(1-e)) tan(E/2)] follow, providing polar coordinates in the orbital plane.^[30]^[31] To obtain Cartesian coordinates in the ecliptic reference frame, the position in the orbital plane (r cos ν, r sin ν, 0) is transformed using rotation matrices that incorporate the Keplerian elements: inclination i, longitude of the ascending node Ω, and argument of periapsis ω. The full rotation matrix R is the product R = R_z(-Ω) R_x(-i) R_z(-ω), applied as \vec{r} = R \begin{pmatrix} r \cos \nu \ r \sin \nu \ 0 \end{pmatrix}, yielding the geocentric or heliocentric position vector. Velocity components are similarly derived from the time derivatives. These transformations assume the two-body model and use the orbital elements as inputs. Conservation of angular momentum in the two-body problem ensures that the specific angular momentum vector \vec{h} = \vec{r} \times \vec{v} remains constant, with magnitude h = √[μ p], where p = a(1 - e²) is the semi-latus rectum. This magnitude h = √[μ a (1 - e²)] defines the size of the orbital plane and is perpendicular to it, fixing the plane's orientation. The constancy of \vec{h} arises directly from the central nature of the gravitational force, which exerts no torque.^[32]^[33] While the two-body equations provide an exact solution for isolated heliocentric motion, real solar system dynamics introduce n-body perturbations from planetary gravity, which qualitatively alter the pure model by causing secular variations in orbital elements like precession of perihelion and changes in eccentricity over long timescales. These effects are small for most asteroids and comets but accumulate, leading to deviations from Keplerian predictions that require numerical integration for accurate long-term propagation.^[34]

Classifications

Bound Orbits

Bound orbits in the heliocentric system are characterized by closed, elliptical paths where the orbital eccentricity satisfies

e < 1

and the specific orbital energy

\varepsilon < 0

, ensuring the object remains gravitationally bound to the Sun and undergoes periodic motion without escaping to infinity.^[35] This contrasts with unbound orbits, which follow open hyperbolic or parabolic trajectories due to non-negative energy. The negative energy arises from the balance where the gravitational potential energy dominates the kinetic energy, confining the orbit within a finite region around the Sun. The orbital period

T

of bound heliocentric orbits follows Kepler's third law, expressed as

T^2 \propto a^3

, where

a

is the semi-major axis, linking the time for one complete revolution to the orbit's average size.^[5] Mean motion resonances occur when the orbital periods of two bodies form a simple integer ratio, such as 3:1 or 5:2 with Jupiter, influencing the distribution of objects; for instance, the Kirkwood gaps in the asteroid belt represent regions depleted by resonant interactions that destabilize orbits over time.^[36] Stability in these orbits is enhanced by low eccentricity and inclination, which keep trajectories nearly coplanar with the ecliptic plane and minimize perturbations from gravitational interactions.^[37] However, chaotic effects can arise from close encounters with massive bodies like planets, leading to unpredictable variations in orbital elements and potential long-term instability.^[38] For small particles in bound orbits, evolutionary changes occur through the Poynting-Robertson drag, a radiation effect that causes gradual loss of angular momentum, resulting in a spiraling decay toward the Sun over timescales of thousands to millions of years.^[39] This drag is particularly significant for dust grains, altering their semi-major axis and eccentricity until they are eventually accreted by the Sun.^[40]

Unbound Orbits

Unbound orbits in the heliocentric frame are open trajectories where celestial objects possess sufficient energy to escape the Sun's gravitational pull permanently. These include parabolic orbits with eccentricity

e = 1

and zero specific orbital energy

\varepsilon = 0

, representing the limiting case, as well as hyperbolic orbits with

e > 1

and

\varepsilon > 0

. The following description focuses on hyperbolic orbits, which are the typical form for interstellar objects approaching from outside the Solar System.^[41]^[42] The asymptotic behavior of hyperbolic orbits is characterized by straight-line paths at infinity, both incoming and outgoing, with the hyperbolic excess velocity

v_\infty

representing the speed relative to the Sun far from its influence. This velocity is given by

v_\infty = \sqrt{\frac{\mu}{|a|}}

v∞=∣a∣μ

, where $\mu$ is the Sun's gravitational parameter and $|a|$ is the magnitude of the semi-major axis (taken positive for convenience in hyperbolic contexts). The impact parameter $b$ , defined as the perpendicular offset from the Sun to the incoming asymptote, governs the geometry of closest approach and is expressed as $b = |a| \sqrt{e^2 - 1}$

. Together, these parameters determine the trajectory's curvature, with smaller $b$ leading to tighter bends and closer perihelia.^[41]^[43] The gravitational interaction imparts a deflection angle $\delta = 2 \arcsin\left(\frac{1}{e}\right)$ , which quantifies the turning of the object's velocity vector during the encounter, akin to a natural slingshot effect. This angle ranges from nearly 0° for large $e$ (minimal deflection, nearly straight path) to approaching 180° as $e$ nears 1 (strong deflection near head-on). Observational signatures of such orbits include high $v_\infty$ values, often exceeding 20 km/s, reflecting interstellar origins, and a prevalence of retrograde inclinations, particularly for objects detected near the ecliptic plane due to the geometry of galactic motion relative to the solar system. These traits have been noted in confirmed interstellar visitors, such as 1I/'Oumuamua (v_∞ ≈ 26 km/s, 2017), 2I/Borisov (v_∞ ≈ 32 km/s, 2019), and 3I/ATLAS (v_∞ ≈ 58 km/s, discovered 2025), aiding their identification amid solar system clutter.^[41]^[44]^[45]

Applications

Natural Bodies

The solar system's eight planets occupy stable, nearly circular heliocentric orbits with low eccentricities (typically e < 0.1) and minimal inclinations relative to the ecliptic plane (i < 8°). These bodies are divided into inner planets (Mercury, Venus, Earth, and Mars), which have semi-major axes less than 2 AU and rocky compositions formed closer to the Sun, and outer planets (Jupiter, Saturn, Uranus, and Neptune), with semi-major axes exceeding 5 AU and gaseous or icy compositions resulting from their distant formation in a cooler environment. For instance, Earth orbits at a semi-major axis of 1 AU with e = 0.017 and i ≈ 0°, providing a reference for the astronomical unit and exemplifying the low-eccentricity, coplanar nature of planetary paths.^[46] Asteroids, remnants of the solar system's early planetesimal disk, populate various heliocentric regions with more varied orbital parameters than planets. The main asteroid belt lies between Mars and Jupiter at semi-major axes of 2.2–3.3 AU, featuring moderate eccentricities (e ≈ 0.1–0.3) and inclinations (i ≈ 10°–15° on average), which result in somewhat elliptical and tilted orbits but keep most objects confined between 1.8 and 3.5 AU perihelion and aphelion. Jupiter's Trojan asteroids reside in stable 1:1 orbital resonance at the L4 and L5 Lagrange points ahead of and behind the planet, with semi-major axes near 5.2 AU, low eccentricities (e < 0.1), and inclinations typically under 20°, allowing them to co-orbit Jupiter without close encounters. Near-Earth objects (NEOs), a subset of asteroids with orbits crossing or approaching Earth's path, pose elevated collision risks due to their dynamical instability; these include Earth-crossers with perihelia under 1.3 AU and eccentricities often exceeding 0.3, enabling potential impacts if alignments occur.^[47]^[48]^[49] Comets, icy bodies that develop tails when nearing the Sun, exhibit highly eccentric heliocentric orbits influenced by their distant origins. Short-period comets, particularly the Jupiter family with periods under 20 years, have semi-major axes less than 7 AU, eccentricities below 0.99, and low inclinations (i < 30°), reflecting gravitational sculpting by Jupiter that confines their paths to the inner solar system. In contrast, long-period comets from the Oort cloud have periods exceeding 200 years, near-parabolic eccentricities (e ≈ 1), and randomly distributed high inclinations (often >30° up to nearly 180°), indicating isotropic perturbations from passing stars that send them inward from a spherical reservoir at 2,000–100,000 AU. Halley's Comet serves as a transitional example, with a 76-year period, e = 0.967, and retrograde inclination of 162° (equivalent to 18° tilt relative to the ecliptic), bridging short- and long-period dynamics through repeated Jupiter interactions.^[50]^[51] Rare interstellar objects temporarily enter the solar system on unbound hyperbolic trajectories with eccentricities greater than 1, unbound by the Sun's gravity. The first detected, 1I/'Oumuamua (discovered in 2017), followed a hyperbolic path with e ≈ 1.2, originating from outside the solar system and exhibiting non-gravitational acceleration possibly from outgassing. Similarly, 2I/Borisov (2019), an active comet-like interloper, had e = 3.36, confirming its extrasolar origin through its high speed at infinity (≈32 km/s) and trajectory unbound by solar perturbations. These intruders highlight the porosity of the heliosphere to galactic wanderers, though their detection remains exceptional due to the vast volume of space.^[52]^[53]

Spacecraft Trajectories

Spacecraft are typically injected into heliocentric orbits through an initial escape from Earth's sphere of influence, achieved via a hyperbolic trajectory relative to Earth. This escape is powered by the launch vehicle, imparting a hyperbolic excess velocity (v_∞) that, when vectorially added to Earth's heliocentric velocity, establishes the spacecraft's initial solar-relative speed and direction. Upon exiting Earth's influence, a dedicated insertion burn adjusts the orbit to the desired semi-major axis (a) and eccentricity (e), tailoring the trajectory for mission objectives such as planetary encounters or solar exploration.^[54] For missions targeting the inner solar system, like the Parker Solar Probe, the injection leverages a high-energy launch to place the spacecraft on an initially elliptical heliocentric path, with subsequent maneuvers refining the orbit. The probe's trajectory aligns considerations of solar magnetic field geometry, akin to the Parker spiral configuration of the interplanetary magnetic field, to optimize in-situ measurements during escape and insertion phases.^[55] Transfer orbits enable efficient relocation between distinct heliocentric paths, with the Hohmann transfer serving as the minimum-energy method for transitioning between two coplanar circular orbits. This involves a single elliptical arc tangent to both orbits, requiring two impulsive burns: one to depart the initial orbit and enter the transfer ellipse, and a symmetric burn upon arrival to circularize at the target radius. The total delta-v (Δv) for such a transfer from an inner radius r₁ to an outer radius r₂ is given by:

\Delta v = \sqrt{\frac{\mu}{r_1}} \left( \sqrt{\frac{2 r_2}{r_1 + r_2}} - 1 \right) + \sqrt{\frac{\mu}{r_2}} \left( 1 - \sqrt{\frac{2 r_1}{r_1 + r_2}} \right)

Δv=r1μ

(r1+r22r2

−1)+r2μ

(1−r1+r22r1

) where μ is the Sun's gravitational parameter. This formulation derives from the vis-viva equation applied at perigee and apogee of the transfer orbit, ensuring the maneuver minimizes propellant use for coplanar, non-resonant transfers.^[56] Gravity assists augment or redirect heliocentric trajectories by exploiting planetary flybys to modify the spacecraft's v_∞ relative to the Sun, effectively altering energy and angular momentum without onboard propulsion. During a flyby, the spacecraft follows a hyperbolic path around the planet, gaining (or losing) velocity depending on the geometry—approaching from behind the planet's orbital motion yields a speed boost in the heliocentric frame. The Voyager missions exemplify this technique, employing sequential Jupiter and Saturn flybys to propel the probes outward, transforming their initial near-Earth heliocentric orbits into hyperbolic escapes toward the outer solar system with minimal delta-v expenditure.^[57] Deep-space probes often combine these elements for complex tours. As of 2024, the Parker Solar Probe has executed a highly elliptical heliocentric orbit, progressively tightening via seven Venus gravity assists to achieve a final perihelion of approximately 0.046 AU (3.83 million miles from the Sun's surface), enabling unprecedented solar corona sampling.^[55] Similarly, the Lucy mission employed multiple Earth gravity assists—completed in 2022 and 2024—and flew by asteroid Donaldjohanson in April 2025, to insert into a resonant orbit matching Jupiter's Trojans, facilitating flybys of eight asteroids across a 12-year tour while maintaining a stable heliocentric path between 1 and 5 AU.^[58]

Info Pages

Talk Pages

Special Pages

Heliocentric orbit

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Heliocentric orbit

Trans-Mars injection

See also

References