Community hub
0 subscribers8 pages, 0 posts
Recent from talks
All channels
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to List of orbits.
Nothing was collected or created yet.
List of orbits
View on Wikipediafrom Wikipedia
- the innermost, the red dotted line represents the orbit of the International Space Station (ISS);
- cyan represents low Earth orbit,
- yellow represents medium Earth orbit,
- The green dashed line represents the orbit of Global Positioning System (GPS) satellites, and
- the outermost, the black dashed line represents geostationary orbit.
This is a list of types of gravitational orbit classified by various characteristics.
Common abbreviations
[edit]List of abbreviations of common Earth orbits
[edit]| Orbit | Name |
|---|---|
| GEO | Geostationary orbit |
| LEO | Low Earth orbit |
| MEO | Medium Earth orbit |
| SSO | Sun-synchronous orbit |
List of abbreviations of other orbits
[edit]| Orbit | Name |
|---|---|
| GSO | Geosynchronous orbit |
| GTO | Geostationary transfer orbit |
| HCO | Heliocentric orbit |
| HEO | Highly elliptical orbit |
| NRHO | Near-rectilinear halo orbit |
| VLEO | Very Low Earth Orbit |
Classifications
[edit]The following is a list of types of orbits:
Centric classifications
[edit]- Galactocentric orbit:[2] An orbit about the center of a galaxy. The Sun follows this type of orbit about the Galactic Center of the Milky Way.
- Heliocentric orbit: An orbit around the Sun. In the Solar System, all planets, comets, and asteroids are in such orbits, as are many artificial satellites and pieces of space debris. Moons by contrast are not in a heliocentric orbit but rather orbit their parent object.
- Geocentric orbit: An orbit around the planet Earth, such as that of the Moon or of artificial satellites.
- Selenocentric orbit (named after Selene): An orbit around Earth's Moon.
- Areocentric orbit (named after Ares): An orbit around the planet Mars, such as that of its moons or artificial satellites.
For orbits centered about planets other than Earth and Mars and for the dwarf planet Pluto, the orbit names incorporating Greek terminology are not as established and much less commonly used:
 | This section needs additional citations for verification. (October 2024) |
- Mercury orbit (Hermeocentric orbit, named after Hermes): An orbit around the planet Mercury.
- Venus orbit (Cytherocentric orbit, named after Cytherea, or Aphrodiocentric, after Aphrodite): An orbit around the planet Venus.
- Jupiter orbit (Zenocentric orbit, named after Zeus,[3] or Latin equivalent Jovicentric): An orbit around the planet Jupiter.
- Saturn orbit (Kronocentric orbit, named after Cronus,[3][failed verification] or Latin equivalent Saturnicentric): An orbit around the planet Saturn.
- Uranus orbit (Uranocentric orbit, named after Uranus): An orbit around the planet Uranus.
Altitude classifications for geocentric orbits
[edit]- Transatmospheric orbit (TAO): geocentric orbits with an apogee above 100 km and perigee that intersects with the defined atmosphere.[4]
- Very low Earth orbit (VLEO) is defined as altitudes between approximately 100 - 450 km above Earth’s surface.[5][6]
- Low Earth orbit (LEO): geocentric orbits with altitudes below 2,000 km (1,200 mi).[7]
- Medium Earth orbit (MEO): geocentric orbits ranging in altitude from 2,000 km (1,200 mi) to just below geosynchronous orbit at 35,786 kilometers (22,236 mi). Also known as an intermediate circular orbit. These are used for Global Navigation Satellite System spacecraft, such as GPS, GLONASS, Galileo, BeiDou. GPS satellites orbit at an altitude of 20,200 kilometers (12,600 mi) with an orbital period of almost 12 hours.[8]
- Geosynchronous orbit (GSO) and geostationary orbit (GEO) are orbits around Earth matching Earth's sidereal rotation period.[1][9] Although terms are often used interchangeably, technically a geosynchronous orbit matches the Earth's rotational period, but the definition does not require it to have zero orbital inclination to the equator, and thus is not stationary above a given point on the equator, but may oscillate north and south during the course of a day. Thus, a geostationary orbit is defined as a geosynchronous orbit at zero inclination. Geosynchronous (and geostationary) orbits have a semi-major axis of 42,164 km (26,199 mi).[10] This works out to an altitude of 35,786 km (22,236 mi). Both complete one full orbit of Earth per sidereal day (relative to the stars, not the Sun).
- High Earth orbit: geocentric orbits above the altitude of geosynchronous orbit (35,786 km or 22,236 mi).[8]
For Earth orbiting satellites below the height of about 800 km, the atmospheric drag is the major orbit perturbing force out of all non-gravitational forces.[11] Above 800 km, solar radiation pressure causes the largest orbital perturbations.[12] However, the atmospheric drag strongly depends on the density of the upper atmosphere, which is related to the solar activity, therefore the height at which the impact of the atmospheric drag is similar to solar radiation pressure varies depending on the phase of the solar cycle.
Inclination classifications
[edit]- Inclined orbit: An orbit whose inclination in reference to the equatorial plane is not 0.
- Polar orbit: An orbit that passes above or nearly above both poles of the planet on each revolution. Therefore, it has an inclination of (or very close to) either 90 degrees or −90 degrees.
- Polar Sun-synchronous orbit (SSO): A nearly polar orbit that passes the equator at the same local solar time on every pass. Useful for image-taking satellites because shadows will be the same on every pass.
- Non-inclined orbit: An orbit whose inclination is equal to zero with respect to some plane of reference.
- Ecliptic orbit: A non-inclined orbit with respect to the ecliptic.
- Equatorial orbit: A non-inclined orbit with respect to the equator.
- Near equatorial orbit: An orbit whose inclination with respect to the equatorial plane is nearly zero. This orbit allows for rapid revisit times (for a single orbiting spacecraft) of near equatorial ground sites.
Directional classifications
[edit]- Prograde orbit: An orbit that is in the same direction as the rotation of the primary (i.e. east on Earth). By convention, the inclination of a Prograde orbit is specified as an angle less than 90°.
- Retrograde orbit: An orbit counter to the direction of rotation of the primary. By convention, retrograde orbits are specified with an inclination angle of more than 90°. Apart from those in Sun-synchronous orbit, few satellites are launched into retrograde orbit on Earth because the quantity of fuel required to launch them is greater than for a prograde orbit. This is because when the rocket starts out on the ground, it already has an eastward component of velocity equal to the rotational velocity of the planet at its launch latitude.
Eccentricity classifications
[edit]There are two types of orbits: closed (periodic) orbits, and open (escape) orbits. Circular and elliptical orbits are closed. Parabolic and hyperbolic orbits are open. Radial orbits can be either open or closed.
- Circular orbit: An orbit that has an eccentricity of 0 and whose path traces a circle.
- Elliptic orbit: An orbit with an eccentricity greater than 0 and less than 1 whose orbit traces the path of an ellipse.
- Geostationary or geosynchronous transfer orbit (GTO): An elliptic orbit where the perigee is at the altitude of a low Earth orbit (LEO) and the apogee at the altitude of a geostationary orbit.
- Hohmann transfer orbit: An orbital maneuver that moves a spacecraft from one circular orbit to another using two engine impulses. This maneuver was named after Walter Hohmann.
- Ballistic capture orbit: a lower-energy orbit than a Hohmann transfer orbit, a spacecraft moving at a lower orbital velocity than the target celestial body is inserted into a similar orbit, allowing the planet or moon to move toward it and gravitationally snag it into orbit around the celestial body.[13]
- Coelliptic orbit: A relative reference for two spacecraft—or more generally, satellites—in orbit in the same plane. "Coelliptic orbits can be defined as two orbits that are coplanar and confocal. A property of coelliptic orbits is that the difference in magnitude between aligned radius vectors is nearly the same, regardless of where within the orbits they are positioned. For this and other reasons, coelliptic orbits are useful in [spacecraft] rendezvous".[14]
- Parabolic orbit: An orbit with the eccentricity equal to 1. Such an orbit also has a velocity equal to the escape velocity and therefore will escape the gravitational pull of the planet. If the speed of a parabolic orbit is increased it will become a hyperbolic orbit.
- Escape orbit: A parabolic orbit where the object has escape velocity and is moving away from the planet.
- Capture orbit: A parabolic orbit where the object has escape velocity and is moving toward the planet.
- Hyperbolic orbit: An orbit with the eccentricity greater than 1. Such an orbit also has a velocity in excess of the escape velocity and as such, will escape the gravitational pull of the planet and continue to travel infinitely until it is acted upon by another body with sufficient gravitational force.
- Radial orbit: An orbit with zero angular momentum and eccentricity equal to 1. The two objects move directly towards or away from each other in a straight-line.
- Radial elliptic orbit: A closed elliptic orbit where the object is moving at less than the escape velocity. This is an elliptic orbit with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit.
- Radial parabolic orbit: An open parabolic orbit where the object is moving at the escape velocity.
- Radial hyperbolic orbit: An open hyperbolic orbit where the object is moving at greater than the escape velocity. This is a hyperbolic orbit with semi-minor axis = 0 and eccentricity = 1. Although the eccentricity is 1, this is not a parabolic orbit.
Synchronicity classifications
[edit]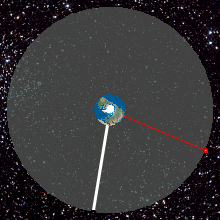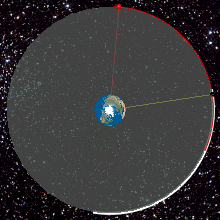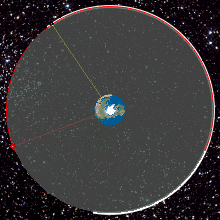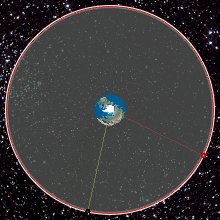
- Synchronous orbit: An orbit whose period is a rational multiple of the average rotational period of the body being orbited and in the same direction of rotation as that body. This means the track of the satellite, as seen from the central body, will repeat exactly after a fixed number of orbits. In practice, only 1:1 ratio (geosynchronous) and 1:2 ratios (semi-synchronous) are common.
- Geosynchronous orbit (GSO): An orbit around the Earth with a period equal to one sidereal day, which is Earth's average rotational period of 23 hours, 56 minutes, 4.091 seconds. For a nearly circular orbit, this implies an altitude of approximately 35,786 kilometers (22,236 mi). The orbit's inclination and eccentricity may not necessarily be zero. If both the inclination and eccentricity are zero, then the satellite will appear stationary from the ground. If not, then each day the satellite traces out an analemma (i.e. a "figure-eight") in the sky, as seen from the ground. When the orbit is circular and the rotational period has zero inclination, the orbit is considered to also be geostationary. Also known as a Clarke orbit after the writer Arthur C. Clarke.[8]
- Geostationary orbit (GEO): A circular geosynchronous orbit with an inclination of zero. To an observer on the ground this satellite appears as a fixed point in the sky. "All geostationary orbits must be geosynchronous, but not all geosynchronous orbits are geostationary."[8]
- Tundra orbit: A synchronous but highly elliptic orbit with significant inclination (typically close to 63.4°) and orbital period of one sidereal day (23 hours, 56 minutes for the Earth). Such a satellite spends most of its time over a designated area of the planet. The particular inclination keeps the perigee shift small.[15]
- Areosynchronous orbit (ASO): A synchronous orbit around the planet Mars with an orbital period equal in length to Mars' sidereal day, 24.6229 hours.
- Areostationary orbit (AEO): A circular areosynchronous orbit on the equatorial plane and about 17,000 km (10,557 miles) above the surface of Mars. To an observer on Mars this satellite would appear as a fixed point in the sky.
- Geosynchronous orbit (GSO): An orbit around the Earth with a period equal to one sidereal day, which is Earth's average rotational period of 23 hours, 56 minutes, 4.091 seconds. For a nearly circular orbit, this implies an altitude of approximately 35,786 kilometers (22,236 mi). The orbit's inclination and eccentricity may not necessarily be zero. If both the inclination and eccentricity are zero, then the satellite will appear stationary from the ground. If not, then each day the satellite traces out an analemma (i.e. a "figure-eight") in the sky, as seen from the ground. When the orbit is circular and the rotational period has zero inclination, the orbit is considered to also be geostationary. Also known as a Clarke orbit after the writer Arthur C. Clarke.[8]
- Subsynchronous orbit: A drift orbit close below GSO/GEO.
- Semi-synchronous orbit: An orbit with an orbital period equal to half of the average rotational period of the body being orbited and in the same direction of rotation as that body. For Earth this means a period of just under 12 hours at an altitude of approximately 20,200 km (12,544.2 miles) if the orbit is circular.[16]
- Molniya orbit: A semi-synchronous variation of a Tundra orbit. For Earth this means an orbital period of just under 12 hours. Such a satellite spends most of its time over two designated areas of the planet. An inclination of 63.4° is normally used to keep the perigee shift small.[15]
- Semi-synchronous orbit: An orbit with an orbital period equal to half of the average rotational period of the body being orbited and in the same direction of rotation as that body. For Earth this means a period of just under 12 hours at an altitude of approximately 20,200 km (12,544.2 miles) if the orbit is circular.[16]
- Supersynchronous orbit: Any orbit in which the orbital period of a satellite or celestial body is greater than the rotational period of the body which contains the barycenter of the orbit.
Orbits in galaxies or galaxy models
[edit]
- Box orbit: An orbit in a triaxial elliptical galaxy that fills in a roughly box-shaped region.
- Pyramid orbit: An orbit near a massive black hole at the center of a triaxial galaxy.[17] The orbit can be described as a Keplerian ellipse that precesses about the black hole in two orthogonal directions, due to torques from the triaxial galaxy.[18] The eccentricity of the ellipse reaches unity at the four corners of the pyramid, allowing the star on the orbit to come very close to the black hole.
- Tube orbit: An orbit near a massive black hole at the center of an axisymmetric galaxy. Similar to a pyramid orbit, except that one component of the orbital angular momentum is conserved; as a result, the eccentricity never reaches unity.[18]
Special classifications
[edit]- Sun-synchronous orbit: An orbit which combines altitude and inclination in such a way that the satellite passes over any given point of the planets's surface at the same local solar time. Such an orbit can place a satellite in constant sunlight and is useful for imaging, spy, and weather satellites.
- Frozen orbit: An orbit in which natural drifting due to the central body's shape has been minimized by careful selection of the orbital parameters.
- Orbit of the Moon: The orbital characteristics of the Moon. Average altitude of 384,403 kilometres (238,857 mi), elliptical-inclined orbit.
- Beyond-low Earth orbit (BLEO) and beyond Earth orbit (BEO) are a broad class of orbits that are energetically farther out than low Earth orbit or require an insertion into a heliocentric orbit as part of a journey that may require multiple orbital insertions, respectively.
- Near-rectilinear halo orbit (NRHO): an orbit currently planned in cislunar space, as a selenocentric orbit that will serve as a staging area for future missions. [19][20] Planned orbit for the NASA Lunar Gateway in circa 2024, as a highly-elliptical seven-day near-rectilinear halo orbit around the Moon, which would bring the small space station within 3,000 kilometers (1,900 mi) of the lunar north pole at closest approach and as far away as 70,000 kilometers (43,000 mi) over the lunar south pole.[21][22][23]
- Distant retrograde orbit (DRO): A stable circular retrograde orbit (usually referring to Lunar Distant Retrograde Orbit). Stability means that satellites in DRO do not need to use station keeping propellant to stay in orbit. The lunar DRO is a high lunar orbit with a radius of approximately 61,500 km.[24] This was proposed[by whom?] in 2017 as a possible orbit for the Lunar Gateway space station, outside Earth-Moon L1 and L2.[20]
- Decaying orbit: A decaying orbit is an orbit at a low altitude that decreases over time due atmospheric resistance. Used to dispose of dying artificial satellites or to aerobrake an interplanetary spacecraft.
- Earth-trailing orbit, a heliocentric orbit that is placed such that the satellite will initially follow Earth but at a somewhat slower orbital angular speed, such that it moves further behind year by year. This orbit was used on the Spitzer Space Telescope in order to drastically reduce the heat load from the warm Earth from a more typical geocentric orbit used for space telescopes.[25]
- Graveyard orbit (or disposal, junk orbit) : An orbit that satellites are moved into at the end of their operation. For geostationary satellites a few hundred kilometers above geosynchronous orbit.[26][27]
- Parking orbit, a temporary orbit.
- Transfer orbit, an orbit used during an orbital maneuver from one orbit to another.
- Lunar transfer orbit (LTO)[clarification needed] accomplished with trans-lunar injection (TLI)
- Mars transfer orbit (MTO) also known as trans-Mars injection (TMI) orbit
- Repeat orbit: An orbit where the ground track of the satellite repeats after a period of time.
- Gangale orbit: a solar orbit near Mars whose period is one Martian year, but whose eccentricity and inclination both differ from that of Mars such that a relay satellite in a Gangale orbit is visible from Earth even during solar conjunction.[28]
Pseudo-orbit classifications
[edit]
- Horseshoe orbit: An orbit that appears to a ground observer to be orbiting a certain planet but is actually in co-orbit with the planet. See asteroids 3753 Cruithne and 2002 AA29.
- Libration point orbits such as halo orbits and Lissajous orbits: These are orbits around a Lagrangian point. Lagrange points are shown in the adjacent diagram, and orbits near these points allow a spacecraft to stay in constant relative position with very little use of fuel. Orbits around the L1 point are used by spacecraft that want a constant view of the Sun, such as the Solar and Heliospheric Observatory. Orbits around L2 are used by missions that always want both Earth and the Sun behind them. This enables a single shield to block radiation from both Earth and the Sun, allowing passive cooling of sensitive instruments. Examples include the Wilkinson Microwave Anisotropy Probe and the James Webb Space Telescope. L1, L2, and L3 are unstable orbits[6], meaning that small perturbations will cause the orbiting craft to drift out of the orbit without periodic corrections.
- P/2 orbit, a highly-stable 2:1 lunar resonant orbit, that was first used with the spacecraft TESS (Transiting Exoplanet Survey Satellite) in 2018.[29][30]
See also
[edit]Notes
[edit]- ^ Orbital periods and speeds are calculated using the relations 4π2R3 = T2GM and V2R = GM, where R = radius of orbit in metres, T = orbital period in seconds, V = orbital speed in m/s, G = gravitational constant ≈ 6.673×10−11 Nm2/kg2, M = mass of Earth ≈ 5.98×1024 kg.
- ^ Approximately 8.6 times when the Moon is nearest (363,104 km ÷ 42,164 km) to 9.6 times when the Moon is farthest (405,696 km ÷ 42,164 km).
References
[edit]- ^ a b "Types of Orbits". Space Foundation.
- ^ "Definition of GALACTOCENTRIC". www.merriam-webster.com. Retrieved 3 June 2020.
- ^ a b Parker, Sybil P. (2002). McGraw-Hill Dictionary of Scientific and Technical Terms Sixth Edition. McGraw-Hill. p. 1772. ISBN 007042313X.
- ^ McDowell, Jonathan (24 May 1998). "Jonathan's Space Report".
Transatmospheric orbit (TAO): orbital flight with perigee less than 80 km but more than zero. Potentially used by aerobraking missions and transatmospheric vehicles, also in some temporary phases of orbital flight (e.g. STS pre OMS-2, some failures when no apogee restart)
- ^ "Stingray VLEO Constellation".
- ^ "Attitude control for satellites flying in VLEO using aerodynamic surfaces".
- ^ "NASA Safety Standard 1740.14, Guidelines and Assessment Procedures for Limiting Orbital Debris" (PDF). Office of Safety and Mission Assurance. 1 August 1995. p. A-2. Archived from the original (PDF) on 15 February 2013.
Low Earth orbit (LEO) – The region of space below the altitude of 2000 km.
, pages 37–38 (6–1,6–2); figure 6-1. - ^ a b c d "Orbit: Definition". Ancillary Description Writer's Guide, 2013. National Aeronautics and Space Administration (NASA) Global Change Master Directory. Archived from the original on 11 May 2013. Retrieved 29 April 2013.
- ^ "Types of orbits".
- ^ Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications. Hawthorne, CA: Microcosm Press. p. 31.
- ^ Krzysztof, Sośnica (1 March 2015). "Impact of the Atmospheric Drag on Starlette, Stella, Ajisai, and Lares Orbits". Artificial Satellites. 50 (1): 1–18. Bibcode:2015ArtSa..50....1S. doi:10.1515/arsa-2015-0001.
- ^ Bury, Grzegorz; Sośnica, Krzysztof; Zajdel, Radosław; Strugarek, Dariusz (28 January 2020). "Toward the 1-cm Galileo orbits: challenges in modeling of perturbing forces". Journal of Geodesy. 94 (2): 16. Bibcode:2020JGeod..94...16B. doi:10.1007/s00190-020-01342-2.
- ^ Hadhazy, Adam (22 December 2014). "A New Way to Reach Mars Safely, Anytime and on the Cheap". Scientific American. Retrieved 25 December 2014.
- ^ Whipple, P. H . (17 February 1970). "Some Characteristics of Coelliptic Orbits – Case 610" (PDF). Bellcom Inc. Washington: NASA. Archived from the original (PDF) on 21 May 2010. Retrieved 23 May 2012.
- ^ a b This answer explains why such inclination keeps apsidial drift small: https://space.stackexchange.com/a/24256/6834
- ^ "Catalog of Earth Satellite Orbits". earthobservatory.nasa.gov. NASA. 4 September 2009. Retrieved 4 May 2022.
- ^ Merritt and Vasilev, ORBITS AROUND BLACK HOLES IN TRIAXIAL NUCLEI", The Astrophysical Journal 726(2), 61 (2011).
- ^ a b Merritt, David (2013). Dynamics and Evolution of Galactic Nuclei. Princeton: Princeton University Press. ISBN 9780691121017.
- ^ Leonard David (15 March 2018). "NASA Shapes Science Plan for Deep-Space Outpost Near the Moon". Space.com.
- ^ a b How a New Orbital Moon Station Could Take Us to Mars and Beyond Oct 2017 video with refs
- ^ Angelic halo orbit chosen for humankind's first lunar outpost. European Space Agency, Published by PhysOrg. 19 July 2019.
- ^ Halo orbit selected for Gateway space station. David Szondy, New Atlas. 18 July 2019.
- ^ Foust, Jeff (16 September 2019). "NASA cubesat to test lunar Gateway orbit". SpaceNews. Retrieved 15 June 2020.
- ^ "Asteroid Redirect Mission Reference Concept" (PDF). www.nasa.gov. NASA. Retrieved 14 June 2015.
- ^ "About Spitzer: Fast Facts". Caltech. 2008. Archived from the original on 2 February 2007. Retrieved 22 April 2007.
- ^ "U.S. Government Orbital Debris Mitigation Standard Practices" (PDF). United States Federal Government. Retrieved 28 November 2013.
- ^ Luu, Kim; Sabol, Chris (October 1998). "Effects of perturbations on space debris in supersynchronous storage orbits" (PDF). Air Force Research Laboratory Technical Reports (AFRL-VS-PS-TR-1998-1093). Bibcode:1998PhDT.......274L. Archived (PDF) from the original on 3 December 2013. Retrieved 28 November 2013.
- ^ Byford, Dorothy (September 2008). "Optimal Location of Relay Satellites for Continuous Communication with Mars".
- ^ Keesey, Lori (31 July 2013). "New Explorer Mission Chooses the 'Just-Right' Orbit". NASA. Retrieved 5 April 2018.
- ^ Overbye, Dennis (26 March 2018). "Meet Tess, Seeker of Alien Worlds". The New York Times. Retrieved 5 April 2018.
Gravitational orbits | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Types |
| ||||||||
| Parameters |
| ||||||||
| Maneuvers | |||||||||
| Orbital mechanics |
| ||||||||
List of orbits
View on Grokipediafrom Grokipedia
A list of orbits is a catalog of distinct orbital trajectories employed by spacecraft around Earth or other celestial bodies, classified primarily by altitude, inclination, period, and shape to serve specific mission objectives such as Earth observation, telecommunications, and interplanetary travel.[1] These orbits range from low-altitude paths that enable detailed imaging to high-altitude stationary positions that facilitate continuous global coverage, with each type optimized for factors like energy efficiency, revisit frequency, and gravitational stability.[2]
Common classifications include low-Earth orbit (LEO), spanning altitudes of approximately 160 to 2,000 kilometers, which supports rapid global data collection for satellites like NASA's Aqua mission at 705 km, often in polar or Sun-synchronous configurations to ensure consistent lighting for imaging.[2] Medium-Earth orbit (MEO), from 2,000 to 35,500 km, is utilized for navigation systems such as the European Space Agency's Galileo constellation at about 23,222 km, allowing for orbits completed in roughly 12 hours with daily equatorial crossings.[2] Higher regimes encompass geosynchronous orbits (GEO) at around 35,786 km, where satellites match Earth's rotation period of 23 hours, 56 minutes, and 4 seconds to appear fixed over a longitude, ideal for weather monitoring and communications as seen in NASA's GOES series.[1][2]
Specialized orbits further diversify applications: polar orbits, with 90-degree inclinations, enable full planetary coverage as the body rotates beneath, supporting mapping missions like NASA's Magellan at Venus.[1] Sun-synchronous orbits, a subset often in LEO, precess to maintain consistent local solar time at each pass, optimizing illumination for Earth-observing satellites such as the Mars Global Surveyor.[1] Walking orbits allow controlled precession of the orbital plane due to gravitational perturbations, adjusting ground track for targeted observations.[3] Transfer orbits, like the elliptical geosynchronous transfer orbit (GTO) with an apogee near 37,000 km, serve as efficient pathways to reach GEO from launch, minimizing propellant use via Hohmann transfers.[1][3]
Beyond Earth-centric paths, halo orbits around Lagrange points—such as L1 or L2—provide stable vantage points for continuous solar observation, exemplified by NASA's Solar and Heliospheric Observatory (SOHO) at the Sun-Earth L1 point, requiring station-keeping to counter instability.[1] Geostationary orbits, a precise equatorial variant of GEO with zero eccentricity, maintain fixed positions for uninterrupted service, known as the Clarke orbit after its proposer.[3] These orbital types, governed by Keplerian mechanics and perturbed by factors like atmospheric drag in LEO or third-body effects in higher regimes, form the foundational framework for spaceflight planning and mission design.[1]
Representative mission examples illustrate these abbreviations. The Voyager 1 and 2 probes, launched in 1977, transitioned to SSE after gravitational assists from outer planets, crossing the heliopause in 2012 and 2018, respectively, to enter interstellar space on unbound trajectories.[8] New Horizons, launched in 2006 and after its Pluto flyby in 2015, is in a heliocentric orbit through the Kuiper Belt region at approximately 60 AU (as of 2025), studying distant Kuiper Belt objects.[9] Emerging designations, such as ISO for interstellar objects, gained prominence with confirmed interstellar visitors like 2I/Borisov (discovered 2019) and 3I/ATLAS (discovered 2025), highlighting hyperbolic paths unbound to the solar system.[10]
Abbreviations
Geocentric Orbit Abbreviations
Geocentric orbit abbreviations refer to standardized shorthand terms used in aerospace engineering and space operations to denote specific types of orbits centered around Earth, facilitating efficient communication in technical documentation and mission planning. These abbreviations primarily describe orbits based on altitude, period, inclination, or synchronization characteristics, all of which are geocentric by definition. They emerged during the mid-20th century space race, with many originating from U.S. satellite programs in the 1950s and 1960s, such as NASA's early communication satellite developments.[4] The abbreviation GEO for Geostationary Orbit, for instance, gained prominence through NASA's Syncom program in the early 1960s, where Syncom 2 (launched in 1963) became the first successful geosynchronous satellite, and Syncom 3 (1964) achieved true geostationary positioning, enabling real-time telecommunications relays.[4] Common misuses include applying LEO to suborbital trajectories, which do not complete full orbits around Earth and thus fall outside orbital classifications. The following table summarizes key geocentric orbit abbreviations, their definitions, and primary parameters:| Abbreviation | Full Name | Definition and Key Parameters |
|---|---|---|
| LEO | Low Earth Orbit | Orbits with altitudes typically ranging from 160 km to 2,000 km above Earth's surface, offering low latency but requiring frequent orbital adjustments due to atmospheric drag.[5] |
| MEO | Medium Earth Orbit | Orbits between approximately 2,000 km and 35,786 km altitude, commonly used for navigation systems like GPS, balancing coverage and signal delay.[5] |
| HEO | Highly Elliptical Orbit | Highly elliptical orbits with apogees exceeding 35,786 km (often much higher), providing extended dwell time over specific regions, such as in Molniya orbits for high-latitude coverage. |
| GSO | Geosynchronous Orbit | Orbits with a sidereal period matching Earth's rotation (23 hours, 56 minutes, 4 seconds), at an average altitude of 35,786 km, appearing fixed relative to Earth's surface from the ground.[6] |
| GEO | Geostationary Orbit | A circular equatorial subset of GSO with zero inclination, maintaining a fixed position over the equator at 35,786 km altitude for continuous regional coverage.[6] |
| SSO | Sun-Synchronous Orbit | Near-polar orbits (inclination ~98°) in the LEO regime where the orbital plane precesses at 0.986° per day to match the Earth's orbital motion around the Sun, ensuring consistent lighting for imaging.[7] |
Non-Geocentric Orbit Abbreviations
Non-geocentric orbit abbreviations refer to shorthand terms used in astronomy and spaceflight for trajectories centered on the Sun, other planets, or regions beyond Earth's immediate gravitational influence, facilitating communication about interplanetary and extrasolar paths. These terms complement geocentric nomenclature by addressing broader solar system dynamics, where orbits are defined relative to the barycenter of the Sun or distant reservoirs of icy bodies. Heliocentric orbits, for instance, describe paths around the Sun with varying semi-major axes, often exceeding 1 AU for outer solar system exploration. The following table lists key abbreviations for non-geocentric orbits, focusing on solar system and interstellar contexts:| Abbreviation | Full Form | Description |
|---|---|---|
| HCO | Heliocentric Orbit | An orbit centered on the Sun, encompassing planetary paths and spacecraft trajectories post-Earth escape, with semi-major axes typically ranging from inner solar system (<1 AU) to outer regions (>1 AU).[8] |
| PCO | Planetocentric Orbit | An orbit around a planet other than Earth, such as Mars or Jupiter, used for planetary missions excluding solar or Earth-centric references.[8] |
| SSE | Solar System Escape | A hyperbolic trajectory escaping the Sun's gravitational influence, achieving interstellar velocities beyond the heliosphere.[8] |
Centric and Altitude Classifications
Centric Classifications
Centric classifications categorize orbits based on the primary gravitating body at the center of the orbit, providing a foundational framework for understanding orbital mechanics across different scales in the universe. These classifications derive from the two-body problem in Newtonian gravity, where the orbit of a smaller body is approximated as an ellipse (or other conic section) around a much more massive central body, governed by the standard gravitational parameter μ = GM, with G as the gravitational constant and M as the mass of the central body. This parameter quantifies the strength of the gravitational field and is essential for calculating orbital elements like semi-major axis and period. For instance, geocentric orbits center on Earth, while broader classifications extend to other celestial bodies or systems.[11] Geocentric orbits are those centered on Earth, encompassing natural satellites like the Moon and artificial ones such as communication and Earth-observation spacecraft. The Earth's standard gravitational parameter is μ = 3.98600435507 × 10^{14} m³ s^{-2}, enabling precise predictions of orbital trajectories within Earth's sphere of influence, approximately 925,000 km in radius. These orbits form the basis for most human space activities, from low-Earth missions to lunar transfers.[11][1] Heliocentric orbits revolve around the Sun, the dominant mass in the solar system, and include the paths of planets, asteroids, and interplanetary probes. The Sun's μ = 1.32712440041279419 × 10^{20} m³ s^{-2} dictates the scale of these orbits, with Earth's orbit serving as a reference at 1 astronomical unit (AU). Such orbits are crucial for missions exploring the outer solar system, where spacecraft like Voyager maintain heliocentric paths after escaping planetary influences.[11][7] Barycentric orbits are defined relative to the solar system's center of mass, or barycenter, which accounts for the collective gravitational pull of the Sun and all planets, shifting its position due to Jupiter's influence but remaining within about 2 solar radii of the Sun's center. Unlike heliocentric approximations that treat the Sun as fixed, barycentric coordinates provide a more accurate inertial reference for deep-space navigation, with the International Celestial Reference System (ICRS) originating at this barycenter. This framework is used in ephemerides for precise trajectory planning in missions beyond Earth's vicinity.[12][13] Areocentric orbits center on Mars, facilitating exploration of the Red Planet and its moons Phobos and Deimos. Mars' μ = 4.2828375816 × 10^{13} m³ s^{-2} results in slower orbital velocities compared to Earth, influencing mission designs like those of the Mars Reconnaissance Orbiter. These orbits operate within Mars' sphere of influence, about 577,000 km, and support landed missions by providing relay capabilities.[11][14] The conceptual shift from geocentric to heliocentric models in the 16th and 17th centuries marked a pivotal evolution in orbital classifications. Nicolaus Copernicus proposed the heliocentric system in his 1543 work De revolutionibus orbium coelestium, arguing that Earth and other planets orbit the Sun, simplifying the geometry over Ptolemy's Earth-centered epicycles. Johannes Kepler refined this in the early 1600s with his three laws of planetary motion, empirically deriving elliptical orbits from Tycho Brahe's observations, thus establishing the Sun as the central body for solar system orbits. This transition laid the groundwork for modern centric classifications, emphasizing the central gravitating body's role.[15][16] In contemporary applications, barycentric orbits exemplify advanced centric classifications for deep-space missions. The James Webb Space Telescope, launched in December 2021, follows a halo orbit around the Sun-Earth L2 Lagrange point, approximately 1.5 million km from Earth, which itself traces a barycentric path within the solar system. This configuration maintains the telescope's alignment with Earth while using barycentric coordinates for navigation, enabling stable infrared observations over its planned 20-year mission.[17][13]Altitude Classifications
Altitude classifications for geocentric orbits divide them based on the altitude above Earth's mean surface, typically measured from the perigee for elliptical paths, influencing factors such as atmospheric interaction, radiation exposure, and mission longevity. Low Earth orbit (LEO) spans altitudes from approximately 160 km to 2,000 km, where satellites experience significant atmospheric drag due to residual air density, necessitating frequent orbital maintenance.[18][7] Medium Earth orbit (MEO) ranges from 2,000 km to 35,786 km, a regime dominated by navigation satellites like the Global Positioning System (GPS) constellation at around 20,200 km altitude, benefiting from reduced drag but increased exposure to radiation. High Earth orbit (HEO) encompasses altitudes above 35,786 km, often involving highly elliptical paths with apogees extending far beyond geosynchronous altitude, suitable for missions requiring prolonged visibility over specific regions.[19][20] In LEO, atmospheric drag is the primary perturbing force, modeled by the drag force equation: where is atmospheric density, is the satellite's velocity, is the drag coefficient, is the cross-sectional area, and is the unit vector in the direction of motion; this force leads to gradual orbital decay, requiring periodic reboosts for sustained operations, as seen with the International Space Station (ISS) at approximately 400 km, which undergoes reboost maneuvers every few months to counteract an average altitude loss of about 100 meters per day.[21][22][23] MEO and HEO orbits traverse the Van Allen radiation belts—inner belt from roughly 1,000 to 6,000 km and outer from 13,000 to 60,000 km—exposing satellites to high-energy protons and electrons that can degrade electronics and solar panels over time, thus demanding robust shielding for long-duration missions. Representative examples include the Hubble Space Telescope in LEO for astronomical observations, GPS satellites in MEO for global navigation, and weather satellites with HEO apogees, such as certain geosynchronous meteorological systems that utilize elliptical paths for extended regional coverage.[7][24] Post-2020 developments have emphasized LEO mega-constellations, exemplified by SpaceX's Starlink, which as of November 2025 has launched over 10,000 satellites, with more than 8,800 operational, primarily at altitudes around 550 km to provide global broadband internet, highlighting intensified drag management challenges and increasing collision risks for large-scale deployments amid rising space traffic.[25]Shape and Orientation Classifications
Eccentricity Classifications
Orbits are classified based on eccentricity , a dimensionless parameter that quantifies the shape of the trajectory relative to a circle, with the central body at one focus of the conic section. A circular orbit features , maintaining a constant radial distance from the central body throughout the motion.[7] Elliptical orbits, characterized by , describe bound, closed paths where the orbiting body varies in distance, approaching closest at perigee and farthest at apogee.[7] Parabolic orbits occur at , marking the threshold of escape where the body has precisely the energy needed to depart to infinity without returning.[7] Hyperbolic orbits, with , represent unbound trajectories where excess kinetic energy allows the body to approach from infinity, interact briefly, and recede indefinitely.[7] These classifications tie directly to the total mechanical energy of the orbit via the vis-viva equation, which gives the speed at any radial distance : Here, is the gravitational constant, the mass of the central body, and the semi-major axis; negative for hyperbolic cases reflects positive energy and unbound motion.[26] Elliptical orbits enable efficient transfers between circular paths, as in the Hohmann maneuver, where eccentricity typically spans 0.1 to 0.7 based on the radial separation of the orbits; for an Earth-to-Mars transfer, .[27][28] Hyperbolic orbits facilitate permanent escapes from the central body's influence, exemplified by Voyager 2's heliocentric trajectory post-Neptune flyby, with .[29] The Molniya orbit, an elliptical type with high , prolongs apogee dwell time over high latitudes for enhanced coverage, originally devised in the Soviet era and planned for use in future GLONASS navigation variants such as GLONASS-V, with deployments expected starting in 2026.[30][31] Eccentricity emerges from conservation of angular momentum in the two-body problem, where the specific angular momentum relates to orbital parameters as for elliptical orbits, with ; solving yields , linking shape to the balance of rotational and radial motion.[26]Inclination Classifications
Orbital inclination, denoted as , measures the angular tilt of an orbit's plane relative to a reference plane, typically the equatorial plane for Earth-centered orbits. It is calculated using the cosine of the angle between the angular momentum vector (where and are the position and velocity vectors) and the reference normal vector , given by .[32] This parameter ranges from 0° to 180°, influencing the orbit's latitudinal coverage and interaction with gravitational perturbations. Orbits are classified by inclination into several types. Equatorial orbits have , lying directly in the reference plane, which maximizes coverage over equatorial regions but limits polar access.[1] Polar orbits feature , allowing satellites to pass over both poles and achieve near-global coverage as Earth rotates beneath them; this is ideal for Earth observation missions like the Landsat series, which uses a near-polar orbit at approximately 98.2° inclination for comprehensive surface imaging.[33] Inclined orbits have for prograde motion (aligned with the reference body's rotation) or for retrograde motion, providing targeted coverage over specific latitude bands.[7] A specialized inclined variant is the sun-synchronous orbit, typically near-polar with , designed so the satellite's orbital plane precesses at a rate matching Earth's revolution around the Sun. This ensures consistent solar illumination angles during repeated passes over the same ground location, crucial for applications in remote sensing and climate monitoring.[7] In low Earth orbit (LEO), inclined orbits experience nodal precession due to Earth's oblateness, primarily the J2 gravitational harmonic, which causes the right ascension of the ascending node to drift at a rate dependent on inclination, semi-major axis, and eccentricity. This perturbation can alter ground track patterns over time, requiring active control for mission longevity.[34] Frozen orbits address stability challenges by selecting specific combinations of inclination and eccentricity that minimize secular variations in argument of perigee and eccentricity, resulting in near-constant altitude profiles despite perturbations. These are particularly valuable for LEO Earth observation CubeSats in the 2020s, such as those in constellations providing daily global imaging, as they reduce fuel needs for station-keeping.[35]Directional Classifications
Directional classifications categorize orbits based on the direction of the orbiting body's motion relative to the rotation of the central body. A prograde orbit occurs when the satellite moves in the same direction as the primary body's rotation, generally corresponding to an orbital inclination below 90 degrees. This alignment leverages the natural spin of the planet, facilitating more efficient orbital insertion for many missions. In contrast, a retrograde orbit features motion opposite to the primary's rotation, typically with an inclination exceeding 90 degrees, which can complicate launches but offers advantages in certain observational geometries.[1] The directional choice significantly influences launch dynamics, particularly the delta-v requirements. For prograde orbits around Earth, launches from eastward trajectories capitalize on the planet's rotational velocity, providing an initial boost that reduces propellant needs. At equatorial sites, this adds approximately 0.465 km/s to the effective velocity, effectively adjusting the launch equation to , where is the desired orbital speed around 7.8 km/s for low Earth orbit. Retrograde orbits, however, launch westward against this rotation, opposing the boost and increasing delta-v by a similar magnitude, often by several hundred meters per second depending on latitude. Prograde orbits dominate artificial satellite deployments due to launch efficiency. The International Space Station, for example, maintains a prograde orbit at 51.6° inclination, enabling routine resupply from multiple launch sites. Retrograde orbits are rarer but employed for specialized applications, such as reconnaissance or Earth observation requiring specific ground tracks. Israel's Ofeq spy satellites, including Ofeq-13 launched in 2023, exemplify this by operating in retrograde orbits to accommodate westward launches from Palmachim Airbase over the Mediterranean for national security. Sun-synchronous satellites like ESA's ERS-1 also utilize slightly retrograde inclinations around 98° to achieve consistent solar lighting for imaging.[37] Retrograde orbits represent high-inclination configurations exceeding 90 degrees, distinguishing them from the degree of tilt emphasized in inclination classifications.Temporal and Special Classifications
Synchronicity Classifications
Synchronicity classifications refer to orbits in which the orbital period of a satellite aligns with the rotational period of the central body, enabling consistent relative positioning over time. These orbits are particularly valuable for applications requiring stable visibility from the surface, such as telecommunications and Earth observation. The defining characteristic is the synchronization of the satellite's orbital period with the body's sidereal rotation, which is the time for one complete rotation relative to distant stars, typically 23 hours, 56 minutes, and 4 seconds for Earth.[7] A geosynchronous orbit (GSO) has an orbital period equal to one sidereal day, causing the satellite to return to the same position in the sky relative to Earth's surface after each orbit.[1] Geostationary orbit (GEO) is a specific subset of GSO that is both circular and equatorial, with zero inclination, resulting in the satellite appearing motionless at a fixed point above the equator.[7] This synchronization is achieved through Kepler's third law, which states that the square of the orbital period is proportional to the cube of the semi-major axis , or .[38] For a GEO, the semi-major axis is approximately 42,164 km from Earth's center, corresponding to an altitude of 35,786 km above the equator.[7] Areosynchronous orbits represent a subtype adapted for Mars, where the orbital period matches Mars' sidereal day of about 24 hours and 37 minutes, enabling similar synchronization benefits for Martian missions. In non-equatorial GSO configurations, satellites experience longitudinal drift rates due to gravitational perturbations, requiring periodic station-keeping maneuvers to maintain position.[7] These orbits are widely used in communications, with fleets like Intelsat's GEO satellites providing global coverage for television broadcasting, internet, and telephony services.[39] Non-zero inclinations in GSO lead to figure-8 shaped ground tracks, as the satellite's path appears to oscillate north-south over the equator while maintaining east-west synchronization.[40] Emerging trends in 2025 include optical GEO systems for laser communications, which leverage the fixed positioning to enable low-latency, high-bandwidth data links between satellites and ground stations, supporting applications in real-time global networking.[41]Special Classifications
Special classifications of orbits encompass unique configurations tailored for particular mission objectives or to address environmental challenges, such as maintaining consistent observational conditions or ensuring post-mission safety. These orbits prioritize functional adaptations like regional coverage optimization or debris avoidance over standard parametric definitions. Sun-synchronous orbits (SSOs) are retrograde, near-polar orbits designed to precess at a rate of 360° per year, aligning the orbital plane's orientation with the Earth's revolution around the Sun to ensure constant local solar time and consistent illumination for Earth-observing satellites.[42] This precession arises primarily from the Earth's oblateness (J2 perturbation), with the nodal precession rate given by where is the second zonal harmonic, is Earth's equatorial radius, is the semi-major axis, is the mean motion, is the inclination, and is the eccentricity; for SSOs, this rate is tuned to approximately -0.9856° per day. Typical SSO altitudes range from 600 to 800 km, enabling applications in remote sensing and meteorology.[7] Molniya orbits represent a highly elliptical, semi-synchronous configuration with an inclination of 63.4° and eccentricity around 0.7, allowing satellites to spend extended periods (up to 8 hours per orbit) at apogee over high northern latitudes for enhanced communications and remote sensing coverage in regions like the Arctic, where geostationary orbits are ineffective.[44] The 12-hour period ensures two orbits per day, with perigee positioned over the southern hemisphere to minimize atmospheric drag.[45] Graveyard orbits serve as disposal regions for end-of-life satellites, particularly those from geostationary missions, by raising them to altitudes exceeding 36,000 km—typically 300 km above the geostationary belt—to prevent collisions with active spacecraft and comply with international mitigation guidelines.[46] This supersynchronous placement ensures long-term stability without interfering with operational slots.[47] Purpose-driven orbits include medium Earth orbits (MEO) for navigation systems like GPS, where satellites at approximately 20,200 km altitude provide global coverage with a 12-hour period and low eccentricity (<0.02) for precise timing signals.[48] In contrast, low Earth orbits (LEO) around approximately 250–1,000 km support reconnaissance missions, as exemplified by the KH-11 satellites, which use sun-synchronous paths for high-resolution, real-time electro-optical imaging.[49] Walker constellations employ delta-i (relative inclination offset) patterns across multiple orbital planes to distribute satellites for uniform global coverage; the Iridium system, for instance, utilizes a Walker Star 86.4°:66/6/2 configuration with 66 active satellites in six planes at 86.4° inclination and 780 km altitude, enhanced by spares for resilience as of 2025.[50] Debris mitigation orbits adhere to standards such as the international 25-year decay rule for LEO missions, mandating that satellites re-enter Earth's atmosphere within 25 years of mission completion to limit long-term population growth and collision risks, often achieved through controlled deorbiting or passive drag enhancement; however, as of 2024, some regulations like the U.S. FCC's require disposal within 5 years for new LEO satellites below 600 km.[51][52] This standard, with a targeted 90% success rate, has proven effective in stabilizing the LEO environment.[53]Advanced Classifications
Multi-Body and Galactic Orbits
In multi-body orbital dynamics, gravitational interactions among three or more significant masses lead to configurations that deviate from simple Keplerian two-body paths, often resulting in stable or quasi-stable resonances and librations.[54] These systems are typically modeled using the restricted three-body problem, where the third body has negligible mass compared to the primary pair, allowing analysis of perturbed orbits around Lagrange points.[54] Key examples include co-orbital configurations like horseshoe and tadpole orbits, which arise in the circular restricted three-body problem and are stabilized by the Jacobi integral, a conserved quantity given by where are coordinates in the rotating frame, and are distances to the primary masses, is the mass ratio, and dots denote velocities; this integral defines forbidden regions and assesses stability.[55] Horseshoe orbits occur when a minor body librates around the primary's orbit in a U-shaped path relative to the line connecting the two massive bodies, spending time on both sides without encircling either.[56] A prominent example is asteroid 3753 Cruithne, a near-Earth object in 1:1 resonance with Earth, completing a full horseshoe cycle every 770 years due to mutual perturbations.[56] In contrast, tadpole orbits involve libration around one of the triangular Lagrange points (L4 or L5), forming a tadpole-like shape ahead or behind the secondary body.[57] Jupiter's Trojan asteroids, numbering over 10,000, predominantly occupy these tadpole orbits at L4 and L5, maintaining stability through the Jacobi integral's constraints over billions of years.[57] Mean-motion resonances provide another multi-body mechanism, where orbital periods align in simple ratios to avoid collisions.[58] Pluto exemplifies this in its 3:2 resonance with Neptune, completing two orbits for every three of Neptune, which keeps their paths separated despite apparent crossings and has preserved stability for over 4 billion years.[58] Galactic orbits describe stellar motions within large-scale structures like the Milky Way, influenced by the distributed mass of stars, gas, and dark matter rather than point masses.[59] In the galactic disk, stars typically follow nearly circular orbits around the center, with speeds determined by the enclosed mass via , where is the central mass concentration and the radial distance.[59] The Sun, at about 8 kpc from the center, orbits at roughly 220 km/s, completing a revolution every 225 million years.[59] Halo stars, however, trace highly eccentric orbits that plunge deep toward the center and extend far outward, often with eccentricities exceeding 0.8, reflecting accretion from disrupted satellite galaxies.[60] The European Space Agency's Gaia mission, positioned in a Lissajous halo orbit around the Sun-Earth L2 point for thermal stability, concluded science operations in January 2025 after delivering data releases including DR3 in 2022, which refined models of galactic dynamics with mappings of halo streams and velocity fields from approximately 1.8 billion sources, primarily stars.[61][62] These observations confirm the eccentric nature of halo populations and their role in tracing the Milky Way's merger history. Extending to exoplanetary systems, the TRAPPIST-1 system features seven Earth-sized planets in a compact multi-body configuration locked in a chain of first-order mean-motion resonances (e.g., 8:5, 5:3, 3:2), which dynamically couple their orbits and enhance long-term stability against perturbations.[63] James Webb Space Telescope observations from 2023 to 2025, including transmission spectroscopy of planets like TRAPPIST-1e, provide constraints on atmospheric retention amid these resonant interactions, suggesting the resonances help mitigate stellar flares' disruptive effects.[63]Pseudo-Orbit Classifications
Pseudo-orbit classifications refer to quasi-equilibrium or librational configurations in multi-body gravitational systems that deviate from classical closed Keplerian ellipses, serving as approximations or stable points in astrodynamics for spacecraft operations. These setups, often analyzed in the restricted three-body problem, include equilibrium points and perturbed paths that balance gravitational and centrifugal forces, enabling prolonged station-keeping with minimal fuel. Unlike bound orbits governed by two-body dynamics, pseudo-orbits are typically unstable or non-periodic in the inertial frame, relying on three-body perturbations for relative stability and requiring active control to prevent drift. Lagrange points, labeled L1 through L5, represent equilibrium positions where a test particle experiences zero net force in the co-rotating frame of two massive bodies. The collinear points L1, L2, and L3 align along the line joining the primaries, with L1 between them, L2 beyond the smaller primary, and L3 opposite the smaller primary; L4 and L5 form equilateral triangular configurations ahead and behind the smaller body. For the collinear points in systems with small mass ratio μ (smaller mass over total), their locations are found by solving the equations of equilibrium numerically. These points arise in the circular restricted three-body problem and extend to elliptical cases with perturbations.[64] The Hill sphere delineates the volume around a secondary body where its gravitational influence prevails over the primary's, defining the practical limit for stable satellite orbits. Its radius is given by , where is the semi-major axis of the secondary's orbit around the primary, the secondary's mass, and the primary's mass; this approximation holds for small mass ratios and circular orbits. In the Earth-Moon system, the Moon's Hill sphere extends roughly 60,000 km from its center, encompassing most lunar satellites.[65] Halo orbits constitute perturbed, periodic librations encircling the collinear Lagrange points L1 or L2 in the synodic frame, forming loop-like paths that avoid eclipsing the primary bodies. These three-dimensional trajectories are inherently unstable, with Lyapunov times on the order of months, necessitating periodic station-keeping thrusts of about 10-50 m/s per year. The Solar and Heliospheric Observatory (SOHO), launched in 1995, exemplifies this application, maintaining a halo orbit around the Sun-Earth L1 point—approximately 1.5 million km from Earth—for continuous solar wind monitoring and imaging of coronal mass ejections.[66][67] Stability near these pseudo-orbits is assessed using Hill's equations, which linearize the variational equations of motion around collinear Lagrange points in the restricted three-body problem, capturing small perturbations from equilibrium. In the lunar context, these equations model the Moon's orbital variations around Earth, revealing unstable modes that decay exponentially and stable oscillatory modes, informing spacecraft trajectory corrections.[68] Distant retrograde orbits (DRO) around the Moon, highly inclined and retrograde relative to the Earth-Moon plane, leverage three-body dynamics for exceptional stability, with perturbations averaging to near-zero drift over years. In the Artemis program, DRO supports extended cislunar missions; the uncrewed Artemis I in 2022 demonstrated this by placing Orion in a lunar DRO spanning approximately 64,000 km (40,000 miles) in apolune with minimal fuel for six days, while the Lunar Gateway station employs a related near-rectilinear halo orbit variant for persistent operations planned for the late 2020s, with assembly starting no earlier than 2028.[69][70]References
- https://science.[nasa](/page/NASA).gov/learn/basics-of-space-flight/chapter14-1/
- https://tfaws.[nasa](/page/NASA).gov/wp-content/uploads/Rickman-Presentation.pdf