Hubbry Logo
Perfect fifthPerfect fifthMain
Open search
Perfect fifth
Community hub
Perfect fifth
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Perfect fifth
Perfect fifth
Perfect fifth
View on Wikipedia
from Wikipedia
Perfect fifth
Equal tempered
Just
perfect fifth
Inverseperfect fourth
Name
Other namesdiapente
AbbreviationP5
Size
Semitones7
Interval class5
Just interval3:2
Cents
12-Tone equal temperament700
Just intonation701.955[1]
The perfect fifth with two strings
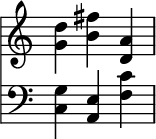
{ << \new Staff \with{ \magnifyStaff #4/3 } \relative c' { \key c \major \clef treble \override Score.TimeSignature #'stencil = ##f \time 3/4 <g' d'> <b fis'> <d, a'> } \new Staff \with{ \magnifyStaff #4/3 } \relative c' { \key c \major \clef bass \override Score.TimeSignature #'stencil = ##f \time 3/4 <c, g'> <a e'> <f' c'> } >> }
Examples of perfect fifth intervals

In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.

In classical music from Western culture, a fifth is the interval from the first to the last of the first five consecutive notes in a diatonic scale.[2] The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C.

The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note.

The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its Greek names, diapente.[3] Its inversion is the perfect fourth. The octave of the fifth is the twelfth.

A perfect fifth is at the start of "Twinkle, Twinkle, Little Star"; the pitch of the first "twinkle" is the root note and the pitch of the second "twinkle" is a perfect fifth above it.

Alternative definitions

[edit]

The term perfect identifies the perfect fifth as belonging to the group of perfect intervals (including the unison, perfect fourth, and octave), so called because of their simple pitch relationships and their high degree of consonance.[4] When an instrument with only twelve notes to an octave (such as the piano) is tuned using Pythagorean tuning, one of the twelve fifths (the wolf fifth) sounds severely discordant and can hardly be qualified as "perfect", if this term is interpreted as "highly consonant". However, when using correct enharmonic spelling, the wolf fifth in Pythagorean tuning or meantone temperament is actually not a perfect fifth but a diminished sixth (for instance G♯–E♭).

Perfect intervals are also defined as those natural intervals whose inversions are also natural, where natural, as opposed to altered, designates those intervals between a base note and another note in the major diatonic scale starting at that base note (for example, the intervals from C to C, D, E, F, G, A, B, C, with no sharps or flats); this definition leads to the perfect intervals being only the unison, fourth, fifth, and octave, without appealing to degrees of consonance.[5]

The term perfect has also been used as a synonym of just, to distinguish intervals tuned to ratios of small integers from those that are "tempered" or "imperfect" in various other tuning systems, such as equal temperament.[6][7] The perfect unison has a pitch ratio 1:1, the perfect octave 2:1, the perfect fourth 4:3, and the perfect fifth 3:2.

Within this definition, other intervals may also be called perfect, for example a perfect third (5:4)[8] or a perfect major sixth (5:3).[9]

Other qualities

[edit]

In addition to perfect, there are two other kinds, or qualities, of fifths: the diminished fifth, which is one chromatic semitone smaller, and the augmented fifth, which is one chromatic semitone larger. In terms of semitones, these are equivalent to the tritone (or augmented fourth), and the minor sixth, respectively.

Pitch ratio

[edit]
Just perfect fifth on D. The perfect fifth above D (A+, 27/16) is a syntonic comma (81/80 or 21.5 cents) higher than the just major sixth above middle C: (A♮, 5/3).[10]
Just perfect fifth below A. The perfect fifth below A (D-, 10/9) is a syntonic comma lower than the just/Pythagorean major second above middle C: (D♮, 9/8).[10]

The justly tuned pitch ratio of a perfect fifth is 3:2 (also known, in early music theory, as a hemiola),[11][12] meaning that the upper note makes three vibrations in the same amount of time that the lower note makes two. The just perfect fifth can be heard when a violin is tuned: if adjacent strings are adjusted to the exact ratio of 3:2, the result is a smooth and consonant sound, and the violin sounds in tune.

Keyboard instruments such as the piano normally use an equal-tempered version of the perfect fifth, enabling the instrument to play in all keys. In 12-tone equal temperament, the frequencies of the tempered perfect fifth are in the ratio or approximately 1.498307. An equally tempered perfect fifth, defined as 700 cents, is about two cents narrower than a just perfect fifth, which is approximately 701.955 cents.

Kepler explored musical tuning in terms of integer ratios, and defined a "lower imperfect fifth" as a 40:27 pitch ratio, and a "greater imperfect fifth" as a 243:160 pitch ratio.[13] His lower perfect fifth ratio of 1.48148 (680 cents) is much more "imperfect" than the equal temperament tuning (700 cents) of 1.4983 (relative to the ideal 1.50). Hermann von Helmholtz uses the ratio 301:200 (708 cents) as an example of an imperfect fifth; he contrasts the ratio of a fifth in equal temperament (700 cents) with a "perfect fifth" (3:2), and discusses the audibility of the beats that result from such an "imperfect" tuning.[14]

Use in harmony

[edit]

W. E. Heathcote describes the octave as representing the prime unity within the triad, a higher unity produced from the successive process: "first Octave, then Fifth, then Third, which is the union of the two former".[15] Hermann von Helmholtz argues that some intervals, namely the perfect fourth, fifth, and octave, "are found in all the musical scales known", though the editor of the English translation of his book notes the fourth and fifth may be interchangeable or indeterminate.[16]

The perfect fifth is a basic element in the construction of major and minor triads, and their extensions. Because these chords occur frequently in much music, the perfect fifth occurs just as often. However, since many instruments contain a perfect fifth as an overtone, it is not unusual to omit the fifth of a chord (especially in root position).

The perfect fifth is also present in seventh chords as well as "tall tertian" harmonies (harmonies consisting of more than four tones stacked in thirds above the root). The presence of a perfect fifth can in fact soften the dissonant intervals of these chords, as in the major seventh chord in which the dissonance of a major seventh is softened by the presence of two perfect fifths.

Chords can also be built by stacking fifths, yielding quintal harmonies. Such harmonies are present in more modern music, such as the music of Paul Hindemith. This harmony also appears in Stravinsky's The Rite of Spring in the "Dance of the Adolescents" where four C trumpets, a piccolo trumpet, and one horn play a five-tone B-flat quintal chord.[17]

Bare fifth, open fifth, or empty fifth

[edit]
{ \set Staff.midiInstrument = "electric guitar (clean)" \omit Score.MetronomeMark \tempo 4=160 \repeat unfold 16 { <e b e'>8-. } \bar "|." }
E5 power chord in eighth notes

A bare fifth, open fifth or empty fifth is a chord containing only a perfect fifth with no third. The closing chords of Pérotin's Viderunt omnes and Sederunt Principes, Guillaume de Machaut's Messe de Nostre Dame, the Kyrie in Mozart's Requiem, and the first movement of Bruckner's Ninth Symphony are all examples of pieces ending on an open fifth. These chords are common in Medieval music, Sacred Harp singing, and throughout rock music. In hard rock, metal, and punk music, overdriven or distorted electric guitar can make thirds sound muddy while the bare fifths remain crisp. In addition, fast chord-based passages are made easier to play by combining the four most common guitar hand shapes into one. Rock musicians refer to them as power chords. Power chords often include octave doubling (i.e., their bass note is doubled one octave higher, e.g. F3–C4–F4).

pacha siku
k'antu

An empty fifth is sometimes used in traditional music, e.g., in Asian music and in some Andean music genres of pre-Columbian origin, such as k'antu and sikuri. The same melody is being led by parallel fifths and octaves during all the piece.

Western composers may use the interval to give a passage an exotic flavor.[18] Empty fifths are also sometimes used to give a cadence an ambiguous quality, as the bare fifth does not indicate a major or minor tonality.

Use in tuning and tonal systems

[edit]

The just perfect fifth, together with the octave, forms the basis of Pythagorean tuning. A slightly narrowed perfect fifth is likewise the basis for meantone tuning.[citation needed]

The circle of fifths is a model of pitch space for the chromatic scale (chromatic circle), which considers nearness as the number of perfect fifths required to get from one note to another, rather than chromatic adjacency.

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Perfect fifth

View on Grokipedia
from Grokipedia
A perfect fifth is a musical interval that spans seven semitones (or half steps) in the , corresponding to a ratio of 3:2 between the two pitches, and is classified as a interval due to its stable and harmonious sound. This interval encompasses five degrees in a major or minor key, such as from to G, and is one of the "perfect" intervals—along with the , fourth, and —that were historically distinguished for their purity in tuning systems. The concept of the perfect fifth traces back to ancient Greek philosophy, particularly attributed to Pythagoras in the 6th century BCE, who reportedly discovered its mathematical basis through observations of vibrating strings or blacksmith hammers producing ratios like 3:2, laying the foundation for Pythagorean tuning where scales are generated by stacking perfect fifths. This tuning system influenced Western music for centuries, emphasizing the interval's role in creating harmonic series approximations. In Western music theory and practice, the perfect fifth serves as a cornerstone of harmony, forming the backbone of power chords in rock and metal, the root-to-fifth structure in triads, and the sequential progression in the circle of fifths, which organizes keys and modulates between them for tonal coherence. Its consonance arises from acoustic principles, where the higher pitch's harmonics align closely with those of the lower, producing minimal beating and a sense of resolution that defines key centers in compositions from classical to contemporary genres.

Fundamentals

Definition

In music theory, the perfect fifth is defined as the interval spanning the first and fifth scale degrees in a major or minor scale. For example, in the key of , it occurs between (the tonic) and G (the dominant). This interval forms a foundational element in Western tonal music, appearing consistently across diatonic scales. The perfect fifth measures exactly seven semitones in and encompasses 7/12 of an . On a musical staff, it is notated as the vertical distance between two notes seven scale steps apart, such as from C4 to G4 in treble clef, where the lower note is placed on the first ledger line below the staff and the upper note on the second line from the bottom. The concept of the perfect fifth originated in around 500 BCE, where identified it as a fundamental consonant interval derived from the harmonic series and incorporated into the structure. This early recognition emphasized its role in establishing basic tonal relationships through simple integer ratios. Unlike imperfect fifths, such as the (enlarged by one ) or diminished fifth (reduced by one ), the perfect fifth maintains a neutral, stable quality without alteration.

Interval Size and Ratio

The perfect fifth in possesses a frequency ratio of 3:2, such that if the lower note has a frequency ff, the upper note has a frequency of 32f\frac{3}{2}f. This ratio arises naturally from the harmonic series produced by vibrating strings or air columns, where the second partial (the first , at 2f2f) and the third partial (at 3f3f) form the interval, with their frequencies in the precise 3:2 proportion. For example, a fundamental of 261.63 Hz (approximating middle C) yields a perfect fifth at approximately 392.44 Hz (approximating G above it). In logarithmic terms, the interval size of a just perfect fifth measures 701.96 cents, derived from the formula 1200log⁡2(32)1200 \log_2 \left( \frac{3}{2} \right), where cents represent equal divisions of the octave on a logarithmic scale. By contrast, in twelve-tone equal temperament, the perfect fifth spans exactly 700 cents (seven semitones), rendering it approximately 1.96 cents narrower than the just intonation version to facilitate modulation across all keys without accumulating errors in the circle of fifths. This tempering distributes the deviation evenly but introduces a subtle flattening relative to the pure 3:2 ratio. Further tempering occurs in meantone tunings, where fifths are narrowed beyond the degree (to about 696.6 cents in quarter-comma meantone) to sharpen major thirds toward their just 5:4 ratio, resulting in most fifths being smaller than 3:2 while one "wolf fifth" becomes significantly expanded (around 737.6 cents) to close the circle. When a fifth deviates from the pure 3:2 ratio, acoustic beats emerge from interference among corresponding partials, with the beat approximating the detuning magnitude; for instance, a 1-cent mistuning produces roughly 0.6 beats per second at typical pitch heights, increasing linearly with greater detuning and minimal at exact intonation.

Musical Characteristics

Consonance and Qualities

The perfect fifth is widely regarded as the second most consonant interval after the in musical , owing to its simple of 3:2, which results in minimal sensory dissonance when the tones are sounded simultaneously. This ranking emerges from neural and psychophysical studies showing robust responses to the perfect fifth, nearly matching those of the and , while surpassing other intervals like the or in pitch salience and stability. In contrast, more complex ratios, such as those in minor seconds or tritones, elicit weaker neural encoding and heightened dissonance. Acoustically, the consonance of the perfect fifth stems from the extensive overlap in the series of its two tones, leading to a low combined complexity and reduced perceptual roughness. When the lower tone's fundamental is at 100 Hz and the upper at 150 Hz, their harmonics align closely (e.g., the third of the lower tone coincides with the second of the upper tone, both at 300 Hz), filling a high of the series and mimicking the structure of unified vocalizations. Theories of sensory dissonance, such as Ernst Terhardt's model, further explain this by quantifying roughness as interference within critical bandwidths; for the perfect fifth, partials are sufficiently spaced to avoid significant beating, yielding near-zero dissonance values independent of musical context. Compared to other perfect intervals, the perfect fifth is more stable than the (ratio 4:3), though less pure than the or , due to its simpler prime factors and greater conformity. Dissonance models assign the perfect fifth a lower tension value than the , reflecting fewer mismatched overtones and stronger fusion in auditory processing. This positions the fifth as a foundational element of stability, bridging the purity of octaves with the relative openness of fourths. Psychologically, the perfect fifth evokes a sense of tension resolution, as demonstrated in studies of chord progressions where its appearance reduces perceived instability through subharmonic convergence, correlating strongly (r = 0.922) with listener ratings of consonance and closure. For instance, transitions involving perfect fifths, such as in dominant-to-tonic motions, trigger neural periodicity detection that enhances emotional release, a pattern observed in both musicians and non-musicians. Cross-cultural ethnomusicological research supports a partial universality in recognizing the perfect fifth's consonance, with preferences evident in groups exposed to Western tonal music but absent in isolated highland communities, suggesting a blend of innate auditory tuning and cultural familiarity. Large-scale analyses of global song databases reveal frequent use of the perfect fifth across diverse traditions, indicating convergent evolutionary roles in signaling social cohesion. Without a third, the perfect fifth feels open or ambiguous, as it lacks the major or minor coloration that defines tonal quality, often termed a bare fifth in perceptual terms. This incompleteness arises from the interval's neutrality, allowing it to support multiple harmonic interpretations without resolving to a specific mode.

Bare, Open, or Empty Fifth

A bare fifth, also referred to as an open fifth or empty fifth, consists of the perfect fifth interval presented as a simple dyad, without the inclusion of a third or any other pitches that would imply a fuller triad. This configuration emphasizes the interval's inherent consonance while stripping away modal or tonal specificity. Historically, bare fifths featured prominently in medieval from the 9th to 12th centuries, where parallel motion at the perfect fifth was added to melodies to create early , as documented in treatises like those attributed to Hucbald. This technique, known as parallel , produced a stark, resonant texture that reinforced the chant's solemnity without introducing dissonance. In the , the bare fifth reemerged in through power chords—distorted guitar dyads of root and fifth—pioneered in the by bands like The Who, whose aggressive use in tracks such as "" (1965) drove the raw energy of and styles. The primary advantages of the bare fifth lie in its structural simplicity and interpretive flexibility. Lacking a third, it generates ambiguity between major and minor modes, enabling melodic lines or surrounding harmonies to imply either quality without commitment, a trait particularly valued in rock for maintaining modal openness amid distortion. In polyphonic contexts like medieval organum, parallel bare fifths simplified voice leading by relying on consonant motion, circumventing the complexities of contrary motion or dissonant intervals that later became standard in Renaissance counterpoint. Additionally, this dyad enhances rhythmic propulsion in genres like rock, where the unadorned interval cuts through dense instrumentation to underscore beats and riffs. Notable examples illustrate the bare fifth's versatility across eras. The iconic riff in Deep Purple's "Smoke on the Water" (1972) relies on sequential power chords (G5 to Bb5 to C5), delivering a memorable, -driven groove that exemplifies the interval's punchy reinforcement in . In Baroque organ repertoire, Johann Sebastian Bach utilized open fifths over pedal points to anchor harmonic progressions, as in the sustained root-fifth dyads supporting the variations in the and in C minor, BWV 582, where they provide a grounded, resonant bass amid upper-voice flux. Acoustically, the dyadic perfect fifth bolsters the perception of the individual fundamentals of its two notes through close alignment in the harmonic series—the upper note's fundamental aligns closely in the harmonic series with the lower note's partials, sharing harmonics such as the third partial of the lower with the second of the upper, creating reinforcement without the spectral interference or "clutter" that additional tones, such as a third, might introduce in fuller chords. This purity contributes to its timeless appeal in minimalistic settings, from ancient parallel to amplified rock.

Applications

Role in Harmony

In Western tonal music, the perfect fifth forms the foundational interval in triads, extending from the to the fifth and providing essential structural support. In a major triad, this perfect fifth combines with a major third between the root and third, resulting in a bright, stable sonority; for example, in a C major triad (C-E-G), the fifth spans C to G. Similarly, the minor triad features the same perfect fifth paired with a minor third, yielding a darker quality, as in the A minor triad (A-C-E) where A to E defines the interval. The perfect fifth also plays a key role in dominant seventh chords, appearing between the root and fifth of the V7 chord, which drives resolution in the V-I cadence central to tonal harmony. During this progression, the root and fifth of the V7 typically resolve in similar motion to form an in the tonic triad, reinforcing closure; for instance, in the key of , the G-D perfect fifth in the chord (G-B-D-F) moves to C-C. This resolution underscores the perfect fifth's contribution to tension and release. In , 18th-century guidelines, as codified by in , prohibit parallel perfect fifths between voices to preserve melodic independence and contrapuntal texture. Instead, smooth progressions favor contrary or oblique motion involving the fifth, ensuring varied intervallic relationships across harmonic changes. The perfect fifth imparts harmonic stability, acting as skeletal support in root-position triads and persisting in inversions and suspensions during the from Bach to Beethoven. In first inversion (third in bass), the fifth remains an upper voice for consonance, while second inversion (fifth in bass) offers temporary instability resolved by progression to root position; Bach's chorales and Beethoven's symphonic developments frequently employ these configurations to build tension and resolution around the fifth's framework. Compound intervals, such as the (a plus an ), function equivalently to the simple perfect fifth in contexts, as the added octave does not alter the core intervallic identity or stability. In modern extensions, voicings often incorporate the perfect fifth above root or guide tones (third and seventh) for added color and resonance, particularly in dominant and extended chords. In atonal and post-tonal music, stacks of perfect fifths create quintal , generating tension through non-tertian structures, as exemplified in Béla Bartók's No. 2.

Usage in Tuning and Tonal Systems

In , the scale is constructed by stacking successive pure perfect fifths with a frequency ratio of 3:2, resulting in a chain of twelve such intervals that spans slightly more than seven octaves, creating the —a discrepancy of the ratio 531441:524288 between the final note and the expected octave equivalent. This tuning system, attributed to , was employed in for tuning tetrachords and forming scales, and it remained the standard in medieval European from the 9th to the 14th centuries, emphasizing consonant fifths and fourths in compositions by figures like and Machaut. Just intonation employs pure 3:2 perfect fifths as foundational intervals within modal structures, allowing for highly consonant harmonies in fixed keys but proving impractical for frequent transpositions due to accumulating discrepancies in interval purity across different modes. This system has historical roots in medieval practices and was revived in the 20th-century movement, particularly in vocal traditions where singers naturally adjust to pure intervals for enhanced timbral clarity, as seen in ensembles like the Deller Consort. In twelve-tone (12-TET), the perfect fifth is tempered to exactly 700 cents—slightly narrower than the just 3:2 interval of approximately 701.96 cents—to divide the into twelve equal semitones, a system mathematically defined by Francisco Salinas in 1577 and increasingly adopted for keyboard instruments from the onward. This compromise enables seamless modulation across all keys without dissonant "wolf" intervals, facilitating the chromatic explorations in by composers such as J.S. Bach. Meantone temperaments, prevalent from the 16th to 19th centuries, produce "sweet" major thirds by narrowing the perfect fifth below the Pythagorean size; for instance, quarter-comma meantone tempers each fifth by one-quarter of the (approximately 696 cents), prioritizing consonant triads over pure fifths. Well-temperaments like Werckmeister III (1691) and Kirnberger III (late ) further distribute tempering unevenly across the fifths—narrowing some by one-quarter comma while widening others—to allow modulation in most keys with varying degrees of consonance, bridging meantone purity and versatility. In non-Western tonal systems, the perfect fifth appears with slight variations from the 3:2 ratio to suit modal frameworks; in , the shuddha pancham serves as the pure fifth above the tonic shadja in sruti-based tunings, integral to ragas like Bilawal for establishing modal stability. Similarly, Arabic maqam scales incorporate a near-perfect fifth (often around 700-702 cents) as a structural pillar within microtonal jins, though flexible intonation allows subtle adjustments for expressive nuance in performance. Modern digital tuning, as standardized in the MIDI protocol, defaults to 12-TET with perfect fifths at 700 cents for and sequencer compatibility, approximating just intervals through equal division while supporting custom scalings via the MIDI Tuning Standard for more precise realizations in software like . This enables to emulate historical tunings or dynamically, though approximations can introduce beating in pure fifth contexts unless retuned.

References

  1. https://www.musictheory.net/lessons/31
  2. https://www.phys.uconn.edu/~gibson/Notes/Section3_2/Sec3_2.htm
  3. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/11-intervals/
  4. https://fiveable.me/key-terms/ap-music-theory/perfect-fifth
  5. https://courses.lumenlearning.com/suny-musicappreciationtheory/chapter/pythagoras/
  6. https://www.uwlax.edu/globalassets/offices-services/urc/jur-online/pdf/2011/hammond.mth.pdf
  7. https://online.berklee.edu/takenote/circle-of-fifths-the-key-to-unlocking-harmonic-understanding/
  8. https://www.beyondmusictheory.org/the-close-relationship-between-tonic-and-fifth
  9. https://www.britannica.com/art/fifth-music
  10. https://musictheory.pugetsound.edu/mt21c/HowToIdentifyIntervals.html
  11. https://plato.stanford.edu/entries/hist-westphilmusic-to-1800/
  12. https://eamusic.dartmouth.edu/~larry/published_articles/divisions_of_the_tetrachord/chapter2.pdf
  13. https://tuning.ableton.com/glossary/intervals/perfect-fifth/
  14. https://web.uniarts.fi/akustiikka/index9abc.html?id=39&la=en
  15. https://sengpielaudio.com/calculator-centsratio.htm
  16. https://www.britannica.com/art/equal-temperament
  17. http://www.tonalsoft.com/enc/w/wolf.aspx
  18. https://link.springer.com/article/10.3758/BF03206236
  19. https://pmc.ncbi.nlm.nih.gov/articles/PMC2804402/
  20. https://www.pnas.org/doi/10.1073/pnas.1505768112
  21. https://pmc.ncbi.nlm.nih.gov/articles/PMC4568680/
  22. https://www.apa.org/pubs/journals/features/xge-a0030830.pdf
  23. http://music.psych.cornell.edu/articles/reviews/Music_psychology-_Tonal_structures_in_perception_and_memory.pdf
  24. https://pmc.ncbi.nlm.nih.gov/articles/PMC7006947/
  25. https://pmc.ncbi.nlm.nih.gov/articles/PMC7350922/
  26. https://www.pnas.org/doi/10.1073/pnas.1414495112
  27. https://www.musictheoryacademy.com/understanding-music/intervals/perfect-fifth/
  28. https://www.academia.edu/112553755/Semitic_music_theory
  29. https://www.jstor.org/stable/738461
  30. https://www.jstor.org/stable/3686161
  31. https://apps.aoi.wsu.edu/onlineMedia/transcripts/mus262_17_v%28c132%29.pdf
  32. https://www.jstor.org/stable/853641
  33. https://digitalcollections.lipscomb.edu/cgi/viewcontent.cgi?article=1273&context=jmtp
  34. https://ecommons.cornell.edu/bitstreams/54fb6dc3-699a-4722-a35f-2b844a47b36e/download
  35. https://open.lib.umn.edu/musiccomposition/chapter/common-practice-era-chord-qualities/
  36. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/13-triads/
  37. https://milnepublishing.geneseo.edu/fundamentals-function-form/chapter/19-the-dominant-seventh-chord/
  38. https://musictheory.pugetsound.edu/mt21c/SpeciesCounterpoint.html
  39. https://musictheory.pugetsound.edu/mt21c/JazzChordVoicings.html
  40. https://musictheory.pugetsound.edu/mt21c/QuintalHarmony.html
  41. http://www.medieval.org/emfaq/harmony/pyth4.html
  42. http://www.medieval.org/emfaq/harmony/pyth.html
  43. https://www.musicandpractice.org/volume-1/intonation-neue-vocalsolisten-stuttgart/
  44. https://archive.org/download/tuningtemperamen00barb/tuningtemperamen00barb.pdf
  45. https://www.kylegann.com/histune.html
  46. http://www.colinpykett.org.uk/handy-guide-to-choosing-temperaments.htm
  47. https://ccrma.stanford.edu/~arvindh/cmt/the_12_notes.html
  48. https://www.academia.edu/8223346/Arabic_maqam
  49. https://www.dynamictonality.com/about.htm
  50. https://www.jstor.org/stable/26777136
Add your contribution
Related Hubs
User Avatar
No comments yet.