Hubbry Logo
RefractionRefractionMain
Open search
Refraction
Community hub
Refraction
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Refraction
Refraction
Refraction
View on Wikipedia
from Wikipedia

A ray of light being refracted in a plastic block

In physics, refraction is the redirection of a wave as it passes from one medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium.[1] Refraction of light is the most commonly observed phenomenon, but other waves such as sound waves and water waves also experience refraction. How much a wave is refracted is determined by the change in wave speed and the initial direction of wave propagation relative to the direction of change in speed.

Optical prisms and lenses use refraction to redirect light, as does the human eye. The refractive index of materials varies with the wavelength of light,[2] and thus the angle of the refraction also varies correspondingly. This is called dispersion and allows prisms[3] and raindrops in rainbows[4] to divide white light into its constituent spectral colors.

Law

[edit]
Refraction of light at the interface between two media of different refractive indices, with n2 > n1. Since the phase velocity is lower in the second medium (v2 < v1), the angle of refraction θ2 is less than the angle of incidence θ1; that is, the ray in the higher-index medium is closer to the normal.

For light, refraction follows Snell's law, which states that, for a given pair of media, the ratio of the sines of the angle of incidence and angle of refraction is equal to the ratio of phase velocities in the two media, or equivalently, to the refractive indices of the two media:[5]


A pen partially submerged in a bowl of water appears bent due to refraction at the water surface.

General explanation

[edit]
When a wave moves into a slower medium the wavefronts get compressed. For the wavefronts to stay connected at the boundary the wave must change direction.

Refraction involves two related parts, both a result of the wave nature of light: a reduced speed in an optical medium and a change in angle when a wave front crosses between different media at an angle.

  1. Light slows as it travels through a medium other than vacuum (such as air, glass or water). This is not because of scattering or absorption. Rather it is because, as an electromagnetic oscillation, light itself causes other electrically charged particles such as electrons, to oscillate. The oscillating electrons emit their own electromagnetic waves which interact with the original light. The resulting combined wave has a lower speed. When light returns to a vacuum and there are no electrons nearby, this slowing effect ends and its speed returns to c.
  2. When light enters a slower medium at an angle, one side of the wavefront is slowed before the other. This asymmetrical slowing of the light causes it to change the angle of its travel. Once light is within the new medium with constant properties, it travels in a straight line again.

Slowing of light

[edit]

As described above, the speed of light is slower in a medium other than vacuum. This slowing applies to any medium such as air, water, or glass, and is responsible for phenomena such as refraction. On the other side of the medium its speed will again be the speed of light in vacuum, c.

A correct explanation rests on light's nature as an electromagnetic wave.[6] Because light is an oscillating electrical/magnetic wave, light traveling in a medium causes the electrically charged electrons of the material to also oscillate. (The material's protons also oscillate but as they are around 2000 times more massive, their movement and therefore their effect, is far smaller). A moving electrical charge emits electromagnetic waves of its own. The electromagnetic waves emitted by the oscillating electrons interact with the electromagnetic waves that make up the original light, similar to water waves on a pond, a process known as constructive interference. When two waves interfere in this way, the resulting "combined" wave may have wave packets that pass an observer at a slower rate. The light has effectively been slowed. When the light leaves the material, this interaction with electrons no longer happens, and therefore the wave packet rate (and therefore its speed) return to normal.

Bending of light

[edit]

Consider a wave going from one material to another where its speed is slower as in the figure. If it reaches the interface between the materials at an angle one side of the wave will reach the second material first, and therefore slow down earlier. With one side of the wave going slower the whole wave will pivot towards that side. This is why a wave will bend away from the surface or toward the normal when going into a slower material. In the opposite case of a wave reaching a material where the speed is higher, one side of the wave will speed up and the wave will pivot away from that side.

Another way of understanding the same thing is to consider the change in wavelength at the interface. When the wave goes from one material to another where the wave has a different speed v, the frequency f of the wave will stay the same, but the distance between wavefronts or wavelength λ = v/f will change. If the speed is decreased, such as in the figure to the right, the wavelength will also decrease. With an angle between the wave fronts and the interface and change in distance between the wave fronts the angle must change over the interface to keep the wave fronts intact. From these considerations the relationship between the angle of incidence θ1, angle of transmission θ2 and the wave speeds v1 and v2 in the two materials can be derived. This is the law of refraction or Snell's law and can be written as[7]

The phenomenon of refraction can in a more fundamental way be derived from the 2 or 3-dimensional wave equation. The boundary condition at the interface will then require the tangential component of the wave vector to be identical on the two sides of the interface.[8] Since the magnitude of the wave vector depend on the wave speed this requires a change in direction of the wave vector.

The relevant wave speed in the discussion above is the phase velocity of the wave. This is typically close to the group velocity which can be seen as the truer speed of a wave, but when they differ it is important to use the phase velocity in all calculations relating to refraction.

A wave traveling perpendicular to a boundary, i.e. having its wavefronts parallel to the boundary, will not change direction even if the speed of the wave changes.

Dispersion of light

[edit]
Rainbows are formed by dispersion of light, in which the refraction angle depends on the light's frequency.

Refraction is also responsible for rainbows and for the splitting of white light into a rainbow-spectrum as it passes through a glass prism. Glass and water have higher refractive indexes than air. When a beam of white light passes from air into a material having an index of refraction that varies with frequency (and wavelength), a phenomenon known as dispersion occurs, in which different coloured components of the white light are refracted at different angles, i.e., they bend by different amounts at the interface, so that they become separated. The different colors correspond to different frequencies and different wavelengths.

On water

[edit]
A pencil part immersed in water looks bent due to refraction: the light waves from X change direction and so seem to originate at Y.

Refraction occurs when light goes through a water surface since water has a refractive index of 1.33 and air has a refractive index of about 1. Looking at a straight object, such as a pencil in the figure here, which is placed at a slant, partially in the water, the object appears to bend at the water's surface. This is due to the bending of light rays as they move from the water to the air. Once the rays reach the eye, the eye traces them back as straight lines (lines of sight). The lines of sight (shown as dashed lines) intersect at a higher position than where the actual rays originated. This causes the pencil to appear higher and the water to appear shallower than it really is.

The depth that the water appears to be when viewed from above is known as the apparent depth. This is an important consideration for spearfishing from the surface because it will make the target fish appear to be in a different place, and the fisher must aim lower to catch the fish. Conversely, an object above the water has a higher apparent height when viewed from below the water. The opposite correction must be made by an archer fish.[9]

For small angles of incidence (measured from the normal, when sin θ is approximately the same as tan θ), the ratio of apparent to real depth is the ratio of the refractive indexes of air to that of water. But, as the angle of incidence approaches 90°, the apparent depth approaches zero, albeit reflection increases, which limits observation at high angles of incidence. Conversely, the apparent height approaches infinity as the angle of incidence (from below) increases, but even earlier, as the angle of total internal reflection is approached, albeit the image also fades from view as this limit is approached.

An image of the Golden Gate Bridge is refracted and bent by many differing three-dimensional drops of water.

Atmospheric

[edit]
Main article: Atmospheric refraction
Comparison of inferior and superior mirages due to differing air refractive indices, n
The sun appears slightly flattened when close to the horizon due to refraction in the atmosphere.

The refractive index of air depends on the air density and thus vary with air temperature and pressure. Since the pressure is lower at higher altitudes, the refractive index is also lower, causing light rays to refract towards the earth surface when traveling long distances through the atmosphere. This shifts the apparent positions of stars slightly when they are close to the horizon and makes the sun visible before it geometrically rises above the horizon during a sunrise.

Heat haze in the engine exhaust above a diesel locomotive

Temperature variations in the air can also cause refraction of light. This can be seen as a heat haze when hot and cold air is mixed e.g. over a fire, in engine exhaust, or when opening a window on a cold day. This makes objects viewed through the mixed air appear to shimmer or move around randomly as the hot and cold air moves. This effect is also visible from normal variations in air temperature during a sunny day when using high magnification telephoto lenses and is often limiting the image quality in these cases. [10] In a similar way, atmospheric turbulence gives rapidly varying distortions in the images of astronomical telescopes limiting the resolution of terrestrial telescopes not using adaptive optics or other techniques for overcoming these atmospheric distortions.

Mirage over a hot road

Air temperature variations close to the surface can give rise to other optical phenomena, such as mirages and Fata Morgana. Most commonly, air heated by a hot road on a sunny day deflects light approaching at a shallow angle towards a viewer. This makes the road appear reflecting, giving an illusion of water covering the road.

In eye care

[edit]

In medicine, particularly optometry, ophthalmology and orthoptics, refraction (also known as refractometry) is a clinical test in which a phoropter may be used by the appropriate eye care professional to determine the eye's refractive error and the best corrective lenses to be prescribed. A series of test lenses in graded optical powers or focal lengths are presented to determine which provides the sharpest, clearest vision.[11] Refractive surgery is a medical procedure to treat common vision disorders.

Mechanical waves

[edit]

Water

[edit]
Main article: Water wave refraction
Water waves are almost parallel to the beach when they hit it because they gradually refract towards land as the water gets shallower.

Water waves travel slower in shallower water. This can be used to demonstrate refraction in ripple tanks and also explains why waves on a shoreline tend to strike the shore close to a perpendicular angle. As the waves travel from deep water into shallower water near the shore, they are refracted from their original direction of travel to an angle more normal to the shoreline.[12]

Sound

[edit]
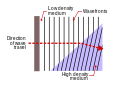
Main article: Refraction (sound)

In underwater acoustics, refraction is the bending or curving of a sound ray that results when the ray passes through a sound speed gradient from a region of one sound speed to a region of a different speed. The amount of ray bending is dependent on the amount of difference between sound speeds, that is, the variation in temperature, salinity, and pressure of the water.[13] Similar acoustics effects are also found in the Earth's atmosphere. The phenomenon of refraction of sound in the atmosphere has been known for centuries.[14] Beginning in the early 1970s, widespread analysis of this effect came into vogue through the designing of urban highways and noise barriers to address the meteorological effects of bending of sound rays in the lower atmosphere.[15]

[edit]
2D simulation: refraction of a wave packet from a potential step. The black half of the background is zero potential, the gray half is a higher potential. White blur represents the probability distribution of finding a particle in a given place if measured.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Refraction

View on Grokipedia
from Grokipedia
Refraction is the change in direction of a wave, such as or , as it passes obliquely from one medium to another in which its speed is different, resulting in a of the wave's path. This occurs because the wave's changes at the interface between the two media, causing the to alter its orientation. In , refraction primarily refers to the behavior of electromagnetic waves, particularly visible , when transitioning between materials with different optical densities. The extent of bending in refraction is quantitatively described by , which states that the product of the of the first medium and the sine of the angle of incidence equals the product of the of the second medium and the sine of the . The (n) of a medium is defined as the ratio of the in a to its speed in that medium, serving as a measure of how much the material slows down light propagation. For example, air has a close to 1, while is approximately 1.33 and around 1.5, leading to noticeable bending when light enters these substances from air. When light travels from a medium with a higher to one with a lower index at an angle greater than the critical angle, occurs instead of refraction, which is fundamental to devices like fiber optics. Refraction plays a crucial role in numerous optical applications, enabling the design of lenses that focus light for vision correction in eyeglasses and contact lenses, as well as in cameras, microscopes, and telescopes. In telecommunications, it underpins the guiding of light signals through optical fibers, where total internal reflection maintains signal integrity over long distances. Atmospheric refraction, caused by varying air density, affects astronomical observations by bending starlight, influencing the apparent positions of celestial bodies. Additionally, refraction is essential in medical imaging techniques, such as ophthalmology for assessing eye refraction errors, and in scientific instruments for precise light manipulation.

Fundamentals

Definition

Refraction is the change in direction of a propagating wave that results from a change in its transmission speed upon passing from one medium to another. This phenomenon occurs for various types of waves, including electromagnetic waves such as light and mechanical waves like sound or water waves, provided the wave encounters a boundary between media with different wave speeds. The bending happens only when the wave approaches the interface at an oblique angle; if incident normally, the wave continues straight without deviation. For wave propagation across such boundaries, the frequency ff of the wave remains invariant, as it is determined by the source and conserved across the interface. However, the speed vv changes due to the medium's properties, such as density or elasticity for mechanical waves, or permittivity and permeability for electromagnetic waves. Consequently, the wavelength λ\lambda adjusts to maintain the fundamental relation v=fλv = f \lambda, resulting in a shorter wavelength in a medium where the wave slows down and a longer one where it speeds up. The phenomenon of refraction was first observed and qualitatively described by scholars, with Claudius providing detailed accounts in his work around 150 AD, including experimental attempts to measure the bending of light rays. 's descriptions focused on visual effects and rudimentary tables of angles, marking an early systematic study. Although earlier attempts existed, including approximate tables by , the precise quantitative relationship was first established by Ibn Sahl in the and rediscovered in the through experiments by Willebrord Snell, later known as . A basic ray diagram for refraction depicts an incident ray striking the boundary between two media at an θi\theta_i to (a line perpendicular to the interface), bending to a refracted ray at θr\theta_r, while remains unchanged. The diagram typically shows the incident ray approaching from the first medium, the straight normal at the point of incidence, and the refracted ray departing into the second medium, illustrating the directional change without altering the wave's overall path if normal incidence occurs.

Snell's Law

Snell's law, also known as the law of refraction, describes the relationship between the angles of incidence and refraction for a light ray passing from one medium to another. It states that the product of the of the first medium and the sine of the angle of incidence equals the product of the of the second medium and the sine of of refraction:
n1sin⁡θ1=n2sin⁡θ2n_1 \sin \theta_1 = n_2 \sin \theta_2
where n1n_1 and n2n_2 are the of the respective media, θ1\theta_1 is the angle between the incident ray and to the interface, and θ2\theta_2 is between the refracted ray and . The refractive index nn of a medium is defined as the ratio of the in cc to the in that medium vv:
n=cv.n = \frac{c}{v}.
This quantity is dimensionless and greater than or equal to 1 for all media, with air having an approximate value of n≈1n \approx 1 under standard conditions. Snell's law can be derived from Fermat's principle, which posits that light travels along the path that minimizes the travel time between two points. Consider a light ray crossing a planar interface from medium 1 (speed v1=c/n1v_1 = c/n_1) to medium 2 (speed v2=c/n2v_2 = c/n_2). The time of travel tt for a path parameterized by the point of incidence is t=l1v1+l2v2t = \frac{l_1}{v_1} + \frac{l_2}{v_2}, where l1l_1 and l2l_2 are the path lengths in each medium. Minimizing tt with respect to the lateral displacement at the interface yields sin⁡θ1v1=sin⁡θ2v2\frac{\sin \theta_1}{v_1} = \frac{\sin \theta_2}{v_2}, or equivalently n1sin⁡θ1=n2sin⁡θ2n_1 \sin \theta_1 = n_2 \sin \theta_2. Alternatively, the law follows from the continuity of wave fronts across the interface using Huygens' principle, ensuring phase matching at the boundary. When light travels from a medium with higher n1n_1 to one with lower n2<n1n_2 < n_1, a critical angle θc\theta_c exists beyond which no refraction occurs into the second medium. This critical angle is given by
sin⁡θc=n2n1,\sin \theta_c = \frac{n_2}{n_1},
derived by setting θ2=90∘\theta_2 = 90^\circ in Snell's law. For incident angles θ1>θc\theta_1 > \theta_c, occurs, with the light entirely reflected back into the first medium at an angle equal to the incident angle, following the law of reflection. A common example is light passing from air (n1≈1n_1 \approx 1) to glass (n2≈1.5n_2 \approx 1.5). For an incident angle of θ1=30∘\theta_1 = 30^\circ, the refracted angle is θ2=arcsin⁡(sin⁡30∘1.5)≈19.5∘\theta_2 = \arcsin\left(\frac{\sin 30^\circ}{1.5}\right) \approx 19.5^\circ. Conversely, from glass to air, the critical angle is θc=arcsin⁡(11.5)≈41.8∘\theta_c = \arcsin\left(\frac{1}{1.5}\right) \approx 41.8^\circ, above which total internal reflection takes place.

Light Refraction

Mechanism of Bending

Refraction occurs when a wave passes from one medium to another with a different , causing the wave front to change direction due to a variation in propagation speed. According to Huygens' principle, every point on an advancing wave front serves as a source of secondary spherical wavelets, and the new wave front is the tangent envelope of these wavelets. In refraction, the differential speed between media leads to an asymmetric expansion of these wavelets: those entering the slower medium lag behind, resulting in an oblique propagation of the overall wave front and bending of the ray. Light travels more slowly in denser media, such as glass compared to air, because the electromagnetic wave interacts with the atoms or molecules, inducing oscillations that re-radiate secondary waves. These re-radiated waves interfere constructively with the incident wave in the forward direction but introduce a phase delay, effectively reducing the phase velocity of the light. The refractive index n=c/vn = c / v, where cc is the speed in vacuum and vv is the speed in the medium, quantifies this slowdown, with higher nn indicating stronger interactions and greater delay. In ray optics, the incident ray strikes the interface at an angle, and upon entering a medium with higher refractive index, the refracted ray bends toward the normal (the perpendicular to the interface), while in a lower index medium, it bends away from the normal. This directional change maintains the continuity of the wave front across the boundary. At normal incidence, where the ray is perpendicular to the interface, no bending occurs despite the speed change, as the wave front advances uniformly. The resulting angular relationship, described by Snell's law, emerges directly from this mechanism of speed variation and wave front reconstruction. From a quantum perspective, consists of , each carrying E=hfE = h f (where hh is Planck's constant and ff is ) and p=E/vp = E / v, with vv the speed in the medium. During refraction, a photon's —and thus —remains constant to conserve at the interface, but its magnitude changes with the speed alteration. The component of parallel to the interface is conserved, ensuring the photon adjusts its direction to satisfy this condition, analogous to a particle while preserving parallel .

Dispersion

Dispersion refers to the variation of the of a medium with the of , causing different s to refract at slightly different angles. In most transparent media, such as or , the refractive index n(λ)n(\lambda) decreases as the λ\lambda increases, a behavior known as normal dispersion. This dependence arises from the interaction of electromagnetic waves with the electrons in the material, leading to greater bending for shorter s (like blue light) compared to longer ones (like red light). As a result, white passing through such media separates into its constituent colors, producing a . An empirical relation often used to approximate this normal dispersion in the visible range is Cauchy's equation: n(λ)=A+Bλ2,n(\lambda) = A + \frac{B}{\lambda^2}, where AA and BB are material-specific constants determined experimentally, with AA representing the refractive index at infinite wavelength and BB accounting for the dispersive contribution. This simple two-term form provides a good fit for many optical glasses away from absorption regions, though more complex models like the Sellmeier equation are used for broader spectral ranges. For example, in crown glass, typical values are A≈1.51A \approx 1.51 and B≈0.0068 μm2B \approx 0.0068 \, \mu \mathrm{m}^2, yielding refractive indices around 1.52 for yellow light. In prisms, this wavelength dependence manifests as angular dispersion, the spread in deviation angles between different colors. For a thin prism with apex angle AA, the deviation for a given wavelength is approximately δ(λ)=(n(λ)−1)A\delta(\lambda) = (n(\lambda) - 1) A, so the angular separation between blue and red light is δb−δr=(nb−nr)A\delta_b - \delta_r = (n_b - n_r) A. The dispersive power ω\omega, a material property measuring the relative dispersion, is defined as ω=nb−nrμ−1\omega = \frac{n_b - n_r}{\mu - 1}, where μ\mu is the mean refractive index (often for yellow light), typically ranging from 0.008 for low-dispersion crown glass to 0.017 for flint glass. This quantifies how effectively the material separates colors without excessive mean deviation. A prominent natural example of dispersion is the formation of rainbows, where refracts, reflects, and disperses within spherical droplets in the atmosphere. In the primary rainbow, each droplet causes one internal reflection, with dispersion separating the colors such that appears on the outer edge (deviation about 42°) and violet on the inner edge (about 40°), forming an arc centered on the . The secondary rainbow, fainter and higher in the sky, results from two internal reflections, reversing the color order ( inner, violet outer) with a larger deviation of about 51°. These phenomena require droplets of roughly 0.1–1 mm diameter and are observable when the sun is low. Anomalous dispersion occurs in rare cases near regions of strong absorption, such as atomic lines or molecular bands, where the increases with (dn/dλ>0dn/d\lambda > 0). Here, the usual order of colors reverses, with longer wavelengths bending more than shorter ones, though this regime is accompanied by high absorption and limited transparency. This effect is described by the Kramers-Kronig relations linking real and imaginary parts of the dielectric function and is observed in gases like sodium vapor near the yellow D-lines or in certain dyed glasses.

Natural Phenomena

Atmospheric Refraction

Atmospheric refraction occurs due to the gradual variation in the of air with altitude, primarily caused by the decrease in air as increases. The of air near is approximately 1.0003 under standard conditions, but it diminishes toward 1 at higher altitudes because lower allows to travel faster. This creates a vertical in refractivity, bending rays concave toward the Earth's surface and making celestial objects appear higher in the sky than their true positions. One common everyday phenomenon is the apparent flattening of the Sun near the horizon at sunrise or sunset. As passes through the denser lower atmosphere, the rays from the Sun's upper edge bend less than those from the lower edge due to the increasing gradient near the ground, compressing the solar disk vertically and giving it an oblate shape. Mirages represent more dramatic effects of this refraction, arising from horizontal temperature gradients that invert the usual profile. An inferior mirage occurs when hot ground air creates a layer less dense than the air above, bending light rays upward and producing illusory images like puddles on a hot road, where the sky appears reflected below the actual object. In contrast, a superior mirage forms under a temperature inversion with colder air near the surface overlaid by warmer air, causing rays to bend downward and elevate distant objects, such as ships appearing to float above the horizon. , a related , magnifies and raises objects when the refractive gradient lifts the apparent horizon, often seen over cold water bodies. In astronomy, necessitates corrections for the observed positions of stars and other celestial bodies, as it displaces their apparent altitude toward the by up to about 35 arcminutes at the horizon. The angular correction [R](/page/R)[R](/page/R) can be approximated by the formula [R](/page/R)≈(n−1)tan⁡[z](/page/Z)[R](/page/R) \approx (n-1) \tan [z](/page/Z), where nn is the at and [z](/page/Z)[z](/page/Z) is the true zenith distance; for small angles, this simplifies to [R](/page/R)≈60′′tan⁡[z](/page/Z)[R](/page/R) \approx 60'' \tan [z](/page/Z), with the result in arcseconds. This effect is most pronounced for objects low on the horizon and requires adjustment in precise observations, such as or . The of stars, or scintillation, results from refraction through turbulent pockets of air with varying densities and temperatures, causing rapid fluctuations in the light's arrival angle and intensity. These small-scale atmospheric cells, driven by wind and , refract starlight irregularly, producing the characteristic shimmer, while appear steadier due to their larger apparent disks averaging out the distortions. Temperature inversions, where warmer air traps cooler air below, exacerbate mirage formation by steepening the gradient and confining light paths to unusual trajectories. Such inversions are common in stable climatic conditions, like over polar seas or calm nights, enhancing superior s and contributing to optical illusions in regions with persistent cold surface layers.

Aquatic Refraction

Aquatic refraction occurs at the interface between water and air, where light bends due to the difference in refractive indices, leading to various optical illusions and adaptations in marine environments. The refractive index of water is approximately 1.33 for visible light, though it varies slightly with temperature, salinity, and wavelength; for instance, freshwater at 20°C has n≈1.333n \approx 1.333, while seawater can reach up to 1.34 due to dissolved salts. This index governs how light rays from air enter water or vice versa, causing phenomena observable in everyday settings and underwater ecosystems. A classic example is the apparent depth of submerged objects, where an item at actual depth dd appears closer to the surface at d′=d/nd' = d / n, making pools or lakes seem shallower than they are; for water, this reduces perceived depth by about 25%. Similarly, a straw or pencil partially immersed in a glass of water appears bent at the water's surface because light rays from the submerged portion refract toward the normal upon entering air, creating a discontinuity in the perceived straight line. From underwater, this refraction culminates in Snell's window, a circular field of view spanning approximately 97° above the observer, beyond which total internal reflection occurs at the critical angle of θc=sin⁡−1(1/n)≈48.6∘\theta_c = \sin^{-1}(1/n) \approx 48.6^\circ, reflecting the underwater scene instead of the surface world. In , refraction influences visual adaptations, particularly in fish vision, where spherical lenses with higher refractive indices compensate for the medium's properties to focus effectively , unlike the corneal-dominated focusing in air-breathing animals. Deep-sea species further adapt to low-light conditions involving , with specialized photoreceptors and lens pigments enhancing detection of narrow-bandwidth blue-green emissions that propagate through water with minimal , aided by the refractive environment.

Optical Applications

In Human Vision

Refraction plays a central role in human vision by bending rays to focus them on the , primarily through the optical properties of the and crystalline lens. The , the eye's transparent front surface, has a of approximately 1.376 and contributes about 43 diopters to the total refractive power. The crystalline lens, with a of around 1.41, adds roughly 17 diopters, resulting in an overall refractive power of about 60 diopters for the relaxed eye. This combined refraction, governed by at the air- and cornea-aqueous humor interfaces, accounts for approximately two-thirds of the eye's focusing ability from the alone. In a normal eye, known as , parallel light rays from distant objects converge precisely on the , producing clear vision without accommodation. Refractive errors disrupt this process: , or nearsightedness, occurs when the focal point falls in front of the due to an elongated eyeball or excessive corneal curvature, making distant objects blurry while near vision remains clear. , or farsightedness, results in the focal point behind the from a shortened eyeball or insufficient refractive power, often causing strain during near tasks. arises from irregular curvature of the or lens, leading to multiple focal points and distorted vision at all distances. Corrective measures address these errors by altering the light path before it enters the eye or by modifying the eye's structure. Spectacles and contact lenses use thin lenses designed via the lensmaker's formula, 1f=(n−1)(1R1−1R2)\frac{1}{f} = (n-1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right), where ff is the , nn is the lens material's , and R1R_1, R2R_2 are the radii of of the lens surfaces, to provide diverging power for or converging power for hyperopia and . LASIK surgery corrects refractive errors by using an to reshape the , flattening it for or steepening it for hyperopia, thereby adjusting its refractive power without altering the lens. The eye's ability to focus on near objects, called accommodation, involves the ciliary muscles contracting to relax zonular fibers, allowing the lens to become more spherical and increase its refractive power by up to 10-12 diopters in . This dynamic refraction enables clear vision from infinity to about 25 cm. , an age-related condition typically onset after age 40, diminishes this capacity as the lens stiffens and loses elasticity, reducing accommodative amplitude to near zero by age 60 and necessitating reading glasses for close work. The development of corrective lenses traces back to the 13th century in Italy, where monks and scholars first crafted convex glass lenses to aid presbyopic reading, marking the earliest known optical correction for refractive errors.

In Lenses and Instruments

Lenses are optical devices that exploit refraction to converge or diverge light rays, forming images through the bending of light at curved surfaces. Converging lenses, often convex in shape, have a positive focal length and focus parallel rays to a single point, while diverging lenses, typically concave, possess a negative focal length and cause parallel rays to spread apart. These effects arise from the variation in refractive index between the lens material and the surrounding medium, governed by Snell's law at each surface./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.05%3A_Thin_Lenses) The behavior of thin lenses, where thickness is negligible compared to , is described by the thin lens equation: 1f=1u+1v\frac{1}{f} = \frac{1}{u} + \frac{1}{v} Here, ff is the , uu is the object distance, and vv is the image distance. This equation derives from applying iteratively at the two refracting surfaces of the lens, combined with the paraxial approximation for small angles. The lensmaker's formula further relates ff to the lens's radii of curvature R1R_1 and R2R_2, and nn: 1f=(n−1)(1R1−1R2)\frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) For a biconvex converging lens, R1>0R_1 > 0 and R2<0R_2 < 0, yielding a positive ff./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.05%3A_Thin_Lenses) Imperfections in lens performance, known as aberrations, degrade image quality. Chromatic aberration occurs because dispersion causes different wavelengths to refract by varying amounts, focusing them at different points along the optical axis. This is corrected in achromatic doublets, which combine a convex crown glass element (low dispersion) with a concave flint glass element (high dispersion) to bring two wavelengths to the same focus. Spherical aberration, meanwhile, results from the stronger refraction at the lens periphery compared to the center for spherical surfaces, blurring the image. Aspheric lenses, with non-spherical surfaces, mitigate this by tailoring the curvature to equalize focal points across the aperture. In microscopes, refraction through objective and lenses enables high linear . The objective forms a real, magnified intermediate image with m=v/um = v/u, where vv and uu are the image and object distances from the thin lens equation. The total is then the product of the objective's linear and the 's angular , often achieving hundreds to thousands of times enlargement for detailed specimen viewing. Telescopes utilize refraction to achieve angular , expanding the apparent size of distant objects. In a , the angular is m=fobj/feyepiecem = f_{\text{obj}} / f_{\text{eyepiece}}, where fobjf_{\text{obj}} and feyepiecef_{\text{eyepiece}} are the focal lengths of the objective and lenses, respectively, allowing resolution of fine celestial details./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/02%3A_Geometric_Optics_and_Image_Formation/2.09%3A_Microscopes_and_Telescopes) Fiber optics rely on refraction via total internal reflection to guide light signals over long distances. The fiber core, with a higher refractive index ncoren_{\text{core}} than the surrounding cladding (nclad<ncoren_{\text{clad}} < n_{\text{core}}), confines light within the core when the incidence angle exceeds the critical angle, defined by Snell's law as sin⁡θc=nclad/ncore\sin \theta_c = n_{\text{clad}} / n_{\text{core}}. This principle enables low-loss transmission in telecommunications, with typical index differences of about 0.01 for single-mode fibers.

Mechanical Waves

Water Waves

Refraction of surface waves occurs when waves propagate from regions of one water depth to another, causing a change in wave direction due to variations in wave speed. This phenomenon is prominent in , coastal areas, and even laboratory ripple tanks, where waves encounter gradually changing depths. The bending of wave crests aligns them more to the depth , altering the distribution of wave along the shore./05:_Coastal_hydrodynamics/5.02:_Wave_transformation/5.2.3:_Refraction) The speed of surface gravity waves depends on water depth relative to the wavelength. In deep water, where the depth hh is greater than half the wavelength λ\lambda, the phase speed vv is given by v=gλ2π,v = \sqrt{\frac{g \lambda}{2\pi}},
Add your contribution
Related Hubs
User Avatar
No comments yet.