Recent from talks
Nothing was collected or created yet.
Transverse wave
View on WikipediaThis article needs additional citations for verification. (May 2019) |
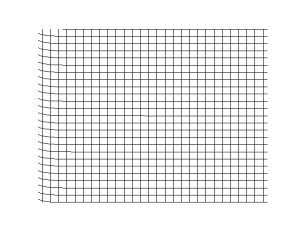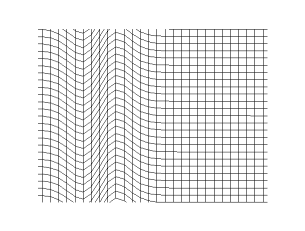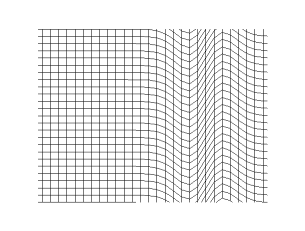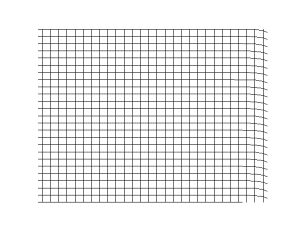
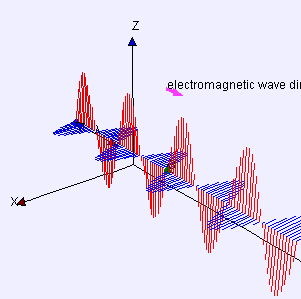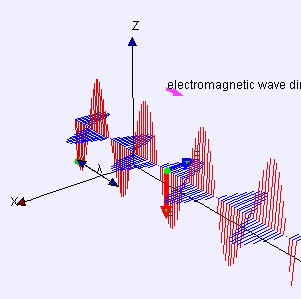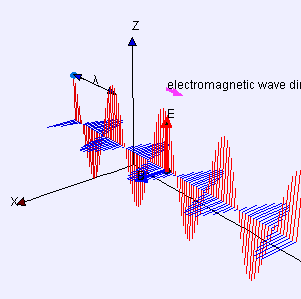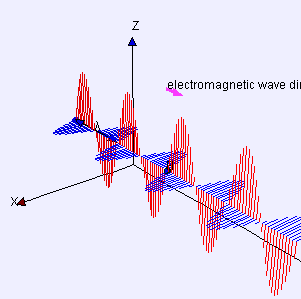
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without transporting the matter in the transmission medium if there is one.[1][2] Electromagnetic waves are transverse without requiring a medium.[3] The designation “transverse” indicates the direction of the wave is perpendicular to the displacement of the particles of the medium through which it passes, or in the case of EM waves, the oscillation is perpendicular to the direction of the wave.[4]
A simple example is given by the waves that can be created on a horizontal length of string by anchoring one end and moving the other end up and down. Another example is the waves that are created on the membrane of a drum. The waves propagate in directions that are parallel to the membrane plane, but each point in the membrane itself gets displaced up and down, perpendicular to that plane. Light is another example of a transverse wave, where the oscillations are the electric and magnetic fields, which point at right angles to the ideal light rays that describe the direction of propagation.
Transverse waves commonly occur in elastic solids due to the shear stress generated; the oscillations in this case are the displacement of the solid particles away from their relaxed position, in directions perpendicular to the propagation of the wave. These displacements correspond to a local shear deformation of the material. Hence a transverse wave of this nature is called a shear wave. Since fluids cannot resist shear forces while at rest, propagation of transverse waves inside the bulk of fluids is not possible.[5] In seismology, shear waves are also called secondary waves or S-waves.
Transverse waves are contrasted with longitudinal waves, where the oscillations occur in the direction of the wave. The standard example of a longitudinal wave is a sound wave or "pressure wave" in gases, liquids, or solids, whose oscillations cause compression and expansion of the material through which the wave is propagating. Pressure waves are called "primary waves", or "P-waves" in geophysics.
Water waves involve both longitudinal and transverse motions.[6]
Mathematical formulation
[edit]Mathematically, the simplest kind of transverse wave is a plane linearly polarized sinusoidal one. "Plane" here means that the direction of propagation is unchanging and the same over the whole medium; "linearly polarized" means that the direction of displacement too is unchanging and the same over the whole medium; and the magnitude of the displacement is a sinusoidal function only of time and of position along the direction of propagation.
The motion of such a wave can be expressed mathematically as follows. Let be the direction of propagation (a vector with unit length), and any reference point in the medium. Let be the direction of the oscillations (another unit-length vector perpendicular to d). The displacement of a particle at any point of the medium and any time t (seconds) will be where A is the wave's amplitude or strength, T is its period, v is the speed of propagation, and is its phase at t = 0 seconds at . All these parameters are real numbers. The symbol "•" denotes the inner product of two vectors.
By this equation, the wave travels in the direction and the oscillations occur back and forth along the direction . The wave is said to be linearly polarized in the direction .
An observer that looks at a fixed point will see the particle there move in a simple harmonic (sinusoidal) motion with period T seconds, with maximum particle displacement A in each sense; that is, with a frequency of f = 1/T full oscillation cycles every second. A snapshot of all particles at a fixed time t will show the same displacement for all particles on each plane perpendicular to , with the displacements in successive planes forming a sinusoidal pattern, with each full cycle extending along by the wavelength λ = v T = v/f. The whole pattern moves in the direction with speed V.
The same equation describes a plane linearly polarized sinusoidal light wave, except that the "displacement" S(, t) is the electric field at point and time t. (The magnetic field will be described by the same equation, but with a "displacement" direction that is perpendicular to both and , and a different amplitude.)
Superposition principle
[edit]In a homogeneous linear medium, complex oscillations (vibrations in a material or light flows) can be described as the superposition of many simple sinusoidal waves, either transverse or longitudinal.
The vibrations of a violin string create standing waves,[7] for example, which can be analyzed as the sum of many transverse waves of different frequencies moving in opposite directions to each other, that displace the string either up or down or left to right. The antinodes of the waves align in a superposition .
Circular polarization
[edit]If the medium is linear and allows multiple independent displacement directions for the same travel direction , we can choose two mutually perpendicular directions of polarization, and express any wave linearly polarized in any other direction as a linear combination (mixing) of those two waves.
By combining two waves with same frequency, velocity, and direction of travel, but with different phases and independent displacement directions, one obtains a circularly or elliptically polarized wave. In such a wave the particles describe circular or elliptical trajectories, instead of moving back and forth.
It may help understanding to revisit the thought experiment with a taut string mentioned above. Notice that you can also launch waves on the string by moving your hand to the right and left instead of up and down. This is an important point. There are two independent (orthogonal) directions that the waves can move. (This is true for any two directions at right angles, up and down and right and left are chosen for clarity.) Any waves launched by moving your hand in a straight line are linearly polarized waves.
But now imagine moving your hand in a circle. Your motion will launch a spiral wave on the string. You are moving your hand simultaneously both up and down and side to side. The maxima of the side to side motion occur a quarter wavelength (or a quarter of a way around the circle, that is 90 degrees or π/2 radians) from the maxima of the up and down motion. At any point along the string, the displacement of the string will describe the same circle as your hand, but delayed by the propagation speed of the wave. Notice also that you can choose to move your hand in a clockwise circle or a counter-clockwise circle. These alternate circular motions produce right and left circularly polarized waves.
To the extent your circle is imperfect, a regular motion will describe an ellipse, and produce elliptically polarized waves. At the extreme of eccentricity your ellipse will become a straight line, producing linear polarization along the major axis of the ellipse. An elliptical motion can always be decomposed into two orthogonal linear motions of unequal amplitude and 90 degrees out of phase, with circular polarization being the special case where the two linear motions have the same amplitude.

Power in a transverse wave in string
[edit](Let the linear mass density of the string be μ.)
The kinetic energy of a mass element in a transverse wave is given by:
In one wavelength, kinetic energy
Using Hooke's law the potential energy in mass element
And the potential energy for one wavelength
So, total energy in one wavelength
Therefore average power is [8]
See also
[edit]- Longitudinal wave
- Luminiferous aether – the postulated medium for light waves; accepting that light was a transverse wave prompted a search for evidence of this physical medium
- Shear wave splitting
- Sinusoidal plane-wave solutions of the electromagnetic wave equation
- Transverse mode
- Elastography
- Shear-wave elasticity imaging
References
[edit]- ^ "Transverse Waves". L.R. Ingersoll Physics Museum. Retrieved 2024-03-06.
- ^ "Explainer: Understanding waves and wavelengths". 2020-03-05. Retrieved 2024-03-06.
- ^ "Transverse Waves". www.memphis.edu. Retrieved 2024-03-06.
- ^ "Physics Tutorial: The Anatomy of a Wave". www.physicsclassroom.com. Retrieved 2024-03-06.
- ^ "Fluid Mechanics II: Viscosity and Shear stresses" (PDF).
- ^ "Longitudinal and Transverse Wave Motion".
- ^ University Physics, Vol. 1, Chapter 16.6, "Standing Waves and Resonance" University of Central Florida, https://pressbooks.online.ucf.edu/osuniversityphysics/chapter/16-6-standing-waves-and-resonance/.
- ^ "16.4 Energy and Power of a Wave - University Physics Volume 1 | OpenStax". openstax.org. 19 September 2016. Retrieved 2022-01-28.
External links
[edit]- Interactive simulation of transverse wave
- Wave types explained with high speed film and animations
- Weisstein, Eric Wolfgang (ed.). "Transverse Wave". ScienceWorld.
- Transverse and Longitudinal Waves Introductory module on these waves at Connexions
Transverse wave
View on GrokipediaFundamentals
Definition
A transverse wave is a type of wave in which the oscillations occur perpendicular to the direction of wave propagation, thereby transferring energy without net displacement in the propagation direction. This includes mechanical transverse waves, where the particles of the medium vibrate perpendicular to the wave's direction, and electromagnetic waves, where the electric and magnetic fields oscillate perpendicular to each other and to the propagation direction.[6][7][2] In mechanical transverse waves, the disturbance causes individual particles to vibrate back and forth—such as up and down or side to side—in a plane orthogonal to the forward progress of the wave itself, forming a repeating pattern that advances through the medium over time.[1][8] This perpendicular motion distinguishes transverse waves as a fundamental mode of propagation, enabling phenomena where the wave's energy travels independently of the medium's bulk movement. This perpendicularity of oscillation to propagation contrasts with longitudinal waves, in which particle motion aligns parallel to the wave's direction.[1]Key Characteristics
Transverse waves are characterized by several fundamental properties that describe their oscillatory behavior and propagation. The amplitude represents the maximum extent of oscillation, such as the displacement of the medium's particles from their equilibrium position in mechanical waves or the peak field strength in electromagnetic waves, determining the wave's intensity or energy carried.[9] The wavelength () is the spatial distance between consecutive crests or troughs of the wave, providing a measure of its spatial periodicity.[10] The frequency () quantifies the number of oscillations or cycles per unit time, typically measured in hertz (Hz), while the period () is the duration of one complete cycle, inversely related to frequency by .[11] The phase indicates the specific position of a point on the wave relative to a reference point in its cycle, often expressed as the argument of the sinusoidal function describing the wave, such as , where it helps determine alignment between different wave components.[12] A defining feature of transverse waves is the directionality of oscillation, perpendicular to the direction of wave propagation. This perpendicularity distinguishes them from other wave types and allows for motion confined to a plane perpendicular to propagation (linear transverse motion) or more complex paths, such as elliptical or circular trajectories in three dimensions when combining components along the two independent perpendicular axes.[13][14] The speed () of a transverse wave depends on the properties of the medium through which it travels (or the vacuum for electromagnetic waves) and relates the other characteristics via the relation , where the wave speed remains constant for a given medium while frequency and wavelength adjust inversely to maintain this balance.[11] These properties collectively enable phenomena like polarization, where the orientation of oscillations influences wave behavior.[9]Comparison with Longitudinal Waves
Transverse waves differ fundamentally from longitudinal waves in the direction of oscillation relative to the direction of wave propagation. In transverse waves, oscillations occur perpendicular to the propagation direction, resulting in crests and troughs, whereas in longitudinal waves, oscillations occur parallel to the propagation direction, producing compressions and rarefactions.[1][7] This distinction arises because mechanical transverse waves require a medium with shear strength to support perpendicular motion, such as solids or taut strings, while longitudinal waves can propagate through media lacking such rigidity, including fluids like air or water. Electromagnetic transverse waves, however, do not require a medium.[15][16] Despite these differences, both transverse and longitudinal waves share core similarities as disturbances that propagate energy without net transport of matter. They exhibit common properties, including wavelength, frequency, amplitude, and speed, which determine their behavior in transmission and interference.[1][7] The following table summarizes key contrasts in oscillation and medium requirements (noting that electromagnetic transverse waves do not require a medium):| Aspect | Transverse Waves (Mechanical) | Longitudinal Waves |
|---|---|---|
| Oscillation Direction | Perpendicular to propagation | Parallel to propagation |
| Oscillation Path | Up-and-down or side-to-side (circular or linear in plane) | Back-and-forth along propagation axis |
| Medium Requirement | Needs shear strength (e.g., solids, strings) | No shear strength needed (e.g., fluids, gases) |
| Propagation Capability | Possible in solids; limited in fluids | Possible in solids, fluids, and gases |
| Occurrence Examples | Vibrations on strings, seismic S-waves | Sound waves in air, seismic P-waves |













