Recent from talks
Nothing was collected or created yet.
Uniform continuity
View on Wikipedia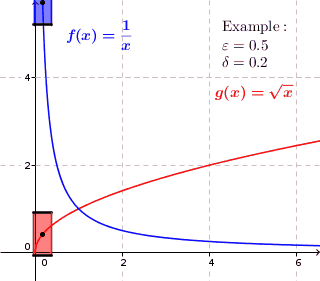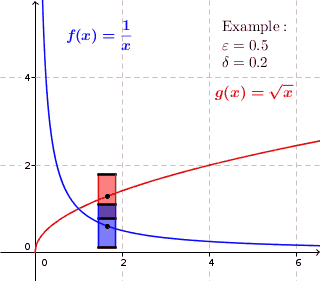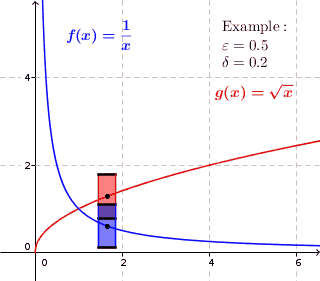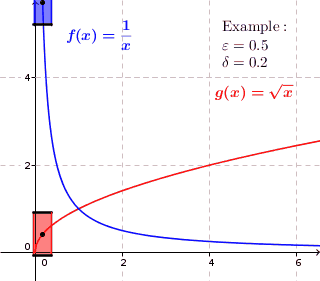
In mathematics, a real function of real numbers is said to be uniformly continuous if there is a positive real number such that function values over any function domain interval of the size are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number , then there is a positive real number such that for any and in any interval of length within the domain of .
The difference between uniform continuity and (ordinary) continuity is that in uniform continuity there is a globally applicable (the size of a function domain interval over which function value differences are less than ) that depends on only , while in (ordinary) continuity there is a locally applicable that depends on both and . So uniform continuity is a stronger continuity condition than continuity; a function that is uniformly continuous is continuous but a function that is continuous is not necessarily uniformly continuous. The concepts of uniform continuity and continuity can be expanded to functions defined between metric spaces.
Continuous functions can fail to be uniformly continuous if they are unbounded on a bounded domain, such as on , or if their slopes become unbounded on an infinite domain, such as on the real (number) line. However, any Lipschitz map between metric spaces is uniformly continuous, in particular any isometry (distance-preserving map).
Although continuity can be defined for functions between general topological spaces, defining uniform continuity requires more structure. The concept relies on comparing the sizes of neighbourhoods of distinct points, so it requires a metric space, or more generally a uniform space.
Definition for functions on metric spaces
[edit]For a function with metric spaces and , the following definitions of uniform continuity and (ordinary) continuity hold.
Definition of uniform continuity
[edit]- is called uniformly continuous if for every real number there exists a real number such that for every with , we have . The set for each is a neighbourhood of and the set for each is a neighbourhood of by the definition of a neighbourhood in a metric space.
- If and are subsets of the real line, then and can be the standard one-dimensional Euclidean distance, yielding the following definition: for every real number there exists a real number such that for every , (where is a material conditional statement saying "if , then ").
- Equivalently, is said to be uniformly continuous if . Here quantifications (, , , and ) are used.
- Equivalently, is uniformly continuous if it admits a modulus of continuity.
Definition of (ordinary) continuity
[edit]- is called continuous if for every real number there exists a real number such that for every with , we have . The set is a neighbourhood of . Thus, (ordinary) continuity is a local property of the function at the point .
- Equivalently, a function is said to be continuous if .
- Alternatively, a function is said to be continuous if there is a function of all positive real numbers and , representing the maximum positive real number, such that at each if satisfies then . At every , is a monotonically non-decreasing function.
Local continuity versus global uniform continuity
[edit]In the definitions, the difference between uniform continuity and continuity is that, in uniform continuity there is a globally applicable (the size of a neighbourhood in over which values of the metric for function values in are less than ) that depends on only while in continuity there is a locally applicable that depends on the both and . Continuity is a local property of a function — that is, a function is continuous, or not, at a particular point of the function domain , and this can be determined by looking at only the values of the function in an arbitrarily small neighbourhood of that point. When we speak of a function being continuous on an interval, we mean that the function is continuous at every point of the interval. In contrast, uniform continuity is a global property of , in the sense that the standard definition of uniform continuity refers to every point of . On the other hand, it is possible to give a definition that is local in terms of the natural extension (the characteristics of which at nonstandard points are determined by the global properties of ), although it is not possible to give a local definition of uniform continuity for an arbitrary hyperreal-valued function, see below.
A mathematical definition that a function is continuous on an interval and a definition that is uniformly continuous on are structurally similar as shown in the following.
Continuity of a function for metric spaces and at every point of an interval (i.e., continuity of on the interval ) is expressed by a formula starting with quantifications
- ,
(metrics and are and for for the set of real numbers ).
For uniform continuity, the order of the first, second, and third quantifications (, , and ) are rotated:
- .
Thus for continuity on the interval, one takes an arbitrary point of the interval, and then there must exist a distance ,
while for uniform continuity, a single must work uniformly for all points of the interval,
Properties
[edit]Every uniformly continuous function is continuous, but the converse does not hold. Consider for instance the continuous function where is the set of real numbers. Given a positive real number , uniform continuity requires the existence of a positive real number such that for all with , we have . But
and as goes to be a higher and higher value, needs to be lower and lower to satisfy for positive real numbers and the given . This means that there is no specifiable (no matter how small it is) positive real number to satisfy the condition for to be uniformly continuous so is not uniformly continuous.
Any absolutely continuous function (over a compact interval) is uniformly continuous. On the other hand, the Cantor function is uniformly continuous but not absolutely continuous.
The image of a totally bounded subset under a uniformly continuous function is totally bounded. However, the image of a bounded subset of an arbitrary metric space under a uniformly continuous function need not be bounded: as a counterexample, consider the identity function from the integers endowed with the discrete metric to the integers endowed with the usual Euclidean metric.
The Heine–Cantor theorem asserts that every continuous function on a compact set is uniformly continuous. In particular, if a function is continuous on a closed bounded interval of the real line, it is uniformly continuous on that interval. The Darboux integrability of continuous functions follows almost immediately from this theorem.
If a real-valued function is continuous on and exists (and is finite), then is uniformly continuous. In particular, every element of , the space of continuous functions on that vanish at infinity, is uniformly continuous. This is a generalization of the Heine-Cantor theorem mentioned above, since .
Examples and nonexamples
[edit]Examples
[edit]- Linear functions are the simplest examples of uniformly continuous functions.
- Any continuous function on the interval is also uniformly continuous, since is a compact set.
- If a function is differentiable on an open interval and its derivative is bounded, then the function is uniformly continuous on that interval.
- Every Lipschitz continuous map between two metric spaces is uniformly continuous. More generally, every Hölder continuous function is uniformly continuous.
- The absolute value function is uniformly continuous, despite not being differentiable at . This shows uniformly continuous functions are not always differentiable.
- Despite being nowhere differentiable, the Weierstrass function is uniformly continuous.
- Every member of a uniformly equicontinuous set of functions is uniformly continuous.
Nonexamples
[edit]- Functions that are unbounded on a bounded domain are not uniformly continuous. The tangent function is continuous on the interval but is not uniformly continuous on that interval, as it goes to infinity as .
- Functions whose derivative tends to infinity as grows large cannot be uniformly continuous. The exponential function is continuous everywhere on the real line but is not uniformly continuous on the line, since its derivative is , and as .
Visualization
[edit]For a uniformly continuous function, for every positive real number there is a positive real number such that two function values and have the maximum distance whenever and are within the maximum distance . Thus at each point of the graph, if we draw a rectangle with a height slightly less than and width a slightly less than around that point, then the graph lies completely within the height of the rectangle, i.e., the graph do not pass through the top or the bottom side of the rectangle. For functions that are not uniformly continuous, this isn't possible; for these functions, the graph might lie inside the height of the rectangle at some point on the graph but there is a point on the graph where the graph lies above or below the rectangle. (the graph penetrates the top or bottom side of the rectangle.)
-
For uniformly continuous functions, for each positive real number there is a positive real number such that when we draw a rectangle around each point of the graph with a width slightly less than and a height slightly less than , the graph lies completely inside the height of the rectangle.
-
For functions that are not uniformly continuous, there is a positive real number such that for every positive real number there is a point on the graph so that when we draw a rectangle with a height slightly less than and a width slightly less than around that point, there is a function value directly above or below the rectangle. There might be a graph point where the graph is completely inside the height of the rectangle but this is not true for every point of the graph.
History
[edit]The first published definition of uniform continuity was by Heine in 1870, and in 1872 he published a proof that a continuous function on an open interval need not be uniformly continuous. The proofs are almost verbatim given by Dirichlet in his lectures on definite integrals in 1854. The definition of uniform continuity appears earlier in the work of Bolzano where he also proved that continuous functions on an open interval do not need to be uniformly continuous. In addition he also states that a continuous function on a closed interval is uniformly continuous, but he does not give a complete proof.[1]
Other characterizations
[edit]Non-standard analysis
[edit]In non-standard analysis, a real-valued function of a real variable is microcontinuous at a point precisely if the difference is infinitesimal whenever is infinitesimal. Thus is continuous on a set in precisely if is microcontinuous at every real point . Uniform continuity can be expressed as the condition that (the natural extension of) is microcontinuous not only at real points in , but at all points in its non-standard counterpart (natural extension) in . Note that there exist hyperreal-valued functions which meet this criterion but are not uniformly continuous, as well as uniformly continuous hyperreal-valued functions which do not meet this criterion, however, such functions cannot be expressed in the form for any real-valued function . (see non-standard calculus for more details and examples).
Cauchy continuity
[edit]For a function between metric spaces, uniform continuity implies Cauchy continuity (Fitzpatrick 2006). More specifically, let be a subset of . If a function is uniformly continuous then for every pair of sequences and such that
we have
Relations with the extension problem
[edit]Let be a metric space, a subset of , a complete metric space, and a continuous function. A question to answer: When can be extended to a continuous function on all of ?
If is closed in , the answer is given by the Tietze extension theorem. So it is necessary and sufficient to extend to the closure of in : that is, we may assume without loss of generality that is dense in , and this has the further pleasant consequence that if the extension exists, it is unique. A sufficient condition for to extend to a continuous function is that it is Cauchy-continuous, i.e., the image under of a Cauchy sequence remains Cauchy. If is complete (and thus the completion of ), then every continuous function from to a metric space is Cauchy-continuous. Therefore when is complete, extends to a continuous function if and only if is Cauchy-continuous.
It is easy to see that every uniformly continuous function is Cauchy-continuous and thus extends to . The converse does not hold, since the function is, as seen above, not uniformly continuous, but it is continuous and thus Cauchy continuous. In general, for functions defined on unbounded spaces like , uniform continuity is a rather strong condition. It is desirable to have a weaker condition from which to deduce extendability.
For example, suppose is a real number. At the precalculus level, the function can be given a precise definition only for rational values of (assuming the existence of qth roots of positive real numbers, an application of the Intermediate Value Theorem). One would like to extend to a function defined on all of . The identity
shows that is not uniformly continuous on the set of all rational numbers; however for any bounded interval the restriction of to is uniformly continuous, hence Cauchy-continuous, hence extends to a continuous function on . But since this holds for every , there is then a unique extension of to a continuous function on all of .
More generally, a continuous function whose restriction to every bounded subset of is uniformly continuous is extendable to , and the converse holds if is locally compact.
A typical application of the extendability of a uniformly continuous function is the proof of the inverse Fourier transformation formula. We first prove that the formula is true for test functions, there are densely many of them. We then extend the inverse map to the whole space using the fact that linear map is continuous; thus, uniformly continuous.
Generalization to topological vector spaces
[edit]In the special case of two topological vector spaces and , the notion of uniform continuity of a map becomes: for any neighborhood of zero in , there exists a neighborhood of zero in such that implies
For linear transformations , uniform continuity is equivalent to continuity. This fact is frequently used implicitly in functional analysis to extend a linear map off a dense subspace of a Banach space.
Generalization to uniform spaces
[edit]Just as the most natural and general setting for continuity is topological spaces, the most natural and general setting for the study of uniform continuity are the uniform spaces. A function between uniform spaces is called uniformly continuous if for every entourage in there exists an entourage in such that for every in we have in .
In this setting, it is also true that uniformly continuous maps transform Cauchy sequences into Cauchy sequences.
Each compact Hausdorff space possesses exactly one uniform structure compatible with the topology. A consequence is a generalization of the Heine-Cantor theorem: each continuous function from a compact Hausdorff space to a uniform space is uniformly continuous.
See also
[edit]- Contraction mapping – Function reducing distance between all points
- Uniform convergence – Mode of convergence of a function sequence
- Uniform isomorphism – Uniformly continuous homeomorphism
References
[edit]Further reading
[edit]- Bourbaki, Nicolas (1989). General Topology: Chapters 1–4 [Topologie Générale]. Springer. ISBN 0-387-19374-X. Chapter II is a comprehensive reference of uniform spaces.
- Dieudonné, Jean (1960). Foundations of Modern Analysis. Academic Press.
- Fitzpatrick, Patrick (2006). Advanced Calculus. Brooks/Cole. ISBN 0-534-92612-6.
- Kelley, John L. (1955). General topology. Graduate Texts in Mathematics. Springer-Verlag. ISBN 0-387-90125-6.
{{cite book}}: ISBN / Date incompatibility (help) - Kudryavtsev, L.D. (2001) [1994], "Uniform continuity", Encyclopedia of Mathematics, EMS Press
- Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 978-0-07-054235-8.
- Rusnock, P.; Kerr-Lawson, A. (2005), "Bolzano and uniform continuity", Historia Mathematica, 32 (3): 303–311, doi:10.1016/j.hm.2004.11.003







































































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)








































