Hubbry Logo
MATLABMATLABMain
Open search
MATLAB
Community hub
MATLAB
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
MATLAB
MATLAB
MATLAB
View on Wikipedia
from Wikipedia

MATLAB (software)
DeveloperMathWorks
Initial release1984; 41 years ago (1984)
Stable release
R2025b[2] Edit this on Wikidata / September 17, 2025; 40 days ago (September 17, 2025)
Written inC/C++, MATLAB
Operating systemWindows, macOS, and Linux[3][4]
PlatformIA-32, x86-64, ARM64
TypeNumerical computing
LicenseProprietary commercial software
Websitemathworks.com
MATLAB (programming language)
Paradigmmulti-paradigm: functional, imperative, procedural, object-oriented, array
Designed byCleve Moler
DeveloperMathWorks
First appearedlate 1970s
Stable release
R2025b[2] Edit this on Wikidata / September 17, 2025; 40 days ago (September 17, 2025)
Typing disciplinedynamic, weak
Filename extensions.m, .p,[5] .mex*,[6] .mat,[7] .fig,[8] .mlx,[9] .mlapp,[10] .mltbx,[11] .mlappinstall,[12] .mlpkginstall[13]
Websitemathworks.com
Influenced by
Influenced
  • MATLAB Programming at Wikibooks

MATLAB (Matrix Laboratory)[18] is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages.

Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems.

As of 2020, MATLAB has more than four million users worldwide.[19] They come from various backgrounds of engineering, science, and economics. As of 2017, more than 5000 global colleges and universities use MATLAB to support instruction and research.[20]

History

[edit]

Origins

[edit]

MATLAB was invented by mathematician and computer programmer Cleve Moler.[21] The idea for MATLAB was based on his 1960s PhD thesis.[21] Moler became a math professor at the University of New Mexico and started developing MATLAB for his students[21] as a hobby.[22] He developed MATLAB's initial linear algebra programming in 1967 with his one-time thesis advisor, George Forsythe.[21] This was followed by Fortran code for linear equations in 1971.[21]

Before version 1.0, MATLAB "was not a programming language; it was a simple interactive matrix calculator. There were no programs, no toolboxes, no graphics. And no ODEs or FFTs."[23]

The first early version of MATLAB was completed in the late 1970s.[21] The software was disclosed to the public for the first time in February 1979 at the Naval Postgraduate School in California.[22] Early versions of MATLAB were simple matrix calculators with 71 pre-built functions.[24] At the time, MATLAB was distributed for free[25][26] to universities.[27] Moler would leave copies at universities he visited and the software developed a strong following in the math departments of university campuses.[28]: 5 

In the 1980s, Cleve Moler met John N. Little. They decided to reprogram MATLAB in C and market it for the IBM desktops that were replacing mainframe computers at the time.[21] John Little and programmer Steve Bangert re-programmed MATLAB in C, created the MATLAB programming language, and developed features for toolboxes.[22]

Commercial development

[edit]

MATLAB was first released as a commercial product in 1984 at the Automatic Control Conference in Las Vegas.[21][22] MathWorks, Inc. was founded to develop the software[26] and the MATLAB programming language was released.[24] The first MATLAB sale was the following year, when Nick Trefethen from the Massachusetts Institute of Technology bought ten copies.[22][29]

By the end of the 1980s, several hundred copies of MATLAB had been sold to universities for student use.[22] The software was popularized largely thanks to toolboxes created by experts in various fields for performing specialized mathematical tasks.[25] Many of the toolboxes were developed as a result of Stanford students that used MATLAB in academia, then brought the software with them to the private sector.[22]

Over time, MATLAB was re-written for early operating systems created by Digital Equipment Corporation, VAX, Sun Microsystems, and for Unix PCs.[22][24] Version 3 was released in 1987.[30] The first MATLAB compiler was developed by Stephen C. Johnson in the 1990s.[24]

In 2000, MathWorks added a Fortran-based library for linear algebra in MATLAB 6, replacing the software's original LINPACK and EISPACK subroutines that were in C.[24] MATLAB's Parallel Computing Toolbox was released at the 2004 Supercomputing Conference and support for graphics processing units (GPUs) was added to it in 2010.[24]

Recent history

[edit]

Some especially large changes to the software were made with version 8 in 2012.[31] The user interface was reworked[citation needed] and Simulink's functionality was expanded.[32]

By 2016, MATLAB had introduced several technical and user interface improvements, including the MATLAB Live Editor notebook, and other features.[24]

Release history

[edit]

For a complete list of changes of both MATLAB an official toolboxes, check MATLAB previous releases.[33]

Versions of the MATLAB product family
Name of release MATLAB Simulink, Stateflow (MATLAB attachments) Year
Volume 8 5.0 1996
Volume 9 5.1 1997
R9.1 5.1.1 1997
R10 5.2 1998
R10.1 5.2.1 1998
R11 5.3 1999
R11.1 5.3.1 1999
R12 6.0 2000
R12.1 6.1 2001
R13 6.5 2002
R13SP1 6.5.1 2003
R13SP2 6.5.2
R14 7 6.0 2004
R14SP1 7.0.1 6.1
R14SP2 7.0.4 6.2 2005
R14SP3 7.1 6.3
R2006a 7.2 6.4 2006
R2006b 7.3 6.5
R2007a 7.4 6.6 2007
R2007b 7.5 7.0
R2008a 7.6 7.1 2008
R2008b 7.7 7.2
R2009a 7.8 7.3 2009
R2009b 7.9 7.4
R2010a 7.10 7.5 2010
R2010b 7.11 7.6
R2011a 7.12 7.7 2011
R2011b 7.13 7.8
R2012a 7.14 7.9 2012
R2012b 8.0 8.0
R2013a 8.1 8.1 2013
R2013b 8.2 8.2
R2014a 8.3 8.3 2014
R2014b 8.4 8.4
R2015a 8.5 8.5 2015
R2015b 8.6 8.6
R2016a 9.0 8.7 2016
R2016b 9.1 8.8
R2017a 9.2 8.9 2017
R2017b 9.3 9.0
R2018a 9.4 9.1 2018
R2018b 9.5 9.2
R2019a 9.6 9.3 2019
R2019b 9.7 10.0
R2020a 9.8 10.1 2020
R2020b 9.9 10.2
R2021a 9.10 10.3 2021
R2021b 9.11 10.4
R2022a 9.12 10.5 2022
R2022b 9.13 10.6
R2023a 9.14 10.7 2023
R2023b 23.2 23.2
R2024a 24.1 24.1 2024
R2024b 24.2 24.2
R2025a 25.1 25.1 2025
R2025b 25.2 25.2

Syntax

[edit]

The MATLAB application is built around the MATLAB programming language.

Common usage of the MATLAB application involves using the "Command Window" as an interactive mathematical shell or executing text files containing MATLAB code.[34]

"Hello, world!" example

[edit]

An example of a "Hello, world!" program exists in MATLAB. 

disp('Hello, world!')

It displays like so: 

Hello, world!

Variables

[edit]

Variables are defined using the assignment operator, =.

MATLAB is a weakly typed programming language because types are implicitly converted.[35] It is an inferred typed language because variables can be assigned without declaring their type, except if they are to be treated as symbolic objects,[36] and that their type can change.

Values can come from constants, from computation involving values of other variables, or from the output of a function.

For example: 

>> x = 17
x =
 17

>> x = 'hat'
x =
hat

>> x = [3*4, pi/2]
x =
   12.0000    1.5708

>> y = 3*sin(x)
y =
   -1.6097    3.0000

Vectors and matrices

[edit]

A simple array is defined using the colon syntax: initial:increment:terminator. For instance: 

>> array = 1:2:9
array =
 1 3 5 7 9

defines a variable named array (or assigns a new value to an existing variable with the name array) which is an array consisting of the values 1, 3, 5, 7, and 9. That is, the array starts at 1 (the initial value), increments with each step from the previous value by 2 (the increment value), and stops once it reaches (or is about to exceed) 9 (the terminator value).

The increment value can actually be left out of this syntax (along with one of the colons), to use a default value of 1. 

>> ari = 1:5
ari =
 1 2 3 4 5

assigns to the variable named ari an array with the values 1, 2, 3, 4, and 5, since the default value of 1 is used as the increment.

Indexing is one-based,[37] which is the usual convention for matrices in mathematics, unlike zero-based indexing commonly used in other programming languages such as C, C++, and Java.

Matrices can be defined by separating the elements of a row with blank space or comma and using a semicolon to separate the rows. The list of elements should be surrounded by square brackets []. Parentheses () are used to access elements and subarrays (they are also used to denote a function argument list). 

>> A = [16, 3, 2, 13  ; 5, 10, 11, 8 ; 9, 6, 7, 12 ; 4, 15, 14, 1]
A =
 16  3  2 13
  5 10 11  8
  9  6  7 12
  4 15 14  1

>> A(2,3)
ans =
 11

Sets of indices can be specified by expressions such as 2:4, which evaluates to [2, 3, 4]. For example, a submatrix taken from rows 2 through 4 and columns 3 through 4 can be written as: 

>> A(2:4,3:4)
ans =
 11 8
 7 12
 14 1

A square identity matrix of size n can be generated using the function eye, and matrices of any size with zeros or ones can be generated with the functions zeros and ones, respectively. 

>> eye(3,3)
ans =
 1 0 0
 0 1 0
 0 0 1

>> zeros(2,3)
ans =
 0 0 0
 0 0 0

>> ones(2,3)
ans =
 1 1 1
 1 1 1

Transposing a vector or a matrix is done either by the function transpose or by adding dot-prime after the matrix (without the dot, prime will perform conjugate transpose for complex arrays): 

>> A = [1 ; 2],  B = A.', C = transpose(A)
A =
     1
     2
B =
     1     2
C =
     1     2

>> D = [0, 3 ; 1, 5], D.'
D =
     0     3
     1     5
ans =
     0     1
     3     5

Most functions accept arrays as input and operate element-wise on each element. For example, mod(2*J,n) will multiply every element in J by 2, and then reduce each element modulo n. MATLAB does include standard for and while loops, but (as in other similar applications such as APL and R), using the vectorized notation is encouraged and is often faster to execute. The following code, excerpted from the function magic.m, creates a magic square M for odd values of n (MATLAB function meshgrid is used here to generate square matrices I and J containing ⁠⁠): 

[J,I] = meshgrid(1:n);
A = mod(I + J - (n + 3) / 2, n);
B = mod(I + 2 * J - 2, n);
M = n * A + B + 1;

Structures

[edit]

MATLAB supports structure data types.[38] Since all variables in MATLAB are arrays, a more adequate name is "structure array", where each element of the array has the same field names. In addition, MATLAB supports dynamic field names[39] (field look-ups by name, field manipulations, etc.).

Functions

[edit]

When creating a MATLAB function, the name of the file should match the name of the first function in the file. Valid function names begin with an alphabetic character, and can contain letters, numbers, or underscores. Variables and functions are case sensitive.[40] 

rgbImage = imread('ecg.png');
grayImage = rgb2gray(rgbImage); % for non-indexed images
level = graythresh(grayImage); % threshold for converting image to binary, 
binaryImage = im2bw(grayImage, level); 
% Extract the individual red, green, and blue color channels.
redChannel = rgbImage(:, :, 1);
greenChannel = rgbImage(:, :, 2);
blueChannel = rgbImage(:, :, 3);
% Make the black parts pure red.
redChannel(~binaryImage) = 255;
greenChannel(~binaryImage) = 0;
blueChannel(~binaryImage) = 0;
% Now recombine to form the output image.
rgbImageOut = cat(3, redChannel, greenChannel, blueChannel);
imshow(rgbImageOut);

Function handles

[edit]

MATLAB supports elements of lambda calculus by introducing function handles,[41] or function references, which are implemented either in .m files or anonymous[42]/nested functions.[43]

Classes and object-oriented programming

[edit]

MATLAB supports object-oriented programming including classes, inheritance, virtual dispatch, packages, pass-by-value semantics, and pass-by-reference semantics.[44] However, the syntax and calling conventions are significantly different from other languages. MATLAB has value classes and reference classes, depending on whether the class has handle as a super-class (for reference classes) or not (for value classes).[45]

Method call behavior is different between value and reference classes. For example, a call to a method: 

object.method();

can alter any member of object only if object is an instance of a reference class, otherwise value class methods must return a new instance if it needs to modify the object.

An example of a simple class is provided below: 

classdef Hello
    methods
        function greet(obj)
            disp('Hello!')
        end
    end
end

When put into a file named hello.m, this can be executed with the following commands: 

>> x = Hello();
>> x.greet();
Hello!

Graphics and graphical user interface programming

[edit]

MATLAB has tightly integrated graph-plotting features. For example, the function plot can be used to produce a graph from two vectors x and y. The code: 

x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)

produces the following figure of the sine function:

MATLAB supports three-dimensional graphics as well: 

[X,Y] = meshgrid(-10:0.25:10,-10:0.25:10);
f = sinc(sqrt((X/pi).^2+(Y/pi).^2));
mesh(X,Y,f);
axis([-10 10 -10 10 -0.3 1])
xlabel('{\bfx}')
ylabel('{\bfy}')
zlabel('{\bfsinc} ({\bfR})')
hidden off
    
[X,Y] = meshgrid(-10:0.25:10,-10:0.25:10);
f = sinc(sqrt((X/pi).^2+(Y/pi).^2));
surf(X,Y,f);
axis([-10 10 -10 10 -0.3 1])
xlabel('{\bfx}')
ylabel('{\bfy}')
zlabel('{\bfsinc} ({\bfR})')
This code produces a wireframe 3D plot of the two-dimensional unnormalized sinc function:     This code produces a surface 3D plot of the two-dimensional unnormalized sinc function:
   

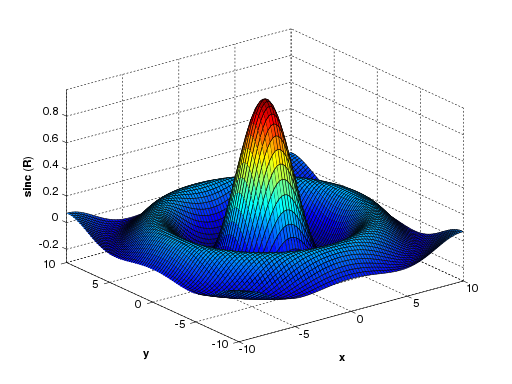
MATLAB supports developing graphical user interface (GUI) applications.[46] UIs can be generated either programmatically or using visual design environments such as GUIDE and App Designer.[47][48]

MATLAB and other languages

[edit]

MATLAB can call functions and subroutines written in the programming languages C or Fortran.[49] A wrapper function is created allowing MATLAB data types to be passed and returned. MEX files (MATLAB executables) are the dynamically loadable object files created by compiling such functions.[50][51] Since 2014 increasing two-way interfacing with Python was being added.[52][53]

Libraries written in Perl, Java, ActiveX or .NET can be directly called from MATLAB,[54][55] and many MATLAB libraries (for example XML or SQL support) are implemented as wrappers around Java or ActiveX libraries. Calling MATLAB from Java is more complicated, but can be done with a MATLAB toolbox[56] which is sold separately by MathWorks, or using an undocumented mechanism called JMI (Java-to-MATLAB Interface),[57][58] (which should not be confused with the unrelated Java Metadata Interface that is also called JMI). Official MATLAB API for Java was added in 2016.[59]

As alternatives to the MuPAD based Symbolic Math Toolbox available from MathWorks, MATLAB can be connected to Maple or Mathematica.[60][61]

Libraries also exist to import and export MathML.[62]

Relations to US sanctions

[edit]

In 2020, MATLAB withdrew services from two Chinese universities as a result of US sanctions. The universities said this will be responded to by increased use of open-source alternatives and by developing domestic alternatives.[63]

See also

[edit]
[edit]

Notes

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

MATLAB

View on Grokipedia
from Grokipedia
MATLAB (an initialism for "matrix laboratory") is a proprietary high-level programming language and interactive computing environment designed for numerical computation, data analysis, algorithm development, and visualization. Developed by The MathWorks, Inc., it originated in the late 1970s as a simple Fortran-based interactive calculator created by Cleve Moler to provide students access to matrix computation libraries like LINPACK and EISPACK without needing to write Fortran code. In 1984, following a rewrite in C by Moler, Jack Little, and Steve Bangert, MathWorks was founded to commercialize and further develop the software, transforming it from a basic tool into a comprehensive platform with a matrix-oriented syntax, built-in graphics capabilities, and a desktop environment optimized for iterative problem-solving in engineering and science. Key features include extensive mathematical function libraries, support for interfacing with other languages such as C, Java, and Python, and specialized toolboxes for domains like signal processing, control systems, and machine learning, enabling users to perform complex simulations, model dynamic systems, and deploy applications. Employed by millions of professionals across academia, industry, and government for tasks ranging from prototyping algorithms to embedded system design, MATLAB's widespread adoption stems from its ease of use for matrix manipulations and its integration with hardware and external data sources, though its proprietary nature and licensing costs have prompted alternatives like open-source options.

History

Origins and Academic Roots

MATLAB originated in the late 1970s as an academic tool developed by , a professor of mathematics and at the , to facilitate matrix computations for teaching and research in . , who had contributed to the development of the EISPACK library (released in versions from 1971 to 1976 for eigenvalue computations) and LINPACK (a 1975 package for solving linear systems), sought to make these Fortran-based routines accessible to students without requiring them to master programming or rely on costly mainframe computers from vendors such as DEC or . The initial version of MATLAB, implemented entirely in , functioned as a simple interactive matrix that wrapped approximately a dozen subroutines from LINPACK and EISPACK, enabling users to perform operations like , inversion, and eigenvalue decomposition through straightforward commands. This design emphasized practical utility for engineering and scientific problem-solving, allowing direct experimentation with core algorithms of —such as and —rooted in established mathematical methods rather than abstract theoretical constructs. By encapsulating complex calls behind an intuitive interface, MATLAB addressed the empirical need for hands-on access to these tools on more affordable computing platforms available in academic settings during the era. Moler first demonstrated MATLAB publicly in February 1979 during a SIAM short course on matrix methods, co-taught with G. W. Stewart, highlighting its role in simplifying the application of linear algebra routines for educational purposes. The tool's academic prioritized enabling empirical validation of computational results over hardware dependencies, fostering its early adoption in courses on matrix theory and numerical methods before any commercial adaptations. This foundational approach ensured MATLAB's focus remained on verifiable, first-order numerical operations essential to engineering analysis.

Commercialization and Early Growth

In 1984, , Jack Little, and Steve Bangert founded , in to commercialize MATLAB, transforming it from an academic teaching tool distributed as into a product. The company's initial operations were modest, with its first mailing address at a rented cabin in the hills above where Little resided. This venture capitalized on the emerging personal computing market, particularly the PC introduced in 1981, by rewriting MATLAB's codebase in C to enable a PC-compatible version known as PC-MATLAB. Early sales targeted universities and engineering departments, where MATLAB's matrix-oriented syntax addressed needs in numerical computing that were underserved by existing tools like libraries or early spreadsheets. PC-MATLAB Version 1.0 debuted publicly in December 1984 at the IEEE Conference on Decision and Control in , marking MATLAB's first commercial release for on IBM-compatible PCs. This version introduced a licensing model that supported ongoing development through updates and expansions, effectively resembling a subscription structure by requiring purchases for new releases and tool extensions. Little and Bangert contributed key enhancements, including improved graphics and elements, which facilitated its appeal to control engineers and signal processors seeking without low-level programming. MATLAB's early growth in the late 1980s and stemmed from the introduction of domain-specific toolboxes, beginning with those for control systems and , which extended the core language to handle specialized applications like analysis and digital filtering. These add-ons, such as the Control System Toolbox (initially released as Pro-MATLAB in the mid-1980s), enabled users to model dynamic systems and design controllers interactively, driving adoption in academia and industry sectors like and where empirical validation through was increasingly valued. The causal mechanism for market expansion lay in this modular extensibility: toolboxes lowered barriers to applying advanced , fostering user-contributed extensions and positioning MATLAB as a for technical computing by the early .

Expansion Through Acquisitions and Milestones

MathWorks pursued strategic acquisitions to bolster MATLAB's capabilities in code verification and simulation. In April 2007, the company acquired , a Grenoble-based firm specializing in static analysis tools for detecting runtime errors in code. This integration added products to the MATLAB and portfolios, enabling methods that mathematically prove the absence of certain errors, such as overflows or divisions by zero, thereby enhancing reliability in industries requiring certified software, including and automotive systems. The acquisition exemplified ' focus on augmenting core simulation strengths with complementary technologies derived from specialized engineering needs. Further expansions included the 2018 acquisition of Vector Zero, developers of software for of road networks in simulation environments. extended MATLAB's and Simulink's reach into autonomous vehicle testing by facilitating rapid creation of drivable 3D scenes from HD maps and OpenDRIVE data, supporting scenario-based verification without external dependencies. These moves, funded through internal revenues as a privately held entity, prioritized empirical enhancements to the ecosystem over subsidized research, aligning with user-driven demands for integrated, high-fidelity modeling tools. Product milestones reinforced this growth, notably the overhaul of in MATLAB R2008a (version 7.6), released in March 2008. This update introduced the classdef syntax, , and property validation, supplanting earlier handle and value class systems to better accommodate complex, modular codebases in workflows. Such adaptations stemmed from community feedback and performance benchmarks, enabling scalable development without shifting to alternative languages. Similarly, the internal development of SimEvents, a toolbox integrated with , expanded hybrid modeling for queues, servers, and stochastic processes, addressing latencies in communication and systems through market-responsive innovation.

Evolution in the 21st Century

In the early 2000s, MATLAB adapted to the proliferation of multi-core processors by introducing the Parallel Computing Toolbox in release R2008a, which enabled distribution of computational workloads across multiple CPU cores using constructs like parfor loops for iterative matrix operations. This shift leveraged hardware advances, with benchmarks indicating near-linear performance gains for embarrassingly parallel tasks, such as large-scale simulations, proportional to the number of available cores on desktops and clusters. By R2010a and R2010b, support extended to GPU acceleration through gpuArray objects, allowing compatible numerical functions to execute on NVIDIA hardware with compute capability 2.0 or higher, thereby reducing computation times for algorithms like FFTs and linear algebra by factors of 10 or more in select cases. The 2010s marked MATLAB's pivot toward cloud-native capabilities amid growing demands for distributed and scalable computing. MATLAB Online, launched as a browser-based platform, permitted execution of MATLAB code on remote servers without local installation, integrating with cloud storage services like AWS S3 for handling datasets exceeding local memory limits. This facilitated collaborative workflows and on-demand resource scaling, aligning with enterprise shifts to hybrid environments where MATLAB scripts could interface with virtual machines for high-throughput tasks. Parallel to hardware and cloud integrations, MATLAB intensified focus on data-intensive domains post-2010, evolving toolboxes to address and statistical modeling needs driven by exponential data growth. The Statistics and Machine Learning Toolbox incorporated advanced algorithms for , regression, and , building on MATLAB's matrix paradigm to streamline workflows from data preprocessing to predictive modeling. These enhancements supported and empirical validation in fields like and , with MATLAB's syntax enabling that outpaced general-purpose languages in iterative analysis cycles.

Release History

Pre-Commercial and Initial Versions

MATLAB originated in the late 1970s as an academic tool developed by at the to provide students with access to the LINPACK and EISPACK libraries for matrix computations without requiring direct programming. This pre-commercial version, written in , functioned as a simple interactive matrix calculator supporting basic operations through an interactive shell and approximately 71 built-in functions, but lacked scripting capabilities, toolboxes, or graphics. It was freely distributed to universities and research institutions prior to 1984, emphasizing empirical numerical paradigms for linear algebra tasks with limited scope confined to dense matrix manipulations. The transition to commercial development began in 1983 when Jack Little and Steve Bangert rewrote the software in C for personal computers, leading to the release of MATLAB 1.0 in December 1984 by the newly founded company. This initial version debuted at the IEEE Conference on Decision and Control, introducing enhancements such as expanded functions, basic graphics, fast Fourier transforms, and early toolbox support like the Control System Toolbox in the subsequent Pro-MATLAB release for Unix workstations in 1985. Subsequent releases progressed incrementally: version 2.0 in 1986 added further matrix handling refinements, while version 3.0 in 1987 incorporated the Toolbox and solvers. By version 3.5 in 1990 and culminating in version 4.0 in 1992, MATLAB established core integration features, including MEX files for embedding C and Fortran code to extend functionality beyond native capabilities, and support for sparse matrices to optimize storage and computation for large-scale linear algebra problems with predominantly zero elements. These upgrades enabled more efficient handling of empirical data sets in scientific computing, with sparse matrix operations demonstrating measurable performance gains in memory usage and solve times for underdetermined systems compared to dense representations. Version 4.0 also previewed broader ecosystem expansions, solidifying MATLAB's foundational role in numerical analysis.

Major Architectural Shifts

In MATLAB R14, released in 2004, implemented a Java-based utilizing the for UI rendering. This architectural pivot improved cross-platform uniformity by minimizing OS-specific variations in interface behavior and appearance across Windows, , and Solaris systems. MATLAB R2016a, issued on March 3, 2016, debuted the Live Editor, an interactive tool for embedding executable code, outputs, and formatted text within scripts. This facilitated reproducible workflows by allowing section-wise execution and inline results, addressing limitations in traditional script-based and . Release R2019b, dated September 18, 2019, overhauled function name resolution precedence, elevating local functions, private functions, and package-scoped elements above path-dependent external files. The revision curbed collisions—where unintended function shadowing disrupted code execution—by enforcing a more predictable search hierarchy, thereby boosting reliability in modular and large-scale projects.

Recent Releases (R2020s)

MATLAB releases in the 2020s have emphasized enhancements in , GPU acceleration, and AI integration to support advanced computational workflows. R2024a introduced major updates to the Deep Learning Toolbox, including new algorithms for designing explainable and robust neural networks, expanded GPU support for training, and improved scalability for large models. These changes facilitated faster model deployment on hardware-accelerated systems, with functions like importNetworkFromPyTorch enabling seamless integration of models into MATLAB environments. R2024b built on these by adding capabilities for converting shallow neural networks from the Statistics and Machine Learning Toolbox into deep learning objects, further bridging classical and modern AI techniques. Parallelization improvements and additional pretrained models enhanced performance for tasks like and . R2025a, released on May 15, 2025, marked a significant architectural shift with a redesigned desktop interface rebuilt using and for improved web compatibility and responsiveness, replacing legacy components to enable a unified codebase across platforms. Key additions included customizable sidebars, dark mode theming, tabbed figure management, and the initial rollout of MATLAB Copilot, an AI assistant providing real-time code suggestions, autocompletions, and natural language-based code generation. This version also evolved the Live Editor for saving scripts in standard .m format and enhanced Python integration for hybrid workflows. R2025b, released in September 2025, focused on stability enhancements and expanded MATLAB Copilot functionality, including advanced aids, explanations, and test case generation to streamline prototyping and refinement. These updates prioritized quality improvements over new features, ensuring reliability for production environments while integrating AI assistance more deeply into coding tasks.

Core Syntax and Language Features

Basic Syntax and "Hello, World" Example

MATLAB employs an interpreted, array-based programming language optimized for numerical computations, where variables represent matrices by default and operations are designed for vectorization to facilitate rapid prototyping without explicit iteration. In this paradigm, scalars function as 1-by-1 matrices, enabling uniform handling of data from single values to multidimensional arrays. The language is case-sensitive for identifiers and commands but insensitive to whitespace, except within array definitions or string literals, which supports concise interactive entry while maintaining readability. A basic "Hello, World" example demonstrates output via the disp function: disp('Hello, World'), which prints the string to the command window without returning a value for assignment. Executing this in MATLAB's interactive environment (the Command Window or REPL-like interface) displays the text immediately, reflecting the language's roots in interactive matrix laboratory sessions for exploratory computation. Appending a to statements, as in disp('Hello, World');, suppresses automatic output display, a convention inherited from its design for efficient session-based workflows where users often prioritize computation over verbose feedback. Vectorized operations exemplify MATLAB's efficiency in avoiding loops: for instance, a = 1:10; generates a row vector [1 2 3 4 5 6 7 8 9 10] using the colon operator for range specification. Then, b = a.^2; computes the element-wise squares [1 4 9 16 25 36 49 64 81 100], leveraging the array-centric syntax to apply the power operator (denoted by .^ for element-wise distinction from matrix power *) across all elements in a single instruction. This approach exploits MATLAB's optimized linear algebra routines, reducing code verbosity and execution time compared to explicit for-loops, as vectorization minimizes overhead in the underlying C/ implementations.

Variables, Vectors, and Matrices

MATLAB employs dynamic typing, wherein variables require no explicit declaration and can alter their , or complexity during execution. Assignment occurs via the equals operator, as in x = 5;, which simultaneously creates the variable if absent and infers its type from the right-hand side value. This approach contrasts with statically typed languages, enabling but necessitating caution with unintended type changes in iterative computations. Vectors form the foundational data structure, treated as 1-by-n row or n-by-1 column matrices. Row vectors arise from space- or comma-separated elements within brackets, such as v_row = [1 2 3];, while column vectors use semicolons: v_col = [1; 2; 3];. The colon operator generates sequences efficiently, e.g., 1:5 yields [1 2 3 4 5], supporting vector creation, indexing, and loop bounds without explicit loops. Matrices extend this by concatenating vectors horizontally with spaces or vertically with semicolons, as in A = [1 2; 3 4]; for a 2-by-2 array. Arithmetic operations distinguish matrix multiplication (A * B) from element-wise multiplication (A .* B), with the former requiring compatible inner dimensions for standard linear algebra tasks. Inversion via inv(A) computes the matrix YY such that AY=YA=IA Y = Y A = I, where II is the identity, but direct inversion risks numerical instability for ill-conditioned matrices; built-in solvers like A \ b (mldivide) prioritize stability by selecting appropriate algorithms, such as LU or QR decomposition, over explicit inverses. The eig(A) function computes eigenvalues and optionally eigenvectors, leveraging optimized LAPACK routines for accuracy on symmetric or general matrices. Since release R2016b, MATLAB supports automatic broadcasting (implicit expansion) in array operations, expanding compatible arrays element-wise without loops or explicit replication via repmat or bsxfun. For instance, adding a row vector to a matrix broadcasts the vector across rows, yielding efficient, readable code. Vectorization—replacing loops with array operations—exploits SIMD instructions, optimized memory access, and multithreading in built-ins, often outperforming explicit loops by orders of magnitude for large arrays, as loops incur overhead from interpreted execution and lack compiler-level optimizations. This paradigm underscores MATLAB's design for numerical computing, where matrix-oriented syntax minimizes errors and accelerates linear algebra workflows compared to scalar-loop alternatives in languages like C or Python without equivalent libraries.

Functions, Structures, and Handles

MATLAB supports modular code organization through functions, which encapsulate reusable computations and promote a paradigm. Functions are defined using the syntax function [outputs] = functionName(inputs), where outputs are optional and enclosed in square brackets if multiple, and the function body follows until an end keyword or file end. Local functions within a script or primary function file begin with their own function statement and share the file's workspace, enabling organized subroutines without separate files. This facilitates and testing, as functions can accept inputs like scalars, arrays, or cell arrays and return corresponding outputs. Structures provide a flexible for heterogeneous , grouping related elements under named fields accessible via dot notation, such as s.fieldName = value. A structure s = struct('field1', value1, 'field2', value2) initializes fields that can hold any MATLAB , including nested structures or arrays of varying sizes across elements. This field-based access supports intuitive organization, akin to records in other languages, and allows dynamic field addition or removal, e.g., s.newField = [];, making structures suitable for representing complex entities like parameters or experimental results without fixed schemas. Function handles, denoted by the @ operator as in fh = @functionName, represent functions as first-class types, enabling their passage to other functions for higher-order operations like or optimization without relying on object-oriented constructs. handles, such as fh = @(x) sin(x), inline simple expressions directly, supporting immediate parameterization and closure over variables. s further enhance modularity by inheriting the scope of enclosing functions, allowing shared access to outer variables without explicit passing, which mitigates reliance on global variables and associated maintenance issues in large-scale codebases. For instance, a can modify an outer loop counter, enforcing lexical scoping that aligns with causal dependencies in computations. MATLAB .m files, used for functions and scripts, support Unicode characters in comments and code. As of R2020a, the Editor saves new .m files by default in UTF-8 encoding without a byte-order mark, enabling seamless storage and display of non-ASCII characters, such as Persian, via standard Save or Save As operations. In earlier versions, non-ASCII characters may appear corrupted; users can mitigate this by selecting UTF-8 in Save As (if available) or saving the file in an external editor like Notepad++ with UTF-8 encoding. For better Unicode display in the console, execute feature('DefaultCharacterSet', 'UTF-8').

Advanced Capabilities

Object-Oriented Programming and Classes

MATLAB introduced support for in release R2008a through the classdef syntax, which defines classes as blocks of code encapsulating data properties and associated methods. This feature enables , polymorphism, and while preserving the language's foundational array-centric paradigm, allowing extensible designs for complex simulations and algorithms without requiring retrofits to built-in functions. Classes consist of properties for and methods for operations, with properties supporting attributes to control behavior. The Dependent attribute designates properties computed dynamically via getter methods upon access, avoiding persistent storage and enabling derived values like calculated from other data. The Transient attribute prevents properties from being saved during object or transmission, useful for temporary or computationally intensive elements that should not persist across sessions. MATLAB's hybrid semantics distinguish value classes, which copy objects on assignment to enforce immutability similar to built-in numeric types, from handle classes, which pass references to permit shared mutable state without duplication. Value classes suit stateless , while handle classes facilitate scenarios like event-driven systems or graphs where modifications should propagate across references, though they introduce method dispatch overhead for property access compared to direct struct usage. In toolboxes, classes underpin extensible components such as custom data types for or iterative solvers, integrating with MATLAB's matrix operations for domain-specific extensions like financial instruments or control systems. For instance, handle classes enable listener patterns in or objects, supporting modular designs; however, benchmarks reveal property read/write latencies in classes exceed those of structs by factors of 10-100 times, limiting their use for high-frequency numerical tasks in favor of lighter alternatives.

Graphics, Visualization, and GUI Development

MATLAB's graphics system supports a wide array of 2D and 3D visualization functions designed for rendering numerical , with the foundational plot function enabling line plots from vectors x and y, customizable via arguments for line styles, markers, colors, and axis properties. These plots can be extended to multiple lines or subplots using handles to figures and axes objects, allowing programmatic control over appearance and interactivity, such as zooming and panning. For plotting matrices with customized x-axis labels, the imagesc function can be used for basic visualization, followed by setting xticks and xticklabels. Example: A = rand(10,5); imagesc(A); xticks(1:5); xticklabels({'Jan','Feb','Mar','Apr','May'}); xlabel('Months'); For enhanced control in releases from R2017a onward, the heatmap function allows direct specification: h = heatmap(A); h.XDisplayLabels = {'label1','label2',...}; This integrates naturally with MATLAB's graphics capabilities for data visualization. For 3D visualizations, the mesh function produces wireframe surfaces from matrix data, displaying edges without filled faces to emphasize grid structure and height variations. Complementing this, surf generates filled surface plots with interpolated faces, where users can apply lighting effects via functions like camlight and light to simulate realistic shading and highlight contours, aiding in the interpretation of complex scalar fields. These tools, integral to MATLAB since its inception for numerical analysis, facilitate rapid prototyping of data-driven insights without reliance on external libraries. GUI development in MATLAB centers on App Designer, available since release R2016a, which provides a drag-and-drop interface for assembling UI components like buttons, sliders, and axes, paired with a code editor for defining callbacks through object handles. This approach supports responsive apps that integrate visualizations directly, such as embedding dynamic plots updated via user interactions, with automatic layout management for desktop and web deployment. Release R2025a introduced a transition from Java-based to WebGL-based rendering for graphics and apps, leveraging and for improved cross-platform consistency, reduced crashes, and enhanced web export capabilities. This shift yields measurable performance gains, including faster rendering speeds in browser environments—up to 2-3 times quicker for complex surfaces in benchmarks—while maintaining full compatibility with existing plot functions.

Parallel Computing and Performance Optimizations

The Parallel Computing Toolbox facilitates scalable computations by distributing workloads across multiple cores, machines, or GPU devices, with core features including parfor loops for automatic parallelization of independent iterations and spmd blocks for explicit single-program multiple-data execution on worker processes. Introduced in November 2004 as the Distributed Computing Toolbox and later expanded, the toolbox manages parallel pools—groups of worker MATLAB sessions—that automatically handle data transfer and synchronization for constructs like parfor, enabling speedups proportional to available cores for embarrassingly parallel tasks such as Monte Carlo simulations. For cluster-scale operations, integration with MATLAB Parallel Server supports job submission to schedulers like PBS or Slurm, distributing arrays via codistributed objects to minimize communication overhead in large-scale linear algebra or parameter sweeps. GPU acceleration, enabled through gpuArray objects since MATLAB R2010b, stores in GPU and extends over 1,195 built-in functions—including matrix multiplications and FFTs—to devices as of R2024b, with automatic kernel generation for element-wise operations via arrayfun or pagefun. Empirical benchmarks demonstrate significant speedups for compute-intensive matrix operations; for instance, vectorized eigenvalue decompositions on a GPU yield up to 35 times faster execution than equivalent CPU loops, though small-array transfers incur latency costs that diminish gains below thresholds like 10,000 elements per . These capabilities leverage GPU parallelism for data-parallel kernels, but require single-precision or batched operations to maximize throughput, as double-precision performance remains limited by hardware architecture. Performance optimizations in MATLAB emphasize vectorization—replacing explicit loops with array-wide operations—as the foundational technique, exploiting pre-optimized and backends like BLAS for linear algebra, which circumvents interpreter overhead and yields 10-100x speedups over scalar loops in prototyping scenarios. This approach causally enables rapid iteration in numerical development, where matrix-oriented syntax aligns with hardware vector units, outperforming naive implementations in compiled languages for exploratory tasks despite MATLAB's interpretive nature. Combining vectorization with parallel features, such as GPU-accelerated parfor, further amplifies ; however, profiling via gputimeit or tic/toc reveals bottlenecks like memory-bound operations, necessitating data-type reductions (e.g., single vs. double) for optimal resource utilization.

Ecosystem and Extensions

Toolboxes for Specialized Domains

MATLAB offers a suite of proprietary toolboxes that extend its core functionality into specialized domains, providing rigorously tested algorithms and functions developed by engineers to address domain-specific challenges with empirical validation through benchmarks and real-world applications. These toolboxes, exceeding 100 in number across categories like , statistics, and , incorporate optimized implementations that reduce the need for users to develop and verify custom code from scratch. Licensing typically occurs as add-ons or bundles, with documentation highlighting time savings in prototyping and analysis as a key benefit, supported by internal testing showing faster execution compared to equivalent user-coded alternatives. The Signal Processing Toolbox includes functions for spectral analysis, such as the fft function, which computes the using algorithms automatically selected based on input size for optimal performance, alongside tools for , resampling, and power spectrum estimation validated on standard signals like sinusoids and noise-corrupted data. The Statistics and Machine Learning Toolbox provides capabilities for hypothesis testing, including t-tests, chi-square tests, and analysis of variance (ANOVA), which assess from sample data against null hypotheses, with functions like ttest and anova1 incorporating assumptions such as normality and verified through empirical distributions and simulations. For advanced applications, the Deep Learning Toolbox enables (CNN) training via functions like trainNetwork, supporting by fine-tuning pretrained models such as on custom datasets, with benchmarks demonstrating accuracies comparable to state-of-the-art on datasets like when adapting layers for feature extraction and . These toolboxes maintain proprietary optimizations, ensuring consistency and reliability across MATLAB releases while linking development to validated outcomes in fields like engineering and . Simulink serves as a graphical extension to , enabling the modeling and simulation of dynamic systems through block diagrams that represent multidomain physical and control systems. This integration allows algorithms to be directly embedded into models via MATLAB Function blocks or S-functions, facilitating parameterization and customization of model behaviors with scripted computations. For instance, users can leverage scripts to generate lookup tables, tune parameters dynamically during simulation, or process simulation outputs for analysis, streamlining the transition from algorithmic prototyping in to system-level verification in . Embedded Coder extends this synergy by automating the generation of optimized C and C++ code from models, supporting deployment to embedded hardware without manual recoding. The tool ensures compliance with industry standards such as for automotive applications and for aerospace certification, as verified through qualified toolchains that produce traceable, production-ready code. In workflows, this capability reduces development time by enabling early verification of generated code against hardware-in-the-loop tests, with case studies in automotive control systems demonstrating reductions in integration issues and improved product quality. Stateflow complements by providing a graphical formalism for designing finite state machines and hybrid systems logic, integrated seamlessly within Simulink models to handle event-driven behaviors alongside continuous dynamics. Transitions and states in Stateflow charts can invoke MATLAB functions for computations, enabling causal modeling of supervisory control and fault management in complex systems. This ecosystem cohesion, part of ' model-based design paradigm, fosters iterative refinement from high-level simulation to deployment, though it reinforces proprietary dependencies by optimizing workflows across MATLAB, , and add-ons like Stateflow for industries requiring certified reliability. Industry applications, such as in automotive reactive systems, highlight how these integrations minimize defects through simulation-driven validation before physical prototyping.

Interoperability and Compatibility

Interfaces with External Languages and APIs

MATLAB supports integration with external languages primarily through MEX files, which enable the execution of C, C++, or Fortran code as native functions within the MATLAB environment to accelerate performance-critical computations. MEX functions are compiled binaries that interface directly with MATLAB's matrix API, allowing seamless data exchange without explicit copying in many cases, though users must manage memory allocation via MATLAB's mxArray utilities. This mechanism is particularly effective for numerical algorithms where MATLAB's interpreted nature incurs overhead, with benchmarks showing speedups of 10-100x for compute-intensive loops compared to pure MATLAB implementations, depending on the algorithm's vectorization potential. For invoking Python code from MATLAB, the py. provides a introduced in release R2014b, permitting direct calls to Python modules and libraries such as or by prefixing function names. Data types are automatically converted between MATLAB arrays and Python equivalents (e.g., double to numpy.ndarray), but this incurs overhead for large datasets, often limiting efficiency to scenarios where Python's offers unique optimizations unavailable in native MATLAB toolboxes. Empirical tests indicate that while small function calls add negligible latency, iterative exchanges of multi-gigabyte matrices can degrade by factors of 2-5 relative to in-process operations, favoring hybrid workflows that minimize boundary crossings. Conversely, the facilitates embedding MATLAB as a computational engine within external applications written in C, , , Python, or .NET, enabling calls to MATLAB functions from host languages for leveraging its matrix operations in non-MATLAB environments. For instance, the Python implementation launches a MATLAB session via the matlab.engine package, supporting synchronous execution and data transfer, which is useful for integrating legacy MATLAB code into Python pipelines but introduces process startup costs (typically 1-5 seconds) and latency. In , the supports both synchronous and asynchronous modes, with similar trade-offs where gains accrue from MATLAB's specialized solvers outweighing marshalling expenses in data-parallel tasks. Overall, these interfaces enable modular architectures but require profiling to balance benefits against invocation overheads, as excessive cross-language calls can negate acceleration from optimized external libraries.

Relations to Open-Source Alternatives

GNU Octave serves as a free, open-source alternative designed for high compatibility with MATLAB's core syntax and matrix-oriented operations, allowing many MATLAB scripts to run with minimal modifications. However, Octave falls short in replicating MATLAB's extensive toolbox ecosystem, with fewer specialized functions for domains like signal processing, control systems, and optimization, often requiring community-contributed packages that lack the rigorous testing and integration of MATLAB's proprietary equivalents. Evaluations indicate that while Octave handles basic numerical computations adequately, its toolboxes exhibit inconsistencies in performance and completeness for advanced applications. Python, augmented by libraries such as for array manipulation, for scientific algorithms, and for visualization, competes as a versatile open-source ecosystem for numerical and scientific . Benchmarks reveal MATLAB's advantages in integrated prototyping speed for linear and matrix operations, where it often outperforms Python by factors of 5-10 in summation and multiplication tasks on large arrays, due to optimized just-in-time . Conversely, Python excels in scalability through parallel processing across multiple cores and broader with machine learning frameworks like , fostering community-driven extensions that address evolving needs beyond MATLAB's core focus. The structure of MATLAB enables sustained in a cohesive, polished environment, including validated toolboxes and optimizations, which supports through dedicated teams. In contrast, open-source alternatives like and Python rely on distributed volunteer contributions, promoting wider accessibility and rapid adaptation to niche innovations but risking fragmented maintenance and slower resolution of specialized gaps, as evidenced by comparative studies on software ecosystems in scientific domains. This dynamic underscores how closed-source models incentivize comprehensive reliability for enterprise use, while open-source prioritizes extensibility at the potential cost of uniformity.

Commercial Model

Licensing Structure and Pricing

MATLAB's licensing is managed exclusively by , offering a range of options tailored to individual users, commercial entities, academic institutions, and personal non-commercial use, all requiring activation through MathWorks accounts. Commercial individual licenses operate on a subscription model at USD 1,015 annually (excluding taxes), encompassing base MATLAB functionality and one year of Software Maintenance Service () for updates, bug fixes, and ; without renewed SMS, users retain access only to the licensed version without new releases. Perpetual licenses remain available for select categories like academic teaching and research or personal use, permitting indefinite operation of the purchased version, though they include only the initial year's SMS, with subsequent renewals—typically 20-30% of the base price—necessary for ongoing enhancements and compatibility. Academic licensing differentiates by scope: student versions, such as the and Student Suite, provide subscription access to core products plus select add-ons at reduced rates (around USD 99-500 annually, varying by region and eligibility), verifiable through institutional affiliation. Campus-wide licenses for universities enable unlimited deployment across faculty, staff, and students, often negotiated per institution and including extensive toolboxes, reflecting bulk pricing that can exceed USD 100,000 annually for large deployments to sustain broad accessibility while funding development. Home licenses for personal, non-commercial use start at approximately USD 149 for perpetual access to a single version or subscription equivalents, explicitly barring professional or educational applications. Toolboxes and add-ons, essential for domain-specific extensions like or , are priced separately as modular purchases, with individual commercial licenses ranging from USD 500 to over USD 4,000 each, bundled in higher-tier plans like startup programs that include 90+ add-ons for USD 500-1,000 monthly during early stages. This structure incentivizes incremental revenue, as base MATLAB alone suffices for basic numerical computing, but advanced workflows—prevalent in engineering and —demand multiple toolboxes, often comprising the majority of total licensing expenditures. Concurrent or network licenses for organizations scale costs by simultaneous users or seats, typically requiring custom quotes to accommodate enterprise deployment. All licenses enforce single-vendor dependency, with no open-source equivalents bundled, ensuring controls updates and feature evolution through mandatory renewals.

Business Sustainability and Market Position

MathWorks, the developer of MATLAB, reported annual revenue of $1.5 billion as of 2025, with consistent profitability achieved every year since the company's founding in 1984. This financial stability stems from a private ownership structure held by co-founders Jack Little and Cleve Moler, which avoids shareholder pressures and enables sustained investment in research and development without reliance on external debt or public markets. The firm employs over 6,500 people across 34 global offices, supporting a diversified customer base that includes academic institutions, government agencies, and enterprises in sectors such as aerospace, automotive, and pharmaceuticals. MATLAB maintains a dominant market position in numerical computing and , serving approximately 5 million users worldwide. Its ecosystem of specialized toolboxes and seamless integration with hardware-in-the-loop testing and —particularly via —creates high for competitors, fostering vendor loyalty in engineering workflows where rapid prototyping and validation are critical. While open-source alternatives like Python with NumPy/SciPy libraries have gained traction for general-purpose due to cost advantages, MATLAB's entrenched role in regulated industries and legacy codebases sustains its revenue streams, with adoption rates remaining robust among companies for tasks requiring certified, domain-specific extensions. Business sustainability faces pressures from the commoditization of basic matrix operations and visualization tools, yet counters this through continuous innovation, such as GPU acceleration and deployment options introduced in recent releases, which extend MATLAB's applicability to large-scale simulations. The company's avoidance of acquisitions for core growth—focusing instead on organic development—has preserved , though a incident in August 2025 disrupted licensing services temporarily without long-term revenue impact. Overall, MATLAB's market position reflects a niche monopoly in high-value applications, where the , including productivity gains from features, outweighs free alternatives for many professional users.

Criticisms and Technical Limitations

Syntax and Usability Shortcomings

MATLAB employs 1-based indexing for arrays, diverging from the 0-based convention dominant in languages such as C, Python, and Java, which predisposes code to off-by-one errors, especially during integration with zero-indexed external libraries or data formats where boundary assumptions mismatch. This design, rooted in mathematical notation for counting from 1, complicates mental mapping for developers accustomed to offset-based addressing, amplifying bugs in loops and slicing operations that span language boundaries. Complementing this, MATLAB's column-major storage order—elements of columns contiguous in memory, akin to —clashes with the row-major layout standard in C-derived ecosystems, requiring explicit transpositions (e.g., via permute or reshape) when exchanging matrix data, a frequent source of shape mismatches and silent errors in hybrid workflows. The square bracket operator [] exacerbates ambiguity by doubling as an empty matrix indicator and a concatenation tool, where horizontal ([A B]) versus vertical ([A; B]) assembly hinges on spacing or semicolons; unintended flattening occurs when juxtaposing cell or arrays, as [] defaults to over preservation, demanding workarounds like explicit cell constructors. Operator overloading introduces further unintuitiveness, as arithmetic symbols apply numeric semantics to non-numeric types: adding an to a character array shifts ASCII values ('a' + 1 yields 'b'), treating text as encoded integers rather than abstract , which derails expectations in mixed-type expressions and necessitates type guards absent in dedicated string operators. Prior to release R2016b, string manipulation relied on character arrays—matrices of numeric codes—lacking native vectorized methods for common tasks like splitting or , forcing reliance on matrix-oriented functions (e.g., strcat for ) that scale poorly and invite dimension errors in text-heavy pipelines. The native string type introduced in R2016b mitigated some issues by enabling array-friendly operations, yet legacy codebases perpetuate friction, with computational scientists reporting cumulative maintenance burdens from these design choices over alternatives like Python's distinct string primitives.

Performance and Scalability Issues

MATLAB's execution model, which relies on just-in-time (JIT) compilation atop an interpreted framework, introduces overhead that can degrade runtime performance relative to fully compiled languages or optimized alternatives. For instance, while MATLAB's vectorized operations leverage highly tuned linear algebra libraries like MKL for competitive speeds in matrix computations, explicit loops often underperform due to interpretive dispatch costs and dynamic typing checks, sometimes by factors of 2x to 10x compared to equivalent in the host implementation language. Benchmarks indicate that Python loops accelerated via Numba—a for numerical —can surpass MATLAB's loop execution times, as Numba generates more aggressively without MATLAB's interpretive layer constraints. This stems from architectural choices prioritizing over low-level optimization, where complex paths limit effectiveness, as seen in pre-2015b and persisting in scenarios with heavy function calls or type variability. Scalability challenges arise prominently in for large-scale arrays, where MATLAB's column-major storage and automatic resizing can trigger out-of-memory (OOM) errors without explicit interventions like preallocation or workspace limits. Creating or expanding arrays exceeding available RAM—such as a 1e10-element vector—frequently exhausts resources on systems with 16 GB or more, necessitating techniques like sparse matrices, clearing unused variables, or tall arrays for workflows. These pitfalls reflect causal reliance on contiguous allocation, which fragments heap space during iterative growth and lacks native support for non-contiguous paging in base MATLAB, contrasting with alternatives that integrate seamlessly with distributed systems. Toolbox dependencies exacerbate footprint inflation, with full installations demanding 4-6 GB of disk space for core functionality plus add-ons, far exceeding lightweight alternatives like Python's NumPy (under 100 MB core) that avoid monolithic bundling. This architectural bloat, driven by proprietary extensions for specialized domains, hinders deployment in resource-constrained environments and amplifies runtime memory demands when multiple toolboxes load shared libraries, verified through comparisons showing MATLAB's effective footprint 10-20x larger for equivalent numerical tasks.

Vendor Lock-In and Documentation Gaps

MATLAB's toolboxes, such as the Signal Processing Toolbox and Image Processing Toolbox, create significant dependencies that impede code portability to open-source alternatives. These toolboxes encapsulate specialized functions and algorithms not natively replicated in environments like Python with / or , often necessitating extensive rewrites or approximations during migration. For instance, dependencies on esoteric toolbox features or integration frequently render direct translation infeasible, as no automated converters handle complex proprietary extensions comprehensively. This lock-in manifests in migration efforts where teams must identify and replace toolbox-specific calls, increasing time and cost; one analysis notes that domain-specific toolboxes pose the primary barrier, requiring equivalents across fragmented open libraries. Evidence from migration experiences underscores these portability hurdles. In engineering and R&D contexts, organizations report challenges in replicating custom algorithms tied to MATLAB's closed toolboxes, with rewrites consuming months for legacy codebases reliant on over 100 specialized add-ons. Blogs detailing transitions to Python highlight that while core matrix operations port easily, toolbox-dependent or control systems code demands manual refactoring, deterring full adoption of cost-free alternatives despite their growing ecosystem maturity. Such dependencies empirically sustain ' licensing revenue—estimated at billions annually—by elevating switching costs, even as open tools demonstrate comparable or superior scalability in community-driven development. MATLAB's documentation has drawn criticism for gaps in covering advanced usage and edge cases, often providing simplistic examples that assume substantial prior expertise. User forums report that function references frequently omit normalization assumptions or boundary behaviors, leading to misleading outcomes in non-trivial applications like quaternion transformations. Similarly, examples are faulted for bloat avoidance at the expense of comprehensive use cases, leaving users to patch deficiencies via community suggestions rather than official completeness. These shortcomings, evident in discussions on undocumented features, exacerbate support quality issues, as incomplete edge-case guidance forces reliance on trial-and-error or external resources, particularly for proprietary toolbox interactions. In combination with lock-in, this contributes to slower transitions to alternatives, where documentation from collaborative projects like offers denser, verifiable coverage without vendor-imposed limitations.

Controversies

US Export Controls and Sanctions Compliance

MATLAB software, developed by the U.S.-based MathWorks, is subject to the Export Administration Regulations (EAR) administered by the Bureau of Industry and Security (BIS). It is typically classified under Export Control Classification Number (ECCN) 5D992.c as mass-market encryption software or as EAR99, allowing no-license-required (NLR) exports to most countries but prohibiting shipments to comprehensively embargoed nations such as Cuba, Iran, North Korea, Syria, and Sudan without BIS authorization. These restrictions stem from longstanding U.S. embargoes—Iran's intensified post-1979 revolution and Cuba's dating to the 1960s—aimed at preventing technology transfers that could support military or prohibited end-uses in adversarial regimes. MathWorks enforces compliance through end-user screening against U.S. denied parties lists, license activation protocols that verify IP geolocation and user affiliations, and explicit prohibitions in its end-user agreements against use in sanctioned regions or by restricted entities. Sales and to embargoed countries have been halted, with documented instances including deactivations for users in following 2022 sanctions and denials to specific Chinese institutions like in June 2020, after their addition to the BIS for military ties. These measures impose operational costs on MathWorks, including dedicated programs to avoid violations, though attempted workarounds—such as third-party purchases by sanctioned entities—have been reported and deemed non-compliant. Critics argue that such controls impede global scientific and in affected nations, potentially stifling empirical advancements in fields reliant on numerical tools like MATLAB, as evidenced by short-term disruptions reported by students and researchers in restricted universities. Proponents counter that the restrictions serve causal objectives by limiting dual-use software access to regimes with proliferation risks, with empirical data showing no broad harm from targeted entity controls, while private firms like absorb compliance burdens without undermining U.S. technological leadership. Geopolitically, these policies reflect broader U.S. efforts to curb technology diffusion amid tensions with , , and others, though they fuel debates over extraterritorial enforcement .

Ethical and Accessibility Debates in Adoption

MATLAB's licensing structure, with standard individual subscriptions costing between $860 and $2,150 annually, imposes significant financial barriers for independent users and institutions in developing countries, where such expenditures can exceed average monthly incomes and divert limited resources from other educational needs. editions, priced at around $49, offer partial mitigation through perpetual access to core functionality but restrict advanced toolboxes, block counts, and certain computational capabilities, thereby limiting their utility for comprehensive research or professional training in resource-constrained environments. Critics argue that these cost barriers exacerbate inequalities in STEM fields by excluding researchers and students from low-income regions, potentially stifling global innovation and reproducibility in scientific computing, as proprietary restrictions hinder code sharing and collaborative verification compared to open-source ecosystems. Proponents counter that revenue from paid licenses sustains MathWorks' investments in reliability, extensive documentation, and specialized toolboxes—features absent or underdeveloped in many free alternatives—evidenced by MATLAB's enduring adoption in validated engineering applications despite alternatives' availability. However, empirical observations indicate that open-source tools like GNU Octave and Python's NumPy/SciPy libraries enable rapid innovation in unconstrained academic and hobbyist communities, with lower total ownership costs (up to 90% savings in some analyses) fostering broader participation and iterative improvements unbound by licensing fees. These debates highlight a tension between incentives for polished, supported software and the democratizing potential of open alternatives, with data from academic forums showing persistent shifts toward free options in cost-sensitive contexts to avoid exclusion, though without quantifiable that MATLAB's model causally impairs overall field progress relative to its reliability contributions.

Impact and Reception

Role in Academia and Education

MATLAB maintains a dominant position in academic curricula, particularly in , and sciences, where it is employed for numerical , , and . According to , the software is used extensively in , research, and student projects at over 6,500 universities worldwide as of 2021, facilitating and visualization that align with introductory coursework needs. This prevalence stems from its matrix-oriented syntax, which simplifies linear algebra and concepts for undergraduates, often integrated into campus-wide licenses that provide unlimited access to students and faculty. Despite this entrenchment, critics argue that MATLAB's pedagogical role perpetuates dependency on tools, fostering habits ill-suited to long-term career versatility and incurring hidden costs through licensing dependencies. Educators and researchers advocate transitioning to open-source alternatives like Python, citing its free availability, extensive libraries (e.g., , ), and general-purpose applicability that better equips students for diverse professional environments beyond academia. Surveys and discussions highlight in curricula, where historical adoption overrides merit-based evaluation, potentially limiting exposure to transferable programming paradigms. Empirically, MATLAB's academic footprint is evident in high citation volumes, with 6,873 articles referencing it in Web of Science-indexed publications from 2000 to 2020, underscoring its utility in research dissemination. However, its proprietary nature poses challenges to principles, as reliance on licensed toolboxes and non-exportable code hinders ; analyses note difficulties in sharing workflows without equivalent access, exacerbating the broader reproducibility crisis in computational fields where verifiable, platform-agnostic code is essential. This has prompted calls for hybrid approaches or migrations to ensure empirical claims in papers remain causally traceable and independently verifiable.

Applications in Industry and Research

MATLAB sees extensive adoption in the sector, where employs it for nonlinear aircraft simulations and spacecraft power capability modeling, as demonstrated in tools for analyzing the Orion spacecraft's electrical power system launched in analyses as recent as November 2024. In specific cases, utilized MATLAB and to accelerate multirotor flight control development and testing by enabling rapid integration of custom algorithms, reducing iteration cycles in hardware-in-the-loop environments as of April 2024. Similarly, MATLAB supported modeling of the I mission's Orion crew capsule dynamics in 2022, facilitating verification of uncrewed lunar flyby trajectories through -based simulations. In the , MATLAB underpins modeling and simulations, with examples including Simulink-based estimation of longitudinal and lateral for handling analysis. Engineers apply it to prototype control algorithms for transmissions, integrating Stateflow for shift logic representation and enabling deployment from to embedded code. These applications extend to full vehicle system modeling using Simscape Driveline, where variants are simulated to evaluate and performance metrics. MATLAB maintains a strong position in (GNC) systems, particularly for vehicles, with blocks for IMU navigation and path-following controllers used in formation flying projects that achieved 50% faster cycles. In , it supports industrial deployments in , , and communications, where engineers analyze time-series and prototype filters before hardware . Toolboxes like SimBiology facilitate research simulations in quantitative systems , while broader validation frameworks ensure compliance with FDA regulations for modeling, though custom MATLAB code often supplements toolbox outputs for specialized requirements. Case studies indicate MATLAB's role in prototyping-to-deployment workflows yields measurable returns, such as NASA's use of Stateflow and Simulink Coder for fault protection code generation, completed within tight 1998 deadlines by automating logic from models to flight software. In non-software-centric firms, these capabilities correlate with reduced time-to-insight, as frameworks quantify ROI through metrics like 20-50% cuts in development time across engineering teams, per vendor-analyzed implementations.

Influence on Numerical Computing and Broader Ecosystem

MATLAB's emphasis on interactive, matrix-oriented computing environments established foundational practices in , promoting and visualization that became benchmarks for the field. By integrating a command-window REPL with script execution and graphical outputs, it shifted workflows from to iterative exploration, influencing the design of later systems like R's interactive console and Jupyter's notebook format, which extended similar paradigms to broader applications. This standardization extended to domain-specific methodologies, where MATLAB toolboxes—such as those for , control systems, and optimization—defined workflows and function signatures that achieved status in subfields, often replicated or emulated in competing tools to maintain . The proprietary model underpinning MATLAB's development fostered disciplined iteration through commercial incentives, yielding polished, reliable extensions that outpaced fragmented open-source efforts in niche reliability during the and 2000s. However, its licensing costs and performance bottlenecks in large-scale computations spurred competitive responses, notably , which prioritizes script compatibility to enable cost-free migration of MATLAB codebases. Similarly, Julia emerged in 2012 as a response to MATLAB's interpretive overhead, leveraging to deliver near-C-level speeds for numerical tasks while retaining high-level syntax familiarity, thereby addressing the "two-language problem" where prototyping in MATLAB necessitated rewrites in faster languages for production. In the broader , MATLAB's dominance accelerated R&D productivity across sectors by enabling quick validation, though quantifiable economic returns remain indirect; its toolboxes have underpinned simulations in and , contributing to efficiencies that proprietary rigor arguably sustains over open-source alternatives' slower consensus-driven progress. This dynamic has diversified the landscape, with Julia's now supporting advanced scientific packages that challenge MATLAB's incumbency in performance-critical applications, reflecting market-driven evolution toward hybrid workflows integrating both paradigms.

References

  1. https://www.mathworks.com/company/technical-articles/a-brief-history-of-matlab.html
  2. https://www.mathworks.com/help/matlab/learn_matlab/product-description.html
  3. https://www.mathworks.com/company/technical-articles/the-origins-of-matlab.html
  4. https://cvw.cac.cornell.edu/matlab/intro/history
  5. https://www.mathworks.com/discovery/what-is-matlab.html
  6. https://www.mathworks.com/products/matlab.html
  7. https://muse.jhu.edu/pub/87/article/235247
  8. https://cse.engineering.nyu.edu/~mleung/CS1133/f09/LectureNotes/MatlabHistory.pdf
  9. https://www.mathworks.com/content/dam/mathworks/tag-team/Objects/t/72887_92020v00Cleve_Growth_MATLAB_MathWorks_Two_Decades_Jan_2006.pdf
  10. https://blogs.mathworks.com/cleve/2018/03/09/matlab-history-pc-matlab-version-1-0/
  11. https://www.eetimes.com/the-mathworks-acquires-polyspace-technologies/
  12. https://www.crunchbase.com/acquisition/mathworks-acquires-vectorzero--6e53ef42
  13. https://blogs.mathworks.com/steve/2008/03/21/matlab-76-r2008a/
  14. https://www.mathworks.com/company/technical-articles/inside-matlab-objects-in-r2008a.html
  15. https://www.mathworks.com/products/simevents.html
  16. https://www.mathworks.com/content/dam/mathworks/mathworks-dot-com/company/events/conferences/matlab-computational-finance-conference-nyc/2015/proceedings/origins-evolution-future-directions-matlab.pdf
  17. https://www.mathworks.com/products/parallel-computing.html
  18. https://www.mathworks.com/help/parallel-computing/gpu-computing-in-matlab.html
  19. https://www.mathworks.com/products/matlab-online.html
  20. https://www.mathworks.com/solutions/cloud.html
  21. https://www.mathworks.com/products/statistics.html
  22. https://www.versionbay.com/resources/history/matlab-history/
  23. http://matlab.izmiran.ru/help/techdoc/rn/r14sp2_env_new.html
  24. https://www.educba.com/matlab-version/
  25. https://www.electronicdesign.com/technologies/embedded/software/article/21801437/matlab-r2016a-adds-live-editing-ide
  26. https://www.mathworks.com/matlabcentral/answers/1632555-is-live-editor-included-in-the-matlab-licence-or-a-separate-program
  27. https://www.mathworks.com/help/matlab/matlab_prog/upgrade-code-for-r2019b-changes-to-function-precedence-order.html
  28. https://nhigham.com/2019/11/12/whats-new-in-matlab-r2019a-and-r2019b/
  29. https://blogs.mathworks.com/deep-learning/2024/03/25/deep-learning-toolbox-r2024a-major-update-and-new-examples/
  30. https://www.mathworks.com/products/new_products/release2024a.html
  31. https://blogs.mathworks.com/deep-learning/2024/12/31/ai-with-matlab-3-things-that-happened-in-2024/
  32. https://blogs.mathworks.com/deep-learning/2024/09/17/r2024b-a-peek-into-new-ai-features/
  33. https://blogs.mathworks.com/matlab/2025/05/15/matlab-r2025a-has-been-released-whats-new/
  34. https://blogs.mathworks.com/matlab/2025/05/16/whats-with-all-the-big-changes-in-r2025a/
  35. https://www.mathworks.com/products/matlab-copilot.html
  36. https://www.mathworks.com/help/matlab-copilot/ug/generate-and-modify-code-using-matlab-copilot.html
  37. https://www.mathworks.com/products/new_products/latest_features.html
  38. https://www.mathworks.com/videos/introducing-matlab-copilot-1758744213958.html
  39. https://www.mathworks.com/company/technical-articles/the-joy-of-generating-c-code-from-matlab.html
  40. https://www.mathworks.com/company/technical-articles/new-functions-for-vectorizing-operations-on-any-data-type.html
  41. https://www.mathworks.com/help/matlab/math/matrices-in-the-matlab-environment.html
  42. https://www.mathworks.com/help/matlab/matlab_prog/case-and-space-sensitivity.html
  43. https://www.mathworks.com/help/matlab/ref/disp.html
  44. https://www.mathworks.com/help/matlab/ref/semicolon.html
  45. https://www.mathworks.com/help/matlab/ref/double.colon.html
  46. https://www.mathworks.com/help/matlab/ref/double.power.html
  47. https://www.mathworks.com/help/coder/data-definition.html
  48. https://www.mathworks.com/matlabcentral/answers/290186-how-do-i-define-a-variable-without-assigning-it-a-value
  49. https://www.mathworks.com/help/hdlcoder/data-definition.html
  50. https://www.mathworks.com/help/matlab/learn_matlab/matrices-and-arrays.html
  51. https://www.mathworks.com/help/simulink/slref/product.html
  52. https://www.mathworks.com/help/matlab/ref/inv.html
  53. https://www.mathworks.com/matlabcentral/answers/469143-doing-matrix-multiplications-and-taking-inverses-of-huge-matrices-sparse-matrices-too-slow
  54. https://www.mathworks.com/help/matlab/ref/eig.html
  55. https://blogs.mathworks.com/loren/2016/10/24/matlab-arithmetic-expands-in-r2016b/
  56. https://www.mathworks.com/help/matlab/matlab_prog/vectorization.html
  57. https://www.mathworks.com/matlabcentral/answers/160161-why-vectorized-calculations-are-faster-than-for-loops
  58. https://www.mathworks.com/help/matlab/matlab_prog/create-functions-in-files.html
  59. https://www.mathworks.com/help/matlab/ref/function.html
  60. https://www.mathworks.com/help/matlab/ref/struct.html
  61. https://www.mathworks.com/help/matlab/structures.html
  62. https://www.mathworks.com/help/matlab/function-handles.html
  63. https://www.mathworks.com/help/matlab/matlab_prog/nested-functions.html
  64. https://www.mathworks.com/help/matlab/matlab_prog/save-and-back-up-code.html
  65. https://www.mathworks.com/matlabcentral/answers/482380-how-to-set-the-encoding-of-matlab-m-files-to-be-utf8
  66. https://www.mathworks.com/help/matlab/ref/classdef.html
  67. https://www.mathworks.com/company/technical-articles/introduction-to-object-oriented-programming-in-matlab.html
  68. https://www.mathworks.com/help/matlab/matlab_oop/property-attributes.html
  69. https://www.mathworks.com/help/matlab/matlab_oop/comparing-handle-and-value-classes.html
  70. https://www.mathworks.com/help/matlab/matlab_oop/which-kind-of-class-to-use.html
  71. https://www.mathworks.com/help/matlab/object-oriented-programming.html
  72. https://www.mathworks.com/matlabcentral/answers/15533-object-oriented-programming-performance-comparison-handle-class-vs-value-class-vs-no-oop
  73. https://www.mathworks.com/help/matlab/ref/imagesc.html
  74. https://www.mathworks.com/help/matlab/ref/heatmap.html
  75. https://www.mathworks.com/help/matlab/graphics.html
  76. https://www.mathworks.com/help/matlab/ref/mesh.html
  77. https://www.mathworks.com/help/matlab/surface-and-mesh-plots-1.html
  78. https://www.mathworks.com/products/matlab/matlab-graphics.html
  79. https://www.mathworks.com/products/matlab/app-designer.html
  80. https://www.mathworks.com/help/matlab/app-designer.html
  81. https://blogs.mathworks.com/graphics-and-apps/2025/06/10/introducing-the-new-graphics-and-app-building-system-in-matlab-r2025a/
  82. https://blogs.mathworks.com/graphics-and-apps/2025/10/20/webgl-matlabs-new-graphics-rendering-system/
  83. https://www.mathworks.com/help/parallel-computing/spmd.html
  84. https://www.mathworks.com/help/parallel-computing/quick-start-parallel-computing-in-matlab.html
  85. https://blogs.mathworks.com/cleve/2024/03/15/twenty-years-of-parallel-matlab/
  86. https://www.mathworks.com/help/parallel-computing/run-code-on-parallel-pools.html
  87. https://blogs.mathworks.com/matlab/2024/09/26/matlab-now-has-over-1000-functions-that-just-work-on-nvidia-gpus/
  88. https://www.mathworks.com/help/parallel-computing/gpuarray.html
  89. https://www.mathworks.com/help/parallel-computing/improve-performance-using-a-gpu-and-vectorized-calculations.html
  90. https://www.mathworks.com/help/parallel-computing/measure-and-improve-gpu-performance.html
  91. https://developer.nvidia.com/blog/high-performance-matlab-gpu-acceleration/
  92. https://www.mathworks.com/help/matlab/matlab_prog/techniques-for-improving-performance.html
  93. https://www.mathworks.com/help/parallel-computing/improve-performance-of-small-matrix-problems-on-the-gpu-using-pagefun.html
  94. https://www.mathworks.com/products.html
  95. https://www.mathworks.com/pricing-licensing.html
  96. https://www.mathworks.com/help/matlab/ref/fft.html
  97. https://www.mathworks.com/discovery/fft.html
  98. https://www.mathworks.com/products/signal.html
  99. https://www.mathworks.com/help/stats/hypothesis-testing.html
  100. https://www.mathworks.com/help/stats/available-hypothesis-tests.html
  101. https://www.mathworks.com/help/deeplearning/ug/transfer-learning-using-alexnet.html
  102. https://www.mathworks.com/products/deep-learning.html
  103. https://www.mathworks.com/help/deeplearning/gs/get-started-with-transfer-learning.html
  104. https://www.mathworks.com/products/simulink.html
  105. https://www.mathworks.com/help/simulink/index.html
  106. https://www.mathworks.com/help/simulink/simulation-integration.html
  107. https://www.mathworks.com/help/ecoder/gs/code-generation-workflows-with-embedded-coder.html
  108. https://www.mathworks.com/campaigns/offers/model-based-design-automotive-control-systems.html
  109. https://www.mathworks.com/help/stateflow/gs/get-started-introduction.html
  110. https://www.mathworks.com/help/stateflow/ug/programming-a-matlab-function-in-a-chart.html
  111. https://www.mathworks.com/solutions/model-based-design.html
  112. https://www.mathworks.com/videos/accelerating-innovation-model-based-design-led-development-for-the-2-3-wheeler-software-development-to-accelerate-time-to-market-ensure-superior-quality-1713860895871.html
  113. https://www.mathworks.com/help/matlab/call-mex-file-functions.html
  114. https://www.mathworks.com/help/matlab/matlab_external/choosing-mex-applications.html
  115. https://stackoverflow.com/questions/20513071/performance-tradeoff-when-is-matlab-better-slower-than-c-c
  116. https://www.mathworks.com/matlabcentral/answers/473245-is-there-any-way-to-call-python-in-r2014a
  117. https://www.mathworks.com/help/matlab/matlab_external/create-object-from-python-class.html
  118. https://www.mathworks.com/help/matlab/matlab_external/introducing-matlab-engine.html
  119. https://www.mathworks.com/help/matlab/matlab-engine-for-python.html
  120. https://www.mathworks.com/help/matlab/matlab-engine-api-for-java.html
  121. https://www.mathworks.com/help/matlab/external-language-interfaces.html
  122. https://stackoverflow.com/questions/3534867/why-when-should-i-prefer-matlab-over-octave
  123. https://userpages.umbc.edu/~gobbert/papers/BrewsterGobbertTR2011.pdf
  124. https://nandanghawate.medium.com/octave-vs-matlab-22ea6a2b971d
  125. https://stackoverflow.com/questions/46067817/comparing-numpy-and-matlab-array-summation-speed
  126. https://codesolid.com/python-vs-matlab/
  127. http://rlhick.people.wm.edu/posts/comparing-the-speed-of-matlab-versus-pythonnumpy-partii.html
  128. https://quix.io/blog/debunking-python-performance-myths-for-matlab-users
  129. https://www.researchgate.net/publication/2559454_Open-Source_vs_Proprietary_Software
  130. https://www.sciencedirect.com/science/article/pii/S0167268125002288
  131. https://nebius.com/blog/posts/open-source-vs-proprietary
  132. https://www.mathworks.com/matlabcentral/answers/1777835-what-is-the-differences-between-annual-and-perpetual-licenses
  133. https://www.mathworks.com/products/matlab/student.html
  134. https://www.mathworks.com/academia/campus/resources/campus-wide-license-products.html
  135. https://www.mathworks.com/products/matlab-home.html
  136. https://www.mathworks.com/campaigns/offers/matlab-toolbox-price-request.html
  137. https://www.reddit.com/r/matlab/comments/hgl7lb/price_for_matlab_for_startups/
  138. https://itassetmanagement.net/2021/01/26/mathworks-licensing-getting-started/
  139. https://www.mathworks.com/content/dam/mathworks/fact-sheet/2025-company-factsheet-8-5x11-8282v25.pdf
  140. https://cybernews.com/security/mathworks-matlab-data-breach-users-exposed/
  141. https://enlyft.com/tech/products/matlab
  142. https://www.rath.org/matlab-is-a-terrible-programming-language.html
  143. https://craftofcoding.wordpress.com/2017/03/12/why-1-based-indexing-is-ok/
  144. https://www.mathworks.com/help/coder/ug/what-are-column-major-and-row-major-representation-1.html
  145. https://www.mathworks.com/matlabcentral/answers/308303-why-does-matlab-transpose-hdf5-data
  146. https://www.mathworks.com/matlabcentral/answers/489127-why-array-of-strings-are-concatenated
  147. https://nhigham.com/2016/10/06/whats-new-in-matlab-r2016b/
  148. https://blogs.mathworks.com/loren/2017/04/24/working-with-text-in-matlab/
  149. https://softwareengineering.stackexchange.com/questions/339866/can-we-make-general-statements-about-the-performance-of-interpreted-code-vs-comp
  150. https://www.mathworks.com/help/matlab/matlab_prog/resolving-out-of-memory-errors.html
  151. https://www.mathworks.com/help/matlab/matlab_prog/memory-allocation.html
  152. https://www.mathworks.com/matlabcentral/answers/46551-out-of-memory-when-assigning-values-to-existing-arrays
  153. https://www.mathworks.com/matlabcentral/answers/102729-how-much-disk-space-do-the-matlab-simulink-products-require
  154. https://eprints.soton.ac.uk/22811/1/Fang_04.pdf
  155. https://iies.in/blog/detailed-code-migration-guide-matlab-to-python/
  156. https://xcorr.net/2020/03/04/rewriting-matlab-code-in-python/
  157. https://stackoverflow.com/questions/65307154/how-to-convert-matlab-code-to-python-code-automatically
  158. https://www.reddit.com/r/matlab/comments/1lu3ek3/shall_i_stop_to_use_matlab_and_migrate_to_python/
  159. https://quix.io/blog/future-proofing-industrial-r-d-why-you-need-to-migrate-from-matlab-to-python-now
  160. https://www.makerluis.com/replacing-matlab-with-python-part-1/
  161. https://www.mathworks.com/matlabcentral/answers/739502-something-wrong-with-quat2angle-function
  162. https://www.mathworks.com/matlabcentral/answers/472624-why-are-all-the-examples-for-matlab-functions-hindered-by-useless-simplistic-examples-that-do-not-s
  163. https://www.mathworks.com/matlabcentral/answers/183012-modify-then-write-data-in-the-given-format
  164. https://www.mathworks.com/matlabcentral/answers/413183-please-provide-the-export-control-number-eccn-for-matlab-compiler-runtime-for-export-compliance-pu
  165. https://umbc.atlassian.net/wiki/display/faq/matlab
  166. https://www.mathworks.com/company/trust-center/recent-sanctions.html
  167. https://www.scmp.com/news/china/diplomacy/article/3088854/us-military-ban-locks-two-chinese-universities-out-popular
  168. https://www.mathworks.com/content/dam/mathworks/mathworks-dot-com/company/aboutus/policies_statements/code-of-business-conduct.pdf
  169. https://news.cgtn.com/news/2020-06-13/Chinese-FM-responds-to-MATLAB-s-ban-on-two-Chinese-universities-Rhx20G3pte/index.html
  170. https://www.csis.org/analysis/did-us-semiconductor-export-controls-harm-innovation
  171. https://www.cnas.org/publications/reports/rethinking-export-controls-unintended-consequences-and-the-new-technological-landscape
  172. https://www.trustradius.com/products/matlab/pricing
  173. https://www.researchgate.net/post/Is-MATLAB-a-barrier-to-scientific-advancement
  174. https://www.mathworks.com/matlabcentral/answers/1815935-how-many-nodes-is-available-for-the-student-version
  175. https://academia.stackexchange.com/questions/80790/is-it-ethical-to-use-proprietary-closed-source-software-for-scientific-computa
  176. https://www.quora.com/Why-do-people-pay-for-MATLAB-when-there-are-many-open-source-alternatives
  177. https://medium.com/%40ujjawalr/the-great-debate-open-source-vs-proprietary-software-weighing-the-pros-cons-and-trade-offs-90fc685cf956
  178. https://opensource.com/alternatives/matlab
  179. https://www.mathworks.com/matlabcentral/answers/1645840-can-matlab-be-made-cheaper
  180. https://in.mathworks.com/content/dam/mathworks/fact-sheet/2021-en-in-cwl-fact-sheet.pdf
  181. https://www.mathworks.com/products/matlab-campus.html
  182. https://www.reddit.com/r/matlab/comments/axb93z/the_future_of_matlab_in_academia/
  183. https://www.tandfonline.com/doi/abs/10.1080/0194262X.2022.2070329
  184. https://www.mathworks.com/videos/the-use-of-matlab-in-open-science-1612769704068.html
  185. https://ntrs.nasa.gov/api/citations/20030013626/downloads/20030013626.pdf
  186. https://www.mathworks.com/videos/nasa-s-spacecraft-power-capability-model-and-applications-using-matlab-1730974096080.html
  187. https://blogs.mathworks.com/autonomous-systems/2024/04/26/how-nasa-langley-is-using-matlab-and-simulink-to-accelerate-development-and-testing-of-multirotor-flight-control/
  188. https://www.mathworks.com/videos/how-nasa-modeled-artemis-i-in-matlab-and-simulink--1671048095326.html
  189. https://www.mathworks.com/help/ident/ug/modeling-a-vehicle-dynamics-system.html
  190. https://www.mathworks.com/help/simulink/slref/modeling-an-automatic-transmission-controller.html
  191. https://www.mathworks.com/help/sdl/vehicle-applications.html
  192. https://www.mathworks.com/help/aeroblks/guidance-navigation-and-control-gnc.html
  193. https://www.mathworks.com/company/user_stories/ohb-develops-satellite-guidance-navigation-and-control-software-for-autonomous-formation-flying.html
  194. https://www.mathworks.com/discovery/digital-signal-processing.html
  195. https://www.mathworks.com/products/simbiology.html
  196. https://www.mathworks.com/solutions/medical-devices/fda-software-validation.html
  197. https://www.mathworks.com/company/user_stories/nasa-uses-stateflow-and-simulink-coder-to-generate-fault-protection-code-for-deep-space-1.html
  198. https://www.mathworks.com/content/dam/mathworks/white-paper/measuring-roi-of-model-based-design.pdf
  199. https://medium.com/data-science/is-matlab-still-relevant-cf5627f171b8
  200. https://cepr.org/voxeu/blogs-and-reviews/which-numerical-computing-language-best-julia-matlab-python-or-r
  201. https://ftp.kcregap.org/scholarship/TBfBtL/3OK057/MatlabProgrammingForEngineersByStephenJChapman.pdf
  202. https://userpages.umbc.edu/~dfrey1/ench445/is-it-worth-the-effort-to-learn-Julia.pdf
  203. https://machaddr.substack.com/p/julia-programming-language-a-powerful
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.