Hubbry Logo
Isogonal figureIsogonal figureMain
Open search
Isogonal figure
Community hub
Isogonal figure
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Isogonal figure
Isogonal figure
Isogonal figure
View on Wikipedia
from Wikipedia

In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces.

Technically, one says that for any two vertices there exists a symmetry of the polytope mapping the first isometrically onto the second. Other ways of saying this are that the group of automorphisms of the polytope acts transitively on its vertices, or that the vertices lie within a single symmetry orbit.

All vertices of a finite n-dimensional isogonal figure exist on an (n−1)-sphere.[1]

The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed from modern ideas such as symmetry groups and graph theory.

The pseudorhombicuboctahedron – which is not isogonal – demonstrates that simply asserting that "all vertices look the same" is not as restrictive as the definition used here, which involves the group of isometries preserving the polyhedron or tiling.

Isogonal polygons and apeirogons

[edit]
Isogonal apeirogons
Isogonal skew apeirogons

All regular polygons, apeirogons and regular star polygons are isogonal. The dual of an isogonal polygon is an isotoxal polygon.

Some even-sided polygons and apeirogons which alternate two edge lengths, for example a rectangle, are isogonal.

All planar isogonal 2n-gons have dihedral symmetry (Dn, n = 2, 3, ...) with reflection lines across the mid-edge points.

D2 D3 D4 D7

Isogonal rectangles and crossed rectangles sharing the same vertex arrangement
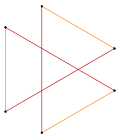Isogonal hexagram with 6 identical vertices and 2 edge lengths.[2]
Isogonal convex octagon with blue and red radial lines of reflection
Isogonal "star" tetradecagon with one vertex type, and two edge types[3]

Isogonal polyhedra and 2D tilings

[edit]
Isogonal tilings
Distorted square tiling
A distorted
truncated square tiling

An isogonal polyhedron and 2D tiling has a single kind of vertex. An isogonal polyhedron with all regular faces is also a uniform polyhedron and can be represented by a vertex configuration notation sequencing the faces around each vertex. Geometrically distorted variations of uniform polyhedra and tilings can also be given the vertex configuration.

Isogonal polyhedra
D3d, order 12 Th, order 24 Oh, order 48
4.4.6 3.4.4.4 4.6.8 3.8.8

A distorted hexagonal prism (ditrigonal trapezoprism)
A distorted rhombicuboctahedron
A shallow truncated cuboctahedron
A hyper-truncated cube

Isogonal polyhedra and 2D tilings may be further classified:

  • Regular if it is also isohedral (face-transitive) and isotoxal (edge-transitive); this implies that every face is the same kind of regular polygon.
  • Quasi-regular if it is also isotoxal (edge-transitive) but not isohedral (face-transitive).
  • Semi-regular if every face is a regular polygon but it is not isohedral (face-transitive) or isotoxal (edge-transitive). (Definition varies among authors; e.g. some exclude solids with dihedral symmetry, or nonconvex solids.)
  • Uniform if every face is a regular polygon, i.e. it is regular, quasiregular or semi-regular.
  • Semi-uniform if its elements are also isogonal but allow for multiple edges lengths
  • Scaliform if all the edges are the same length.
  • Noble if it is also isohedral (face-transitive).

N dimensions: Isogonal polytopes and tessellations

[edit]

These definitions can be extended to higher-dimensional polytopes and tessellations. All uniform polytopes are isogonal, for example, the uniform 4-polytopes and convex uniform honeycombs.

The dual of an isogonal polytope is an isohedral figure, which is transitive on its facets.

k-isogonal and k-uniform figures

[edit]

A polytope or tiling may be called k-isogonal if its vertices form k transitivity classes. A more restrictive term, k-uniform is defined as a k-isogonal figure constructed only from regular polygons. They can be represented visually with colors by different uniform colorings.


This truncated rhombic dodecahedron is 2-isogonal because it contains two transitivity classes of vertices. This polyhedron is made of squares and flattened hexagons.
This demiregular tiling is also 2-isogonal (and 2-uniform). This tiling is made of equilateral triangle and regular hexagonal faces.
2-isogonal 9/4 enneagram (face of the final stellation of the icosahedron)

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Isogonal figure

View on Grokipedia
from Grokipedia
In , an isogonal figure is a (such as a or ) or a tiling in which all vertices are equivalent under the symmetries of the figure, meaning the symmetry group acts transitively on the set of vertices, or equivalently, the figure is vertex-transitive. This property ensures that every vertex has an identical local configuration, with the same arrangement of incident edges and faces, though the faces and edges themselves may vary in shape or size across the figure. Isogonal figures encompass a broad class of symmetric geometric objects beyond regular polytopes, including semi-regular or uniform polyhedra like the Archimedean solids, where vertices are indistinguishable but faces are regular polygons of more than one type. For polygons, isogonality implies that the figure is both cyclic—all vertices lie on a common —and equiangular—all interior angles are equal—though sides may differ in length. In three dimensions, finite isogonal polyhedra have all vertices lying on a common , generalizing the cyclic property of polygons. The study of isogonal figures extends to tilings of the plane and higher-dimensional spaces, where exactly 91 types of plane isogonal tilings exist, of which 34 are also isohedral (face-transitive) and 63 can be realized with convex tiles. These structures are fundamental in combinatorial geometry and symmetry theory, often serving as to isohedral figures, and they highlight the interplay between vertex uniformity and overall symmetry groups.

Definition and Fundamental Properties

Core Definition

An isogonal figure is a polygon, polyhedron, or higher-dimensional analogue that is vertex-transitive, meaning its symmetry group acts transitively on the set of vertices, rendering all vertices equivalent under the figure's symmetries. This property ensures that the local configuration around each vertex is indistinguishable via the figure's isometries, though the global structure may vary. In group-theoretic terms, the vertices form a single orbit under the action of the symmetry group. For finite isogonal figures in nn-dimensional , the vertices lie on a common (n−1)(n-1)-. This circumscribed hypersphere is a direct consequence of the vertex-transitivity, as the symmetries preserve distances from . Not all isogonal figures are uniform polyhedra or polytopes, which additionally require that all faces (or facets) are regular polygons. Isogonal figures may possess irregular faces while maintaining vertex equivalence under symmetries. The term "isogonal" dates back to at least the early , with significant advancements in the mid- through the work of H. S. M. Coxeter and collaborators on uniform polyhedra.

Symmetry Characteristics

An isogonal figure is characterized by its full , consisting of isometries that preserve the figure, acting transitively on the set of vertices. This transitivity implies that the group orbits include all vertices, ensuring every vertex can be mapped to any other via a . In two-dimensional cases, such as isogonal polygons, the frequently coincides with the DnD_n of order 2n2n, where nn is the number of vertices, encompassing rotations by multiples of 2π/n2\pi/n and reflections across axes through vertices or midpoints of opposite sides. This group structure facilitates the equivalence of vertices under both rotational and reflectional symmetries. The duality of an yields an , which is face-transitive under its . In this dual construction, each vertex of the isohedral dual corresponds to a face of the original isogonal figure, while each face of the dual corresponds to a vertex of the primal. This correspondence interchanges the roles of vertices and faces, transforming vertex-transitivity into face-transitivity, and highlights the complementary properties between primal and dual figures. Vertex figures in isogonal figures, defined as the polygonal sections obtained by intersecting the figure with a sufficiently close to a vertex ( to the line from the vertex to the ) or equivalently by connecting midpoints of incident edges, are congruent across all vertices. The transitive action of the maps any to another, preserving their geometric configuration and ensuring uniform local structure at each vertex. This property underscores the homogeneity of vertex environments in isogonal figures. The -stabilizer theorem provides a quantitative link between the global and local symmetries: the size of the vertex , which equals the total number of vertices ∣V∣|V| due to transitivity, is ∣V∣=∣G∣/∣Stab(v)∣|V| = |G| / |\mathrm{Stab}(v)|, where GG is the and Stab(v)\mathrm{Stab}(v) is the stabilizer fixing a particular vertex vv. The stabilizer Stab(v)\mathrm{Stab}(v) captures the symmetries local to that vertex, such as rotations around an axis through vv. This formula is fundamental for analyzing the scale of in isogonal figures. Contemporary computational methods enhance the verification of these symmetry properties, particularly for intricate or higher-dimensional isogonal figures. Software like the GAP system computes the from vertex coordinates or incidence structures and checks transitivity by examining group orbits on vertices, confirming whether the action yields a single orbit. Such tools have been instrumental in classifying and validating isogonal polyhedra beyond classical examples.

Two-Dimensional Isogonal Figures

Isogonal Polygons

An isogonal polygon is a two-dimensional whose symmetry group acts transitively on its vertices, meaning that there exists a symmetry of the polygon that maps any given vertex to any other vertex. This property ensures that all vertices are equivalent in terms of their local geometry and position relative to the figure's symmetries. The term "isogonal" derives from for "equal angles," reflecting the congruent vertex figures, though the defining characteristic is vertex-transitivity rather than strict equiangularity in all cases. All regular n-gons and regular star polygons, such as the pentagram {5/2}, are isogonal, as their dihedral symmetry group DnD_n (of order 2n2n) acts transitively on the nn vertices. For odd nn, the only isogonal polygons are the regular ones, since any transitive action requires the full rotational symmetry of order nn, forcing equal edge lengths and angles. For even nn, additional irregular examples exist; a non-square rectangle is an isogonal quadrilateral under D2D_2 symmetry, where the alternating edge lengths (two pairs of equal opposite sides) preserve vertex equivalence via 180-degree rotations and reflections across axes through opposite vertices and midpoints of opposite sides. Similarly, rhombi (non-square) are isogonal under D2D_2, and higher even-sided polygons can feature alternating or patterned edge lengths while maintaining vertex-transitivity. Isogonal polygons are constructed by starting with a and distorting its edge lengths in a manner compatible with the desired , ensuring that the vertex-transitivity is preserved; this often places vertices on a common for full dihedral . For even n≥6n \geq 6, such constructions yield infinite families parameterized by ratios of edge lengths, as seen in isogonal octagons (with up to four independent edge types under D4D_4 or D2D_2 symmetries) and tetradecagons. The vertex configuration at each vertex is identical up to , denoted either by a of edge lengths (e.g., ababab for an alternating ) or, for regular and star cases, by the {n/k}\{n/k\}, where kk and nn are coprime and 1<k<n/21 < k < n/2. This congruence arises directly from the transitive action of the . The dihedral symmetry group DnD_n for an isogonal n-gon with full symmetry has 2n2n elements—nn rotations and nn reflections—and acts transitively on the vertices by design. Lower symmetries, such as Dn/2D_{n/2} for even nn, allow for more varied edge configurations while still achieving transitivity, contributing to the diversity of forms. For odd nn, only the regular type exists, while even nn admit infinite continuous families under varying symmetries.

Isogonal Apeirogons and Tilings

Isogonal apeirogons are infinite polygons that exhibit vertex-transitivity under their symmetry groups, extending the concept of finite isogonal polygons to unbounded structures in the plane. The regular apeirogon, denoted by the Schläfli symbol {∞}, consists of an infinite sequence of equal-length edges meeting at equal angles of 180 degrees, forming a straight line with dihedral symmetry group D_∞, which includes all rotations and reflections preserving the figure. Zig-zag apeirogons, in contrast, feature vertices that alternate between two parallel lines while maintaining equal edge lengths, resulting in a coplanar but non-collinear configuration with frieze group symmetry of order 2∞, generated by glide reflections. These structures are skew polygons despite their planarity, and their isogonal nature ensures all vertices are equivalent under the symmetry operations. In two-dimensional Euclidean space, isogonal tilings fill the plane periodically with polygons such that the symmetry group acts transitively on the vertices, combining translational symmetries with rotational and reflectional elements to maintain congruence of vertex configurations. Archimedean tilings, also known as uniform tilings, represent a subset of these, comprising 11 distinct types that use regular polygons in edge-to-edge arrangements with identical vertex figures across the plane; notable examples include the snub square tiling (3.4.3.4), where triangles and squares alternate around each vertex, and the truncated hexagonal tiling (3.12.12). All Archimedean tilings are inherently isogonal due to their vertex-transitivity. Beyond uniform tilings, broader classes of isogonal tilings incorporate irregular polygons while preserving congruent vertex figures, such as distorted hexagonal tilings where hexagons deviate from regularity but maintain uniform angular arrangements at vertices, or isogonal pentagonal tilings featuring congruent pentagons with varied edge lengths. A comprehensive classification identifies exactly 91 types of normal isogonal tilings in the plane, where "normal" implies bounded tiles and proper intersections; of these, 63 can be realized with convex tiles, and 34 are also isohedral (face-transitive). The Wythoff construction provides a method to generate many such isogonal tilings from regular triangular tilings by selecting points in the fundamental domain of the symmetry group and taking convex hulls of their orbits, yielding periodic structures with combined rotational and translational symmetries. Classifications of non-uniform isogonal tilings use notations such as orbifold signature to describe symmetry types and enumerate structures with irregular but congruent vertex figures that extend beyond the edge-to-edge constraint of Archimedean examples.

Three-Dimensional Isogonal Figures

Isogonal Polyhedra

Isogonal polyhedra are three-dimensional figures, either convex or non-convex star polyhedra, characterized by transitive vertex symmetries, where the symmetry group acts transitively on the vertices, rendering all vertices equivalent under the polyhedron's symmetries. This property ensures that the vertex figure—a polygon formed by connecting the midpoints of edges incident to a vertex—is congruent across all vertices. All uniform polyhedra, which have regular polygonal faces and are vertex-transitive, are thus isogonal; excluding infinite families of prisms and antiprisms, there are exactly 75 finite uniform polyhedra. These uniform isogonal polyhedra are classified into several categories based on their symmetry and face arrangements. The five Platonic solids represent the regular isogonal polyhedra, featuring identical regular faces and full symmetry at vertices, edges, and faces. Quasi-regular polyhedra include the cuboctahedron and icosidodecahedron, which have regular triangular and square (or pentagonal) faces alternating around each vertex. The 13 Archimedean solids, often termed semi-regular, are convex isogonal polyhedra with regular faces of two or more types meeting in the same configuration at each vertex, such as the rhombicuboctahedron with vertex configuration (3.4.4.4), including chiral examples like the snub cube and snub dodecahedron, which exhibit rotational symmetries without reflection. Non-convex uniform isogonal polyhedra encompass the four Kepler-Poinsot star polyhedra—small stellated dodecahedron, great dodecahedron, great stellated dodecahedron, and great icosahedron—as well as 53 additional star polyhedra with intersecting faces. Beyond uniform polyhedra, isogonal polyhedra include non-uniform examples where faces are irregular polygons but vertex-transitivity is preserved, such as distorted prisms and antiprisms that maintain equivalent vertices through adjusted edge lengths or angles. These distortions form continuous families of realizations for certain combinatorial types, demonstrating the abundance of isogonal polyhedra beyond the discrete 75 uniform cases. In star polyhedra, the density—measuring the number of face windings around a point—can be computed from the Schläfli symbol {p/q, r}; for instance, the small stellated dodecahedron {5/2, 5} has density 3, while the great stellated dodecahedron {5/2, 3} has density 7, as derived from winding number formulas. Modern enumerations, extending Coxeter's 1954 catalog, confirm infinitely many such isogonal polyhedra through these deformable realizations and additional combinatorial types.

Isogonal Space-Filling Polyhedra

Isogonal space-filling polyhedra are vertex-transitive polyhedra capable of tessellating three-dimensional Euclidean space without gaps or overlaps, forming the cells of isogonal honeycombs where the overall symmetry acts transitively on all vertices. These structures generalize finite isogonal polyhedra by extending their vertex symmetry to infinite periodic arrangements, often leveraging lattice symmetries for complete spatial coverage. A key class consists of the convex uniform honeycombs, in which every cell is a uniform polyhedron—characterized by regular polygonal faces and vertex transitivity—and vertices in the honeycomb are equivalent under the symmetry group. There are exactly 28 such convex uniform honeycombs in Euclidean 3-space. In these honeycombs, all cells are inherently isogonal, ensuring consistent local geometry at every vertex. Representative examples include the cubic honeycomb, composed of regular cubes with eight meeting at each vertex, governed by the full cubic space group OhO_h that transitively maps vertices across the integer lattice. Another is the bitruncated cubic honeycomb, featuring truncated octahedra as cells, with four meeting at each vertex and preserving vertex transitivity under the same cubic symmetry. These uniform cases highlight how isogonal cells enable efficient, symmetric tilings. Classifications extend beyond uniform honeycombs to semi-uniform variants, where cells mix uniform polyhedra but maintain overall vertex transitivity, and to distorted versions that deform faces while preserving congruent vertex figures and transitivity. The symmetry groups involved are crystallographic space groups acting transitively on the vertex set of the lattice, such as the 230 space groups of 3D Euclidean space, with cubic subgroups common for high-symmetry examples. Since isogonal polyhedra possess isohedral duals (face-transitive), the dual honeycombs feature space-filling cells like the , dual to the and tiling space in the rhombic dodecahedral honeycomb under face-transitive symmetries. Non-uniform isogonal space-fillers include the Hill tetrahedra, a family of disphenoid tetrahedra with four congruent triangular faces and vertex-transitive symmetry, discovered in 1896 and capable of periodic tessellation. These provide examples of irregular yet symmetric cells beyond uniform constructions, filling space via infinite families parameterized by edge lengths.

Higher-Dimensional and Generalized Isogonal Figures

Isogonal Polytopes in N Dimensions

In higher dimensions, the concept of an isogonal figure generalizes to n-polytopes (for n ≥ 4), which are vertex-transitive polytopes whose symmetry group acts transitively on the set of vertices, ensuring that all vertices are equivalent under the polytope's isometries. This property implies that the vertex figure—a polytope formed by connecting the adjacent vertices to a given vertex—is identical at every vertex and is itself an (n-1)-dimensional polytope. All uniform n-polytopes, which have regular facets and vertex-transitive symmetry, are thus isogonal by definition. Prominent examples in four dimensions include uniform polychora such as the 16-cell (icositetrachoron, with Schläfli symbol {3,3,4}) and the snub 24-cell, both of which exhibit full vertex transitivity while incorporating irregular but uniform cells like tetrahedra and octahedra. In five dimensions, analogues include the uniform 5-simplex, 5-cube, and 5-orthoplex, alongside more complex uniform polytera that maintain isogonal symmetry. These structures extend the three-dimensional case of isogonal polyhedra, where vertex transitivity ensures a consistent local geometry at each vertex. Enumeration of isogonal n-polytopes is primarily achieved through uniform cases, as complete classifications remain elusive beyond low dimensions due to the complexity of symmetry groups. In four dimensions, Coxeter's analysis identifies 64 convex uniform polychora, including 6 regular ones (the 5-cell, tesseract, 16-cell, 24-cell, 120-cell, and 600-cell). Higher dimensions yield exponentially more uniform polytopes; for instance, five dimensions feature hundreds of known uniform polytera, with numbers growing rapidly as dimensionality increases, reflecting the expanding possibilities of Coxeter reflection groups. Key properties of convex isogonal n-polytopes include the fact that their vertices lie on a common (n-1)-dimensional hypersphere, a consequence of vertex transitivity preserving distances from the center. The symmetry groups are often finite Coxeter groups; for example, the 120-cell and 600-cell in four dimensions are governed by the H_4 group of order 14,400, which facilitates their vertex-transitive action. Non-uniform isogonal 4-polytopes, beyond the uniform subset, have been explored in recent research through kaleidoscopic constructions based on reflection groups, yielding structures like non-Wythoffian perfect 4-polytopes that maintain full vertex transitivity without deriving from standard Wythoffian operations. These include a new class constructed by embedding symmetric 3-polytopes into facet-transitive 4-polytopes while preserving the overall symmetry.

Isogonal Tessellations in N Dimensions

Isogonal tessellations in n-dimensional Euclidean space for n ≥ 4, also known as uniform n-honeycombs, are vertex-transitive tilings composed of uniform polytopes as cells, ensuring all vertices are equivalent under the symmetry group. These structures fill space without gaps or overlaps, with examples including the 5-cell honeycomb, denoted by the Schläfli symbol {3,3,3,4}, where regular 5-cells meet three around each face and sixteen at each vertex, governed by the Coxeter group [3,3,4,3]. Another representative is the quarter-cubic honeycomb, a uniform tetracomb with tetrahedral and truncated tetrahedral cells, arising from the alternated cubic lattice and classified under the Coxeter group Q₅. In total, there are 143 such uniform tetracombs in 4D Euclidean space, enumerated via Wythoff constructions from Coxeter-Dynkin diagrams of rank 5. In hyperbolic n-space (H^n), infinite isogonal tessellations are generated by irreducible Coxeter groups of rank n+1 acting as reflection groups, producing uniform honeycombs with potentially infinite or Euclidean cells in paracompact cases. For n=4, there are five compact regular hyperbolic tetracombs, such as {3,3,3,5}, alongside four regular star variants like {5,3,3,5}/2, all vertex-transitive and filling H^4 compactly. Paracompact examples include the cubic honeycomb tetracomb {4,3,3,4}∞, which incorporates infinite Euclidean cubic honeycombs as cells, and two additional regular paracompact forms like {3,4,3,4}. Higher dimensions yield no compact cases beyond 4D, but infinite paracompact and hypercompact uniform tessellations exist, such as the 5D {3,3,3,4,3}∞ and 6D variants with Euclidean facets, classified by their Coxeter diagrams where branch marks satisfy hyperbolic density conditions (e.g., sum of reciprocals <1). These are enumerated systematically using rank and extended Schläfli symbols, with Wythoffian derivatives providing non-regular uniform variants. The duals of isogonal n-honeycombs are isohedral tessellations, which are cell-transitive (facet-transitive in the dual sense), filling space such that all cells are equivalent under symmetries, preserving the uniform nature but transposing vertex and cell roles. For instance, the dual of the 5-cell honeycomb is the 16-cell honeycomb {4,3,3,3}, with transitive hyperoctahedral cells. Computational verification of these symmetries in higher dimensions relies on tools like the Magma computational algebra system, which computes automorphism and isometry groups of polytopes to confirm vertex-transitivity via transitive action on vertices, as updated in version 2.29 (2025) for n-dimensional convex polytopes. Such models facilitate enumeration and symmetry checking for complex hyperbolic cases, including paracompact structures.

k-Isogonal Figures

A k-isogonal figure is defined as a geometric figure, such as a , tiling, or higher-dimensional , whose vertices fall into exactly k distinct orbits under the action of its , with the group acting transitively within each individual orbit. This generalizes the concept of fully isogonal figures, where k=1 and all vertices are equivalent under the symmetries. In three dimensions, the rhombic dodecahedron serves as a classic example of a 2-isogonal polyhedron, featuring two vertex classes: eight vertices incident to three rhombic faces and six vertices incident to four rhombic faces, while maintaining the full octahedral symmetry group that transits within each class. Similarly, the truncated rhombic dodecahedron is 2-isogonal, preserving two transitivity classes of vertices derived from its parent structure. For tilings, 2-isogonal examples include demiregular patterns like variants of the snub trihexagonal tiling, where vertices divide into two orbits under the symmetry group, allowing for reduced but structured vertex configurations. The of k-isogonal figures involves a reduced group action compared to full vertex-transitivity, as the symmetry group does not map vertices between different orbits; however, subclasses may exhibit edge-transitivity or face-transitivity, as seen in the rhombic dodecahedron, which is edge-transitive despite its multiple vertex orbits. For k > 1, this partial transitivity enables more flexible structures while retaining significant . Examples with k ≥ 3 remain less enumerated in three and four dimensions, though recent explorations of multi-orbit polyhedra highlight their potential in constructing complex convex forms with layered vertex classes under finite symmetry groups. Such figures find applications in modeling quasicrystals and aperiodic tilings, where partial vertex captures the ordered yet non-periodic arrangements observed in these structures, facilitating of rotational symmetries without full translational invariance. k- figures generalize the concept of figures by allowing the to partition the vertices into k distinct transitivity classes, while requiring all faces to be regular polygons and every vertex to share the identical vertex configuration—a consistent cyclic of face types meeting at each vertex. This ensures that, despite the lack of full vertex-transitivity for k > 1, the local geometry at each vertex remains . All 1- figures coincide with fully isogonal figures, as their symmetries act transitively on all vertices, combining regular faces with complete vertex equivalence. In two dimensions, k-uniform tilings by regular polygons have been systematically enumerated for small k. There are 20 such 2-uniform Euclidean tilings, each featuring two vertex classes with the same configuration, such as the tiling with vertex configuration (3.12.12) where vertices fall into two orbits. For 3-uniform tilings, 61 examples exist, expanding the combinatorial possibilities while preserving edge-to-edge regularity. Post-2000 enumerations extended this to higher k, identifying 151 4-uniform, 332 5-uniform, and 673 6-uniform tilings, providing a comprehensive catalog up to k=6 and highlighting the increasing complexity as k grows. These counts update earlier work, such as Krötenheerdt's 1969 enumeration for k=2 and Chavey's 1984 analysis for subsets of k=3, by incorporating computational verification from Galebach (2002). In three dimensions, the notion of k-uniform extends to space-filling , where figures with k > 1 vertex classes but regular polygonal faces and vertex configurations are classified as k-uniform. This framework applies to infinite families, such as certain prismatic or pyramidal extensions, though finite convex polyhedra with k > 1 typically revert to full uniformity due to closure constraints. Related classifications include scaliform figures, which are isogonal (1-uniform) with regular faces but permit unequal edge lengths in dimensions greater than 3, allowing for more flexible geometries in higher-dimensional analogs. Noble figures represent another refinement, defined as both isogonal and isohedral—transitive on both vertices and faces—encompassing dual pairs like the regular polyhedra and their catalan solids, with infinite families under symmetry groups in hyperbolic spaces. The vertex classes in k- figures can be distinguished through colorings, where edges or faces are consistently across classes to reflect the partial , effectively modeling the orbits as separate components in a vertex- graph. This approach aids visualization and , particularly in software tools like Stella4D, which supports rendering and exploration of (k=1) polychora and can be adapted for partial-transitivity cases in 4-polytopes. Post-2000 efforts, including computational of 4-polytopes exceeding 40,000 distinct forms, provide a foundation for extending k- classifications to higher dimensions, though full counts for k > 1 remain ongoing due to .

References

  1. http://faculty.washington.edu/moishe/branko/BG201.Metamorphoses.pdf
  2. https://mathworld.wolfram.com/DualPolyhedron.html
  3. https://mathresearch.utsa.edu/wiki/index.php?title=Definition_of_Polygons
  4. http://faculty.washington.edu/moishe/branko/BG112.Isogonal.tilings.pdf
  5. http://isogpolys.info/
  6. https://www.cambridge.org/core/journals/proceedings-of-the-royal-society-of-edinburgh/article/abs/xiiisohedral-and-isogonal-generalizations-of-the-regular-polyhedra/D4761AF1B35F34B2AC9F574C72F70D76
  7. https://royalsocietypublishing.org/doi/10.1098/rsta.1954.0003
  8. https://arxiv.org/pdf/1411.1782
  9. https://kconrad.math.uconn.edu/blurbs/grouptheory/dihedral.pdf
  10. http://www.csun.edu/~ctoth/Handbook/chap18.pdf
  11. https://www.sas.rochester.edu/mth/sites/doug-ravenel/otherpapers/grunbau.pdf
  12. https://bendwavy.org/klitzing/explain/isogonal.htm
  13. https://mathworld.wolfram.com/Apeirogon.html
  14. https://polytope.miraheze.org/wiki/Zigzag
  15. https://www.sciencedirect.com/science/article/pii/S0012365X14003288
  16. https://www.ams.org/journals/tran/1978-242-00/S0002-9947-1978-0496813-3/S0002-9947-1978-0496813-3.pdf
  17. https://www3.mpifr-bonn.mpg.de/staff/pfreire/polyhedra/wythoff.htm
  18. https://www.researchgate.net/publication/263488290_The_Orbifold_Notation_for_Two-Dimensional_Groups
  19. http://www.numericana.com/answer/polyhedra.htm
  20. https://mathworld.wolfram.com/UniformPolyhedron.html
  21. http://faculty.washington.edu/moishe/Prismatoids.new.text
  22. https://www.cambridge.org/core/services/aop-cambridge-core/content/view/8C077D63C4F653593D3CF956BE12A0CF/S0305004100010318a.pdf/densities_of_the_regular_polytopes.pdf
  23. https://www.arxiv.org/pdf/2412.00048
  24. https://www.tandfonline.com/doi/full/10.1080/10586458.2019.1691090
  25. https://link.springer.com/article/10.1007/s00004-022-00607-x
  26. https://arxiv.org/pdf/2412.00048
  27. https://link.springer.com/article/10.1007/s00454-025-00764-z
  28. https://arxiv.org/pdf/1403.2125
  29. https://arxiv.org/html/2403.01323v1
  30. https://arxiv.org/pdf/2312.01282
  31. https://n.ethz.ch/~vkuperber/vertexpolytopes.pdf
  32. https://arxiv.org/pdf/1102.1132
  33. http://people.eecs.berkeley.edu/~sequin/CS39/LECT_2017/ProjectReports/SpencerHill_RegConvexUniform-Polyhedra.pdf
  34. https://arxiv.org/pdf/1106.2957
  35. https://math.stackexchange.com/questions/1907058/proving-vertex-transitive-polytopes-can-be-circumscribed
  36. https://bendwavy.org/4HONEYS.pdf
  37. https://bendwavy.org/klitzing/dimensions/hyperbolic.htm
  38. https://magma.maths.usyd.edu.au/magma/handbook/convex_polytopes_and_polyhedra
  39. http://www.csun.edu/~ctoth/Handbook/chap3.pdf
  40. https://archium.ateneo.edu/context/mathematics-faculty-pubs/article/1047/viewcontent/Taganap_and_De_Las_Penas_Kisocoronalt_tilings.pdf
  41. https://www.academia.edu/42263804/Mathematical_Analysis_of_Rhombic_Dodecahedron_Application_of_HCRs_Theory_of_Polygon_
  42. https://drops.dagstuhl.de/storage/00lipics/lipics-vol226-fun2022/LIPIcs.FUN.2022.6/LIPIcs.FUN.2022.6.pdf
  43. https://www.science.smith.edu/~jorourke/Papers/RollingFUN.pdf
  44. https://www.diva-portal.org/smash/get/diva2:444746/FULLTEXT01.pdf
  45. https://oeis.org/A068599
  46. http://rcsr.net/downloads/TouristGuide.pdf
  47. https://bendwavy.org/klitzing/explain/scaliform.htm
Add your contribution
Related Hubs
User Avatar
No comments yet.